Арифметические основы ЭВМ. Лекция 2

1.

ФГБОУ ВО БАШКИРСКИЙ
ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
Институт истории и
государственного
управления
Кафедра управления
информационной
безопасностью
Уфа - 2020

2.

ФГБОУ ВО БАШКИРСКИЙ
ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
Специальность
10.05.05 Безопасность
информационных технологий в
правоохранительной сфере
Аппаратные средства
вычислительной техники
Составитель: И.В. Салов

3.

Аппаратные средства вычислительной техники
Лекция 2 (2 часа)
Тема лекции:
Арифметические основы ЭВМ.
Цель занятия:
Изучить арифметические основы ЭВМ.
План занятия:
1. Счисления с разными основаниями.
2. Битовые операции.
3. Логические основы ЭВМ.
4. Основные положения алгебры логики.
5. Законы и тождества алгебры логики.
6. Правила старшинства логических операций.
7. Таблица истинности.
8. Логические основы компьютера.
3

4.

Арифметические основы ЭВМ
• В цифровых устройствах обработки информации
используется двоичная система счисления с основанием
2, в которой используется два элемента обозначения: 0 и 1.
Веса разрядов слева направо от младших разрядов к
старшим увеличиваются в 2 раза, то есть имеют такую
последовательность: 8421. В общем виде эта
последовательность имеет вид:
2n…25,24,23,22,21,20,2-1,2-2,2-3…2–n
и используется для перевода двоичного числа в десятичное.
Например, двоичное число 101011 эквивалентно десят
ичному числу 43:
25·1+24·0+23·1+22·0+21·1+20·1=43
4

5.

Арифметические основы ЭВМ
Бит или двоичный разряд определяет значение
одного какого-либо знака в двоичном числе.
Например, двоичное число 101 имеет три бита или
три разряда. Крайний справа разряд, с наименьшим
весом, называется младшим, а крайний слева, с
наибольшим весом, — старшим.
5

6.

Арифметические основы ЭВМ
Байт
определяет
8-разрядную
информацию,
1 байт=23 бит, например,
10110011 или 01010111 и т.д.,
1 кбайт = 210 байт,
1 Мбайт = 210 кбайт = 220 байт.
единицу
6

7.

Арифметические основы ЭВМ
Основанием
шестнадцатеричной
системы
счисления является число 16=24, в которой используется
16 элементов обозначения:
числа от 0 до 9 и буквы A, B, C, D, E, F.
7

8.

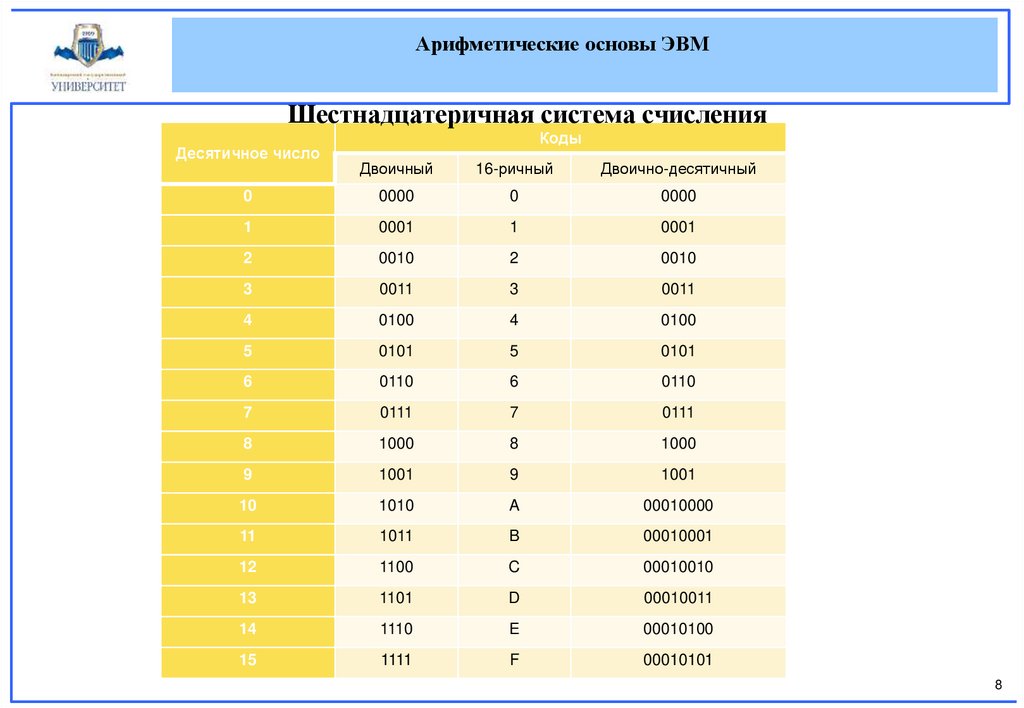
Арифметические основы ЭВМ
Шестнадцатеричная система счисления
Десятичное число
Коды
Двоичный
16-ричный
Двоично-десятичный
0
0000
0
0000
1
0001
1
0001
2
0010
2
0010
3
0011
3
0011
4
0100
4
0100
5
0101
5
0101
6
0110
6
0110
7
0111
7
0111
8
1000
8
1000
9
1001
9
1001
10
1010
A
00010000
11
1011
B
00010001
12
1100
C
00010010
13
1101
D
00010011
14
1110
E
00010100
15
1111
F
00010101
8

9.

Арифметические основы ЭВМ
Двоично-десятичный код образуется заменой
каждой десятичной цифры числа четырёхразрядным
двоичным представлением этой цифры в двоичном коде.
Например, число 15 представляется как 00010101 BCD
(Binary Coded Decimal). При этом в каждом байте
располагаются две десятичные цифры. Заметим, что
двоично-десятичный код при таком преобразовании не
является двоичным числом, эквивалентным десятичному
числу.
9

10.

Основные положения алгебры логики
Логическая формула функции двух переменных
записывается в виде:
y=f(X1, X2),
где X1, X2 — входные переменные
10

11.

Основные положения алгебры логики
Таблица истинности – таблица содержащая все
возможные комбинации входных переменных и
соответствующее им значения на выходе.
Таблица истинности содержит 2n строк, где n –
число входных переменных, и n+m – столбцы, где m –
выходные переменные.
11

12.

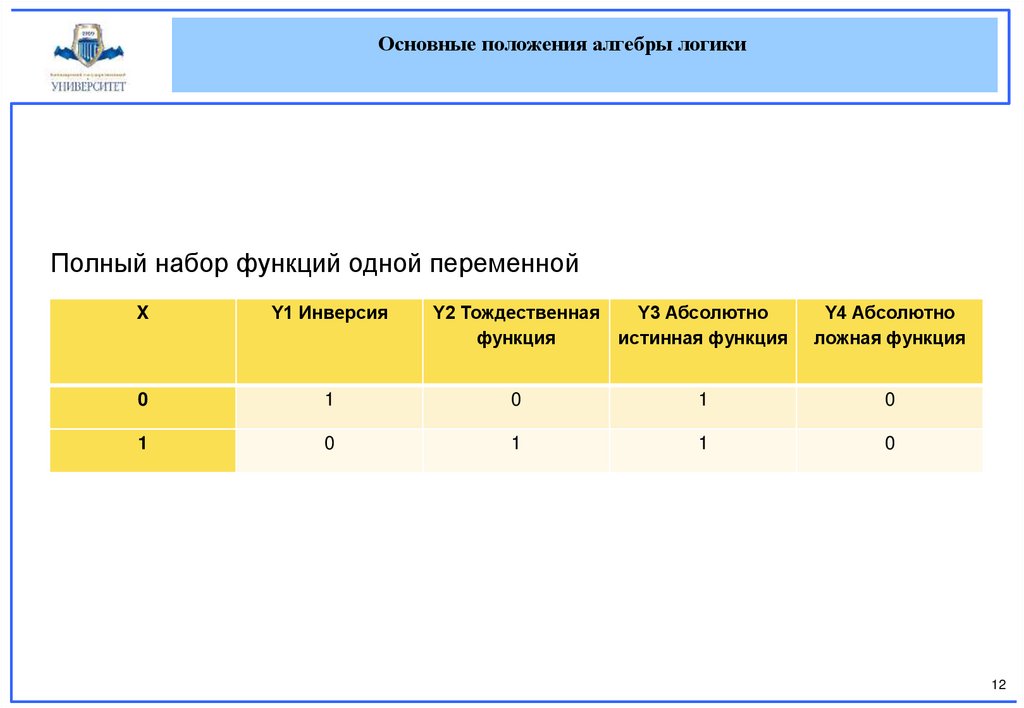
Основные положения алгебры логики
Полный набор функций одной переменной
X
Y1 Инверсия
Y2 Тождественная
Y3 Абсолютно
функция
истинная функция
Y4 Абсолютно
ложная функция
0
1
0
1
0
1
0
1
1
0
12

13.

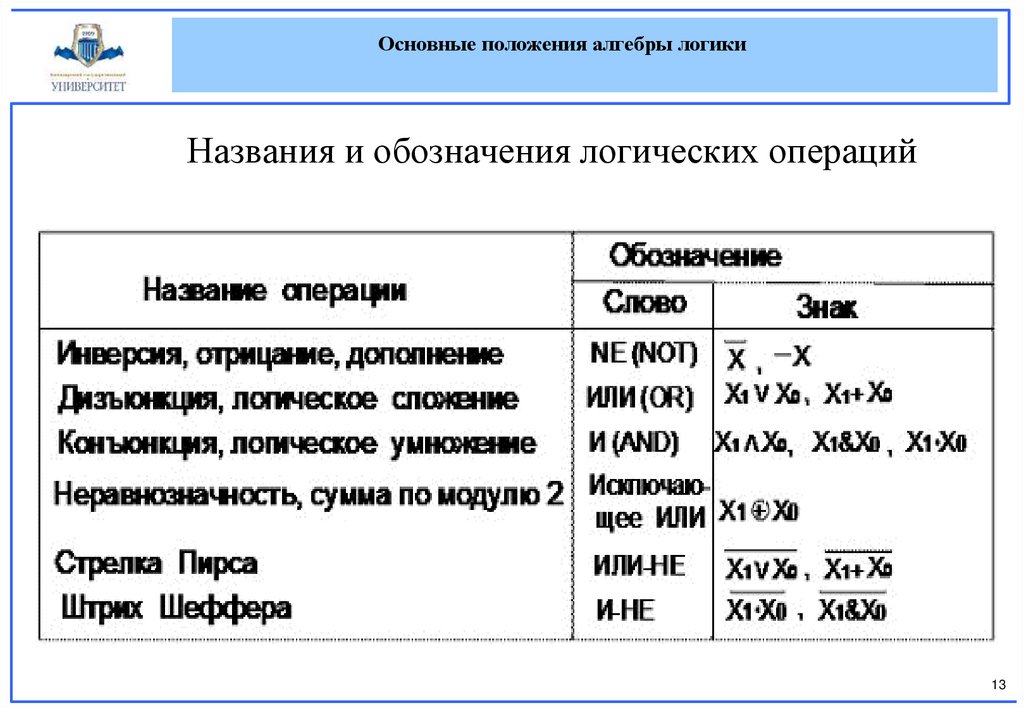
Основные положения алгебры логики
Названия и обозначения логических операций
13

14.

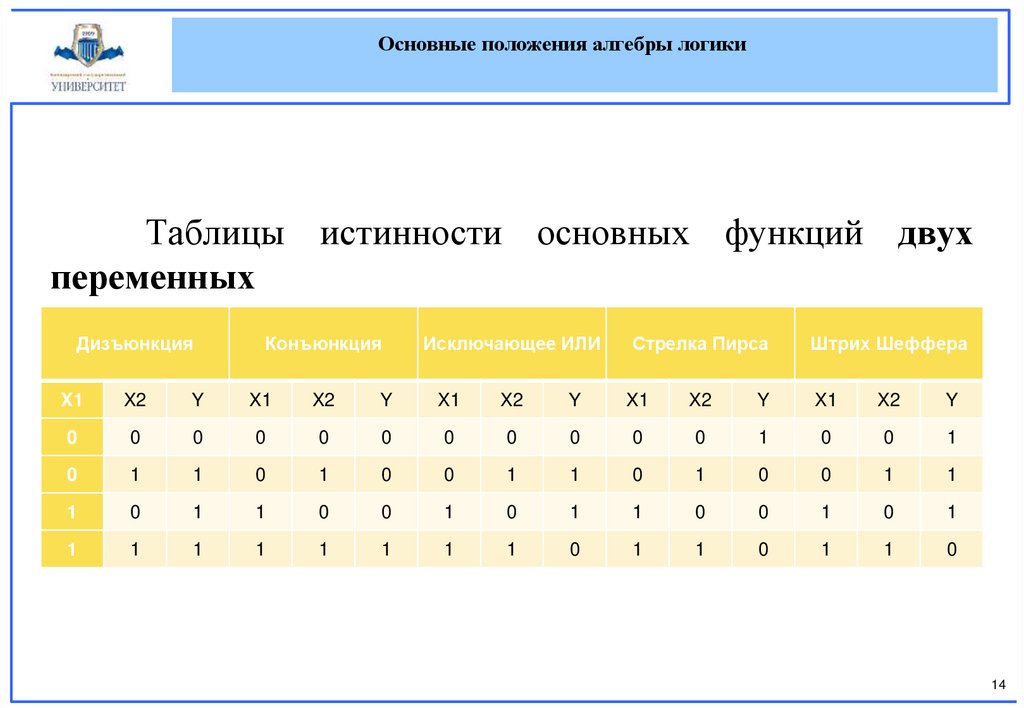
Основные положения алгебры логики
Таблицы истинности основных функций двух
переменных
Дизъюнкция
Конъюнкция
Исключающее ИЛИ
Стрелка Пирса
Штрих Шеффера
X1
X2
Y
X1
X2
Y
X1
X2
Y
X1
X2
Y
X1
X2
Y
0
0
0
0
0
0
0
0
0
0
0
1
0
0
1
0
1
1
0
1
0
0
1
1
0
1
0
0
1
1
1
0
1
1
0
0
1
0
1
1
0
0
1
0
1
1
1
1
1
1
1
1
1
0
1
1
0
1
1
0
14

15.

Основные положения алгебры логики
• Дизъюнкция.
В отличие от обычного арифметического или
алгебраического суммирования здесь наличие двух
единиц даёт в результате единицу. Поэтому при
обозначении логического суммирования предпочтение
следует отдать знаку (∨) вместо знака (+).
15

16.

Основные положения алгебры логики
• Дизъюнкция.
Первые две строчки таблицы истинности операции
дизъюнкции (x1=0) определяют закон сложения с нулём:
x ∨ 0 = x, а вторые две строчки (x1 = 1) — закон сложения
с единицей: x ∨ 1 = 1.
16

17.

Основные положения алгебры логики
• Конъюнкция.
Таблица убедительно показывает тождественность
операций обычного и логического умножений. Поэтому
в качестве знака логического умножения возможно
использование привычного знака обычного умножения в
виде точки.
17

18.

Основные положения алгебры логики
• Конъюнкция.
Первые две строчки таблицы истинности
операции конъюнкции определяют закон умножения на
ноль: x·0 = 0, а вторые две — закон умножения
на единицу: x·1 = x.
18

19.

Основные положения алгебры логики
Исключающее ИЛИ.
• Под функцией «Исключающее ИЛИ» понимают
следующее: единица на выходе появляется тогда, когда
только на одном входе присутствует единица. Если
единиц на входах две или больше, или если на всех
входах нули, то на выходе будет нуль.
19

20.

Основные положения алгебры логики
Исключающее ИЛИ.
• Операция аналогична операции арифметического
суммирования, но, как и другие логические операции,
без образования переноса. Поэтому она имеет другое
название сумма по модулю 2 и обозначение ⊕, сходное
с обозначением арифметического суммирования.
20

21.

Основные положения алгебры логики
• Стрелка Пирса и штрих Шеффера. Эти операции
являются инверсиями операций дизъюнкции и
конъюнкции и специального обозначения не имеют.
21

22.

Законы и тождества алгебры логики
Законы:
1) Переместительный:
X ∨ Y = Y ∨ X;
X · Y = Y · X.
2) Cочетательный:
X ∨ Y ∨ Z = (X ∨ Y) ∨ Z = X ∨(Y ∨ Z);
X · Y · Z = (X · Y) · Z = X· (Y· Z).
.
22

23.

Законы и тождества алгебры логики
Законы:
3) Идемпотентности (рефлексивности):
X ∨ X = X; X · X = X.
4) Распределительный:
(X ∨ Y)· Z = X· Z ∨ Y· Z.
23

24.

Законы и тождества алгебры логики
Законы:
5) Двойное отрицание:
.
6) Закон двойственности (Правило де Моргана):
24

25.

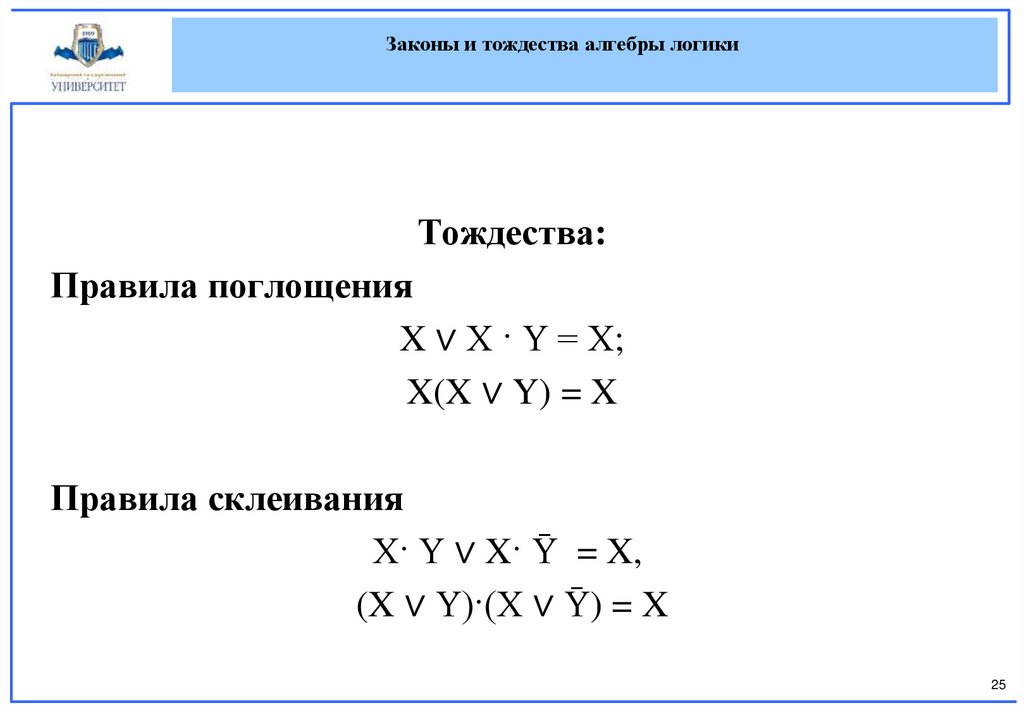
Законы и тождества алгебры логики
Тождества:
Правила поглощения
X ∨ X · Y = X;
X(X ∨ Y) = X
Правила склеивания
X· Y ∨ X· Ȳ = X,
(X ∨ Y)·(X ∨ Ȳ) = X
25

26.

Правила старшинства логических операций
1) Отрицание — логическое действие первой ступени.
2) Конъюнкция — логическое действие второй ступени.
3) Дизъюнкция — логическое действие третьей ступени.
26

27.

Основные положения алгебры логики
Если в логическом выражении встречаются
действия различных ступеней, то сначала выполняются
первой ступени, затем второй и только после этого
третьей ступени. Всякое отклонение от этого порядка
должно быть обозначено скобками.
27

28.

Аксиомы алгебры логики
• 1) ¬(¬x)=x, x=¬(¬x);
• 2) x*(¬x)=0;
• 3) x+1=1;
• 4) x+x=x, x=x+x+x;
• 5) x+0=x;
• 6) x*x=x, x=x*x*x;
28

29.

Аксиомы алгебры логики
• 7) x*0=0;
• 8) x*1=x;
• 9) x+(¬x)=1.
29

30.

Аппаратные средства вычислительной техники
Источники информации:
1.
Айдинян, А.Р. Аппаратные средства вычислительной техники : учебник
/[Электронный ресурс]/ А.Р. Айдинян. - Москва ; Берлин : Директ-Медиа, 2016. 125 с. - Режим доступа URL: http://biblioclub.ru/index.php?page=book&id=443412
2.
Волкова, Т.В. Основы проектирования компонентов автоматизированных
систем : учебное пособие [Электронный ресурс]/ / Т.В. Волкова ; Министерство
образования и науки Российской Федерации, Оренбургский Государственный
Университет, Кафедра программного обеспечения вычислительной техники и
автоматизированных систем. - Оренбург : ОГУ, 2016. - 226 с. Режим доступа URL: http://biblioclub.ru/index.php?page=book&id=471129
3.
Синицын, Ю.И. Сети и системы передачи информации : учебное
пособие[Электронный ресурс]/ Ю.И. Синицын, Е. Ряполова, Р.Р. Галимов ;
Министерство образования и науки Российской Федерации, Федеральное
государственное бюджетное образовательное учреждение высшего образования
«Оренбургский государственный университет». - Оренбург : ОГУ, 2017. - 190 с. –
Режим доступа : http://biblioclub.ru/index.php?page=book&id=485524
30

31.

Аппаратные средства вычислительной техники
Задание
для самостоятельной работы студентов
1.
Двоичное преставление целых чисел.
2.
Двоично-десятичное представление целых чисел.
3.
Название и обозначения логических операций, их
таблица истинности.
4.
Законы и тождества алгебры логики.
5.
Правила старшинства логических операций.
6.
Битовые операции. Примеры. Назначение.
31