Арифметические и логические основы ЭВМ

1. АРИФМЕТИЧЕСКИЕ И ЛОГИЧЕСКИЕ ОСНОВЫ ЭВМ

2. Формы представления информации

• Информационное сообщение может существовать
в самых разнообразных видах и формах:
• в виде знаков: это цифры и арифметические знаки,
используемые в математике, условные графические
изображения;
• в виде символов, которые могут быть представлены
буквами алфавита, специальными обозначениями, используемыми для
создания текстов и рисунков;
• в форме звуковых, световых сигналов и радиоволн,
применяемых в радиовещании, телефонии, телевизионной трансляции;
• в форме устной речи;
• в форме магнитных полей;
• в форме электрического тока или напряжения, на которых основана
работа двигателей, генераторов и других технических устройств

3. Единицы измерения количества информации

• В электронно-вычислительных машинах используется объемный способ
измерения информации, учитывающий количество символов,
содержащихся в сообщении.
• Наименьшей единицей измерения информации является Бит. Это
двоичная ячейка памяти, которая может находиться в двух состояниях:
«0» (тока нет) и «1» (ток есть).
• Блоки данных, объединяющие 8 Бит, называют Байтами, а их номера —
адресами (1 байт – минимальный адресуемый объем данных в ЭВМ). В
свою очередь, определенная количественная совокупность Байт
называется машинным словом (2 байта).
• На практике чаще используют более крупные единицы измерения
информации:
• 1 кБайт = 2^10 Байт;
• 1 МБайт = 2^20 Байт;
• 1 ГБайт = 2^30 Байт;
• 1 терабайт = 2^40 байт; 1 петабайт = 2^50 байт.

4. Кодирование информации

• Информация разнообразных видов и форм
кодируется, поступая в ЭВМ.
• Кодирование — перевод значения в двоичный код
• Система счисления — это способ наименования и
изображения чисел с помощью символов, имеющих
определенные количественные значения.
• В зависимости от способа изображения чисел
системы делятся на
• позиционные и непозиционные

5.

• В позиционной системе счисления
количественное значение каждой цифры
зависит от ее местоположения (позиции) в
числе.
• В непозиционной системе счисления
цифры не меняют своего количественного
значения при изменении их положения в
числе. – РИМСКАЯ система
• I = 1; V = 5; X = 10; L = 50; С = 100; D = 500;
M = 1000.

6.

• Количество цифр, используемых для изображения
числа в позиционной системе счисления,
называется основанием системы.
• Десятичная (р = 10) система счисления —
используется в математике для записи числа,
основание которого равно 10 (количеству
используемых цифр от 0 до 9). Таким образом,
любое число может быть представлено набором
цифр с запятой или без нее. Если запятая
присутствует, то последовательность чисел,
расположенных до нее (запятой), называется целой
частью числа. А последовательность чисел,
расположенных после запятой, называется дробной
частью числа.

7.

Для перевода двоичных чисел в десятичные
используются таблицы перевода
10 с.с.
2 с.с.
8 с.с.
16 с.с.
0
0
0
0
1
1
1
1
2
10
2
2
3
11
3
3
4
100
4
4
5
101
5
5
6
110
6
6
7
111
7
7
8
1000
10
8
9
1001
11
9
10
1010
12
A
11
1011
13
B
12
1100
14
C
13
1101
15
D
14
1110
16
E
15
1111
17
F
16
10000
20
10
2^n = 1(0…0) n раз

8. Алгоритм перевода десятичных чисел в двоичные. Целая часть

• 1.Разделить число на 2. Зафиксировать остаток (0 или 1) и частное.
• 2. Если частное не равно 0, то разделить его на 2, и так далее, пока
частное не станет равно 0. Если частное равно 0, то записать все
полученные остатки, начиная с первого, справа налево.
• В примере ответ 10111.

9. Запись любого смешанного числа в системе счисления с основанием р

• Запись представляет собой ряд следующего вида:
• am-1Pm-1+ am-2Pm-2+…+ a1P1+ a0P0+ a-1P-1+
+a-2P-2+…+ a-3P-3
• где нижние индексы определяют местоположение цифры в
числе (разряд):
• положительные значения индексов — для целой части числа (m
разрядов);
• отрицательные значения — для дробной части
(s разрядов).
• 395,47110(10) = 3 • 102 + 9 • 101 + 5 • 100 + 4 •10-1 +
• + 7 •10-2 + 1 •10-3

10.

• Двоичная система счисления (р=2)
• Используется для преобразования чисел
в два символа «0» и «1», а двоичное
число 1011,01(2) представляется
следующей последовательностью :
• 1011,012= 1*23 + 0*22 + 1*21 + 1*2° + 0*2-1
+ 1*2 -2 = 11,2510 (10).

11.

• Восьмеричная система счисления (р=8)
• Кодирует информацию с помощью восьми
символов (0 …7)
• 542= 5*82 + 4*81 + 2*8° = 35410
• Шестнадцатеричная система счисления (р=16)
• использует для кодирования 16 символов:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, А(10), В(11), С(12),
D(13), E(14), F(15). Таким образом, запись
F5C,E6 соответствует следующему ряду:
F5C,F616= F*162 + 5*161 + С*16° + Е*16-1 +
6*16-2 = 3932,910

12. ЛОГИЧЕСКИЕ ОСНОВЫ ПОСТРОЕНИЯ ПК

• Для анализа и синтеза схем в ЭВМ при
алгоритмизации и программировании решения
задач широко используется математический
аппарат алгебры логики.
• Алгебра логики – это раздел математической
логики, значения всех элементов которой
определены в двухэлементном множестве: 0 и 1
(ложь и истина).

13. Элементы алгебры логики

• Основной объект алгебры логики –
высказывание.
• Высказыванием называется любое
предложение, о котором можно судить,
истинно оно или ложно.
• Высказывание должно удовлетворять закону
исключенного третьего, т.е. высказывание не
должно быть одновременно истинным и
ложным.

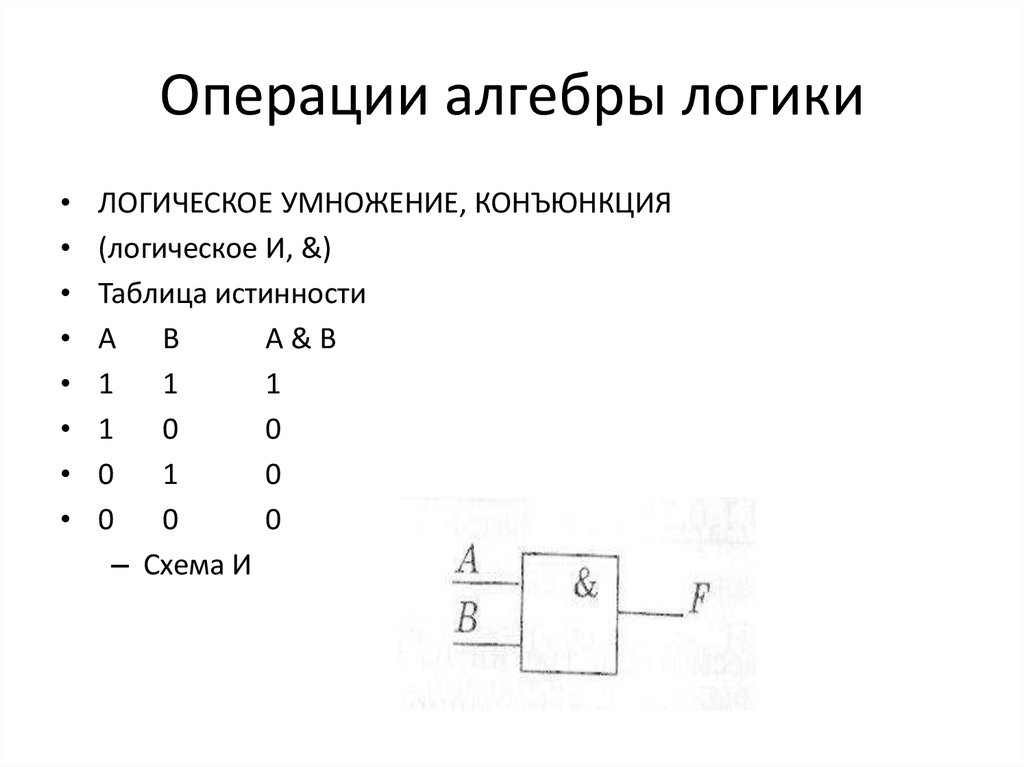
14. Операции алгебры логики

ЛОГИЧЕСКОЕ УМНОЖЕНИЕ, КОНЪЮНКЦИЯ
(логическое И, &)
Таблица истинности
A B
A&B
1
1
1
1
0
0
0
1
0
0
0
0
– Схема И

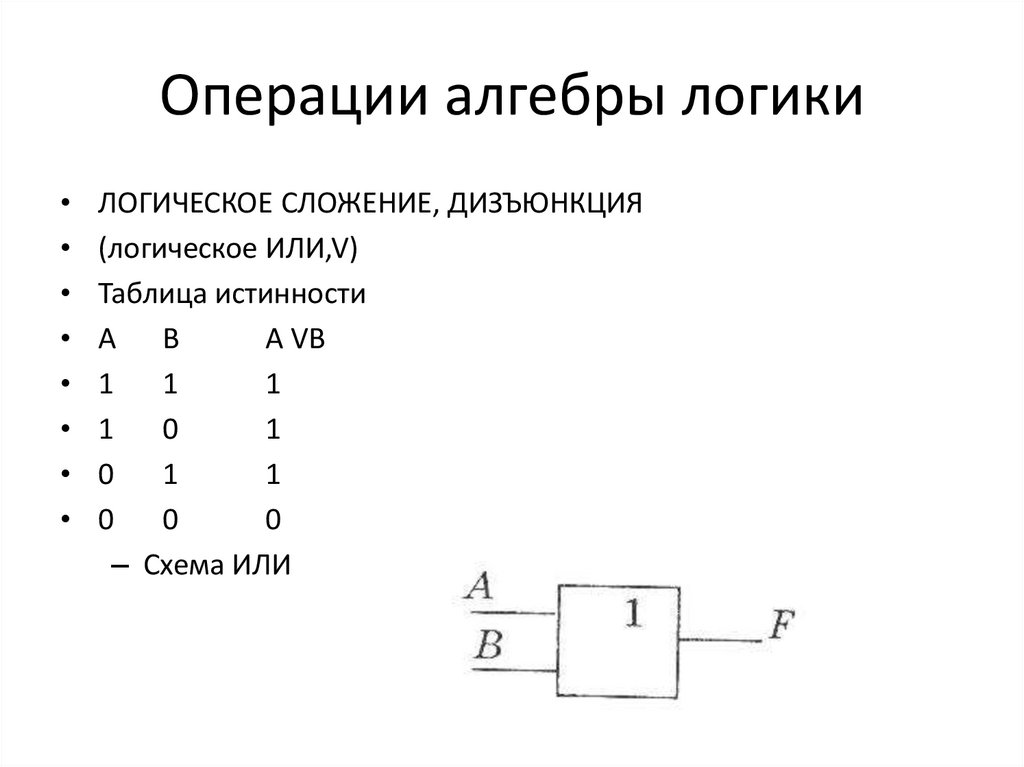
15. Операции алгебры логики

ЛОГИЧЕСКОЕ СЛОЖЕНИЕ, ДИЗЪЮНКЦИЯ
(логическое ИЛИ,V)
Таблица истинности
A B
A VB
1
1
1
1
0
1
0
1
1
0
0
0
– Схема ИЛИ

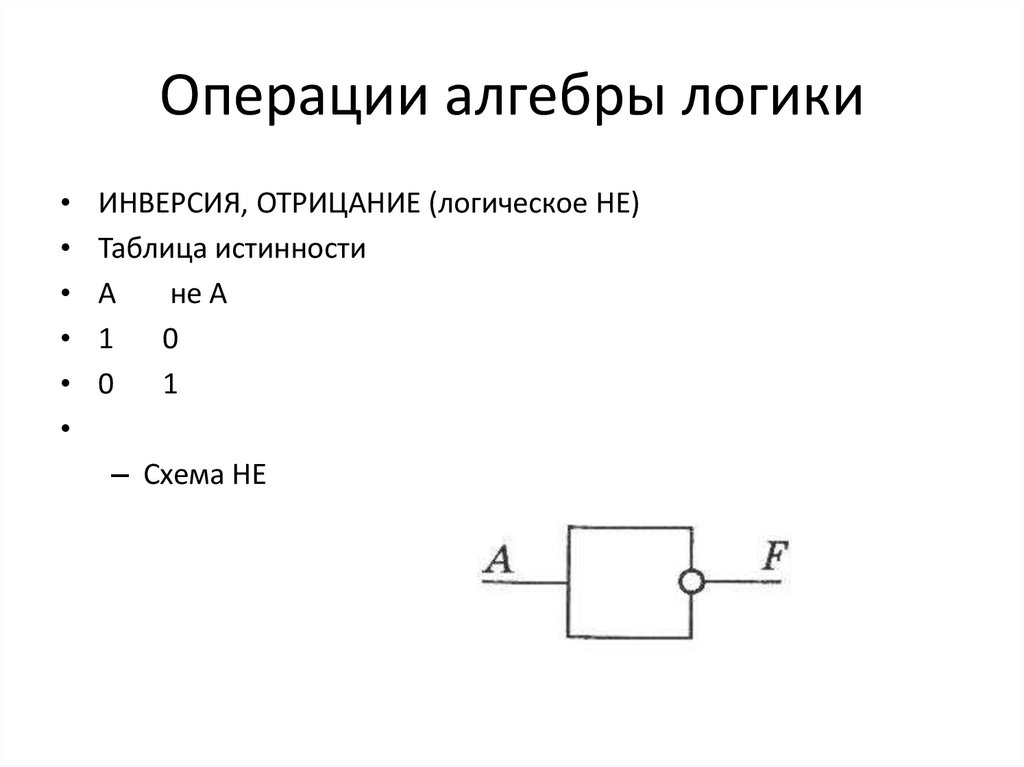
16. Операции алгебры логики

ИНВЕРСИЯ, ОТРИЦАНИЕ (логическое НЕ)
Таблица истинности
A
не A
1
0
0
1
– Схема НЕ

17. Операции алгебры логики

• ИМПЛИКАЦИЯ (логическое следование,
«если…, то …», ->)
Таблица истинности
A B
A ->B
1
1
1
1
0
0
0
1
1
0
0
1

18. Операции алгебры логики

• ЭКВИВАЛЕНЦИЯ (A B, тождественно, (“если и
только если”, “необходимо и достаточно”, “…
равносильно …”)
Таблица истинности
A B
A <->B
1
1
1
1
0
0
0
1
0
0
0
1

19. Законы алгебры логики

• Сочетательный
• (a+b)+c=a+(b+c); (a*b)*c=a*(b*c)
• Переместительный
• a+b=b+a; a*b=b*a
• Распределительный
• a*(b+c)=a*b+a*c
• (a+b)*c=a*c+b*c

20. Законы

• Поглощения
• а и (а или с)=а; а или (а и с)=а
• Склеивания
• (а или с) и (не а или с)=с
• (а и с) или (не а и с)=с
• Непротиворечия а и не а=0
• Исключенного третьего
• а или не а = 1

21. Законы

• Идемпотентности
• а или а = а; а и а = а
• Де Моргана (общей инверсии)
• Не(а или с)=не а и не с
• Не(а и с)=не а или не с
• Исключения констант
• A или 1 = 1; A или 0= А
• A и 1 = A; A и 0= 0
• Контрапозиции A -> B=не B -> не A