Similar presentations:
Вычислительные машины
1. Вычислительные машины
2. Учебно-методические материалы
Точи Р.Дж., Уидмер Н.С. Цифровые системы. Теорияи практика, 8-е изд.: Пер. с англ. -М.: Издательский
дом «Вильямс», 2004.
Пухальский Г.И., Новосельцева Т.Я. Цифровые
устройства: Учебное пособие для втузов. -СПб.:
Политехника, 1996.
Угрюмов Е.П. Цифровая схемотехника. - СПб.: БХВ –
Санкт-Петербург, 2000.
Савельев А.Я. Прикладная теория цифровых
автоматов: Учебник для вузов по спец. ЭВМ. -М.:
Высшая школа, 1987.
3.
Путков В.Н. и др. Электронные вычислительныеустройства: Учеб. пособие для радиотехн. спец.
вузов / В.Н.Путков, И.И.Обросов, С.В.Бекетов. -Мн.:
Вышэйшая школа, 1981.
Цилькер Б.Я., Орлов С.А. Организация ЭВМ и
систем: Учебник для вузов. -СПб.: Питер, 2004.
Закревский А.Д., Поттосин Ю.В., Черемисинова Л.Д.
Основы логического проектирования. Кн. 2.
Оптимизация в булевом пространстве. -Мн.: ОИПИ
НАН Беларуси, 2004.
Закревский А.Д., Поттосин Ю.В., Черемисинова Л.Д.
Основы логического проектирования Кн. 3.
Проектирование устройств логического управления. Мн.: ОИПИ НАН Беларуси, 2006.
4.
Позиционные системы счисления.Позиционная система счисления – это система, в которой
значение символа зависит от его позиции в цепочке символов
(цифр), изображающих число.
Основание системы счисления – это количество S
различных символов, используемых в пределах одного
разряда.
В двоичной системе (S=2) используются символы 0,1.
В восьмеричной – символы 0,1, 2,…, 7.
В десятичной – символы 0,1,2,…,9.
В шестнадцатеричной – символы 0,…,9,A,B,C,D,E,F.
Числа в позиционных системах представляются
последовательностью ряда цифр, разделенных на две
группы: группа разрядов, задающая целую часть числа, и
группа разрядов, задающая дробную часть.
5.
Пусть X s a2a1a0 , a 1a 2 ....- число в системе счисления с основанием S.
Любое число X в позиционной системе счисления с
основанием S может быть представлено в виде:
S – основание; i – номер разряда; n+1 (n, n-1, …,
1, 0) – количество целых разрядов; m – количество
дробных разрядов; n - старший разряд; -m - младший
разряд; ai - разрядные коэффициенты; Si - вес i-го
разряда.
Пример. 71,25 = 7×101 +1×100,+2×10−1+5×10−2
6.
В вычислительной технике применяется двоичнаясистема (X =2), в ней для записи числа используются
две цифры: 0 и 1.
Сложение
0+0=0;
0+1=1;
1+0=1;
1+1=10
Вычитание
0-0=0;
1-0=1;
1-1=0;
10-1=1
Умножение
0 0=0;
0 1=0;
1 0=0;
1 1=1
Деление чисел в двоичной системе производится по
правилам умножения и вычитания.
7.
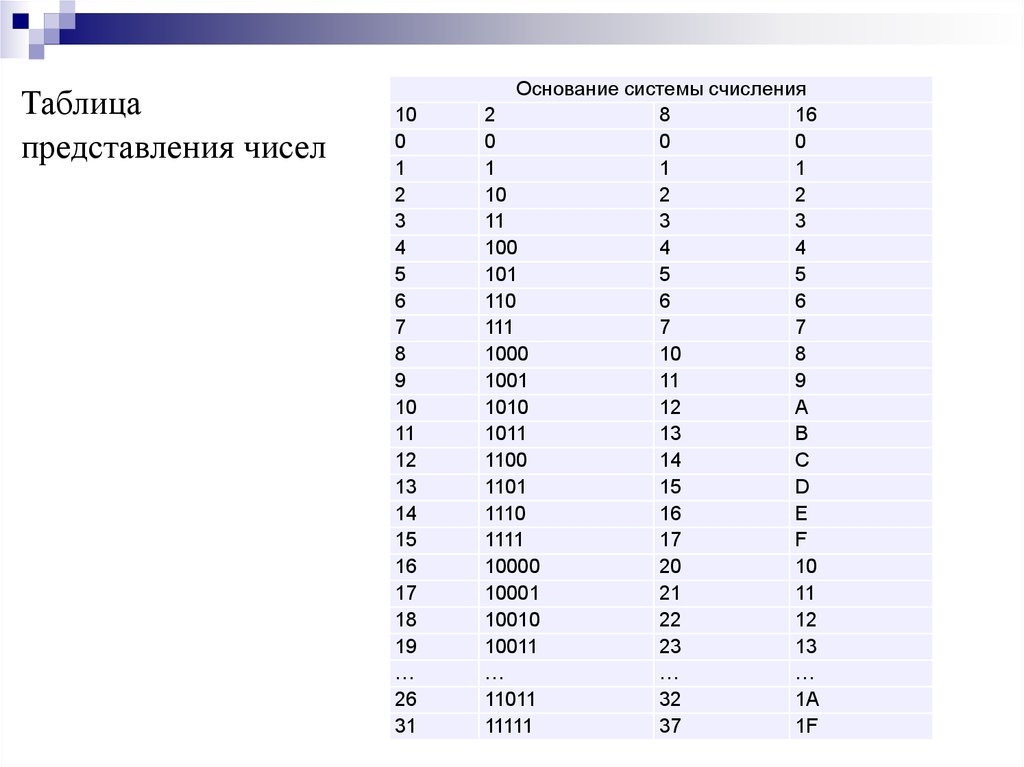
Таблицапредставления чисел
10
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
…
26
31
Основание системы счисления
2
8
16
0
0
0
1
1
1
10
2
2
11
3
3
100
4
4
101
5
5
110
6
6
111
7
7
1000
10
8
1001
11
9
1010
12
A
1011
13
B
1100
14
C
1101
15
D
1110
16
E
1111
17
F
10000
20
10
10001
21
11
10010
22
12
10011
23
13
…
…
…
11011
32
1A
11111
37
1F
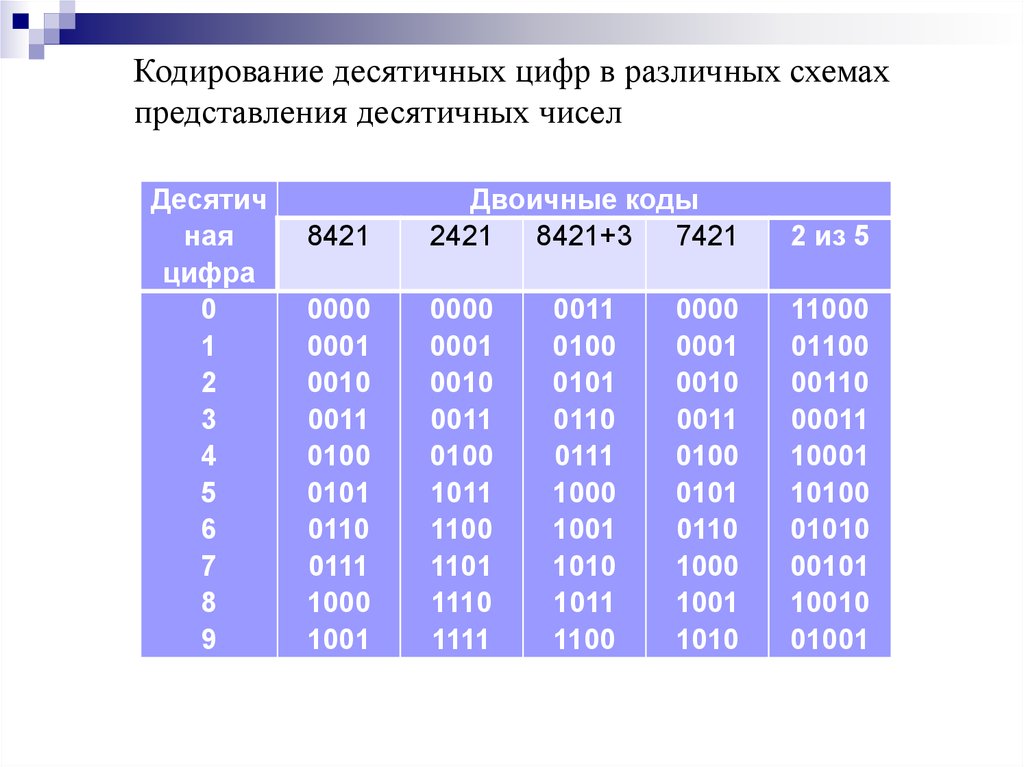
8.
Пример двоично-десятичного кода0001 1001 1000 0100(D) = 1984(10)
Перевод из двоичной в восьмеричную и
шестнадцатеричную системы и обратно
1) перевод 1101111001.11012 в восьмеричное
001 101 111 001 . 110 100 = 1571.648;
1
5
7
1
6
4
2) перевод 11111111011.1001112 в шестнадцатеричное
0111 1111 1011 . 1001 1100 = 7FB.9C16.
7
F
B
9
C
9.
Правило перевода целых чисел.Пример. Перевести целое десятичное число 43 в
двоичную и шестнадцатеричную системы счисления.
Следовательно, 4310 ==>1010112; 4310 ==> 2В16.
10.
Перевод из недесятичной позиционной системысчисления в десятичную
Пример. Перевести двоичное число 110110,1 в
десятичную систему счисления: 110110,12 ==> 1⋅25 +
1⋅24 + 0⋅23 + 1⋅22 + 1⋅21 + 0⋅20 + 1⋅2-1 ==>
==>32+16+4+2+0,5=54,510.
11.
Перевод дробейПример. Перевести десятичную дробь 0,375 в
двоичную (а) и шестнадца-теричную (б) системы
счисления.
а 0,375
х
2
———
0,750
х
2
———
1,500
х
2
———
1,000
б
Следовательно, 0,37510 ==>0,0112;
0,375
х
16
———
6,000
0,375 10 ==>0,616.
12.
Пример: десятичной дроби 0,7689 соответствует6
двоичная дробь 0,110001 с точностью 2
0,7689
x
2
1,5378
x
2
1,0756
x
2
0,1512
x
2
0,3024
х
2
0,6048
х
2
1,2096
13.
Перевод неправильной дробиПример. Последовательно перевести число X=524,6 (8-ричная
система счисления) в следующие системы счисления: десятичную;
двоичную; 16-ричную; десятичную; восьмеричную.
Перевод (8) (10)
X= 5 82 2 81 4 80 6 8 1 320 16 4 0,75 340,75
Перевод (10) (2)
340/2=170(ост 0); 170/2=85(0); 85/2=42(1); 42/2=21(0);
21/2=10(1); 10/2=5(0); 5/2=2(1); 2/2=1(0). Целая часть 101010100
0,75x2=1,5; 0,5x2=1,0. Дробная часть 0,11
X=101010100,11
14.
Перевод (2) (16)(0001)(0101)(0100),(1100)
1
5
4
C
X=154,C.
Перевод (16) (10)
X= 1 162 5 161 4 160 12 16 1 340,75
Перевод (10) (8)
340/8=42(4); 42/8=5(2);
0,75x8=6,0
X=524,6
15.
Основы алгебры логикиРассмотрим некоторую функцию y = f ( x1 ,..., xn )
от n аргументов, где аргументы x1 ,..., xn и функция y
принимает значение 0,1 из множества B={0,1}.
Булевой (логической) функцией называется двоичная
функция от двоичных аргументов.
Булева функция задает отображение булева
n
элементов – n-компонентных
2
пространства (состоящего из
двоичных векторов) в множество {0,1}:
f : Bn B
16.
Число всех булевых функций, зависящих от n аргументов, равноИмеются только 4 булевы функции от одного аргумента:
2
Имеется 16 булевых функций от двух аргументов:
Функции (двухместные логические операции) дизъюнкции f 7 ,
коньнкции f1 и отрицания f12(инверсии) образуют булеву
алгебру.
2n
17.
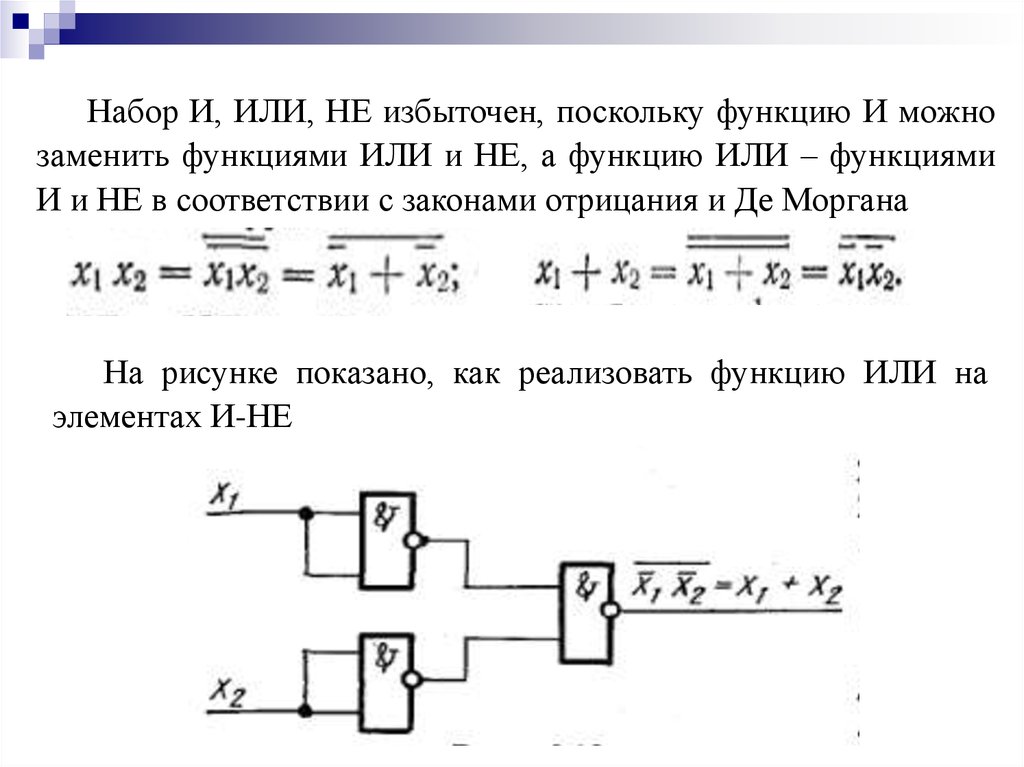
Алгебру логики составляют следующие операции: одноместнаяоперация отрицания (инверсирования) и двухместные операции,
заданные в таблице
Дизъюнкция Конъюнкция Сумма по Импликация
модулю 2
x1 x2
Эквиваленция
~
0
0 0
0
0
1
1
0
1 1
0
1
0
0
1
0 1
0
1
1
0
1
1 1
1
0
1
1
18.
Обозначения логических элементов19.
Основные законы и аксиомы (тождества) алгебры логики.Закон исключенного третьего
A A 0
A A 1
Закон отрицания отрицания (двойного отрицания)
Умножение на константу
Сложение с константой
Идемпотентность
A 0 0
A 1 A
A 0 A
A 1 1
A A A
A A A
A A
20.
КоммутативностьA B B A
A B B A
Ассоциативность
A ( B C) ( A B) C
A ( B C ) ( A B) C
Дистрибутивность A ( B C) ( A B) ( A C)
A ( B C) ( A B) ( A C)
Поглощение
A( A B) A
A AB A
Законы де Моргана
A B A B
A B A B
21.
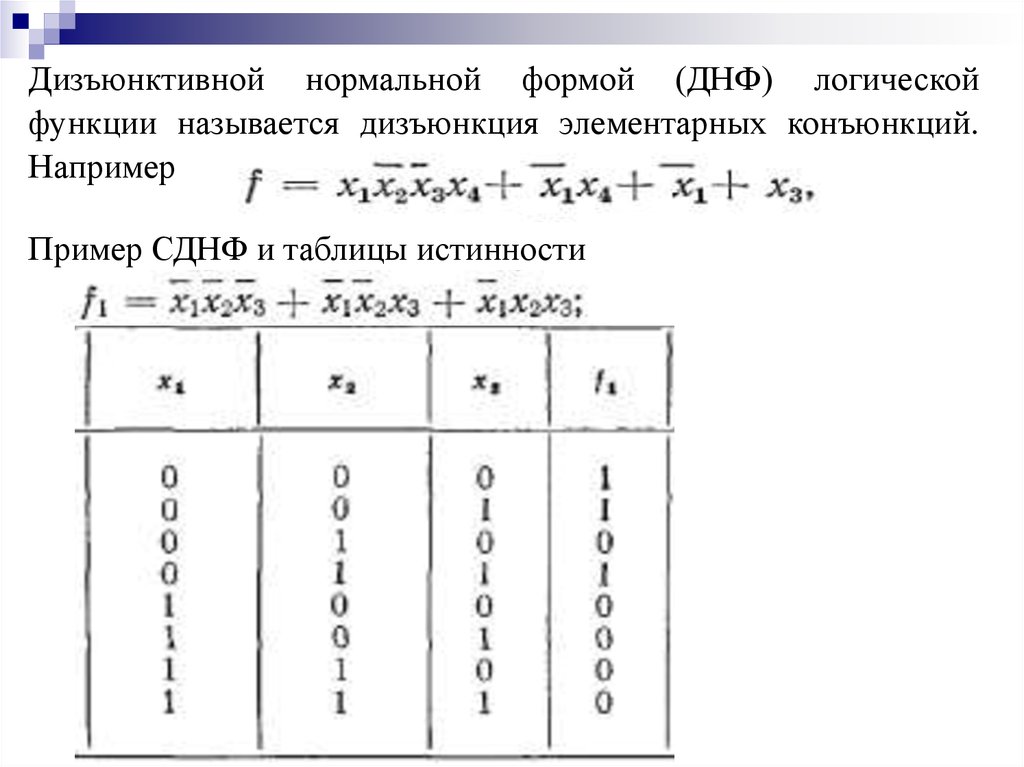
Аналитическое представление булевых функцийf ( x1, x2 , x3 ) x1x2 x3 x1x2 x3 x1 x2 x3 x1 x2 x3 x1 x2 x3
Табличное задание
22.
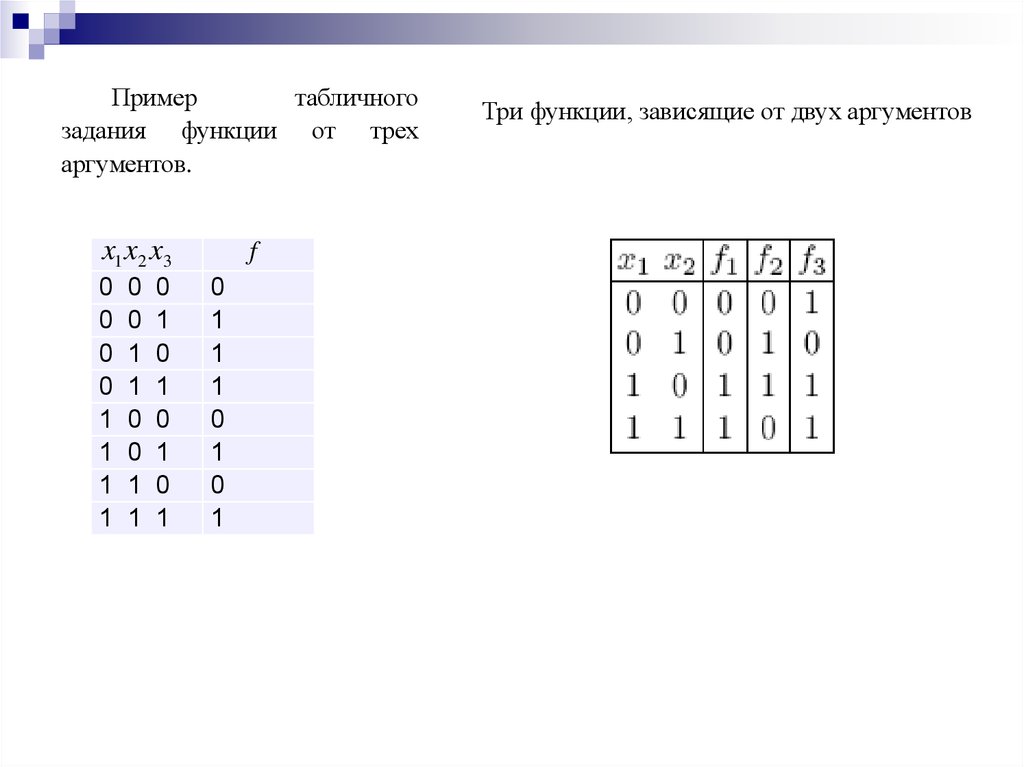
Примертабличного
задания функции от трех
аргументов.
x1 x2 x3
0
0
0
0
1
1
1
1
0
0
1
1
0
0
1
1
0
1
0
1
0
1
0
1
f
0
1
1
1
0
1
0
1
Три функции, зависящие от двух аргументов
23.
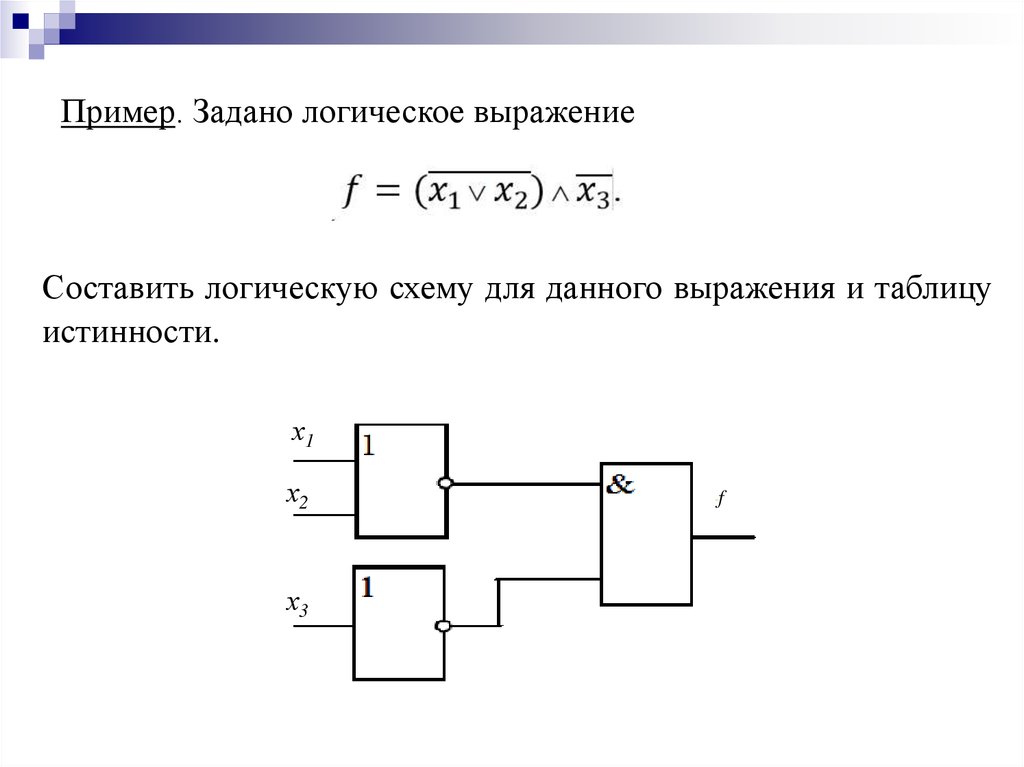
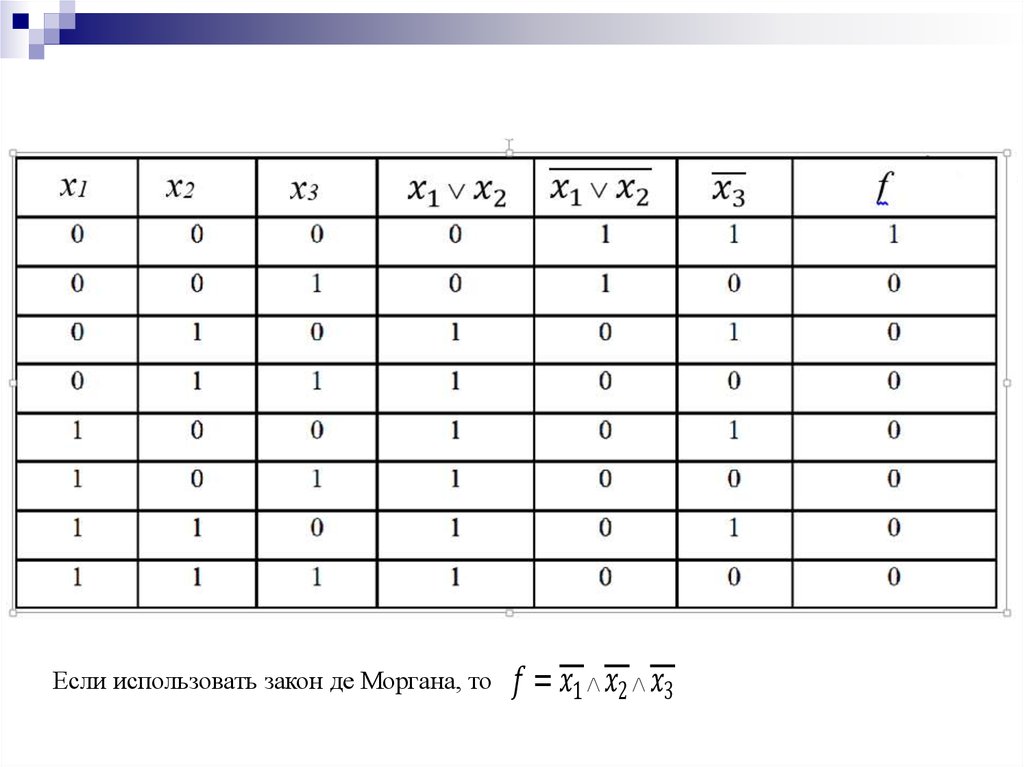
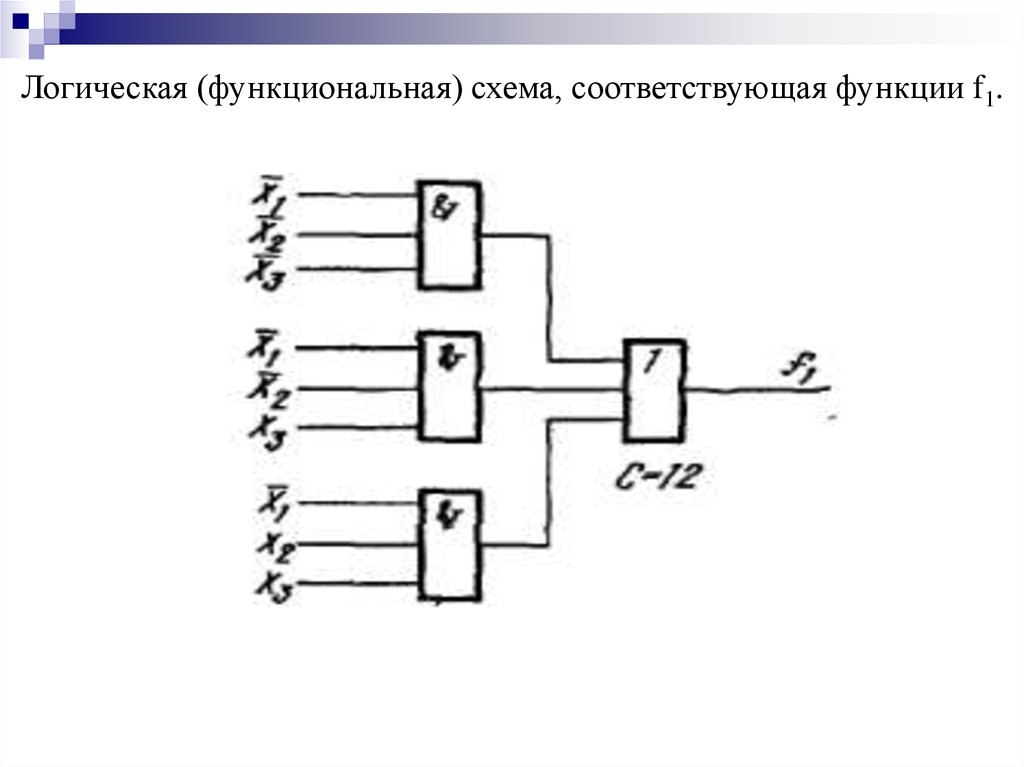
Пример. Задано логическое выражениеСоставить логическую схему для данного выражения и таблицу
истинности.
х1
х2
х3
f
































































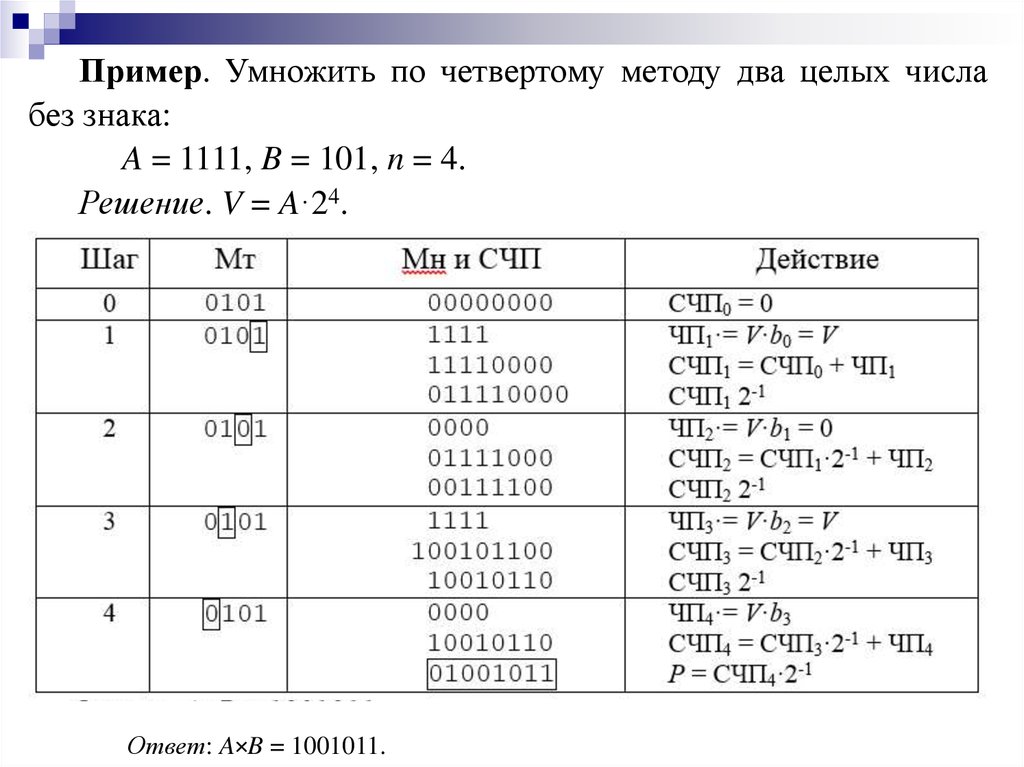
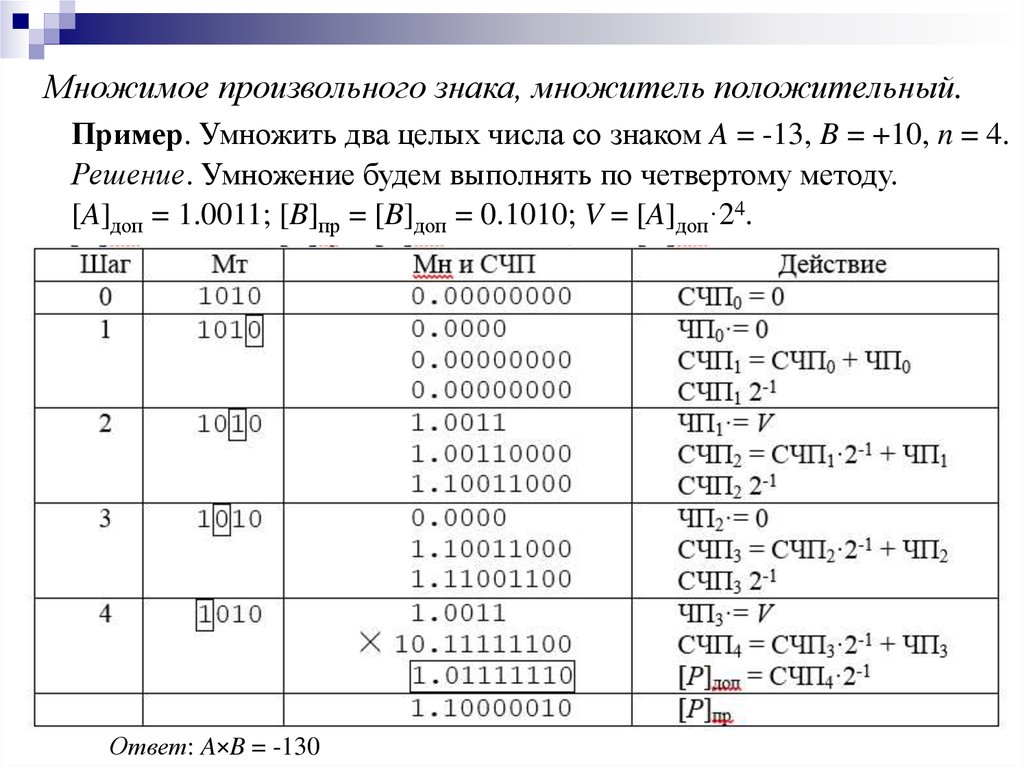
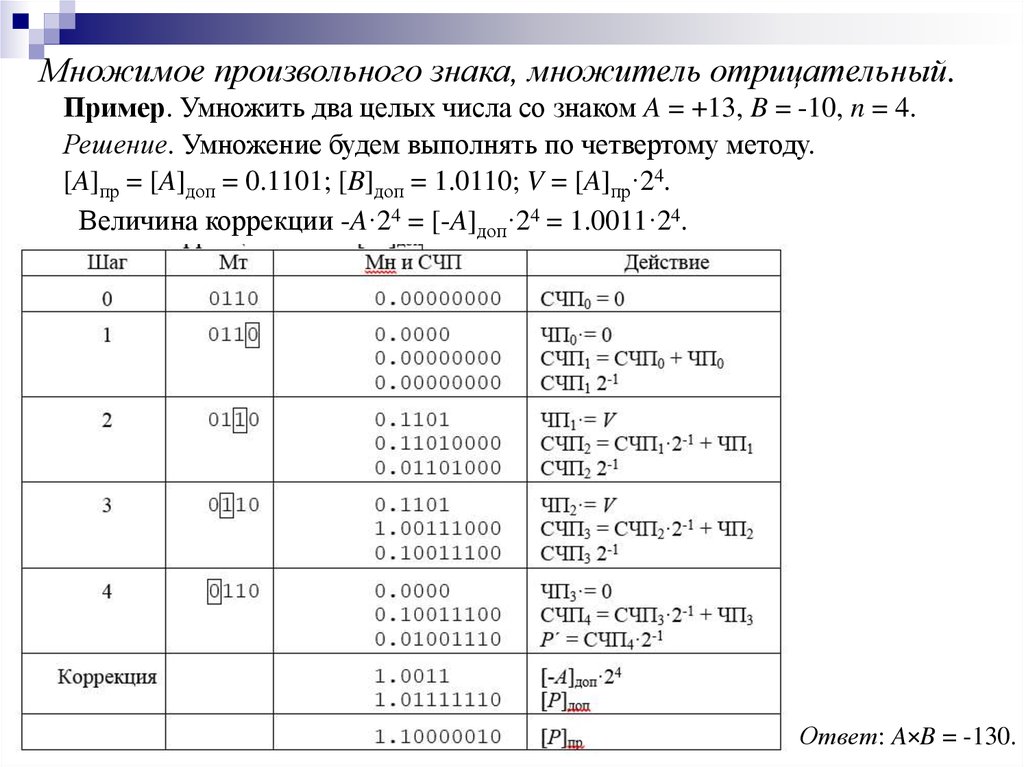


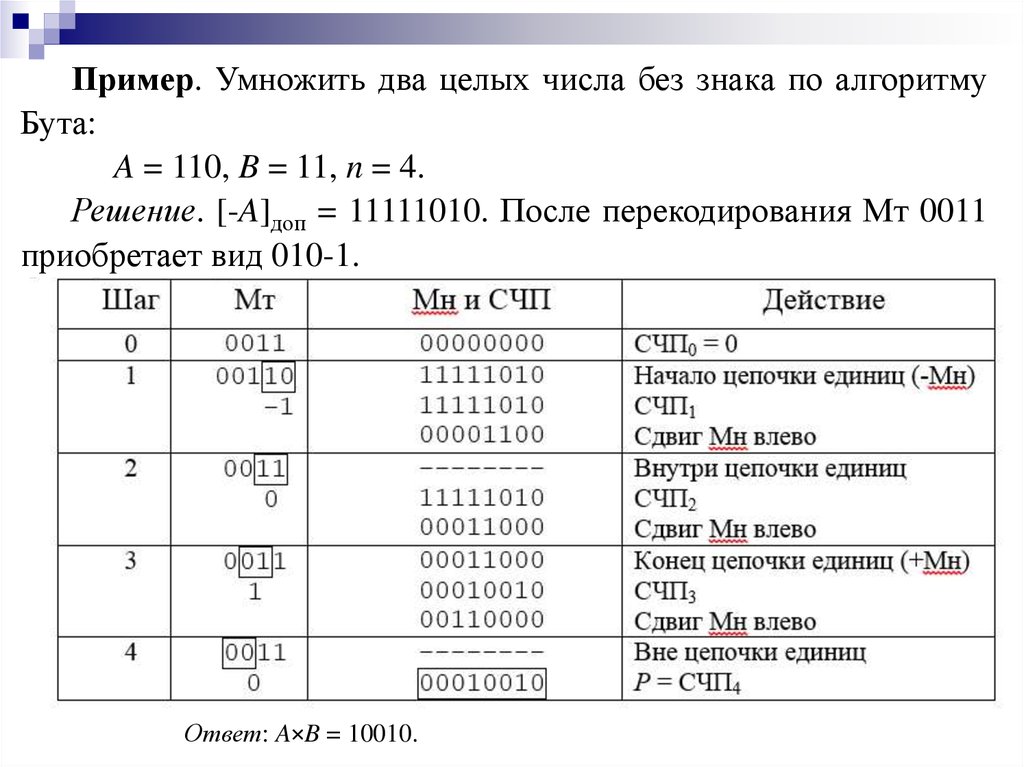
















































 informatics
informatics








