Similar presentations:
Синтез комбинационных схем
1.
СИНТЕЗ КОМБИНАЦИОННЫХ СХЕМКурсовая работа
по дисциплине “Дискретная математика”
2.
Задание.Построить комбинационные схемы в различных
базисах, реализующие не полностью
определенную булеву функцию
f(Х) = f (x1, x2, x3, x4, x5 ),
которая принимает значение 1 при условии:
2 X4X5X1 - X2X3 5
и неопределенное значение на наборах, для
которых X4 X5 = 0.
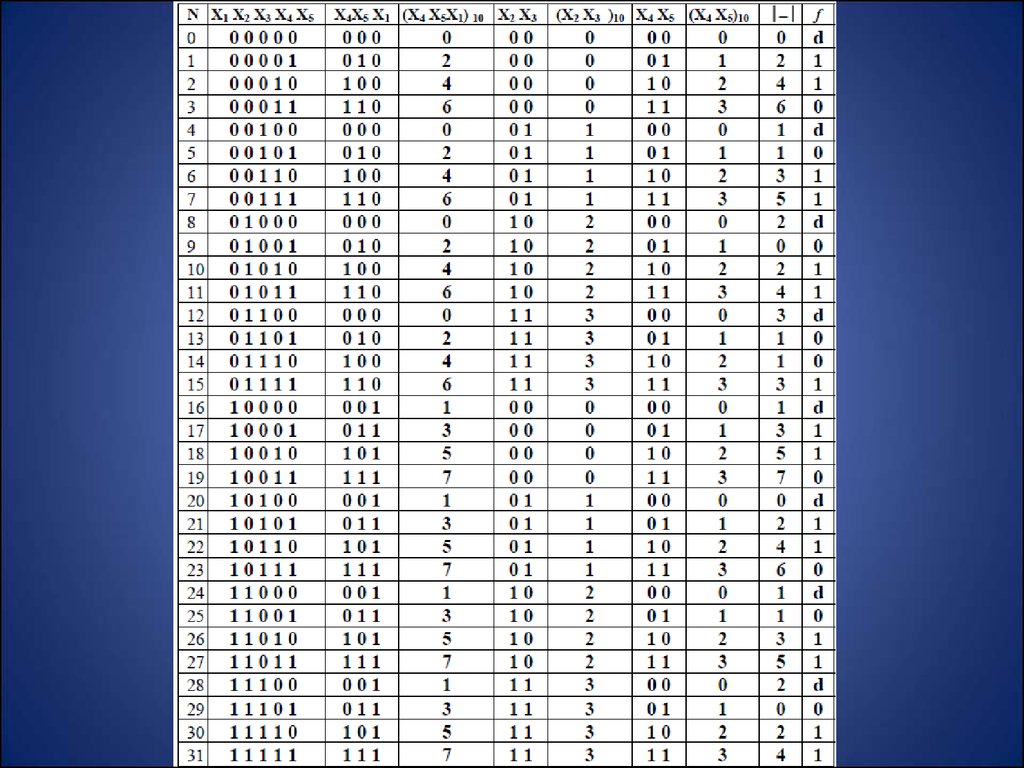
3.
4.
Представление булевой функции в аналитическом видеКДНФ : f x 1 x 2 x 3 x 4 x5 x 1 x 2 x 3 x4 x 5 x 1 x 2 x3 x4 x 5 x 1 x 2 x3 x4 x5 x 1 x2 x 3 x4 x 5
x 1 x2 x 3 x4 x5 x 1 x2 x3 x4 x5 x1 x 2 x 3 x 4 x5 x1 x 2 x 3 x4 x 5 x1 x 2 x3 x 4 x5 x1 x 2 x3 x4 x 5
x1 x2 x 3 x4 x 5 x1 x2 x 3 x4 x5 x1 x2 x3 x4 x 5 x1 x2 x3 x4 x5
ККНФ : f ( x1 x2 x3 x 4 x 5 )( x1 x2 x 3 x4 x 5 )( x1 x 2 x3 x4 x 5 )
( x 1 x2 x 3 x 4 x 5 )( x1 x 2 x3 x4 x 5 )( x 1 x 2 x3 x4 x 5 )
( x1 x 2 x 3 x4 x 5 )( x1 x 2 x 3 x 4 x5 )( x 1 x2 x3 x 4 x 5 )
5.
Минимизация булевой функцииметодом Квайна –Мак-Класки
Нахождение простых импликант
(максимальных кубов).
6.
7.
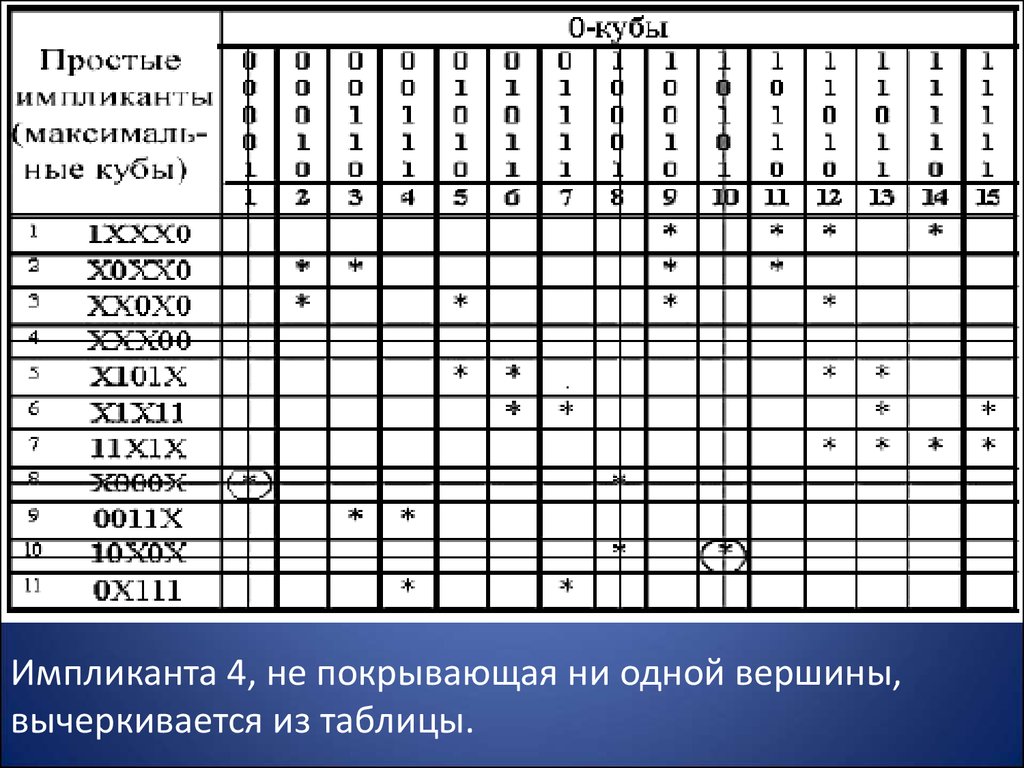
Составление импликантной таблицы.Импликантная таблица содержит 11 строк (по
числу простых импликант) и 15 столбцов (по числу
существенных вершин).
8.
Импликанта 4, не покрывающая ни одной вершины,вычеркивается из таблицы.
9.
Определение существенных импликант.Импликанты 8 и 10 – существенные, так как они
покрывают вершины 1 и 10 соответственно, не
покрытые другими импликантами. Вычеркнем из
таблицы строки, соответствующие этим
импликантам, а также столбцы, соответствующие
вершинам, покрываемым существенными
импликантами.
Множество существенных импликант образует
ядро покрытия как его обязательную часть:
10X0X
Т
X000X
Получаем упрощенную импликантную таблицу.
10.
Определение минимального покрытияМетод Петрика. Выпишем булево выражение Y,
определяющее условие покрытия всех 0-кубов
(существенных вершин), не покрываемых существенными
импликантами, в соответствии с таблицей
Y=(B C)(B G)(G H)(C D)(D E)(E H)(A B C)(A B)
(A C D F)(D E F)(A F)(E F).
11.
Применим закон поглощения к дизъюнктивнымтермам, в результате чего в выражении остаются
только двухбуквенные термы
Y=(B C)(B G)(G H)(C D)(D E)(E H)(A B)(A F)(E F)
Выполняя операции попарного логического
умножения применительно к термам, содержащим одинаковые буквы, с последующим применением закона поглощения, приведем исходную
конъюнктивную форму Y к дизъюнктивной
Y=ABDEG ACEG ABCEH ABDEH ACDFGH
BDEFG BCEFG BCEFH BDFH.
12.
Возможны следующие варианты покрытия:13.
14.
Дальнейшее упрощение импликантной таблицы. К упрощеннойимпликантной таблице применим операцию удаления “лишних”
столбцов (существенных вершин).
В отношении “множество-подмножество“ находятся
отметки следующих пар столбцов: g и a, g и h, k и d, k
и m , l и e, l и n. Таким образом из таблицы можно
удалить столбцы g, k и l, после чего получим новую
таблицу.
15.
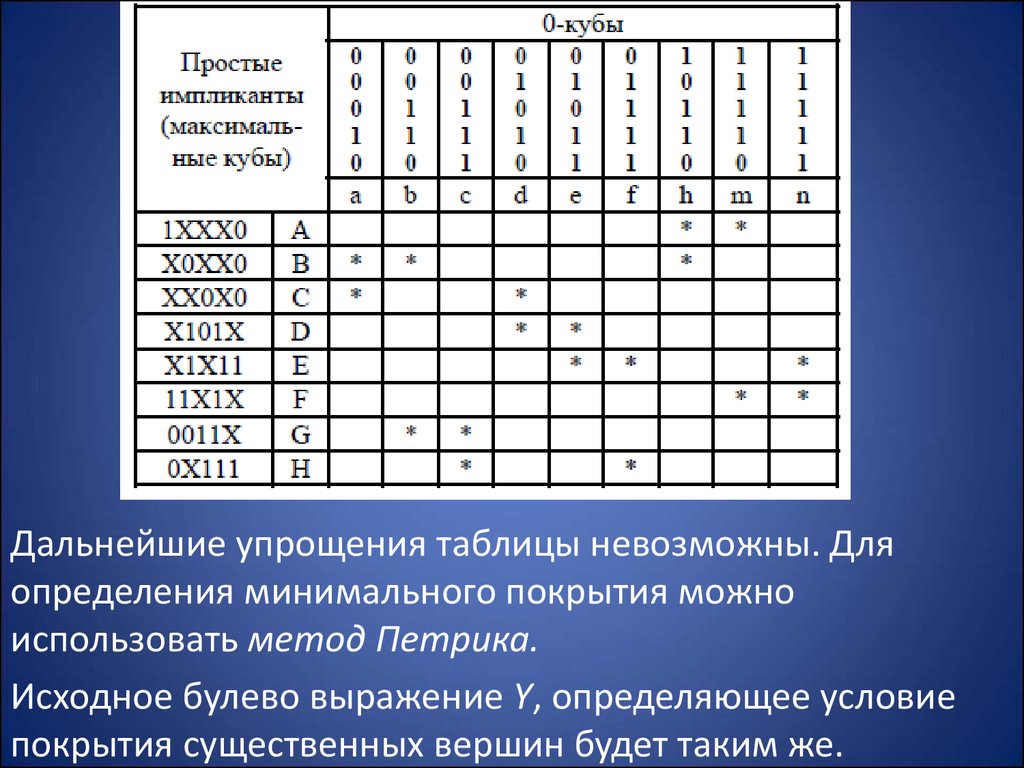
Дальнейшие упрощения таблицы невозможны. Дляопределения минимального покрытия можно
использовать метод Петрика.
Исходное булево выражение Y, определяющее условие
покрытия существенных вершин будет таким же.
16.
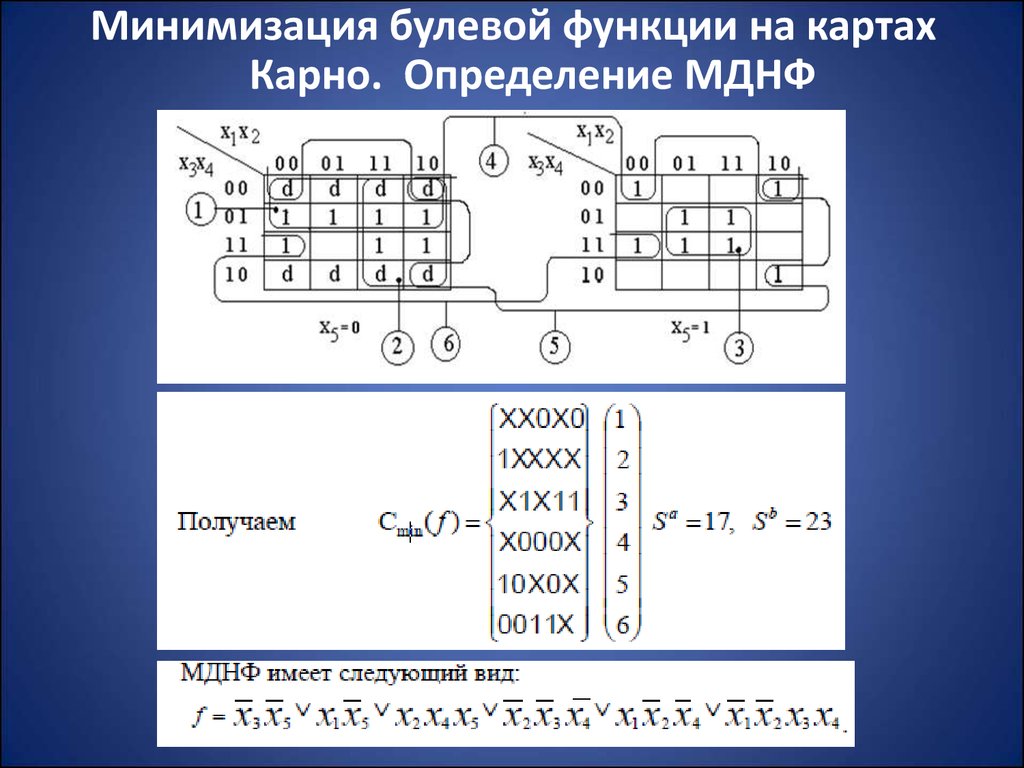
Минимизация булевой функции на картахКарно. Определение МДНФ
17.
Определение МКНФ,
,
,
18.
Преобразование минимальных форм булевойфункции
Факторное преобразование для МДНФ:
f x3 x5 x1 x5 x2 x4 x5 x2 x3 x4 x1 x2 x4 x1 x2 x3 x4
(SQ=23)
x5 ( x1 x3 ) x2 x4 x5 x2 x4 ( x1 x3 ) x1x2 x3 x4
(SQ=20)
( x1 x3 )( x2 x4 x5 ) x2 x4 x5 x1 x2 x3 x4 .
(SQ=18)
Решим задачу декомпозиции применительно к
полученной форме. Для этого введем вспомогательную функцию ( x1 , x3 ) x1 x3
Инверсия этой функции имеет вид x1 x3 .
С учетом новой функции последнее выражение
преобразуется к виду:
19.
f ( x 2 x 4 x5 ) x2 x4 x5 x 2 x4 .Реализация комбинационной схемы по этому
выражению с учетом затрат на вспомогательную
функцию и ее инверсию дает цену схемы SQ=18,
такую же, как и для построенной схемы, но
задержка схемы будет больше.
Факторное преобразование для МКНФ:
f ( x2 x4 ) ( x1 x3 x4 ) ( x1 x2 x3 x5 )
( x2 x3 x4 x5 ) ( x1 x2 x4 x5 )
(SQ=22)
( x4 x2 ( x1 x3 )) ( x2 x4 x5 x1 x3 )
( x x x x ).
1
2
3
5
(SQ=19)
20.
Следует отметить, что вынесение x4 из первыхдвух термов МКНФ не дает уменьшения цены
схемы: SQ = 0 (m=1, k=2, p=1, =2), однако
является целесообразным для дальнейшей
декомпозиции за счет введения вспомогательной
функции , такой же как и в предыдущем случае.
Выражение после декомпозиции примет вид:
x1 x3 , f ( x4 x2 )( x2 x4 x5 )( x2 x5 ), (SQ 17)
для которого цена схемы дает абсолютный
минимум при условии, что синтезируемая схема
строится на элементах булева базиса с
парафазными входами.
21.
Синтез комбинационных схем в булевом базисеКомбинационные схемы, реализующие заданную
функцию по последней форме, в булевом базисе с
парафазными входами и с однофазными
входами
22.
Задержка схемы с парафазными входами Т=4 ,цена схемы SQ=17. Для схемы с однофазными
входами Т=5 , цена схемы SQ=21.
23.
Синтез комбинационных схем в универсальныхбазисах
Базис ИЛИ-НЕ
а) Приведение последнего выражения к базису
ИЛИ-НЕ осуществляется заменой операций булева
базиса на операцию стрелка Пирса путем
использования законов двойственности.
x1 x3 x1 x3 x1 x3 ; x1 x3 .
f ( x4 x2 )( x2 x4 x5 )( x2 x5 )
x4 x2 x2 x4 x5 x2 x5
( x4 ( x2 )) ( x2 x4 x5 ) ( x2 x5 ).
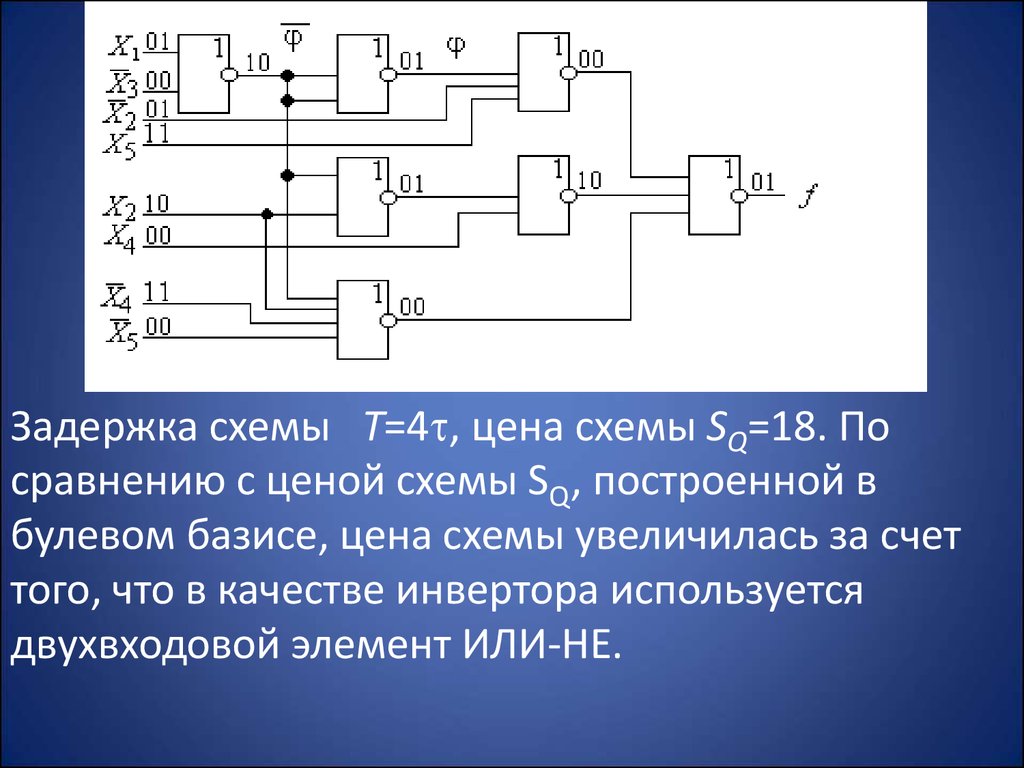
По полученному выражению строим схему с
парафазными входами в базисе ИЛИ-НЕ
24.
Задержка схемы Т=4 , цена схемы SQ=18. Посравнению с ценой схемы SQ , построенной в
булевом базисе, цена схемы увеличилась за счет
того, что в качестве инвертора используется
двухвходовой элемент ИЛИ-НЕ.
25.
б) Преобразование схемы из булева базиса вуниверсальный.
Заменим элементы булева базиса в соответствии с
логическими эквивалентами из таблицы. В результате
получим следующую схему. Пунктирной линией на ней
выделены логические эквиваленты элементов булева
базиса.
Элемент
булева
базиса
Базис И-НЕ
Формула
Логический
элемент
Базис ИЛИ-НЕ
Формула
a a a
a a a
a b a b
a b a b
a b a b
a b a b
Логический
элемент
26.
Исключим из схемы лишние инверторы. К ним относятся:•входной инвертор для инверсии переменной x2
(логический эквивалент элемента 4);
•пары последовательных инверторов на связях с выходов
логических эквивалентов элементов 3, 5 и 6 на входы
логического эквивалента элемента 7.
27.
Кроме того, пары последовательных инверторовсоставляют выходной инвертор логического
эквивалента элемента 1, на котором реализуется
вспомогательная функция , и входной инвертор
логического эквивалента элемента 4, а также
логический эквивалент элемента 2. Однако из двух
последовательных инверторов обеих пар
исключается только один, замыкающий пару, на
котором реализуется инверсия вспомогательной
функции . Лидирующий инвертор пары
сохраняется для подачи значения на вход
логического эквивалента элемента 3.
28.
После удаления замыкающих инверторов обеихпар, на выходах которых реализуется инверсия ,
входы логических эквивалентов элементов 4 и 5,
связанные с выходом удаляемых инверторов,
переключаются к выходу первого элемента логического эквивалента 1, на котором формируется
требуемое значение инверсии . После исключения лишних инверторов получим окончательную
схему в базисе ИЛИ-НЕ, аналогичную приведенной
выше.
Базис И-НЕ
а) Приведение аналитического выражения к
базису И-НЕ осуществляется заменой операций
29.
булева базиса на операцию штрих Шеффера(отрицание конъюнкции) путем использования
законов двойственности.
x1 x3 x1 x3 x1x3 x1 | x3.
f ( x4 x2 )( x2 x4 x5 )( x2 x5 )
x4 x2 x2 x4 x5 x2 x5
( x4 | ( x2 | )) | ( x2 | x4 | x5 | ) | ( x2 | x5 | ).
Цена схемы в базисе И-НЕ: SQ=20. Увеличение
цены схемы на три по сравнению со схемой в
булевом базисе связано, во-первых, с реализацией
инверсии вспомогательной функции и, вовторых, с использованием выходного инвертора.
30.
Для построения схемы с меньшей ценойцелесообразно использовать форму, полученную
по МДНФ с ценой SQ=18 для булева базиса.
f ( x1 x3 )( x2 x4 x5 ) x2 x4 x5 x1 x2 x3 x4
x1 x3 x 2 x 4 x5 x2 x4 x5 x1 x2 x3 x4
x1 x3 x 2 x 4 x5 x2 x4 x5 x1 x2 x3 x4
x1 x3 x 2 x 4 x5 x2 x4 x5 x1 x2 x3 x4
(( x1 | x3 ) | (( x2 | x4 ) | x5 )) | ( x2 |x 4 | x5 ) | ( x1 | x2 | x3 | x4 )
31.
Задержка схемы Т=4 , цена схемы SQ=18 совпадаетс ценой для булева базиса.
б) Преобразование схемы из булевого базиса в
базис И-НЕ осуществляется так же как и для базиса
ИЛИ-НЕ.
32.
Синтез комбинационной схемы с учетомкоэффициента объединения
При построении схемы в универсальном базисе с
учетом ограничения на количество входов в
логические элементы, определяемого
коэффициентом объединения по входам I,
целесообразно предварительно преобразовать
исходное выражение для реализуемой функции в
булевом базисе, разделяя аргументы булевых
операций конъюнкции и дизъюнкции на группы с
числом аргументов, не превышающим заданного
значения I.
33.
Если в выражении для функции имеются трехместные операции, то при I=2 для уменьшения задержки синтезируемой схемы целесообразнее объединять в пару более простые элементы операции,оставляя более сложные элементы уединенными.
Преобразуем полученное выражение для коэффициента объединения I = 2, вводя в нем дополнительные скобки. При этом в трехместной операции
дизъюнкции в правой скобке объединим в пару
входные переменные x2 и x5, уединив функцию ,
реализуемую отдельной подсхемой и следовательно, являющуюся более сложным элементом этой
скобки.
34.
Кроме того, при объединении скобок какэлементов трехместной операции конъюнкции
уединим среднюю скобку, как более сложный
элемент. В результате исходное выражение
преобразуется к виду:
f (( x4 x2 )(( x2 x5 ) ))(( x2 x4 ) ( x5 )).
Преобразуем это выражение к базису ИЛИ-НЕ,
заменяя операции булева базиса операцией
стрелка Пирса подобно тому, как это делалось
ранее, но с учетом скобок. Это означает, что
каждая операция стрелка Пирса должна быть
двухместной.
35.
x1 x 3 f (( x x )(( x x ) ))(( x x ) ( x ))4
2
2
5
2
4
5
( x4 x2 ( x2 x5 ) )(( x2 x4 ) ( x5 ))
(( x4 ( x2 )) (( x2 x5 ) )) (( x2 x4 ) ( x5 ))
(( x4 ( x2 )) (( x2 x5 ) )) (( x2 x4 ) ( x5 ))
Инверсии реализуются в схеме, построенной по
этому выражению, на элементах ИЛИ-НЕ с
запараллеленными входами.
36.
Задержка схемы Т=6 , цена схемы SQ=30. Посравнению со схемой в базисе ИЛИ-НЕ,
построенной без ограничений на число входов в
элементы, задержка схемы и ее цена значительно
увеличились.
37.
Замечание. Использование в качестве исходноговыражения f ( x1 x3 )( x2 x4 x5 ) x2 x4 x5 x1 x2 x3 x4 .
с последующей дополнительной факторизацией
путем вынесения за скобки x4 из двух последних
термов позволяет построить схему на двухвходовых элементах ИЛИ-НЕ с ценой SQ=22 и задержкой
Т=7 . Преобразованное к базису выражение имеет
вид z x1 x3 , f ( z (( x2 x4 ) x5 )) ( x4 (( x2 x5 ) ( z x2 )))
Если использовать аналогичное преобразование
для двухвходового базиса И-НЕ, то цена схемы и
задержка схемы уменьшатся (SQ=20, Т=6 ) за счет
отсутствия в ней выходного инвертора.
38.
Анализ комбинационных схемПо таблице истинности булевой функции выберем
наборы аргументов (входных переменных), на которых функция принимает значения 0 и 1, например,
01101 и 10101, и определим реакцию построенных
схем на эти наборы. Для этого на схеме отмечаются
значения входных переменных и далее определяются
значения выходных сигналов каждого из логических
элементов с учетом функции, реализуемой им.
Последовательно продвигаясь по схеме от ее входов к
выходу, получим значение выходного сигнала схемы.
Сравнив его со значением булевой функции для
выбранного набора аргументов по таблице
истинности, можно утверждать, что, по крайней мере,
39.
Синтез многовыходных комбинационных схемПРИМЕР 2. Синтезировать комбинационную схему,
выполняющую операцию сложения двух
двухразрядных двоичных чисел:
C=A+B, где A=(a1 , a2) B=(b1 , b2) C=(C0 , C1 , C2).
Закон функционирования синтезируемой схемы
описывается системой булевых функций
C 0 f 0 ( a 1 , a 2 , b1 , b 2 )
C1 f1 ( a 1 , a 2 , b1 , b 2 )
C f ( a , a , b , b ),
2
1
2
1
2
2
аргументами которых являются значения двоичных разрядов операндов
40.
1. Составление таблицы истинностиТаблица истинности системы булевых
функций строится с учетом правил двоичного
сложения и представлена в таблице
2. Минимизация булевых функций системы
Для минимизации воспользуемся картами
Карно.
1X1X
Cmin (C0 ) 11X1
X111
a
b
S 8, S 11
41.
a10
0
0
0
0
0
0
0
1
1
1
1
1
1
1
1
a2
0
0
0
0
1
1
1
1
0
0
0
0
1
1
1
1
b1
0
0
1
1
0
0
1
1
0
0
1
1
0
0
1
1
b2
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
C0
0
0
0
0
0
0
0
1
0
0
1
1
0
1
1
1
C1
0
0
1
1
0
1
1
0
1
1
0
0
1
0
0
1
C2
0
1
0
1
1
0
1
0
0
1
0
1
1
0
1
0













































 informatics
informatics electronics
electronics








