Стандартные схемы. Тема 6

1.

Стандартные схемы
• Схема программы - абстракция
императивной программы, в которой
базовые операции заменены
абстрактными символами.
• Интерпретация = смысл базовых
операций + значения входных данных
• Программа = схема программы +
интерпретация.

2.

Базис
• X = {x1,x2,…, y1,y2,…} – переменные
• C = {a,b,c,…} – константы
• F = {f,g,h,….} – функциональные
символы
• P={p,q,…} – предикатные символы
• {старт, стоп, петля, (, ), ,, := } –
специальные символы
• Местность символа: r : F P N

3.

Термы
• Функциональный терм T:
– x – терм, если x X
– a – терм, если a C
– f ( 1,…, n) – терм, если f F, r(f)=n
и 1,…, n – термы,
– других нет
• Предикатные термы :
– p ( 1,…, n) – терм, если p P, r(p)=n
и 1,…, n – функциональные термы

4.

Операторы
• старт(x1,…,xn) – начальный
• стоп( 1,…, n) – заключительный,
останов
• x := – присваивание
• – условный, тест, распознаватель
• петля – зацикливание,

5.

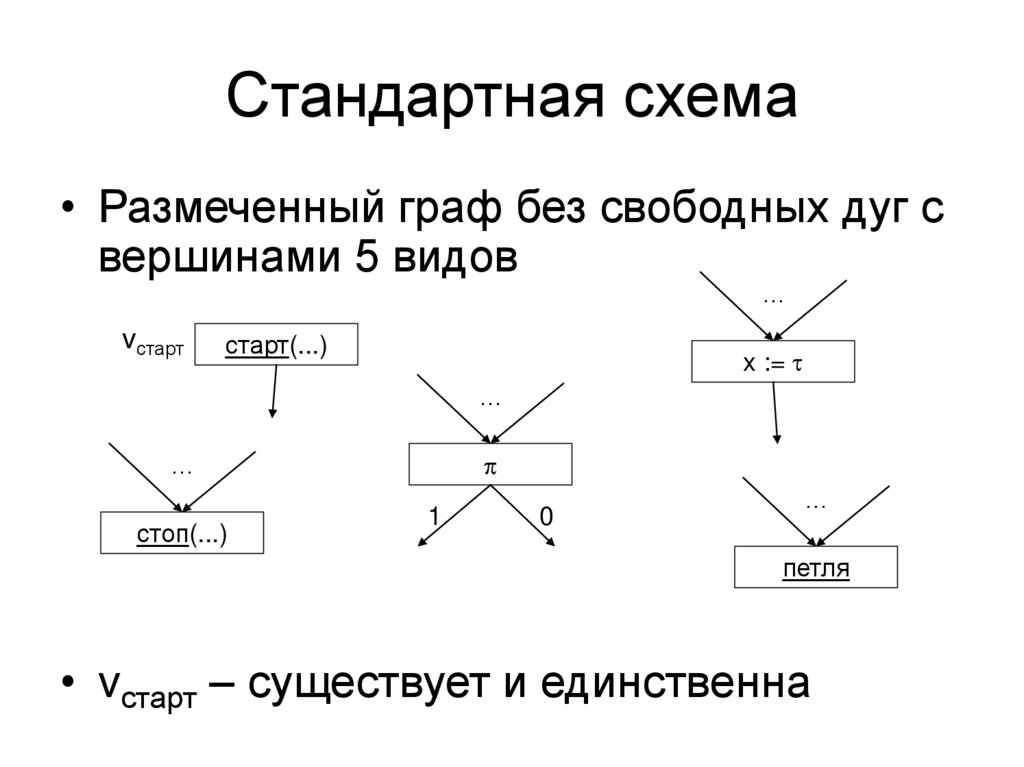
Стандартная схема
• Размеченный граф без свободных дуг с
вершинами 5 видов
…
vстарт
старт(...)
x :=
…
…
стоп(...)
1
0
…
петля
• vстарт – существует и единственна

6.

Аргументы и результаты
• Аргументы терма арг( ), арг( ) – все
переменные, входящие в терм
• Аргументы оператора (вершины)
арг
старт(x1,…,xn)
стоп( 1,…, n)
x :=
петля
арг( 1) … арг( n)
арг( ),
арг( )
рез
{x1,…,xn}
{x}

7.

Правильная схема
• Стандартная схема правильная, если
любая переменная присваивается
раньше, чем используется:
e1,…,en - маршрут :
нач(е1) = vстарт & x арг(кон(en))
i<n : x рез(нач(ei))
• Далее только правильные схемы.

8.

Интерпретация
• Область интерпретации D
• Интерпретация I:
I:X D
I:C D
I : F(n) (Dn D)
I : P(n) (Dn {0,1})
где
– F(n) и P(n) – множества функциональных и
предикатных символов местности n, соотв.
– I(f) всюду определена для любого f

9.

Свободные интерпретации
• Область интерпретации – T (множество
функциональных термов)
Ih(x) = ‘x’
Ih(f)( 1,…, n) =
‘f(’ + 1 + ‘,’ + … + ‘,’ + n + ‘)’
Ih(p) – свободно
• Любые две свободные интерпретации
отличаются только тем, как они
определяют предикатные символы.

10.

Значение терма
• Состояние памяти W : X D
• Значение функционального терма при
интерпретации I на состоянии памяти W:
I : W D
– W(x), если = x
– I(a) , если = a
– I(f)( 1I(W),…, nI(W)), если = f ( 1,…, n)
• Значение предикатного терма при
интерпретации I на состоянии памяти W:
I : W {0,1}
– I(p)( 1I(W),…, nI(W)), если = p( 1,…, n)

11.

Протокол
Протокол схемы S при интерпретации
I: прот(S,I) = (v0,W0),…, (vi,Wi), …
1. v0 = vстарт
x : W0(x) = I(x)
1. Начальная вершина:
Wi+1=Wi
vi
старт(...)
vi+1
...

12.

Протокол
…
3. Присваивание:
Wi+1=Wi[x↦a]
x :=
vi+1
3. Распознаватель
vi+1=vb, где b = I(Wi)
Wi+1=Wi
...
…
vi
1
v1
...
0
v2
...

13.

Протокол
5. Заключительный:
– Протокол конечен
vi
– Результат программы
рез(S,I) = ( 1I(Wi),…, nI(Wi))
5. Зацикливание
vi+1=vi
Wi+1=Wi
- протокол бесконечен
…
стоп( 1,…, n)
…
vi
петля

14.

Функциональная
эквивалентность (не разреш.)
• Стандартные схемы S1 и S2
функционально эквивалентны (S1≈S2),
если
I : (прот(S1,I) бесконечен
& прот(S2,I) бесконечен)
рез(S2,I)=рез(S1,I)
• Стандартная схема S пуста, если
I : прот(S,I) бесконечен
• Стандартная схема S тотальна, если
I : прот(S,I) конечен

15.

Логико-термальная
эквивалентность
• Замечание. Далее рассматриваем только
маршруты =e1,…en, в которых
кон(ei)=нач(еi+1).
• Термальное значение x переменной x вдоль
маршрута ’e:
– x, если ’ - пуст.
– ’, если нач(e) = x:= .
– x ’, иначе
• Термальное значение терма вдоль
маршрута :
[x1/x1 ’,…, xn/xn ’],
где x1,…xn –переменные входящие в .

16.

Логико-термальная
эквивалентность
• Логико-термальная история lt( ) для
маршрута ’e
– , если ’ = .
– lt( ’) pb( 1 ’,…, n ’), если нач(е) –
распозначатель p( 1,…, n), а b {0,1} –
пометка дуги e.
– lt( ’) 1 ’… n ’, если кон(е) – останов
стоп( 1,…, n).

17.

Логико-термальная
эквивалентность
• Детерминант det(S) схемы S:
det(S) = { lt( ) | =e1,...,en, (все возм
маршр)
нач(e1) = vстарт,
кон(еn) – останов стоп(…)}
(бескон. мн-во)
• Схемы S1 и S2 логико-термально
эквивалентны (S1≈лтS2), если det(S1) =
det(S2) ()

18.

Корректность ≈лт
• Теорема. S1≈лтS2 S1≈S2
• Доказательство. Интерпретация I
согласована с лт-историей h= … pibi( 1i,…,
ni)…, 1,… k, если
bi= I(W0),
где = pi( 1i,…, ni), x : W0(x) = I(x).
– Любая интерпретация I, приводящая к останову,
согласована с единственной лт-историей
– Любая интерпретация I, не приводящая к останову,
не согласована ни с одной лт-историей.

19.

Доказательство
1. (S1,I) зацикливается I не согласована ни с
одной лт-историей из det(S1) и из det(S2)
и (S2,I) зацикливается.
2. (S1,I) останавливается I согласована с h
из det(S1).Так как det(S1)= det(S2), то
h det(S2) (S2,I) останавливается.
Совпадение результатов: рез(Si,I) =
( 1(W0),…, k(W0))
• Конец доказательства.

20.

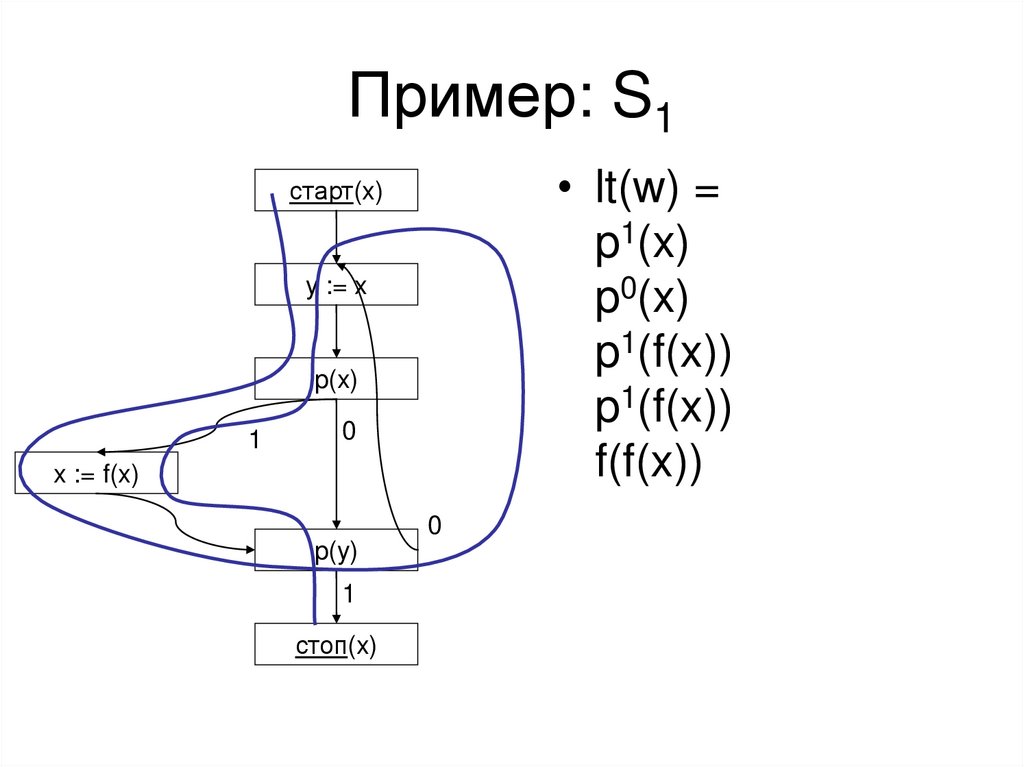
Пример: S1
• lt(w) =
p1(x)
p0(x)
p1(f(x))
p1(f(x))
f(f(x))
старт(x)
y := x
p(x)
1
0
x := f(x)
0
p(y)
1
стоп(x)

21.

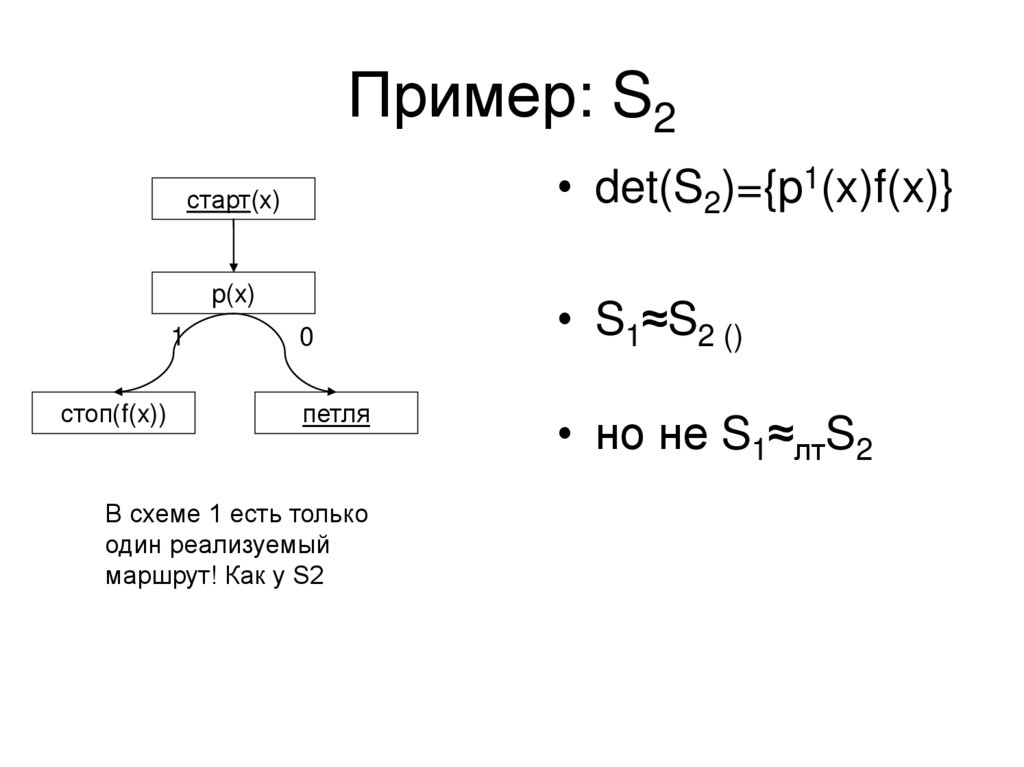
Пример: S2
• det(S2)={p1(x)f(x)}
старт(x)
p(x)
1
стоп(f(x))
0
петля
В схеме 1 есть только
один реализуемый
маршрут! Как у S2
• S1≈S2 ()
• но не S1≈лтS2

22.

Информационные связи
• Информационный маршрут =e1,...,en
для переменной x
– x рез(нач(e1))
– x арг(кон(en))
– i 2..n-1 : x рез(нач(ei))

23.

Информационный граф
• Информационный граф DFG=(O, ↝) схемы S
– ориентированный граф, где
– Множество вершин O – множество вхождений
переменных в схеме S
– Информационная связь o1↝o2 от вхождения o1
переменной x в вершине v1 к вхождению o2
переменной x в вершине v2: существует
информационный маршрут =e1,...,en для
переменной x, нач(e1) = v1 и кон(en) = v2.
• Будем говорить, что подтверждает
информационную связь o1↝o2.

24.

ЗГА для DFG
Обозначения
– O – множество вхождений переменных
– (o) X – переменная, соответствующая
вхождению о.
– o-рез(v) и о-арг(v) – множество вхождений
переменных для результатов и
аргументов вершины v, соответственно.

25.

ЗГА для DFG
1. Граф: граф схемы S
2. Полурешётка: (O, }
3. Начальная разметка:
0(eстарт) = o-рез(vстарт),
если нач(eстарт)= vстарт
0(e) = , иначе
4. Функция переноса (дистрибутивная?):
f(e1,e2)(S) = S \ { o | (o) рез(v) }
o-рез(v),
если v=кон(e1)=нач(e2)
f(e1,e2)(S) = , иначе

26.

Информационный граф: пример
1
старт(x)
• Начальная
разметка
• Стационарная
разметка
• Информационные
зависимости
{1}
2
3
y := x
{1,2,5}
4
p(x)
{1,2,5}
5
6
x := f(x)
{2,5}
1
0{1,2,5}
7
p(y)
1{1,2,5}
8
стоп(x)
0
{1,2,5}

27.

Компоненты связности DFG
• Два информационных маршрута
зацеплены, если они имеют общую дугу.
• Компоненты связности Q1 и Q2
информационного графа зацеплены,
если существует связь из Qi,
подтверждаемая маршрутом i, (i=1..2),
причем 1 и 2 зацеплены.

28.

Переименование
• Требования:
– Все вхождения из любой компоненты
связности должны быть обозначены одной
и той же переменной
– Если две компоненты связности
зацеплены, то принадлежащие им
вхождения должны быть обозначены
разными переменными.

29.

Переименование
Сведение к задаче раскраски графов:
• Граф зацеплённости компонент связности:
– вершины – компоненты связности
– ребро – компоненты связности зацеплены.
• Раскраска графа: приписать вершинам
«цвета» так, чтобы любые две смежные
вершины были «покрашены» в разные цвета.
– «цвета» = новые переменные.
• Сложность нахождения минимальной
раскраски: NP

30.

Информационный граф: пример
старт(a, b, c, d)
y1 := add(a, b)
y2 := mult(y1, c)
y3 := sub(d, c)
y4 := mult(a, y3)
y5 := add(y4, y2)
y6 := add(d, c)
y7 := mult(b, y6)
y8 := sub(y2, y7)
стоп(y5, y8)
• X = {a,b,c,d,
y1,y2,y3,y4,
y5,y6,y7,y8}
• F = {add,mult,sub}

31.

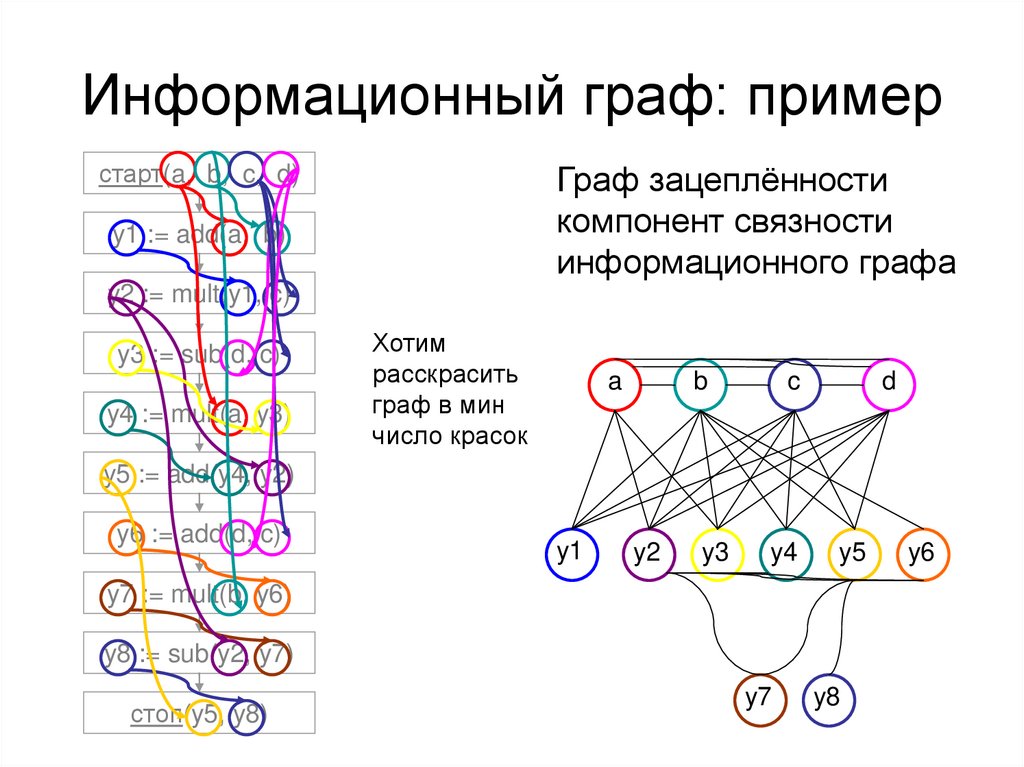
Информационный граф: пример
старт(a, b, c, d)
Граф зацеплённости
компонент связности
информационного графа
y1 := add(a, b)
y2 := mult(y1, c)
y3 := sub(d, c)
y4 := mult(a, y3)
Хотим
расскрасить
граф в мин
число красок
a
b
c
y3
y4
d
y5 := add(y4, y2)
y6 := add(d, c)
y1
y2
y5
y7 := mult(b, y6)
y8 := sub(y2, y7)
стоп(y5, y8)
y7
y8
y6

32.

Информационный граф: пример
старт(x4,x1,x3,x5)
x2 := add(x4,x1)
Замена переменных:
a
b
c
d
y1 y2 y3 y4 y5 y6 y7 y8
x4 x1 x3 x5 x2 x2 x6 x4 x4 x3 x1 x1
x2 := mult(x2, x3)
x6 := sub(x5,x3)
x4 := mult(x4,x6)
x4 := add(x4, x2)
x3 := add(x5,x3)
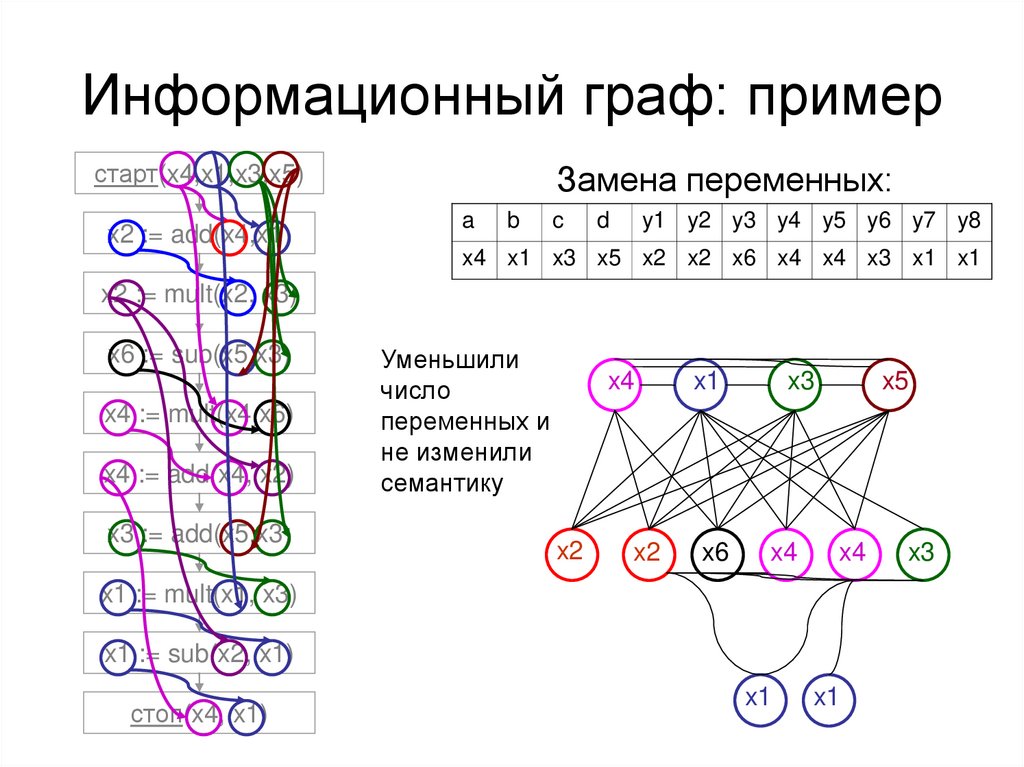
Уменьшили
число
переменных и
не изменили
семантику
x4
x2
x2
x1
x3
x6
x4
x5
x4
x1 := mult(x1, x3)
x1 := sub(x2, x1)
стоп(x4, x1)
x1
x1
x3

33.

Информационный граф: пример
старт(x4,x1,x3,x5)
x2 := add(x4,x1)
Замена переменных:
a
b
c
d
y1 y2 y3 y4 y5 y6 y7 y8
x4 x1 x3 x5 x2 x2 x6 x4 x4 x3 x1 x1
x2 := mult(x2, x3)
x6 := sub(x5,x3)
x4 := mult(x4,x6)
x4 := add(x4, x2)
x3 := add(x5,x3)
x1 := mult(x1, x3)
x1 := sub(x2, x1)
стоп(x4, x1)