Similar presentations:
Углы в пространстве
1.
2.
3.
Образовательные :рассмотрение всех возможных комбинаций углов в пространстве (угол
между двумя прямыми, угол между прямой и плоскостью, угол между
двумя плоскостями), решение геометрических задач классическим и
координатно-векторным методами; формирование навыков чтения
чертежей,
умений
проводить
дополнительные
построения
и
вычисления;
Развивающие:
формирование умения выполнять обобщение и конкретизацию, развитие
качества мышления: гибкость, целенаправленность, рациональность,
критичность с учетом индивидуальных особенностей;
Воспитательные:
Развитие взаимовыручки и взаимопомощи, умение вести культурную
дискуссию, умение четко организовывать самостоятельную и
индивидуальную работу.
4.
Кто не знает, в какую гавань он плывет,для того нет попутного ветра.
Сенека
1. Угол между скрещивающимися прямыми.
классический
координатно-векторный
2. Угол между прямой и плоскостью.
классический
координатно-векторный
3. Угол между двумя плоскостями.
классический
координатно-векторный
4. Теорема о трех перпендикулярах
5. Теорема косинусов
6. Нормаль к плоскости
5.
Углом между скрещивающимися прямыми называетсяугол между пересекающимися прямыми, соответственно
параллельными данным скрещивающимися.
b
a
m
M
a
b
0
0
90
Точку М можно выбрать произвольным образом.
В качестве точки М удобно взять любую точку на одной
из скрещивающихся прямых.
0
6.
Углом между прямой и плоскостью, пересекающей эту прямую и не перпендикулярнойк ней, называется угол между прямой и ее
проекцией на плоскость.
М
перпендикуляр
А
проекция
0
0
Н
90
0
7.
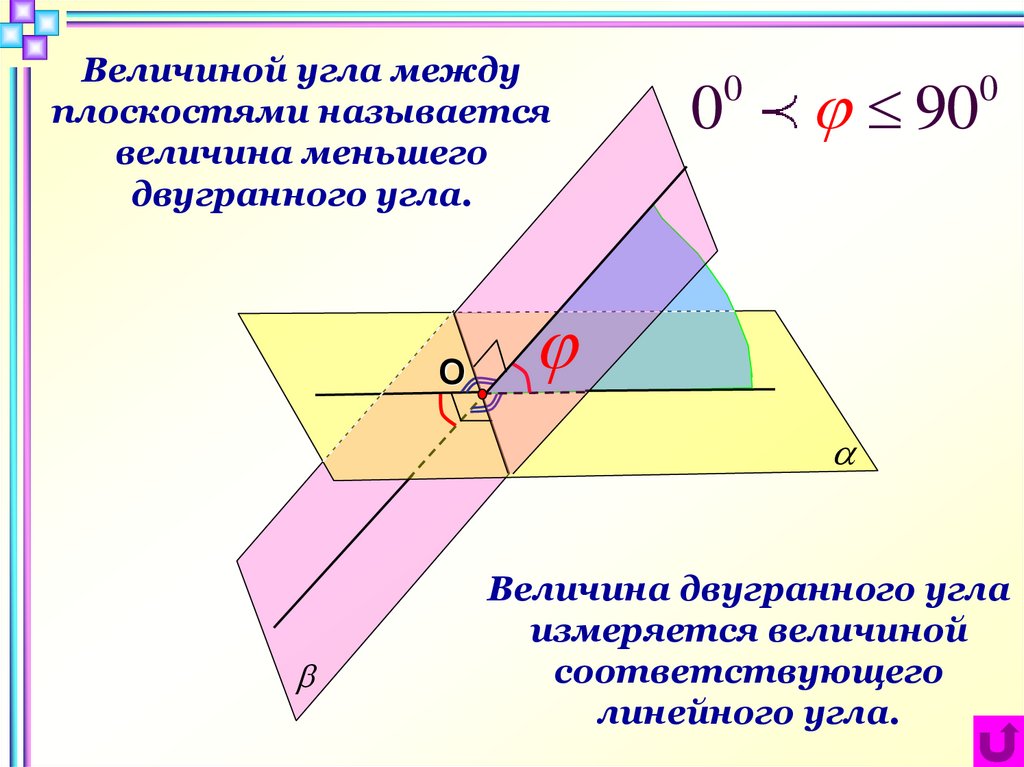
Величиной угла междуплоскостями называется
величина меньшего
двугранного угла.
О
0
0
90
0
Величина двугранного угла
измеряется величиной
соответствующего
линейного угла.
8.
a AB a ACTTП
а
В
перпендикуляр
a AC a AB
TTП
С
А
9.
Квадрат сторонытреугольника равен
сумме квадратов двух
других сторон минус
удвоенное произведение
этих сторон на косинус
угла между ними.
а-?
в
с
a b c 2bc cos
2
2
2
b c a
cos
2bc
2
2
2
10.
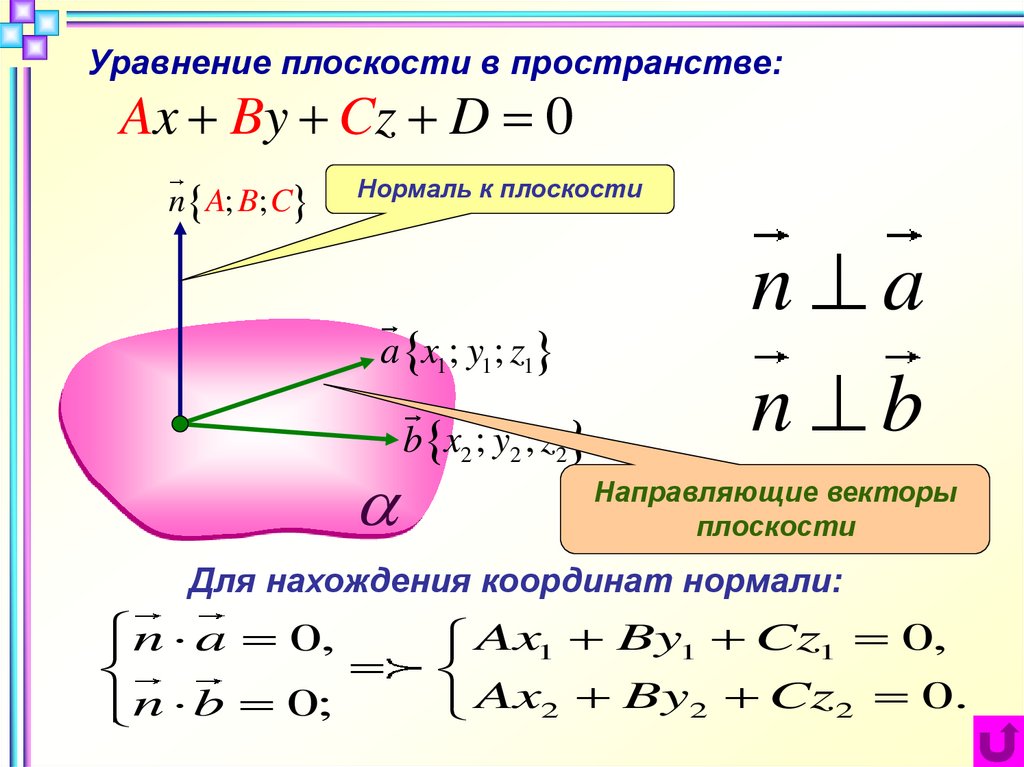
Уравнение плоскости в пространстве:Ax By Cz D 0
n A; B; C
Нормаль к плоскости
a x1; y1; z1
b x2 ; y2 ; z2
n a
n b
Направляющие векторы
плоскости
Для нахождения координат нормали:
n a 0,
n b 0;
Ax1 By1 Cz1 0,
Ax2 By2 Cz2 0.
11.
1 Точка Е – середина ребра ВВ1 куба ABCDA1B1C1D1.Найти угол между прямыми АЕ и СА1.
2
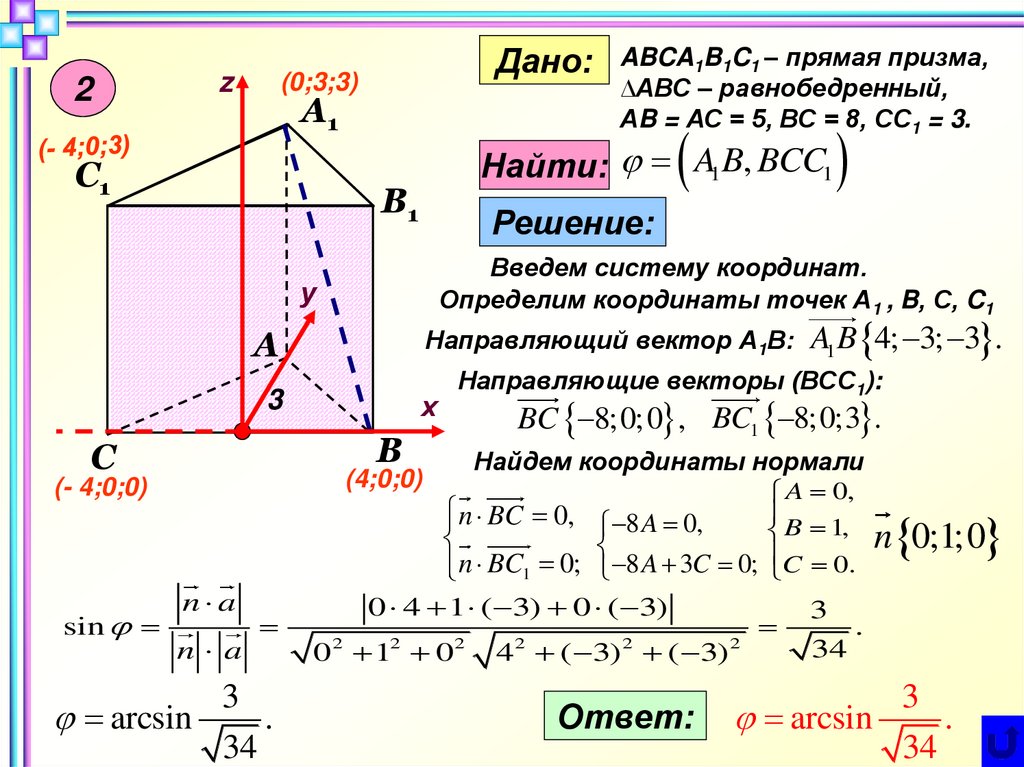
Основанием прямой призмы АВСА1В1С1 является
равнобедренный треугольник АВС. АВ = АС = 5,
ВС = 8. Высота призмы равна 3. Найти угол
между прямой А1В и плоскостью ВСС1.
3
В правильной четырехугольной призме
ABCDA1B1C1D1 стороны основания равны 1, а
боковые ребра равны 5. На ребре АА1 отмечена
точка Е так, что АЕ : ЕА1 = 2 : 3. Найти угол
между плоскостями АВС и ВЕD1.
12.
F1
1
2
C1
Дано: ABCDA1B1C1D1 – куб, BE = EB1.
Найти: AE, CA1
B1
D1
A1
Е
Решение:
Из ∆ ACA1 найдем СА1: CA1 3.
Проведем через А1 прямую А1F ll AE.
C
B
2
D
1
A
AE, CA1 CA1F .
Из ∆ A1B1F (∟B1 = 900) найдем А1F:
A1 F A1 B12 B1 F 2
5
2
Из ∆ CBF (∟B = 900) найдем CF: CF CB 2 BF 2
13
2
CA12 A1 F 2 CF 2
15
cos
:
cos
.
Из ∆ CA1F найдем
2 CA1 A1 F
15
15
15
arccos
.
.
Ответ: arccos
15
15
13.
z1
B1
C1
Е (1;0;1/2)
A1
B
C
x
y
cos
AE CA1
AE CA1
arccos
0 1 1 1
15
.
15
0 1
2
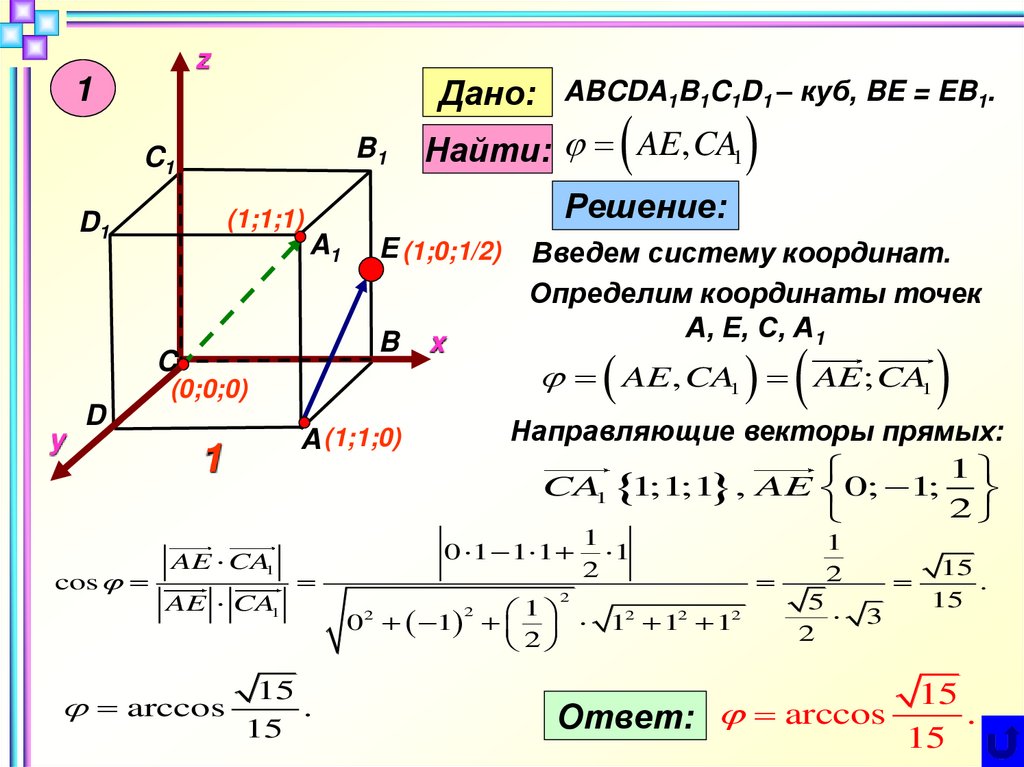
Направляющие векторы прямых:
1
CA1 1;1;1 , AE 0; 1;
2
A (1;1;0)
1
Введем систему координат.
Определим координаты точек
А, Е, С, А1
AE , CA1 AE; CA1
(0;0;0)
D
Решение:
(1;1;1)
D1
Дано: ABCDA1B1C1D1 – куб, BE = EB1.
Найти: AE, CA1
2
2
1
1
2
1
12 12 12
2
1
2
5
2
3
15
.
15
15
.
Ответ: arccos
15
14.
2С1
Дано:
А1
3
М
В1
5
А
С
ABCA1B1C1 – прямая призма,
∆АВС – равнобедренный
АB = АС = 5, ВС = 8, СС1 = 3.
Найти: A1B, BCC1
Решение:
Из ∆A1В1С1 : А1М ┴ ( ВСС1 )
ВМ – проекция А1В на ( ВСС1 )
A1B, BCC1 A1BM .
В
Т.к. В1М = 4, ВВ1 = 3, то ВМ = 5
A1M A1B12 B1M 2 3.
A1M 3
0, 6. arctg 0, 6.
Из ∆А1ВМ: tg
MB 5
Ответ: arctg 0, 6.
15.
z2
Дано:
(0;3;3)
А1
С1
Найти: A1B, BCC1
В1
Введем систему координат.
Определим координаты точек А1 , B, С, C1
А
Направляющий вектор А1В:
3
sin
х
(4;0;0)
n a
n a
arcsin
3
.
34
A1B 4; 3; 3 .
Направляющие векторы (ВСС1):
BC 8;0;0 , BC1 8;0;3 .
В
(- 4;0;0)
Решение:
у
С
ABCA1B1C1 – прямая призма,
∆АВС – равнобедренный,
АB = АС = 5, ВС = 8, СС1 = 3.
Найдем координаты нормали
A 0,
n BC 0, 8 A 0,
B 1,
n BC1 0; 8 A 3C 0;
C 0.
0 4 1 ( 3) 0 ( 3)
02 12 02
42 ( 3) 2 ( 3) 2
Ответ:
n 0;1;0
3
.
34
arcsin
3
.
34
16.
С1D1
3
А1
Е
K А
A1D1E
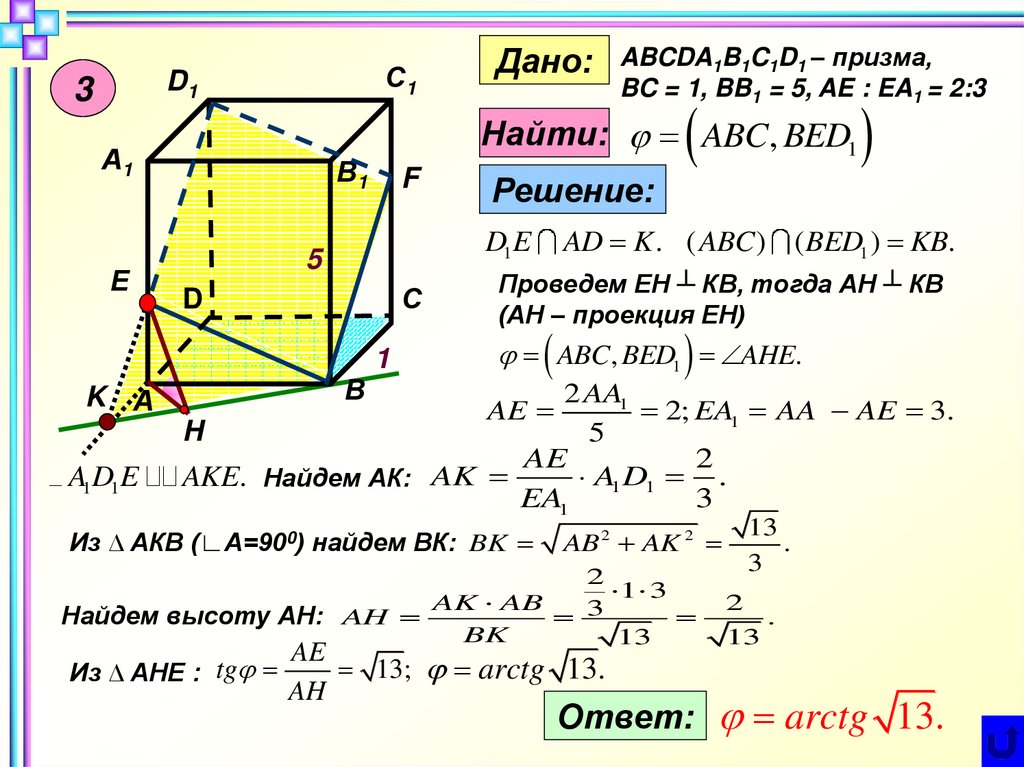
Дано:
Найти: ABC, BED1
В1
F
С
D
1
Решение:
AD K . ( ABC ) ( BED1 ) KB.
D1E
5
В
ABCDA1B1C1D1 – призма,
BC = 1, BB1 = 5, AE : EA1 = 2:3
Проведем ЕН ┴ КВ, тогда АН ┴ КВ
(АН – проекция ЕН)
ABC, BED1 AHE.
2 AA1
2; EA1 AA AE 3.
H
5
AE
2
A1 D1 .
AKE. Найдем АК: AK
EA1
3
AE
Из ∆ АКВ (∟А=900) найдем ВК: BK
AB 2 AK 2
2
1 3
AK AB
3
Найдем высоту АН: AH
BK
13
Из ∆ АНЕ : tg
AE
13; arctg 13.
AH
Ответ:
13
.
3
2
.
13
arctg 13.
17.
D1 (1;1;5)3
z
А1
Е
y
1
Таким образом
cos
n1 n2
Решение:
Введем систему координат.
Определим координаты точек
A, B, С, E, D1
С (1;0;0) Направляющие векторы плоскостей:
В (0;0;0)
A 0,
n1 BA 0, 1
1)
B1 0,
n1 BC 0; C 1.
1
x
D
n1 n2
F
5
А (0;1;0)
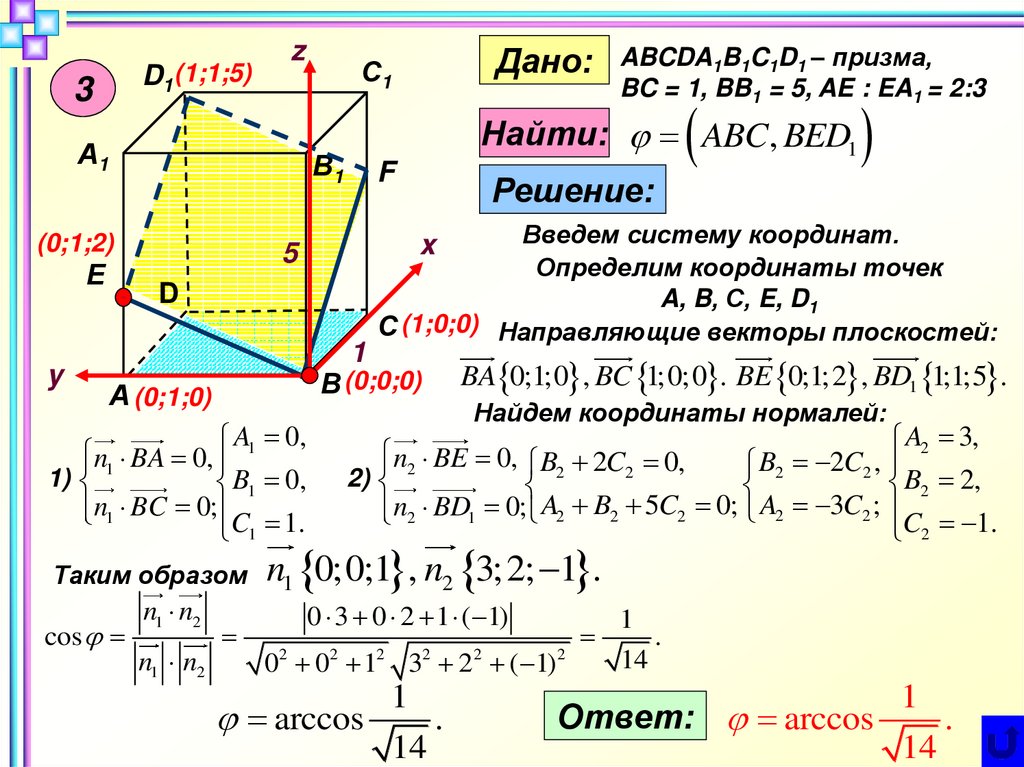
ABCDA1B1C1D1 – призма,
BC = 1, BB1 = 5, AE : EA1 = 2:3
Найти: ABC, BED1
В1
(0;1;2)
Дано:
С1
BA 0;1;0 , BC 1;0;0 . BE 0;1; 2 , BD1 1;1;5 .
Найдем координаты нормалей:
A2 3,
n2 BE 0, B 2C 0,
B2 2C2 ,
2
2
2)
B2 2,
n2 BD1 0; A2 B2 5C2 0; A2 3C2 ; C 1.
2
n1 0;0;1 , n2 3; 2; 1 .
0 3 0 2 1 ( 1)
02 02 12 32 22 ( 1) 2
1
arccos
.
14
1
.
14
Ответ: arccos
1
.
14
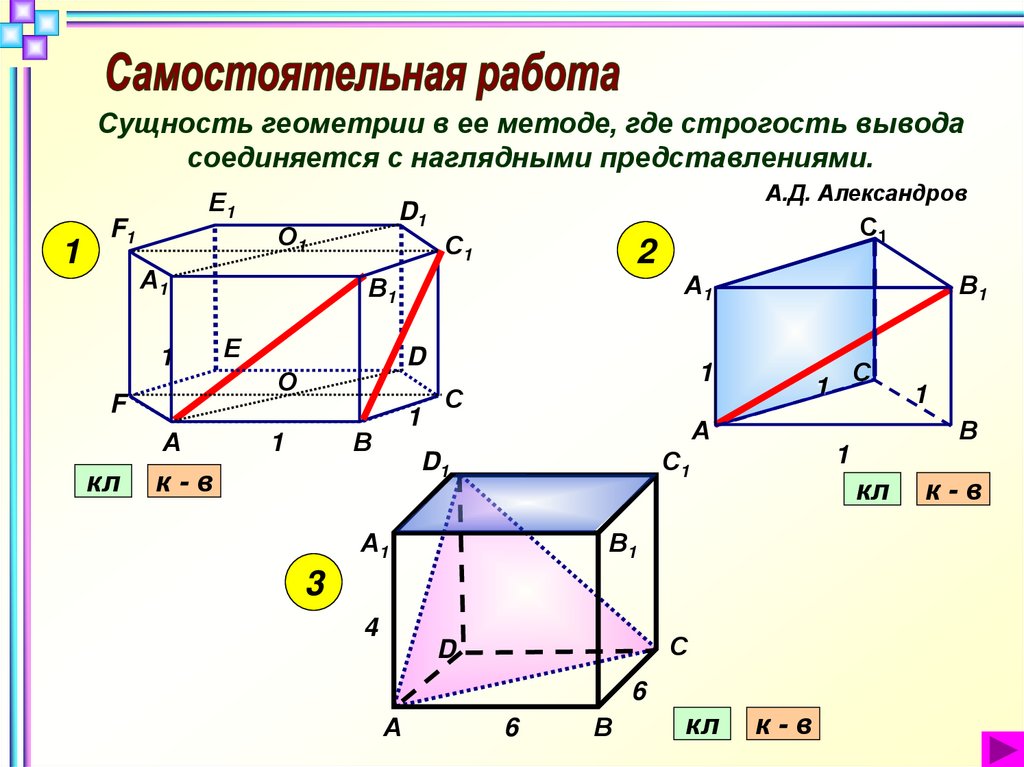
18.
Сущность геометрии в ее методе, где строгость выводасоединяется с наглядными представлениями.
1
Е1
F1
О1
А1
1
F
А
кл
А.Д. Александров
D1
С1
2
А1
В1
Е
С1
D
О
1
В
1
1
С
1
кл
В1
3
С
D
6
А
6
В
кл
1
В
С1
А1
4
С
1
А
D1
к-в
В1
к-в
к-в
19.
1. Точка М – середина стороны ВС основания АВС правильной призмы ABCA1B1C1.Боковое ребро призмы равно 39, а сторона основания равна 12 .Найти угол
между прямой B1M и плоскостью боковой грани ABB1 A1
2. В правильной пирамиде SABC с основанием АВС известны ребра AB 8 3
и SC 17. Найти угол, образованный плоскостью основания и прямой АМ, где
М – точка пересечения медиан грани SBC.
20.
Ответьте на вопросы1) Как определить угол между скрещивающимися
прямыми классическим или координатно-векторным
методом ?
2) Как определить угол между прямой и плоскостью
классическим или координатно-векторным методом ?
3) Как определить угол между двумя плоскостями
классическим или координатно-векторным методом ?
21.
Тренировочные работыЕГЭ 2014 (МИОО)
№ 6, 7,11
Дополнительная задача:
На шаровой поверхности лежат все вершины
треугольника АВС. Точка О – центр шара. Найти
угол между прямой АО и плоскостью треугольника,
если АВ = АС = 10, ВС = 12, АО = 12,5.
22.
ПритчаЧто ты делал целый день?
Первый с ухмылкой ответил, что
целый день возил проклятые камни.
Второй ответил, что
добросовестно выполнял свою работу.
Третий ответил, что
принимал участие в строительстве храма.














 mathematics
mathematics