Similar presentations:
Решение простейших тригонометрических неравенств
1.
МатематикаРешение простейших
тригонометрических
неравенств
2.
Тригонометрическиенеравенства
Решим неравенство:
1
sin x
2
3.
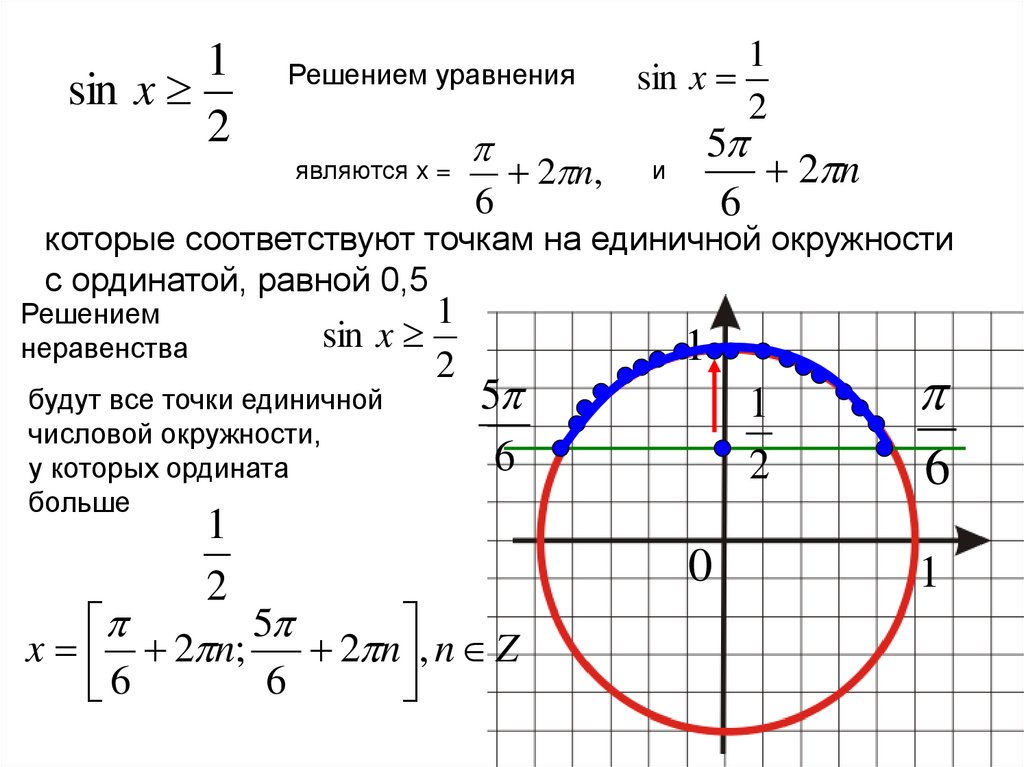
1sin x
2
Решением уравнения
являются x =
6
2 n,
1
sin x
2
5
2 n
6
и
которые соответствуют точкам на единичной окружности
с ординатой, равной 0,5
1
sin x
2
Решением
неравенства
будут все точки единичной
числовой окружности,
у которых ордината
больше
5
6
1
2
5
x 2 n;
2 n , n Z
6
6
1
1
2
0
6
1
4.
1sin x
2
6
5
6
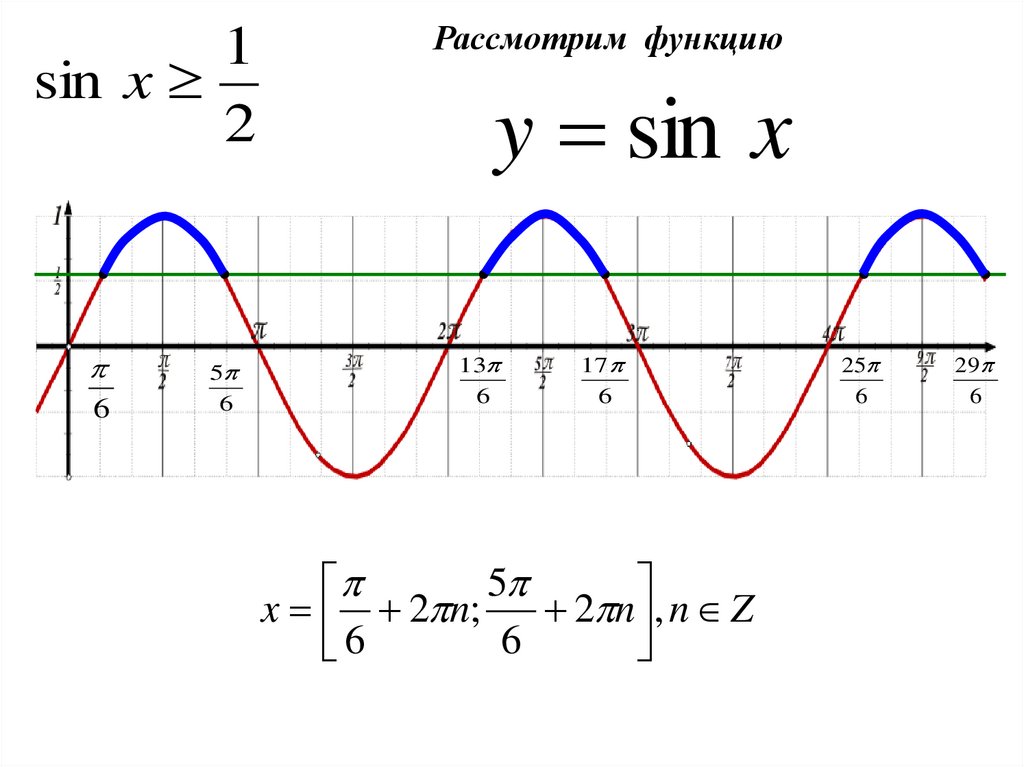
Рассмотрим функцию
y sin x
13
6
17
6
5
x 2 n;
2 n , n Z
6
6
25
6
29
6
5.
Рассмотрим неравенство :1
sin x
2
6.
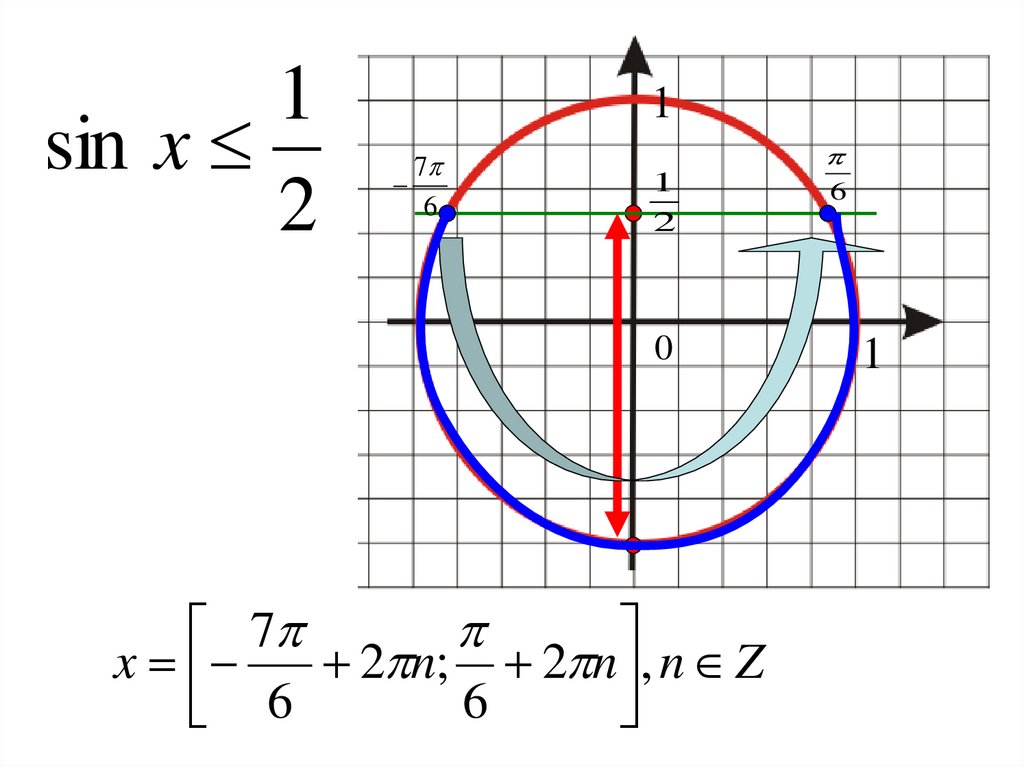
1sin x
2
1
7
6
1
2
0
7
x
2 n; 2 n , n Z
6
6
6
1
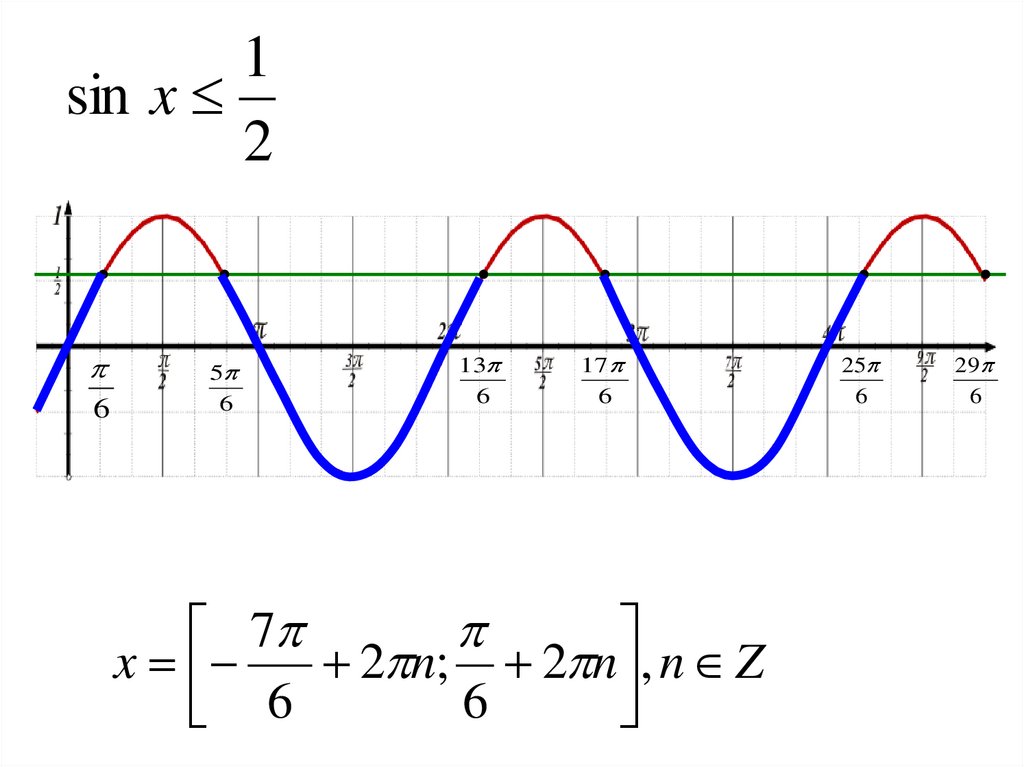
7.
1sin x
2
6
5
6
13
6
17
6
7
x
2 n; 2 n , n Z
6
6
25
6
29
6
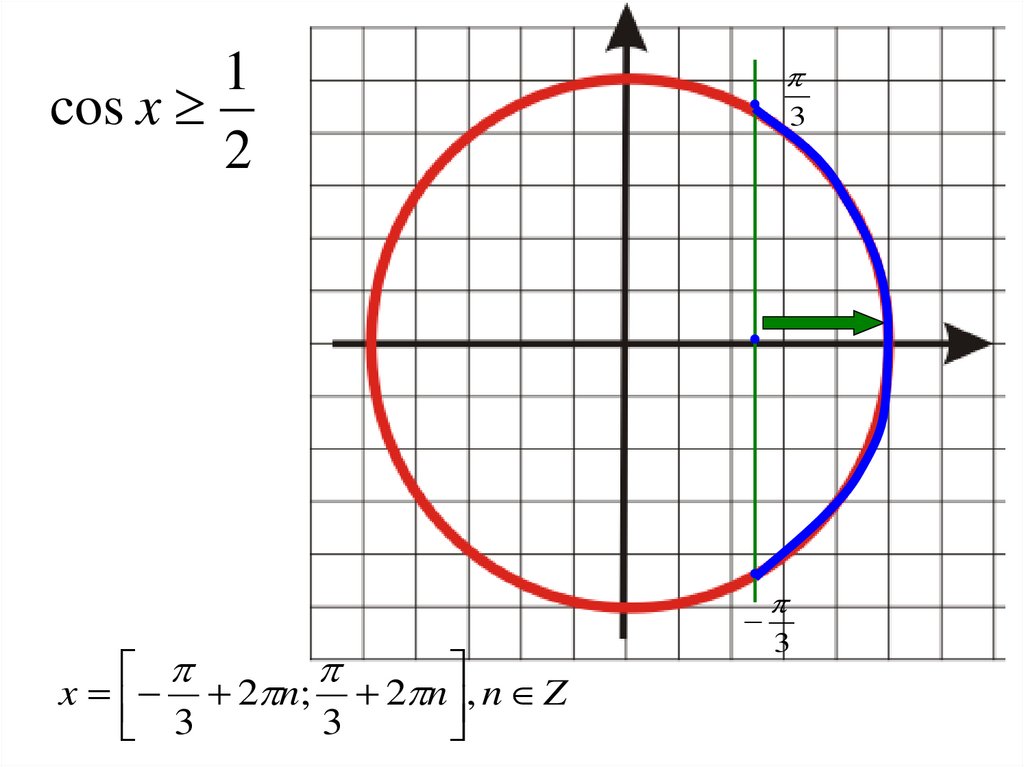
8.
1cos x
2
3
x 2 n; 2 n , n Z
3
3
3
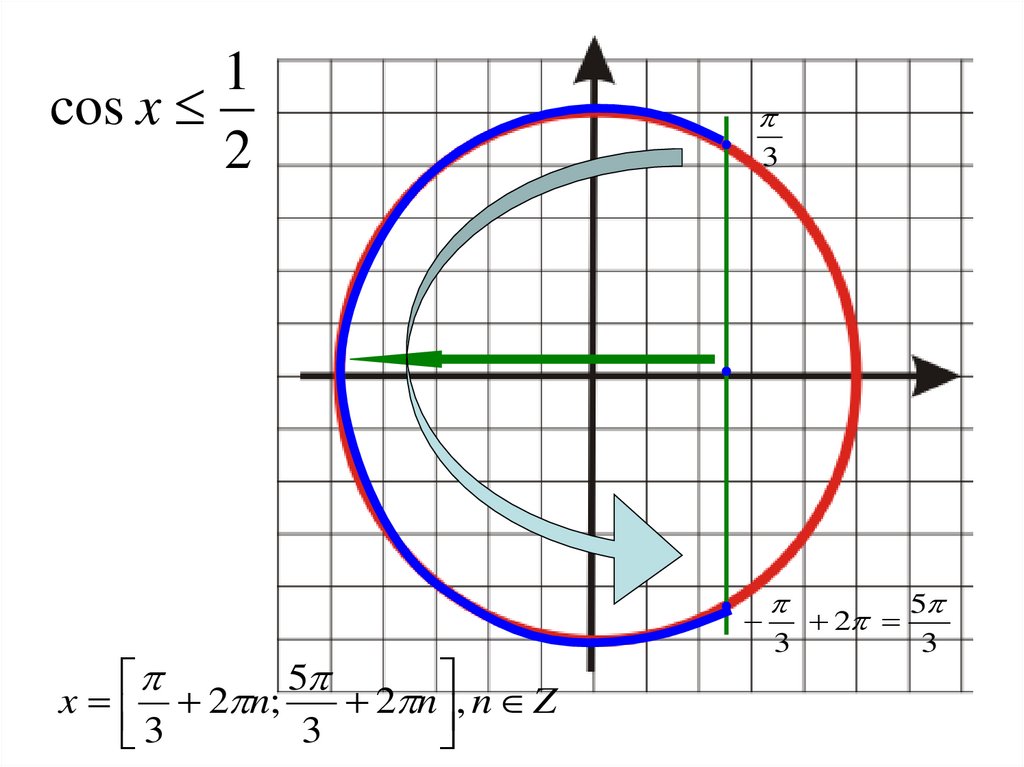
9.
1cos x
2
3
5
x 2 n;
2 n , n Z
3
3
3
2
5
3
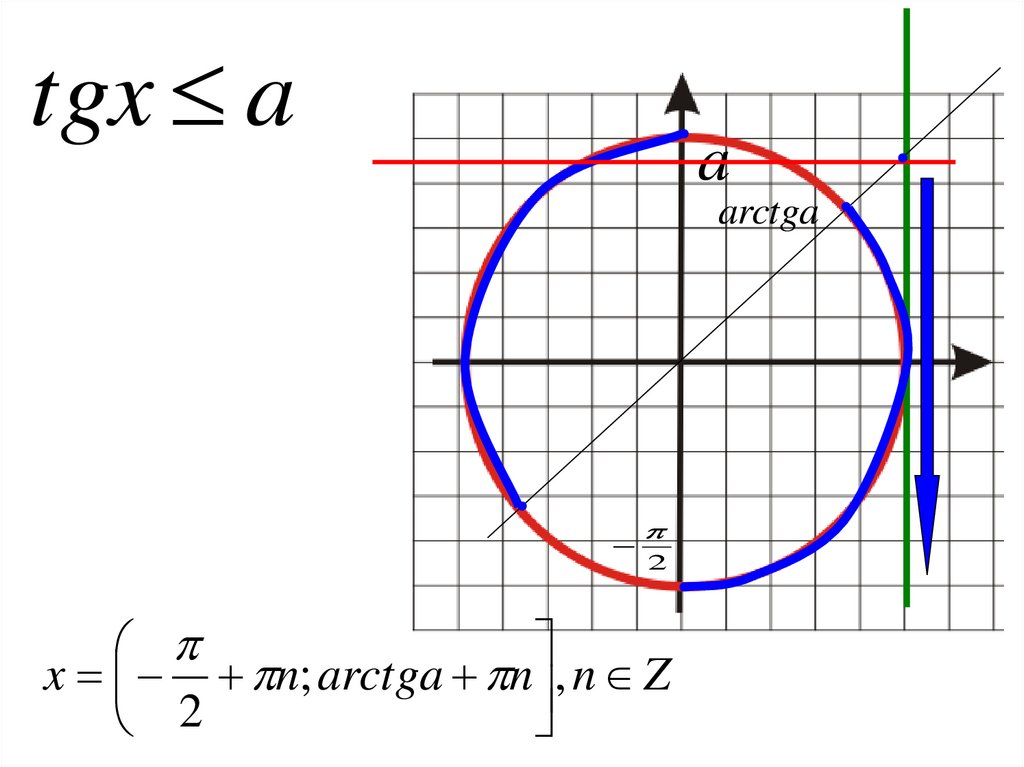
10.
tgx aa
arctga
2
x n; arctga n , n Z
2


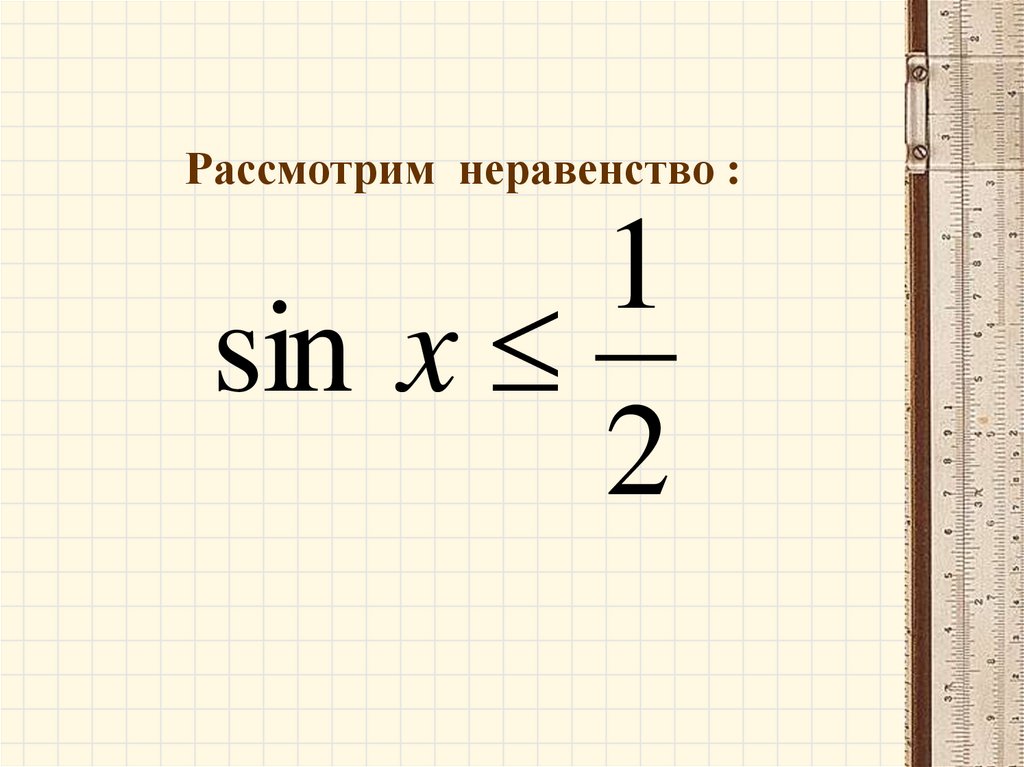
 mathematics
mathematics








