Занятие №9 "Сдвиг (срез) и смятие. Кручение"

1.

1
20.02.02
ОП.02 Техническая механика
Тема 1.4. «Сдвиг (срез), смятие и
кручение»
Разработал: Трунов А.И. ГПОУ
ЯО Переславский колледж им.
А. Невского
08.11.2020

2.

2
Разработал: Трунов А.И. ГПОУ
ЯО Переславский колледж им.
А. Невского
08.11.2020
1. Сформировать знание методики
выполнения основных расчетов на сдвиг
(срез), смятие и кручение.
2. Сформировать умение производить расчеты
деталей на прочность при сдвиге (срезе),
смятии и кручении.

3.

3
Разработал: Трунов А.И. ГПОУ
ЯО Переславский колледж им.
А. Невского
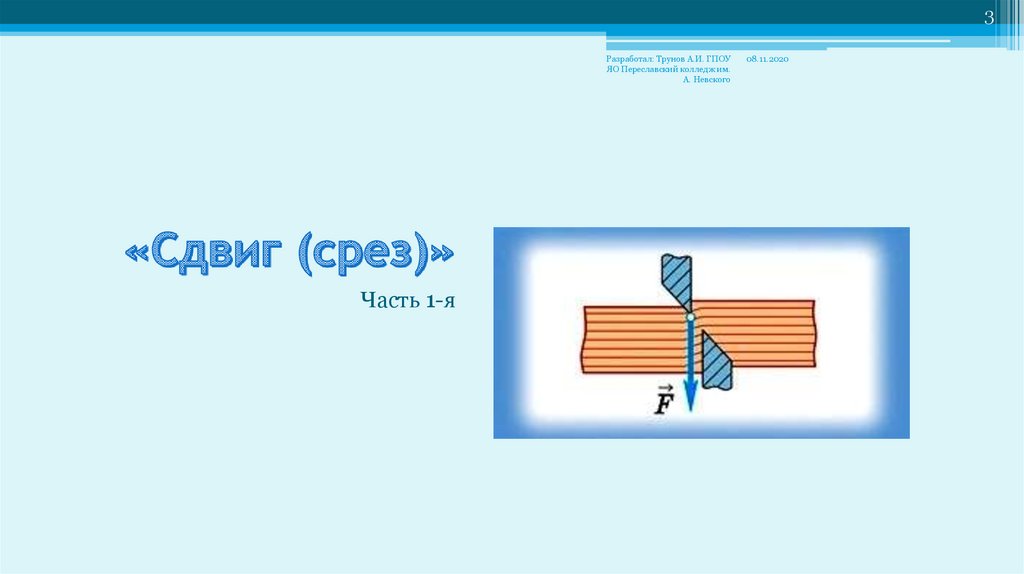
Часть 1-я
08.11.2020

4.

4
Разработал: Трунов А.И. ГПОУ
ЯО Переславский колледж им.
А. Невского
называется такой
вид деформации,
при которой в
любом поперечном
сечении бруса
возникает только
поперечная сила Q
08.11.2020
Q

5.

5
Разработал: Трунов А.И. ГПОУ
ЯО Переславский колледж им.
А. Невского
08.11.2020
деформация сдвига, доведенная до разрушения
материала (применительно к металлическим
деталям),
или скалыванием (применительно к
неметаллическим конструкциям).

6.

6
Разработал: Трунов А.И. ГПОУ
ЯО Переславский колледж им.
А. Невского
можно наблюдать,
например, при резке
ножницами металлических
полос или прутков.
08.11.2020

7.

7
Разработал: Трунов А.И. ГПОУ
ЯО Переславский колледж им.
А. Невского
08.11.2020
и других отраслях деформацию сдвига (среза)
испытывают заклепки, болты, оси и другие детали

8.

8
Разработал: Трунов А.И. ГПОУ
ЯО Переславский колледж им.
А. Невского
08.11.2020
площадью поперечного
сечения А,
перпендикулярно оси
которого приложены
две равные и
противоположно
направленные силы F;
Для определения поперечной силы Q
применим метод сечений

9.

9
Разработал: Трунов А.И. ГПОУ
ЯО Переславский колледж им.
А. Невского
08.11.2020
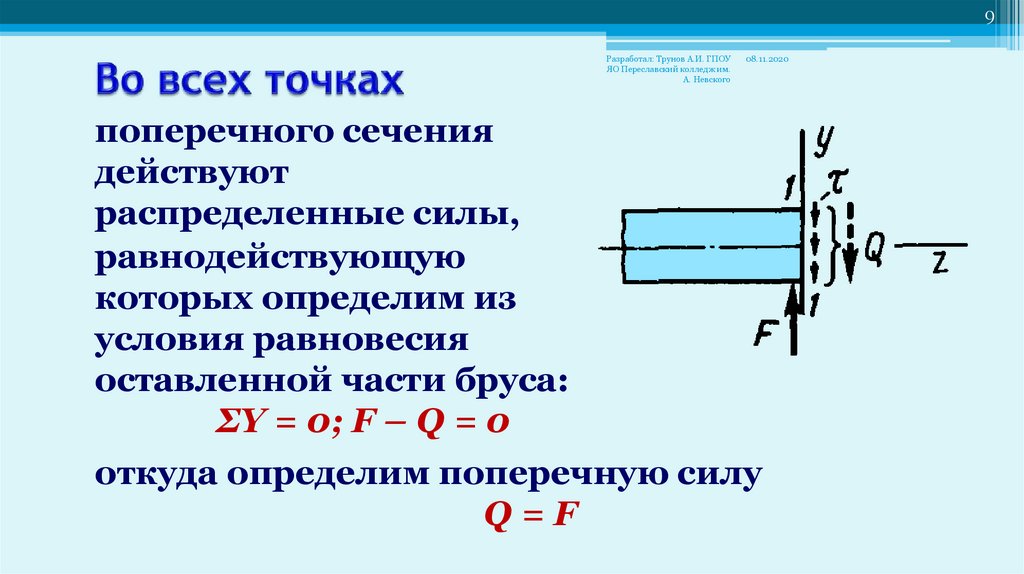
поперечного сечения
действуют
распределенные силы,
равнодействующую
которых определим из
условия равновесия
оставленной части бруса:
ΣY = 0; F – Q = 0
откуда определим поперечную силу
Q=F

10.

10
Разработал: Трунов А.И. ГПОУ
ЯО Переславский колледж им.
А. Невского
08.11.2020
есть равнодействующая внутренних
касательных сил в поперечном сечении при
сдвиге.
При сдвиге в поперечном сечении бруса
действуют только касательные напряжения τ
Предполагаем, что эти напряжения
распределены по сечению равномерно и,
следовательно, их можно вычислить по
формуле
τ = Q/A

11.

11
Разработал: Трунов А.И. ГПОУ
ЯО Переславский колледж им.
А. Невского
08.11.2020
касательных напряжений при сдвиге
приближенный, так как линии действия сил F
и Q не направлены по одной прямой и, строго
говоря, эти силы не являются уравновешенной
системой, а представляют собой пару сил.
Однако момент этой пары (ввиду малого
плеча) невелик и соответствующими ей
напряжениями можно пренебречь.

12.

12
Разработал: Трунов А.И. ГПОУ
ЯО Переславский колледж им.
А. Невского
08.11.2020
детали конструкции заключается в том, что
наибольшее возникающее в ней напряжение
(рабочее напряжение) не должно превышать
допускаемое
Расчетная формула при сдвиге
τ = Q/A [τ]
читается следующим образом: касательное
По этой расчетной формуле проводят
напряжение при сдвиге, вычисленное по
проектный и проверочный расчеты и
формуле τ = Q/А, не должно превышать
определяют допускаемую нагрузку.
допускаемое.

13.

13
Разработал: Трунов А.И. ГПОУ
ЯО Переславский колледж им.
А. Невского
08.11.2020
напряжение на срез выбирают для пластичных
материалов в зависимости от предела
текучести.
В машиностроении для штифтов, болтов,
шпонок и т. п. принимают
[τср] = (0,25...0,35) т.
Расчеты
При
расчетах
соединений
на срез на
в случае,
срез обычно
если соединение
сопровождают
осуществляется
проверкой
прочности
несколькими
этих соединений
одинаковыми
на смятие.
деталями (болтами, заклепками и т. д.), полагают,
что все они нагружены одинаково.

14.

14
Разработал: Трунов А.И. ГПОУ
ЯО Переславский колледж им.
А. Невского
параметров, характеризующих
деформацию при сдвиге,
рассмотрим элемент бруса в
виде параллелепипеда аbсd,
на грани которого действуют
только касательные
напряжения τ, а
противоположную грань
параллелепипеда представим
жестко защемленной.
08.11.2020

15.

15
Разработал: Трунов А.И. ГПОУ
ЯО Переславский колледж им.
А. Невского
08.11.2020
в указанном элементе
заключается в перекашивании
прямых углов параллелепипеда за
счет поступательного
перемещения грани bс по
отношению к сечению,
принятому за неподвижное.
Деформация сдвига характеризуется углом γ и
называется углом сдвига или относительным
сдвигом

16.

16
Разработал: Трунов А.И. ГПОУ
ЯО Переславский колледж им.
А. Невского
08.11.2020
на которую смещается подвижная
грань относительно неподвижной,
называется абсолютным сдвигом.
Относительный сдвиг γ выражается
в радианах.
Напряжения и деформации при
сдвиге связаны между собой
зависимостью, которая называется
законом Гука при сдвиге.

17.

17
Разработал: Трунов А.И. ГПОУ
ЯО Переславский колледж им.
А. Невского
08.11.2020
при сдвиге справедлив лишь в определенных
пределах нагружения и формулируется так:
касательное напряжение прямо
пропорционально относительному сдвигу.
Математически закон Гука можно
записать в виде равенств
τ = Gγ

18.

18
Разработал: Трунов А.И. ГПОУ
ЯО Переславский колледж им.
А. Невского
08.11.2020
пропорциональности G характеризует
жесткость материала (т. е. способность
сопротивляться упругим деформациям) при
сдвиге и называется модулем сдвига или
модулем упругости второго рода.
Модуль упругости и напряжение выражаются
в одинаковых единицах:
[G] = [τ] / [γ] = Па.

19.

19
Разработал: Трунов А.И. ГПОУ
ЯО Переславский колледж им.
А. Невского
08.11.2020
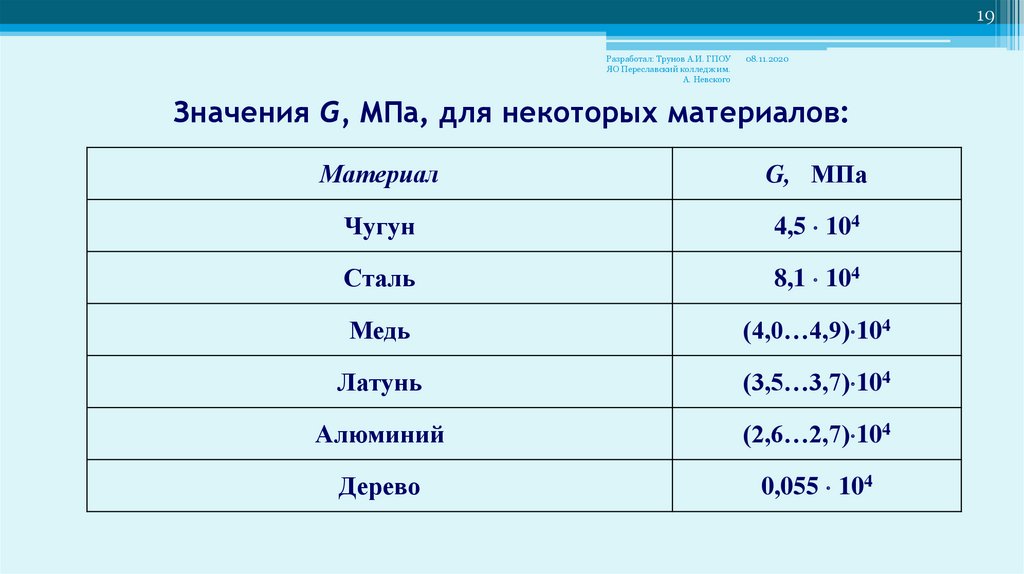
Значения G, МПа, для некоторых материалов:
Материал
G, МПа
Чугун
4,5 104
Сталь
8,1 104
Медь
(4,0…4,9) 104
Латунь
(3,5…3,7) 104
Алюминий
(2,6…2,7) 104
Дерево
0,055 104

20.

20
Разработал: Трунов А.И. ГПОУ
ЯО Переславский колледж им.
А. Невского
08.11.2020
тремя упругими постоянными Е, G и
существует следующая зависимость:
G = E/[2(1 + )]
Принимая для сталей 0,25, получим
Gст 0,4Ест

21.

21
Разработал: Трунов А.И. ГПОУ
ЯО Переславский колледж им.
А. Невского
08.11.2020
Эрдеди А.А. Теоретическая
механика. Сопротивление
материалов. §19.9. стр. 190

22.

22
Разработал: Трунов А.И. ГПОУ
ЯО Переславский колледж им.
А. Невского
Часть 2-я
08.11.2020

23.

23
Разработал: Трунов А.И. ГПОУ
ЯО Переславский колледж им.
А. Невского
08.11.2020
это деформация поверхностей деталей,
возникающая при значительной
внешней сжимающей нагрузке,
приложенной к небольшой площади
контакта.
Для предотвращения
смятия, например, под
гайки и головки болтов
подкладывают шайбы

24.

24
Разработал: Трунов А.И. ГПОУ
ЯО Переславский колледж им.
А. Невского
08.11.2020
полагают, что при контакте по плоскости
возникают нормальные напряжения смятия,
равномерно распределенные по площади
контакта.
Расчетное уравнение на смятие имеет вид
см = F/Асм [ см],
где F — сжимающая сила;
[ см] — допускаемое напряжение на смятие;
Асм — площадь контакта.

25.

25
Разработал: Трунов А.И. ГПОУ
ЯО Переславский колледж им.
А. Невского
08.11.2020
по
цилиндрической
Поэтому
при расчете на
смятие
цилиндрических
поверхности
(например,
отверстий
в расчетную
заклепочное
соединение)
формулу
подставляют не
закон распределения
площадь боковой
напряжений
смятия по
поверхности полуцилиндра, а
поверхности
контакта
значительно меньшую
сложен
условную площадь смятия
Тогда Асм = dδ
где d — диаметр отверстия; δ — толщина соединяемой
детали (высота цилиндра).

26.

26
Разработал: Трунов А.И. ГПОУ
ЯО Переславский колледж им.
А. Невского
08.11.2020
соединяемых деталей в расчетную формулу
подставляют меньшую толщину.
В машиностроении допускаемые напряжения на
смятие для болтовых, штифтовых и шпоночных
соединений из низкоуглеродистой стали принимают в
пределах [ см] = 100... 120 МПа,
для клепаных соединений [ см] = 240...320 МПа,
для древесины (сосна, дуб) [ см] = 2,4... И МПа в
зависимости от сорта древесины и направления
сжимающей силы по отношению к направлению
волокон.

27.

27
Разработал: Трунов А.И. ГПОУ
ЯО Переславский колледж им.
А. Невского
Эрдеди А.А. Теоретическая
механика. Сопротивление
материалов. §19.9. стр. 190
08.11.2020