Similar presentations:
Кригинг
1.
КригингПринципы
Кригинг - это интерполяционный метод, базирующийся на основных
статистических свойствах данных (Среднее значение и Дисперсия).
Предположение :
Стационарность
– Среднее значение не должно меняться по
латерали
– Отсутствие трендов
Входные данные:
Набор значений
Вариограмма и функция распределения
Использование и ограничения:
Поиск тренда и визуализация трендов
Сглаженный и точный результат
Плохо работает с экстремально высокими значениями
2.
КригингОценка
Пример:
На 2D поверхности или 3D гриде известная значения (например,
пористость) – это скважины. Все другие ячейки грида должны
быть рассчитаны:
n
z ( x0 ) i z ( xi )
i
Неизвестные значения z(x0) вычисляется как взвешенная сумма
известных значений
Коэффициенты взвешивания λi вычисляются по модели
вариограммы (неверно – как решения нормальной системы, в которой коэфициенты
“вычисляются по модели вариограммы”)
Известные значения z(xi),например, скважинные данные
3. Кригинг Взвешенная линейная оценка (Всё – бррр!)
Кригинг использует взвешенную линейную оценку; т.е. сочетаетизвестные значения, чтобы рассчитать неизвестные значения Z
в точке Xo
Влияние ранга вариограммы на весы веса
n
X0 ?
z ( x0 ) i z ( xi )
i
Направление наибольшей непрерывности
Данные с известными значениями, Z(Xi)
Точка, в которой нужно найти значение, Z(X0)
Фактор взвешивания, взятый из
вариограммы: (опять неверно!)
• Как близко к точке?
• Преимущественное направление
(анизотропия)
Z (Xo) неизвестно, но мы можем посчитать дисперсию ошибки, так как мы знаем
статистические параметры: среднее, дисперсию и вариограмму
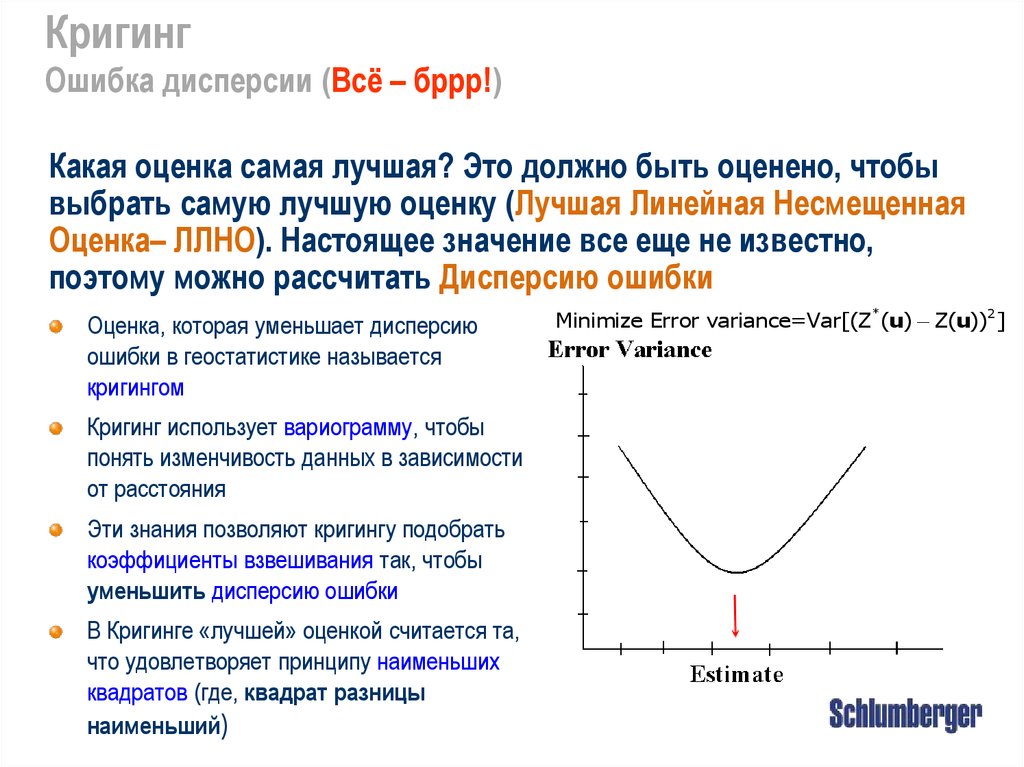
4. Кригинг Ошибка дисперсии (Всё – бррр!)
Какая оценка самая лучшая? Это должно быть оценено, чтобывыбрать самую лучшую оценку (Лучшая Линейная Несмещенная
Оценка– ЛЛНО). Настоящее значение все еще не известно,
поэтому можно рассчитать Дисперсию ошибки
Оценка, которая уменьшает дисперсию
ошибки в геостатистике называется
кригингом
Кригинг использует вариограмму, чтобы
понять изменчивость данных в зависимости
от расстояния
Эти знания позволяют кригингу подобрать
коэффициенты взвешивания так, чтобы
уменьшить дисперсию ошибки
В Кригинге «лучшей» оценкой считается та,
что удовлетворяет принципу наименьших
квадратов (где, квадрат разницы
наименьший)
Minimize Error variance=Var[(Z* (u) Z(u))2 ]
5.
KригингTипы (Всё – бррр!)
Простой кригинг (Simple) – среднее значение известно
n
n
i
i
z ( x0 ) i z ( xi ) [1 i ]m
Сумма весовых коэффициентов i может быть меньше, чем 1
Чем меньше весовые коэффициенты, тем большее влияние математического
ожидания m на вычисленное значение Z в точке x0
Глобальное среднее используется кригинг алгоритмом для расчета весовых
коэффициентов. И среднее значение предполагается известным
По умолчанию в Petrel используется этот кригинг алгоритм
6.
KригингTипы
Обычный кригинг (Ordinary) – локальная оценка среднего
n
z ( x 0 ) i z ( x i )
i
Сумма весовых параметров
i
ВСЕГДА равна 1
Значение локального математического ожидания используется в кригинг
алгоритме при расчете весовых параметров. Среднее предполагается равное
константе, но неизвестно
7.
КригингОт модели вариограммы до конечной оценки– 1
Алгоритм кригинга основан на взаимосвязи параметров
вариограммы и локально близлежащих данных.
Простой пример пояснения кригинга
Расстояние в проектных единицах (m,ft)
Spherical Variogram (Sill=1; Range=60m)
X2 (0.22)
В скобках значение свойства
1,20
1,00
60
X0 (?)
40
X1 (0.25)
Gamma
30
42
0,80
0,60
0,40
0,20
0,00
20
0
20
60
80
100
Distance
55
X3 (0.30)
Сферическая
40
3 h 1 h 3
h c0 c1 * *
2 a 2 a
модель вариограммы
(From Akin/Siemes: Praktische Geostatistik p. 120ff)
c0 = Наггет эффект
c1 = Порог
h = Расстояние
a = Ранг
8.
КригингОт модели вариограммы до конечной оценки– 2
Линейная система уравнений должна быть решена, чтобы найти
значение в точке xo.
Матрица со значениями дисперсии между соседними данными и
данными в точках расчета задана с помощью весов Кригинга
n
Линейная система уравнений для решения:
( x11 ) ( x12 )
( x ) ( x )
22
21
...
...
( xn1 ) ( xn 2 )
1
1
... ( x1n ) 1 1 ( x10 )
... ( x2 n ) 1 2 ( x20 )
...
...
... * ... ...
... ( xnn ) 1 n ( xn 0 )
1
1
0 1
z ( x 0 ) i z ( x i )
i
Неизвестные
коэффициеты
весов
60
2 0.291 3 0.524
0.0425
Z(xo) = 0.185 * 0.25 + 0.291 * 0.22 + 0.524 * 0.30 = 0.267
30
X0 (?)
40
X1
(0.25)
1 0.185
X2
(0.22)
42
20
55
X3
(0.30)
9.
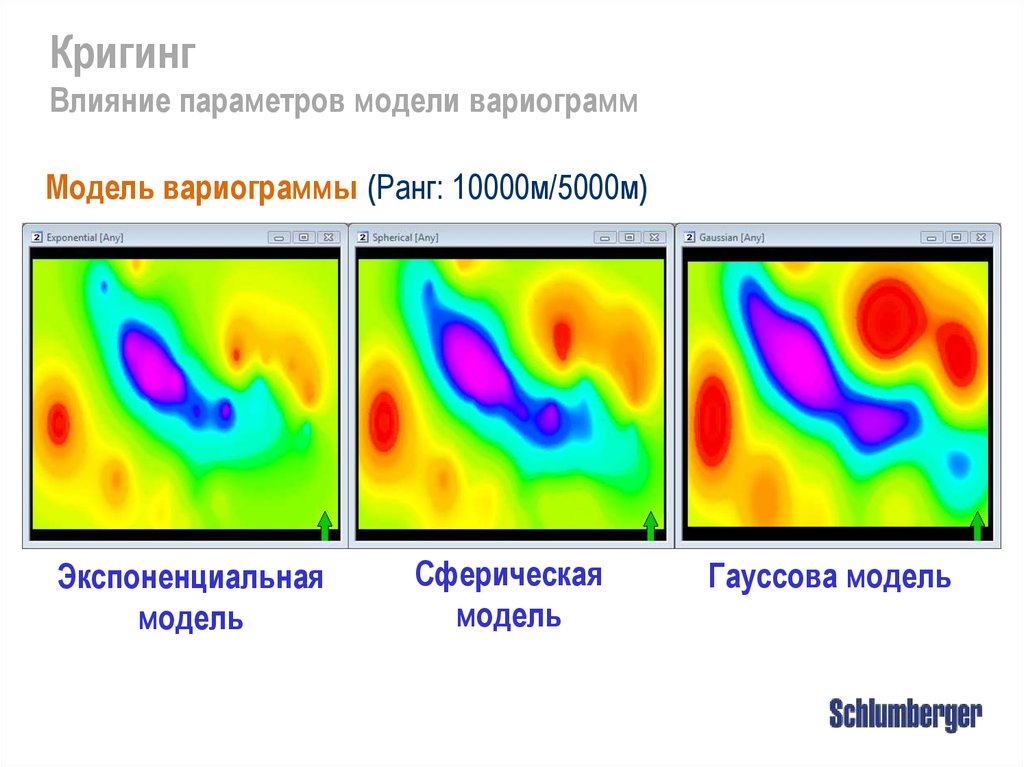
КригингВлияние параметров модели вариограмм
Модель вариограммы (Ранг: 10000м/5000м)
Экспоненциальная
модель
Сферическая
модель
Гауссова модель
10.
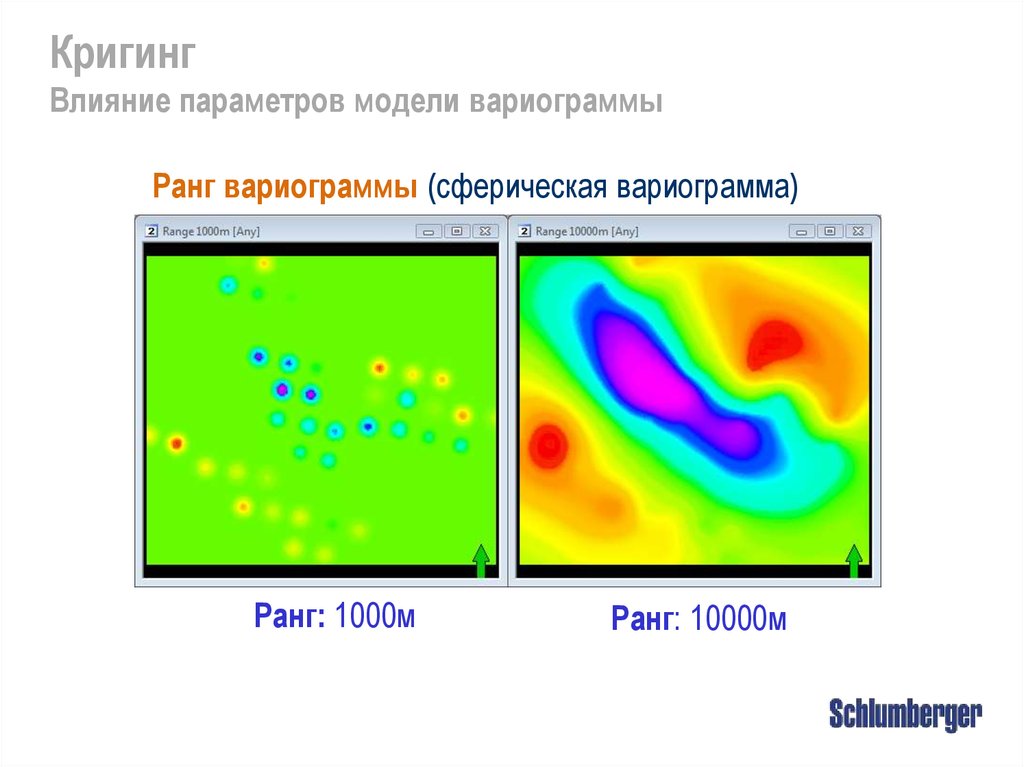
КригингВлияние параметров модели вариограммы
Ранг вариограммы (сферическая вариограмма)
Ранг: 1000м
Ранг: 10000м
11.
КригингВлияние параметров модели ваиограммы
Азимут (сферическая вариограмма)
Плохо
Хорошо
Анизотропия: +45 градусов
Анизотропия : -45 градусов
Ранг: 10000м / 5000м
Ранг: 10000м / 5000м
12.
КригингВлияние параметров модели ваиограммы
Наггет (сферическая вариограмма)
Анизотропия: -45 градусов
Анизотропия: -45 градусов
Ранг : 10000m / 5000m
Ранг : 10000m / 5000m
Наггет: 0.99
Наггет : 0.1
13.
КригингАлгоритмы кригинга, доступные в Petrel
Интерполяционный кригинг
Использует данные только внутри ранга вариограммы.
Кригинг Gsilb
Есть Collocated co-kriging и экспертные настройки,
но производительность ниже, чем у кригинга.
Кригинг
Работает с большим количеством данных, комбинируя многопоточность
и алгоритмы умного поиска. Включает параллелизацию, быстрый
алгоритм Collocated co-kriging и экспертные настройки.
Предпочтителен











 mathematics
mathematics








