Строение вещества. Второй закон термодинамики

1.

СТРОЕНИЕ ВЕЩЕСТВА.
Второй закон термодинамики
1. Смысл и значение 2-го закона термодинамики
2. Неравновесные и равновесные (квазистатические) процессы
3. Идеальная тепловая машина Карно.
Цикл Карно–Клапейрона. Теорема Карно–Клаузиуса
4. 2-ой закон термодинамики как закон возрастания энтропии S
5. Расчёт ΔS в некоторых физико-химических процессах
6. Статистический характер 2-го закона термодинамики
1

2.

СТРОЕНИЕ ВЕЩЕСТВА.
Второй закон термодинамики
Энергия Вселенной постоянна, энтропия
Вселенной непрерывно возрастает до
максимума
(Die Energie der Welt ist Konstant;
die Entropia der Welt strebt einen Maximum zu)
Р. Клаузиус.
О различных удобных для применения формах основных
уравнений механической теории теплоты
(Über verschiedene, für die Anwendung bequeme Formen der
Hauptgleichungen der mechanischen Wärmetheorie), 1865
Рудольф Юлиус Эмануэль
Готтлиб (Клаузиус)
(1822–1888), 1888
2

3.

СТРОЕНИЕ ВЕЩЕСТВА.
1. Смысл и значение 2-го закона термодинамики
Самопроизвольные процессы – это процессы, протекающие без вмешательства со стороны окружающей
среды и сопровождающиеся уменьшением внутренней энергии системы и передачей энергии в окружающую
среду в форме работы и/или теплоты. Такие процессы завершаются равновесным состоянием, из которого
сама система без сообщения ей энергии извне выйти уже не сможет.
Равновесное состояние – это такое термодинамическое состояние системы, когда при постоянных внешних
условиях параметры системы(Р, V, Т, состав и т. д.) не изменяются во времени.
Несамопроизвольные процессы – это процессы, которые не могут совершаться без передачи энергии из
окружающей среды в виде работы и/или теплоты. В изолированной системе такие процессы протекать не
могут ввиду отсутствия внешнего воздействия.
Примеры самопроизвольных и несамопроизвольных процессов
Самопроизвольный процесс
Расширение газа
и заполнение им свободного объёма
Несамопроизвольный процесс
Сжатие газа до меньшего объёма
Переход теплоты от горячего тела к холодному
Диффузия вещества из области большей
концентрации в область меньшей концентрации
Любая реакция, используемая в работающем
гальваническом элементе
(например, в свинцовом аккумуляторе)
Переход теплоты от холодного тела к горячему
(осуществляется в холодильных машинах)
Диффузия вещества из области меньшей
концентрации в область большей концентрации
Зарядка аккумулятора
от внешнего источника тока
Pb 0 Pb 4 O 2 2H 2 SO 4 2Pb 2 SO 4 2H 2 O
Электролитическое разложение воды
на водород и кислород
Сгорание водорода с образованием воды
1
2H 2 O 2 2H 2 O 2
0
0
3

4.

СТРОЕНИЕ ВЕЩЕСТВА.
1. Смысл и значение 2-го закона термодинамики.
Частные формулировки 2-го закона
Михаил Васильевич
Ломоносов
(1711–1765), 1757
(М.В. Ломоносов, 1747)
Рудольф Юлиус Эмануэль
Готтлиб (Клаузиус )
(1822–1888), 1850
Теплота не может переходить сама собой от более холодного тела
к более горячему без каких-либо изменений в системе или
окружающей среде.
(Р. Клаузиус, 1850)
Уильям Томсон
лорд Кельвин
(1824–1907), 1900
Никакая совокупность процессов не может сводиться только к
превращению теплоты в работу, тогда как превращение работы в
теплоту может быть единственным результатом процесса.
(У. Кельвин, 1851)
Людвиг Эдуард Больцман
(1844–1906), 1902
Каждая система, будучи предоставлена сама себе, в среднем
меняется в сторону состояния с наибольшей вероятностью.
(Л. Больцман, 1872)
Вильгельм Фридрих
Оствальд
(1853–1932), 1913
Холодное тело В, погружённое в тёплое тело А, не может
воспринять большую степень теплоты, чем А.
Невозможно создание вечного двигателя второго рода, т. е. такого
двигателя, который производил бы работу только за счёт
поглощения теплоты из окружающей среды без передачи части
теплоты холодильнику.
(В. Оствальд, 1888)
4

5.

СТРОЕНИЕ ВЕЩЕСТВА.
2. Неравновесные и равновесные (квазистатические) процессы
Константин Каратеодори
(1873–1950), ~1910
Неравновесные процессы – термодинамические процессы, включающие неравновесные состояния.
Необратимые процессы – термодинамические процессы, после проведения которых систему и
окружающую среду нельзя одновременно вернуть в прежнее состояние. Если систему можно вернуть к
первоначальному состоянию, в окружающей среде останутся некоторые изменения, «следы»
необратимого процесса (например, изменится энергия).
Равновесные процессы – термодинамические процессы, которые протекают бесконечно медленно и через
непрерывный ряд состояний, бесконечно близких к равновесным состояниям. Равновесные процессы также
называют квазистатическими (от лат. quasi – как будто и греч. statikh – равновесие). Термин был
предложен К. Каратеодори (1909).
Обратимые процессы – термодинамические процессы, после которых можно вернуть и систему, и
окружающую среду в прежнее состояние через ту же последовательность промежуточных состояний,
проходимых в обратном порядке, без каких-либо изменений в системе и окружающей среде.
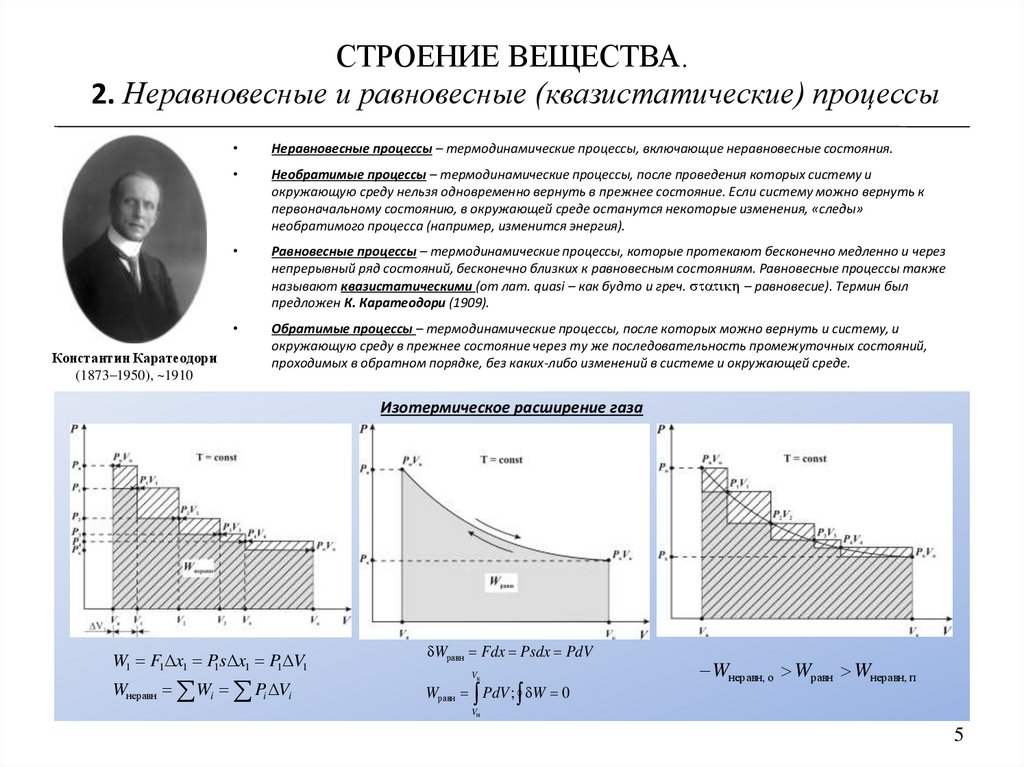
Изотермическое расширение газа
W1 F1Δx1 P1sΔx1 P1ΔV1
Wнеравн Wi Pi ΔVi
Wравн Fdx Psdx PdV
Vк
Wравн PdV ; W 0
Wнеравн, о Wравн Wнеравн, п
Vн
5

6.

СТРОЕНИЕ ВЕЩЕСТВА.
3. Идеальная тепловая машина Карно. Цикл Карно–Клапейрона.
Теорема Карно–Клаузиуса
Николя Леонар
Сади Карно
(1796–1832), 1813
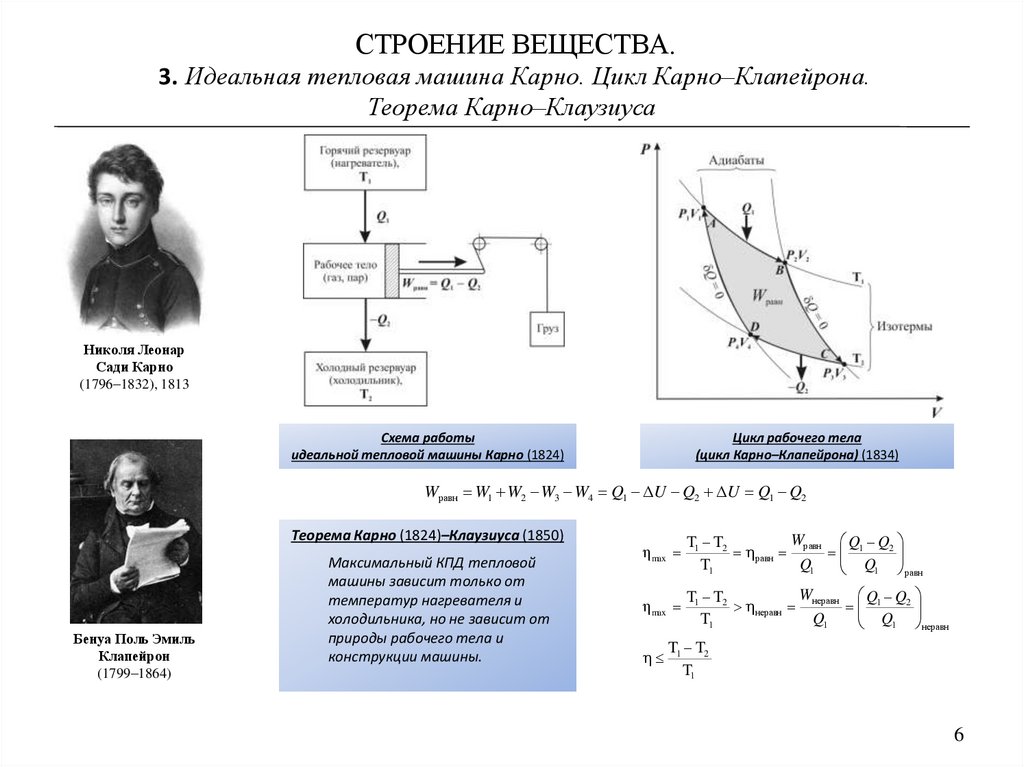
Схема работы
идеальной тепловой машины Карно (1824)
Цикл рабочего тела
(цикл Карно–Клапейрона) (1834)
Wравн W1 W2 W3 W4 Q1 ΔU Q2 ΔU Q1 Q2
Теорема Карно (1824)–Клаузиуса (1850)
Бенуа Поль Эмиль
Клапейрон
(1799–1864)
Максимальный КПД тепловой
машины зависит только от
температур нагревателя и
холодильника, но не зависит от
природы рабочего тела и
конструкции машины.
ηmax
W
Q Q2
T1 T2
hравн равн 1
T1
Q1
Q1 равн
ηmax
W
Q Q2
T1 T2
hнеравн неравн 1
T1
Q1
Q1 неравн
h
T1 T2
T1
6

7.

СТРОЕНИЕ ВЕЩЕСТВА.
4. 2-ой закон термодинамики как закон возрастания энтропии
Равновесный обратимый процесс
Q1 Q2
Q
Q2
T T
1 2 1
0
T1
Q1 равн
T1 равн T2 равн
n
Qi
i 1
T
i
равн
0; n 28
n
Q
δQ
n i
0
T равн
i 1 Ti равн
Рудольф Юлиус Эмануэль
Готтлиб (Клаузиус)
(1822–1888)
Q
dS
T равн
δQ
ΔS S B S A
T равн
A
B
Неравновесный необратимый процесс
Энтропия S
(от греч. εν – энергия,
τροπια – поворот, превращение)
Q1 Q2
Q
Q2
T T
1 2 1
0
T1
Q1 неравн
T1 неравн T2 неравн
T
Qi
2-ой закон термодинамики
δQ
dS
δQ
0;
0
T неравн
i 1 i неравн
n
Мемуары о механической
теории тепла
(Abhandlung über die
mechanische Wärmetheorie),
1864–67
Аппроксимация произвольного цикла
серией циклов Карно
T
δQ
δQ
dS
dS
T неравн
T неравн
равн
δQ
δQ
dS
T неравн T
Q
dU TdS PdV
T
dU PdV
dS
T
dSU ,V 0; ΔSU ,V 0
7

8.

СТРОЕНИЕ ВЕЩЕСТВА.
5. Расчёт ΔS в некоторых физико-химических процессах
1. Нагревание (охлаждение) вещества
QV dU V TdSV CV dT
QP dH P TdS P C P dT
T2
SP2
C P a bT cT 2
T2
ΔS P
a bT cT dT
T1
C
S dS P T TP dT
P
1
2
T
T
c
ΔS P aln 2 b T2 T1 T22 T12
2
T1
2
C P a bT c T
1
T2
CP
dT
T
T1
ΔS P
a bT c T dT
ΔS
С P const
P
T1
T
ΔS P C P ln 2
T1
1200
2
T2
T
T
c 1
1
ΔS P aln 2 b T2 T1 2 2
2 T2 T1
T1
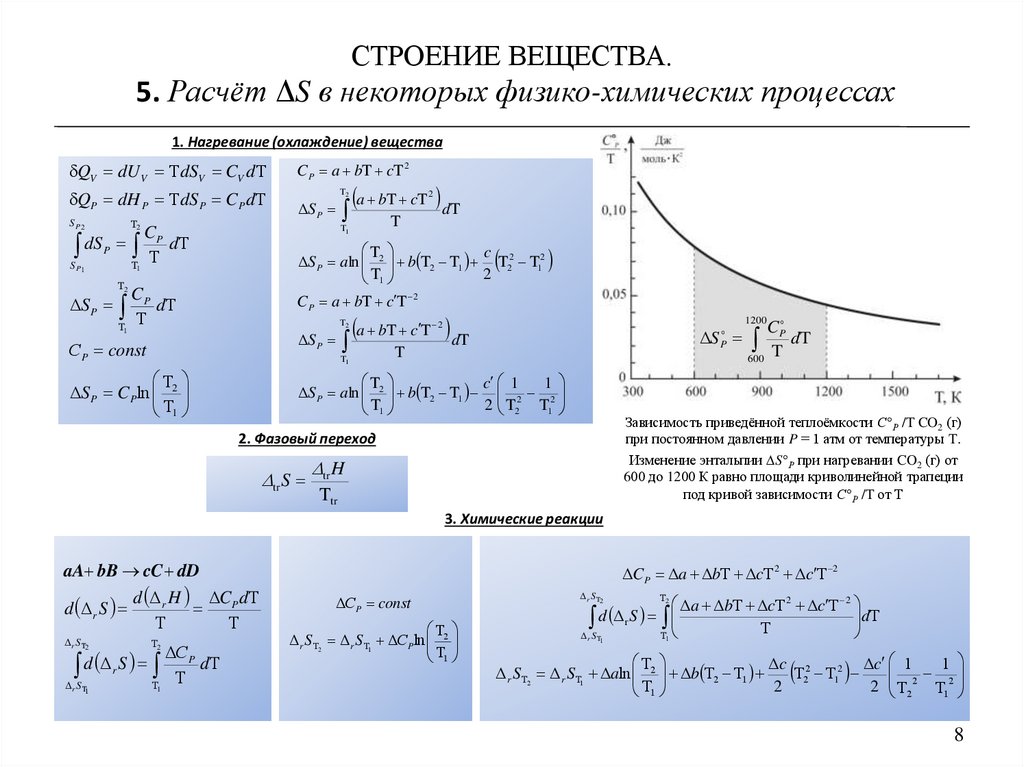
Зависимость приведённой теплоёмкости С Р /T CO2 (г)
при постоянном давлении P = 1 атм от температуры T.
Изменение энтальпии S Р при нагревании CO2 (г) от
600 до 1200 К равно площади криволинейной трапеции
под кривой зависимости С Р /T от Т
2. Фазовый переход
tr S
CP
dT
T
600
ΔS
P
tr H
Ttr
3. Химические реакции
aA bB cC dD
d Δ r H ΔCP dT
d Δ r S
T
T
Δ r S T2
T2
ΔС P
d Δ S T dT
r
Δ r S T1
T1
ΔCP Δa ΔbT ΔcT 2 Δc T 2
ΔСP const
T
Δ r ST2 Δ r ST1 ΔСP ln 2
T1
Δ r S T2
T2
Δa ΔbT ΔcT 2 Δc T 2
dT
d Δ r S
T
Δ r S T1
T1
T
Δc 2
Δc 1
1
Δ r ST2 Δ r ST1 Δaln 2 Δb T2 T1
T2 T12
2
2 T2 2 T12
T1
8

9.

СТРОЕНИЕ ВЕЩЕСТВА.
6. Статистический характер 2-го закона термодинамики
Atomyriades
Nature, it seem, is the popular name
For milliards and milliards and milliards
Of particles playing their infinite game
Of billiards and billiards and billiards.
Природа – лишь имя, я мыслю порой,
Для множеств числом в миллиард
Частичек, реальность творящих игрой
В бесконечный дурной бильярд.
Piet Hein
Статистика Максвелла – Больцмана (1871)
Задача о распределении n частиц по 2-м ячейкам
n = 4 (A, B, C, D), N = 2, Nn = 24 = 16)
Каждая частица A, B, C, D обладает индивидуальными свойствами.
Перестановка частиц между ячейками учитывается, внутри ячеек не учитывается.
№
1
2
3
4
5
6
7
8
Левая
ячейка
Правая
ячейка
№
AB
AC
AD
CD
BD
BC
ABC
ABD
CD
BD
BC
AB
AC
AD
D
C
9
10
11
12
13
14
15
16
Левая
ячейка
Правая
ячейка
ACD
BCD
D
C
B
A
ABCD
–
B
A
ABC
ABD
ACD
BCD
–
ABCD
Биномиальное распределение:
Джеймс Клерк Максвелл
(1831–1879), 1855
Людвиг Эдуард Больцман
(1844–1906), 1869
n
x y n! x m y n m ; n, m N 0
m 0 m! n m !
w
4!
1
w0 4 C40
1; p 0 4 0 n4 4 0,0625
0!4!
N
2
w1 3 4
4!
1
w1 3 C4
4; p 1 3 n 4 0,25
1!3!
N
2
4!
w
6
w2 2 C42
6; p 2 2 2 n2 4 0,375
2!2!
N
2
w
4!
4
w3 1 C43
4; p 3 1 3 n1 4 0,25
3!1!
N
2
w
4!
1
w4 0 C44
1; p 4 0 4 n0 4 0,0625
4!0!
N
2
n
p(m)
Формула (принцип)
Больцмана–Планка
(1872)
0,55
n=2
0,5
S kln w
0,45
R
ln w
NA
3
0,4
4
0,35
5
6
0,3
7
0,25
8
9
10
0,2
0,15
0,1
0,05
0
0
1
2
3
4
5
6
7
8
9
10
m
9