Системы счисления

1.

ГБПОУ "МППК им. В.В.Арнаутова"
A16FF179D
10101001100010
31545625
Системы счисления
Подготовил:
преподаватель информатики
Попова Екатерина Викторовна

2.

Система счисления
!
Система счисления — это знаковая
система,
в
которой
числа
записываются по определённым
правилам с помощью символов
некоторого алфавита, называемых
цифрами.
Системы счисления

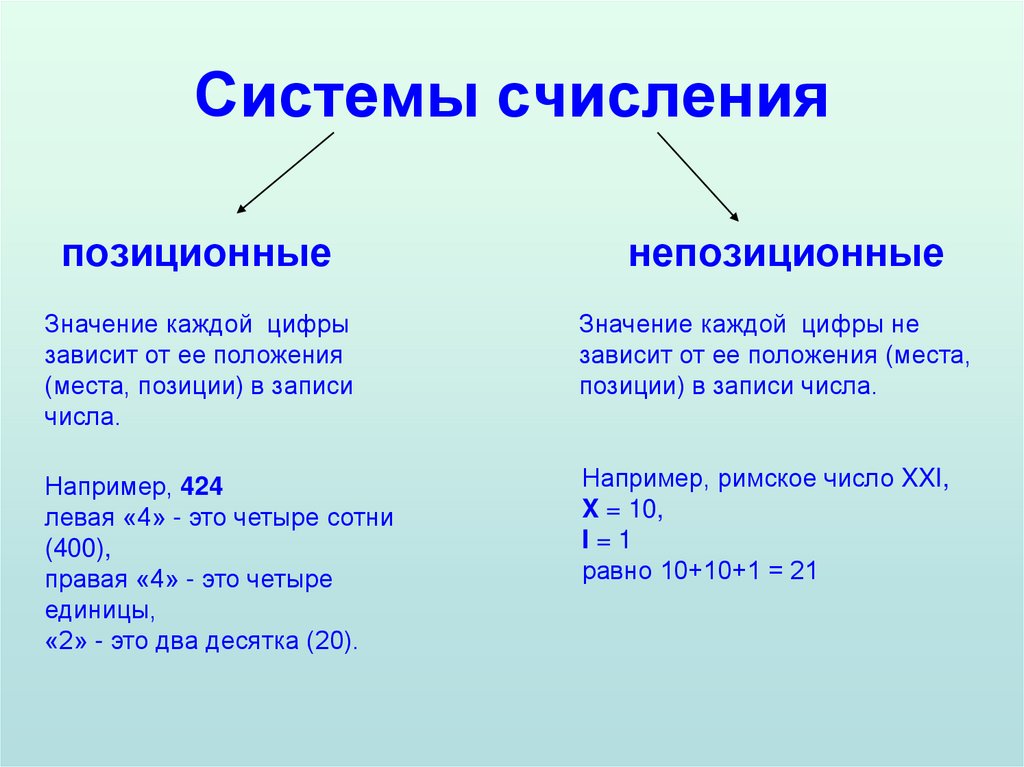
3. Системы счисления

позиционные
непозиционные
Значение каждой цифры
зависит от ее положения
(места, позиции) в записи
числа.
Значение каждой цифры не
зависит от ее положения (места,
позиции) в записи числа.
Например, 424
левая «4» - это четыре сотни
(400),
правая «4» - это четыре
единицы,
«2» - это два десятка (20).
Например, римское число XXI,
X = 10,
I=1
равно 10+10+1 = 21

4.

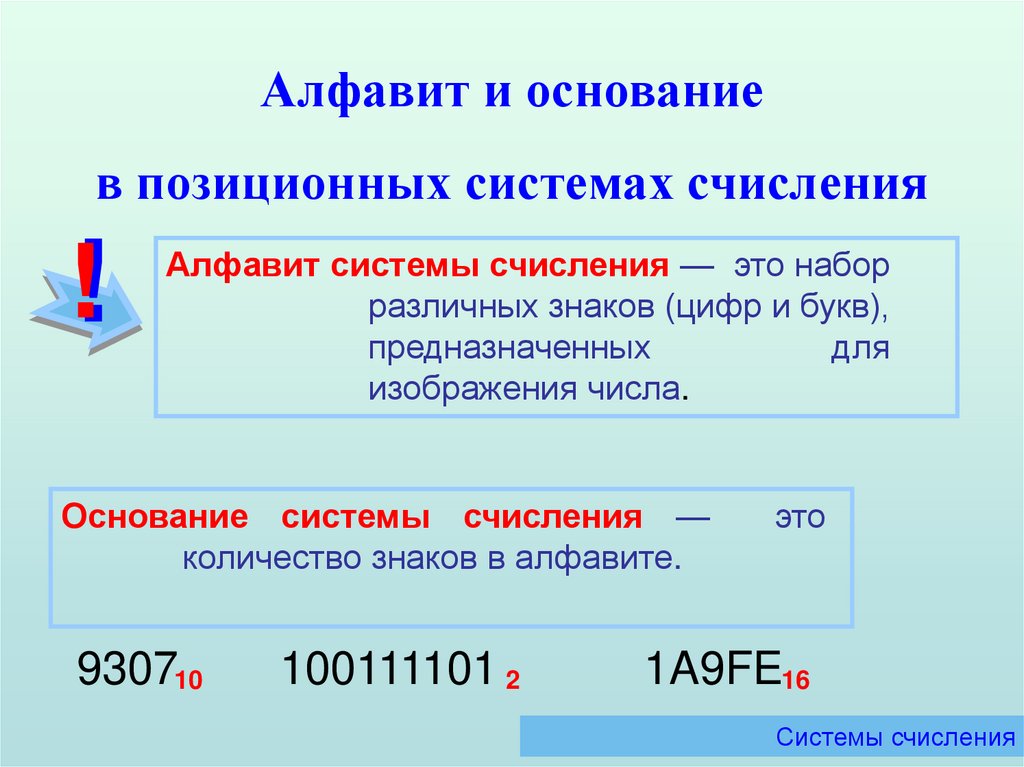
Алфавит и основание
в позиционных системах счисления
!
Алфавит системы счисления — это набор
различных знаков (цифр и букв),
предназначенных
для
изображения числа.
Основание системы счисления —
количество знаков в алфавите.
930710
100111101 2
это
1A9FE16
Системы счисления

5.

Примеры чисел в различных системах
счисления
Двоичная система
счисления
Восьмеричная
Десятеричная
система
система
счисления
счисления
Пример
1011
9071
1706
Алфавит
0,1
0,1,2,3,4,5,6,7
0,1,2,3,4,5,6,7,8,9
Основание
2
10
8
8
10
2
Системы счисления

6. Пример непозиционной системы счисления

В римской СС в качестве цифр
используются некоторые буквы
латинского алфавита:
I = 1,
V = 5,
X = 10,
L =50,
С = 100,
D =500,
M = 1000

7.

Перевод чисел из десятичной системы
счисления в любую другую систему
счисления
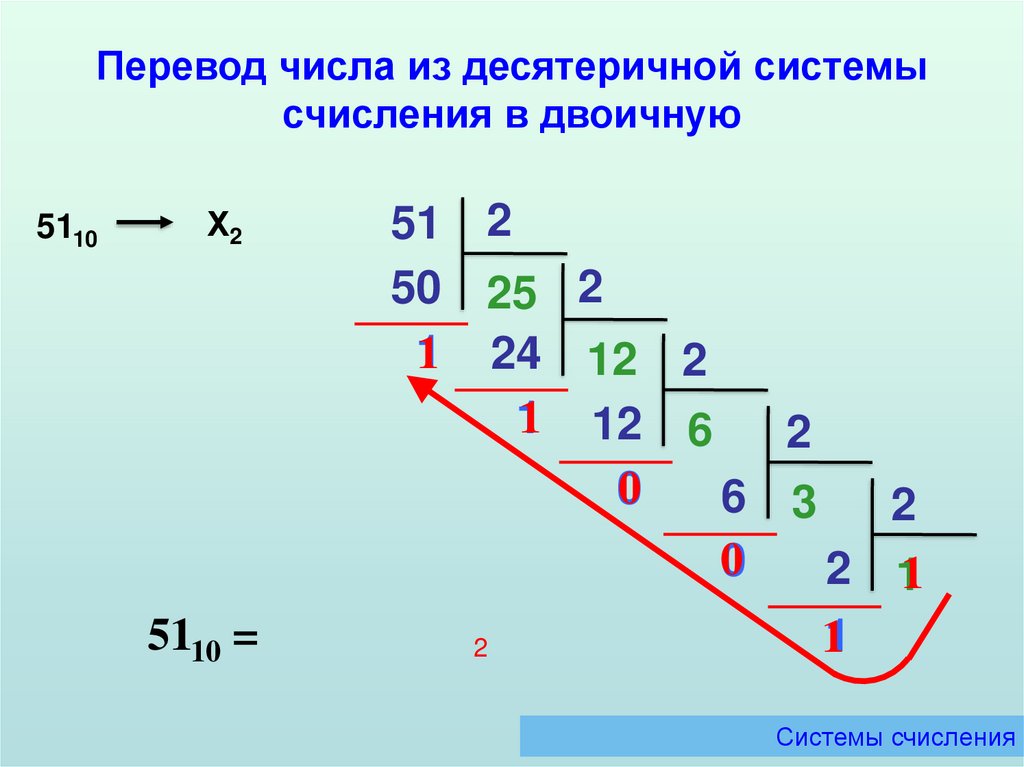
Для перевода числа из десятичной системы
счисления в любую другую следует последовательно
делить это число на основание системы счисления, в
которую переводим до тех пор, пока частное не станет
меньше делителя.
Результат перевода записывается, начиная с
последнего частного и включая все остатки, начиная с
последнего до первого.
Системы счисления

8.

Перевод числа из десятеричной системы
счисления в двоичную
5110
Х2
5110 =
51 2
50 25 2
1 24 12 2
1 12 6
2
0
6 3
2
0
2 11
11
2
Системы счисления

9.

Перевод чисел из любой позиционной
системы счисления в десятичную
Для перевода числа из любой системы счисления в 10-ю
систему счисления число представляют в развёрнутой
форме и производят вычисления в десятичной системе
счисления.
2 1 0
2368 → Х10
4 3 2 10
110012 → X10
2368=2*82+3*81+6*80=128+24+6=15810 → 2368=15810
110012=1*24+1*23+0*22+0*21+1*20 =16+8+0+0+1=2510
110012 =2510
Системы счисления

10.

Перевод из 2-й системы счисления
в 8-ю, 16-ю системы счисления
При переводе целого числа из двоичной системы счисления в
8-ю или в 16-ю систему счисления это число разбивается
справа налево на группы по 3 цифры (триады) для 8-ой системы
счисления или по 4 цифры (тетрады) для 16-й системы
счисления.
Недостающие разряды в группе заполняются нулями слева.
Каждая группа заменяется цифрой соответствующей системы
счисления.
11010110112→Х8 , Х16
Х8 = 1.101.011.011 = 001.101.011.011 = 15338
Х16 = 11.0101.1011 = 0011.0101.1011 = 35B16
Системы счисления

11.

Перевод из 8-й и 16-й систем счисления в
2-ю систему счисления
Для перевода числа из 8-й или 16-й систем счисления в
двоичную необходимо каждую цифру этого числа заменить
её двоичным кодом соответствующей системы счисления.
Пример: B2F16=1011
0010 11112
В
2
F
4568=100 101 1102
4
5
6
Системы счисления

12.

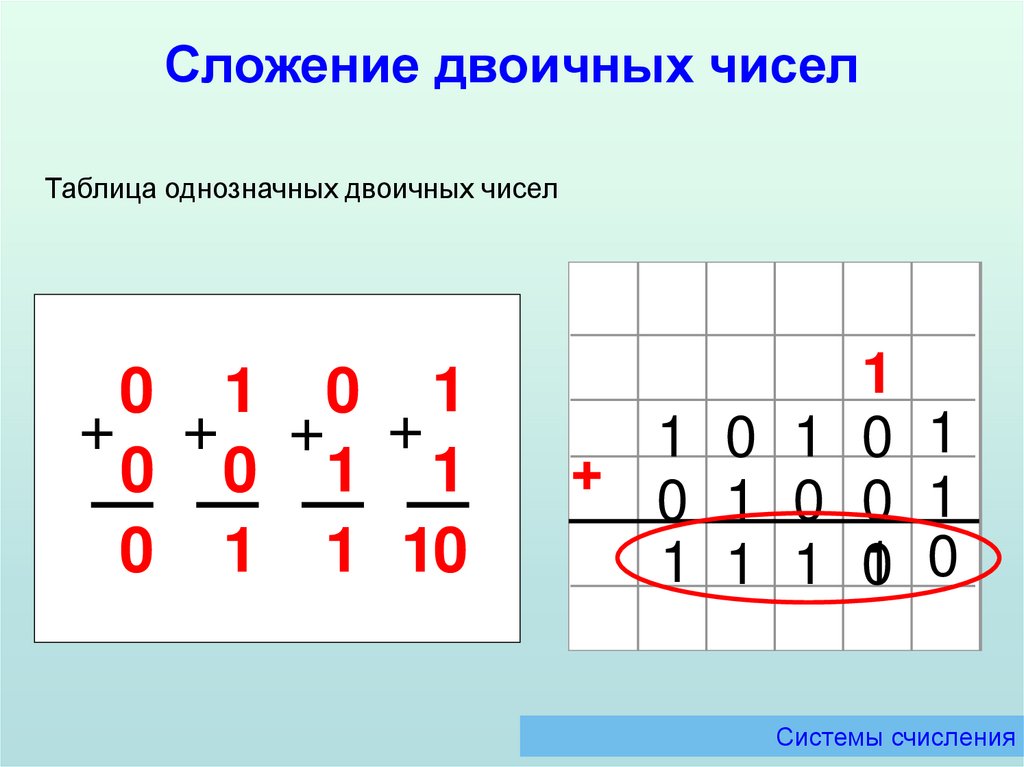
Сложение двоичных чисел
Таблица однозначных двоичных чисел
0 1 0 1
+ + + +
0 0 1 1
0 1 1 10
1
1 0 1 0 1
+
0 1 0 0 1
1 1 1 0
1 0
Системы счисления

13.

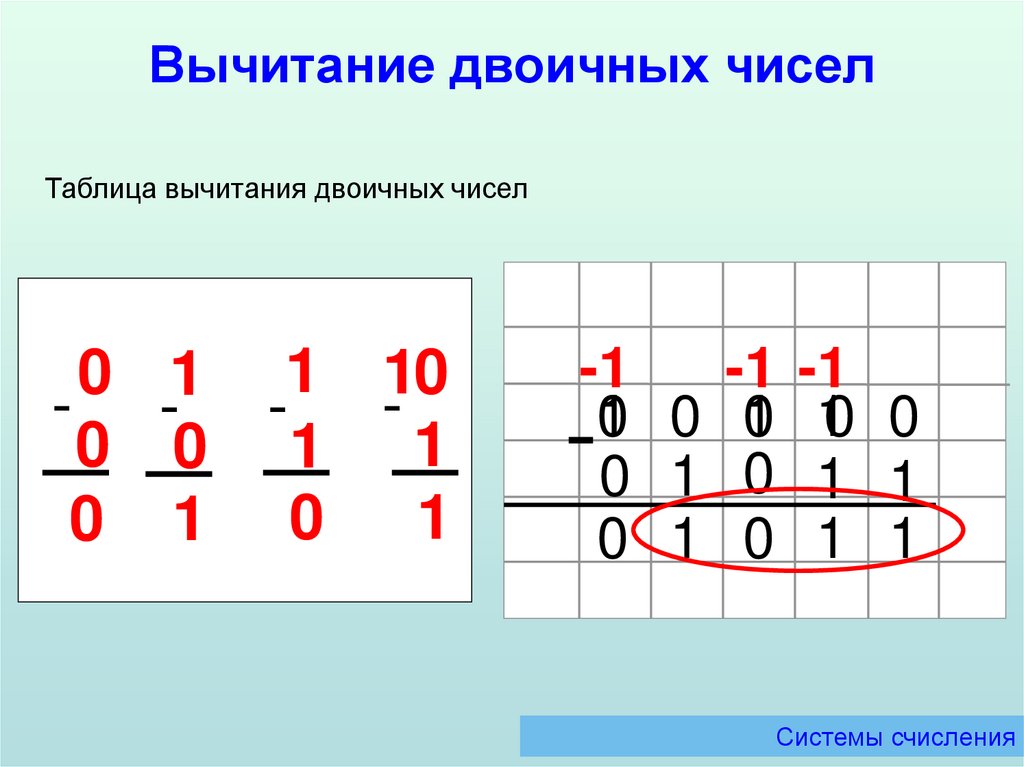
Вычитание двоичных чисел
Таблица вычитания двоичных чисел
0
0
0
1 1 -10
- 0 1 1
1 0 1
-1
-1 -1
1 0 0
0
1 10 0
0 1 0 1 1
0 1 0 1 1
Системы счисления

14.

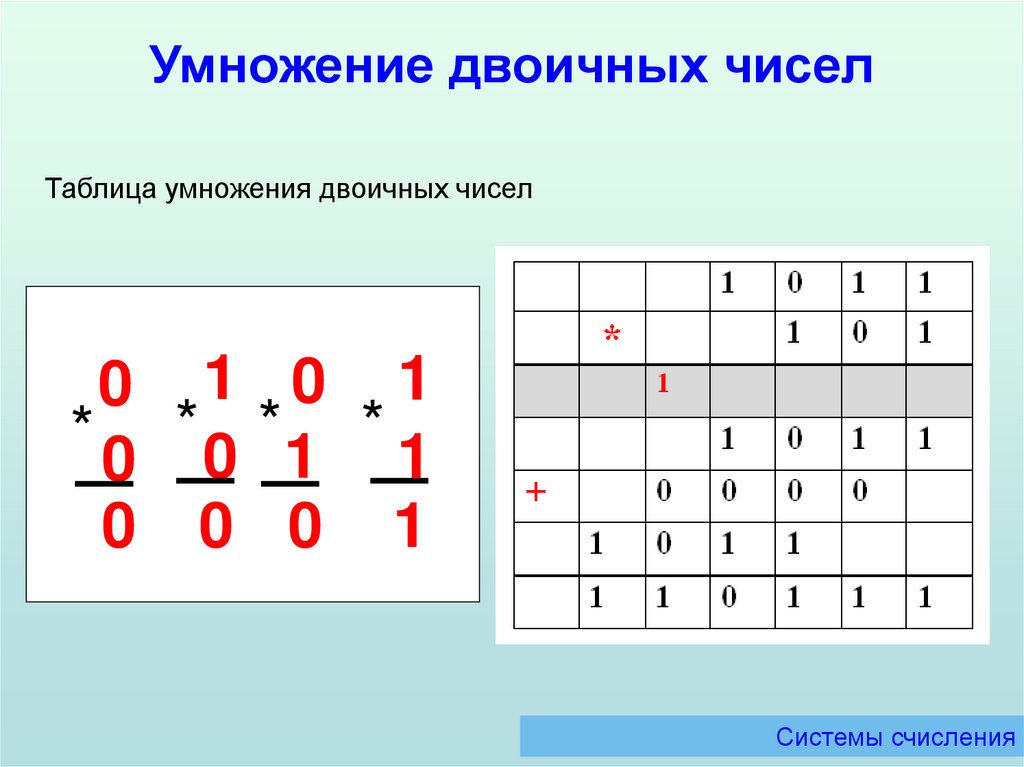
Умножение двоичных чисел
Таблица умножения двоичных чисел
0 1 0 1
* 0 * 0 *1 * 1
0 0 0 1
Системы счисления

15.

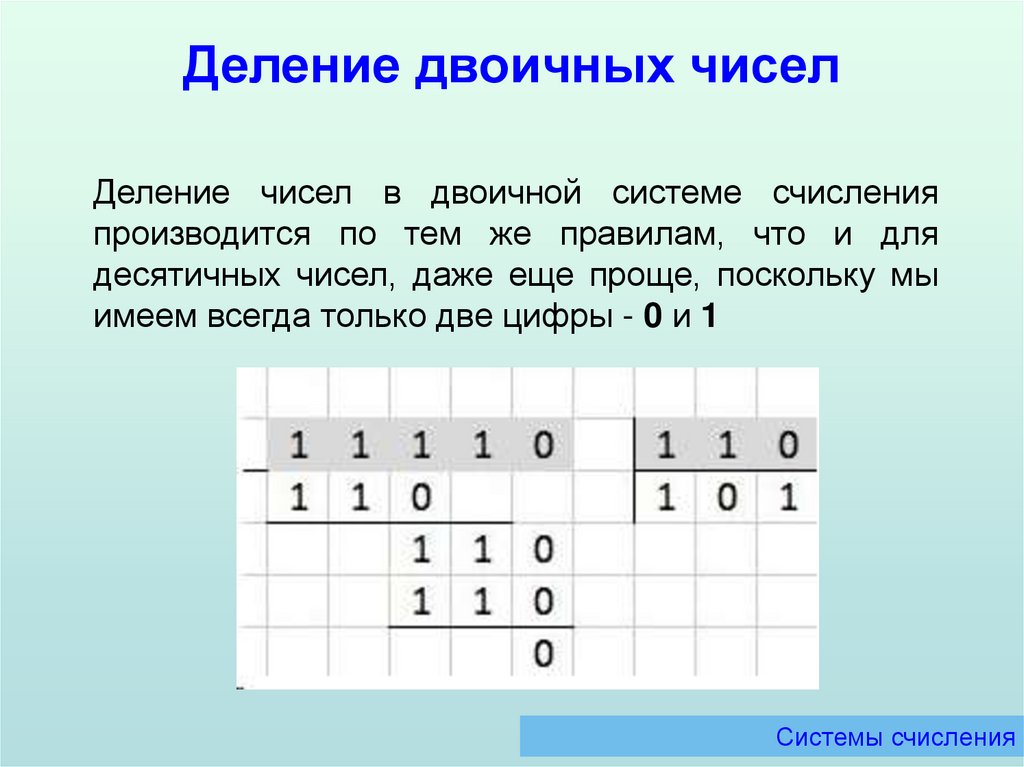
Деление двоичных чисел
Деление чисел в двоичной системе счисления
производится по тем же правилам, что и для
десятичных чисел, даже еще проще, поскольку мы
имеем всегда только две цифры - 0 и 1
Системы счисления