Similar presentations:
Системы счисления
1. Системы счисления
Непозиционные и позиционные системы счисления
Перевод чисел из десятичной С.С. в двоичн
ую (
I способ)
Перевод чисел из десятичной С.С. в
двоичную (II способ)
Перевод чисел из 2-й С.С. в 10-ю
Перевод чисел из 2-й С.С. В 8-ю и 16-ю С.С
Арифметические операции в позиционных
С.С.
2.
Система счисления –это знаковая система, в которой
числа записываются по
определенным правилам с
помощью символов
некоторого алфавита,
называемых цифрами.
3. Для представления чисел используются непозиционные и позиционные системы счисления.
4. В непозиционных системах счисления количественный эквивалент каждой цифры не зависит от её положения (места, позиции) в записи
числа.5. I (1), V (5), X(10), L (50), C(100), D (500), M (1000)
6. Десятичное число имеет следующее представление XCIX = -10 + 100 – 1 + 10
7. Десятичное число 1998 будет выглядеть следующим образом: MCMXCVIII = 1000 +(1000 – 100) +(100 – 10) + 5 +1 +1 +1
8. Недостатки непозиционных систем счисления:
существует постоянная потребностьвведения новых знаков для записи
больших чисел;
невозможно представить дробные и
отрицательные числа;
сложно выполнить арифметические
операции, так как не существует
алгоритмов их выполнения.
9. В позиционных системах счисления количественное значение цифры зависит от её позиции в числе.
10. В позиционных системах счисления основание системы равно количеству цифр (знаков в её алфавите) и определяет, во сколько раз
различаютсязначения одинаковых цифр,
стоящих в соседних позициях.
11.
Система счисления Основа Алфавитние
Десятичная
10
0, 1, 2, 3, 4, 5, 6, 7, 8, 9
Двоичная
2
0, 1
Восьмеричная
8
0, 1, 2, 3, 4, 5, 6, 7
Шестнадцатеричная 16
0, 1, 2, 3, 4, 5, 6, 7, 8, 9,
А(10), B (11), C (12),
D (13), E (14), F (15)
12. Десятичное число А10=4718,63 в развернутой форме запишется так: А10 =4*103 + 7*102 + 1*101+ 8*100 + 6*10-1 +
3*10-2=4000+700+10+8+6
3
+
10 100
13. Двоичное число А2 = 110010,11 в развернутой форме запишется так: А2 = 1*25 + 1*24 + 0*23 + 0*22 + 1*21 +0*20 + 1*2-1 + 1*2-2
14. Существует два способа перевода числа из десятичной системы счисления в двоичную.
Первый способ: деление числа наоснование двоичной системы счисления
15.
7810 ->2
78
2
78 39 2
0 -38
19
2
1 18 9 2
1 8 -4 2
1 4 2 2
0 2 1
0
16.
Второй способ перевода чиселиз десятичной системы
счисления в двоичную.
17.
2 =126 = 64
21 = 2
27 = 128
0
22 = 4
23 = 8
28 = 256
2 = 16
29 = 512
25 = 32
210 = 1024
4
18.
7810 -> 1001110 278
64
14
8
6
4
- 2
2
0
6
3
2
1
6 5 4
3 2 1 0
10 0 1 1 1 0
19.
Перевод чисел из двоичнойсистемы счисления в
десятичную.
20.
1001110 2 -> 78106
5
4
3
2
1
0
6
5
=
1*2
+
0*2
+
1 0 0 1 1 1 0
+ 0*24 + 1*23 + 1*22 + 1*21 + 0*20 =
= 64 + 0 + 0 + 8 + 4 + 2 + 0 = 78
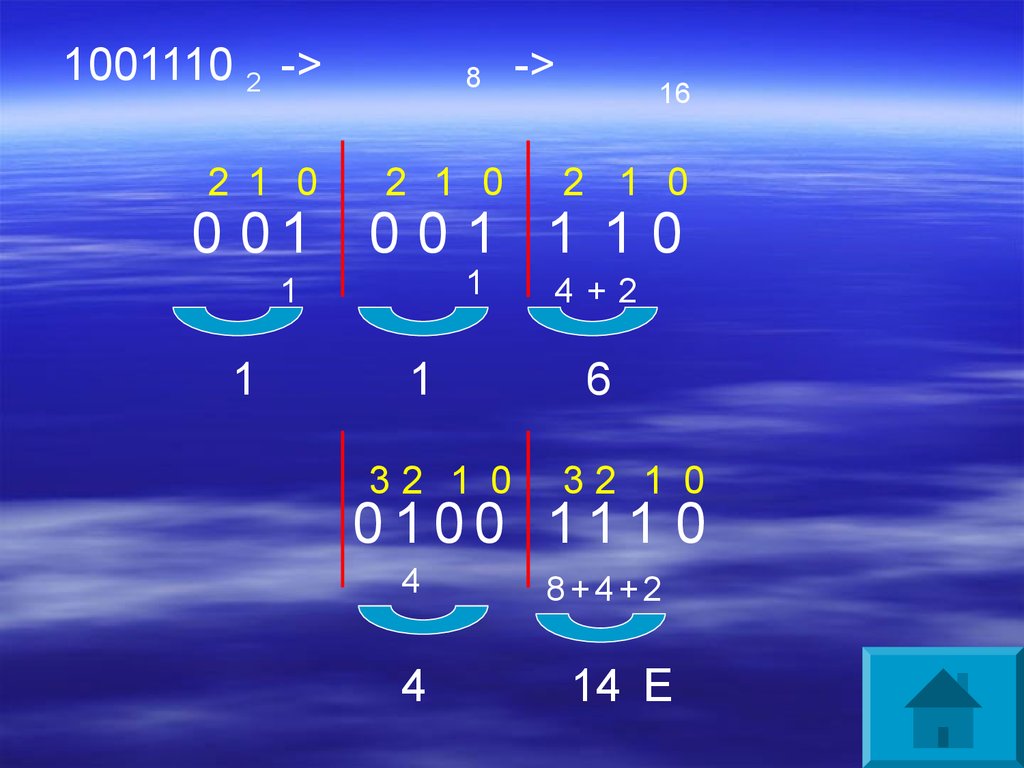
21. Перевод чисел из двоичной в восьмеричную и шестнадцатеричную системы счисления
22.
1001110 2 ->2 1 0
0 01
8
2 1 0
16
2 1 0
001 1 10
1
1
1
->
1
32 1 0
4+2
6
32 1 0
0100 111 0
4
4
8+4+2
14 Е
23. Арифметические операции в позиционных системах счисления
24. Операция сложения в двоичной системе счисления
0+0=00+1=1
1+0=1
1 + 1 = 10
25.
11102 + 1012= 1001121
11 1 0
+ 1 01
10 011
26. Операция вычитания в двоичной системе счисления
0-0=01-0=1
1-1=0
10 - 1 = 1
27.
100112 – 1012 = 111021+1 1+1
10 0 11
1 01
1110
28. Операция умножения в двоичной системе счисления
0*0=00*1=0
1*0=0
1*1=1
29.
1102 * 112 =100102
110
* 11
+1 1 1 0
11 0
1 0 01 0
30. Операция деления выполняется по алгоритму, подобному алгоритму выполнения операции деления в десятичной системе счисления.
31.
100011012 : 112= 10111121
2 2
1
0
0
0
1
1
0
1
1
1
112
1
0
1
1
1
1
1
0
1
- 11
2
1
0
1
- 11
2 2
1
1
0
0
- 11
11






























 informatics
informatics








