Similar presentations:
Поток прямой радиации на произвольно ориентированную поверхность
1. Практическая работа №2
ПРАКТИЧЕСКАЯ РАБОТА №22. Поток прямой радиации на произвольно ориентированную поверхность
ПОТОК ПРЯМОЙ РАДИАЦИИ НА ПРОИЗВОЛЬНООРИЕНТИРОВАННУЮ ПОВЕРХНОСТЬ
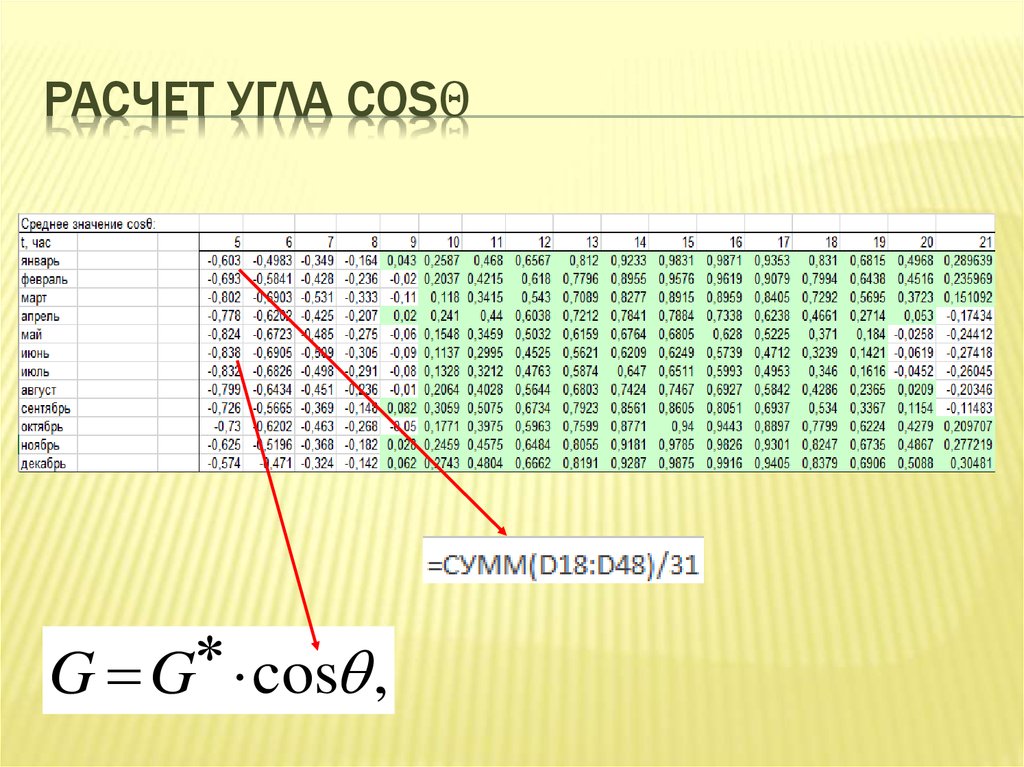
G G cos ,
где
G -
поток на площадку, перпендикулярную прямым лучам
- угол между направлением потока излучения и нормалью к
Поверхности приемника
3. Поток прямой радиации на ортогональную поверхность
ПОТОК ПРЯМОЙ РАДИАЦИИ НАОРТОГОНАЛЬНУЮ ПОВЕРХНОСТЬ
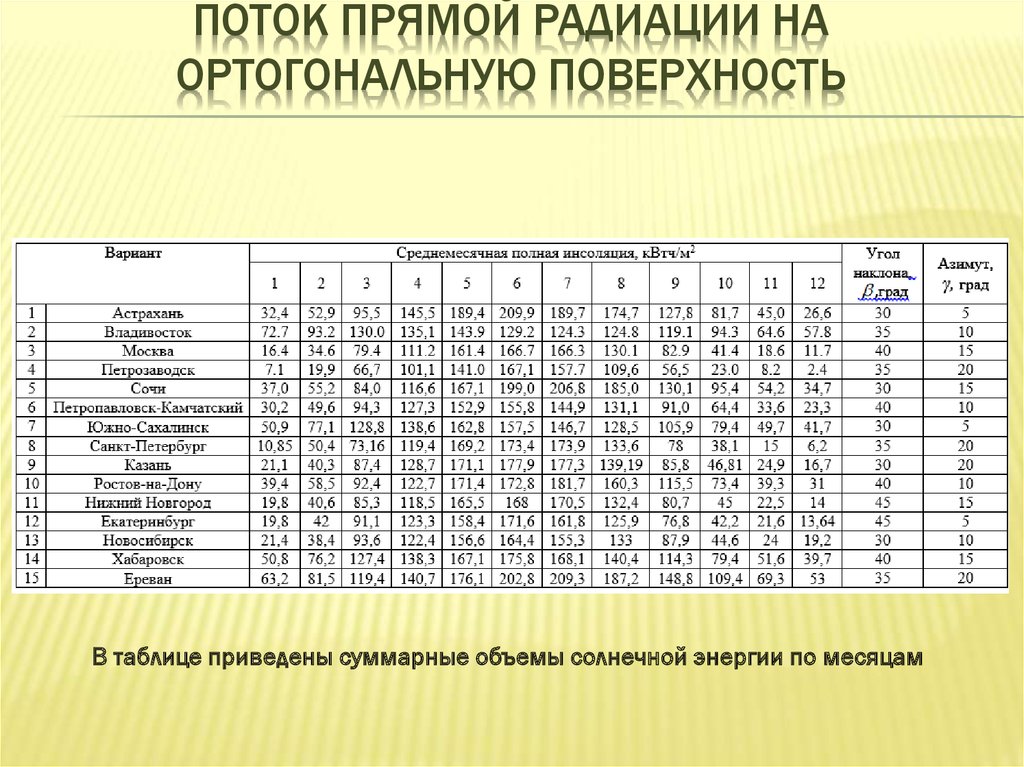
В таблице приведены суммарные объемы солнечной энергии по месяцам
4. Поток прямой радиации на ортогональную поверхность
ПОТОК ПРЯМОЙ РАДИАЦИИ НАОРТОГОНАЛЬНУЮ ПОВЕРХНОСТЬ
http://eosweb.larc.nasa.gov/sse/RETScreen/
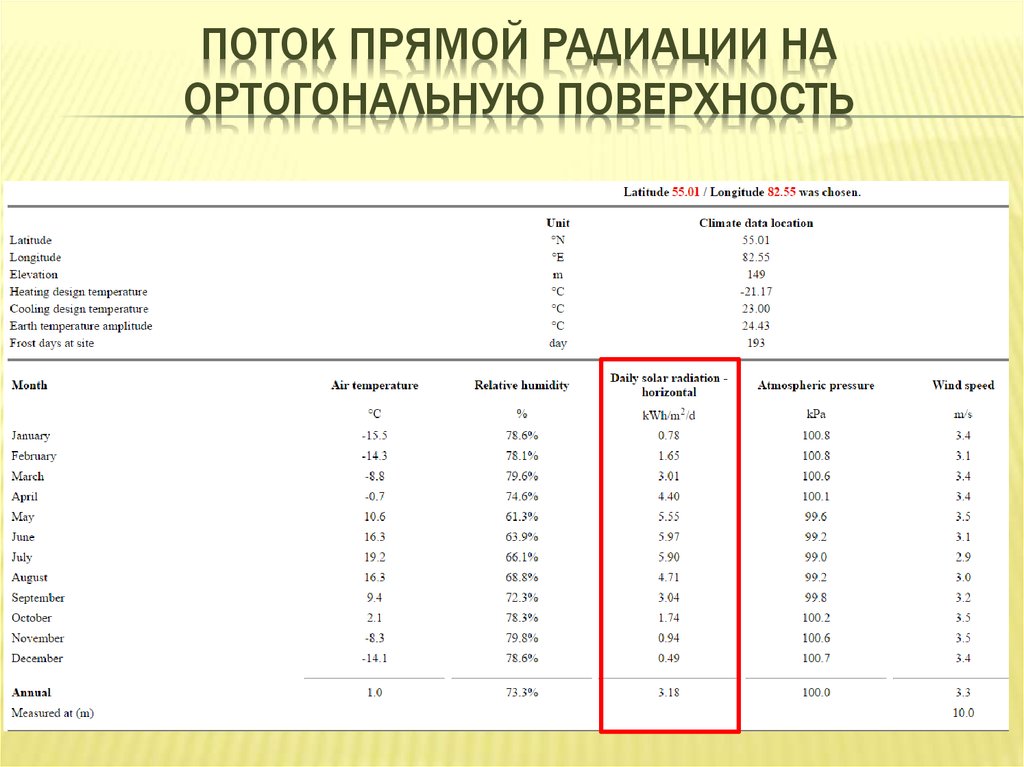
5. Поток прямой радиации на ортогональную поверхность
ПОТОК ПРЯМОЙ РАДИАЦИИ НАОРТОГОНАЛЬНУЮ ПОВЕРХНОСТЬ
6. Угол наклона
УГОЛ НАКЛОНАУгол между рассматриваемой плоскостью и горизонтальной
(0<β<90˚ для поверхностей, обращенных к экватору;
90˚<β<180˚ для поверхностей, повернутых от экватора);
β
7. Азимут
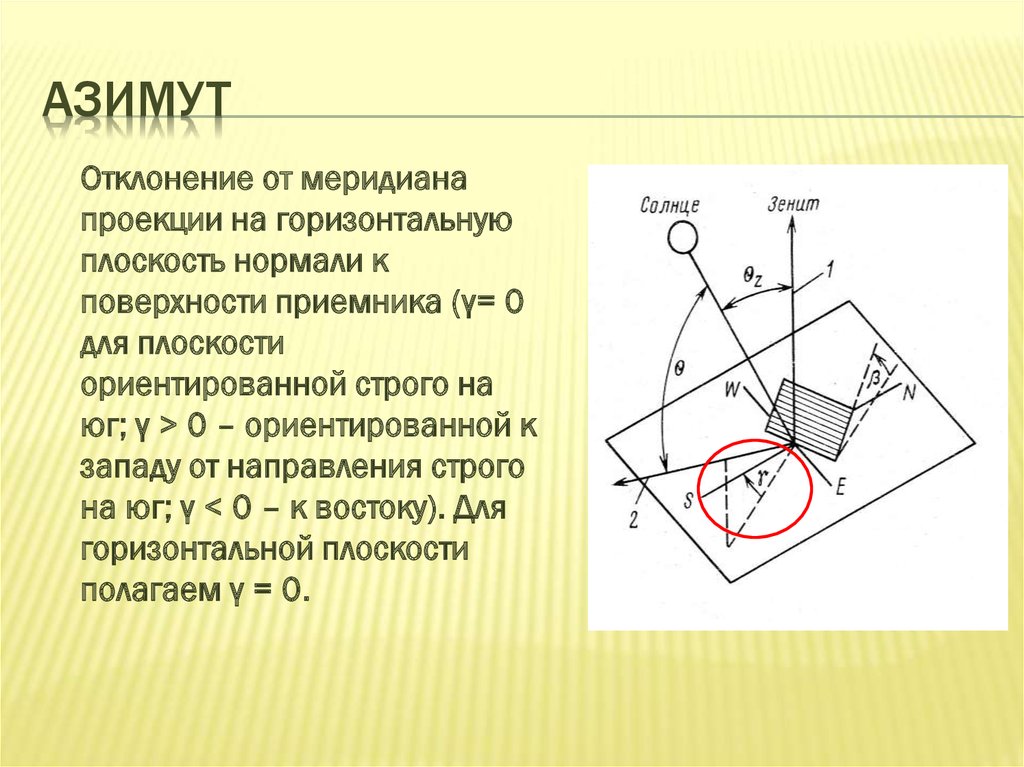
АЗИМУТОтклонение от меридиана
проекции на горизонтальную
плоскость нормали к
поверхности приемника (γ= 0
для плоскости
ориентированной строго на
юг; γ > 0 – ориентированной к
западу от направления строго
на юг; γ < 0 – к востоку). Для
горизонтальной плоскости
полагаем γ = 0.
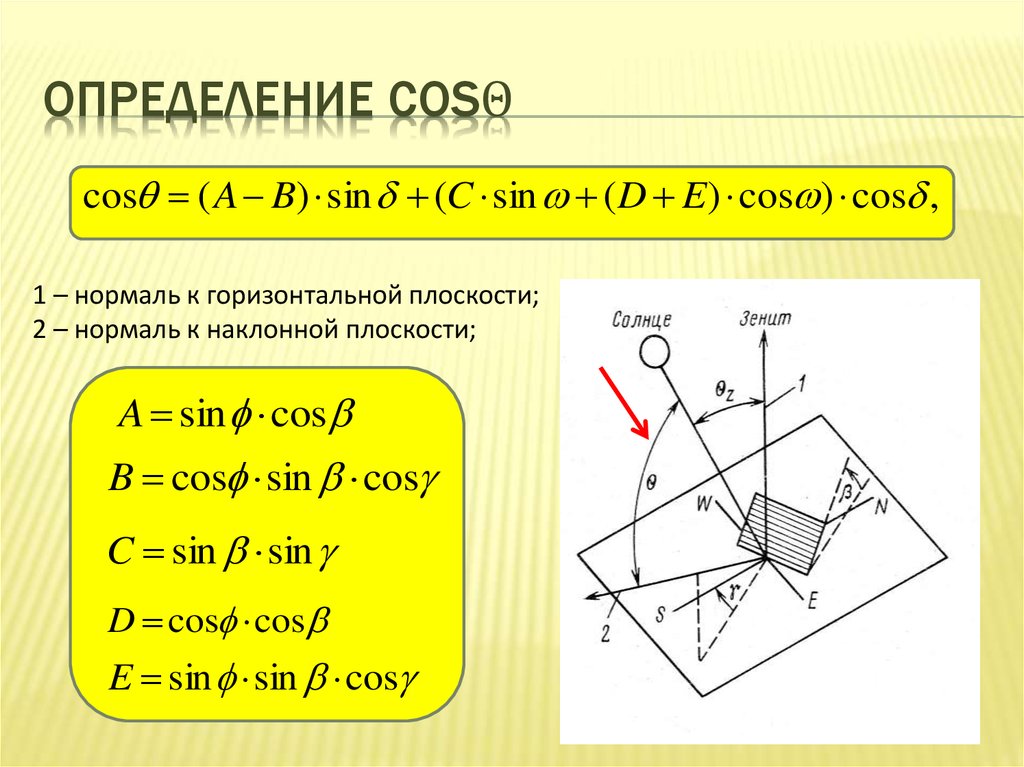
8. Определение cosθ
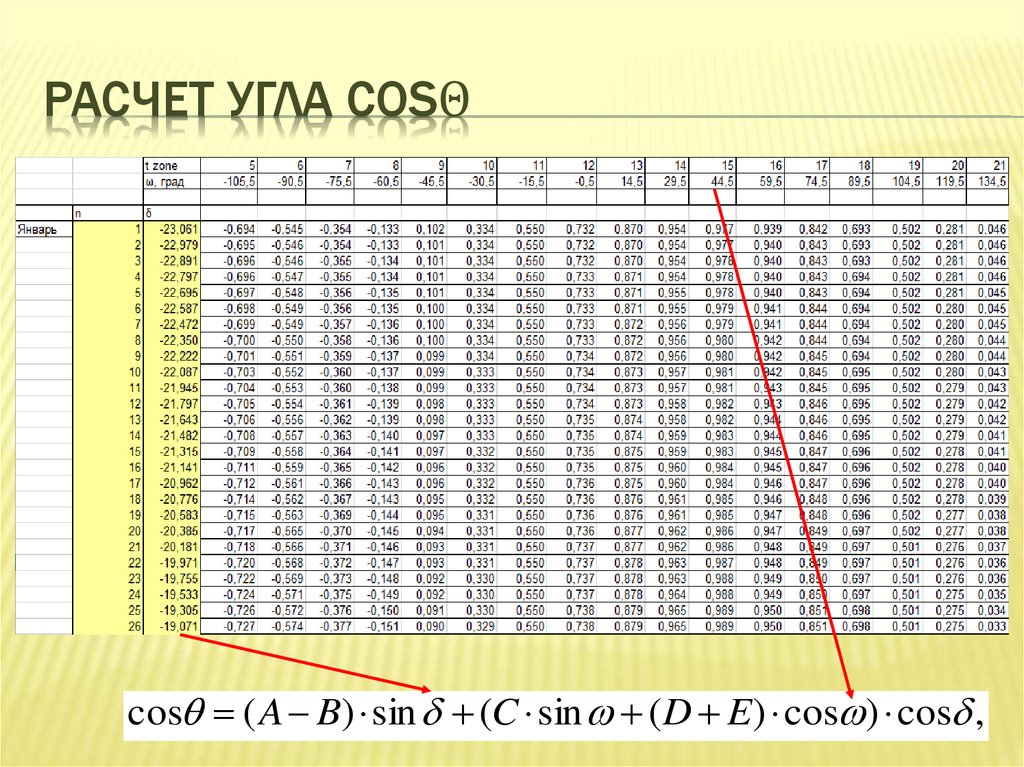
ОПРЕДЕЛЕНИЕ COSΘcos ( A B) sin (C sin ( D E) cos ) cos ,
1 – нормаль к горизонтальной плоскости;
2 – нормаль к наклонной плоскости;
A sin cos
B cos sin cos
C sin sin
D cos cos
E sin sin cos
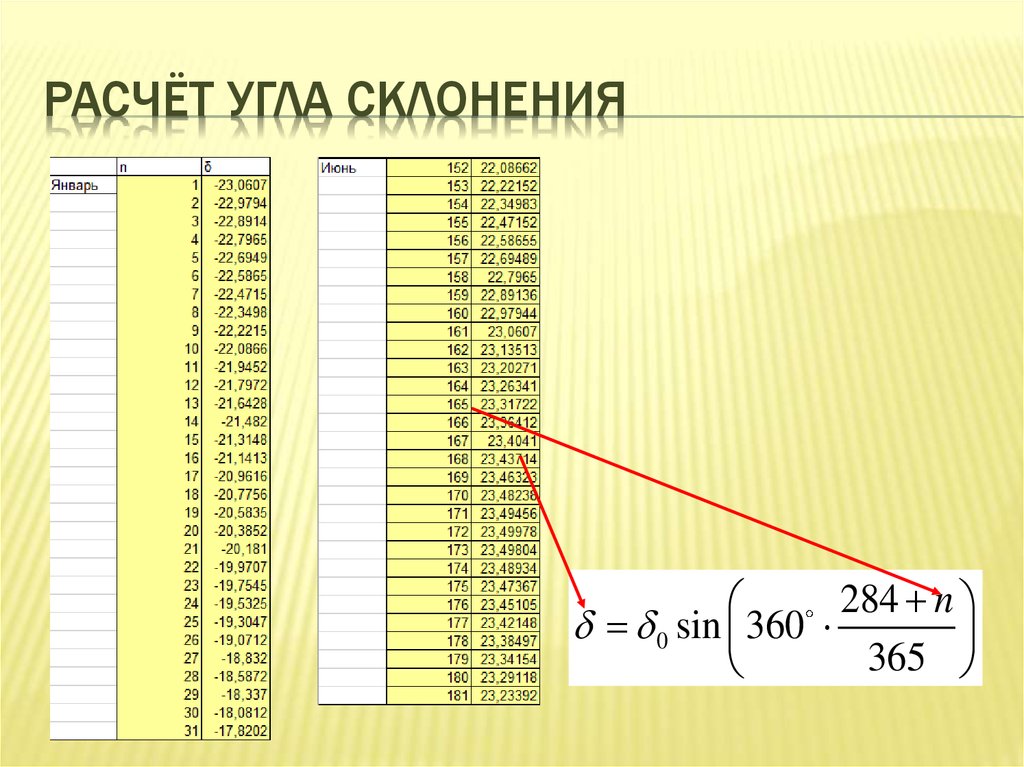
9. Угол склонения
УГОЛ СКЛОНЕНИЯУгол между направлением к Солнцу и экваториальной
плоскостью, является мерой сезонных изменений.
284 n
0 sin 360
365
δ0 = 23,5˚
n – рассматриваемый день года (первое января – 1,
первое февраля – 32, первое марта – 61)
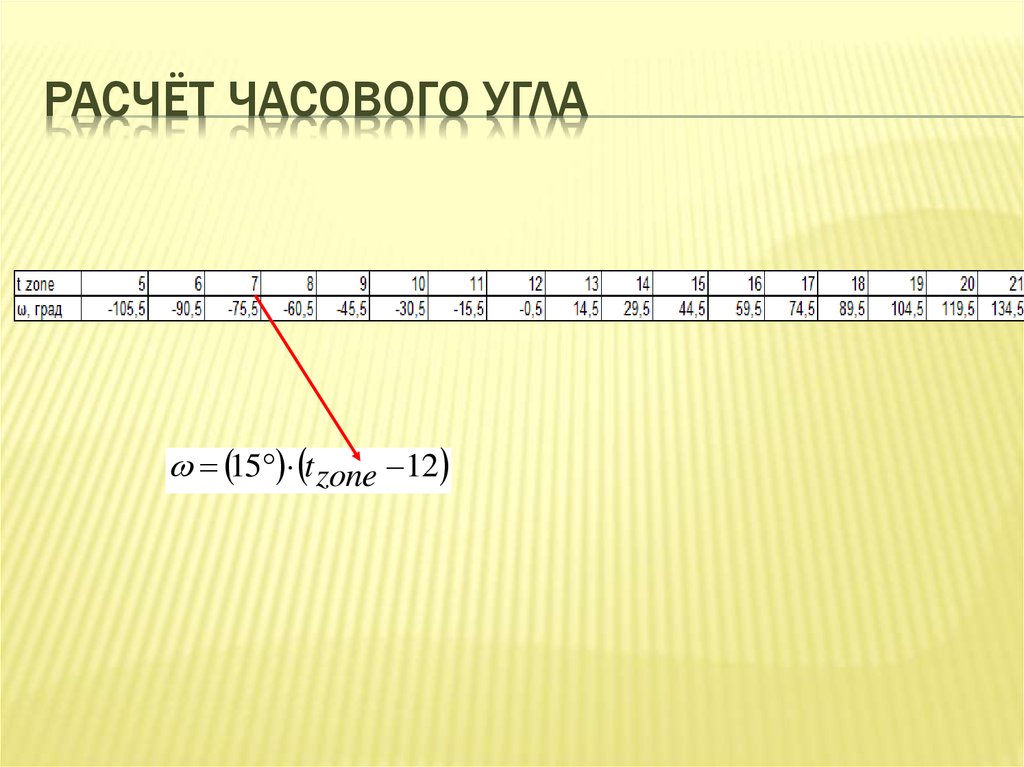
10. Часовой угол
ЧАСОВОЙ УГОЛУгол на который Земля поворачивается с момента
солнечного полдня. Один раз каждые 24 часа Солнце
попадает в меридиональную плоскость. Это – полдень по
солнечному времени для всех точек, имеющих данную
долготу.
15 ч-1 t zone 12ч zone
t zone - декретное время (в часах)
zone - долгота на которой находится солнце, когда t zone
соответствует полудню
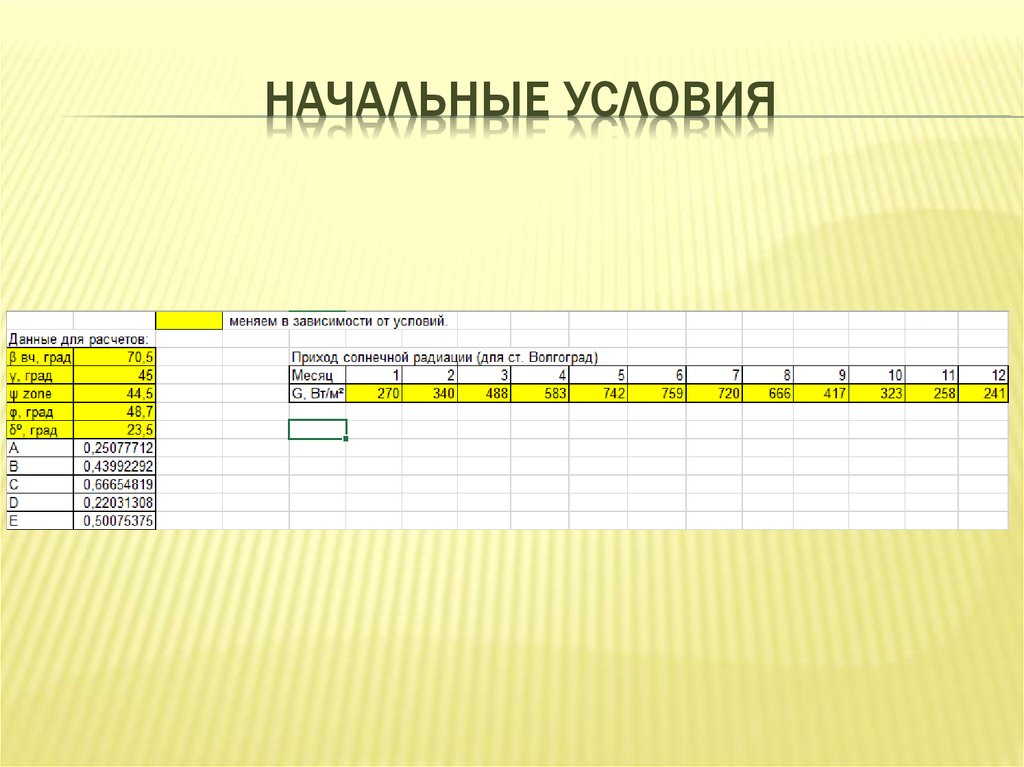
11. Начальные условия
НАЧАЛЬНЫЕ УСЛОВИЯ12. Расчёт часового угла
РАСЧЁТ ЧАСОВОГО УГЛА15 t zone 12
13. Расчёт угла склонения
РАСЧЁТ УГЛА СКЛОНЕНИЯ284 n
0 sin 360
365
14. Расчет угла cosθ
РАСЧЕТ УГЛА COSΘcos ( A B) sin (C sin ( D E) cos ) cos ,
15. Расчет угла cosθ
РАСЧЕТ УГЛА COSΘG G cos ,
16. Содержание отчёта
СОДЕРЖАНИЕ ОТЧЁТА• Титульный лист
• Краткая теория
• Пример расчета в развернутом виде
• Расчеты, сведенные в таблицы
• Значения среднемесячной инсоляции на
произвольно ориентированную поверхность