Similar presentations:
Треугольник Паскаля. Бином Ньютона
1.
Треугольник ПаскаляБином Ньютона
2.
Блез ПаскальСамой известной математической работой
Блеза Паскаля является "Трактат об
арифметическом треугольнике"
(треугольник Паскаля), который имеет
применение в теории вероятностей и обладает
удивительными и занимательными свойствами
3.
Треугольник ПаскаляОпределение:
ТРЕУГОЛЬНИК ПАСКАЛЯ —
это бесконечная числовая
таблица "треугольной
формы", в которой по
боковым сторонам стоят
единицы и всякое число,
кроме этих боковых
единиц.
4.
Треугольник ПаскаляСвойства:
Если очертить треугольник Паскаля,
то получится равнобедренный
треугольник. В этом треугольнике на
вершине и по бокам стоят единицы.
Каждое число равно сумме двух
расположенных над ним чисел.
Например:
2=1+1
3=1+2
6=3+3 и т.д.
Продолжать треугольник можно
бесконечно.
5.
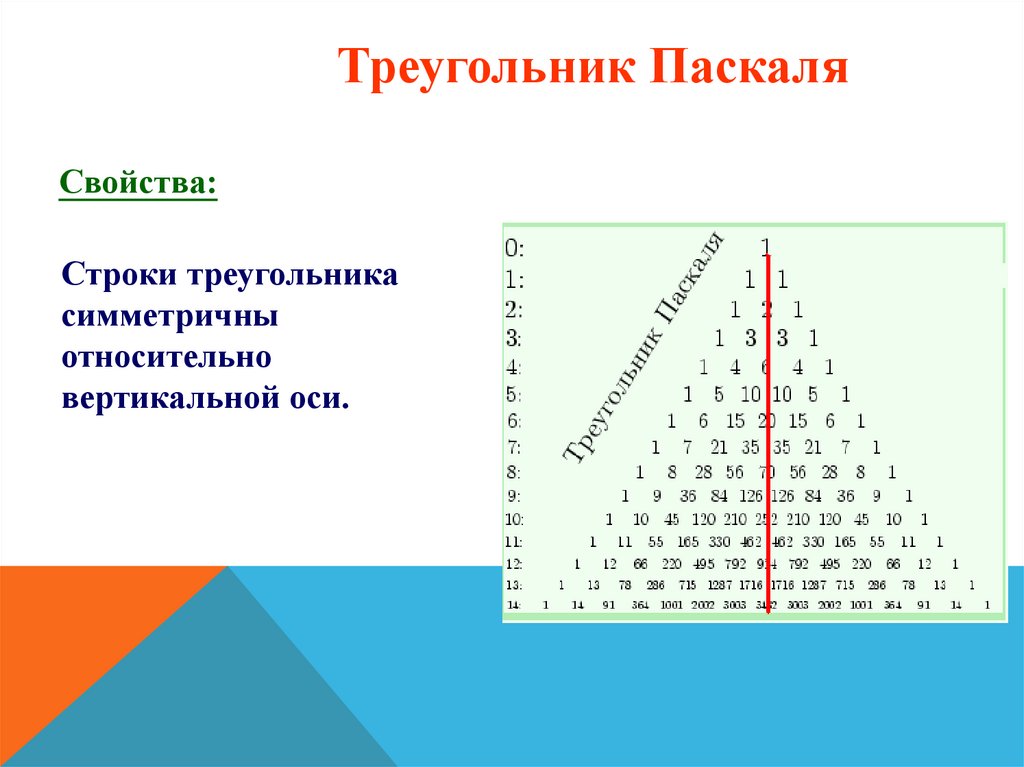
Треугольник ПаскаляСвойства:
Строки треугольника
симметричны
относительно
вертикальной оси.
6.
Треугольник ПаскаляСвойства:
Треугольные числа показывают,
сколько касающихся кружков можно
расположить в виде треугольника
Классический пример: начальная
расстановка шаров в бильярде.
7.
Треугольник ПаскаляСвойства:
Следующая зеленая линия
покажет нам
тетраэдральные числа –
один шар мы можем положить на
три – итого четыре, под три
подложим шесть - итого десять,
и так далее.
8.
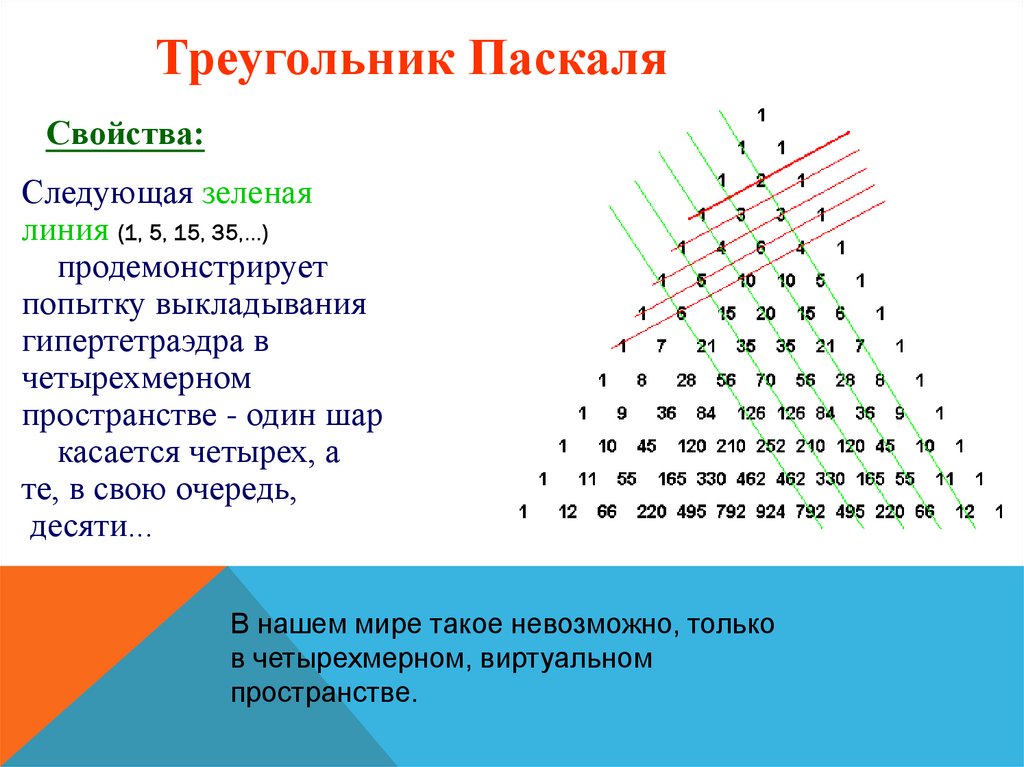
Треугольник ПаскаляСвойства:
Следующая зеленая
линия (1, 5, 15, 35,...)
продемонстрирует
попытку выкладывания
гипертетраэдра в
четырехмерном
пространстве - один шар
касается четырех, а
те, в свою очередь,
десяти...
В нашем мире такое невозможно, только
в четырехмерном, виртуальном
пространстве.
9.
Треугольник ПаскаляПрименение:
Чтобы найти сумму чисел, стоящих на
любой диагонали от начала до
интересующего нас места, достаточно
взглянуть на число, расположенное снизу
и слева от последнего слагаемого.
Пусть, например, мы хотим вычислить
сумму чисел натурального ряда от 1 до 9.
"Спустившись" по диагонали до числа 9,
мы увидим слева снизу от него число 45.
Оно то и дает искомую сумму.
Чему равна сумма первых восьми треугольных
чисел? Отыскиваем восьмое число на второй
диагонали и сдвигаемся вниз и влево. Ответ: 120.
10.
Треугольник ПаскаляПрименение:
Биномиальные коэффициенты есть
коэффициенты разложения многочлена
по степеням x и y
11.
Бином Ньютона.«Би»-удвоение, раздвоение …
«Ном»(фран. nombre) –номер, нумерация.
«Бином» -»два числа»
Числа, стоящие во второй, третьей и четвертой строках
треугольника Паскаля, появляются при возведении
двучлена (бинома) a+b в первую, вторую (квадрат) и третью
(куб) степень
12.
Треугольник Паскаля:1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
13.
Степени суммы двух чисел:а в а в;
2
2
2
а в а 2 ав
в;
3
2
2
2 3
а в а 3 ав 3 ав
в
1
14.
Треугольник Паскаля:0
0
C
0 1
C1 C1
0 1 2
C2C2C2
0 1 2 3
C3 C3C3 C3
0 1 2 3
4
C4C4C4C4C4
...
15.
Степени суммы двух чисел:а в Сав Сав;
1
0 10
1
1 01
1
а в Сав Сав Сав;
2
0 20
2
1 11
2
2 02
2
а в Сав Сав Сав Сав;
3
0 30
3
1 21
3
2 12
3
3 03
3
16.
Правило Паскаля:n
1
m
С C C
n
m
1
n
m
17.
Биноминальные коэффициенты:m!
n
Сm
n! ( m n )!
O! 1
C
0
m
C
1
m
C
m
m
1
C
m 1
m
m
18.
Биноминальные коэффициенты:n
1
m
n
m
n
1
m
1
n
m
С
C
C
n
m
1
С
C
C
n
m
1
m
1
m
С
C
...
C
C
2
0
m
1
m
m
m
m
19.
4 степень суммы двух чисел:4
3
(a+ b) = (a+ b) ⋅ (a+ b)
0
3
1
2
2
2
3 3
(C 3⋅ a + C 3⋅ a ⋅ b+ C 3⋅ a⋅ b + C 3⋅ b )⋅ (a+ b)
0
4
1
3
2
2 2
3
3
C 3⋅ a + C 3⋅ a ⋅ b+ C 3⋅ a ⋅ b + C 3⋅ a⋅ b
0
3
1
2 2
2
3
3 4
+ C 3⋅ a ⋅ b+ C 3⋅ a ⋅ b + C 3⋅ a⋅ b + C 3⋅ b
0
4
1
0
3
2
1
2 2
C 3⋅ a + (C 3+ C 3 )⋅ a ⋅ b+ (C 3 + C 3 )⋅ a ⋅ b
3
2
3
3 4
+ (C 3+ C 3 )⋅ a⋅ b + C 3⋅ b
20.
4 степень суммы двух чисел:Учитывая, что:
0
0
3
4
3
3
C =C
1
3
0
3
1
4
2
3
1
3
C +C =C
C +C =C
2
3
3
4
C + C 3 = C 4 C 3= C 4
Получаем формулу:
4
2
4
(a+ b)
0
4
1
3
2
2 2
3
3
4 4
C 4⋅ a + C 4⋅ a ⋅ b+ C 4⋅ a ⋅ b + C 4⋅ a⋅ b + C 4⋅ b
21.
Бином Ньютона:а
b
т
0
m1
m
1
m
m
m
1m
1 m
m
m
m
С
а
C
a
b
...
C
ab
C
b
m
∑ C ⋅a
k
m
k= 0
m− k
⋅b
k
22.
Задачи:1. Вычислите:
а) 20 ! ;
б)
5!⋅ 16 !
Р6 − Р 5
;
5!
2. Найдите n, если:
а) А = 18⋅ A
; б) А ⋅ P
5
n
4
n
4
n− 2
n− 4
в)
А620+ А520
= 42⋅ P n − 2 ;
А420
; г)
в) 12⋅ С
n− 1
n+ 3
3. Возведите в степень:
а) (х+ 1) ; б) (х− у ) ; в) (1+ i) ; г) (х2− у )6
7
5
6
Р6⋅ (С 57+ С 47 )
7
А10
2
= 55⋅ An+ 1
; г)
1
2
12⋅ С n + C n+ 4 = 126
; д) (3⋅ a2 − 2⋅ b)5
23.
Треугольник Паскаля так прост, чтовыписать его сможет даже
десятилетний ребенок. В то же
время он таит в себе неисчерпаемые
сокровища и связывает воедино
различные аспекты математики, не
имеющие на первый взгляд между
собой ничего общего. Столь
необычные свойства позволяют
считать треугольник Паскаля одной
из наиболее изящных схем во всей
математике[2].
Мартин Гарднер














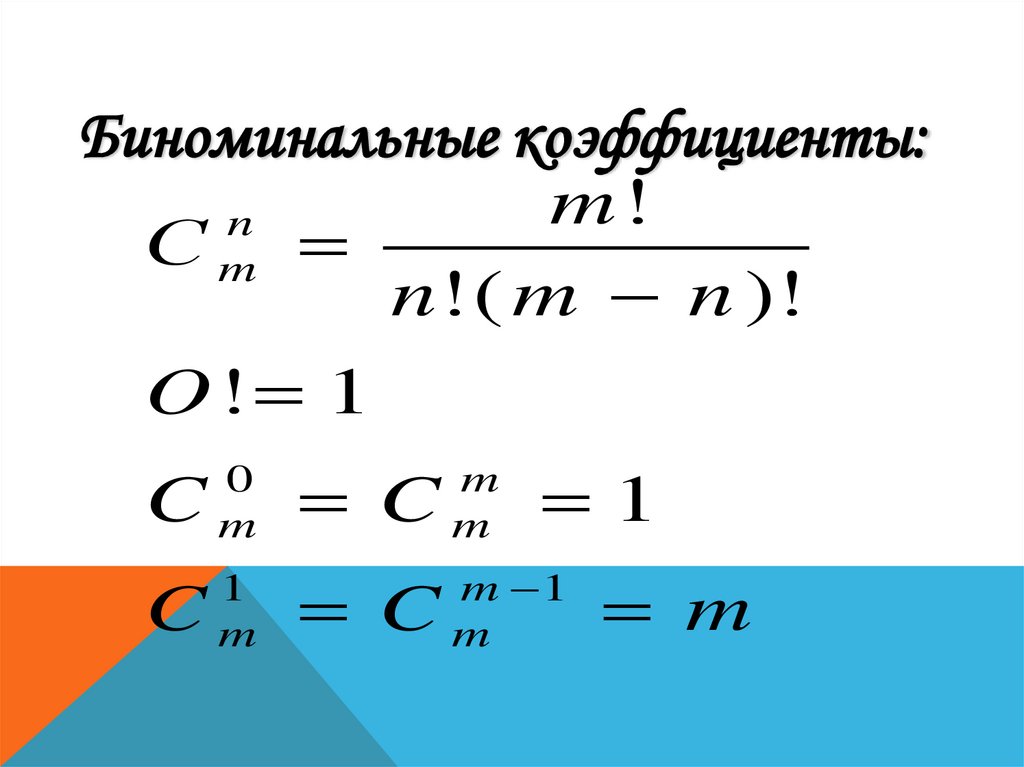

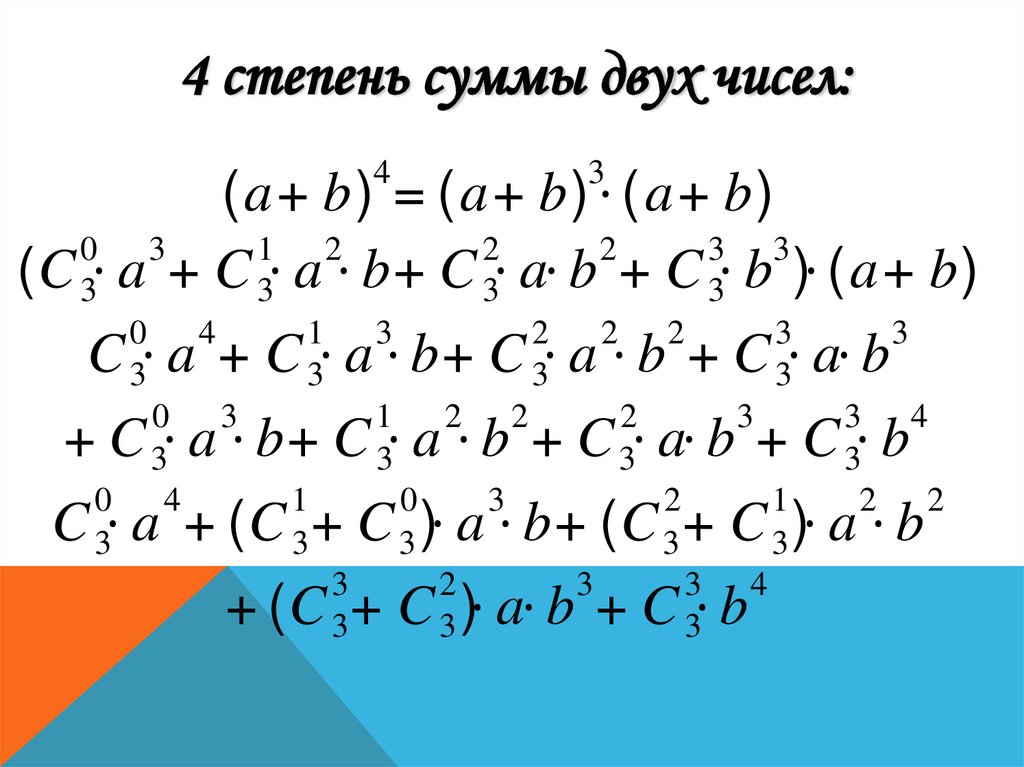




 mathematics
mathematics








