Similar presentations:
Прямой упругоплатический расчет пролетных строений железнодорожного моста с большими перемещениями
1.
1Ленинградцы Товарищи Братья и Сестры Солдаты и
Офицеры Однополчане 4 июня 2023 в 18 00 в
воскресенье в актовом зале горкома КПРФ состоится
конференция Все для Фронта Все для Победы и
перспективы освобождения нашей Родины от
паразитов, приспособленцев и эффективных
менеджеров по маме, по адресу Лиговский пр 207Б (Метро "Обводный канал" тел (950) 664-27-92, (904)
603-82-14 stalincom21@yandex.ru
www.npeterburg.ru Метелица Иван горкома 347-72-22
С докладом на конференции выступит Президент
организации «Сейсмофонд» при СПб ГАСУ , ветеран
боевых действий в Чеченской Республике 1994-1995
гг ОГРН:1022000000824, ИНН: 2014000780 Мажиев
Хасан Нажоевич и Коваленко Александр Иванович
по теме
ПРЯМОЙ УПРУГОПЛАТИЧЕСКИЙ РАСЧЕТ ПРОЛЕТНЫХ
СТРОЕНИЙ ЖЕЛЕЗНОДОРОЖНОГО МОСТА С БОЛЬШИМИ ПЕРЕМЕЩЕНИЯМИ НА
ПРЕДЕЛЬНОЕ РАВНОВЕСИЕ И ПРИСПОСОБЛЯЕМОСТЬ, НА ПРИМЕРЕ БЫСТРО
СОБИРАЕМОГО АМЕРИКАНСКОГО МОСТА, ДЛЯ ПЕРЕПРАВЫ ЧЕРЕЗ РЕКУ СУОН В
ШТАТЕ МОНТАНА, СКОНСТРУИРОВАННОГО СО ВСТРОЕННЫМ БЕТОННЫМ
НАСТИЛОМ, С ИСПОЛЬЗОВАНИЕМ УПРУГОПЛАСТИЧЕСКИХ ПРОЛЕТНЫХ
СТРОЕНИЙ фермы МОСТА, СКРЕПЛЕННЫХ БОЛТОВМИ СОЕДЕИНЯИМИ, С
ДИАГОНАЛЬНЫМИ НАТЯЖНЫМИ РАСКОСАМИ, ВЕРХНЕГО И НИЖНЕГО ПОЯСА
УДК 69.059.22
Уздин Александр Михайлович ПГУПС проф. дтн: uzdin@mail.ru ( 921) 788-33-64
Мажиев Хасан Нажоевич Президент организации «Сейсмофонд» при CПб ГАСУ ИНН: 2014000780
E-Mail: 6947810@mail.ru т/ф (812) 694-78-10, ( 921) 962-67-78, Коваленко Елена Ивановна заместитель Президента организации "Сейсмофонд" при СПб ГАСУ fax8126947810@gmail.com
1
2.
2(911) 175-84-65. Коваленко Александр Ивановича - зам .Президент организации "Сейсмофонд" при
СПб ГАСУ. ОГРН: 1022000000824. (981) 886-57-42? (981) 276-49-92 8126947810@internet.ru
9111758465@bk.ru
Рис. 1. Пролетное строение из упруго пластинчатых балок, через реку Суон, штат Монтана, США
построенное в 2017 по изобретениям проф дтн Уздина А.М
Рис. 1. Пролетное строение из упруго пластинчатых балок, через реку Суон, штат Монтана, США
построенное в 2017 по изобретениям проф дтн Уздина А.М
Ключевые слова: Сборно-разборные мосты, временные мосты, быстровозводимые мосты, мостовые
сооружения, мостовые конструкции, реконструкция мостов.
В данной работе описывается разработанный авторами прямой метод упругопла- стического
анализа стальных пространственных ферм в условиях больших перемещений, для ускоренного
монтажа временной надвижки длиной 60 метров шириной 3 метра упругопластинчетых
пространственных пролетных ферм быстро -собираемого моста с применением замкнутых
гнутосварных профилей прямоугольного сечения типа "Молодечно! ( серия 1.460-3-14 ГПИ
"Ленпроектстальконструкция" для системы несущих элементов и элементов проезжей части
пролетного надвижного строения моста с быстросъмеными упруго пластическими
компенсаторами ( заявка на изобретение: "Антисейсмическое фланцевое фрикционно -подвижное
2
3.
3соединение для трубопроводов " № 2018105803 F16L 23/02 от -7.06.2018 ФИПС заявитель СПб
ГАСУ ) , со сдвиговой фрикционо -демпфирующей жесткостью, приспособленных на предельную
нагрузку и приспособляемость с учетом больших перемещений за счет использования медной
обожженной гильзы, бронзовой втулки, тросовой гильзы стального троса в полимерной оплетке
или фрикци-болта с забитым медным обожженным клином в прорезанный паз болгаркой в
стальной шпильке стягивающего -контрольным натяжением болта, расположенного в длинных
овальных отверстиях , согласно изобретениям проф ПГУПС А.М.Уздина №№ 1143895Ю
1168755, 1174616, 2010136746, 2550777, 165076, 1760020, 154506
За основу был принят инкрементальный метод геометрически нелинейного анализа
пространственных ферм, разработанный ранее одним из авторов, и выполнена его модификация,
позволяющая учесть текучесть и пластические деформации в стержнях ферм. Предложенный
метод реализован в виде программного приложения на платформе Java. При помощи этого
приложения выполнен ряд примеров, описанных в данной работе. Приведенные примеры
демонстрируют, что прямой расчет пространственных ферм на пластическое предельное
равновесие и приспособляемость при больших перемещениях может быть успешно реализован в
программе. Алгоритмы охватывают широкий спектр упругопластического поведения фермы:
упругую работу, приспособляемость, прогрессирующие пластические деформации и разрушение при
формировании механизма. Программное приложение может быть использовано в качестве
тестовой платформы для исследования упругопластического поведения ферм и как инструмент для
решения прикладных задач.
КЛЮЧЕВЫЕ СЛОВА: стальная ферма, большие перемещения, пластичность, для ускоренного
монтажа временной надвижки длиной 60 метров шириной 3 метра упругопластинчетых
пространственных пролетных ферм быстро -собираемого моста с применением замкнутых
гнутосварных профилей прямоугольного сечения типа "Молодечно! ( серия 1.460-3-14 ГПИ
"Ленпроектстальконструкция" для системы несущих элементов и элементов проезжей части
пролетного надвижного строения моста с быстросъмеными упруго пластическими
компенсаторами ( заявка на изобретение: "Антисейсмическое фланцевое фрикционно -подвижное
соединение для трубопроводов " № 2018105803 F16L 23/02 от -7.06.2018 ФИПС заявитель СПб
ГАСУ ) , со сдвиговой фрикционо -демпфирующей жесткостью, приспособленных на предельную
нагрузку и приспособляемость с учетом больших перемещений за счет использования медной
обожженной гильзы, бронзовой втулки, тросовой гильзы стального троса в полимерной оплетке
или фрикци-болта с забитым медным обожженным клином в прорезанный паз болгаркой в
стальной шпильке стягивающего -контрольным натяжением болта, расположенного в длинных
3
4.
4овальных отверстиях , согласно изобретениям проф ПГУПС А.М.Уздина №№ 1143895Ю
1168755, 1174616, 2010136746, 2550777, 165076, 1760020, 154506
1. Теоретические основы расчета на пластическое предельное равновесие и приспособляемость
Деформации и устойчивость стальных конструкций зависят от геометрической и физической
нелинейности их поведения. При больших перемещениях конструкции условия равновесия и
зависимости «перемещения-деформации» нелинейны. Если материал в отдельных частях
конструкции достигает предела текучести, то изменяются соотношения «напряжениядеформации», а также отношения жесткостей элементов конструкции, и в ней могут
образовываться механизмы. Данная статья посвящена анализу таких конструкций при помощи
компьютерных моделей и для ускоренного монтажа временной надвижки длиной 60 метров
шириной 3 метра упругопластинчетых пространственных пролетных ферм быстро собираемого моста с применением замкнутых гнутосварных профилей прямоугольного сечения
типа "Молодечно! ( серия 1.460-3-14 ГПИ "Ленпроектстальконструкция" для системы несущих
элементов и элементов проезжей части пролетного надвижного строения моста с
быстросъмеными упруго пластическими компенсаторами ( заявка на изобретение:
"Антисейсмическое фланцевое фрикционно -подвижное соединение для трубопроводов " №
2018105803 F16L 23/02 от -7.06.2018 ФИПС заявитель СПб ГАСУ ) , со сдвиговой фрикционо демпфирующей жесткостью, приспособленных на предельную нагрузку и приспособляемость с
учетом больших перемещений за счет использования медной обожженной гильзы, бронзовой
втулки, тросовой гильзы стального троса в полимерной оплетке или фрикци-болта с забитым
медным обожженным клином в прорезанный паз болгаркой в стальной шпильке стягивающего контрольным натяжением болта, расположенного в длинных овальных отверстиях , согласно
изобретениям проф ПГУПС А.М.Уздина №№ 1143895Ю 1168755, 1174616, 2010136746, 2550777,
165076, 1760020, 154506
Теоретические основы расчета на предельную пластическую нагрузку и приспособляемость
изложены в сопутствующей статье [1]. Показано, что при малых перемещениях такие задачи
традиционно решаются при помощи методов оптимизации. При использовании методов
оптимизации, рассматривается последовательность статически возможных состояний
конструкции и определяется максимальный коэффициент нагружения, называемый
коэффициентом надежности приспособляемости. Альтернативно, может быть рассмотрена
последовательность кинематически возможных перемещений конструкции и определен
минимальный коэффициент нагружения.
В прямом методе расчета, излагаемом в данной работе, удовлетворяются как статические, так и
кинематические условия, и оптимизация не требуется. Прямой метод требует расчета
последовательности конфигураций конструкции, так как при наступлении пластичности ее
жесткость изменяется. Если какой-то из стержней фермы достигает пластического состояния
или наоборот, если стержень восстанавливает упругое состояние при разгрузке, должно быть
выполнено переформирование и разложение матрицы жесткости системы. На начальных этапах
развития теории предельного пластического равновесия и приспособляемости мощности
компьютеров не соответствовали объему вычислений прямого метода. В связи с этим,
предпочтение отдавалось методам, основанным на теории оптимизации, для которых был
разработан ряд теорем.
4
5.
5Все теоремы оптимизации, рассмотренные в [1] основаны на линейной суперпозиции нагрузок при
формировании их сочетаний. Если поведение конструкции геометрически нелинейно, то
суперпозиция нагрузок неправомерна. В этом случае теоремы теряют справедливость, и
оптимизационный подход не может быть использован для анализа приспособляемости.
При современном уровне развития компьютеров преимущество непрямого оптимизационного
подхода становится спорным даже для задач с малыми перемещениями. В представленной работе
5
6.
6поставлена задача оценить возможность использования прямого метода упругопластического
расчета для практических инженерных задач расчета стальных пространственных ферм.
Инкрементальный метод геометрически нелинейного анализа пространственных ферм, который
использован в настоящем исследовании, был описан в ряде публикаций [2-7], и поэтому в данной
статье не представлен. Авторами статьи была выполнена модификация этого метода,
позволяющая учесть текучесть и пластические деформации в стержнях ферм.
2. Упругопластическое поведение стального стержня для ускоренного монтажа временной
надвижки длиной 60 метров шириной 3 метра упругопластинчетых пространственных
пролетных ферм быстро -собираемого моста с применением замкнутых гнутосварных профилей
прямоугольного сечения типа "Молодечно! ( серия 1.460-3-14 ГПИ
"Ленпроектстальконструкция" для системы несущих элементов и элементов проезжей части
пролетного надвижного строения моста с быстросъмеными упруго пластическими
компенсаторами ( заявка на изобретение: "Антисейсмическое фланцевое фрикционно -подвижное
соединение для трубопроводов " № 2018105803 F16L 23/02 от -7.06.2018 ФИПС заявитель СПб
ГАСУ ) , со сдвиговой фрикционо -демпфирующей жесткостью, приспособленных на предельную
нагрузку и приспособляемость с учетом больших перемещений за счет использования медной
обожженной гильзы, бронзовой втулки, тросовой гильзы стального троса в полимерной оплетке
или фрикци-болта с забитым медным обожженным клином в прорезанный паз болгаркой в
стальной шпильке стягивающего -контрольным натяжением болта, расположенного в длинных
овальных отверстиях , согласно изобретениям проф ПГУПС А.М.Уздина №№ 1143895Ю
1168755, 1174616, 2010136746, 2550777, 165076, 1760020, 154506
Ускоренный способ надвижки американского автомобильного быстро-собираемого моста (
длиной 205 футов = 60 метров ) в штате Монтана ( США ) ,для переправы через реку Суон в 2017
сконструированного со встроенном бетонным настилом в полевых условиях с использованием
упруго пластических стальных ферм, скрепленных ботовыми соединениями между
диагональными натяжными элементами верхнего и нижнего пояса пролетного строения моста, с
экономией строительным материалов до 26 %
Аннотация. В статье приведен краткий обзор характеристик существующих временных мостовых
сооружений, история создания таких мостов и обоснована необходимость проектирования
универсальных быстровозводимых мостов построенных в штате Монтана через реку Суон в США
Стальные ферменные мосты являются эффективным и эстетичным вариантом для пересечения
автомобильных дорог. Их относительно небольшой вес по сравнению с пластинчато-балочными
системами делает их желательной альтернативой как с точки зрения экономии материалов, так и с
точки зрения конструктив-ности. Прототип сварной стальной фермы, сконструированной со
встроенным бетонным настилом, был предложен в качестве потенциальной альтернативы для
проектов ускоренного строительства мостов (ABC) в Монтане. Эта система состоит из сборноразборной сварной стальной фермы, увенчанной бетонным настилом, который может быть отлит на
заводе-изготовителе (для проектов ABC) или в полевых условиях после монтажа (для обычных
проектов). Чтобы исследовать возможные решения усталостных ограничений некоторых сварных
соединений элементов в этих фермах, были оценены болтовые соединения между диагональными
натяжными элементами и верхним и нижним поясами фермы. В этом исследовании для моста со
стальной фермой, скрепленной болтами /сваркой, были оценены как обычная система настила на
месте, так и ускоренная система настила моста (отлитая за одно целое с фермой). Для более точного
расчета распределения нагрузок на полосу движения и грузовые автомобили по отдельным фермам
6
7.
7была использована 3D-модель конечных элементов. Элементы фермы и соединения для обоих
вариантов конструкции были спроектированы с использованием нагрузок из комбинаций нагрузок
AASHTO Strength I, Fatigue I и Service II. Было проведено сравнение между двумя конфигурациями
ферм и длиной 205 футов. пластинчатая балка, используемая в ранее спроектированном мосту через
реку Суон. Оценки материалов и изготовления показывают, что стоимость традиционных и
ускоренных методов строительства на 10% и 26% меньше, соответственно, чем у пластинчатых
балок, предназначенных для переправы через реку Суон.
Специальные технические условия надвижки пролетного строения из стержневых
пространственных структур с использованием рамных сбороно-разборных конструкций с
использованием замкнутых гнутосварных профилей прямоуголного сечения, типа "Молодечно"
(серия 1.460.3-14 ГПИ "Ленпроектстальконструция"), МАРХИ ПСПК", "Кисловодск" ( RU 80471
"Комбинированная пространсвенная структура" ) на фрикционно -подвижных соедеиний для
обеспечения сейсмостойкого строительства железнодорожных мостов в Киевской Руси https://pptonline.org/1148335
Предпосылкой для необходимости проектирования новой временной мостовой конструкции
послужили стихийные бедствия в ДНР, ЛНР во время специальной военной операции на Украине в
20222012 г., где будут применены быстровозводимых сооружений, что могло бы значительно
увеличить шансы спасения человеческих жизней.
Разработанную, в том числе автором, новую конструкцию моста, можно монтировать со скорость
не менее 25 метров в сутки без применения тяжелой техники и кранов и доставлять в любой
пострадавший район воздушным транспортом. Разрезные пролетные строения могут достигать в
длину от 3 до 60 метров, при этом габарит пролетного строения так же варьируется. Сечение моста
подбирается оптимальным из расчета нагрузка/количество металла.
Рис. 2. Пролетное строение из упруго пластинчатых балок, через реку Суон, штат Монтана, США
построенное в 2017 по изобретениям проф дтн Уздина А.М
На настоящий момент построена экспериментальная модель моста в штате Минесота , через реку
Суон. Американской стороной проведены всесторонние испытания, показавшие высокую
корреляцию с расчетными значениями (минимальный запас 4.91%). Мостовое сооружение не имеет
аналогов на территории Российской Федерации.
На конструкцию армейского моста получен патенты №№ 1143895, 1168755, 1174616, 168076,
2010136746. Доработан авторами , в том числе авторами способ бескрановой установки надстройки
опор при строительстве временного железнодорожного моста № 180193 со сборкой на фланцевых
фрикционно-подвижных соединениях проф дтн А.М.Уздина для сборно-разборного
железнодорожного моста демпфирующего компенсатора гасителя динамических колебаний и
сдвиговых напряжений с учетом сдвиговой жесткости в ПК SCAD ( согласно СП 16.1330.2011
SCAD п.7.1.1 сдвиговая с учетом действий поперечных сил ) антисейсмическое фланцевое
7
8.
8фрикционное соединение для сборно-разборного быстрособираемого железнодорожного моста
из стальных конструкций покрытий производственных здании пролетами 18, 24 и 30 м с
применением замкнутых гнутосварных профилей прямоугольного сечения типа «Молодечно»
(серия 1.460.3-14 ГПИ «Ленпроект-стальконструкция» ) для системы несущих элементов и
элементов проезжей части армейского сборно-разборного пролетного надвижного строения
железнодорожного моста, с быстросъемными упругопластичными компенсаторами, со сдвиговой
фрикционно-демпфирующей прочностью и предназначенные для сейсмоопасных районов с
сейсмичностью до 9 баллов, серийный выпуск. В районах с сейсмичностью более 9 баллов,
необходимо использование демпфирующих компенсаторов с упругопластическими шарнирами на
фрикционно-подвижных соединениях, расположенных в длинных овальных отверстиях, с целью
обеспечения многокаскадного демпфирования при импульсных растягивающих и динамических
нагрузках согласно изобретениям, патенты: №№ 1143895, 1174616, 1168755 (автор: проф. д.т.н.
ПГУПС А.М.Уздин) , 2010136746 ,165076 , 2550777, с использованием сдвигового демпфирующего
гасителя сдвиговых напряжений , согласно заявки на изобретение «КОНСТРУКЦИЯ УЧАСТКА
ПОСТОЯННОГО ЖЕЛЕЗОБЕТОННОГО МОСТА НЕРАЗРЕЗНОЙ СИСТЕМЫ,
ВОССТАНОВЛЕННОГО С ПРИМЕНЕНИЕМ типовых структурных серии 1.460.3-14 ГПИ
"Ленпроектстальконструкция", стальные конструкции покрытий производственных» № 2022111669
от 25.05.2022, «Сборно-разборный железнодорожный мост» № 2022113052 от 27.05.2022,
«Сборно-разборный универсальный мост» № 2022113510 от 21.06.2022, «Антисейсмический
сдвиговой компенсатор для гашения колебаний пролетного строения моста» № 2022115073 от
02.06.2022 ФИПС : "Огнестойкого компенсатора -гасителя температурных напряжений" заявка №
2022104632 от 21.02.2022 , вх 009751, "Фрикционно-демпфирующий компенсатор для
трубопроводов" заявка № 2021134630 от 29.12.2021, "Термический компенсатор гаситель
температурных колебаний" Заявка № 2022102937 от 07.02.2022 , вх. 006318, "Термический
компенсатор гаситель температурных колебаний СПб ГАСУ № 20222102937 от 07 фев. 2022, вх
006318, «Огнестойкий компенсатор –гаситель температурных колебаний»,-регистрационный
2022104623 от 21.02.2022, вх. 009751, "Фланцевое соединения растянутых элементов трубопровода
со скошенными торцами" № а 20210217 от 23 сентября 2021, Минск, "Спиральная
сейсмоизолирующая опора с упругими демпферами сухого трения" № а 20210051, "Компенсатор
тов. Сталина для трубопроводов" № а 20210354 от 22 февраля 2022 Минск , заявка № 2018105803
от 27.02.2018 "Антисейсмическое фланцевое фрикционно-подвижное соединение для
трубопроводов" № а 20210354 от 22.02. 2022, Минск, "Антисейсмическое фланцевое фрикционноподвижное соединение для трубопроводов № 2018105803 от 15.02.2018 ФИПС, для обеспечения
сейсмостойкости сборно-разборных надвижных армейских быстровозводимых мостов в
сейсмоопасных районах в сейсмичностью более 9 баллов
8
9.
99
10.
10Рис. 3. Показано пролетное строение из упруго пластинчатых балок, через реку Суон, штат
Монтана, США
В результате стихийных бедствий (наводнение, сход сели, землетрясение, техногенная
катастрофа), военных или других чрезвычайных ситуаций происходит разрушение мостов и
путепроводов. Разрыв транспортных артерий существенно осложняет оказание помощи
пострадавшим местам. Максимально быстрое возобновление автомобильного и железнодорожного
движения является одной из главных задач восстановления жизнеобеспечения отрезанных стихией
районов. Мостовой переход - это сложное инженерное сооружение, состоящее из отдельных
объектов (опор, пролетных строений, эстакад, подходных насыпей и т.д.), капитальный ремонт или
новое строительство которых может длится годы. Поэтому в экстренных случаях используют
временные быстровозводимые конструкции, монтаж которых занимает всего несколько суток, а
иногда и часов. Последовательно рассмотрим существующие варианты восстановления мостового
перехода.
В исключительных случаях, при возникновении чрезвычайной ситуации могут сооружать
примитивные мосты, например, срубив дерево и опрокинув его на другой берег. На рисунке 1.
показан такой способ переправы, мост через реку Суон США , штат Монтана.
Примитивные мосты - это и подвесные мосты, сооруженные из подручных материалов.
Сплетенные из лиан и других ползучих растений веревки натягивают через ущелье, горный поток
или овраг, пространство между ними застилают или досками.. Ненадежность конструкции, низкая
10
11.
11грузоподъѐмность все это практически исключает примитивные мосты для серьезного использования
при ликвидации последствий стихийных бедствий.
Самым распространенным и самым быстрым способом устройства мостового перехода на
сегодняшний день является наведение понтонной переправы. Для еѐ монтажа требуется доставить
понтоны к месту строительства и спустить на воду, после чего происходит их объединение.
Плавучие элементы несут нагрузку за счет герметично устроенного корпуса.
Также возникают проблемы в организации такой переправы на быстротоках и мелководье. Для
доставки и монтажа требуется мощная, как правило, венная техника.
Дешевой и быстровозводимой разновидностью понтонных мостов через водную преграду
являются понтонно-модульные платформы. На каждой платформе предусмотрены специальные
проушины, которые позволяют собирать конструкцию любого габарита и любой длины.
Существенный недостаток этих мостов - низкая грузоподъемность. Максимальная нагрузка на
пластиковый модуль не превышает 400 кгс/м2. Применение таких мостов оправдано для переправы
людей в экстренных ситуациях, а так же для устройства причалов или плавучих ферм.
В основном, существующие в Российской Федерации временные сборно-разборные мостовые
переходы разработаны еще во времена СССР и «морально» устарели. Их конструкции, как правило,
не универсальны, т.е. неизменны по длине и величине пропускаемой нагрузки. Максимальная длина
одного балочного разрезного пролетного строения составляет 33 метра. Пролетное строение моста
через реку Суон 60 метров в Монтане США . Это влечет необходимость устройства
промежуточных опор при перекрытии широких препятствий, что не всегда возможно и занимает
дополнительное время. У всех рассмотренных сборно-разборных конструкций невозможна
оптимизация сечений элементов в зависимости от массы пропускаемой нагрузки. Единственным
решением, которое смогло исключить этот недостаток, является разрезное пролетное строение с
двумя решетчатыми фермами (патент РФ №2010136746, 1143895, 1168755, 1174616, 2550777,
165076, ). В конструкции этого моста имеется два варианта грузоподъемности: обычный и
повышенный. Для монтажа практически всех без исключения существующих решений временных
сооружений необходимо применение тяжелой техники и большого числа монтажников.
Соответственно, даже при возможности быстрого монтажа самой конструкции, доставка в район
постройки необходимой техники займет много времени. Целью данного исследования является
обеспечение возобновление пешеходного, автодорожного или железнодорожного движения в зоне
стихийного бедствия в кратчайшие сроки за счет применения при временном восстановлении
мостовых сооружений универсальной, сборно-разборной конструкции временного моста.
7. Заключение
Примеры, приведенные в данной статье, демонстрируют, что прямой расчет пространственных
ферм на пластическое предельное равновесие и приспособляемость при больших перемещениях
может быть успешно реализован в программе. Алгоритмы охватывают широкий спектр
упругопластического поведения фермы: упругую работу, приспособляемость, прогрессирующие
пластические деформации и разрушение при формировании механизма.
Полный набор результатов расчета включает переменные состояния узлов и стержней на всех
шагах нагружения всех шагов по времени во всех циклах для всех коэффициентов надежности и
является чрезвычайно объемным. Так как состояние стержня не изменяется на шаге нагружения,
на печать выводятся лишь каждое изменение состояния каждого стержня фермы. Эта детальная
информация позволяет выполнить тщательный анализ поведения конструкции.
11
12.
12Разработанное программное приложение позволяет определять последовательность, в которой
стержни достигают текучести, величину нагрузки, при которой это происходит, накопление
пластических деформаций в стержнях, остаточные напряжения в стержнях, а также
перемещения узлов при знакопеременной пластичности. Оно может быть использовано в качестве
тестовой платформы для исследования упругопластического поведения ферм и как инструмент для
решения многих прикладных задач.
Рис. 11. История перемещений узлов n5 и щ3 при коэффициенте X= 4,22656
Время, требуемое для расчета описанной выше двухпролетной фермы при 25 бисекциях и
максимальном количестве циклов для каждой бисекции равном 24, составляет 5 секунд для
стандартного портативного компьютера. Требуемое время зависит в основном от времени,
затрачиваемого на составление и решение систем уравнений. Ожидаемое время расчета
аналогичной фермы с 300 узлов - менее 1 часа. Для инженерной точности расчета время может
быть сокращено до 30 минут. Задачи большей размерности могут решаться на компьютерах
большей производительности, в том числе вычислительных кластерах.
Литература
1. Хейдари А., Галишникова В.В. Аналитический обзор теорем о предельной нагрузке и
приспособляемости в упругопластическом расчете стальных конструкций // Строительная
механика инженерных конструкций и сооружений.- 2014.- № 3. - С. 318.
2. Галишникова В.В. Вывод разрешающих уравнений задачи геометрически нелинейного
деформирования пространственных ферм на основе унифицированного подхода // Вестник
ВолгГАСУ, серия: Строительство и архитектура. - Волгоград, 2009.-Вып. 14(33). - С. 39-49.
3. Галишникова В.В. Постановка задачи геометрически нелинейного деформирования
пространственных ферм на основе метода конечных элементов // Вестник ВолгГА- СУ, серия:
Строительство и архитектура. - Волгорад, 2009. -Вып.14(33). - С. 50-58.
4. Галишникова В.В. Модификация метода постоянных дуг, основанная на использовании
матрицы секущей жесткости // Вестник МГСУ. - Москва, 2009. №2. - С. 63-69.
5. Галишникова В.В. Конечно-элементное моделирование геометрически нелинейного поведения
пространственных шарнирно-стержневых систем // Вестник гражданских инженеров (СПбГАСУ).
- СПб, 2007. -№ 2(11). - С. 101—106.
6. Галишникова В.В. Алгоритм геометрически нелинейного расчета пространственных шарнирностержневых конструкций на устойчивость // МСНТ «Наука и технологии»: Труды XXVII
Российской школы. - М.: РАН, 2007. - С. 235—244.
7. Галишникова В.В. Обобщенная геометрически нелинейная теория и численный анализ
деформирования и устойчивости пространственных стержневых систем. Диссертация на
соискание ученой степени доктора технических наук. -М.: МГСУ, 2011.
Refeгences
1. Heidari, А, Galishnikova, VV. (2014). A Review of Limit Load and Shakedown Theorems for the
Elastic-Plastic Analysis of Steel Structures.Structural Mechanics of Engineering Constructions and
Buildings, № 3, 3-18.
2. Galishnikova, VK(2009). Derivation of the governing equations for the problem of geometrically
nonlinear deformation of space trusses on the basis of unified approach. J. of Volgograd State University for
Architecture and Civil Engineering.Civil Eng. & Architecture, 14(33), 39-49 (in Russian).
3. Galishnikova, VV. (2009). Finite element formulation of the problem of geometrically nonlinear
deformations of space trusses. Journal of Volgograd State University for Architecture and Civil
Engineering.Civil Eng. & Architecture, 14(33), 50-58 (in Russian).
4. Galishnikova, VV. (2009). Modification of the constant arc length method based on the secant matrix
formulation. Journal of Moscow State University of Civil Engineering, №2, 63-69 (in Russian).
12
13.
135. Galishnikova, VV. (2007). Finite element modeling of geometrically nonlinear behavior of space
trusses. Journal of Civil Engineers. Saint-Petersburg University if Architecture and Civil Engineering,
2(11), 101—106 (in Russian).
6. Galishnikova, VV. (2007). Algorithm for geometrically nonlinear stability analysis of space trussed
systems. Proceedings of the XXVII Russian School "Science and Technology". Moscow: Russian Academy of
Science, 235-244 (in Russian).
7. Galishnikova VV. (2011). Generalized geometrically nonlinear theory and numerical deformation and
stability analysis of space trusses.Dissertation submitted for the degree of Dr. of Tech. Science. Moscow
State University of Civil Engineering, 2011.
DIRECT ELASTIC-PLASTIC LIMIT LOAD AND SHAKEDOWN ANALYSIS OF STEEL SPACE TRUSSES
WITH LARGE DISPLACEMENTS
A. Heidari, V.V. Galishnikova
Peoples Friendship University of Russia, Moscow
A direct method for elastic-plastic limit load and shakedown analysis of steel space trusses with large
displacements is treated in this paper. The incremental method for the geometrically nonlinear analysis of
space trusses, developed by one of the authors was modified to account for yielding and plastic strains in the
bars of the truss. The new method has been implemented in computer software. The examples in this paper
show that the direct analysis of space trusses with large displacements can be implemented successfully for
both the limit and the shakedown analysis of space trusses on the Java platform. The algorithms cover a
wide range of elastic-plastic truss behavior: purely elastic behavior, shakedown, ratcheting and collapse
due to the formation of a mechanism. The sequence in which the bars yield, the load levels at which this
occurs, the accumulation of the plastic strains in the bars, the residual stresses in the bars and the node
displacements during ratcheting can all be evaluated. The computer application is therefore suitable as a
test platform for elastic-plastic truss behavior. It can be applied to many other problems of elastic-plastic
space truss analysis.
KEY WORDS: steel space trusses, large displacements, plasticity, limit analysis, shakedown.
Строительная механика инженерных конструкций и сооружений, 2014, № 3
13
14.
1414
15.
1515
16.
1616
17.
1717
18.
1818
19.
1919
20.
2020
21.
2121
22.
22Из проведенных выше данных следует, что такая мостовая конструкция должна соответствовать
следующим современным требованиям:
1. Максимальная длина пролетного строения не менее 60 метров, ширина 3,5 метра , однопутный
, армейский для ДНР, ЛНР ;
2. Длина пролета должна быть переменной и кратной 3 метрам для случая его использования на
сохранившихся опорах капитального моста;
22
23.
233. Максимальный вес любого элемента пролетного строения, не должен превышать одной тонны, что
позволит ограничиться легким крановым оборудованием;
4. Конструкция пролетного строения должна обеспечивать возможность изменять его
геометрические характеристики, определяющие его несущую способность, в зависимости от массы и
габарита пропускаемой нагрузки;
5. Продолжительность монтажа пролетных строений для малых и средних мостов не должна
превышать 2-3 суток, что соответствует скорости его монтажа примерно 25 метров в сутки;
6. Конструкция должна обеспечивать многократность применения;
7. Время доставки конструкций моста в любую точку России не должно превышать одних суток.
С учетом всех вышеперечисленных требований, были разработаны конструкция и технология
сооружения временного моста, названного УЗДИН, по аналогу моста ТАЙПАН. Основная идея
состоит в том, что мост собирают подобно конструктору из отдельных элементов (панель,
поперечная балка, ортотропная плита, опорная стойка) максимальной массой 800 кг и габаритом 3,00
х 1,50 х 0,12 м. Ортотропные плиты проезда покрыты полимерным материалом, обеспечивающим
надежное сцепление колес автомобиля с проезжей частью.
Сборка не требует применения спецтехники: собирается жесткий каркас посредством различных
сборно-разборных соединений. При отсутствии опор, либо при невозможности их устройства (в
случае, когда необходим максимально быстрый монтаж конструкции), фундаментом могут служить
любые близлежащие бетонные блоки, при достаточности их размеров.
Отдельные конструктивные элементы пролетного строения и общий вид моста приведены на
рисунке 7. На конструкцию моста получен патент №137558, кл. E01D 15/133 от 20.02.2014 года.
Применение коротких блоков позволяет получить мосты практически любой длины, как с
разрезными, так и неразрезными балочными пролетными строениями, рассчитанными на пропуск
автомобильной нагрузки А11 и Н11 или колонны танков массой до 70 тонн каждый.
Промежуточные опоры собирают из тех же элементов, что и пролетное строение. В качестве
фундамента и устоев могут быть использованы любые бетонные блоки или бескрановая установка
надстроечных опор по изобретению № 180193 .
Сборка пролетного строения происходит на берегу соединением элементов жесткого каркаса
шплинтами, в необходимых случаях с применением легкого кранового оборудования - автомобиля с
гидроманипулятором (самопогрузчик). По предварительным оценкам скорость монтажа составит не
менее 25 метров в сутки. После сборки пролетного строения производят его надвижку в русло. При
надвижке необходимо использовать аванбек, который позволяет отказаться от противовеса.
Надвижку осуществляет либо группа людей (например, рота солдат), либо бульдозер, толкающий
пролетное строение.
Предельные автомобильно-дорожные нагрузки А11 и Н11 (одиночная нагрузка 80 тонн: 4 оси по
20 тонн) . При тех же характеристиках, грузоподъемность моста достаточна для пропуска колонны
танков до 50 тонн каждый.
Все элементы моста типовые и схемы сооружений отличаются большим или меньшим их
количеством. Основными несущими элементами являются панели размером 3х1.5 метра, которые
связывают между собой при помощи шарнирных соединений - пинов, а левый и правый пояса моста
объединяют поперечными балками. Таким образом, можно оптимизировать конструкцию исходя из
заданых задач - длина и грузоподъемность, тем самым обеспечив рациональную материалоемкость
(меньше нагрузка - меньше металла).
Транспортировку элементов можно выполнять автомобилями или по железной дороге. Доставка
конструкций моста в труднодоступные районы может быть осуществлена по воздуху в контейнерах,
так как это показано на рисунке 10.
23
24.
24Материалы хранятся
6947810@mail.ru
в библиотеке СПб ГАСУ
24
190005, 2-я Красноармейская дом 4
25.
25Рис. 6. Пролетное строение из упруго пластинчатых балок, через реку Суон, штат Монтана,
25
США
26.
2626
27.
2727
28.
2828
29.
2929
30.
3030
31.
3131
32.
3232
33.
3333
34.
3434
35.
3535
36.
3636
37.
3737
38.
3838
39.
3939
40.
4040
41.
4141
42.
4242
43.
4343
44.
44Рис. 3. Проверка состояния стержня в конце цикла итерации, для
ускоренного монтажа временной надвижки длиной 60
метров шириной
3 метра упругопластинчетых
пространственных пролетных ферм быстро -собираемого
моста с применением замкнутых гнутосварных профилей
прямоугольного сечения типа "Молодечно! ( серия 1.4603-14 ГПИ "Ленпроектстальконструкция" для системы
несущих элементов и элементов проезжей части
пролетного надвижного строения моста с
быстросъмеными упруго пластическими компенсаторами
( заявка на изобретение: "Антисейсмическое фланцевое
фрикционно -подвижное соединение для трубопроводов "
№ 2018105803 F16L 23/02 от -7.06.2018 ФИПС
заявитель СПб ГАСУ ) , со сдвиговой фрикционо демпфирующей жесткостью, приспособленных на
предельную нагрузку и приспособляемость с учетом
больших перемещений за счет использования медной
обожженной гильзы, бронзовой втулки, тросовой гильзы
стального троса в полимерной оплетке или фрикци-болта
с забитым медным обожженным клином в прорезанный паз
болгаркой в стальной шпильке стягивающего -контрольным
натяжением болта, расположенного в длинных овальных
отверстиях , согласно изобретениям проф ПГУПС
А.М.Уздина №№ 1143895Ю 1168755, 1174616,
2010136746, 2550777, 165076, 1760020, 154506
Стержень, упругий в начале шага, остается упругим в конце
шага нагружения, если абсолютное значение напряжения в нем
меньше предела текучести. В противном случае стержень в конце
шага считается достигшим текучести. Коэффициент снижения
нагрузки вычисляется следующим образом:
44
45.
45Рассмотрим стержень, состояние которого на шаге было
принято пластическим состоянием. Для упругой и пластической
деформаций задаются пределы погрешностей Se и ѐр. Типичными
значениями пределов погрешностей можно
считать 5S = 10-10 и 5р = 10 6 . Стержень испытывает на шаге
пластическую
деформацию, если значение абсолютной величины инкремента
пластической деформации | sp| превосходит погрешность ѐр. В
противном случае стержень во время шага был упругим вопреки
допущению, принятому в начале шага, и в программе
устанавливаются соответствующие флажки.
Если проверка состояния стержней в конце первого цикла
итераций показывает, что ни один их стержней не изменил
состояния, то цикл считается завершенным. Если хотя бы один
из стержней перешел в упругое состояние, шаг нагружения
повторяется с использованием новых состояний стержней.
В противном случае хотя бы один из стержней перешел в
пластическое состояние, и вычисляется наименьший
коэффициент редуцирования rmm. Пробное состояние
масштабируется при помощи этого коэффициента, и цикл
завершается.
В начале второго и всех последующих циклов итераций на шаге
нагруже- ния, состояние стержня принимается равным его
состоянию в конце предыдущего цикла. Вычисляется матрица
секущей жесткости для текущих инкрементов перемещений и
состояния стержней. Процедура продолжается так же, как и в
предыдущем цикле. Итерации на шаге нагружения завершаются,
когда норма погрешности пробного решения становится меньше
заданного предельного значения. Пошаговое нагружение
завершается, когда достигается предельная нагрузка или когда
выполняется заданное число шагов нагружения. Предельная
45
46.
46нагрузка считается достигнутой, когда максимальное заданное
число делений длины хорды в методе постоянных дуг не приводит
к формированию положительно определенной матрицы секущей
жесткости или к сходимости метода для пробного состояния
фермы на шаге нагружения.
4. Расчет двухпролетной фермы на предельную нагрузку Данный пример демонстрирует
применение прямого метода расчета на предельную пластическую нагрузку, описанного в разделе 3,
к анализу двухпролетной фермы, для ускоренного монтажа временной надвижки длиной 60
метров шириной
3 метра упругопластинчетых пространственных пролетных ферм быстро
-собираемого моста с применением замкнутых гнутосварных профилей прямоугольного сечения
типа "Молодечно! ( серия 1.460-3-14 ГПИ "Ленпроектстальконструкция" для системы несущих
элементов и элементов проезжей части пролетного надвижного строения моста с
быстросъмеными упруго пластическими компенсаторами ( заявка на изобретение:
"Антисейсмическое фланцевое фрикционно -подвижное соединение для трубопроводов " №
2018105803 F16L 23/02 от -7.06.2018 ФИПС заявитель СПб ГАСУ ) , со сдвиговой фрикционо демпфирующей жесткостью, приспособленных на предельную нагрузку и приспособляемость с
учетом больших перемещений за счет использования медной обожженной гильзы, бронзовой
втулки, тросовой гильзы стального троса в полимерной оплетке или фрикци-болта с забитым
медным обожженным клином в прорезанный паз болгаркой в стальной шпильке стягивающего контрольным натяжением болта, расположенного в длинных овальных отверстиях , согласно
изобретениям проф ПГУПС А.М.Уздина №№ 1143895Ю 1168755, 1174616, 2010136746, 2550777,
165076, 1760020, 154506
Рис. 4. Аксонометрическая проекция двухпролетной фермы (диагонали на показаны) для ускоренного
монтажа временной надвижки длиной 60 метров шириной 3 метра упругопластинчетых
пространственных пролетных ферм быстро -собираемого моста с применением замкнутых
гнутосварных профилей прямоугольного сечения типа "Молодечно! ( серия 1.460-3-14 ГПИ
"Ленпроектстальконструкция" для системы несущих элементов и элементов проезжей части
пролетного надвижного строения моста с быстросъмеными упруго пластическими
компенсаторами ( заявка на изобретение: "Антисейсмическое фланцевое фрикционно -подвижное
соединение для трубопроводов " № 2018105803 F16L 23/02 от -7.06.2018 ФИПС заявитель СПб
ГАСУ ) , со сдвиговой фрикционо -демпфирующей жесткостью, приспособленных на предельную
нагрузку и приспособляемость с учетом больших перемещений за счет использования медной
обожженной гильзы, бронзовой втулки, тросовой гильзы стального троса в полимерной оплетке
46
47.
47или фрикци-болта с забитым медным обожженным клином в прорезанный паз болгаркой в
стальной шпильке стягивающего -контрольным натяжением болта, расположенного в длинных
овальных отверстиях , согласно изобретениям проф ПГУПС А.М.Уздина №№ 1143895Ю
1168755, 1174616, 2010136746, 2550777, 165076, 1760020, 154506
Конструкция фермы состоит из четырех поясов, крестовой решетки и вертикальных связейдиафрагм, установленных в каждой панели длиной 2 м. Площади сечения элементов поясов и
диагональных элементов равны 0,0008 м2; площади сечения вертикальных и горизонтальных
элементов связей - 0,0006м2. Опоры в середине длины фермы представляют собой неподвижные
шарниры (перемещения по трем направлениям координационных осей равны нулю), крайние опоры подвижные шарниры (перемещения по направлениям осей х2и х3 равны нулю, перемещение вдоль оси
x1 возможно). Все стержни имеют пре5
2
8
2
дел текучести 2,4^10 кН/м и модуль упругости 2,1^10 кН/м . Схема нагружения состоит из двух
вертикальных сосредоточенных сил в 100 кН каждая, приложенных в средних узлах верхнего пояса
правого пролета фермы (см. рис. 4). Результаты расчета приведены на рис. 5 для грани фермы x2 =
0 с учетом симметрии задачи. Стержни, находящиеся на шаге нагружения в пластическом
состоянии, показаны на рисунке сплошной жирной линией. Стержни, достигающие предела
текучести на данном шаге, показаны жирным пунктиром. На рисунке показаны все изменения в
состояниях стержней и нагрузки, при которых они происходят. При уровне нагрузки 435,787 кН
наступает текучесть в поперечной связи между загруженными узлами, и формируется механизм
разрушения конструкции. Предельный коэффициент нагружения равен 4,542.
На рис. 6 показаны графики зависимости вертикальных перемещений от нагрузки для трех
свободных узлов нижнего пояса правого пролета фермы n11, n13 и n15 (см. рис. 5). Поведение
фермы остается почти линейным до уровня нагрузки около 370,0 кН, что составляет 81,5% от
предельной. Время, затраченное на выполнение прямого пошагового расчета 36-узловой фермы на
предельную пластическую нагрузку, составляет долю секунды. для ускоренного монтажа
временной надвижки длиной 60 метров шириной
3 метра упругопластинчетых
пространственных пролетных ферм быстро -собираемого моста с применением замкнутых
гнутосварных профилей прямоугольного сечения типа "Молодечно! ( серия 1.460-3-14 ГПИ
"Ленпроектстальконструкция" для системы несущих элементов и элементов проезжей части
пролетного надвижного строения моста с быстросъмеными упруго пластическими
компенсаторами ( заявка на изобретение: "Антисейсмическое фланцевое фрикционно -подвижное
соединение для трубопроводов " № 2018105803 F16L 23/02 от -7.06.2018 ФИПС заявитель СПб
ГАСУ ) , со сдвиговой фрикционо -демпфирующей жесткостью, приспособленных на предельную
нагрузку и приспособляемость с учетом больших перемещений за счет использования медной
обожженной гильзы, бронзовой втулки, тросовой гильзы стального троса в полимерной оплетке
или фрикци-болта с забитым медным обожженным клином в прорезанный паз болгаркой в
стальной шпильке стягивающего -контрольным натяжением болта, расположенного в длинных
овальных отверстиях , согласно изобретениям проф ПГУПС А.М.Уздина №№ 1143895, 1168755,
1174616, 2010136746, 2550777, 165076, 1760020, 154506
47
48.
4848
49.
4949
50.
5050
51.
5151
52.
5252
53.
5353
54.
5454
55.
5555
56.
5656
Рис. 6. Пролетное строение из упруго пластинчатых балок, через реку Суон, штат Монтана,
США
57.
5757
58.
5858
59.
5959
60.
6060
61.
6161
62.
6262
63.
6363
64.
6464
65.
6565
66.
6666
67.
6767
68.
6868
69.
6969
70.
7070
71.
7171
72.
7272
73.
7373
74.
7474
75.
7575
76.
7676
77.
7777
78.
78Рис. 3. Проверка состояния стержня в конце цикла итерации, для
ускоренного монтажа временной надвижки длиной 60
метров шириной
3 метра упругопластинчетых
пространственных пролетных ферм быстро -собираемого
моста с применением замкнутых гнутосварных профилей
прямоугольного сечения типа "Молодечно! ( серия 1.4603-14 ГПИ "Ленпроектстальконструкция" для системы
78
79.
79несущих элементов и элементов проезжей части
пролетного надвижного строения моста с
быстросъмеными упруго пластическими компенсаторами
( заявка на изобретение: "Антисейсмическое фланцевое
фрикционно -подвижное соединение для трубопроводов "
№ 2018105803 F16L 23/02 от -7.06.2018 ФИПС
заявитель СПб ГАСУ ) , со сдвиговой фрикционо демпфирующей жесткостью, приспособленных на
предельную нагрузку и приспособляемость с учетом
больших перемещений за счет использования медной
обожженной гильзы, бронзовой втулки, тросовой гильзы
стального троса в полимерной оплетке или фрикци-болта
с забитым медным обожженным клином в прорезанный паз
болгаркой в стальной шпильке стягивающего -контрольным
натяжением болта, расположенного в длинных овальных
отверстиях , согласно изобретениям проф ПГУПС
А.М.Уздина №№ 1143895Ю 1168755, 1174616,
2010136746, 2550777, 165076, 1760020, 154506
Стержень, упругий в начале шага, остается упругим в конце
шага нагружения, если абсолютное значение напряжения в нем
меньше предела текучести. В противном случае стержень в конце
шага считается достигшим текучести. Коэффициент снижения
нагрузки вычисляется следующим образом:
Рассмотрим стержень, состояние которого на шаге было
принято пластическим состоянием. Для упругой и пластической
деформаций задаются пределы погрешностей Se и ѐр. Типичными
значениями пределов погрешностей можно
считать 5S = 10-10 и 5р = 10 6 . Стержень испытывает на шаге
пластическую
79
80.
80деформацию, если значение абсолютной величины инкремента
пластической деформации | sp| превосходит погрешность ѐр. В
противном случае стержень во время шага был упругим вопреки
допущению, принятому в начале шага, и в программе
устанавливаются соответствующие флажки.
Если проверка состояния стержней в конце первого цикла
итераций показывает, что ни один их стержней не изменил
состояния, то цикл считается завершенным. Если хотя бы один
из стержней перешел в упругое состояние, шаг нагружения
повторяется с использованием новых состояний стержней.
В противном случае хотя бы один из стержней перешел в
пластическое состояние, и вычисляется наименьший
коэффициент редуцирования rmm. Пробное состояние
масштабируется при помощи этого коэффициента, и цикл
завершается.
В начале второго и всех последующих циклов итераций на шаге
нагруже- ния, состояние стержня принимается равным его
состоянию в конце предыдущего цикла. Вычисляется матрица
секущей жесткости для текущих инкрементов перемещений и
состояния стержней. Процедура продолжается так же, как и в
предыдущем цикле. Итерации на шаге нагружения завершаются,
когда норма погрешности пробного решения становится меньше
заданного предельного значения. Пошаговое нагружение
завершается, когда достигается предельная нагрузка или когда
выполняется заданное число шагов нагружения. Предельная
нагрузка считается достигнутой, когда максимальное заданное
число делений длины хорды в методе постоянных дуг не приводит
к формированию положительно определенной матрицы секущей
жесткости или к сходимости метода для пробного состояния
фермы на шаге нагружения.
80
81.
814. Расчет двухпролетной фермы на предельную нагрузку Данный
пример демонстрирует применение прямого метода расчета на
предельную пластическую нагрузку, описанного в разделе 3, к
анализу двухпролетной фермы, для ускоренного монтажа
временной надвижки длиной 60 метров шириной
3
метра упругопластинчетых пространственных
пролетных ферм быстро -собираемого моста с
применением замкнутых гнутосварных профилей
прямоугольного сечения типа "Молодечно! ( серия 1.4603-14 ГПИ "Ленпроектстальконструкция" для системы
несущих элементов и элементов проезжей части
пролетного надвижного строения моста с
быстросъмеными упруго пластическими компенсаторами
( заявка на изобретение: "Антисейсмическое фланцевое
фрикционно -подвижное соединение для трубопроводов "
№ 2018105803 F16L 23/02 от -7.06.2018 ФИПС
заявитель СПб ГАСУ ) , со сдвиговой фрикционо демпфирующей жесткостью, приспособленных на
предельную нагрузку и приспособляемость с учетом
больших перемещений за счет использования медной
обожженной гильзы, бронзовой втулки, тросовой гильзы
стального троса в полимерной оплетке или фрикци-болта
с забитым медным обожженным клином в прорезанный паз
болгаркой в стальной шпильке стягивающего -контрольным
натяжением болта, расположенного в длинных овальных
отверстиях , согласно изобретениям проф ПГУПС
А.М.Уздина №№ 1143895Ю 1168755, 1174616,
2010136746, 2550777, 165076, 1760020, 154506
81
82.
82Рис. 4. Аксонометрическая проекция двухпролетной фермы (диагонали на показаны) для ускоренного
монтажа временной надвижки длиной 60 метров шириной 3 метра упругопластинчетых
пространственных пролетных ферм быстро -собираемого моста с применением замкнутых
гнутосварных профилей прямоугольного сечения типа "Молодечно! ( серия 1.460-3-14 ГПИ
"Ленпроектстальконструкция" для системы несущих элементов и элементов проезжей части
пролетного надвижного строения моста с быстросъмеными упруго пластическими
компенсаторами ( заявка на изобретение: "Антисейсмическое фланцевое фрикционно -подвижное
соединение для трубопроводов " № 2018105803 F16L 23/02 от -7.06.2018 ФИПС заявитель СПб
ГАСУ ) , со сдвиговой фрикционо -демпфирующей жесткостью, приспособленных на предельную
нагрузку и приспособляемость с учетом больших перемещений за счет использования медной
обожженной гильзы, бронзовой втулки, тросовой гильзы стального троса в полимерной оплетке
или фрикци-болта с забитым медным обожженным клином в прорезанный паз болгаркой в
стальной шпильке стягивающего -контрольным натяжением болта, расположенного в длинных
овальных отверстиях , согласно изобретениям проф ПГУПС А.М.Уздина №№ 1143895Ю
1168755, 1174616, 2010136746, 2550777, 165076, 1760020, 154506
Конструкция фермы состоит из четырех поясов, крестовой решетки и вертикальных связейдиафрагм, установленных в каждой панели длиной 2 м. Площади сечения элементов поясов и
диагональных элементов равны 0,0008 м2; площади сечения вертикальных и горизонтальных
элементов связей - 0,0006м2. Опоры в середине длины фермы представляют собой неподвижные
шарниры (перемещения по трем направлениям координационных осей равны нулю), крайние опоры подвижные шарниры (перемещения по направлениям осей х2и х3 равны нулю, перемещение вдоль оси
x1 возможно). Все стержни имеют пре5
2
8
2
дел текучести 2,4^10 кН/м и модуль упругости 2,1^10 кН/м . Схема нагружения состоит из двух
вертикальных сосредоточенных сил в 100 кН каждая, приложенных в средних узлах верхнего пояса
правого пролета фермы (см. рис. 4). Результаты расчета приведены на рис. 5 для грани фермы x2 =
0 с учетом симметрии задачи. Стержни, находящиеся на шаге нагружения в пластическом
состоянии, показаны на рисунке сплошной жирной линией. Стержни, достигающие предела
текучести на данном шаге, показаны жирным пунктиром. На рисунке показаны все изменения в
состояниях стержней и нагрузки, при которых они происходят. При уровне нагрузки 435,787 кН
наступает текучесть в поперечной связи между загруженными узлами, и формируется механизм
разрушения конструкции. Предельный коэффициент нагружения равен 4,542.
На рис. 6 показаны графики зависимости вертикальных перемещений от нагрузки для трех
свободных узлов нижнего пояса правого пролета фермы n11, n13 и n15 (см. рис. 5). Поведение
фермы остается почти линейным до уровня нагрузки около 370,0 кН, что составляет 81,5% от
предельной. Время, затраченное на выполнение прямого пошагового расчета 36-узловой фермы на
предельную пластическую нагрузку, составляет долю секунды. для ускоренного монтажа
временной надвижки длиной 60 метров шириной
3 метра упругопластинчетых
82
83.
83пространственных пролетных ферм быстро -собираемого моста с применением замкнутых
гнутосварных профилей прямоугольного сечения типа "Молодечно! ( серия 1.460-3-14 ГПИ
"Ленпроектстальконструкция" для системы несущих элементов и элементов проезжей части
пролетного надвижного строения моста с быстросъмеными упруго пластическими
компенсаторами ( заявка на изобретение: "Антисейсмическое фланцевое фрикционно -подвижное
соединение для трубопроводов " № 2018105803 F16L 23/02 от -7.06.2018 ФИПС заявитель СПб
ГАСУ ) , со сдвиговой фрикционо -демпфирующей жесткостью, приспособленных на предельную
нагрузку и приспособляемость с учетом больших перемещений за счет использования медной
обожженной гильзы, бронзовой втулки, тросовой гильзы стального троса в полимерной оплетке
или фрикци-болта с забитым медным обожженным клином в прорезанный паз болгаркой в
стальной шпильке стягивающего -контрольным натяжением болта, расположенного в длинных
овальных отверстиях , согласно изобретениям проф ПГУПС А.М.Уздина №№ 1143895, 1168755,
1174616, 2010136746, 2550777, 165076, 1760020, 154506
83
84.
8484
85.
8585
86.
8686
87.
8787
88.
8888
89.
8989
90.
9090
91.
9191
92.
9292
93.
9393
94.
9494
95.
9595
96.
9696
97.
9797
98.
9898
99.
9999
100.
100100
101.
101101
102.
102102
103.
103103
104.
104104
105.
105105
106.
106106
107.
107107
108.
108108
109.
109109
110.
110110
111.
111111
112.
112112
113.
113113
114.
114114
115.
115115
116.
116116
117.
117117
118.
118118
119.
119119
120.
120120
121.
121121
122.
122122
123.
123123
124.
124124
125.
125125
126.
126126
127.
127127
128.
128128
129.
129129
130.
130130
131.
131131
132.
132132
133.
133133
134.
134134
135.
135135
136.
136136
137.
137137
138.
138138
139.
139139
140.
140140
141.
141141
142.
142142
143.
143РОССИЙСКИЙ УНИВЕРСИТЕТ ДРУЖБЫ НАРОДОВ
143
144.
144ИНЖЕНЕРНЫЙ ФАКУЛЬТЕТ
КАФЕДРА СТРОИТЕЛЬНЫХ КОНСТРУКЦИЙ И
СООРУЖЕНИЙ
«К защите допускается»: Заведующий
кафедрой к.т.н., доцент
Галишникова В.В.
«__ »_____________2014 г.
диссертации на соискание ученой степени кандидата
технических наук
Прямой упругопластический расчет стальных
пространственных ферм на предельную нагрузку и
приспособляемость с учетом больших перемещений
(название)
Выполнил
Аспирант Хейдари Алиреза Ф.И.О.
(подпись)
Научный руководитель Галишникова Вера Владимировна
Ф.И.О.
к.т.н., доцент (подпись)
(ученая степень, звание)
Москва, 2014
ЭЛЕМЕНТЫ ТЕОРИИ ТРЕНИЯ,
РАСЧЕТ И ТЕХНОЛОГИЯ ПРИМЕНЕНИЯ
ФРИКЦИОННО-ПОДВИЖНЫХ СОЕДИНЕНИЙ
УЗДИН А.М., ЕЛИСЕЕВ О.Н., , НИКИТИН А.А., ПАВЛОВ В.Е., СИМКИН А.Ю.,
КУЗНЕЦОВА И.О.
144
145.
145ЭЛЕМЕНТЫ ТЕОРИИ ТРЕНИЯ,
РАСЧЕТ И ТЕХНОЛОГИЯ ПРИМЕНЕНИЯ
ФРИКЦИОННО-ПОДВИЖНЫХ СОЕДИНЕНИЙ
145
146.
146СОДЕРЖАНИЕ
1
Введение
3
2
Элементы теории трения и износа
6
3
Методика расчета одноболтовых ФПС
18
3.1
Исходные посылки для разработки методики расчета ФПС
18
3.2
Общее уравнение для определения несущей способности ФПС.
20
3.3
Решение общего уравнения для стыковых ФПС
21
3.4
Решение общего уравнения для нахлесточных ФПС
22
4
Анализ экспериментальных исследований работы ФПС
26
5
Оценка
параметров
диаграммы
деформирования
многоболтовых
фрикционно-подвижных соединений (ФПС)
31
5.1
Общие положения методики расчета многоболтовых ФПС
31
5.2
Построение уравнений деформирования стыковых многоболтовых ФПС
32
5.3
Построение уравнений деформирования нахлесточных многоболтовых 38
ФПС
6
Рекомендации по технологии изготовления ФПС и сооружений с такими
соединениями
6.1
42
Материалы болтов, гаек, шайб и покрытий контактных поверхностей
стальных деталей ФПС и опорных поверхностей шайб
42
6.2
Конструктивные требования к соединениям
43
6.3
Подготовка
контактных
поверхностей
элементов
и
методы
контроля
6.4
45
Приготовление и нанесение протекторной грунтовки ВЖС 83-0287. Требования к загрунтованной поверхности. Методы контроля
6.4.1
Основные требования по технике безопасности при работе с
грунтовкой ВЖС 83-02-87
6.4.2
Транспортировка
и
47
хранение
элементов
законсервированных грунтовкой ВЖС 83-02-87
6.5
46
и
деталей,
49
Подготовка и нанесение антифрикционного покрытия на опорные 49
поверхности шайб
6.6
Сборка ФПС
49
7
Список литературы
51
146
147.
147147
148.
148В данной работе описывается разработанный авторами
прямой метод упругопла- стического анализа стальных
пространственных ферм в условиях больших перемещений. За
основу был принят инкрементальный метод геометрически
нелинейного анализа пространственных ферм, разработанный
ранее одним из авторов, и выполнена его модификация,
позволяющая учесть текучесть и пластические деформации в
стержнях ферм. Предложенный метод реализован в виде
программного приложения на платформе Java. При помощи этого
приложения выполнен ряд примеров, описанных в данной работе.
Приведенные примеры демонстрируют, что прямой расчет
пространственных ферм на пластическое предельное равновесие и
приспособляемость при больших перемещениях может быть
успешно реализован в программе. Алгоритмы охватывают
широкий спектр упругопластического поведения фермы: упругую
работу, приспособляемость, прогрессирующие пластические
деформации и разрушение при формировании механизма.
Программное приложение может быть использовано в качестве
тестовой платформы для исследования упругопластического
поведения ферм и как инструмент для решения прикладных задач.
КЛЮЧЕВЫЕ СЛОВА: стальная ферма, большие перемещения,
пластичность.
1. Теоретические основы расчета на пластическое предельное
равновесие и приспособляемость
148
149.
149Деформации и устойчивость стальных конструкций зависят от
геометрической и физической нелинейности их поведения. При
больших перемещениях конструкции условия равновесия и
зависимости «перемещения-деформации» нелинейны. Если
материал в отдельных частях конструкции достигает предела
текучести, то изменяются соотношения «напряжениядеформации», а также отношения жесткостей элементов
конструкции, и в ней могут образовываться механизмы. Данная
статья посвящена анализу таких конструкций при помощи
компьютерных моделей.
Теоретические основы расчета на предельную пластическую
нагрузку и приспособляемость изложены в сопутствующей
статье [1]. Показано, что при малых перемещениях такие задачи
традиционно решаются при помощи методов оптимизации. При
использовании методов оптимизации, рассматривается
последовательность статически возможных состояний
конструкции и определяется максимальный коэффициент
нагружения, называемый коэффициентом надежности
приспособляемости. Альтернативно, может быть рассмотрена
последовательность кинематически возможных перемещений
конструкции и определен минимальный коэффициент нагружения.
В прямом методе расчета, излагаемом в данной работе,
удовлетворяются как статические, так и кинематические
условия, и оптимизация не требуется. Прямой метод требует
расчета последовательности конфигураций конструкции, так как
при наступлении пластичности ее жесткость изменяется. Если
какой-то из стержней фермы достигает пластического
состояния или наоборот, если
стержень восстанавливает упругое состояние при разгрузке,
должно быть выполнено переформирование и разложение
матрицы жесткости системы. На начальных этапах развития
теории предельного пластического равновесия и
149
150.
150приспособляемости мощности компьютеров не соответствовали
объему вычислений прямого метода. В связи с этим, предпочтение
отдавалось методам, основанным на теории оптимизации, для
которых был разработан ряд теорем.
Все теоремы оптимизации, рассмотренные в [1] основаны на
линейной суперпозиции нагрузок при формировании их сочетаний.
Если поведение конструкции геометрически нелинейно, то
суперпозиция нагрузок неправомерна. В этом случае теоремы
теряют справедливость, и оптимизационный подход не может
быть использован для анализа приспособляемости.
При современном уровне развития компьютеров преимущество
непрямого оптимизационного подхода становится спорным даже
для задач с малыми перемещениями. В представленной работе
поставлена задача оценить возможность использования прямого
метода упругопластического расчета для практических
инженерных задач расчета стальных пространственных ферм.
Инкрементальный метод геометрически нелинейного анализа
пространственных ферм, который использован в настоящем
исследовании, был описан в ряде публикаций [2-7], и поэтому в
данной статье не представлен. Авторами статьи была выполнена
модификация этого метода, позволяющая учесть текучесть и
пластические деформации в стержнях ферм.
2. Упругопластическое поведение стального стержня
ш
<=
F пластичность
Рис. 1. Зависимость осевого усилия в стержне от осевой
деформации
Е
150
151.
151На рис.1 показано изменение состояния стержня как функция
инкремента осевой деформации на шаге нагружения. В точках A,
D и G стержень остается упругим при положительных и
отрицательных инкрементах деформации. В
Каждый стержень фермы рассматривается как конечный
элемент постоянного поперечного сечения, подверженный
действию лишь осевого усилия. Стержни соединяются в узлах
шарнирно. Упругая потеря устойчивости отдельных стержней не
рассматривается. Если стержень достигает пластичности, то
полагается, что он может нести осевую нагрузку,
соответствующую напряжению текучести. Считается, что
каждый стержень фермы на шаге нагружения находится либо в
упругом, либо в пластическом состоянии. Величина шага
вычисляется в алгоритме решения таким образом, чтобы
справедливость этого положения не нарушалась. Вклад каждого
стержня в секущую матрицу фермы вычисляется при помощи
выражений, выведенных для геометрически нелинейного расчета
ферм [4]. Если стержень достиг пластичности, то его вклад в
секущую матрицу жесткости фермы равен нулю.
точках B и C стержень будет упругим при отрицательных
инкрементах деформации и пластическим - при положительных
инкрементах деформации. В точках E и F стержень будет
упругим при положительных инкрементах деформации и
пластическим - при отрицательных.
Пусть st, se и sp - полные, упругие и пластические деформации в
стержне соответственно. Верхним индексом (5) будем
обозначать значение переменной в начале шага, а индексом (t) - ее
значение в конце шага нагружения. Обозначим через vk
компоненты координат перемещения в исходной системе
координат, и vk1- их производные по осевой координате y\. Полная
осевая деформация
в стержне задана следующим выражением [2]:
2 2 2 2 st = V11 + 0,5( v2i + v2,i + V31)2 . (1)
151
152.
152Если стержень на шаге нагружения остается упругим, то его
деформация в пробном состоянии равна
s?) = s?) -s« (2) sP = s« (3)
Пусть m - переходный коэффициент между координатами
второго тензора Пиолы - Кирхгофа и координатами вектора
технических напряжений:
m = ^ (1 + V11)2 + vf i + V32i . (4)
Тогда напряжение а и осевое усилие f в стержне в пробном
состоянии определятся из следующих уравнений:
a(t) = m(t) E s?), (5) f(t) = Aa(t) .
(6)
Если стержень на шаге нагружения является пластичным, то
его деформация в пробном состоянии определяется следующим
образом:
set) = s«, (7)
s« =sP5) + Asp, Asp =s(t) -si5).
(8)
Напряжение а и осевое усилие f в стержне, достигшем
пластичности, в пробном состоянии равны:
a(t) = а( 5), (9) f(t) = f(5). (10)
3. Прямой метод расчета по предельному равновесию
В прямом методе расчета на пластическое предельное
равновесие задается схема нагружения (модельная нагрузка),
которая затем умножается на коэффициент нагружения X ,
давая значение нагрузки на шаге нагружения. Определяется
максимальное значение коэффициента нагружения, при котором
конструкция сохраняет устойчивость. Так как предполагается,
что конструкция испытывает большие перемещения, то заранее
не известно, какое предельное состояние наступит раньше:
потеря устойчивости формы конструкции или образование
пластического механизма.
На рис. 2 показана структурная схема алгоритма расчета
фермы на предельную нагрузку. Алгоритм учитывает
геометрическую и физическую нелинейность и состоит из двух
вложенных циклов. Во внешнем цикле выполняется пошаговый
расчет до достижения заданного коэффициента нагружения или
152
153.
153наступления предельного состояния фермы. Во внутреннем цикле
производится итерационное вычисление матрицы секущей
матрицы для шага нагружения в соответствии с инкрементами
перемещения и изменениями состояний стержней.
Истинное состояние стержней на шаге нагружения
определяется итерационно. В начале первого шага нагружения все
стержни упруги и свободны от
напряжений. В первом цикле итераций на всех последующих шагах
нагружения полагается, что стержень пластичен, если он был
пластичен в конце предыдущего шага нагружения. В противном
случае, стержень полагается упругим. Эти предположения могут
оказаться некорректными, и будут уточняться в конце каждого
шага нагружения.
С
J
Начало расчета
^Увеличить коэффициент нагружения J
Итерации секущей матрицы J<
\
1
Вычисление и разложение матрицы
\
1
нет
да
да
^Матрица положительно определена?^>\
, Да
153
154.
154Вычисление пробного состояния
\
г
С
Стержень стал упругим?
Изменилось состояние стержня?
\
, Да
масштабировать пробное состояние
\
г
погрешность состояния < Mm
нет
да
С
цикл итерации < max
нет
уменьшить длину дуги вдвое
да
С
восстановить состояние фермы в начале шага нагружения
да
-Ждлина дуги > min
нет
Q достигнута предельная нагрузка )
сохранить состояние фермы
154
155.
155коэффициент нагружения < max
С
3
конец расчета
Рис. 2. Структурная схема алгоритма расчета фермы на
предельную нагрузку
В первом цикле итераций вычисляется матрица касательной
жесткости фермы и выполняется ее разложение. Инкремент
коэффициента нагружения на цикле, а также перемещения и
реакции в пробном состоянии в конце цикла определяются по
алгоритму геометрически нелинейного анализа, описанному в
работе [7]. При этом выявляются изменение в состояниях
стержней и отмечаются в программе флажками, в которых
значение true имеет следующие смыслы: estart - стержень
является упругим в начале шага нагружения;
eend - стержень является упругим в конце шага нагружения;
dc - по крайней мере один из стержней изменил состояние на
шаге;
de - по крайней мере один из стержней стал упругим на шаге;
dp - по крайней мере один из стержней достиг пластичности на
шаге.
На рис. 3 показан алгоритм проверки состояния стержней.
С
3
начало проверки
estart == trUe
,да
155
156.
156с(,)
<су ((a(s) > 0)л(DSp >SE})> ((с« < 0)л(DSp <SE})
estart = true
dc = true de = true
\
!
return J
да
eend = false
!
< DEP
>5с >
t да
dp = true
Рис. 3. Проверка состояния стержня в конце цикла итерации
Стержень, упругий в начале шага, остается упругим в конце
шага нагружения, если абсолютное значение напряжения в нем
меньше предела текучести. В противном случае стержень в конце
шага считается достигшим текучести. Коэффициент снижения
нагрузки вычисляется следующим образом:
с, -с<д)
c(t) -сО -с, -с<д)
c(t) -с«
(t)
(11) (12)
> 0:
с
r=
(t)
< 0:
156
157.
157с
r=
Рассмотрим стержень, состояние которого на шаге было
принято пластическим состоянием. Для упругой и пластической
деформаций задаются пределы погрешностей Se и ѐр. Типичными
значениями пределов погрешностей можно
считать 5S = 10-10 и 5р = 10 6 . Стержень испытывает на шаге
пластическую
деформацию, если значение абсолютной величины инкремента
пластической деформации | sp| превосходит погрешность ѐр. В
противном случае стержень во время шага был упругим вопреки
допущению, принятому в начале шага, и в программе
устанавливаются соответствующие флажки.
Если проверка состояния стержней в конце первого цикла
итераций показывает, что ни один их стержней не изменил
состояния, то цикл считается завершенным. Если хотя бы один
из стержней перешел в упругое состояние, шаг
55
нагружения повторяется с использованием новых состояний
стержней. В противном случае хотя бы один из стержней
перешел в пластическое состояние, и вычисляется наименьший
коэффициент редуцирования rmm. Пробное состояние
масштабируется при помощи этого коэффициента, и цикл
завершается.
В начале второго и всех последующих циклов итераций на шаге
нагруже- ния, состояние стержня принимается равным его
состоянию в конце предыдущего цикла. Вычисляется матрица
секущей жесткости для текущих инкрементов перемещений и
состояния стержней. Процедура продолжается так же, как и в
предыдущем цикле. Итерации на шаге нагружения завершаются,
157
158.
158когда норма погрешности пробного решения становится меньше
заданного предельного значения. Пошаговое нагружение
завершается, когда достигается предельная нагрузка или когда
выполняется заданное число шагов нагружения. Предельная
нагрузка считается достигнутой, когда максимальное заданное
число делений длины хорды в методе постоянных дуг не приводит
к формированию положительно определенной матрицы секущей
жесткости или к сходимости метода для пробного состояния
фермы на шаге нагружения.
4. Расчет двухпролетной фермы на предельную нагрузку Данный
пример демонстрирует применение прямого метода расчета на
предельную пластическую нагрузку, описанного в разделе 3, к
анализу двухпролетной фермы, показанной на рисунке 4.
x
2,0
2
100 кН 100 кН
к
2,0
x
2,0
2,0
2,0
2,0
2,0
2,0
Х8,0
2,0 -Л- 2,0
8,0
158
159.
159Рис. 4. Аксонометрическая проекция двухпролетной фермы
(диагонали на показаны)
Конструкция фермы состоит из четырех поясов, крестовой
решетки и вертикальных связей-диафрагм, установленных в
каждой панели длиной 2 м. Площади сечения элементов поясов и
диагональных элементов равны 0,0008 м2; площади сечения
вертикальных и горизонтальных элементов связей - 0,0006м2.
Опоры в середине длины фермы представляют собой
неподвижные шарниры (перемещения по трем направлениям
координационных осей равны нулю), крайние опоры - подвижные
шарниры (перемещения по направлениям осей х2и х3 равны нулю,
перемещение вдоль оси x1 возможно). Все стержни имеют пре5 2 8 2
дел текучести 2,4^10 кН/м и модуль упругости 2,1^10 кН/м . Схема
нагружения состоит из двух вертикальных сосредоточенных сил в
100 кН каждая, приложенных в средних узлах верхнего пояса
правого пролета фермы (см. рис. 4). Результаты расчета
приведены на рис. 5 для грани фермы x2 = 0 с учетом симметрии
задачи. Стержни, находящиеся на шаге нагружения в
пластическом состоянии, показаны на рисунке сплошной жирной
линией. Стержни, достигающие предела текучести на данном
шаге, показаны жирным пунктиром. На рисунке показаны все
изменения в состояниях стержней и нагрузки, при которых они
происходят. При уровне нагрузки 435,787 кН наступает
текучесть в поперечной связи между загруженными узлами, и
формируется механизм разрушения конструкции. Предельный
коэффициент нагружения равен 4,542.
На рис. 6 показаны графики зависимости вертикальных
перемещений от нагрузки для трех свободных узлов нижнего пояса
правого пролета фермы n11, n13 и n15 (см. рис. 5). Поведение
фермы остается почти линейным до уровня нагрузки около 370,0
кН, что составляет 81,5% от предельной. Время, затраченное на
159
160.
160выполнение прямого пошагового расчета 36-узловой фермы на
предельную пластическую нагрузку, составляет долю секунды.
W = 348,207
W = 435,785 J
W = 435,787
W = 381,818
W = 436,397 J
W = 452,517
W = 397,150,,
W = 420,658
W = 454,188 J
W = 423,241
Рис. 5. Последовательный переход стержней фермы в
пластическое состояние 5. Прямой метод расчета на
приспособляемость
Рассмотрим конструкцию с множеством векторов модельных
нагрузок p k. История нагружения q (t) конструкции представляет
собой линейную
комбинацию модельных нагрузок с коэффициентами нагружения
ak(t), которые являются циклическими функциями псевдовремени t
с периодом T:
вертикальное перемещение (мм)
Рис. 6. Вертикальные перемещения узлов правого пролета
q (t) = Zak (t) pk, ak (t) = «? (t + mT).
(13)
k=1
160
161.
161Конструкция подвержена нагрузке X q (t), где X - коэффициент
надежности приспособляемости. Целью расчета на
приспособляемость является определение наибольшее значение
Xmax коэффициента надежности, при котором конструкция испытывает пластические деформации в первых
нескольких циклах нагружения, а затем вновь становится упругим
и остается упругим в последующих циклах нагружения.
Приспособляемость под действием циклической нагрузки
анализируется путем вычисления упругопластического поведения
фермы для нагрузки X q (t) для ряда циклов нагружения.
Приспособляемость считается наступившей в цикле нагружения,
если в данном цикле ни один из стержней не испытывает
пластической деформации. Если конструкция не
приспосабливается после заданного числа циклов, то полагается,
что для принятого коэффициента надежности
приспособляемости не наступает.
Максимальный коэффициент надежности приспособляемости
определяется при помощи метода бисекции интервала,
заключающегося в следующем. Задается начальный коэффициент
надежности X0, и ферма рассчитывается на нагрузку X0q(t). Если
ферма для принятой нагрузки не приспосабливается, то
коэффициент надежности умножается на коэффициент 2/3.
Если ферма приспосабливается, коэффициент надежности
умножается на 3/2. Процедура повторяется до тех пор, пока не
отыскивается коэффициент надежности для которого
приспособляемость наступает, и коэффициент X2, для которого
приспособляемость не наступает. Максимальный коэффициент
надежности приспособляемости лежит в интервале Х2].
Интервал, содержащий максимальный коэффициент надежности
приспособляемости, делится пополам и ферма рассчитывается
для среднеарифметического коэффициента надежности = 0,5(^1
161
162.
162+ X2). Если ферма приспосабливается, то интервал заменяется
на [Xm, X2] в
противном случае он заменяется на Xm]. После 10 циклов бисекции
интервал сокращается до 1/1024 от своего первоначального
размера, после 20 циклов - приблизительно до 1/106 начального
размера.
Упругопластический расчет для заданного коэффициента
надежности выполняется пошагово, как и расчет на предельное
пластическое равновесие, однако, для определения инкрементов
нагрузки не используется метод постоянных дуг. Вместо этого,
период T разделяется на заданное число nT интервалов по времени
At = T / nj . Нагрузка в точках на границах интервалов
определяется при
помощи выражения (13) и коэффициента надежности
приспособляемости X.
Если ферма находится в упругом состоянии, то один шаг по
времени совпадает с одним циклом по нагрузке. Если во время шага
по времени хотя бы один из стержней фермы изменяет свое
состояние, то этот шаг разделяется на несколько шагов
нагружения. Конец каждого шага нагружения, за исключением
последнего, совпадает с изменением в состоянии одного или
нескольких стержней. Последний шаг нагружения в интервале
времени задается так, чтобы сумма инкрементов нагрузки по
шагам нагружения была равна инкременту нагрузки на шаге по
времени. На рис. 7 приведена структурная схема алгоритма
определения максимального коэффициента надежности
приспособляемости пространственной фермы для заданной
истории нагружения q(t). Алгоритм состоит из четырех
вложенных циклов. Внешний цикл выполняется по периодам
времени до выявления приспособляемости или ее отсутствия.
Второй цикл выполняется по временным шагам в одном периоде.
Третий цикл выполняется по шагам на- гружения в одном
временном шаге. Во внутреннем цикле итерационно вычисляется
матрица секущей жесткости на шаге нагружения.
162
163.
163Расчет на приспособляемость состоит из последовательности
расчетов с изменяющимися коэффициентами надежности. Если
для заданного коэффициента надежности ферма остается
упругой в первом цикле, то она останется упругой во всех
последующих циклах, и, следовательно, приспосабливается. 58
С
J
С
3
Начало расчета
л
Цикл по периодам
т
Цикл по шагам по времени в периоде J i
Задание инкремента нагрузки на шаге
3Z '
Цикл по шагам нагружения
J)
С
>
Итерации на секущей МЖ
Вычисление и разложение секущей МЖ
у
I
да
Матрица положительно определена
I
Вычисление пробного состояния
С
да
163
164.
164Стержень стал упругим
да
да
Изменилось состояние стержня
\|/ Да
Редуцирование пробного состояния
Погрешность < limit \|/нет ~
Цикл итераций < maximum
Деление интервала пополам
Длина отрезка > minimum
Г" Достигнута предельная нагрузка Л
Сохранение состояния фермы
у+
да
Восстановить состояние фермы в начале шага нагружения
да
Макс, шаг нагрузки на шаге t \|/нет
Полный инкремент нагрузки на шаге t
да
Последний шаг по времени в периоде \|/ да
Приспособляемость J
Пластические деформации в периоде" \|/ Да Последний период
да
С
3
Приспособляемости нет
164
165.
165Рис. 7. Структурная схема алгоритма расчета фермы на
приспособляемость
Если ферма на шаге нагружения теряет устойчивость, то
приспособляемость не наступит. Если ферма испытывает
пластические деформации в первом цикле,
но восстанавливает упругость в следующем цикле и сохраняет ее
в последующих, то она считается приспособившейся. Если ферма
испытывает пластические деформации в последнем цикле
расчета, то она не приспосабливается. Расчет на
приспособляемость прекращается после того, как интервал,
содержащий наибольший коэффициент надежности
приспособляемости, уменьшен до заданного размера. Это размер
может меняться, в зависимости от назначения программы. Для
практических задач он может быть задан большим, чем для
исследовательских.
Разработанный алгоритм реализован в программном
приложении на платформе Java 2, при помощи которого
авторами выполнен ряд примеров.
6. Расчет двухпролетной фермы на приспособляемость
Данный пример иллюстрирует положения расчета на
приспособляемость, изложенные в разд. 5. Здесь использована
конструктивная схема фермы, описанная в разд. 4 (см. рис. 4). На
ферму действуют периодические вертикальные сосредоточенные
силы: силы W1, приложенные в двух верхних узлах в середине
левого пролета и силы W2, приложенные в двух верхних узлах в
середине правого пролета фермы. Графики изменения нагрузок по
времени показаны на рис. 8. В задаче определяется максимальный
коэффициент приспособляемости.
а
1.00
0.50
о.оо
8 псевдовремя t
165
166.
1660 12 3 нагрузка W,,
а
нагрузка W2
Рис. 8. Периодичность изменения нагрузок, действующих на
двухпролетную ферму
Результаты расчета фермы на приспособляемость приведены в
таблице 1. Вычисленный интервал максимального коэффициента
приспособляемости равен [4,206045; 4,206046].
Упругопластическое поведение фермы характеризуется
следующими параметрами:
максимальный коэффициент упругой работы Xe= 3,281;
максимальный коэффициент приспособляемости Х= 4,206;
коэффициент предельной пластической нагрузки Xu= 4,542.
Таблица 1. Результаты расчета фермы на приспособляемость
Xs
Приспособляемость
Xs
Приспособляемость
Xs
Приспособляемость
1,000000
да
4,144531
да
4,205894
да
1,500000
да
4,185547
да
166
167.
1674,205975
да
2,750000
да
4,206055
нет
4,206015
да
5,375000
нет
4,200928
да
4,206035
да
4,062500
да
4,203491
да
4,206045
да
4,718750
нет
4,204773
да
4,206050
нет
4,390635
нет
4,205414
да
4,206047
нет
4,226562
нет
167
168.
1684,205734
да
4,206046
нет
Интервал [4,206045; 4,206046] коэффициента надежности
приспособляемости определен при 25-ти бисекциях. После 14
бисекций был получен интервал [4,2054; 4,2061], который
является достаточно точным для инженерных целей. На
точность определения интервала оказывает влияние
максимальное количество циклов приложения нагрузки.
Коэффициент возрастает на 1,8% при увеличении количества
циклов от 8 (X = 4,130330) до 24 (X = 4,206045 ), а затем
остается постоянным до 40 циклов. Заданное максимальное
количество в 20 шагов нагружения во временном шаге не было
достигнуто.
Для коэффициентов надежности 1,00, 1,50 и 2,75 все стержни
фермы оставались упругими. При коэффициенте надежности
5,375 была достигнута нагрузка предельного равновесия 454,2 кН
между временными точками 1 и 2 в цикле 0. Стержни достигали
пластического состояния в последовательности, описанной в
предыдущем примере (см. рис. 5). Приспособляемость не
наступила.
W, = 360,236
W = 360,236
W, = 366,668
W2 = 366,668
Коэффициент надежности был уменьшен до 4,0625. Временная
точка 2 в цикле 0 была достигнута за 4 шага нагружения, как и
для коэффициента надежности 5,375, однако максимальное
значение нагрузки в 406,25 кН меньше предельной нагрузки 454,2
кН. В процессе разгрузки до временных точек 3 и 4, а также
дальнейшего нагружения до временной точки 5 ферма оставалась
упругой. Точка 6 цикла 0 была достигнута за 6 шагов нагружения.
168
169.
169На рисунке 9 показана последовательность наступления
текучести в стержнях. Разгрузка до точки 8 была полностью
упругой.
W = 347,200
W2 = 347,200
W = 348,222
W2 = 348,222
W, = 406,250
W2 = 358,491
W = 358,491
W2 = 406,250
Рис. 9. Текучесть в стержнях на шаге по времени 5 - 6 Так
как ферма испытала пластические деформации в цикле 0,
выполнялись следующие циклы нагружения. Пластические
деформации продолжались до цикла 4, но ферма оставалась
упругой в течение всего цикла 5, следовательно, при
коэффициенте надежности 4,0625 ферму можно считать
приспособившейся.
Следовательно, максимальный коэффициент надежности
приспособляемости лежит в интервале [4,6025; 5,3750]. В
таблице 1 приведены результаты для значений коэффициентов
надежности, исследовавшихся в дальнейшей процедуре бисекции.
169
170.
170На рис. 10 показано изменение абсолютных значений пластических
деформаций в наиболее нагруженном поясе и диагональном
стержне в зависимости от псевдовремени для коэффициентов X
=4,60250 и 4,22656. Увеличение коэффициента надежности всего
лишь на 3,8% весьма существенно изменяет историю
пластических деформаций. Для коэффициента надежности
4,22656 пластическая деформация продолжает нарастать во всех
циклах. Для этого коэффициента приспособляемость не
наступает, а происходит прогрессирующая деформация.
ni3 bi:
b
5
Е
8000
F
(О
7000
о
6000
^
170
171.
171s
3
со >
5000
о
о
#
4000
ш
ч:
к го
3000
^
о
ш
т
2000
s
н
о
го
171
172.
172с;
1000
с
0
b
Р
1 2 3 4 5 6 7 ЦИКЛ
К-т 4.06250
К-т 4,22656
Рис. 10. История пластических деформаций в стержнях Ь13иЬ71
b
13
13
0
В табл. 2 приведены остаточные напряжения в стержнях для
коэффициента надежности 4,22656. Значения определялись в
конце цикла. Также, как и пластические деформации, остаточные
напряжения продолжают изменяться во всех восьми циклах.
Таблица 2. Остаточные напряжения (кН/м2) для коэффициента X
= 4,22656
Цикл
0
1
2
3
4
5
6
7
b13
172
173.
173-30861
-40595
-44077
-4626
-48064
-48614
-48856
-48989
b71
48517
48315
48113
47984
47897
47837
47776
47709 На рис. 11 показана история перемещений узлов n5 и n13 в
середине пролета нижнего пояса фермы (см. рис. 10) для
коэффициента надежности 4,22656. В первой половине каждого
цикла узел n13 загруженного пролета перемещается вниз, а узел n5
в незагруженном пролете перемещается вверх. Во второй
половине цикла оба узла перемещаются вверх. Перемещение вниз
обоих узлов последовательно нарастает в течение
рассматриваемых восьми периодов.
7. Заключение
Примеры, приведенные в данной статье, демонстрируют, что
прямой расчет пространственных ферм на пластическое
предельное равновесие и приспособляемость при больших
перемещениях может быть успешно реализован в программе.
Алгоритмы охватывают широкий спектр упругопластического
поведения фермы: упругую работу, приспособляемость,
прогрессирующие пластические деформации и разрушение при
формировании механизма.
173
174.
174Полный набор результатов расчета включает переменные
состояния узлов и стержней на всех шагах нагружения всех шагов
по времени во всех циклах для всех коэффициентов надежности и
является чрезвычайно объемным. Так как состояние стержня не
изменяется на шаге нагружения, на печать выводятся лишь
каждое изменение состояния каждого стержня фермы. Эта
детальная информация позволяет выполнить тщательный анализ
поведения конструкции.
Разработанное программное приложение позволяет определять
последовательность, в которой стержни достигают текучести,
величину нагрузки, при которой это происходит, накопление
пластических деформаций в стержнях, остаточные напряжения в
стержнях, а также перемещения узлов при знакопеременной
пластичности. Оно может быть использовано в качестве
тестовой платформы для исследования упругопластического
поведения ферм и как инструмент для решения многих прикладных
задач.
Рис. 11. История перемещений узлов n5 и щ3 при коэффициенте
X= 4,22656
Время, требуемое для расчета описанной выше двухпролетной
фермы при 25 бисекциях и максимальном количестве циклов для
каждой бисекции равном 24, составляет 5 секунд для
стандартного портативного компьютера. Требуемое время
зависит в основном от времени, затрачиваемого на составление и
решение систем уравнений. Ожидаемое время расчета
аналогичной фермы с 300 узлов - менее 1 часа. Для инженерной
точности расчета время может быть сокращено до 30 минут.
Задачи большей размерности могут решаться на компьютерах
большей производительности, в том числе вычислительных
кластерах.
174
175.
175175
176.
176176
177.
177177
178.
178178
179.
179179
180.
180180
181.
181181
182.
182182
183.
183183
184.
184184
185.
185185
186.
186186
187.
187187
188.
188188
189.
189189
190.
190190
191.
191191
192.
192Время
Мероприятие
Место проведения^О
30 ноября 2022 года (среда)
с 10:00
Заседания круглых столов
Аудитории ПГУПС
10:00
Заседание Общественного совета при Федеральной службе
по надзору в сфере транспорта
7 корпус, ауд. 7-227 Конференц-зал
11:00
Публичные обсуждения результатов правоприменительной
практики УГАН НОТБ СЗФО Ространснадзора за IV
квартал 2022 года
1 корпус Дубовый зал
1 декабря 2022 года (четверг)
^09:30 - 15:00
Конференция Международной ассоциации колледжей
транспорта
СПТЖТ ул. Бородинская, д. 6
10:00 - 12:00
Научно-практическая конференция
«Инженерное предпринимательство: новые решения на
транспорте и в логистике»
Дворец Юсуповых Белый зал
11:00
192
193.
193Расширенное заседание Совета Ассоциации технических
университетов, посвященное 30-летию создания системы
университетского технического образования в России
1 корпус Актовый зал
. 14:30
Круглый стол
(Совета Ассоциации технических университетов)
«Технологическое лидерство университетов в условиях
формирования единого научно-образовательного
пространства СНГ»
1 корпус Дубовый зал
16:15
Круглый стол
(Совета Ассоциации технических университетов)
«Проблемы, опыт и перспективы в освоении ресурсов
Арктики, Арктической зоны и Дальнего Востока»
1 корпус Дубовый зал
17:00
Экскурсии для желающих по Музею ПГУПС
Дворец Юсуповых Музей ПГУПС
18:00
Прием для участников Форума и заседания Совета
Ассоциации технических университетов
Дворец Юсуповых Белый зал IV Бетанкуровский дддьии
международный инженерный форум
./л.
ПРОГРАММА мероприятии
Место проведения
Время
Мероприятие
193
194.
1942 декабря 2022 года (пятница)
Открытые лекции
Аудитории ПГУПС
09:00
руководителей ОАО «РЖД», строительных и
промышленных предприятий
Конференция
СПТЖТ ул. Бородинская, д. 6
09:00 - 11:00
Международной ассоциации колледжей транспорта
IT Форум
1 корпус, ауд. 1-217
09:30 - 11:00
«Цифровое пространство современного вуза»
3 корпус, ауд. 3-237 «Большая химическая
аудитория им. Д.И. Менделеева»
10:00
Встреча студентов П1УПС с первым министром путей
сообщения РФ, первым президентом ОАО «РЖД»,
советником генерального директора ОАО «РЖД» Г.М.
Фадеевым: «О важности гражданской позиции
железнодорожников, основанной на созидании и
194
195.
195преданности делу, а также значимости их вклада в
развитие России»
.С)
6 корпус, ауд. 6-302 Большая физическая аудитория
Ш1
12:00
Пленарное заседание Форума «Инженерное образование всемирное наследие. Готовы ли современные образование и
наука обеспечить технологический суверенитет страны?»
Прием
по окончании Пленарного заседания
1 корпус Дубовый зал
0
для участников Пленарного заседания Форума
3 корпус, ауд. 3-237 «Большая химическая
аудитория им. Д.И. Менделеева»
15:00
Встреча студентов ПГУПС с генеральным директором
ООО «ТС Строй» Попковым А.Н. «Организация трудовой
деятельности студенческого строительного отряда
ПГУПС «Байкал» на участке Восточно-Сибирской
железной дороги»
10:00
8-9 декабря 2022 года (четверг, пятница)
195
196.
196Форум поколений ЦДИ
15:00
10:00
П/7ППШ
VII Студенческая конференция первокурсников ПГУПС
15 декабря 2022 года (четверг)
Октябрьский центр инновационного развития,
Библиотечный переулок, д. 4
Хакатон
2 корпус, ауд. 2-402, 2-409
плплпп
Пленарное заседание
«Инженерное образование - всемирное наследие. Готовы ли
современные образование и наука обеспечить
технологический суверенитет страны?»
Время
IV Бетанкуровский международный инженерный форум
Выступление
Кофе-брейк
Торжественное открытие заседания
Панельная дискуссия
Модератор пленарного заседания:
• Николай Зусик - российский журналист и телеведущий
канала «Россия-1»
Спикеры панельной дискуссии:
196
197.
197• Константин Анатольевич Пашков - директор
Административного департамента Минестерства
Транспорта Российской федерации
• Владимир Николаевич Княгинин - вице-губернатор СанктПетербурга
• Игорь Геннадьевич Малыгин - директор Института
проблем транспорта им. Н.С. Соломенко
• Валерий Фаритович Танаев - начальник Московской
железной дороги
• Анатолий Александрович Александров - президент
Ассоциации технических университетов, президент МГТУ
им. Н.Э. Баумана
• Андрей Владимирович Шепель - директор по логистике АО
«Апатит»
• Николай Николаевич Казаков - проректор по учебной
работе Белорусского государственного транспортного
университета
• Андрей Рюрикович Федоров - председатель Совета
Директоров Группы компаний «Диджитал Дизайн»
11.30-12.00
12.00-12.05
12.05-14.00
»»>
s
• Виктор Георгиевич Голомолзин - начальник Октябрьской
железной дороги
14.00-14.05
14.05-14.10
197
198.
19814.10-14.15
• Александр Юрьевич Панычев - ректор Петербургского
государственного университета путей сообщения
Императора Александра I
Вручение сертификата на брендированную аудиторию АО
«Апатит»
Вручение наград начальником Горьковской железной дороги
Дорофеевским С.А. сотрудникам Университета
Подписание Соглашений о сотрудничестве
Традиционное вручение в день основания Университета
дипломов почетного профессора и почетного
преподавателя ПГУПС
14.15-14.20
14.20
Закрытие пленарного заседания Форума
плплпп
Абу-Хасан Махмуд - декан факультета «Промышленное и
гражданское строительство»
30 ноября
Заседания круглых столов
Аудитория
Время
10.00
3-237
198
199.
199Кабанов Александр Васильевич? декан факультета
«Экономика и менеджмент»
10.00
9-120
IV Бетанкуровский международный инженерный форум
Название круглого стола
Новейшие технологии восстановления и форсированного
развития объектов транспортной и строительной
инфраструктуры
Актуальные компетенции в мобильности сетей поставок
транспортных коридоров
Цифровые технологические модели логистической
деятельности железных дорог в современных условиях
10.45
7-320
Бадецкий Александр Петрович ? и.о. декана факультета
«Управление перевозками
и логистика»
Решение стратегических задач транспортного
строительства в современных условиях
импортозамещения, восстановления и развития
транспортной инфраструктуры
Безопасная транспортная экосистема магистральной
инфраструктуры и современные вызовы
Перспективы развития подвижного состава,
технологических и энергетических комплексов
1-418
199
200.
20013.15
15.00
5-403
15.00
в условиях импортозамещения
Чуян Сергей Николаевич - декан факультета
«Транспортные
Бушуев Николай Сергеевич - декан факультета
«Транспортное строительство»
Степанская Ольга Андреевна - декан факультета
«Автоматизация и интеллектуальные технологии»
200
201.
201201
202.
202202
203.
203203
204.
204Более подробно : Перспективы применения
быстровозводимых мостов и переправ очевидны. Не
имея хорошей методической, научной, технической
и практической базы, задачи по быстрому
временному восстановлению мостовых переходов
204
205.
205будут невосполнимы. Это приведет к
непредсказуемым потерям.
Splice Connection Design
Structural calculations for steel beam splice connection design
We provide steel beam splices calculations to BS5950 or Eurocode 3 design codes, ensuring your
splice connection complies with Building Regulation standards.
Our structural engineers will design your splice connection to suit your exact beam size
and loading requirements and provide design calculations that are accepted by Building Control
departments nationwide.
Fast service and detailed output
We supply as standard detailed connection drawings and installation instructions so fabricators
know exactly what to make and installers know exactly how the connection should be fitted.
205
206.
206Our fast online service ensures a quick turnaround helping you to avoid delays and keep your
project on schedule. You can also contact us for a quote.
Order Online | Fast Turnaround | £195+VAT
Includes structural calculations and drawings
suitable for submission to Building Control
Go to order form
Why use a bolted splice connection?
Bolted splice connections are the quickest and easiest way for steel beams to be joined on site in
a quality assured manner and avoid the fire risk and quality control difficulties of on-site welding.
Reducing long beams into shorter and more manageable sections is often necessary for ease of
transport, safe handling or to facilitate installation, particularly when installing steelwork in loft
conversions and existing buildings.
Which splice connection type?
A bolted splice connection can be formed using 'cover plate' splices or bolted 'end plate' splices
(see images). Both are designed to transmit bending moment and shear forces across the joint,
allowing a spliced beam to behave as a continuous member and each have their pros and cons see box below for more technical information.
The size and thickness of steel plates, grade, diameter and quantity of bolts and weld specification
(where relevant) vary depending on beam size and applied loads so it's important splices are
designed to suit each application.
206
207.
207Cover Plate Splice Connection
End Plate Splice Connection
207
208.
208Hollobolt® Splice Connection
https://www.smartbuild.uk.com/steel-beam-splice-design
208
209.
209209
210.
210210
211.
211211
212.
212212
213.
213213
214.
214214
215.
215215
216.
216216
217.
217217
218.
218218
219.
219219
220.
220220
221.
221221
222.
222222
223.
223223
224.
224224
225.
225225
226.
226226
227.
227227
228.
228228
229.
229229
230.
230230
231.
231231
232.
232232
233.
233233
234.
234234
235.
235235
236.
236236
237.
237237
238.
238238
239.
239239
240.
240http://www.mem50212.com/MDME/MEMmods/MEM30007A/properties/Properties.html Introduction
240
241.
241When a material is subject to forces (loads), they will deform (elongate, compress, twist) by some amount. It
may be a small amount, but never zero. Engineers calculate these forces in order to predict the behaviour of
the materials.
Materials scientists learn about these mechanical properties by testing materials. Results from the tests
depend on the size and shape of material to be tested (specimen), how it is held, and the way of performing
the test. That is why we use common procedures, or standards, such as NATA.
What is a Property?
A property is something that will be measured the same regardless of the size of a piece of material. For
example, density is a property, but mass is not.
Important Properties for Engineering
There are many material properties used for all sorts of things, like how well the material conducts heat, or
magnetism, or resists electricity or how much it expands with heat etc etc. (Thermal conductivity,
Magnetic permeability, Resistivity, Coefficient of thermal expansion etc)
Mechanical properties are more focussed on how the material behaves under stress. Here are the key
properties;
Elasticity
The ability of the material to return to its original size (or shape) after being deformed. (stretched,
compressed, twisted, bent etc) Rubber is elastic, so is glass and spring steel
Plasticity
The ability of the material to be deformed and stay like that after load is removed. (Opposite of elasticity)
Lead is quite plastic.
There are some specific types of plasticity.
Ductility = tensile plasticity. A material that can be stretched. (Like chewing gum - it stretches when you
pull it). Good examples are copper, and plastics like polypropylene.
Malleability = compressive plasticity. A material that can be compressed or hammered. (Like wet clay - it
squashes when you press it, but doesn't stretch much). Engineering example; lead. Most plastic materials
show a bit of both - ductile and malleable.
Stress
The intensity of force inside a solid material. It is just like pressure except that it has a set direction (wheras
pressure is in every direction). Stress acts through a cross-section of the material where the forces are
applied on EACH SIDE of that cross-sectional area. So there is a SET of 2 forces - when they are pulling it
is tensile, if they push towards each other it is compressive.
241
242.
242Definition of Stress
f = F / A where
f is the average stress, also called engineering or nominal stress, and
F is the force acting over the area - and perpendicular to it.
The SI unit for stress is the pascal (symbol Pa), which is a shorthand name for
The unit for stress is the same as that of pressure, which is also a measure of Fo
usually measured in megapascals (MPa) or gigapascals (GPa). We always wo
in MPa, because 1 MPa = 1N / 1mm2.
Example:
In the diagram at left, assume a force of 2000N up and 2000N down.
The area of cross-section is 50 square mm.
Stress = 2000 / 50 = 40 MPa
Strength: The amount of Stress a material can 'take'. Where 'take' might be before it breaks, before it
deforms permanently, etc
Yield Strength: The stress that makes the material begin to have some plasticity.
Ultimate Strength. The highest stress the material can get to - any more and it will break.
Tensile Strength. Pulling - yield or ultimate.
Compressive Strength: Compressing strength
Shear Strength: Sliding or distorting, twisting. Yield or ultimate.
Fatigue Strength: The stress the material can handle when applied on and off many times.
Strain
The relative stretch of a material. It the material started with a length L, the amount of change (deformation)
is x as a result of a tensile or compressive stress. This is not a property because it depends on how long the
object is, so we have a property Strain, where
= /L
The Stress/Strain Curve
Elastic deformation. When the stress is removed, the material returns to the dimension it had before the load
was applied. Valid for small strains (except the case of rubbers).
Deformation is reversible, non permanent.
Plastic deformation. When the stress is removed, the material does not return to its previous dimension but
there is a permanent (irreversible) deformation.
242
243.
243Introduction
When a material is subject to forces (loads), they will deform (elongate, compress, twist) by some amount. It
may be a small amount, but never zero. Engineers calculate these forces in order to predict the behaviour of
the materials.
Materials scientists learn about these mechanical properties by testing materials. Results from the tests
depend on the size and shape of material to be tested (specimen), how it is held, and the way of performing
the test. That is why we use common procedures, or standards, such as NATA.
What is a Property?
A property is something that will be measured the same regardless of the size of a piece of material. For
example, density is a property, but mass is not.
Important Properties for Engineering
There are many material properties used for all sorts of things, like how well the material conducts heat, or
magnetism, or resists electricity or how much it expands with heat etc etc. (Thermal conductivity,
Magnetic permeability, Resistivity, Coefficient of thermal expansion etc)
Mechanical properties are more focussed on how the material behaves under stress. Here are the key
properties;
Elasticity
The ability of the material to return to its original size (or shape) after being deformed. (stretched,
compressed, twisted, bent etc) Rubber is elastic, so is glass and spring steel
Plasticity
The ability of the material to be deformed and stay like that after load is removed. (Opposite of elasticity)
Lead is quite plastic.
There are some specific types of plasticity.
Ductility = tensile plasticity. A material that can be stretched. (Like chewing gum - it stretches when you
pull it). Good examples are copper, and plastics like polypropylene.
Malleability = compressive plasticity. A material that can be compressed or hammered. (Like wet clay - it
243
244.
244squashes when you press it, but doesn't stretch much). Engineering example; lead. Most plastic materials
show a bit of both - ductile and malleable.
Stress
The intensity of force inside a solid material. It is just like pressure except that it has a set direction (wheras
pressure is in every direction). Stress acts through a cross-section of the material where the forces are
applied on EACH SIDE of that cross-sectional area. So there is a SET of 2 forces - when they are pulling it
is tensile, if they push towards each other it is compressive.
Definition of Stress
f = F / A where
f is the average stress, also called engineering or nominal stress, and
F is the force acting over the area - and perpendicular to it.
The SI unit for stress is the pascal (symbol Pa), which is a shorthand name for
The unit for stress is the same as that of pressure, which is also a measure of Fo
usually measured in megapascals (MPa) or gigapascals (GPa). We always wo
in MPa, because 1 MPa = 1N / 1mm2.
Example:
In the diagram at left, assume a force of 2000N up and 2000N down.
The area of cross-section is 50 square mm.
Stress = 2000 / 50 = 40 MPa
Strength: The amount of Stress a material can 'take'. Where 'take' might be before it breaks, before it
deforms permanently, etc
Yield Strength: The stress that makes the material begin to have some plasticity.
Ultimate Strength. The highest stress the material can get to - any more and it will break.
Tensile Strength. Pulling - yield or ultimate.
Compressive Strength: Compressing strength
Shear Strength: Sliding or distorting, twisting. Yield or ultimate.
Fatigue Strength: The stress the material can handle when applied on and off many times.
Strain
The relative stretch of a material. It the material started with a length L, the amount of change (deformation)
is x as a result of a tensile or compressive stress. This is not a property because it depends on how long the
object is, so we have a property Strain, where
= /L
The Stress/Strain Curve
Elastic deformation. When the stress is removed, the material returns to the dimension it had before the load
was applied. Valid for small strains (except the case of rubbers).
Deformation is reversible, non permanent.
244
245.
245Plastic deformation. When the stress is removed, the material does not return to its previous dimension but
there is a permanent (irreversible) deformation.
Stiffness
In tensile tests, if the deformation is elastic, the stress-strain relationship is called Hooke's law:
E=f/e E is the slope of the stress-strain curve, called Young's modulus or modulus of elasticity. In some cases
(especially plastics and high speed loadings), the relationship is not linear so that E can be defined
alternatively as the local slope: E = df/de
Shear stresses also produce strains according to: G=f/e
where G is the shear modulus.
Elastic moduli measure the stiffness of the material. They are related to the second derivative of the
interatomic potential, or the first derivative of the force vs. internuclear distance. By examining these curves
we can tell which material has a higher modulus. Due to thermal vibrations the elastic modulus decreases
with temperature. E is large for ceramics (stronger ionic bond) and small for polymers (weak covalent
bond). Since the interatomic distances depend on direction in the crystal, E depends on direction (i.e., it is
anisotropic) for single crystals. For randomly oriented policrystals, E is isotropic.
Anelasticity
Here the behavior is elastic but not the stress-strain curve is not immediately reversible. It takes a while for
the strain to return to zero. The effect is normally small for metals but can be significant for polymers. This
is a type of friction effect and is sensitive to the speed of loading.
Poisson's Ratio (lateral shrinking)
245
246.
246Materials subject to tension shrink laterally. Those subject to compression, bulge. The ratio of lateral and
axial strains is called the Poisson's ratio . = lateral/ axial
The elastic modulus, shear modulus and Poisson's ratio are related by E = 2G(1+ ), so Poisson's ratio can be
worked out from measurements of G and E.
Tensile Properties
Yield point. If the stress is too large, the strain deviates from being proportional to the stress. The point at
which this happens is the yield point because there the material yields, deforming permanently (plastically)
Yield stress. Hooke's law is not valid beyond the yield point. The stress at the yield point is called yield
stress, and is an important measure of the mechanical properties of materials. In practice, the yield stress is
chosen as that causing a permanent strain of 0.002 (strain offset, Fig. 6.9.) The yield stress measures the
resistance to plastic deformation.
Plastic deformation: The reason for plastic deformation, in normal materials, is not that the atomic bond is
stretched beyond repair, but the motion of dislocations, which involves breaking and reforming
bonds. Plastic deformation is caused by the motion of dislocations.
Tensile strength. When stress continues in the plastic regime, the stress-strain passes through a maximum,
called the tensile strength ( TS) , and then falls as the material starts to develop a neck and it finally breaks at
the fracture point (Fig. 6.10). Note that it is called strength, not stress, but the units are the same, MPa. So
strength is a certain stress a material can take.For structural applications, the yield stress is usually a more
important property than the tensile strength, since once the it is passed, the structure has deformed beyond
acceptable limits.
Ductility. Tensile Plasticity. The ability to deform before braking. It is the opposite of brittleness. Ductility
can be given either as percent maximum elongation max or maximum area reduction. %EL = max x 100
%, %AR = (A0 - Af)/A0 These are measured after fracture (repositioning the two pieces back together).
Malleability. Compressive Plasticity.
Toughness. Ability to absorb energy up to fracture. The energy per unit volume is the total area under the
strain-stress curve. It is also measured by an impact test.
Resilience. Capacity to absorb energy elastically. The energy per unit volume is the area under the strainstress curve in the elastic region.
246
247.
247True Stress and Strain. When one applies a constant tensile force the material will break after reaching the
tensile strength. The material starts necking (the transverse area decreases) but the stress cannot increase
beyond TS. The ratio of the force to the initial area, what we normally do, is called the engineering stress. If
the ratio is to the actual area (that changes with stress) one obtains the true stress.
Elastic Recovery During Plastic Deformation. If a material is taken beyond the yield point (it is deformed
plastically) and the stress is then released, the material ends up with a permanent strain. If the stress is
reapplied, the material again responds elastically at the beginning up to a new yield point that is higher than
the original yield point (strain hardening, Ch. 7.10). The amount of elastic strain that it will take before
reaching the yield point is called elastic strain recovery
Compressive, Shear, and Torsional Deformation. Compressive and shear stresses give similar behavior to
tensile stresses, but in the case of compressive stresses there is no maximum in the curve, since no
necking occurs.
Hardness. Hardness is the resistance to plastic deformation (e.g., a local dent or scratch). Thus, it is a
measure of plastic deformation, as is the tensile strength, so they are well correlated. Historically, it was
measured on an empirically scale, determined by the ability of a material to scratch another, diamond being
the hardest and talc the softer. Now we use standard tests, where a ball, or point is pressed into a material
and the size of the dent is measured. There are a few different hardness tests: Rockwell, Brinell, Vickers,
etc. They are popular because they are easy and non-destructive (except for the small dent).
Variability of Material Properties. Tests do not produce exactly the same result because of variations in
the test equipment, procedures, operator bias, specimen fabrication, etc. But, even if all those parameters are
controlled within strict limits, a variation remains in the materials, due to uncontrolled variations during
fabrication, non homogenous composition and structure, etc. The measured mechanical properties will show
scatter, which is often distributed in a Gaussian curve (bell-shaped), that is characterized by the mean value
and the standard deviation (width).
Design/Safety Factors. To take into account variability of properties, designers use, instead of an average
value of, say, the tensile strength, the probability that the yield strength is above the minimum value
tolerable. This leads to the use of a safety factor N > 1 (typ. 1.2 - 4). Thus, a working value for the tensile
strength would be W = TS / N.
Bolt Grades
Grades are stamped into the head of the bolt (for high strength bolts). The larger the number, the stronger the
bolt.
247
248.
248The first number is the ultimate tensile strength (UTS) in 100 x MPa. The second number (if shown) is the
yield strength (YS) as a proportion of UTS. So, for 8.8 bolt, UTS=800MPa, YS = 0.8x800 = 640MPa.
More details given below
Grade
Nominal Size
Proof Stress
YS
UTS
Hardness R (core)
Min.
Max.
4.6
M5-M100
225
240
400
B67
B95
4.8
M1.6-M16
310
340
420
B71
B95
5.8
M5-M24
380
420
520
B82
B95
8.8
M16-M72
600
660
830
C23
C34
9.8
M1.6-M16
650
720
900
C27
C36
10.9
M5-M100
830
940
1040
C33
C39
12.9
M1.6-M100
970
1100
1220
C38
C44
Fatigue
If stress is cycled on and off, the material can fail at a much lower stress than the yield or ultimate strength.
This is due to fatigue - the slow growth of a crack each time the load is re-applied. If stresses are low, and
the number of cycles is high, we use the S-N diagram, or Wohler diagram. (High = 100,000 or more)
The S-N diagram plots stress S versus cycles to failure N. The graph is usually displayed on a log-log plot,
with the actual S-N line representing the mean of the data from several tests.
248
249.
249Endurance Limit: (Material A) Some materials have a fatigue limit or endurance limit - the stress level
below which the material never fails. This is characteristic of steel and titanium in benign environmental
conditions.
Many non-ferrous metals and alloys, such as aluminum, magnesium, and copper alloys, do not exhibit welldefined endurance limits. These materials instead display a continuously decreasing S-N response, similar
to Curve B above. In such cases a fatigue strength Sf for a given number of cycles must be specified. An
effective endurance limit for these materials is sometimes defined as the stress that causes failure at 1E8 or
5E8 loading cycles.
The concept of an endurance limit is used in infinite-life or safe stress designs. It is due to interstitial
elements (such as carbon or nitrogen in iron) that pin dislocations, thus preventing the slip mechanism that
leads to the formation of microcracks. Care must be taken when using an endurance limit in design
applications because it can disappear due to:
Periodic overloads (unpin dislocations)
Corrosive environments (due to fatigue corrosion interaction)
High temperatures (mobilize dislocations)
The endurance limit is not a true property of a material, since other significant influences such as surface
finish cannot be entirely eliminated. However, a test values (Se') obtained from polished specimens provide
a baseline to which other factors can be applied. Influences that can affect (i.e. decrease) the endurance limit
include:
Surface Finish (rough)
Temperature (higher)
Stress Concentrations (geometry that increases stress)
Size (larger)
Fatigue usually begins from a stress concentration at the surface. The fatigue cracks grow slowly and usually
leaves a striated pattern that looks like a smooth sea shell. Then, when the crack has gone far enough, the
object will break suddenly due to the stress in the small remaining area exceeding the ultimate strength. This
sudden fracture will usually look different - rough or torn looking.
Creep
Creep is the slow stretching of a material over time - especially at "high temperature". Boilers, gas turbine
engines, and ovens are some of the systems that have components that experience creep. For some materials
"high temperature" could be room temperature - like lead. Many plastics is also very prone to creep. Failures
involving creep usually involves deformation, but failures may appear ductile or brittle.
249
250.
250In a creep test a constant load is applied to a tensile specimen maintained at a constant temperature. Strain is
then measured over a period of time. The slope of the curve, identified in the above figure, is the strain rate
of the test during stage II or the creep rate of the material.
Primary creep, Stage I, is a period of decreasing creep rate. Primary creep is a period of primarily transient
creep. During this period deformation takes place and the resistance to creep increases until stage II.
Secondary creep, Stage II, is a period of roughly constant creep rate. Stage II is referred to as steady state
creep. Tertiary creep, Stage III, occurs when there is a reduction in cross sectional area due to necking or
effective reduction in area due to internal void formation.
Quiz Study: (Multiple choice questions)
1. Ability of a material to be deformed and then return to its original size after removing the load.
2. Ability of a material to resist indentation or abrasion.
3. Ability of a material to sustain a high load for its size.
4. A material that requires a high stress to deform a small amount is...
5. Ultimate Tensile Strength is a measure of the ........ a material can take.
6. A material that takes a lot of energy to break has a high level of...
7. A tough material will exhibit both...
8. The ability of a material to absorb energy without permanent deformation.
9. Percentage elongation is a measure of a material's...
10. The rate of creep is higher when you increase ...
11. Which of the following would most likely be a CREEP problem?
12. Deformation that increases gradually is likely to be due to...
13. A crack which grows gradually through a shaft is likely to be due to...
14. Shot peening of springs is used to...
15. How does shot peening work?
16. What is a Fatigue Strength?
17. What is the Endurance Limit?
18. Which of the following would most likely be a FATIGUE problem?
19. Which graph indicates Mild Steel?
20. Which is FALSE?
21. The slope of the curve up to the yield point tells you the ...
22. The area under the entire stress-strain curve is an indication of a material's ...
23. Yield Point: Which is ... F A L S E ?
250
251.
25124. A bolt has 12.9 stamped on the head. This means it has maximum strength of ...
25. Comparison between a 25x1 spring steel ruler and 25x1 mild steel strip under bending. If the yield
point of MS is 250MPa and SS is 400MPa, which is TRUE?
26. A Mild Steel beam deflects 0.3mm under load and springs back on removal. Which is FALSE?
27. A bent nail is an example of going beyond the .................
28. A new chain broke while attempting to drag a large fallen tree. This is an example of going beyond
the .................
29. If the stress was between the Yield point and UTS then...
30. If the stress was below the Yield point then...
31. If the stress was above the UTS then...
32. Which is stiffer, mild steel or high tensile steel? (Up to yield point)
33. Which is stronger, Mild steel or High tensile steel?
34. Steel has a Modulus of Elasticity of about;
35. A 10m steel rod is stretched by 1cm. What is the Strain?
36. An electrical wire (cross section = 1 square mm) holds 12 N weight. The stress is;
37. How much will a 100m fence wire stretch if it is tensioned to 100MPa?
38. You are designing an aluminium crank for a bicycle. Which entry is most relevant to ensure it does
not crack?
Whiteboard Photos
251
252.
252252
253.
253253
254.
254Questions: Assignment:
Review Test #10101.
Do a practice test 10101cp
Relevant pages in MDME
Mechanical Properties practice test: 10101cp
Web Links
Google search:
Mechanical Properties of Materials (Ref http://www.virginia.edu/bohr/mse209/chapter6.htm)
254
255.
255255
256.
256256
257.
257257
258.
258258
259.
259259
260.
260260
261.
261261
262.
262262
263.
263263
264.
264264
265.
265265
266.
266A BREAKDOWN OF THE DIFFERENT STYLES OF
UNISTRUT BEAM CLAMPS
When it comes to securing channel to existing structural steel, Unistrut beam clamps are an easy, costeffective solution. Beam clamps provide you with a simple beam-to-strut connection solution that doesn’t
require welding or drilling.
Unistrut beam clamps come in a variety of styles to accommodate a range of beam styles, sizes, applications,
and attachment preferences. This variety also means there are several different styles of beam clamps that
can affect how channel is attached and the total load that can be secured to the beam. Here are some of the
more common styles of beam clamps offered by Unistrut Service Company.
UNISTRUT FLANGE BEAM CLAMPS
HOW THEY WORK
Unistrut flange beam clamps, also known as Unistrut C style beam clamps, are named for their distinctive
shape. Flange beam clamps are designed to secure channel to beams by clamping down on the flanges of a
beam with a set screw. Depending on the design of the flange beam clamp, the channel is either sandwiched
between the flange and the clamp or attached to the clamp with a threaded rod.
Examples
Unistrut PLF3037 thru PLF3075 Flange Clamps
266
267.
267Unistrut P2675 Beam Clamp
UNISTRUT WINDOW STYLE BEAM CLAMPS
HOW THEY WORK
Unistrut window style beam clamps secure channel to existing beams using a “window” cut out of a bent
plate and a set screw. A pair of window style beam clamps are placed on both sides of a beam and a channel
is fed through the windows. Once in place, the window style beam clamp is secured to the beam with the set
screw, which also holds the channel in place.
Example
Unistrut P1796S Window Beam Clamp
267
268.
268UNISTRUT U STYLE BEAM CLAMPS
HOW THEY WORK
Unistrut U style beam clamps feature a piece of bent plate and a u-bolt that is threaded on both sides to
secure channel in place. The channel is fed through the u-bolt, which is then tightened to secure both the
plate to the beam and the channel to the plate. U style beam clamps can be used to secure channel to either
the underside of the beam or the inside of the beam, depending on the configuration of the clamp.
Examples
Unistrut P2785 U-Bolt Beam Clamp
268
269.
269Unistrut P2868 U-Bolt Beam Clamp
UNISTRUT J STYLE BEAM CLAMPS
HOW THEY WORK
Unistrut J style beam clamps feature a hook shaped like a “J” to help them secure channel to existing beams.
While other beam clamp styles are designed to use in pairs to secure both sides of a beam, J style beam
clamps are designed for use as a stand-alone clamp (unless indicated otherwise). This is possible as the hook
secures the j style beam clamp to the opposite side of the beam.
Examples
Unistrut P2867 J-Bolt Beam Clamp
269
270.
270Unistrut P2824 J-Bolt Beam Clamp
270
271.
271UNISTRUT COLUMN INSERTS
HOW THEY WORK
Unistrut column inserts are used to secure channel between the flanges of a beam. The column inserts are
attached to the interior walls of the flanges with set screws, securing the channel between them for use.
Example
Unistrut P3087 Column Insert Beam Clamp
271
272.
272ORDER THE RIGHT UNISTRUT BEAM CLAMPS
There are many ways to connect strut to beams, but it’s important to find the right option for your
suspension needs. Connection style, load capabilities, and minimum safety factors are all important aspects
that play into which beam clamps are best way to attach for your channel to existing structures. Be sure to
consult the engineering catalog to determine load capacity of the clamp you are contemplating using for
your project.
Unistrut Service Company can supply you with the right beam clamps for your suspension project. You
can download the Unistrut Beam Clamp Catalog for details on each product and order Unistrut beam clamps
online through our website. If you need some assistance determining which clamps are right for your
situation, you can contact Unistrut to talk to one of our experts about the needs of your project.
Tags: flange clamps
c clamps
j-bolt clamps
u-bolt clamps
window clamps
hinged beam clamps
column inserts
Categories: Unistrut Beam Clamps
Connect with Unistrut
Tell us about your application’s needs, and we’ll suggest proven products, services and solutions to exceed
your expectations.
272
273.
273273
274.
274274
275.
275275
276.
276276
277.
277277
278.
278278
279.
279279
280.
280280
281.
281281
282.
282282
283.
283283
284.
284284
285.
285285
286.
286286
287.
287287
288.
288288
289.
289289
290.
290290
291.
291291
292.
292292
293.
293293
294.
294294
295.
295295
296.
296296
297.
297297
298.
298298
299.
299299
300.
300300
301.
301301
302.
302302
303.
303303
304.
304304
305.
305305
306.
306306
307.
307307
308.
308308
309.
309309
310.
310310
311.
311311
312.
312312
313.
313313
314.
314314
315.
315315
316.
316316
317.
317317
318.
318318
319.
319319
320.
320320
321.
321321
322.
322322
323.
323323
324.
324324
325.
325325
326.
326326
327.
327327
328.
328328
329.
329329
330.
330330
331.
331331
332.
332332
333.
333333
334.
334334
335.
335335
336.
336336
337.
337337
338.
338338
339.
339339
340.
340340
341.
341341
342.
342342
343.
343343
344.
344344
345.
345345
346.
346346
347.
347347
348.
348348
349.
349349
350.
350350
351.
351351
352.
352352
353.
353353
354.
354354
355.
355355
356.
356356
357.
357357
358.
358358
359.
359359
360.
360360
361.
361361
362.
362362
363.
363363
364.
364364
365.
365365
366.
366366
367.
367https://disk.yandex.ru/d/jsuUAp-0Un_GkA https://ppt-online.org/941232
https://ru.scribd.com/document/515600203/Ispolzovaniy-Gasiteley-Dinamicheskix-Kolebaniy-Obrusheniem-Pyatogo-EtajaObespecheniya-Seismostoykosti-351-Str
367
368.
368368
369.
369369
370.
370370
371.
371371
372.
372372
373.
373373
374.
374374
375.
375375
376.
376376
377.
377377
378.
378378
379.
379379
380.
380380
381.
381381
382.
382382
383.
383383
384.
384384
385.
385385
386.
386386
387.
387387
388.
388388
389.
389389
390.
390390
391.
391391
392.
392392
393.
393393
394.
394394
395.
395395
396.
396396
397.
397397
398.
398398
399.
399399
400.
400400
401.
401401
402.
402402
403.
403403
404.
404404
405.
405405
406.
406406
407.
407407
408.
408408
409.
409409
410.
410410
411.
411411
412.
412412
413.
413413
414.
414414
415.
415415
416.
416416
417.
417417
418.
418418
419.
419419
420.
420420
421.
421Газета «Армия Защитников Отечества", ИА "Русская Народная
Дружина" при СПб ГАСУ № 7 (7) от 05.04.23
421
422.
422422
423.
423ОО "Сейсмофонд" (812) 694-78-10
6947810@mail.ru (921) 962-67-78, (911) 175-84-65 ИНН 2014000780
ФГБОУ СПб ГАСУ № RA.RU.21СТ39 от 27.05.2015, 190005, СПб, 2-я
Красноармейская ул. д 4, ФГБОУ ВПО ПГУПС № SP01.01.406.045 от 27.05.2014,
190031, Организация «Сейсмофонд» при СПб ГАСУ ИНН: 2014000780
t9516441648@gmail.com c6947810@yandex.ru (911) 175-84-65, УТВЕРЖДАЮ протокол
испытаний узлов и фрагентов упругоплатических шарниров для армейского моста и специальные
423
424.
424технические условия изготовления пластинчатых ферм-балок из сверхпрочных и сверхлегких
полимерных материалов
Президент ОО «Сейсмофонд» при СПб ГАСУ ОГРН: 1022000000824
Направляется расчет в ПК SCA 3D и американский
расчет для Bailey bridge и USA изобретения по
изготовлению пластинчатых ферм-балок по запросу
Минстроя ЖКХ Минпромторга Минтраса
Минобороны для включения в план НИОКР и
описание изобретения по способу производства и
изготовления временных опор для переправ
Просим администрацию Президента и Правительство
РФ проинформировать и включить в план НИОКР
НИР на 2023 год а не на 2024 г
Расчет упругоплатических стальных ферм -балок с учетом пластических деформаций при
больщих перемещениях на предельное равновесие и сприспособдяемость и специальные
технические условия надвижки пролетного строения из стержневых пространственных
структур с использованием рамных сбороно-разборных конструкций с использованием
замкнутых гнутосварных профилей прямоуголного сечения, типа "Молодечно" (серия 1.460.314 ГПИ "Ленпроектстальконструция"), МАРХИ ПСПК", "Кисловодск" ( RU 80471
"Комбинированная пространсвенная структура" ) на фрикционно -подвижных соедеиний для
обеспечения сейсмостойкого строительства железнодорожных мостов в Киевской Руси
Основной докладчик на Всероссйском съезже по фундаменталдьным прроблемам
теоретической и прикладной механике полковник Шендаков Михпаил https://pptonline.org/1148335 https://dis
Стажер СПб ГАСУ инжеер -патентовед, Кононенко Роман Игоревич 9111758465@bk.ru
(812) 694-78-10 (981) 886-57-42
424
факс:
425.
425Стажер СПб ГАСУ инжеер -патентовед, Бороденчик Вяеслав Иванович 911758465@bk.ru
rodinailismert@list.ru факс: (812) 694-78-10 (981) 276-49-92
Стажер СПб ГАСУ инжеер -патентовед, Щендаков Михаил Антольевич t8126947810@inbox.ru
t9812764892@yandex.ru m6947810@yandex.ru
факс: (812) 694-78-10 (911) 175-84-65
Стажер СПб ГАСУ проф Матвеев Владимир Владимирович
79111940880 rodinailismert@list.ru t9111758465@outlok.com
070355mvv@gmail.com
Конструктивные системы в природе и строительной технике Темнов В. Г. 1987 г.
https://dwg.ru/lib/1147 m6947810@yand.ru spb6947810@yandex.ru
В книге освещены вопросы организации конструктивных систем организмов живой природы в процессе эволюции. Рассмотрены бионические принципы оптимизации конструктивных систем. Впервые предложены алгоритмы
синтеза оптимальных конструктивных систем на основе бионических принципов. Представлены строительные конструкции, созданные на основе бионических принципов, и освещен опыт их применения в практике строительства.
Книга предназначена для научных и инженерно-технических работников.
ПРИНЯТИЕ РЕШЕНИЙ ПРИ ПРОЕКТИРОВАНИИ ИСКУССТВЕННОЙ СРЕДЫ ОБИТАНИЯ С
ИСПОЛЬЗОВАНИЕМ БИОНИЧЕСКИХ ПРИНЦИПОВ КОНСТРУИРОВАНИЯ
1
ТЕМНОВ ВЛАДИМИР ГРИГОРЬЕВИЧ 1
Петербургский государственный университет путей сообщения
https://www.elibrary.ru/item.asp?id=17303643
https://cyberleninka.ru/article/n/ekologiya-i-arhitekturnaya-tektonika-stroitelnyh-obektov-gorodskoy-sredyobitaniya
Книга Темновва В Г СПб ГАСУ зам президента "Сейсмофонд" при СПб ГАСУ ОГРН:
Темнов В Г дтн, проф ПГУПС аттестата испытательной лаборатории СПб ГАСУ №
RA.RU.21СТ39 от 27.05.2015 (999) 535-47-29 Темнов В Н Подтверждение компетентности
Номер решения о прохождении процедуры подтверждения компетентности 8590-гу (А-5824)
Сведения об аккредитации проф СПб ГАСУ В. Г.Темнова
https://pub.fsa.gov.ru/ral/view/26088/applicant
Егорова Ольга Александровна Преподаватель ПГГУПС Теоретическая механика (МТ)
9219626778@inbox.ru
911-175-84-64
факс (812) 694-78-10
425
426.
426Президент организации «СейсмоФонд» при СПб ГАСУ Х.Н.Мажиев , ИНН 2014000780
rodinailismert@list.ru (921) 962-67-78 факс 812 694-78-10
СПб ГАСУ проф. дтн Ю.Л.Рутман СПб ГАСУ автор статьи "Пластичность при сейсмическом
проектировании зданий и сооружений" для гашения динамических колебаний
тел (911) 175-8465
СПб ГАСУ доц. ктн И.У.Аубакирова , (812) 694-78-10 89219626778 6947810@mail.ru ( 911) 17584-65 8126947810@rambler.ru
СПб ГАСУ проф дтн Ю М Тихонов 89219626778@mail.ru 9967982654@mail.ru ( 951) 644-16-48
СПб ГАСУ инжеер -патентовед Андреева Е И 9111758465@bk.ru
sber2202200786697605@gmail.com
факс: (812) 694-78-10
Морозов В И научный консультант , доктор технических наук, профессор, заведующий кафедрой
железобетонных и каменных конструкций, советник РААСН, лауреат премии Правительства РФ,
почетный работник высшей школы РФ rodinailismert@list.ru
(961) 886-57-42
Суворова Т В , руководитель ИЦ "ПКТИ-СтройТЕСТ" 91117588465@bk.ru
te9219626778@gmail.com ( 981) 276-49-92 kart2202200786697605@gmail.com
426
427.
427Черный А.Г , научный консультант, заведующий кафедрой металлических и деревянных
конструкций, доктор технических наук, профессор СПб ГАСУ 8126947810@rambler.ru (921)
962-67-78 kartf2202200640855233@gmail.com
Стажер СПб ГАСУ инжеер -патентовед, Коваленко Александр Иванович 9111758465@bk.ru
факс: (812) 694-78-10 (981) 886-57-42
Преодоление водных препятствий всегда было существенной
проблемой для армии. Все изменилось в начале 1983 году благодаря
проф дтн ЛИИЖТ А.М.Уздину , который получил патент №
1143895, 1168755, 1174616, 2550777 на сдвиговых болтовых
соединениях, а инженер -механик Андреев Борис Иванович получил
патент № 165076 "Опора сейсмостойкая" и № 2010136746
"Способ защита здания и сооружений " который спроектировал
необычный сборно-разборный универсальный железнодорожный
мост" с использование антисейсмических фланцевых сдвиговых
компенсаторов для сборно-разборного моста" , названный в честь
его имени в честь русского ученого, изобретателя "Мост Уздина".
Но сборно-разборный мост "ТАЙПАН" со сдвиговым
компенсатором проф дтн ПГУПС Уздина , пока на бумаге. Sbornorazborniy bistrosobiraemiy universalniy most UZDINA PGUPS 453
str https://pptonline.org/1162626 https://disk.yandex.ru/d/iCyG5b6MR568RA
Зато, западные партнеры из блока НАТО , уже внедрили
изобретения проф дтн ПГУПС Уздина А М. по использованию
сдвигового компенсатора под названием Bailey bridge
Однако, на переправе Северский Донец из выжило очень мало
русский солдат. В Луганской области при форсировании реки
Северский Донец российская армия потеряла много
военнослужащих семьдесят четвѐртой мотострелковой бригады.
Об этом сообщил американский Институт изучения войны. «11
мая украинская артиллерия с гаубиц М 777 уничтожила
427
428.
428российские понтонные мосты и плотно сконцентрированные
вокруг них российские войска и технику, в результате чего, как
сообщается, погибло много человек и было повреждено более 80
единиц техники», — отмечается в публикации. По оценке
института, войска РФ допустили значительные тактические
ошибки при попытке форсирования реки в районе Кременной, что
привело к таким потерям. Ранее в Институте изучения войны
отмечали, что российские войска сосредотачиваются на битве за
Северодонецк, отказавшись от плана крупномасштабного
окружения ВСУ и выхода на административные границы
Донецкой области
Более подробно новом сборно-разборном мосте "ТАЙПАН"
смотри поданную заявку на изобретение ( отправлено в ФИПС
27.04.2022, регистрационный 2022111669 , входящий 024521
Роспатент , Л.Б Добренкова ) под названием : "КОНСТРУКЦИЯ
УЧАСТКА ПОСТОЯННОГО ЖЕЛЕЗОБЕТОННОГО МОСТА
НЕРАЗРЕЗНОЙ СИСТЕМЫ, ВОССТАНОВЛЕННОГО С
ПРИМЕНЕНИЕМ типовых структурных серии 1.460.3-14 ГПИ
"Ленпроектстальконструкция", стальные конструкции покрытий
производственных зданий пролетами 18, 24 и 30 метров с
применением замкнутых, гнутых профилей прямоугольного
сечения типа "Молодечно" E01D 12/00 , аналог изобретения № №
69086, 68528
Просьба направить изобретения проф проф ПГУПС Уздина А М
сборно-разборный мост "ТАЙПАН" многократного применения
Соболеву Виктор Ивановичу КПРФ ОБЩЕРОССИЙСКОЕ
ОБЩЕСТВЕННОЕ ДВИЖЕНИЕ «В ПОДДЕРЖКУ АРМИИ,
ОБОРОННОЙ ПРОМЫШЛЕННОСТИ И ВОЕННОЙ НАУКИ»
127051, г. Москва, ул. Трубная, д. 19/12 стр.2 Тел. +7(905) 782-8266 sobolev@duma.gov,ru
428
429.
429429
430.
430430
431.
431Доклад для Тринадцатого Всероссийского съезда по
фундаментальным проблемам теоретической и прикладной
механике , который состоится в Политехническом Университете
СПб 21-25 августа 2023 по теме:
Прямой расчет в SCAD статически неопределимой упруго
пластического шарнира для стальной фермы балки
железнодорожного моста с большими перемещениями на
предельное равновесие и приспособляемость т/ф (812) 6947810
(911) 175-84-65, OO "Сейсмофонд" при СПб ГАСУ ОГРН
1022000000824 ИНН 201400780 rodinailismert@list.ru
Direct calculation in SCAD of a statically
indeterminate elastic plastic hinge for a steel girder
431
432.
432beam of a railway bridge with large displacements for
ultimate equilibrium and adaptability
Расчет ПК SCAD стальных конструкции покрытия
производственных зданий пролетом 30 метров с
применением замкнутых гнутосварных профилей
прямоугольного сечения типа "Молодечно" (серия
1.460.3-14 ГПИ "Ленпроектстальконструкция")
расчетная нагрузка 3 тонны
Максимальная нагрузка на снег для стальных
ферм балок пролетом 30 метров для России для
расчет в ПК SCAD
432
433.
433433
434.
434434
435.
435435
436.
436436
437.
437437
438.
438438

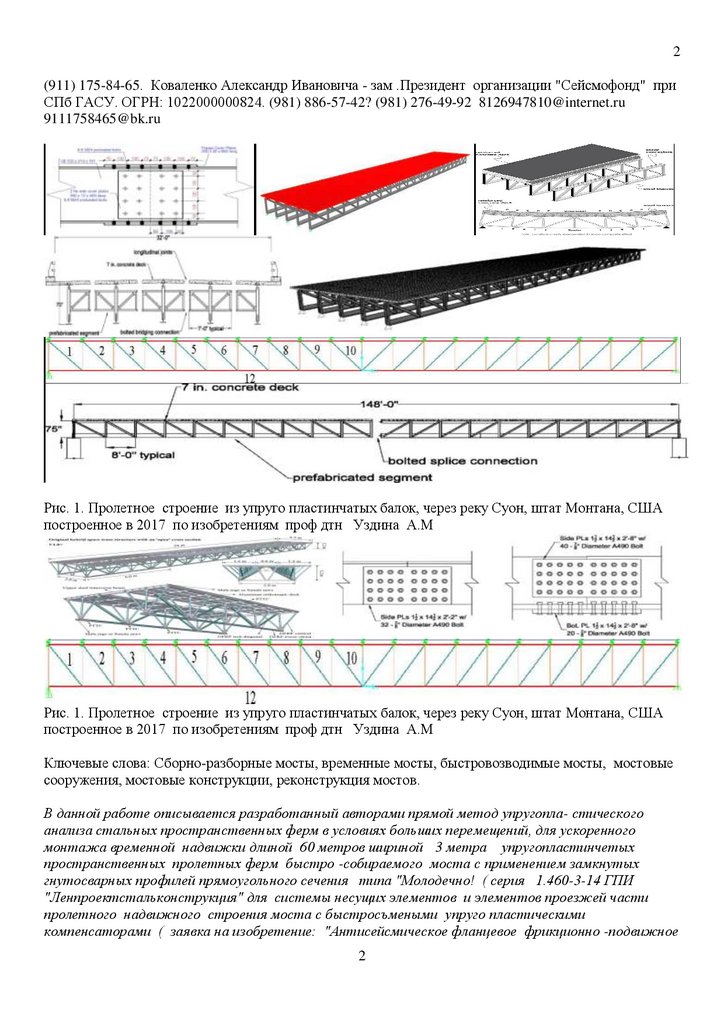


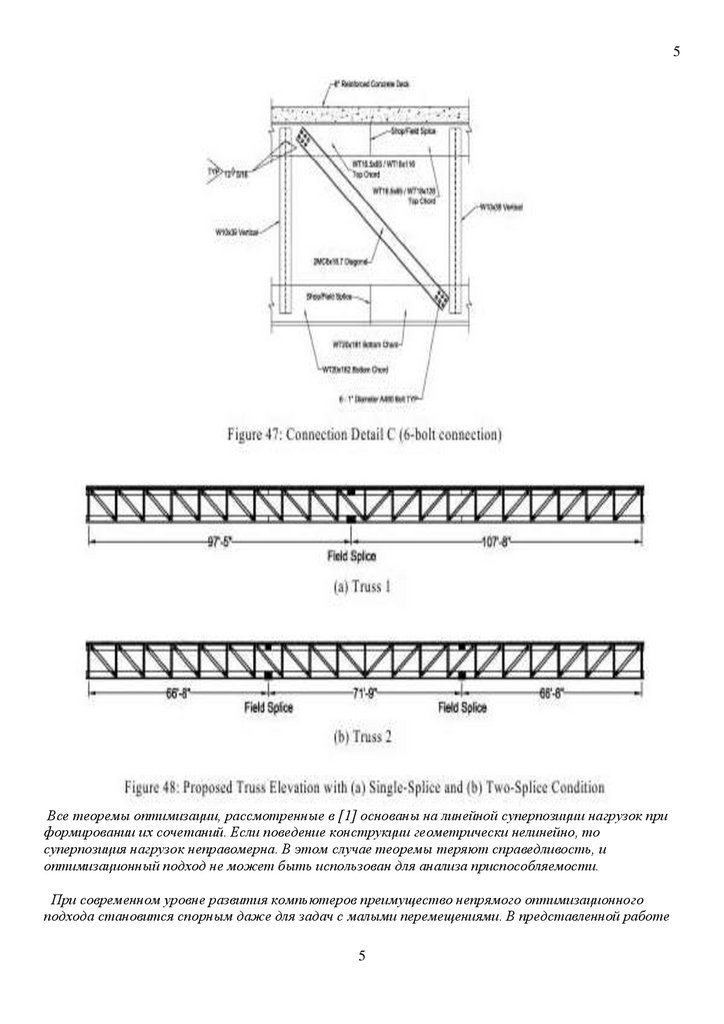



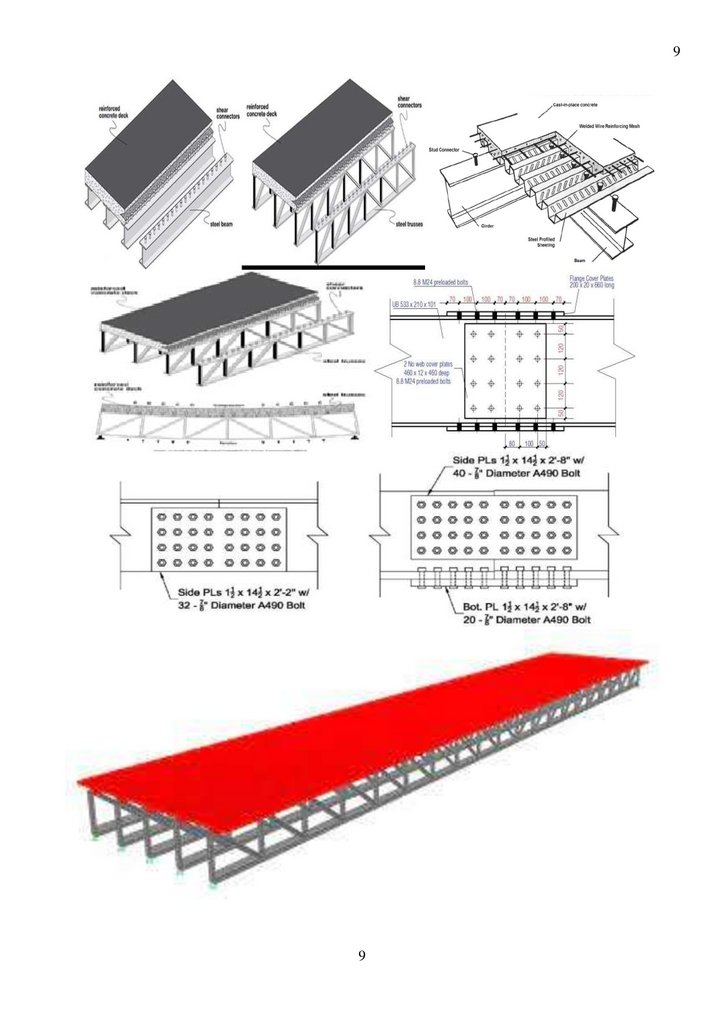




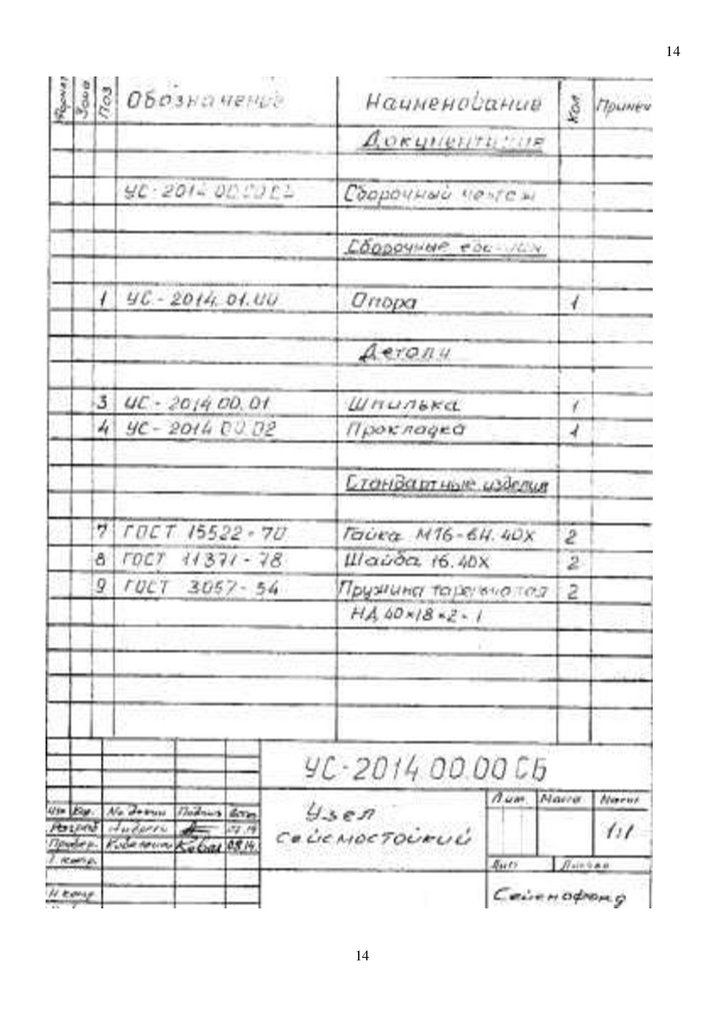
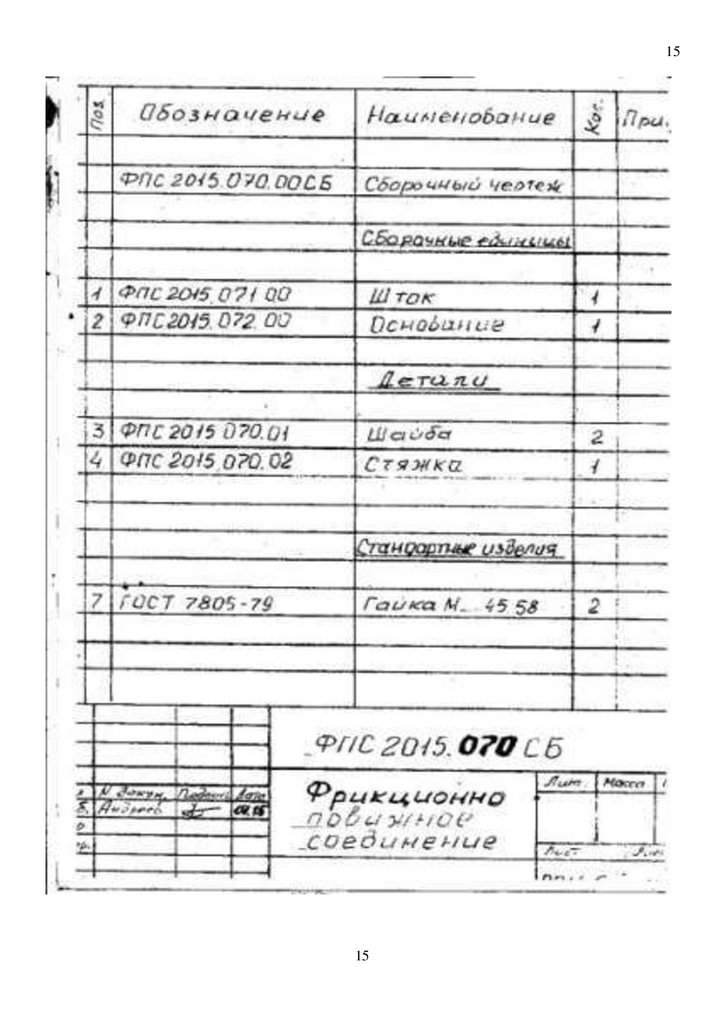
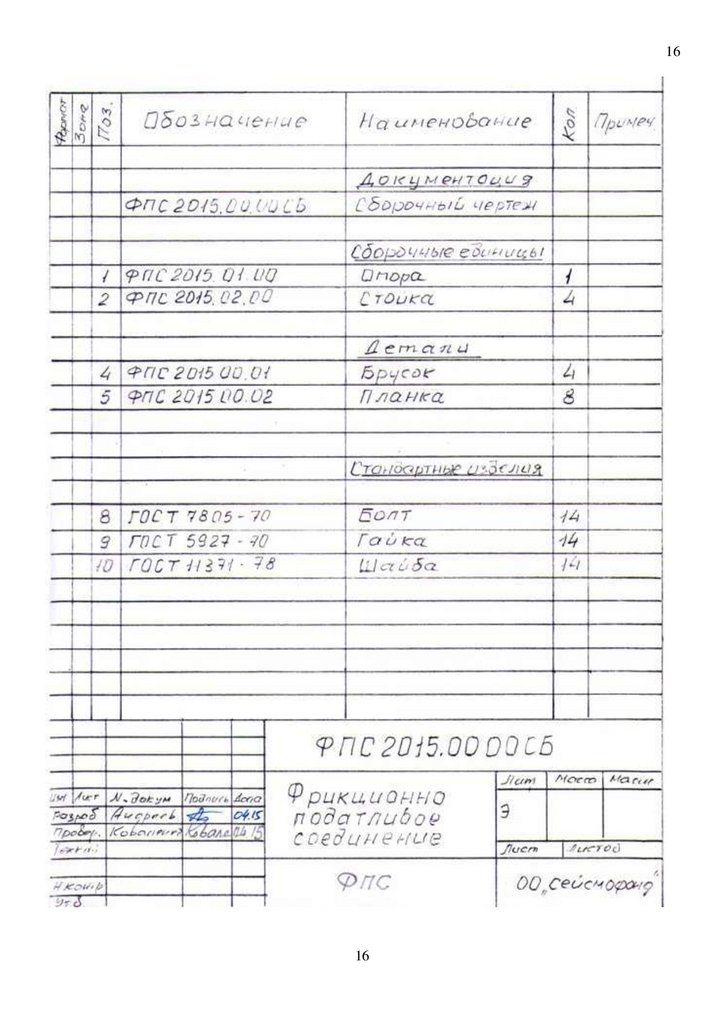
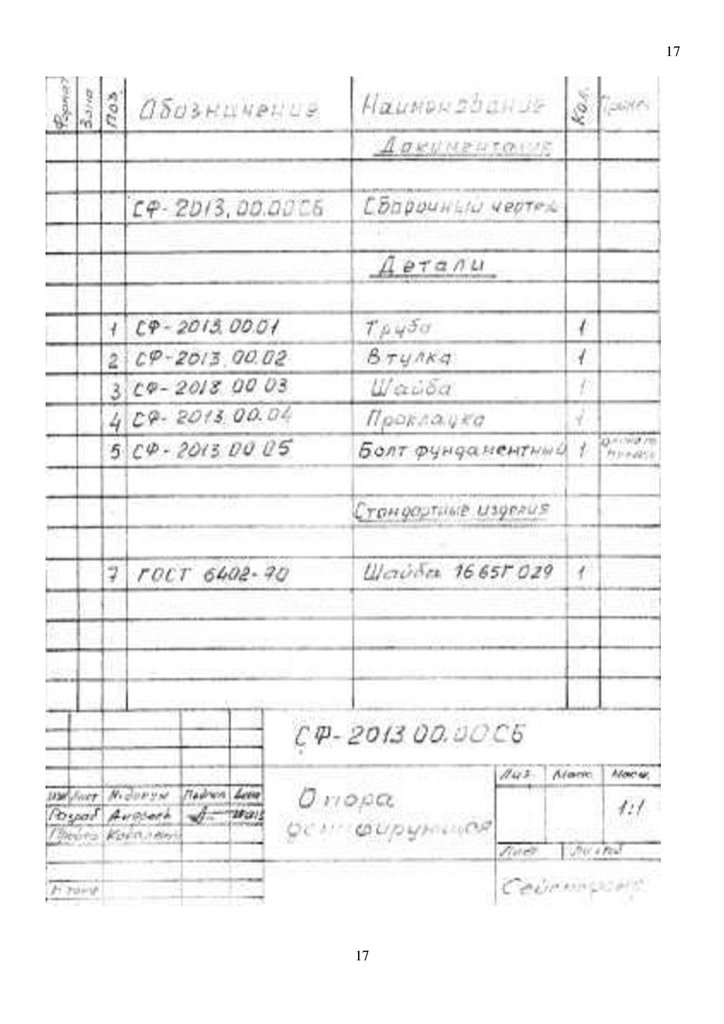
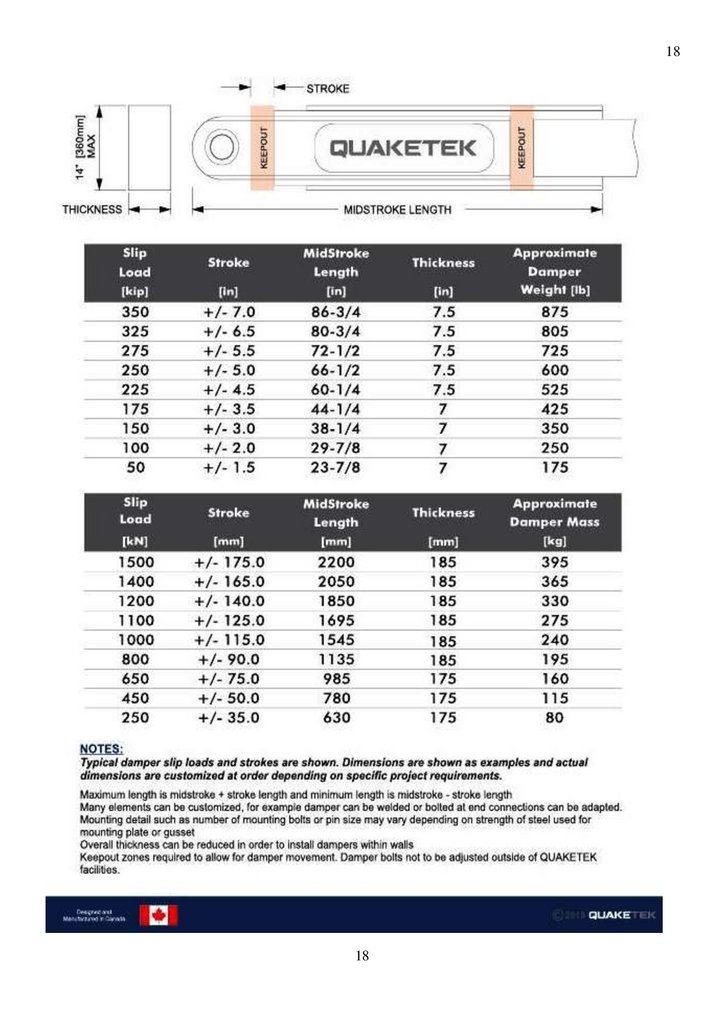
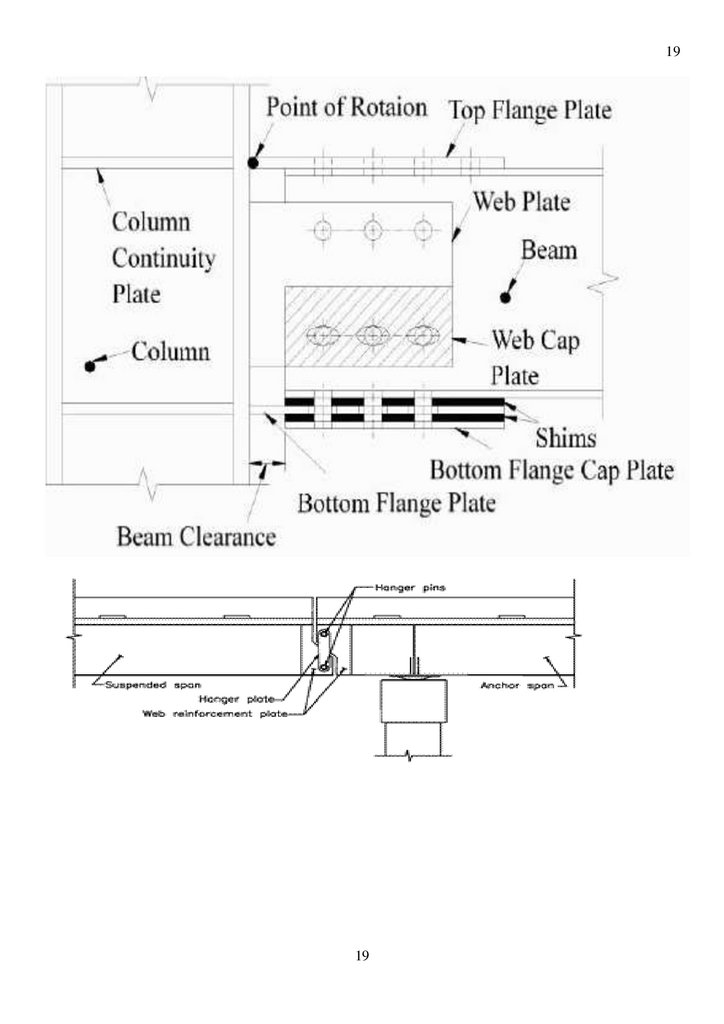





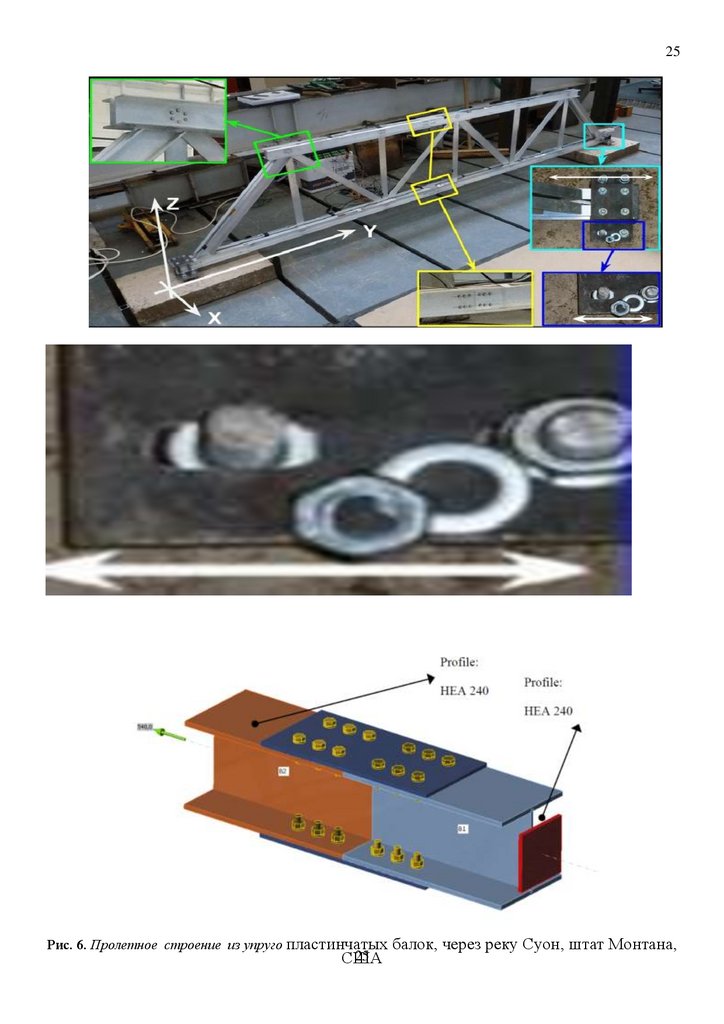
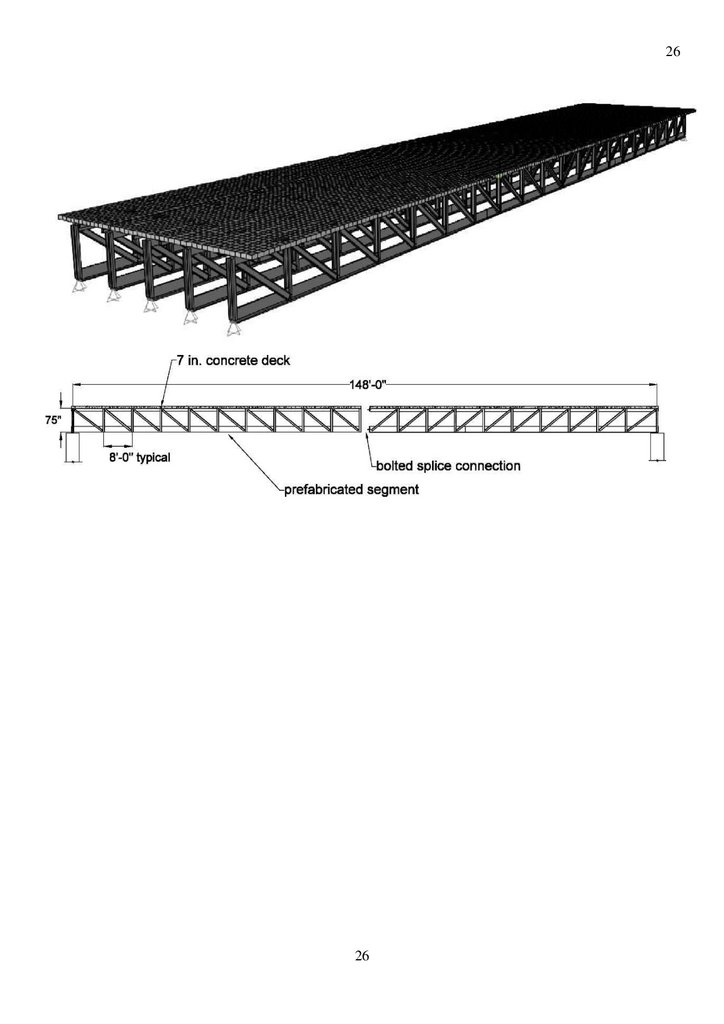
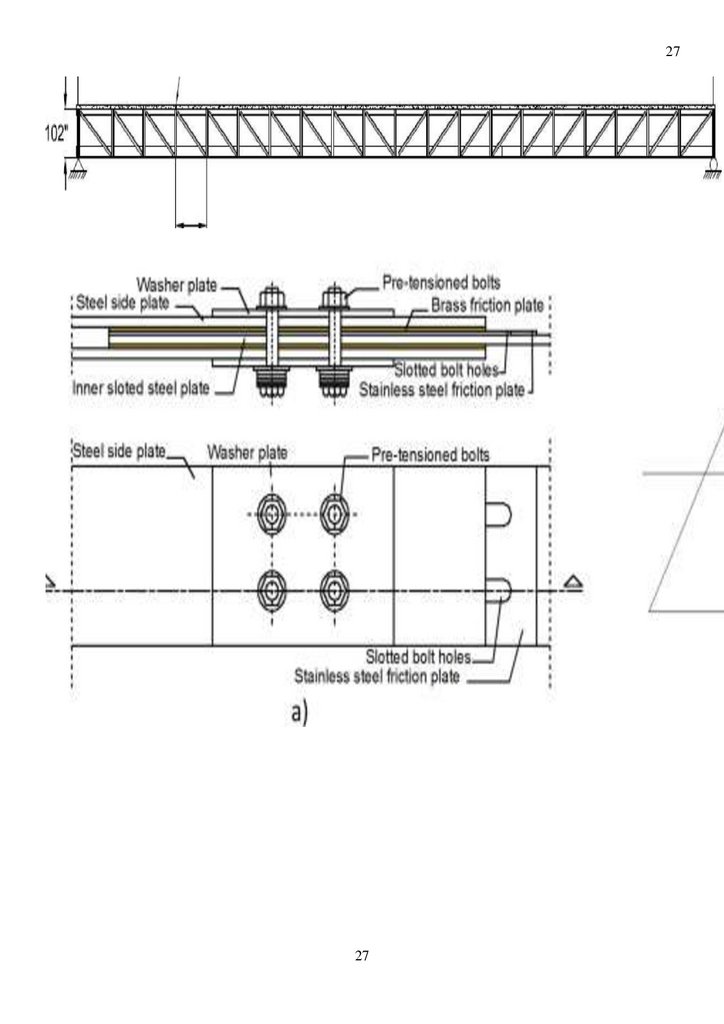
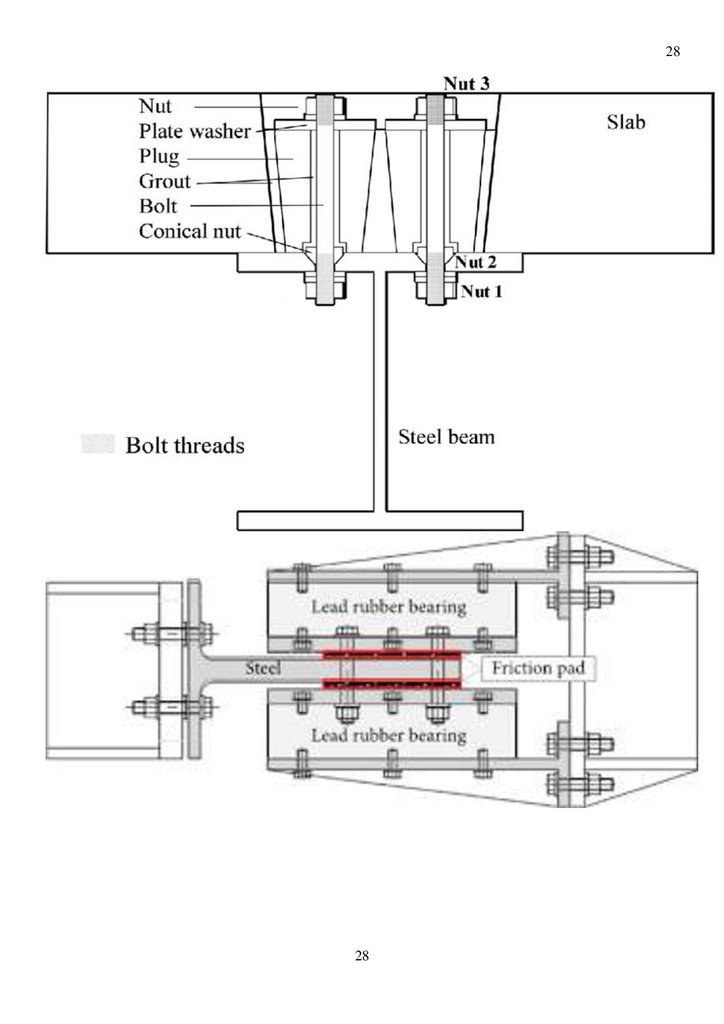
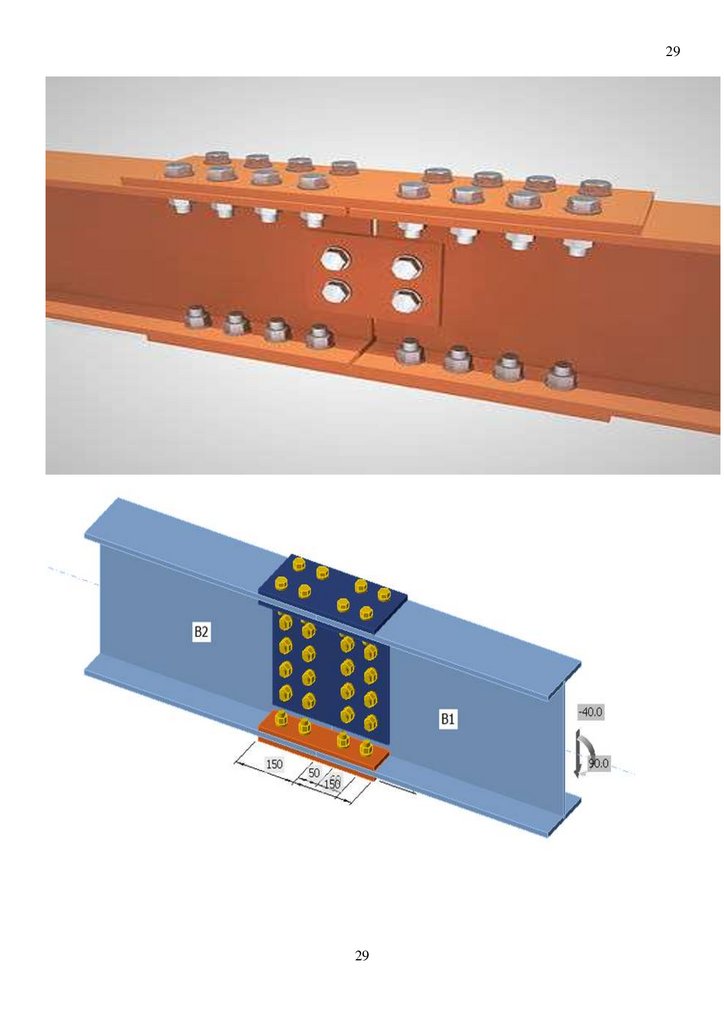

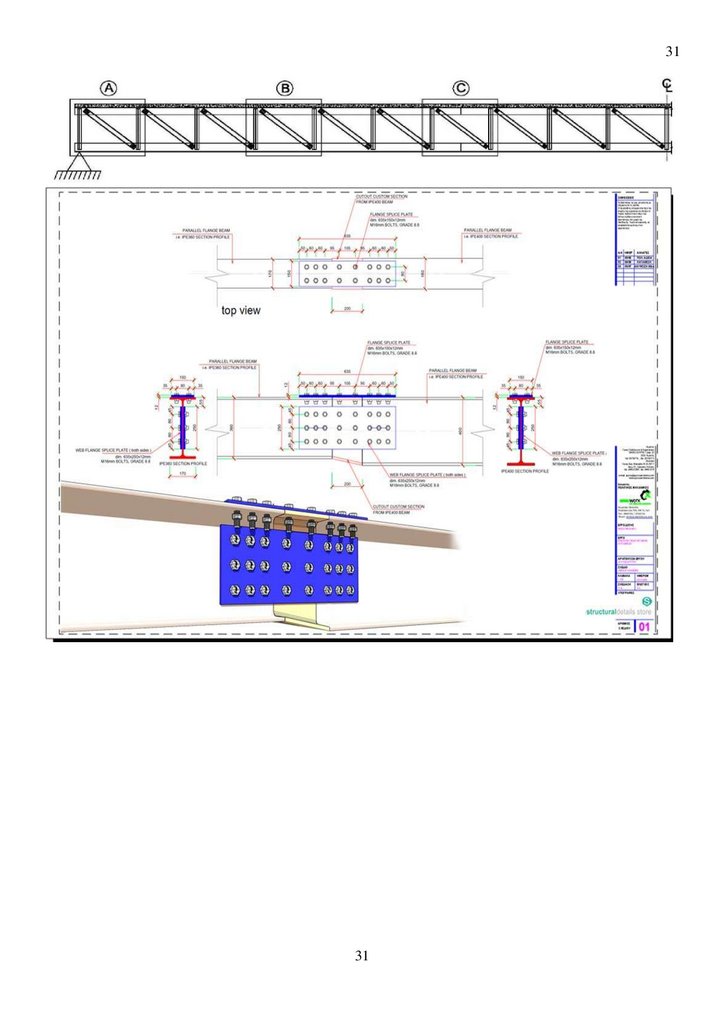
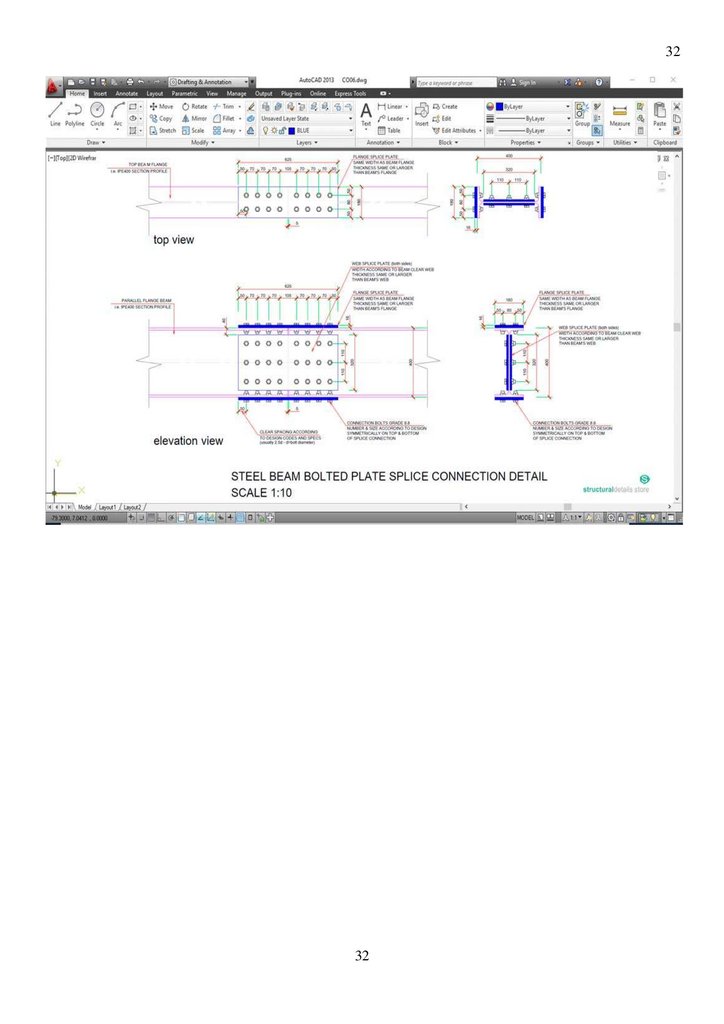
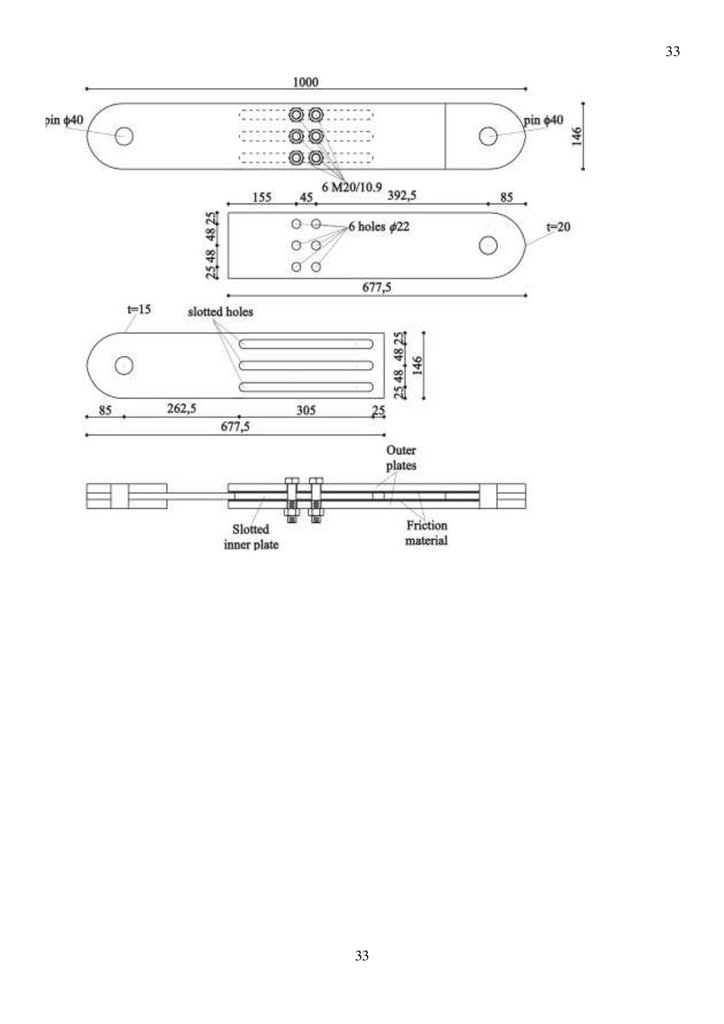
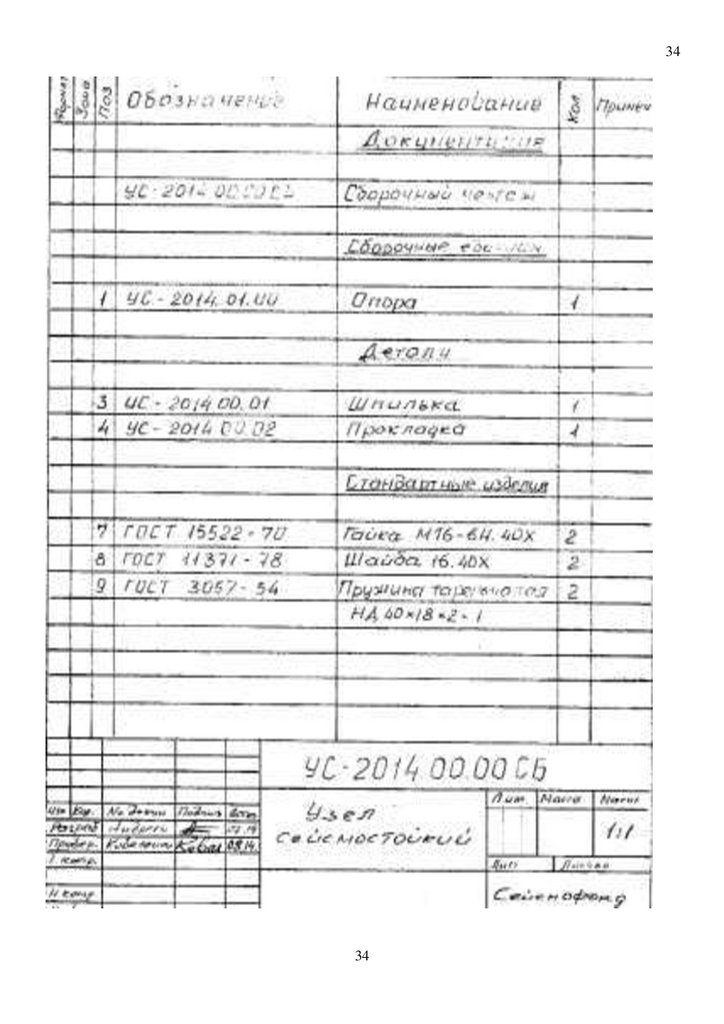
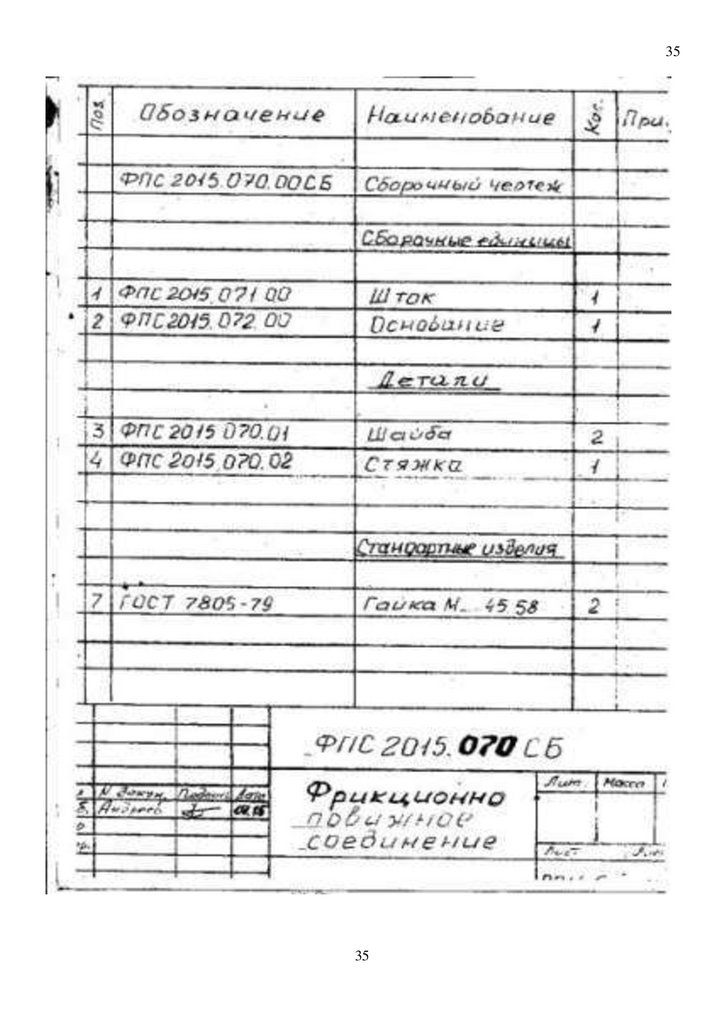
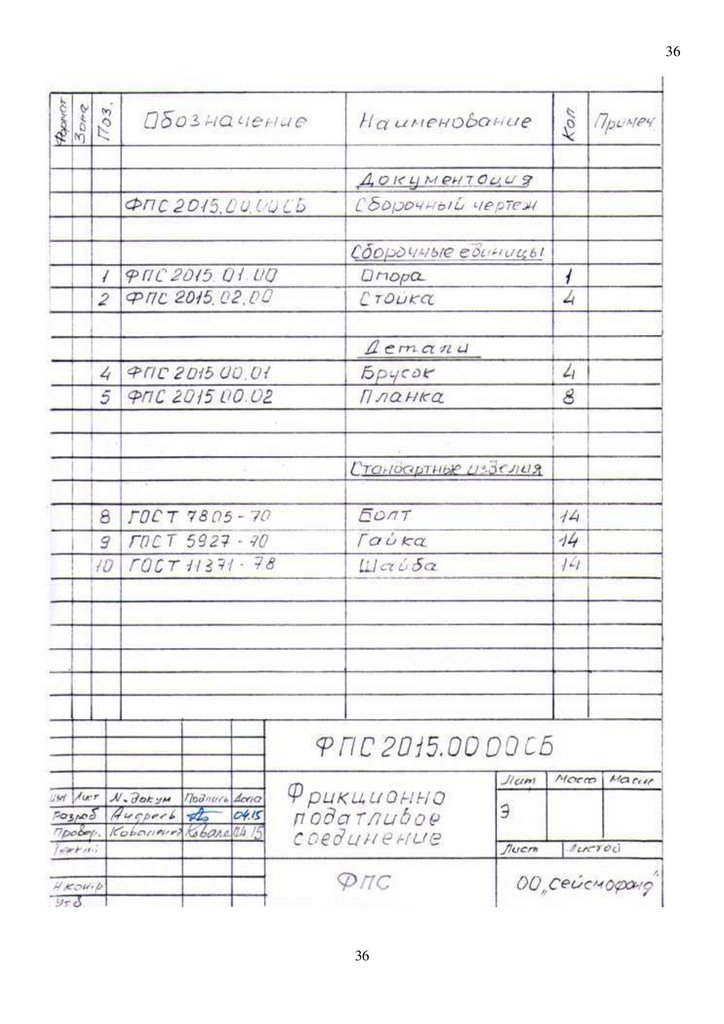
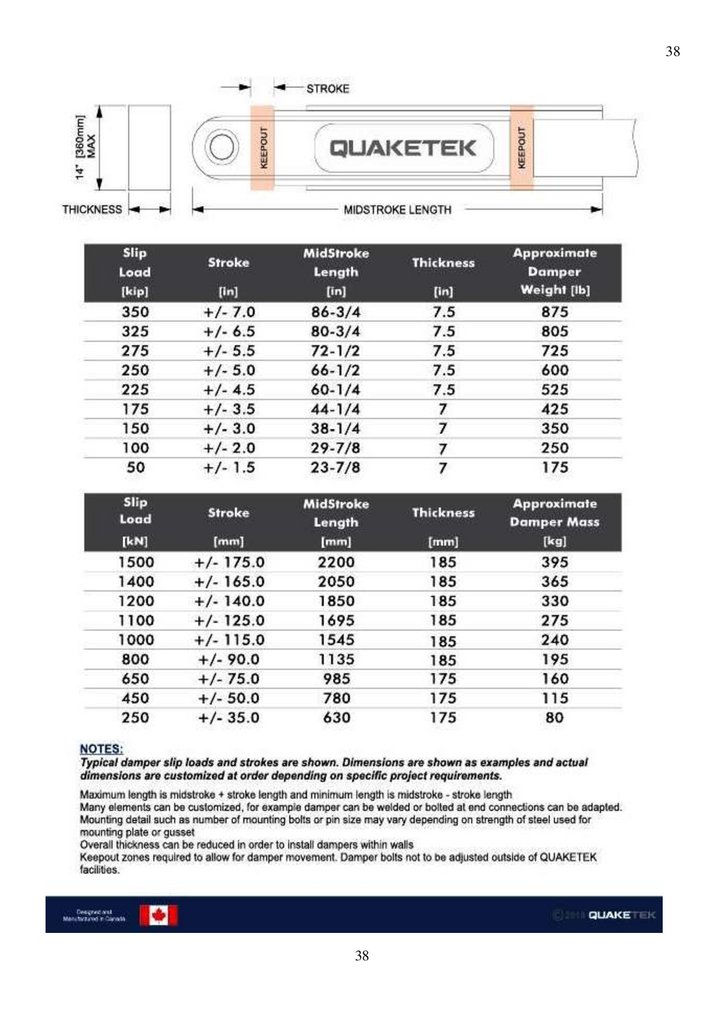
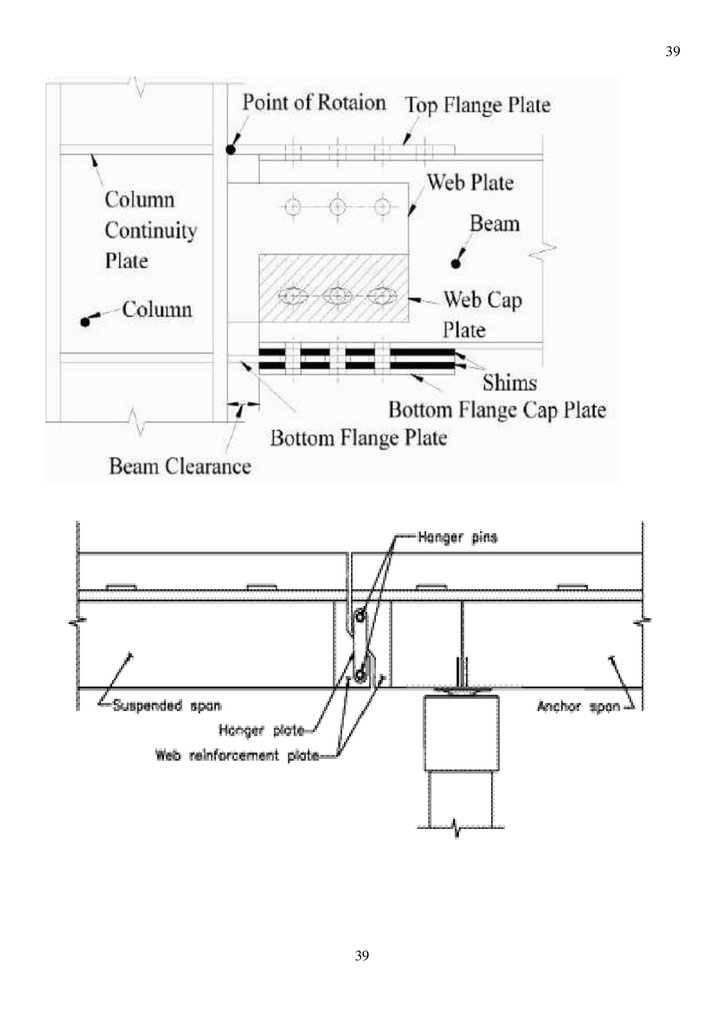

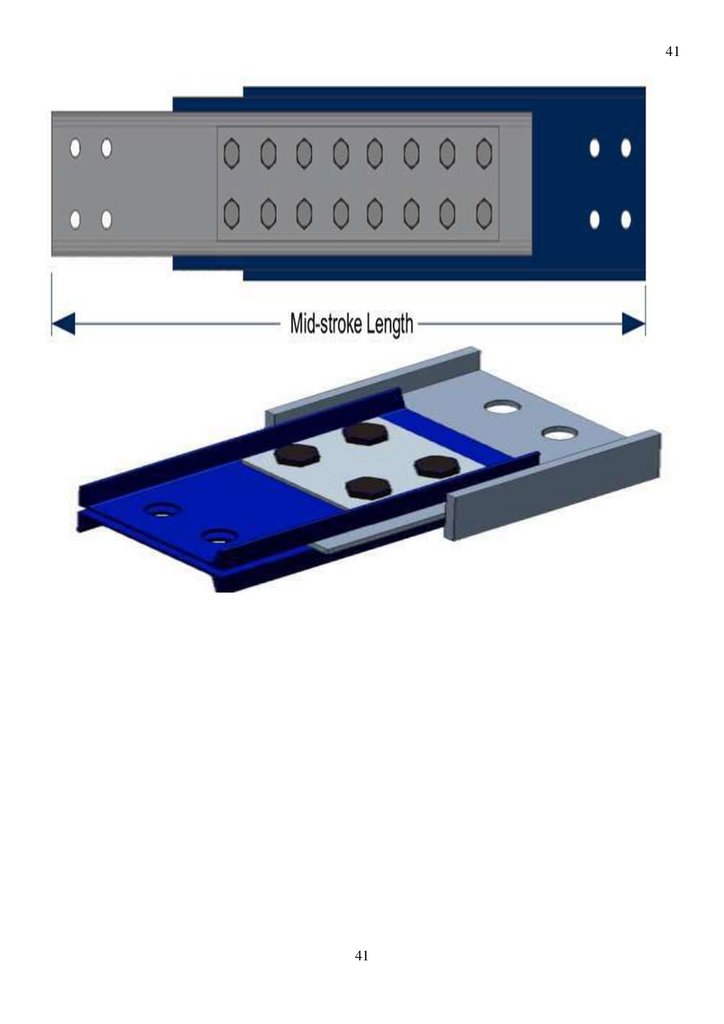






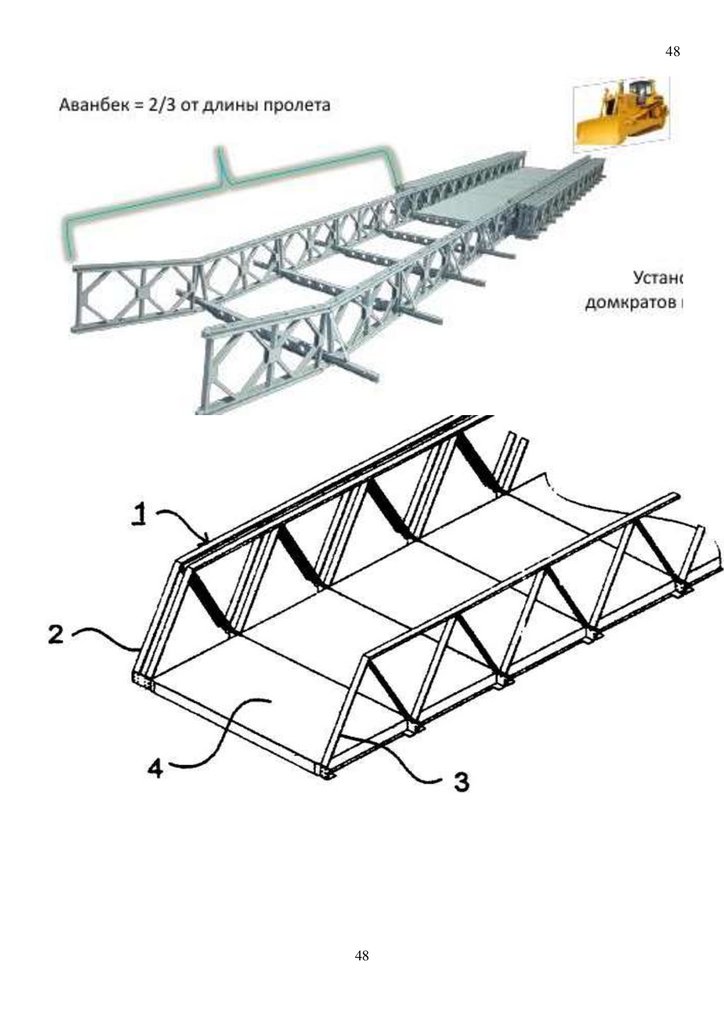
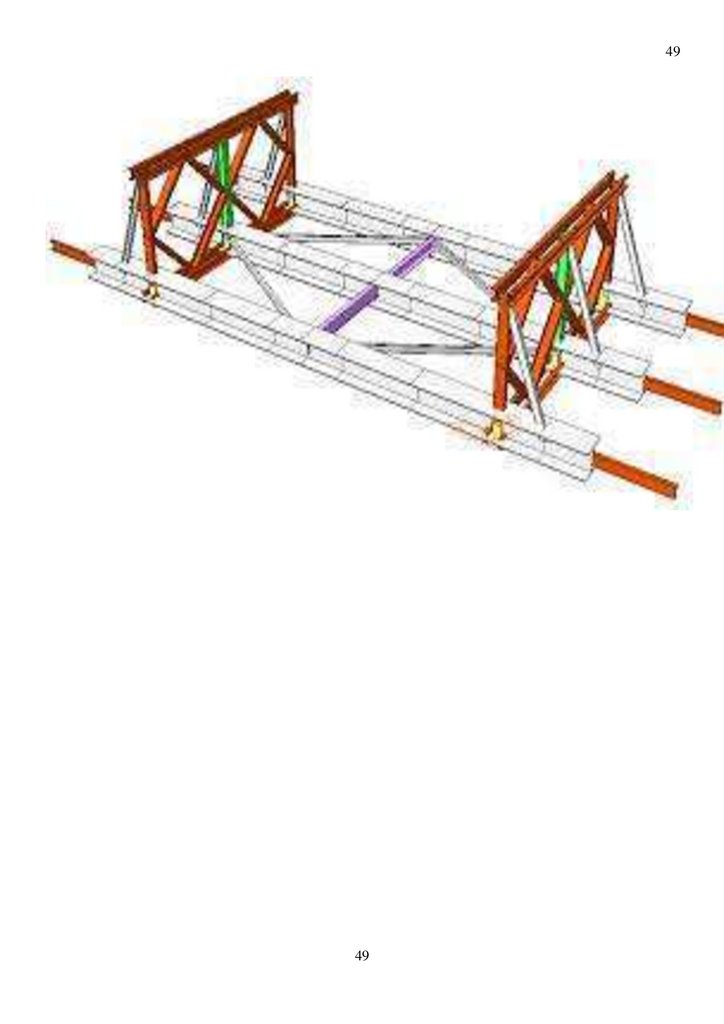
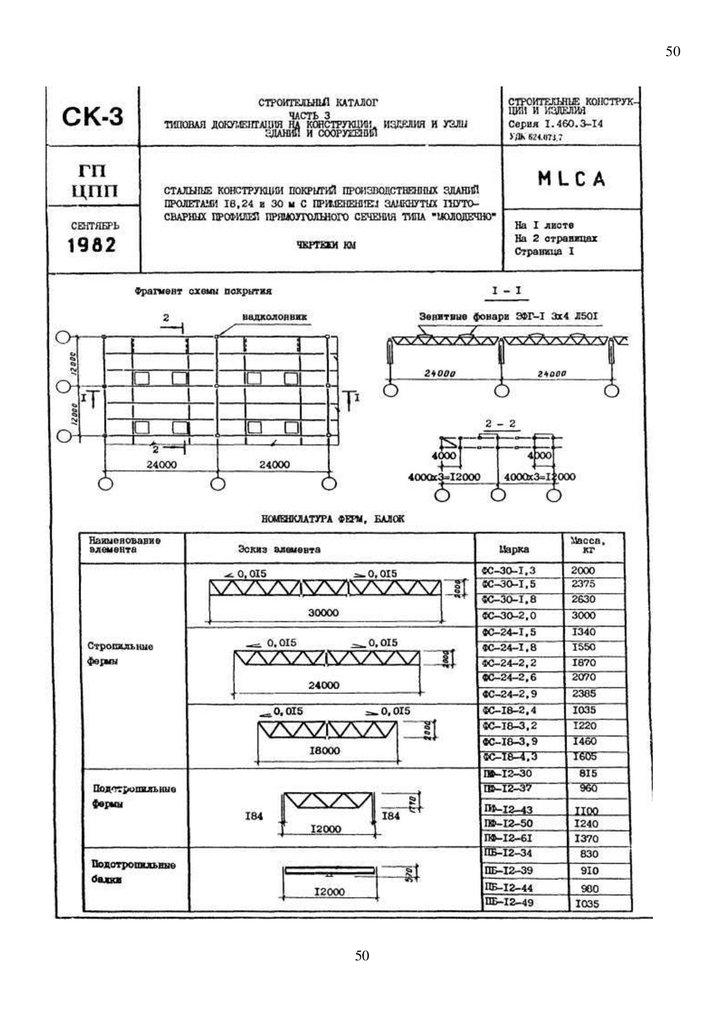
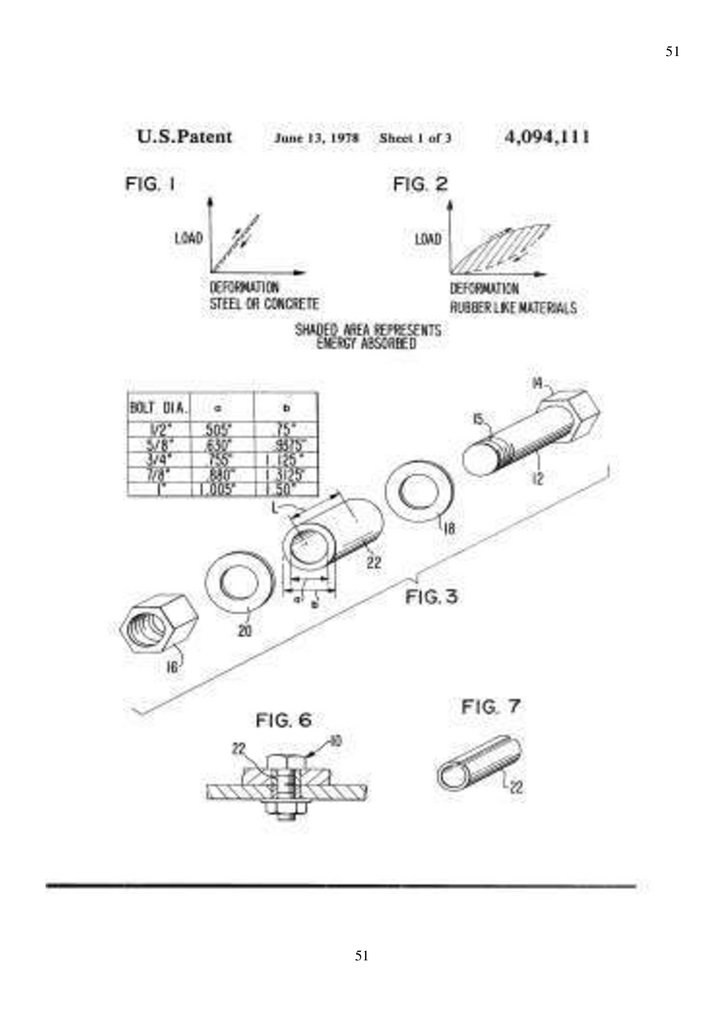
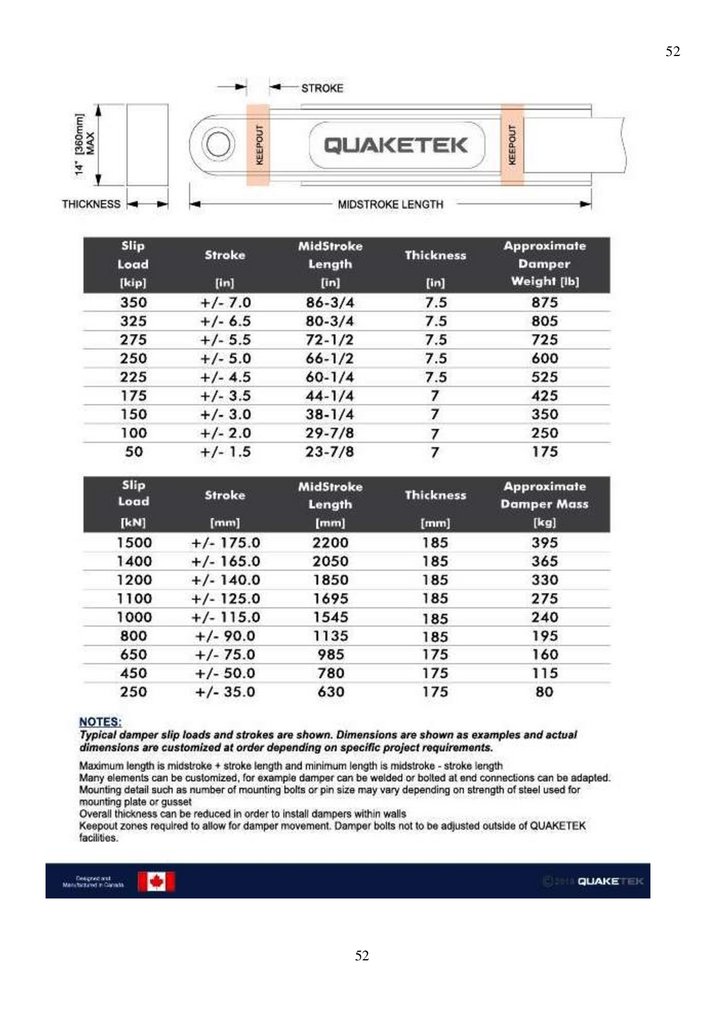
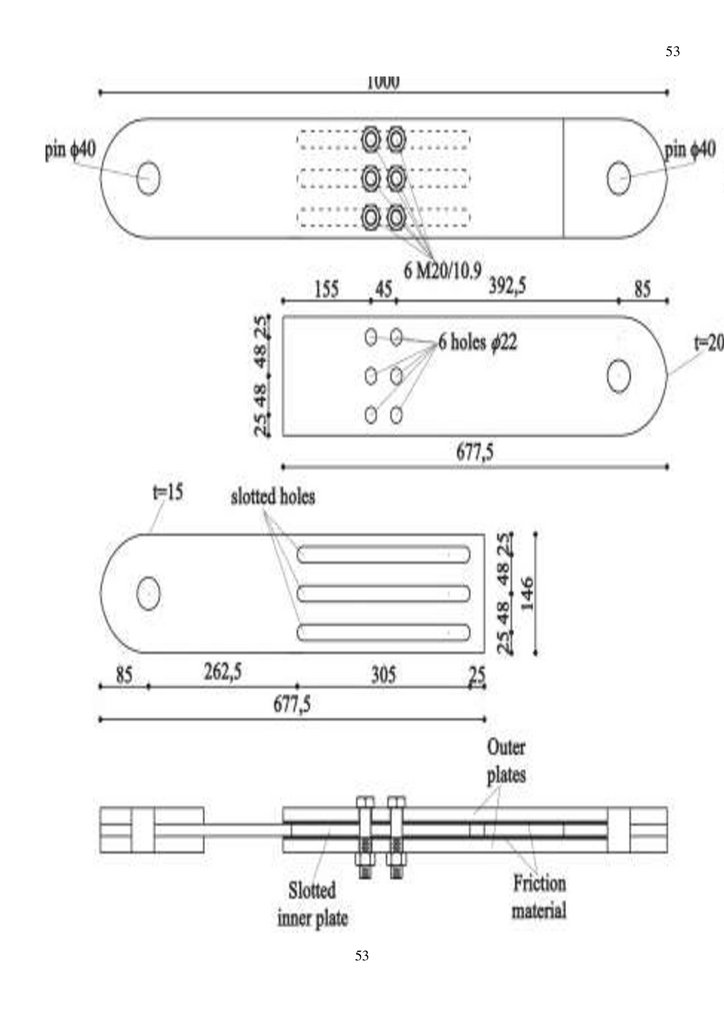
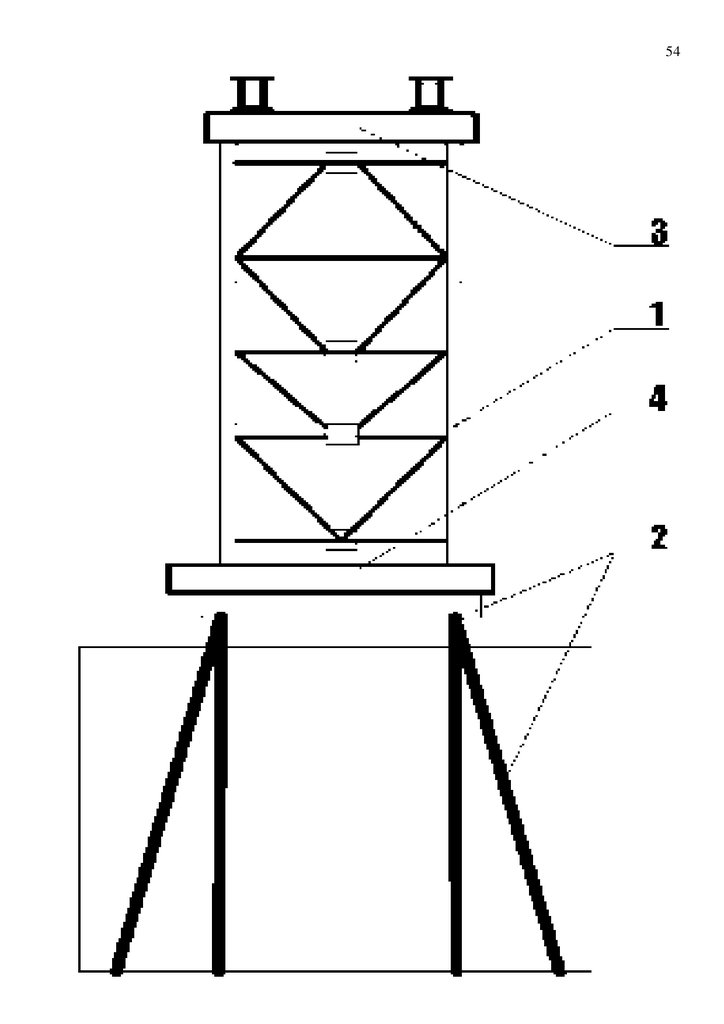
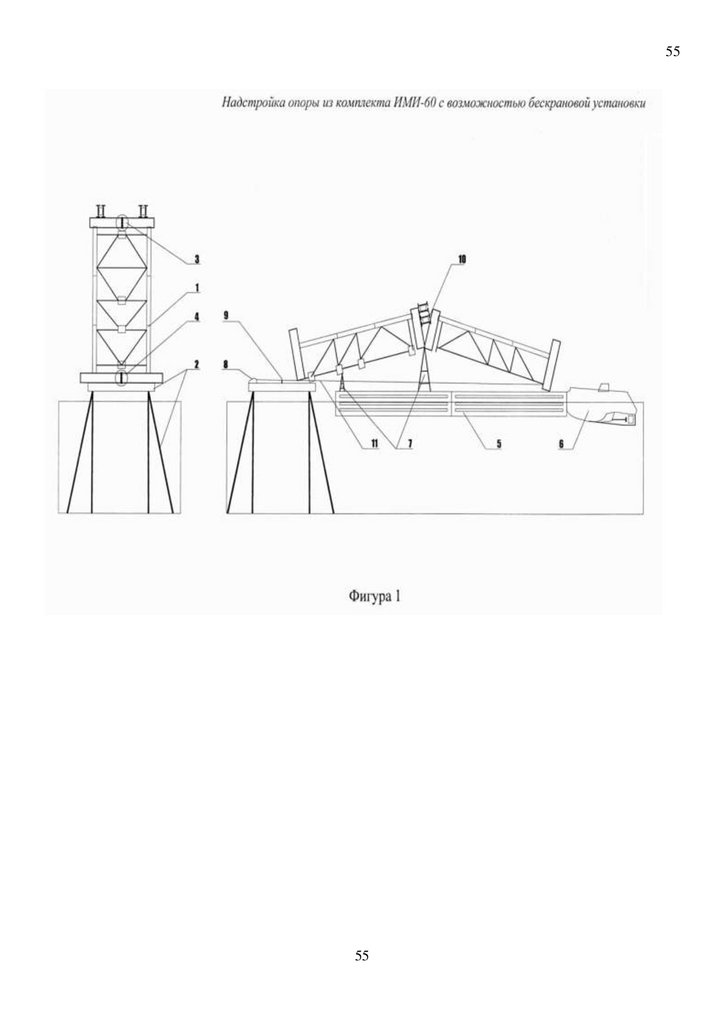
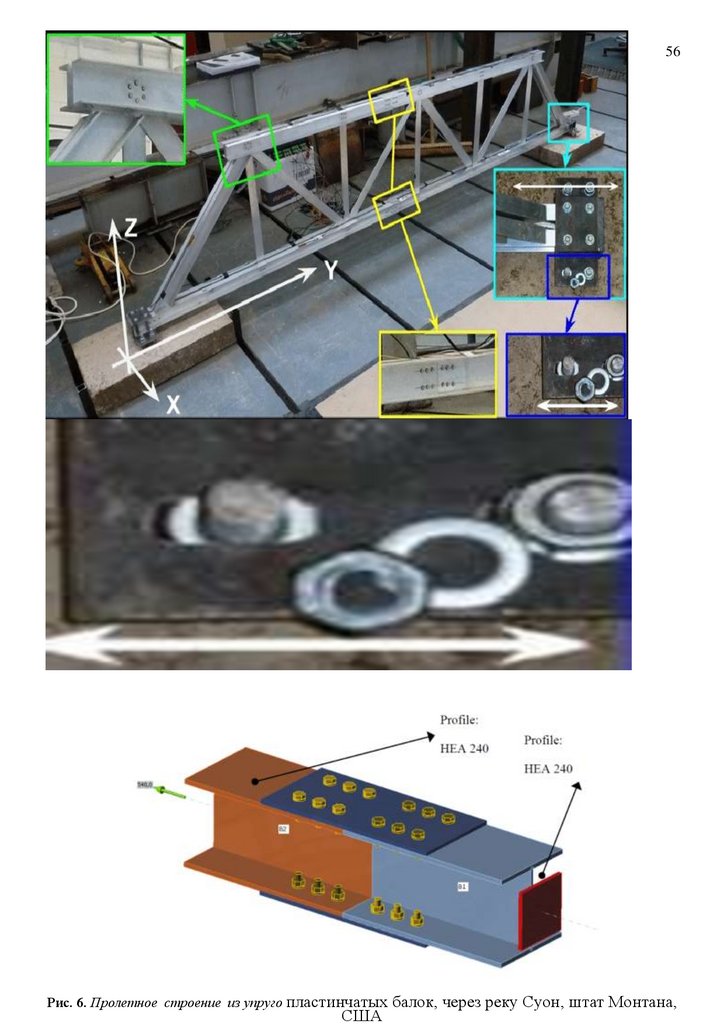
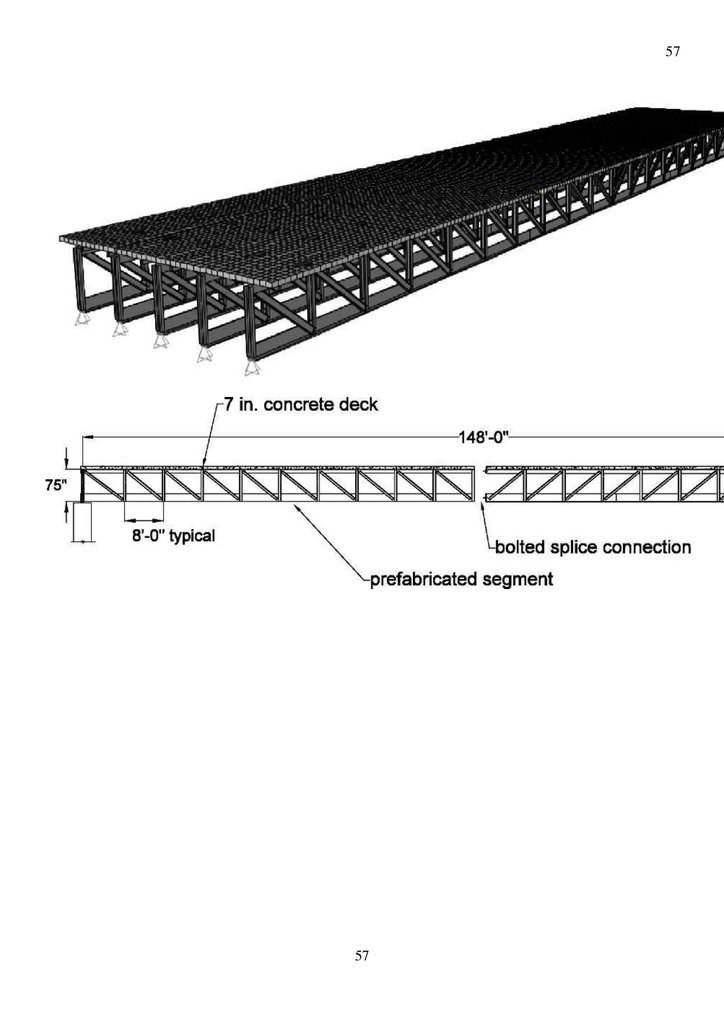
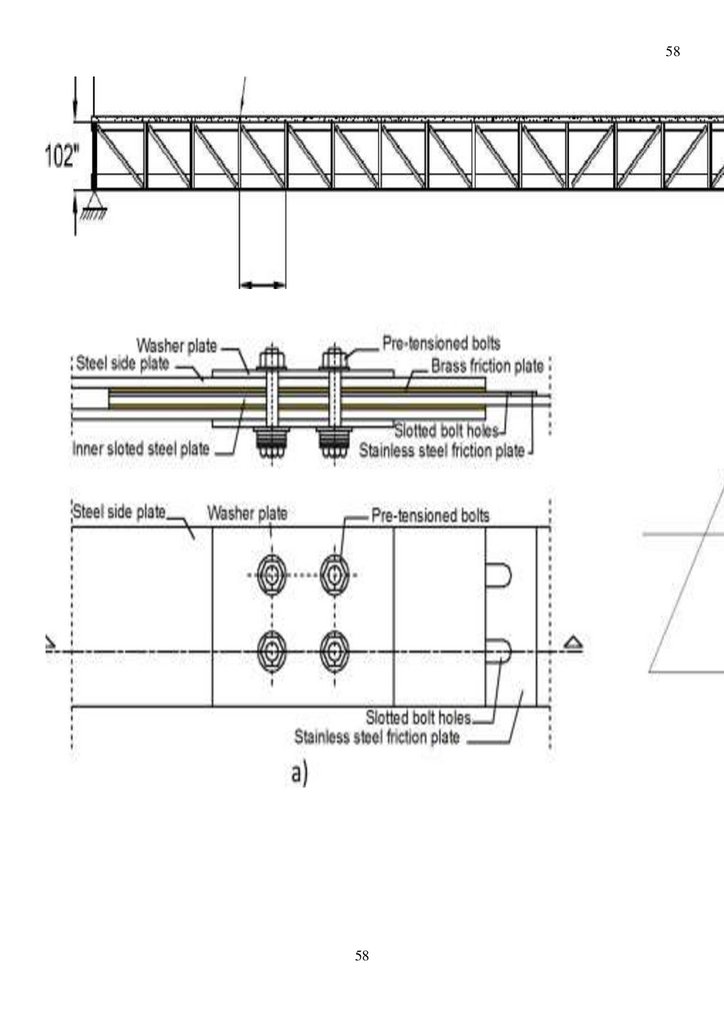
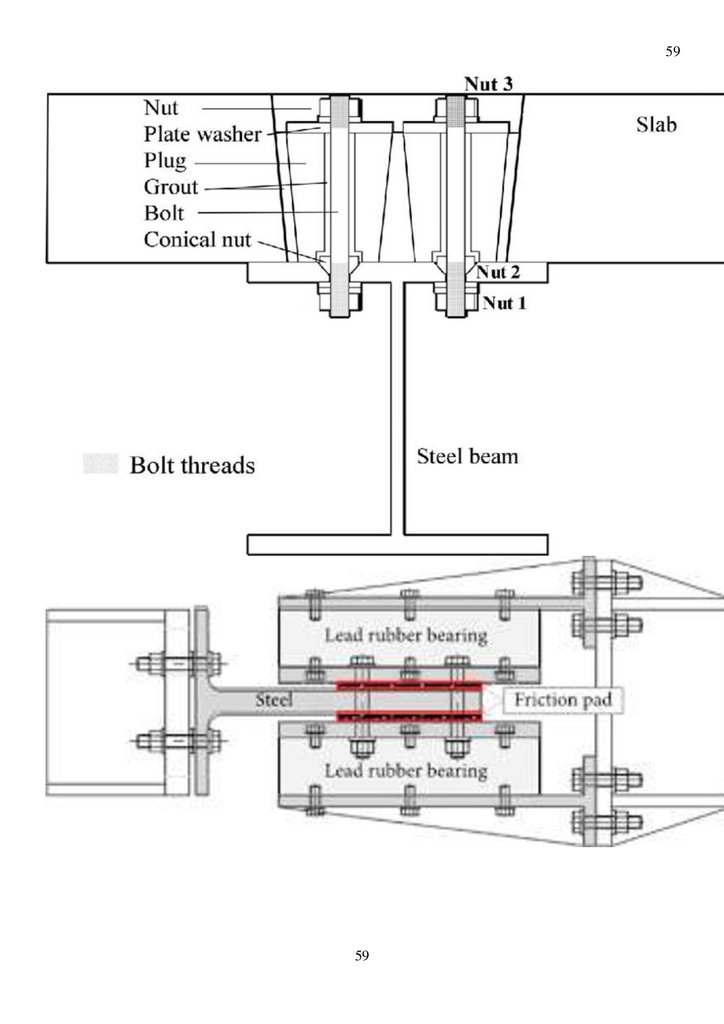
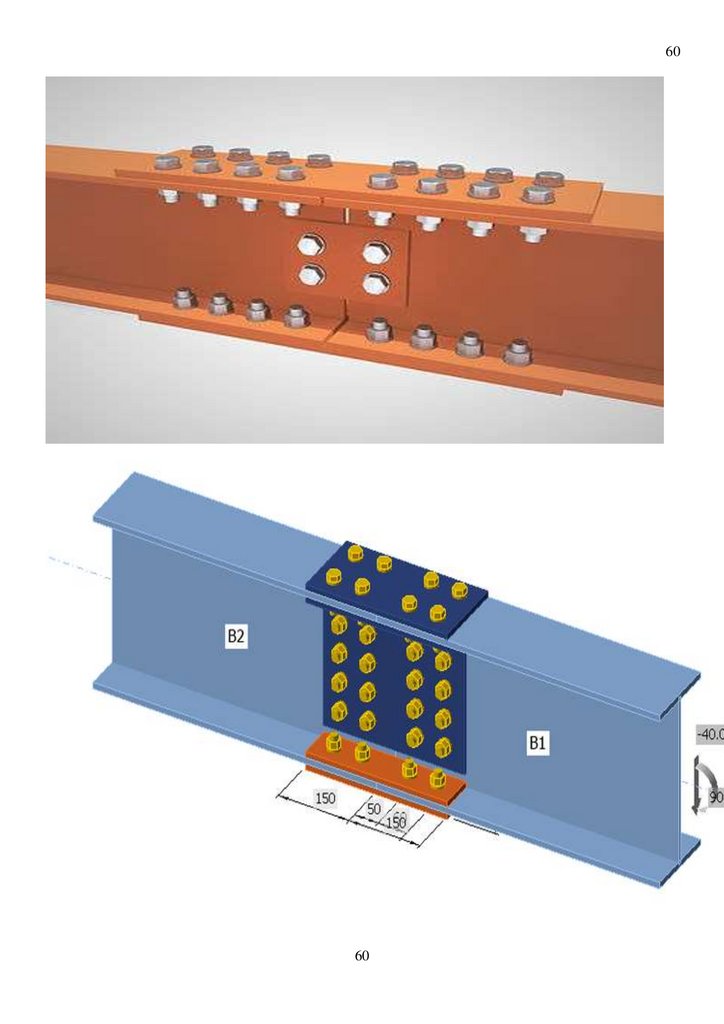

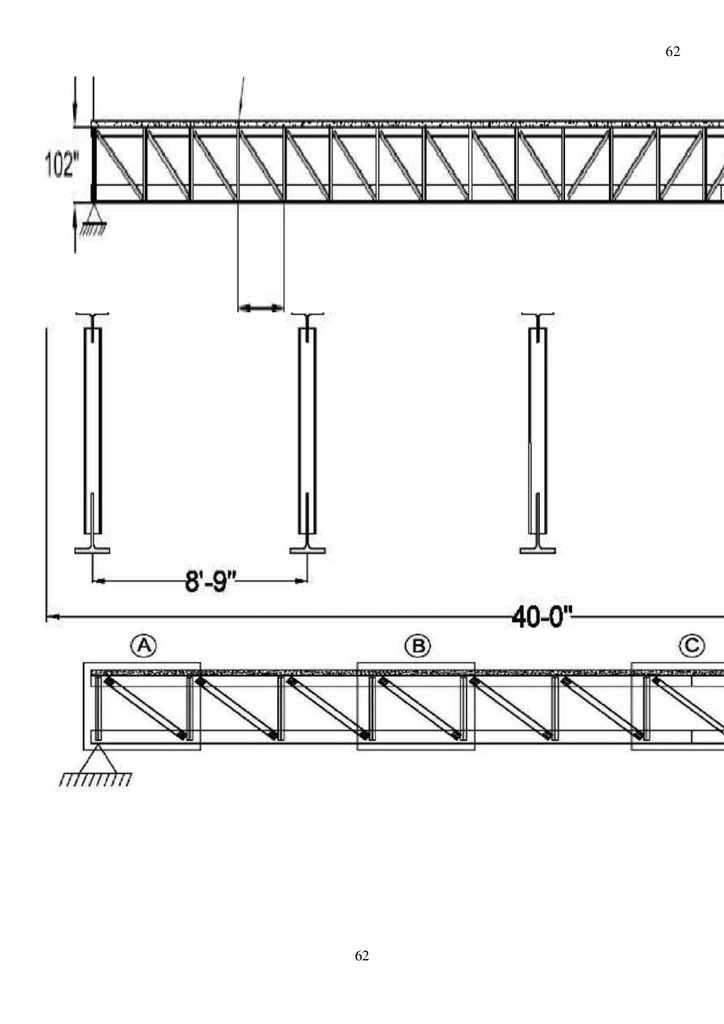
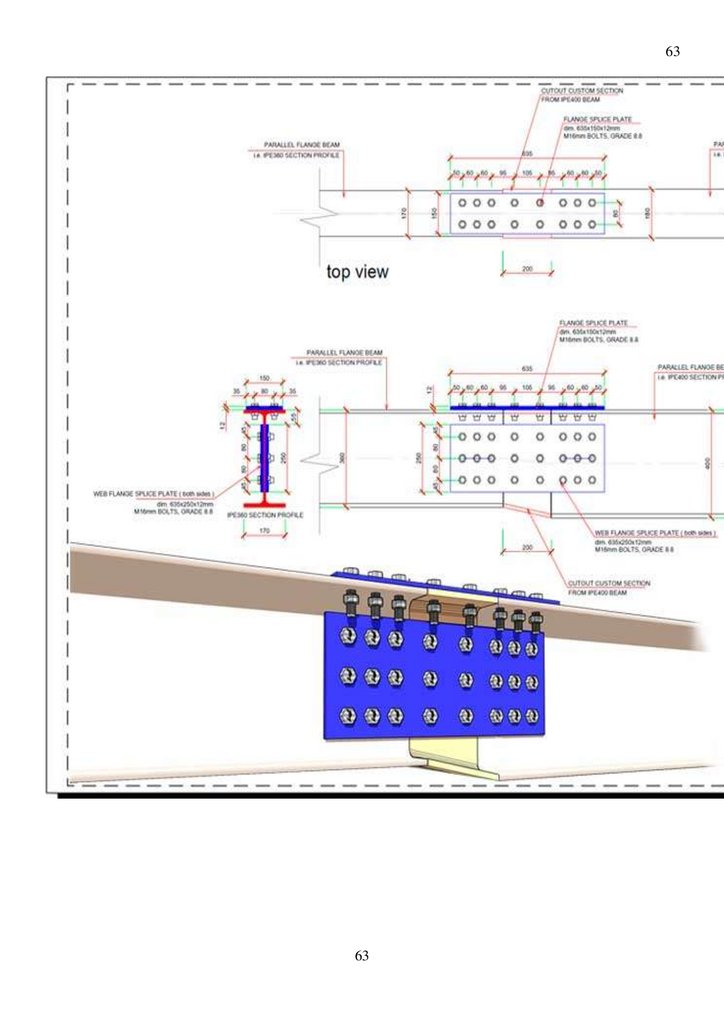
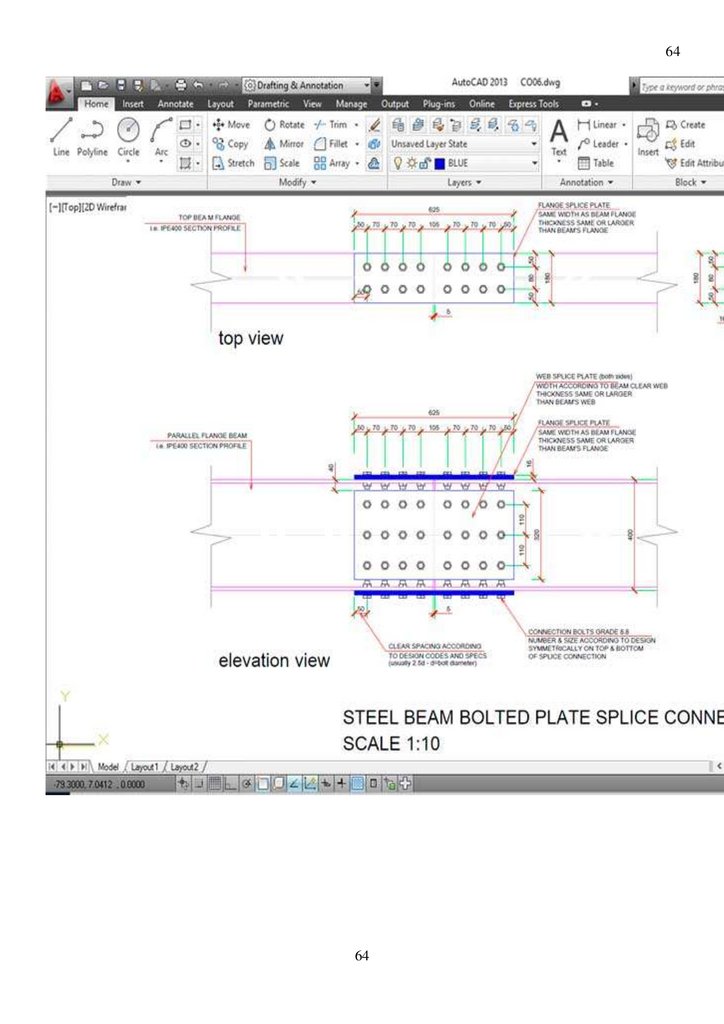
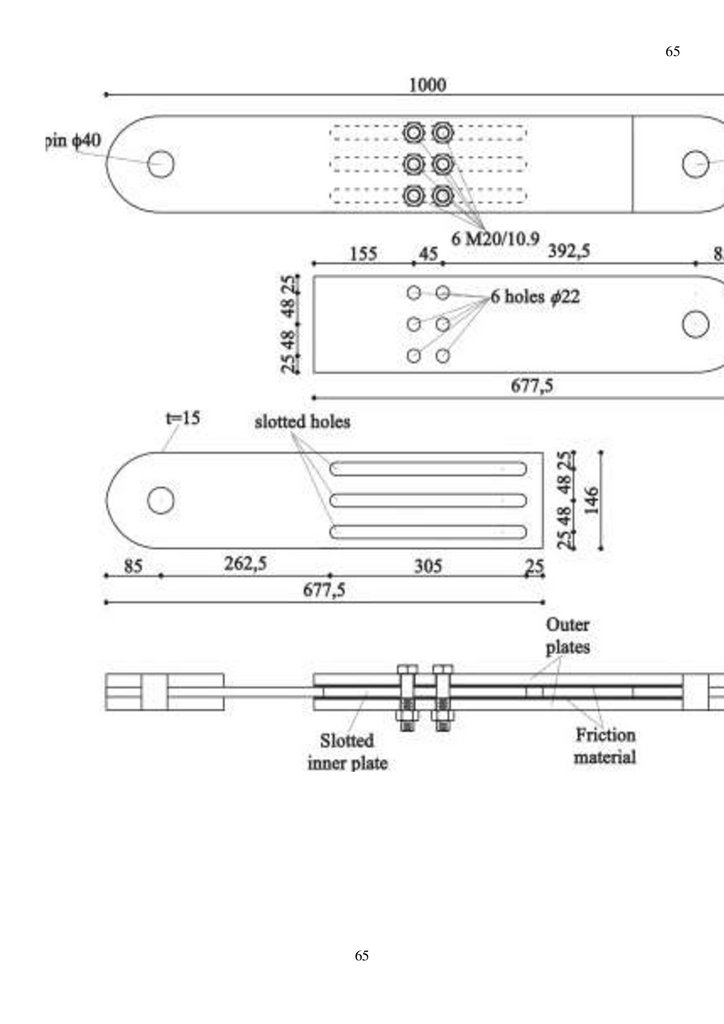
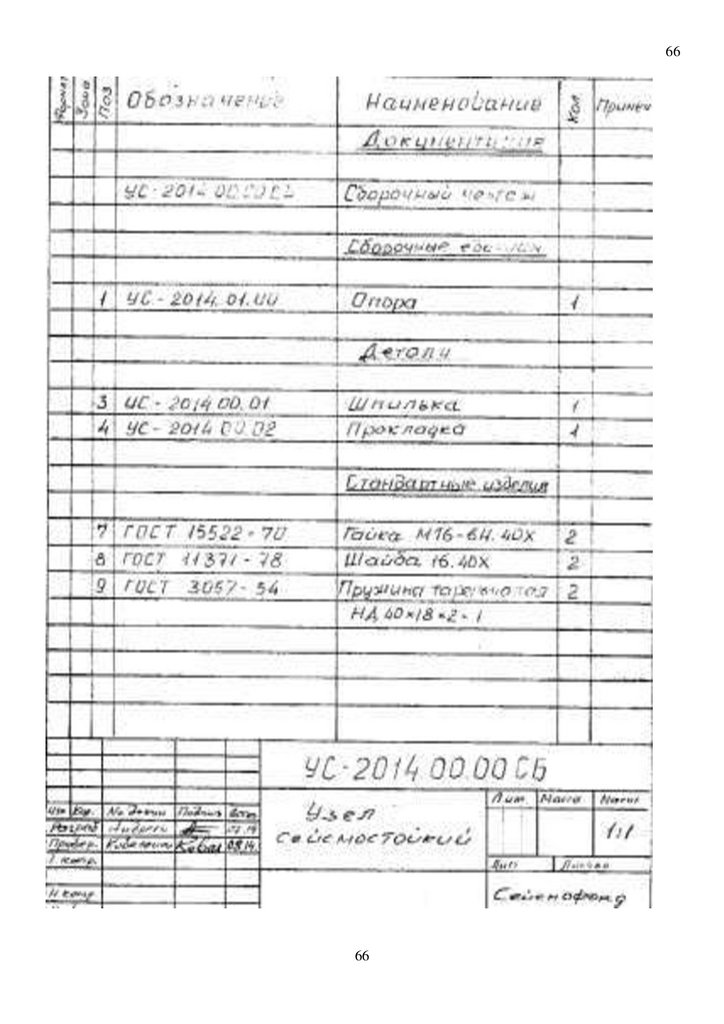
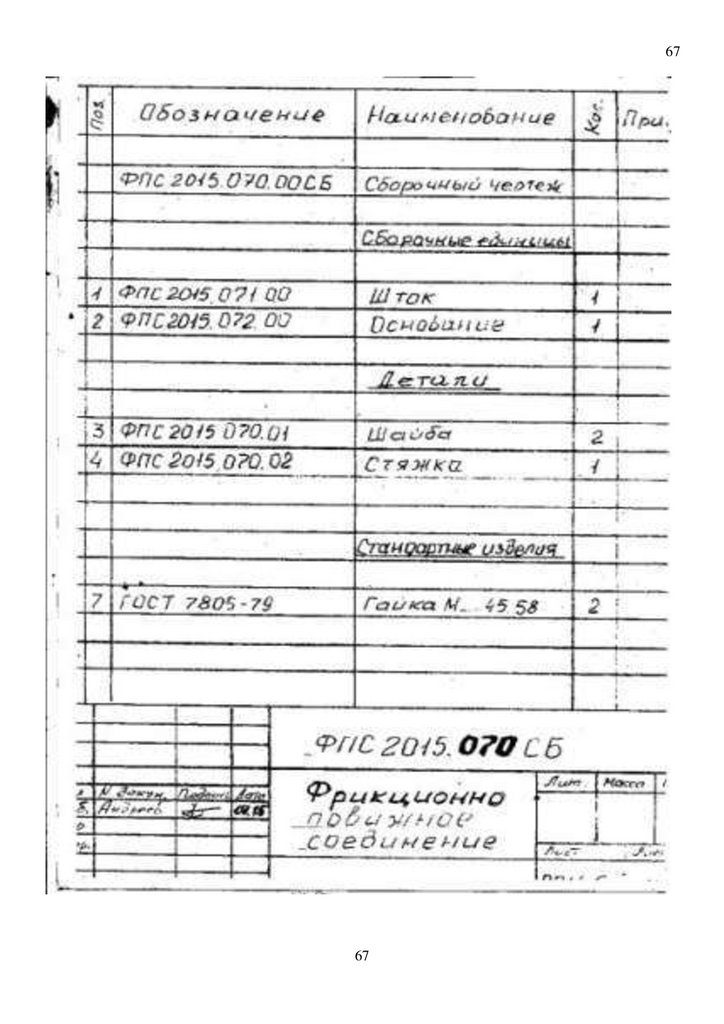
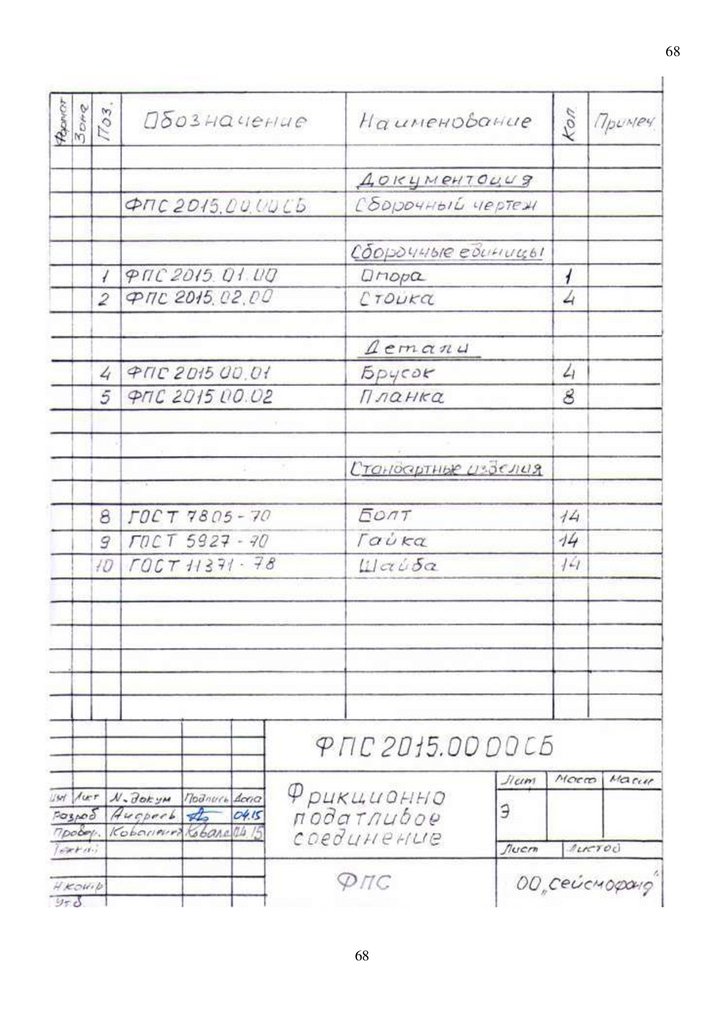
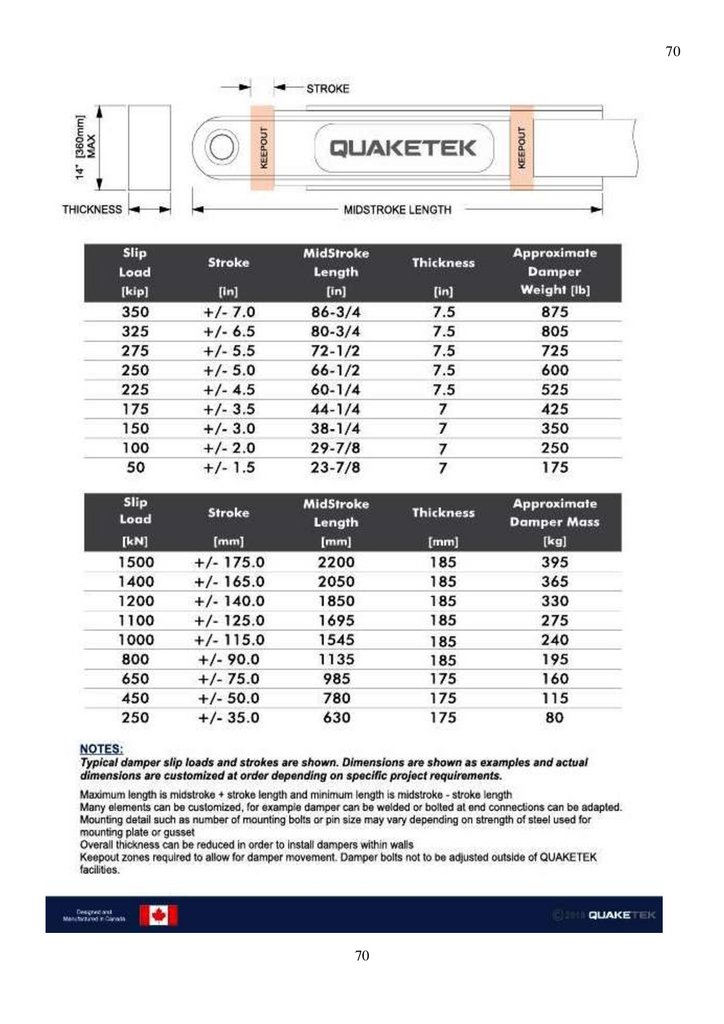
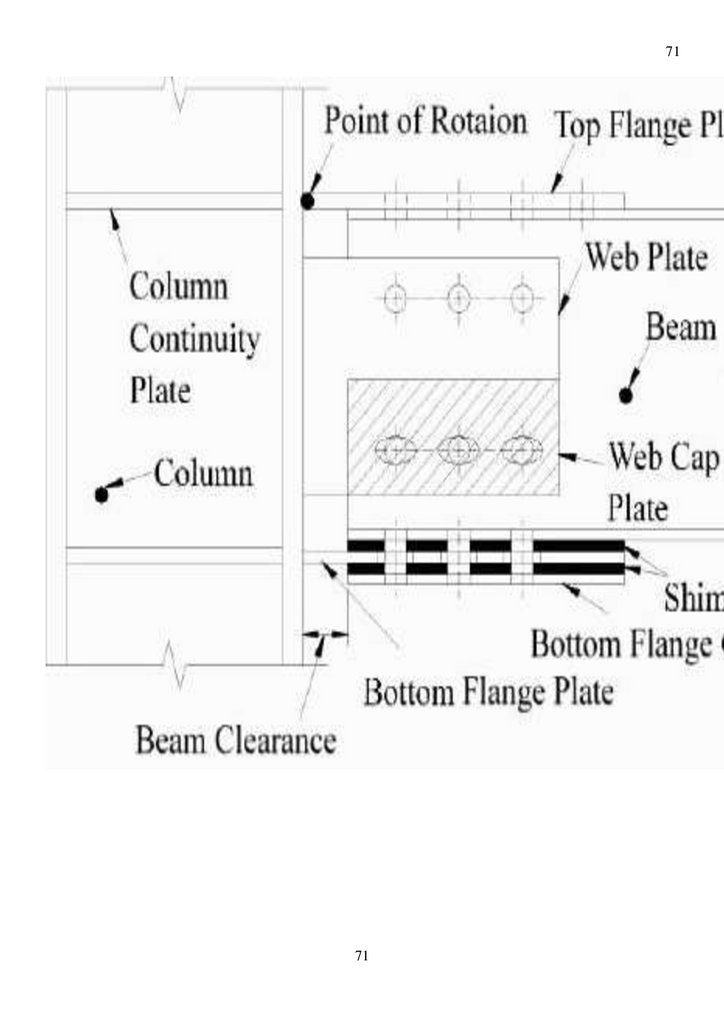
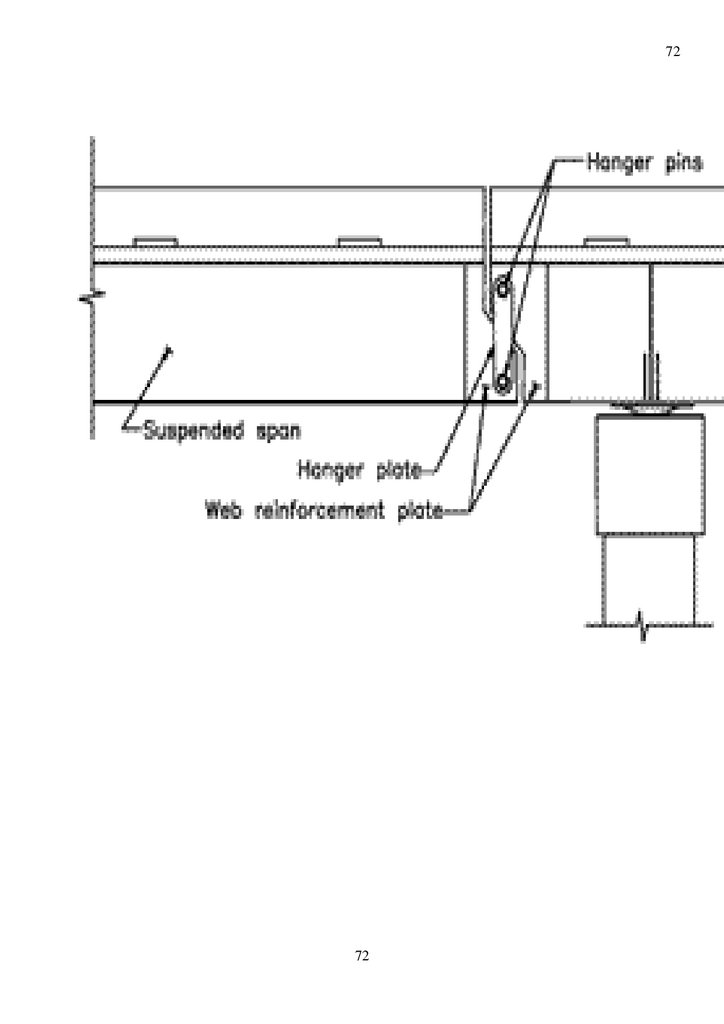

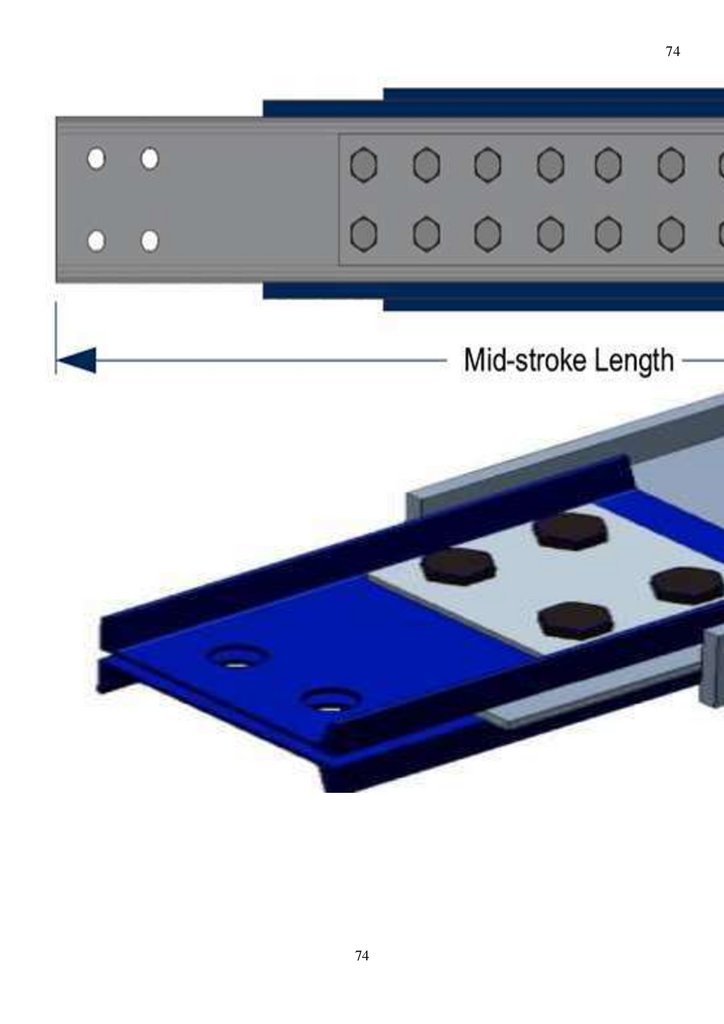









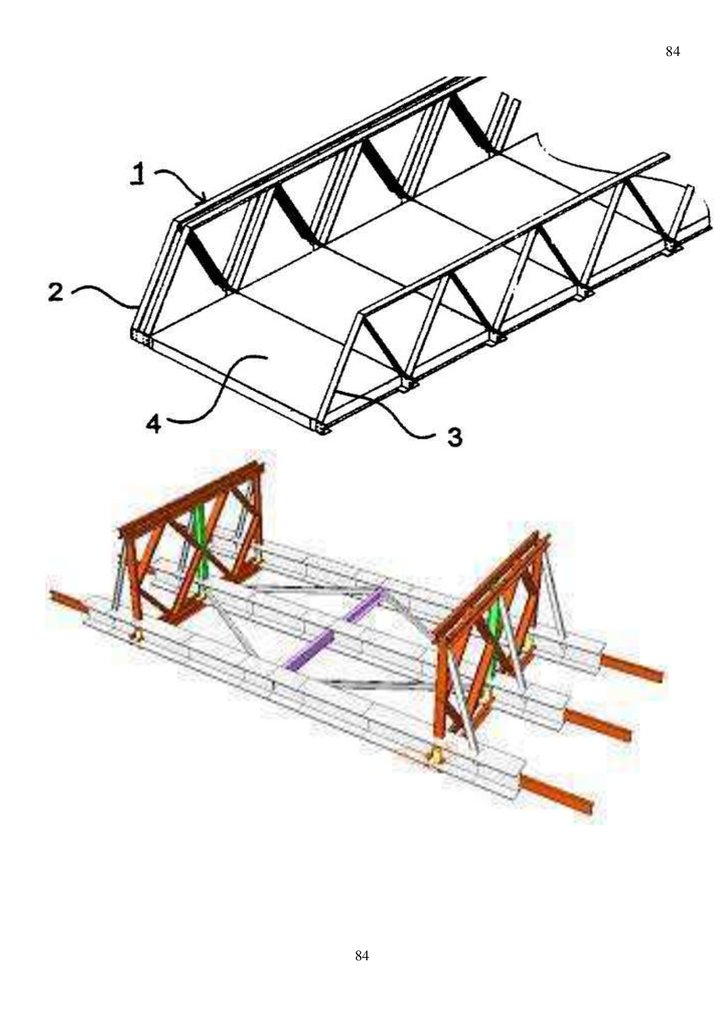
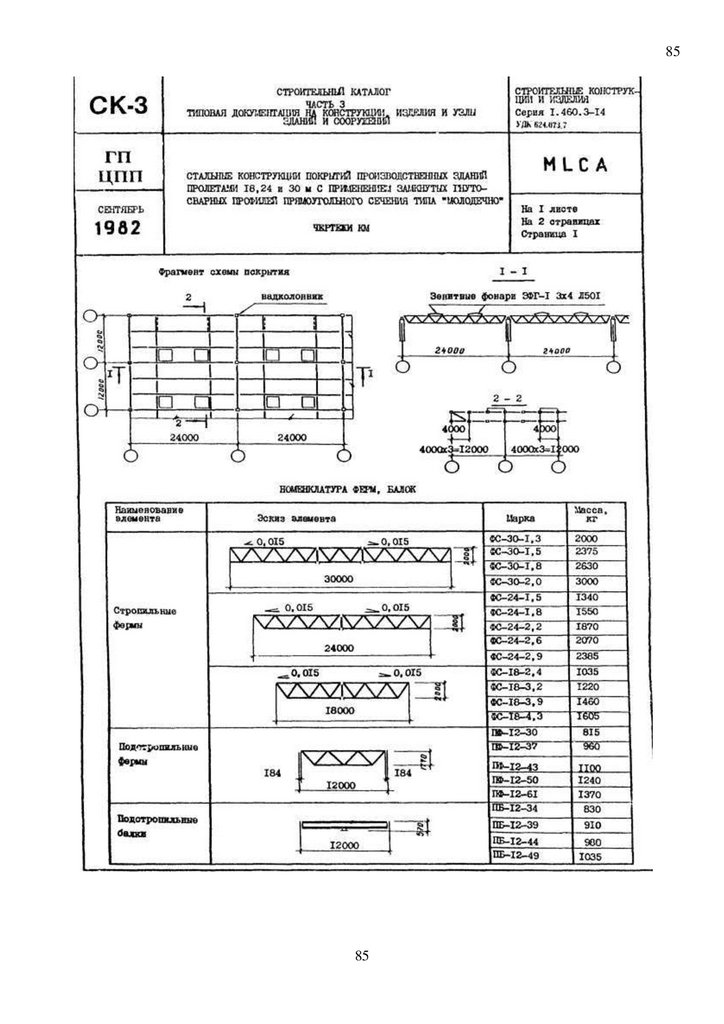
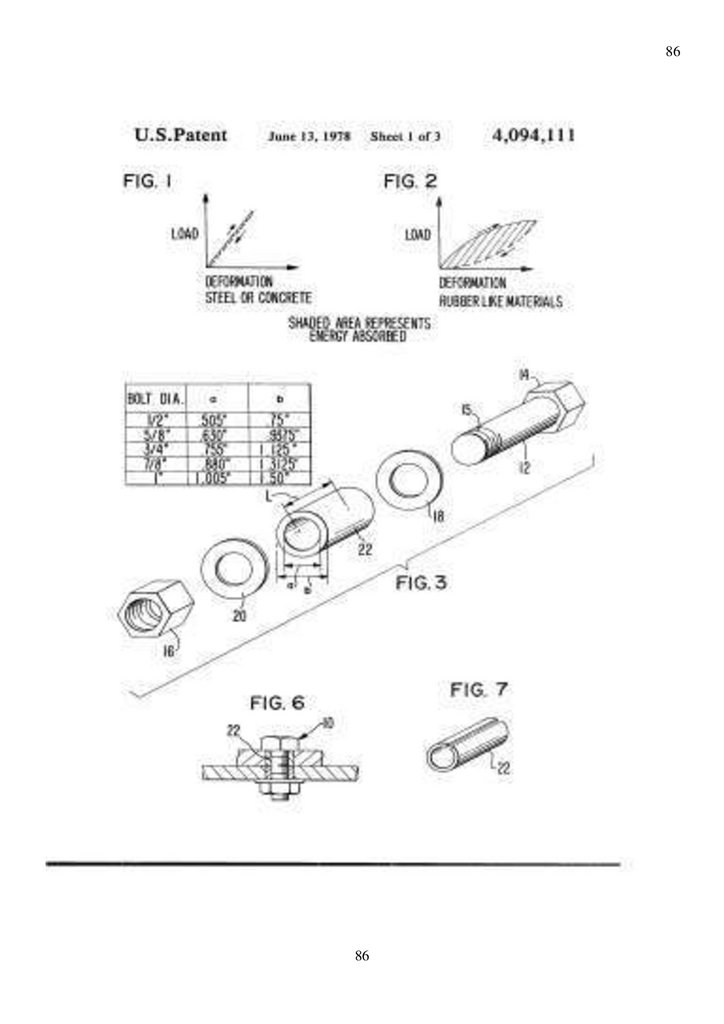
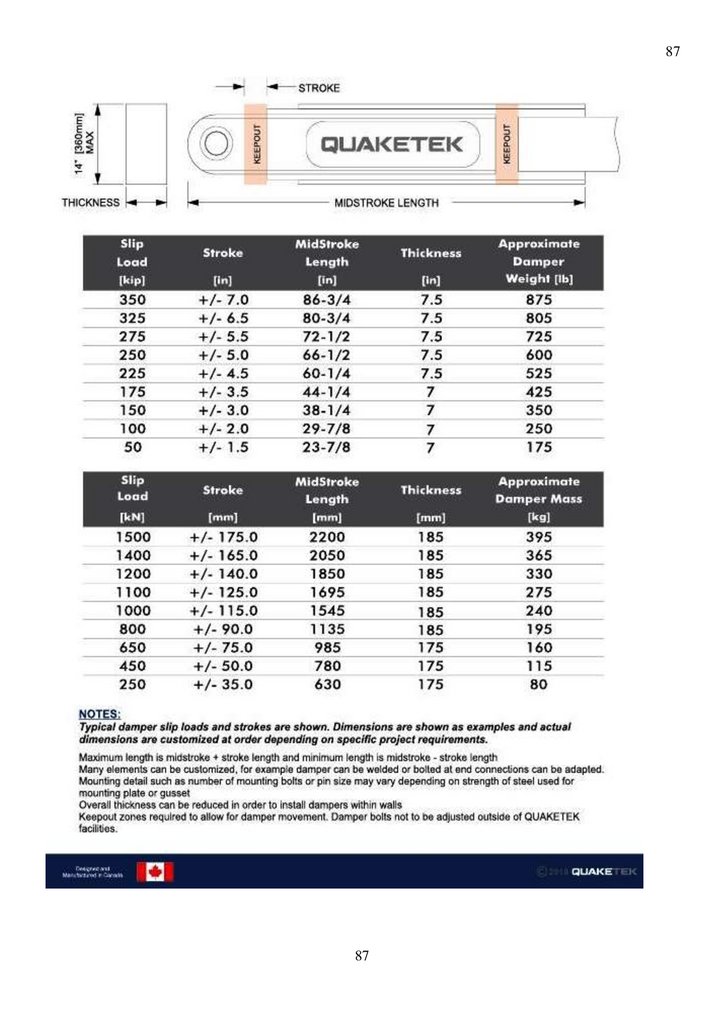
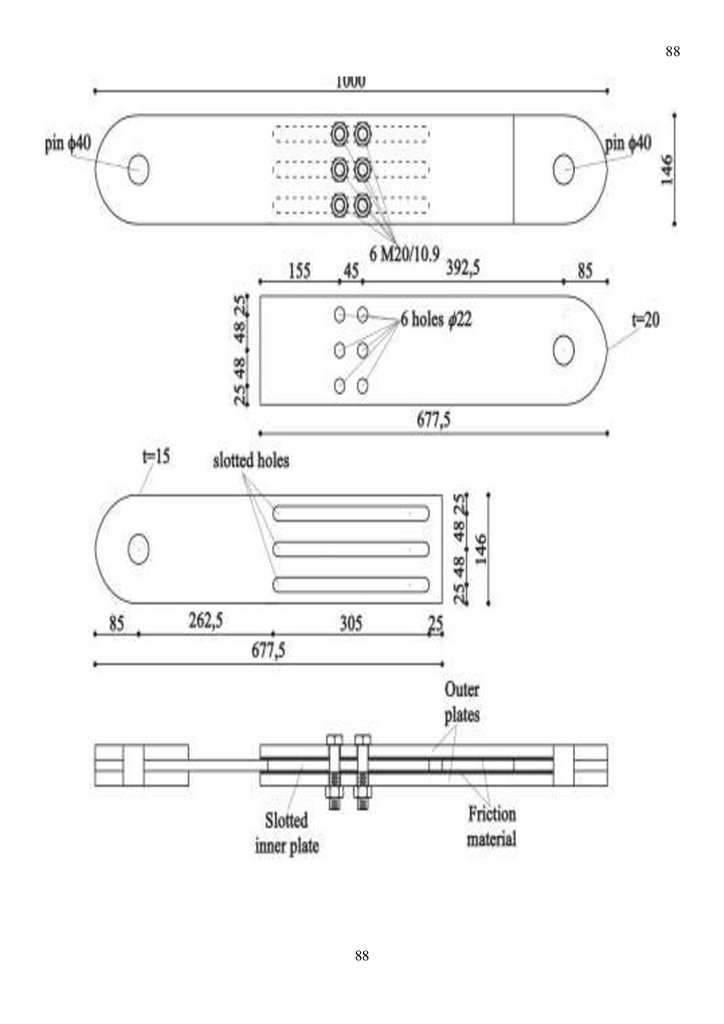
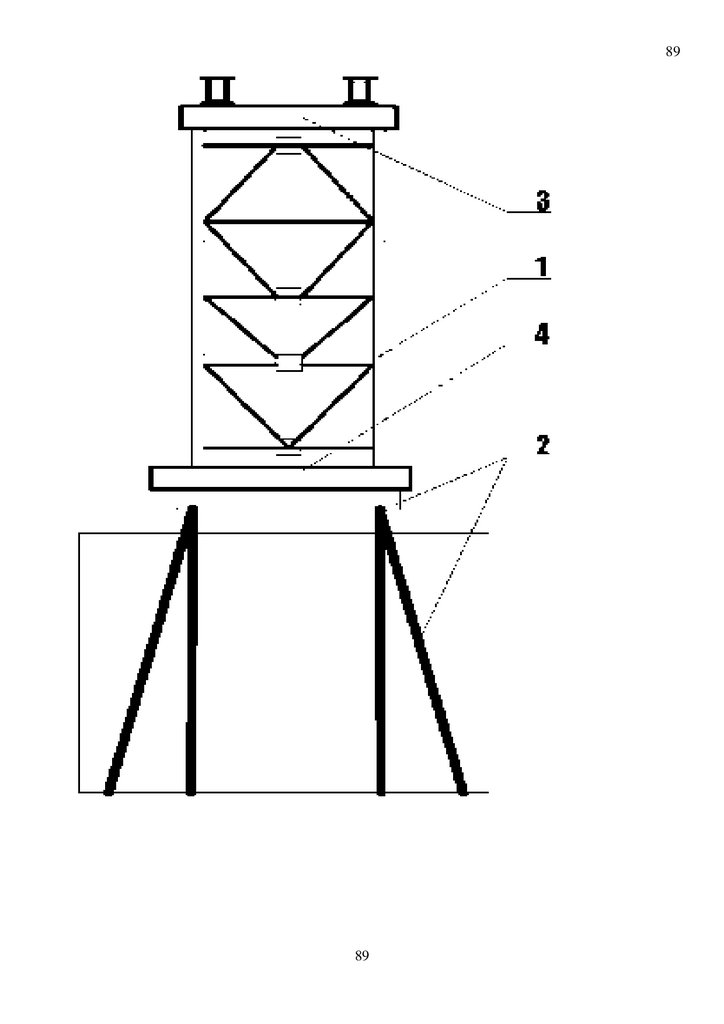
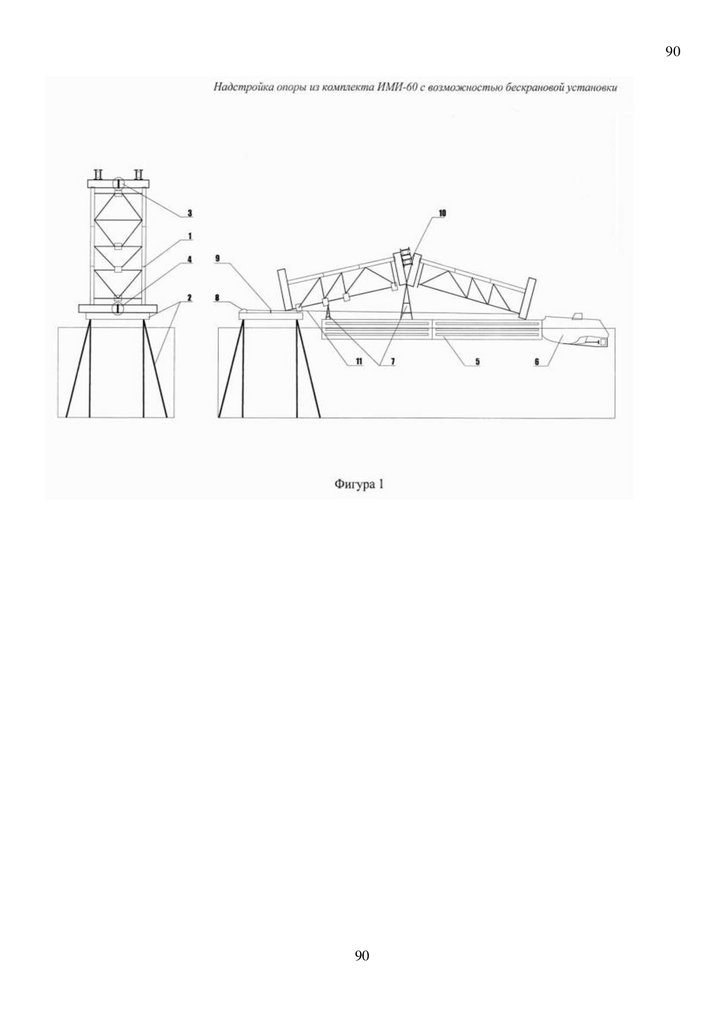












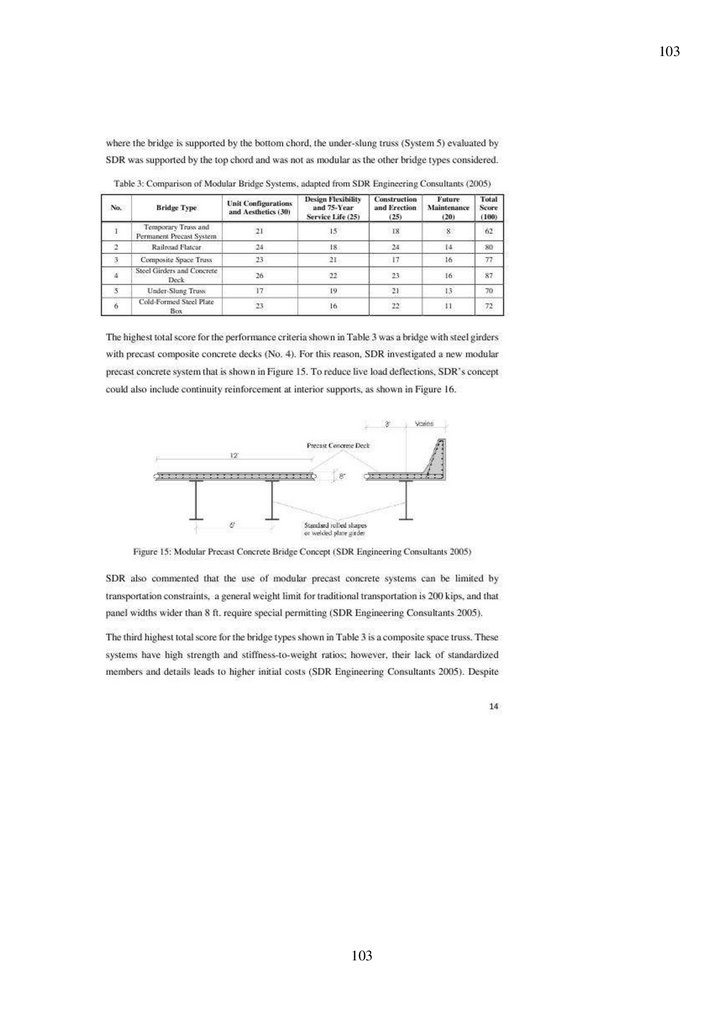


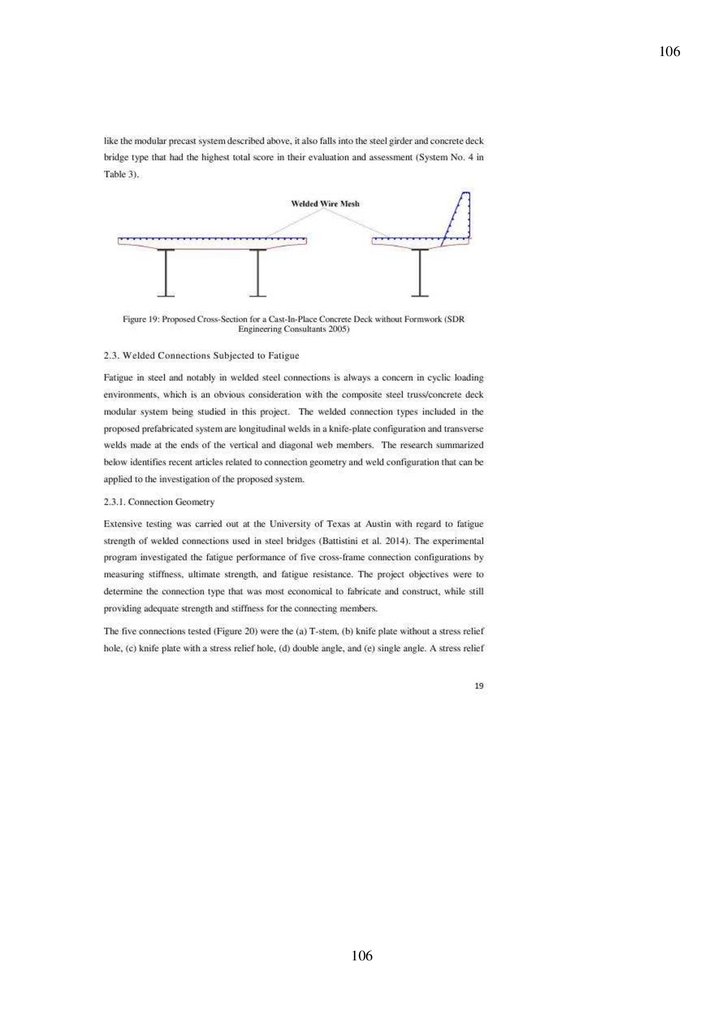









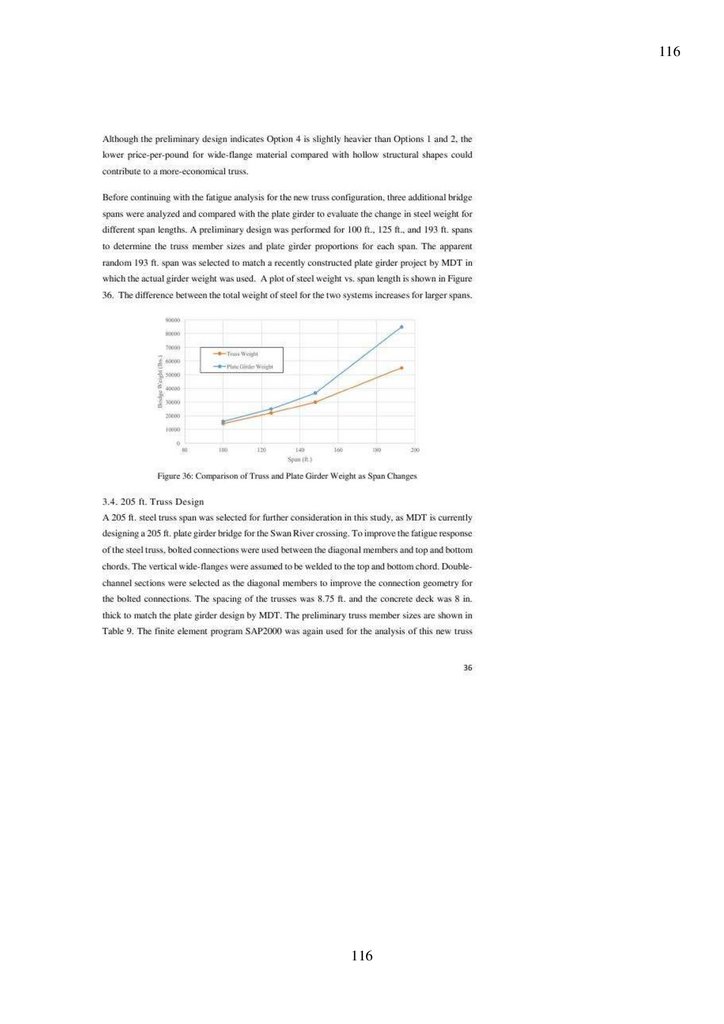














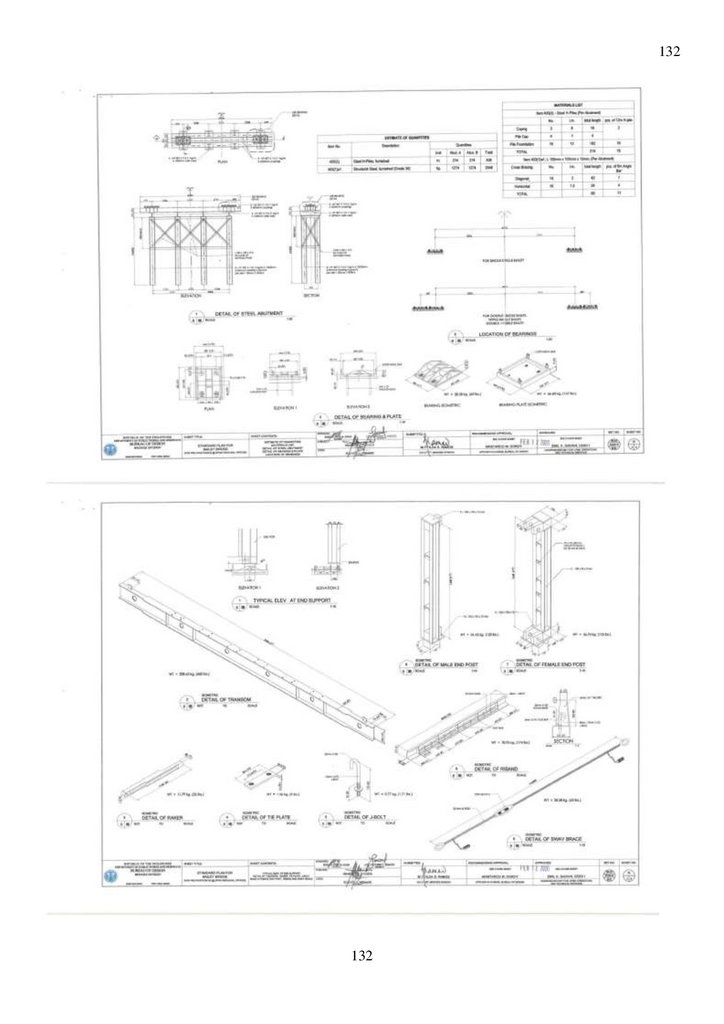

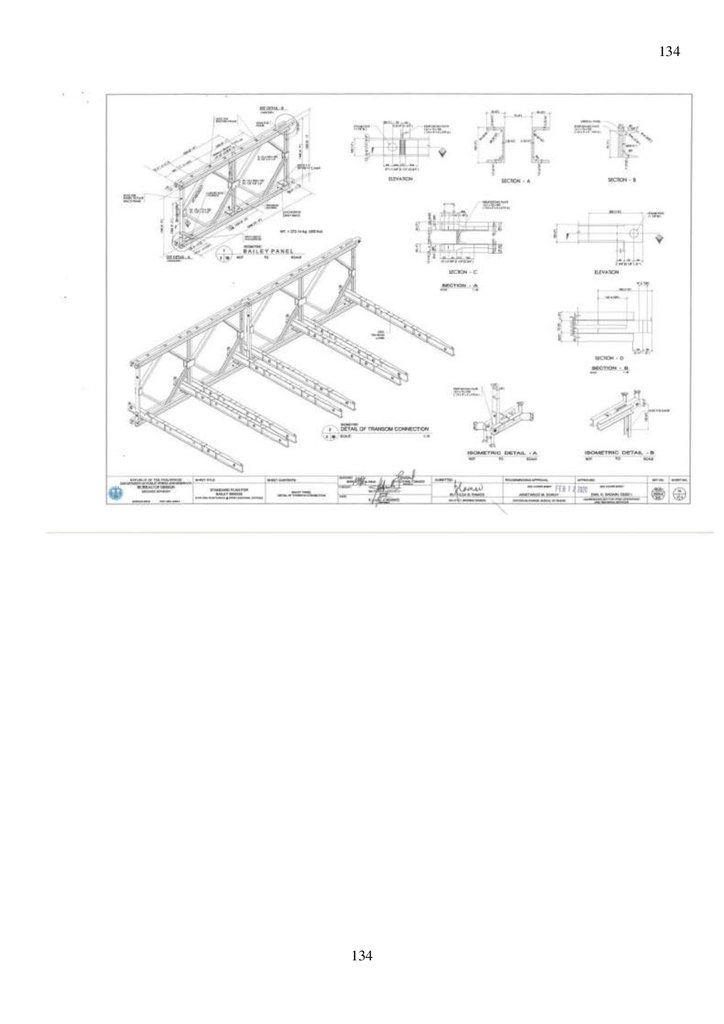






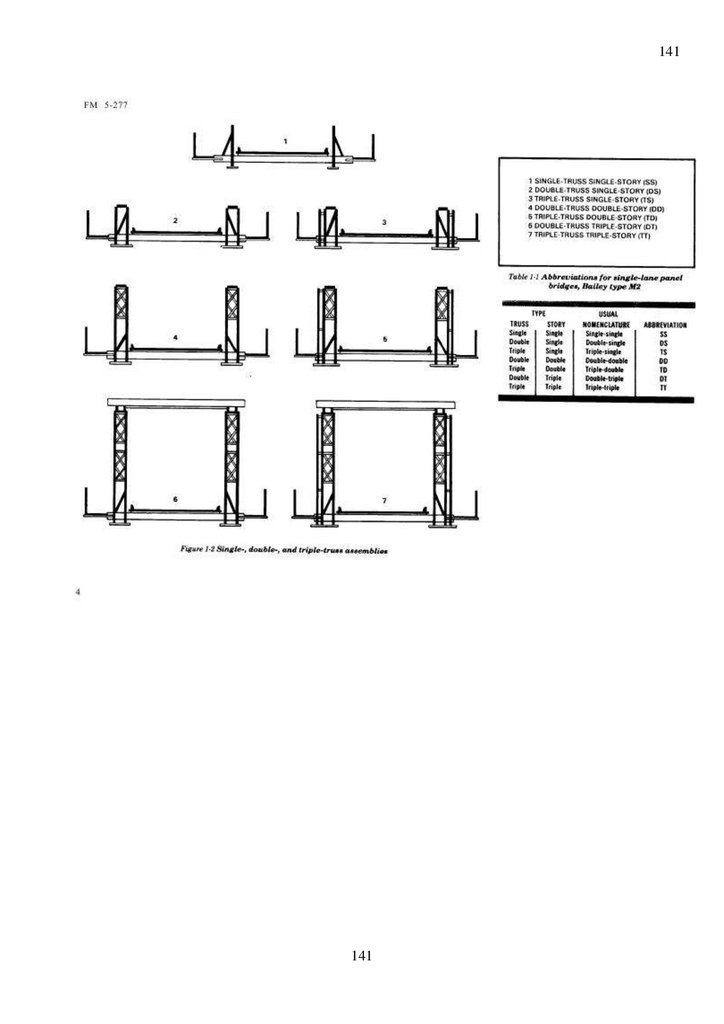
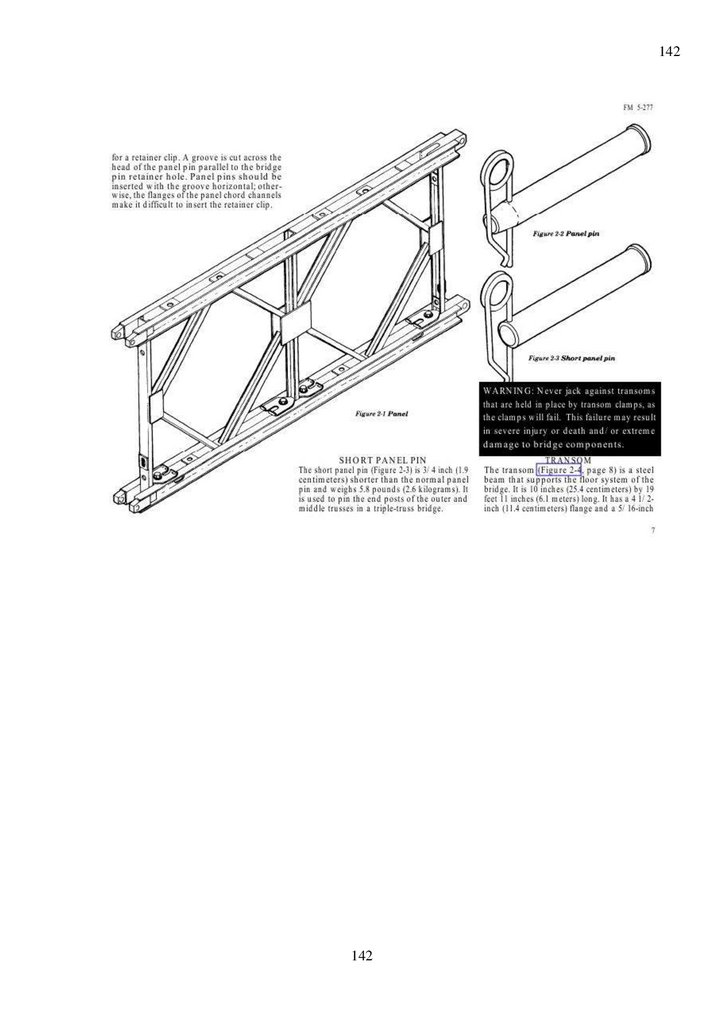




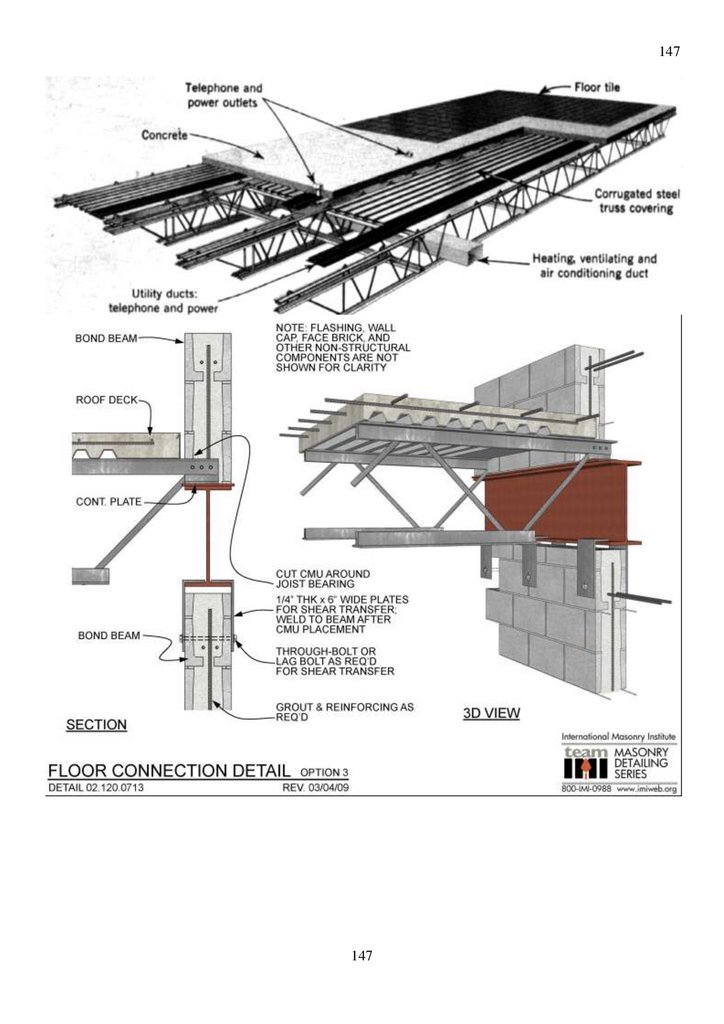




























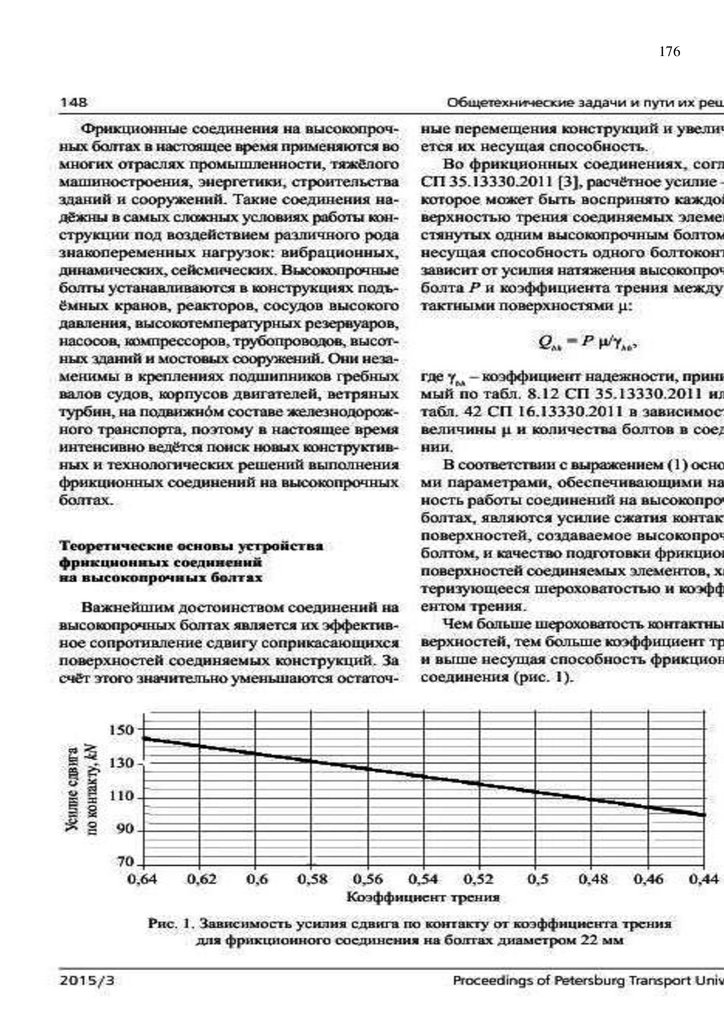










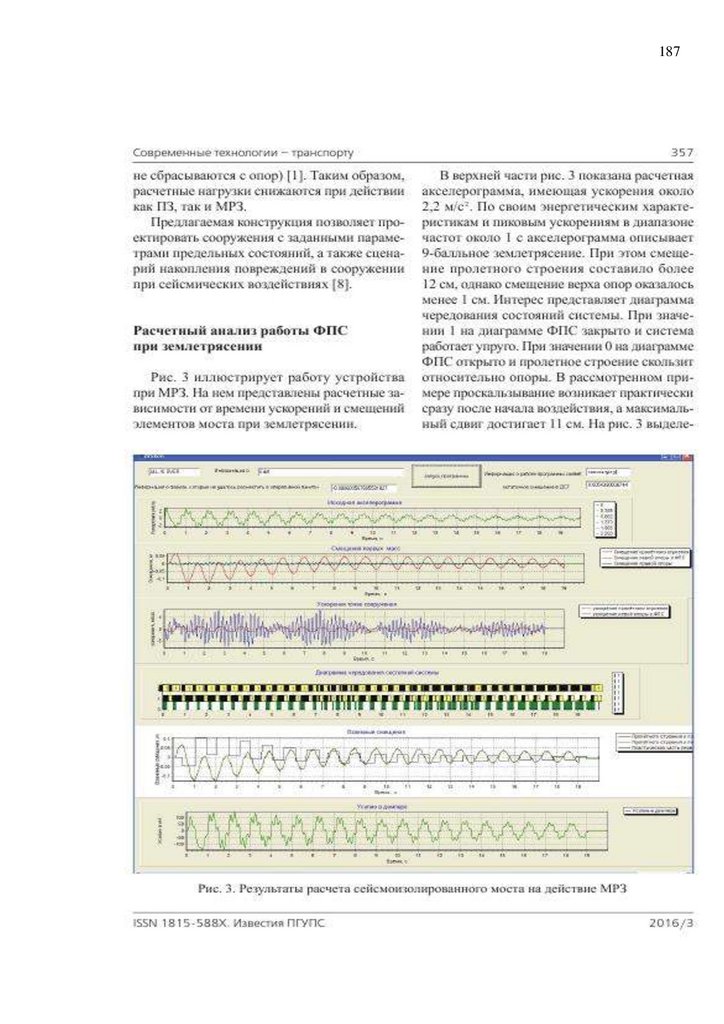













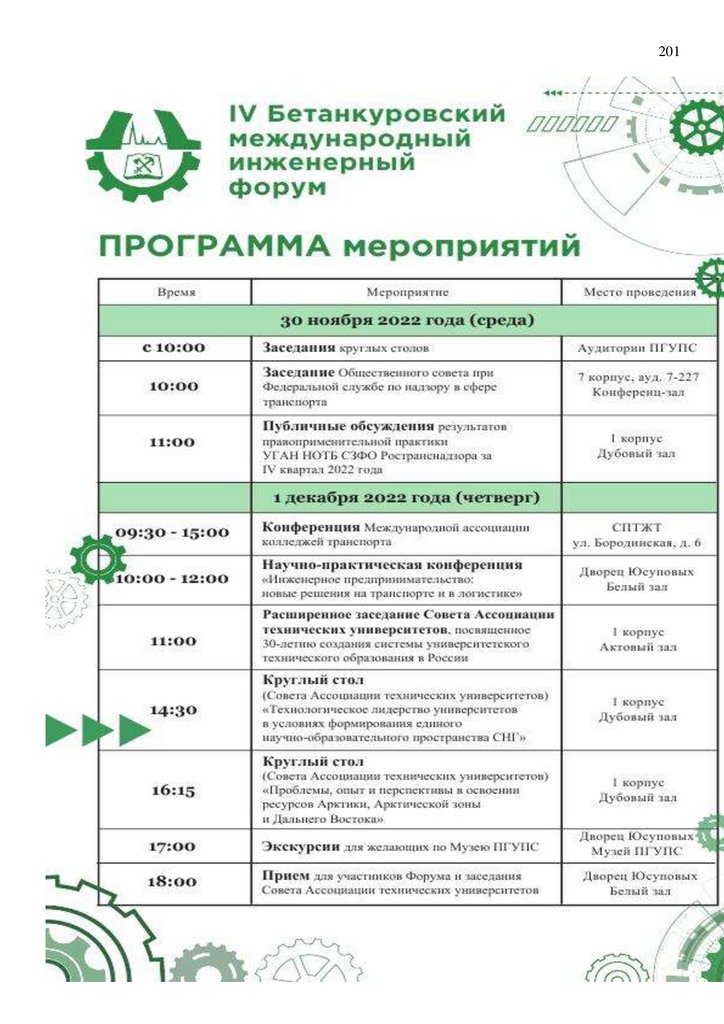







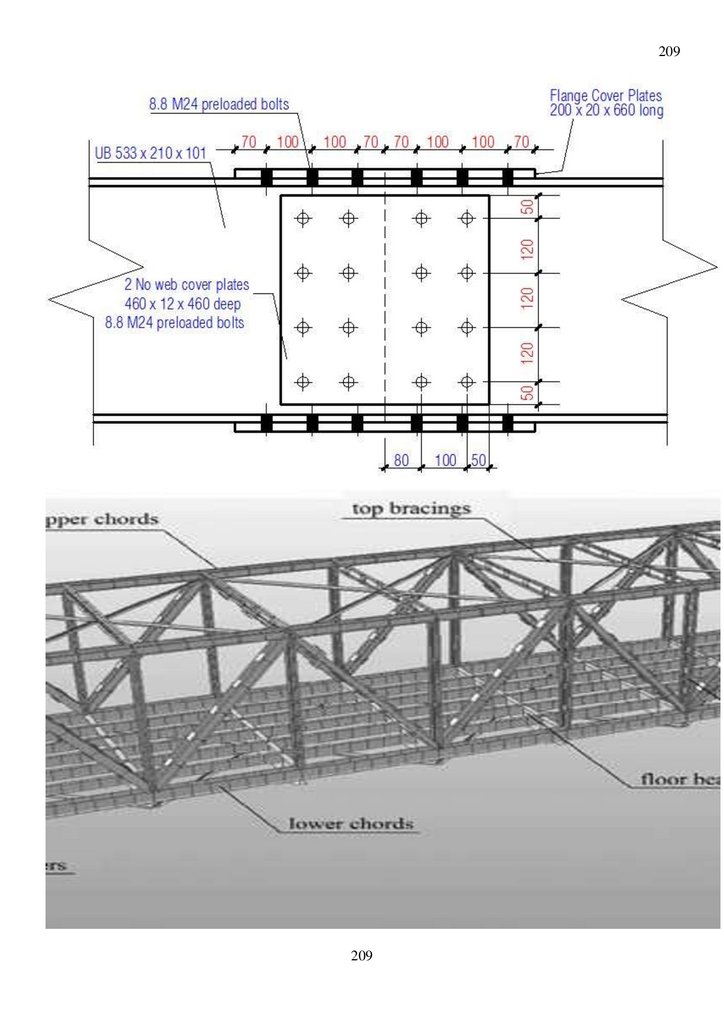
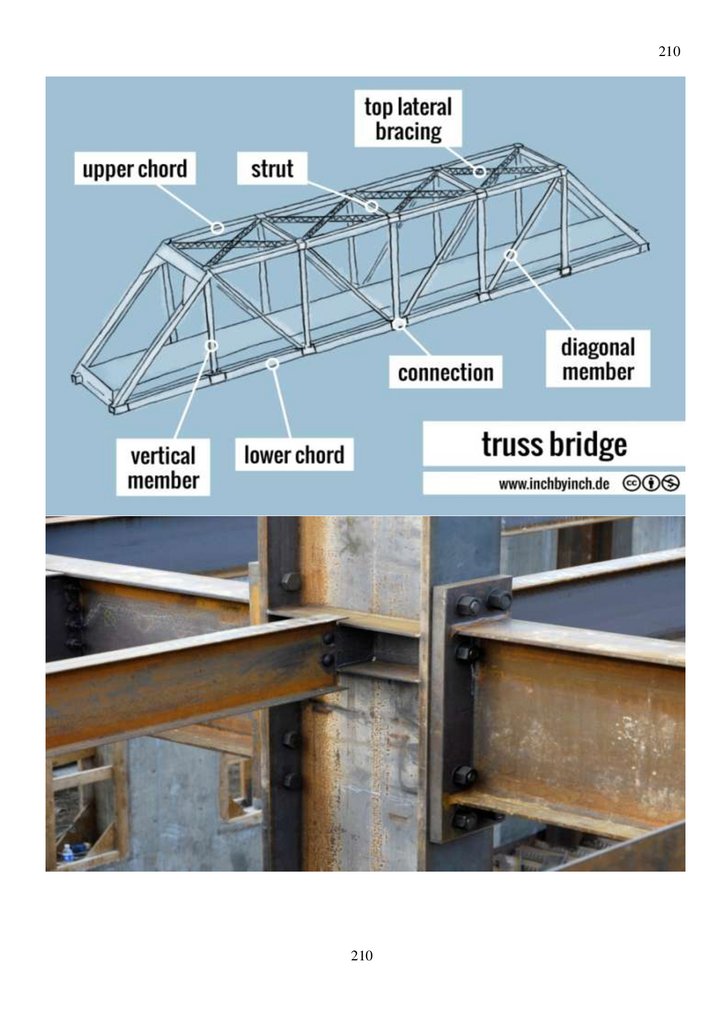
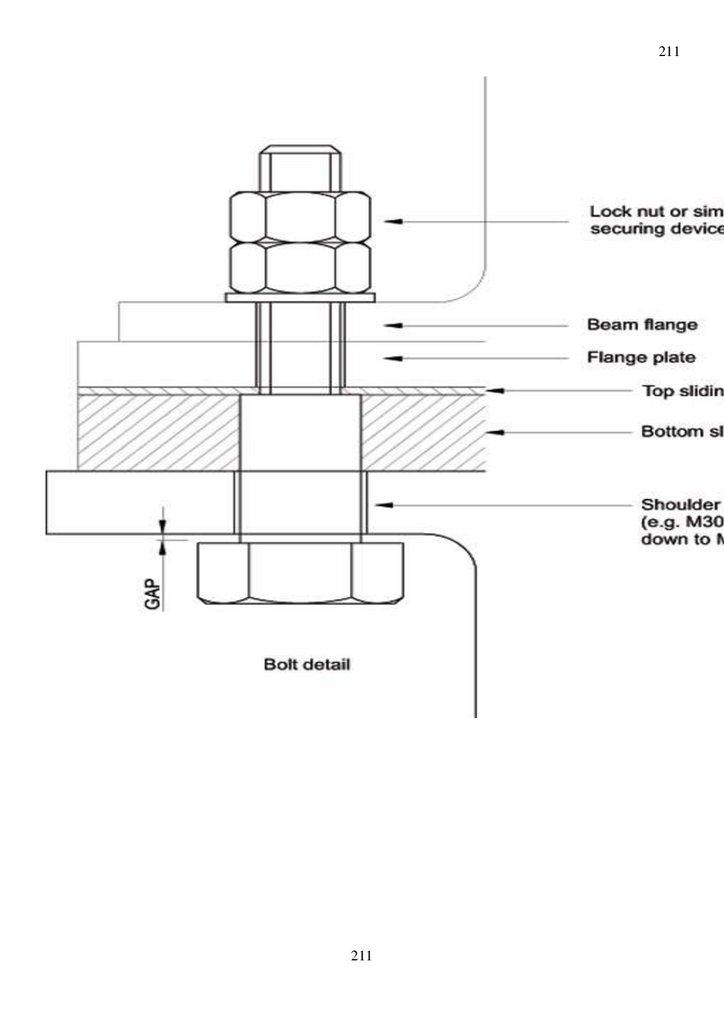
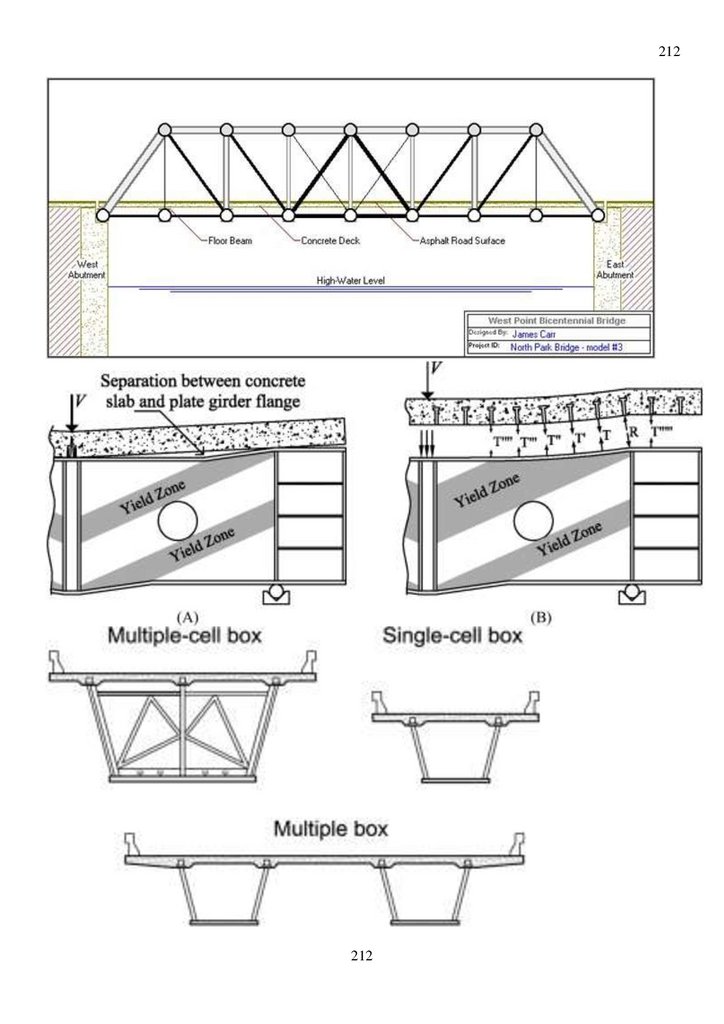
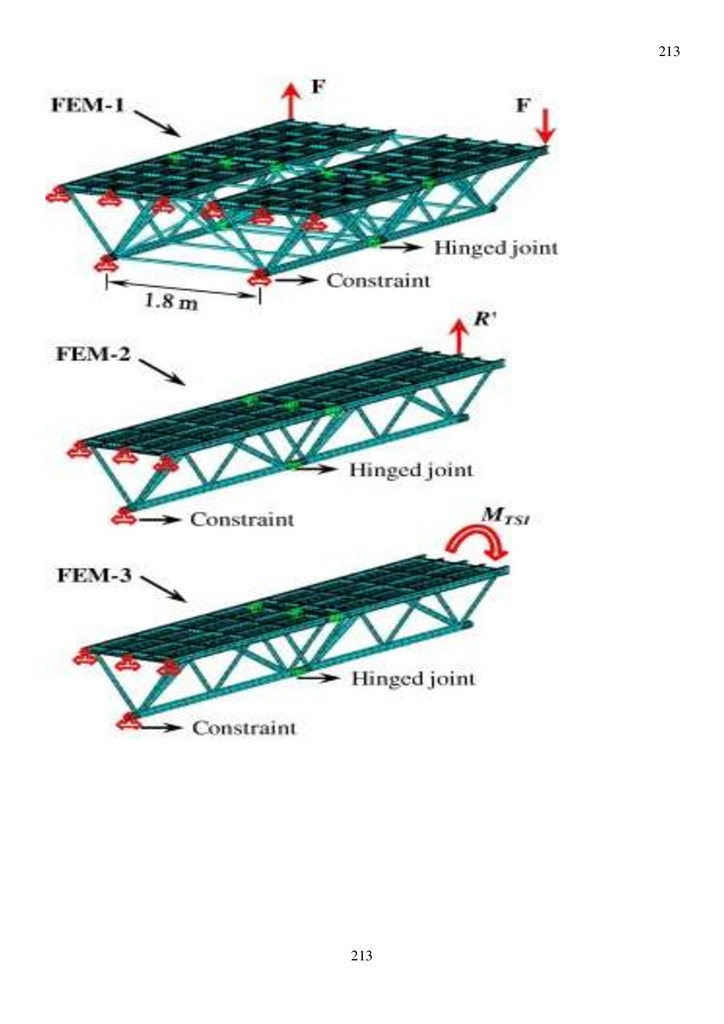
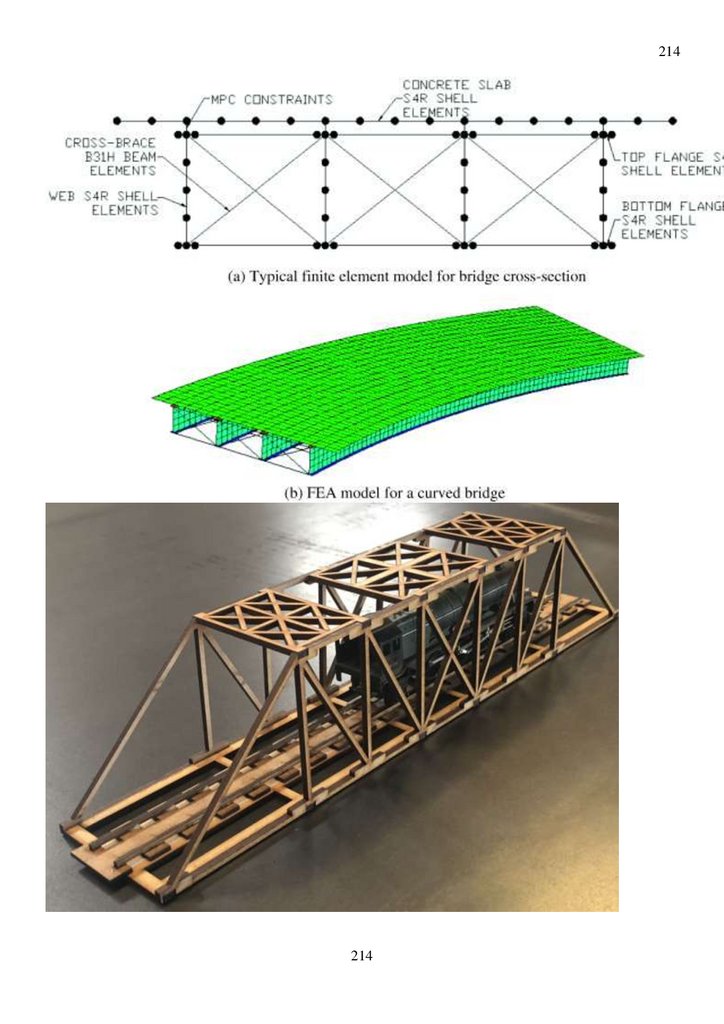
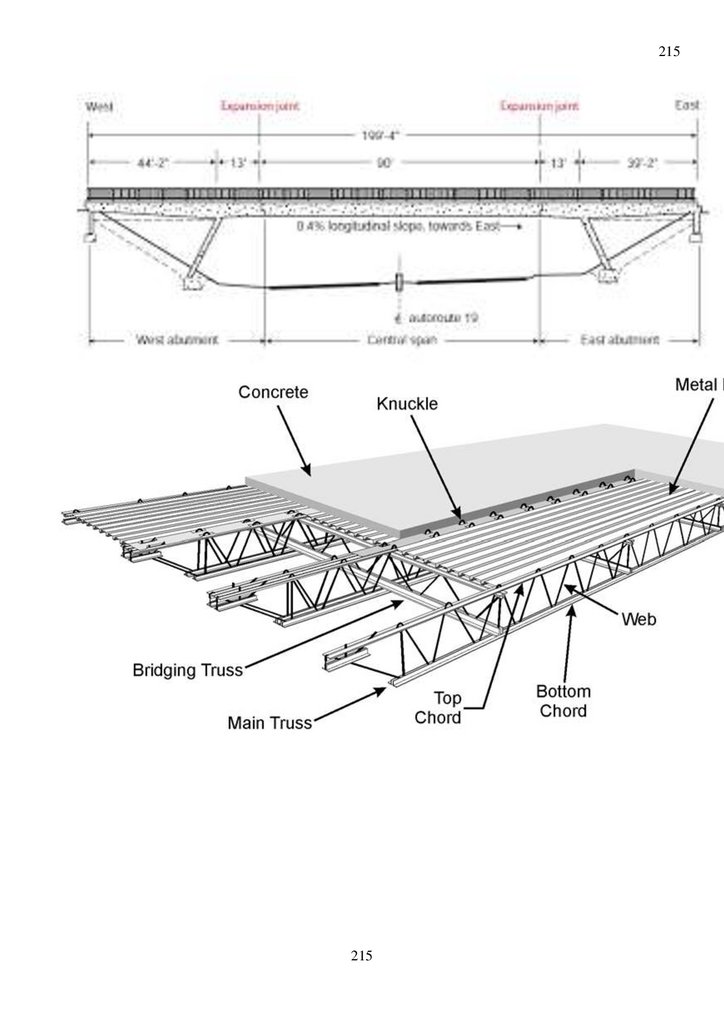
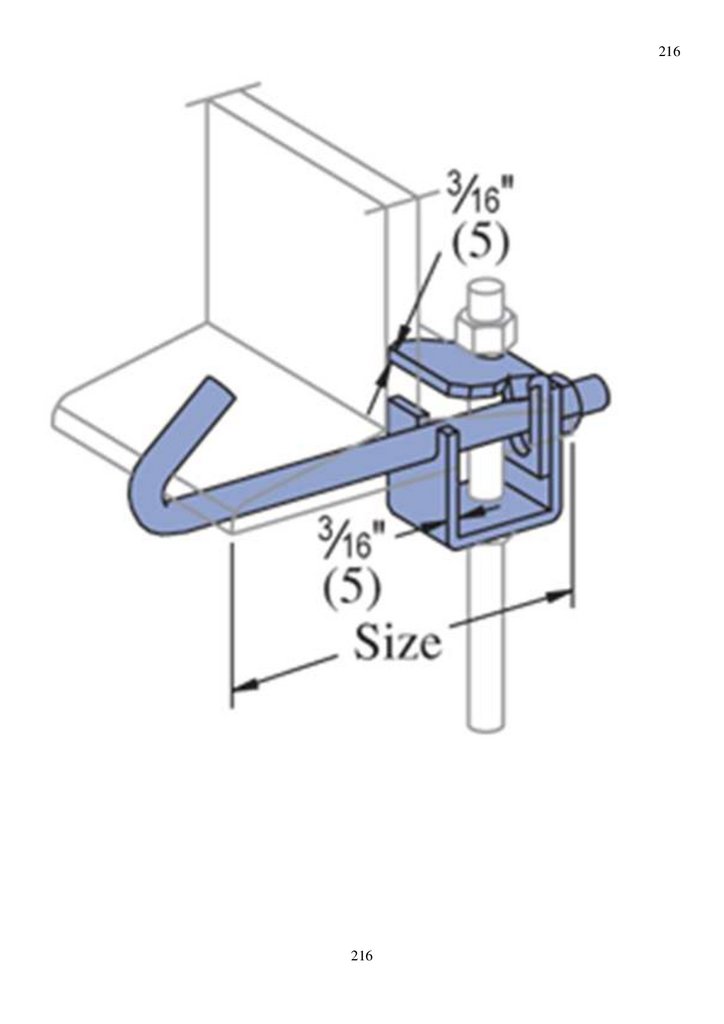
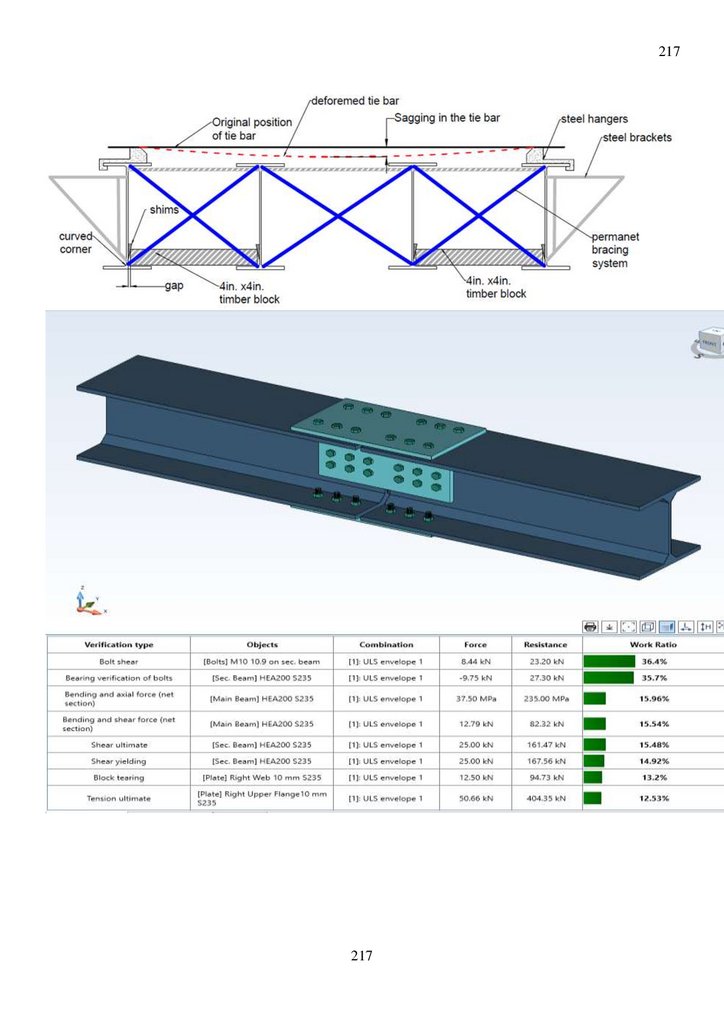


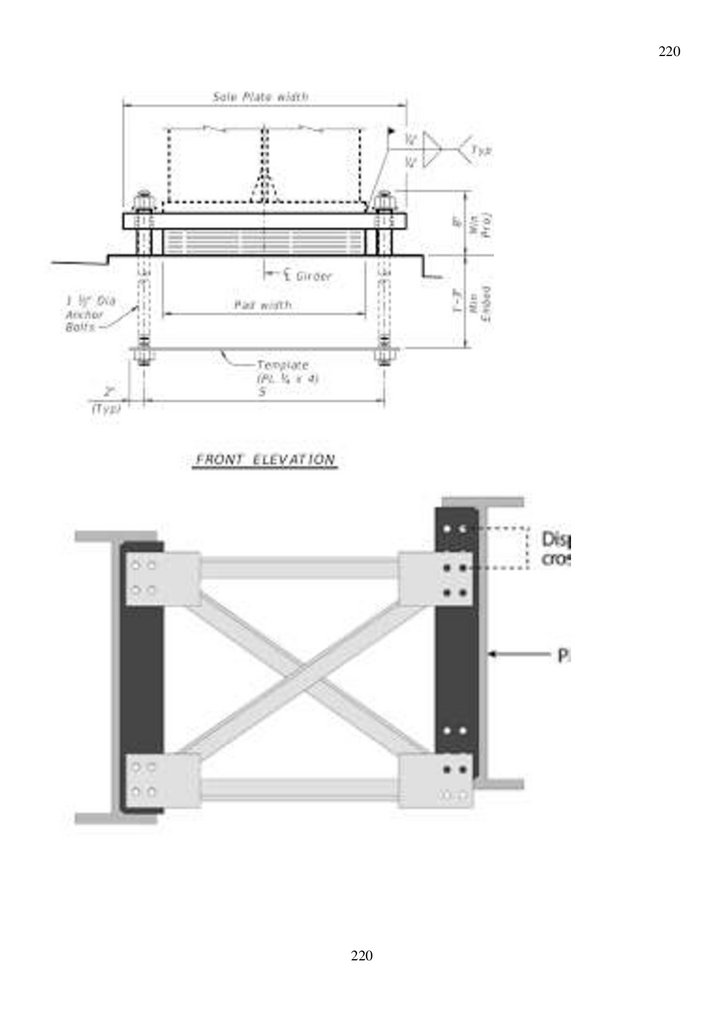
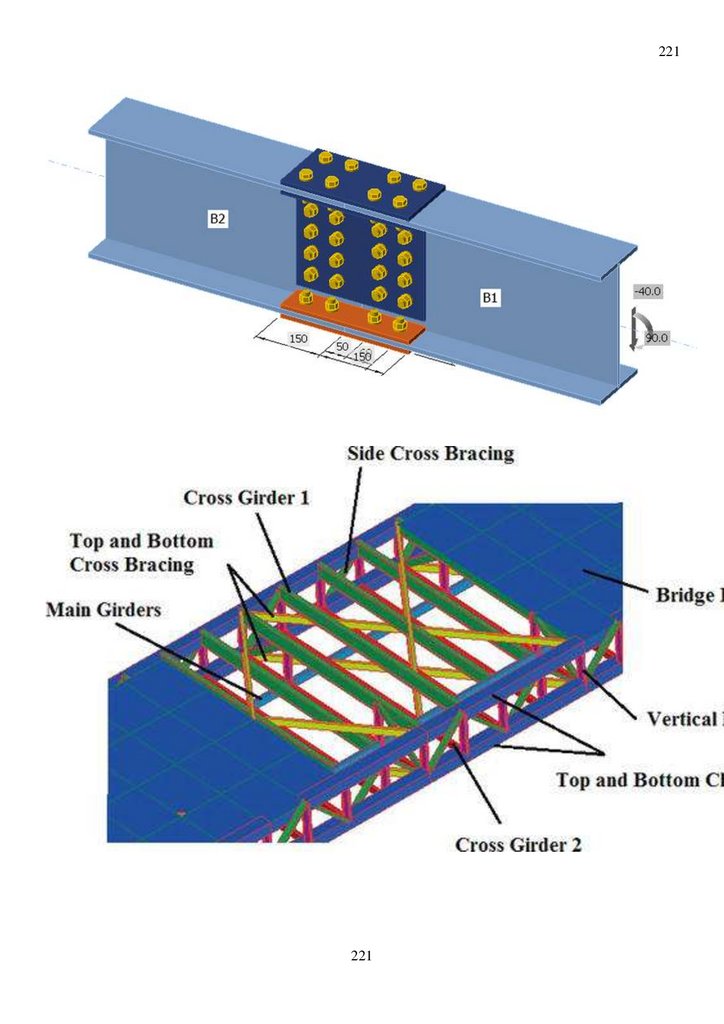
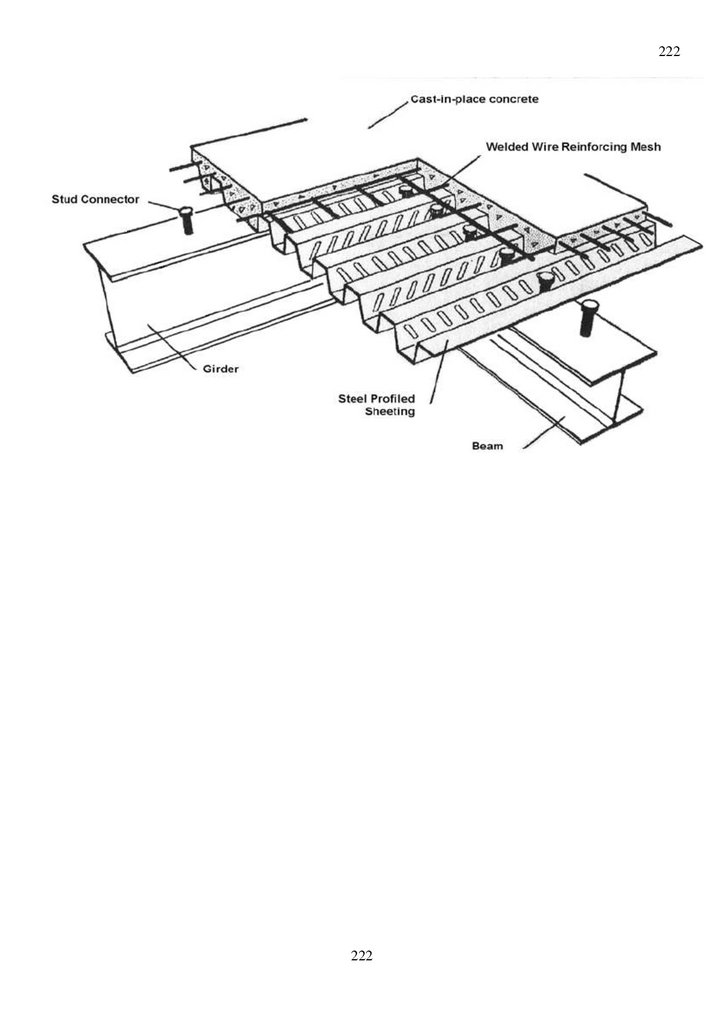
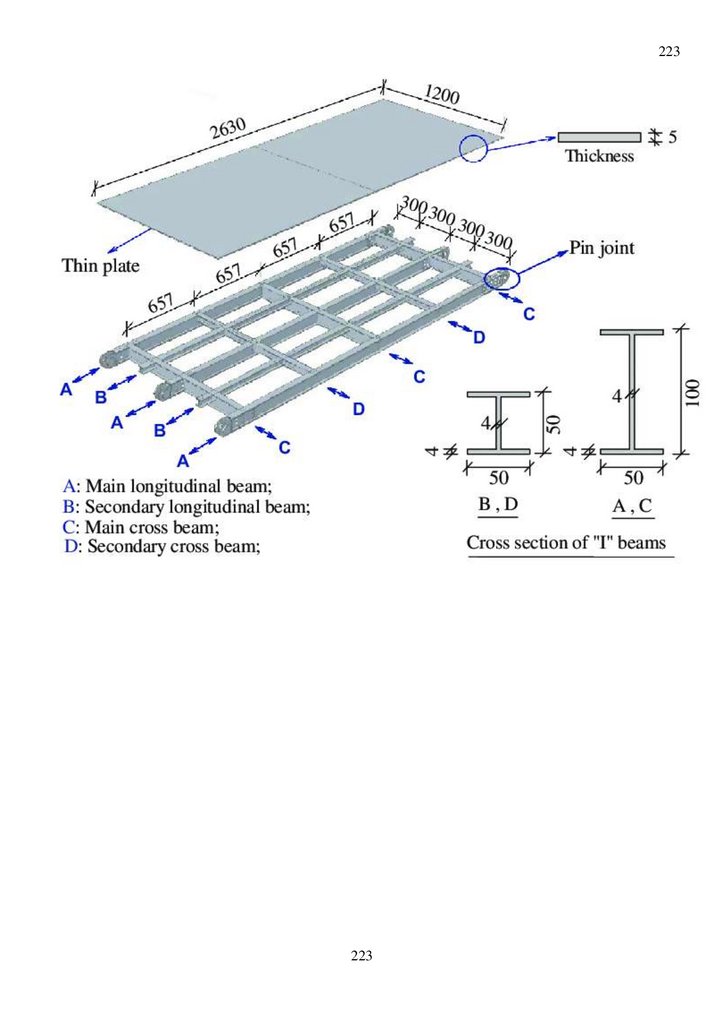
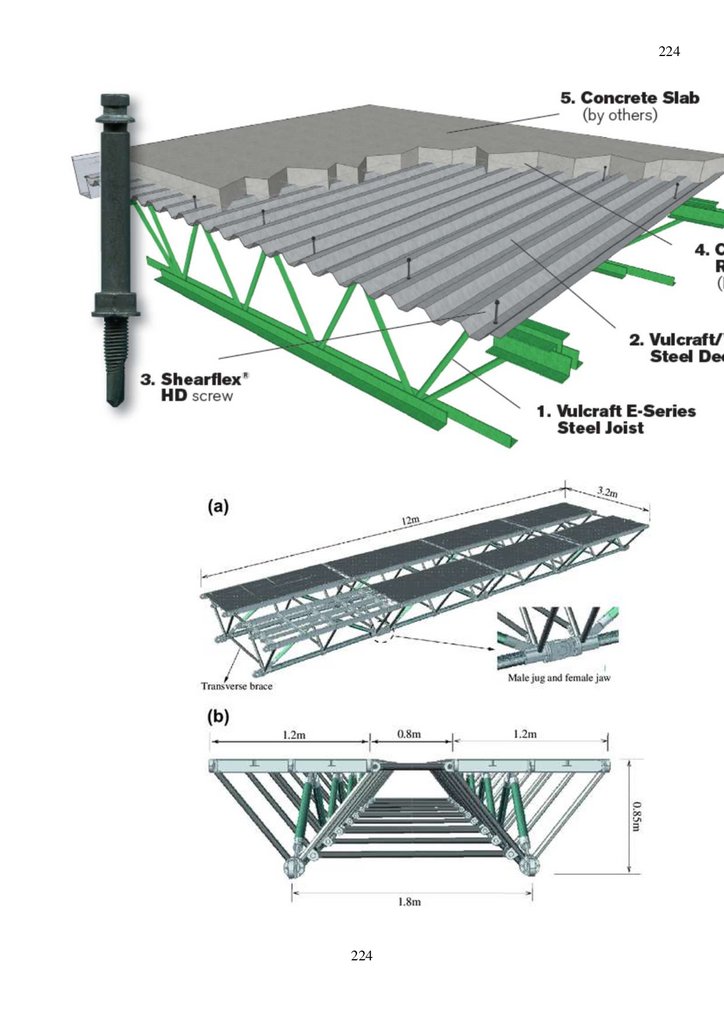
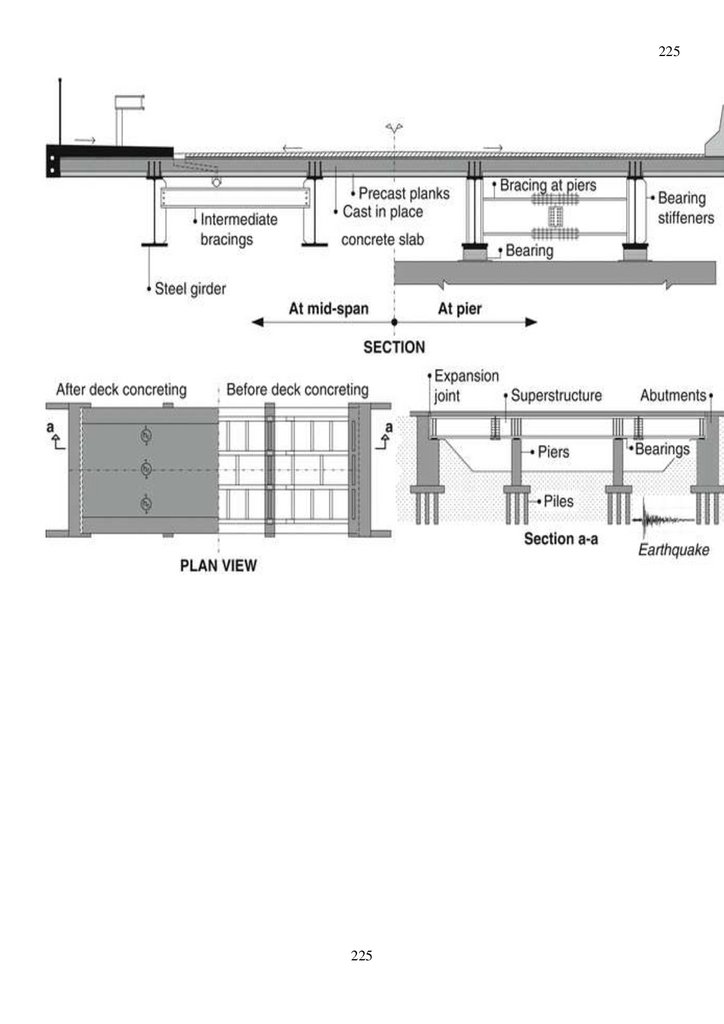
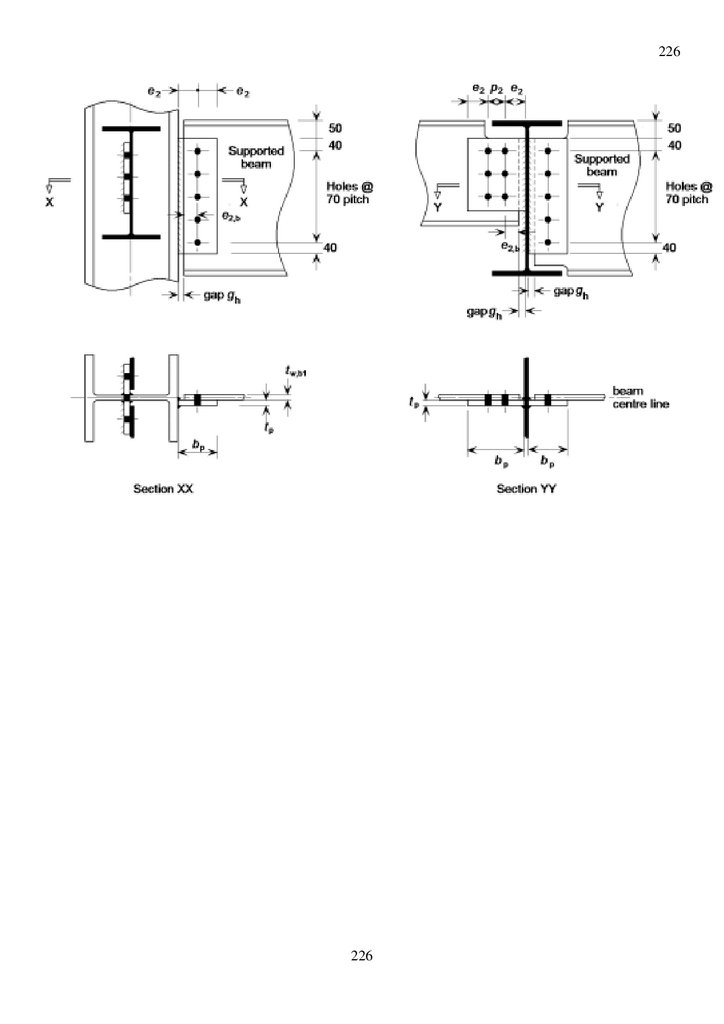
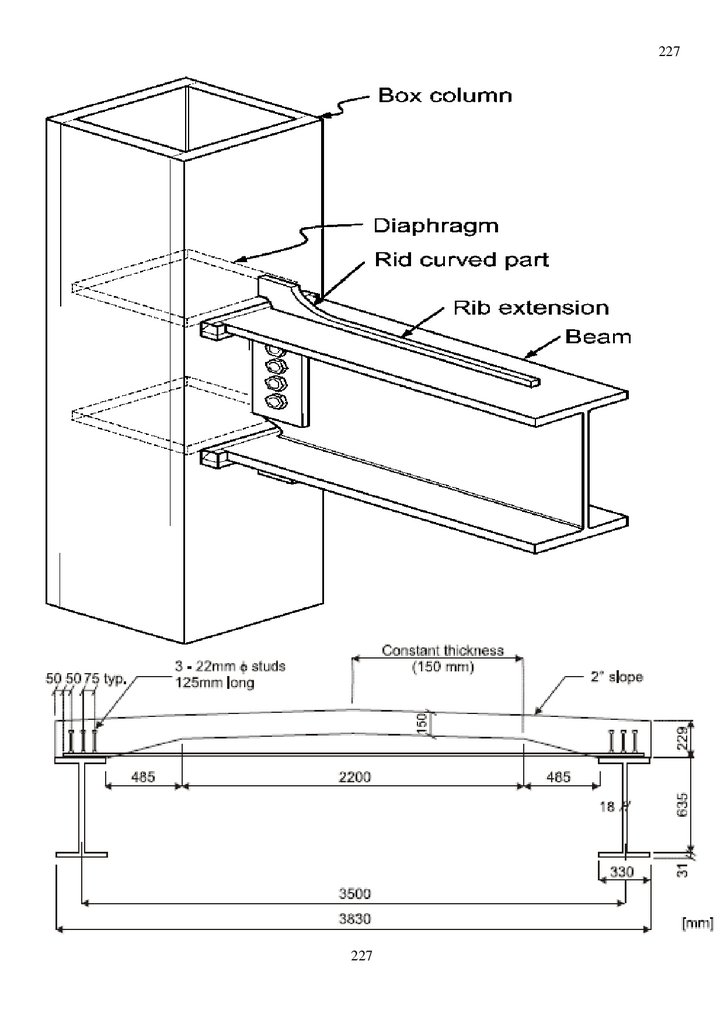
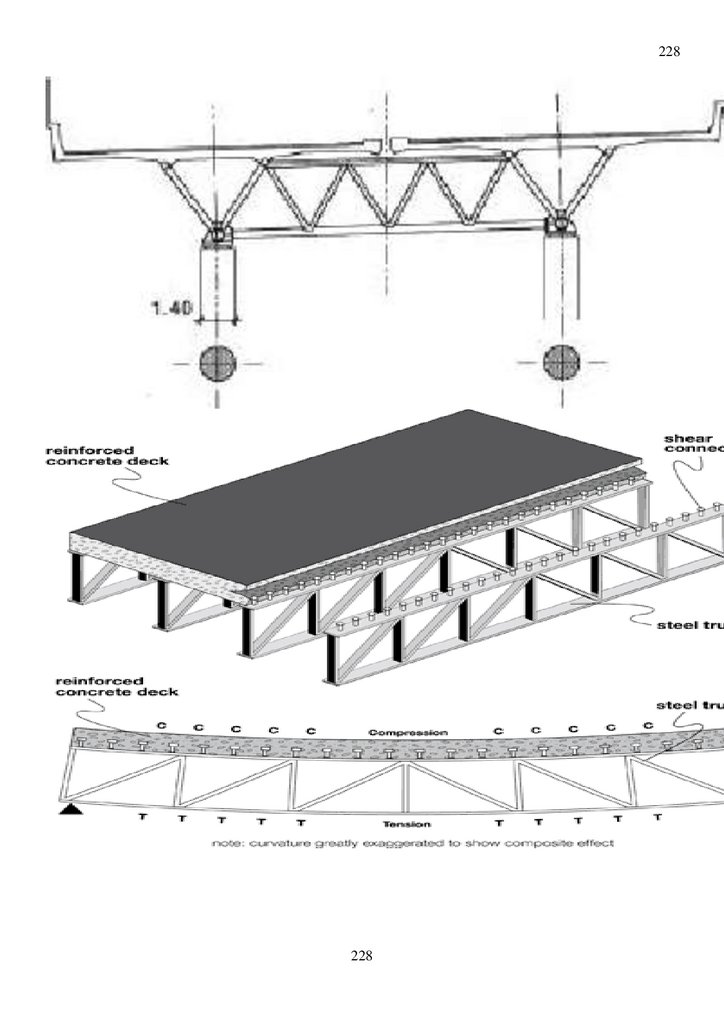
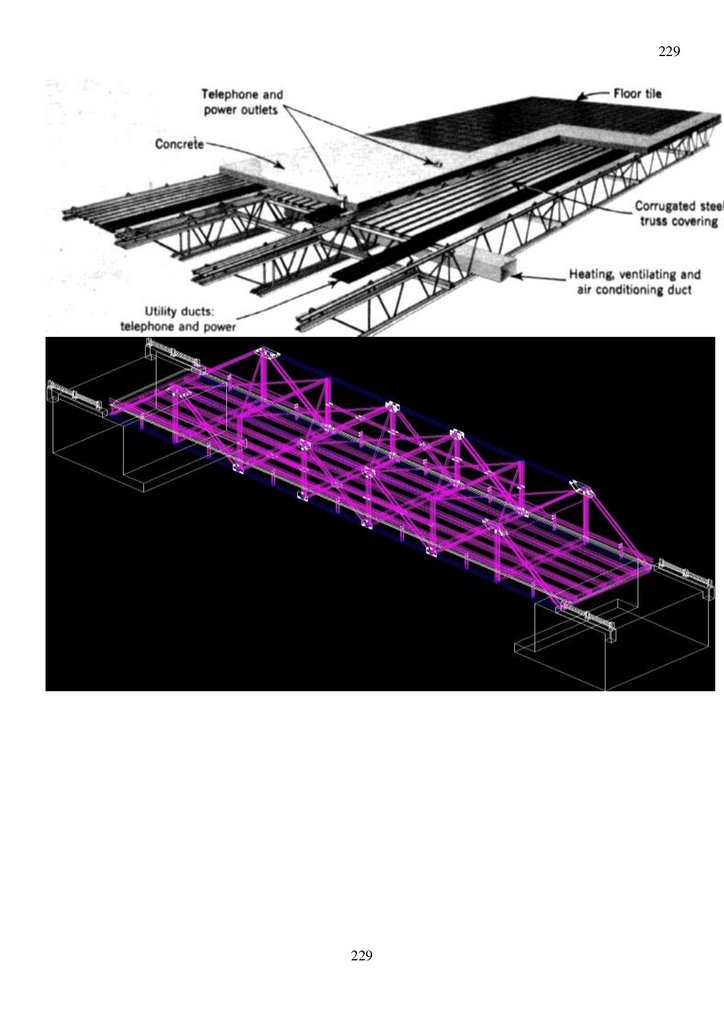
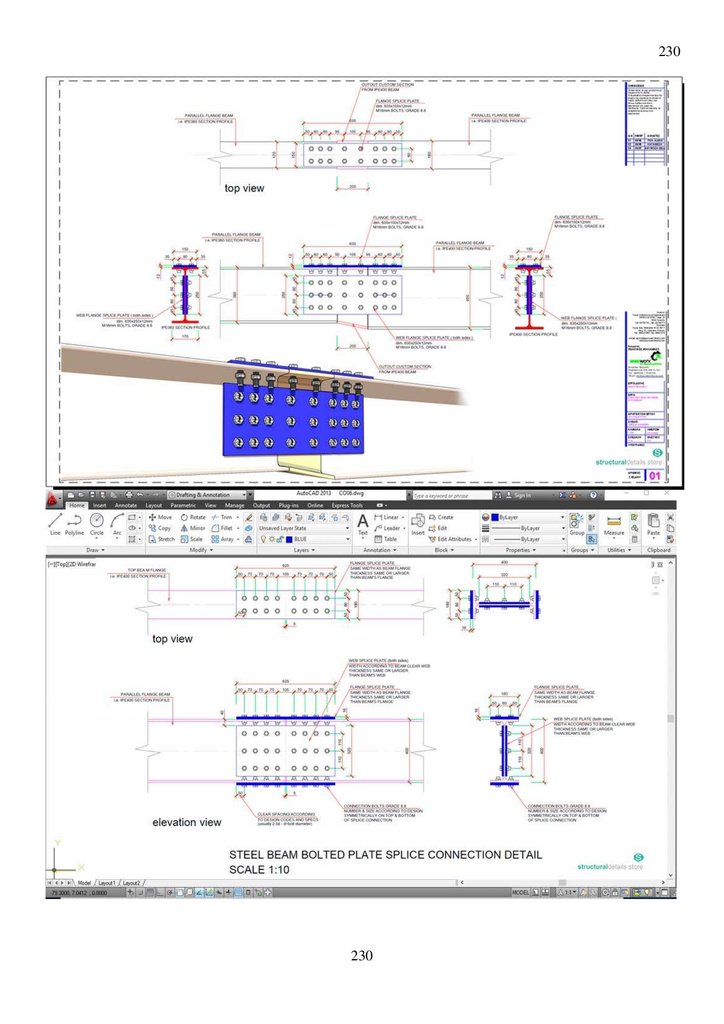




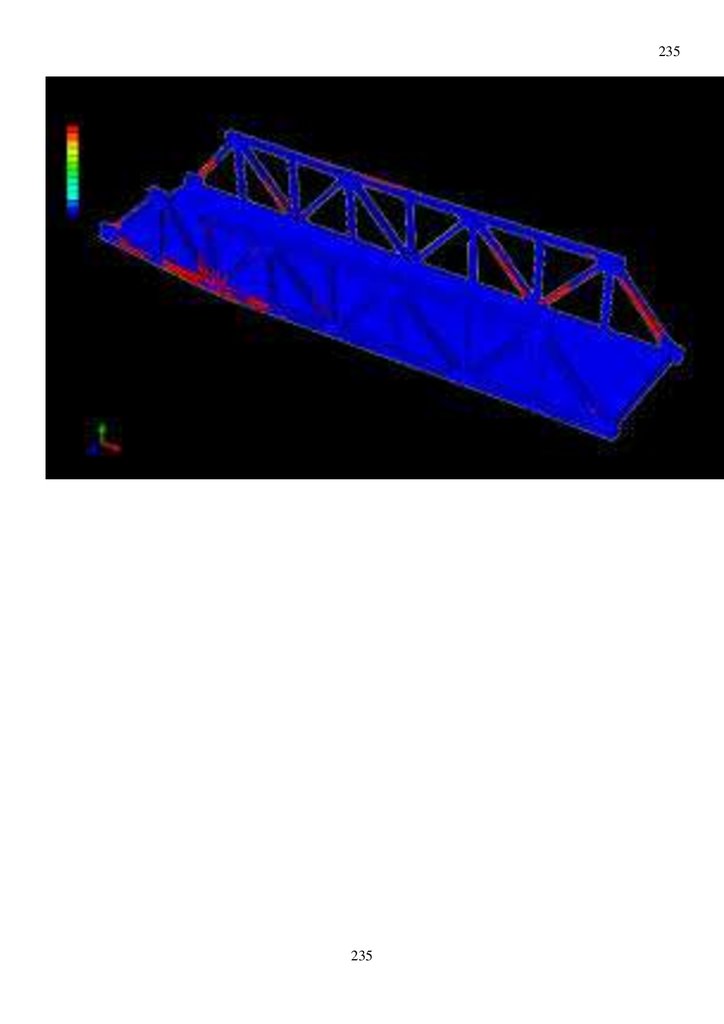
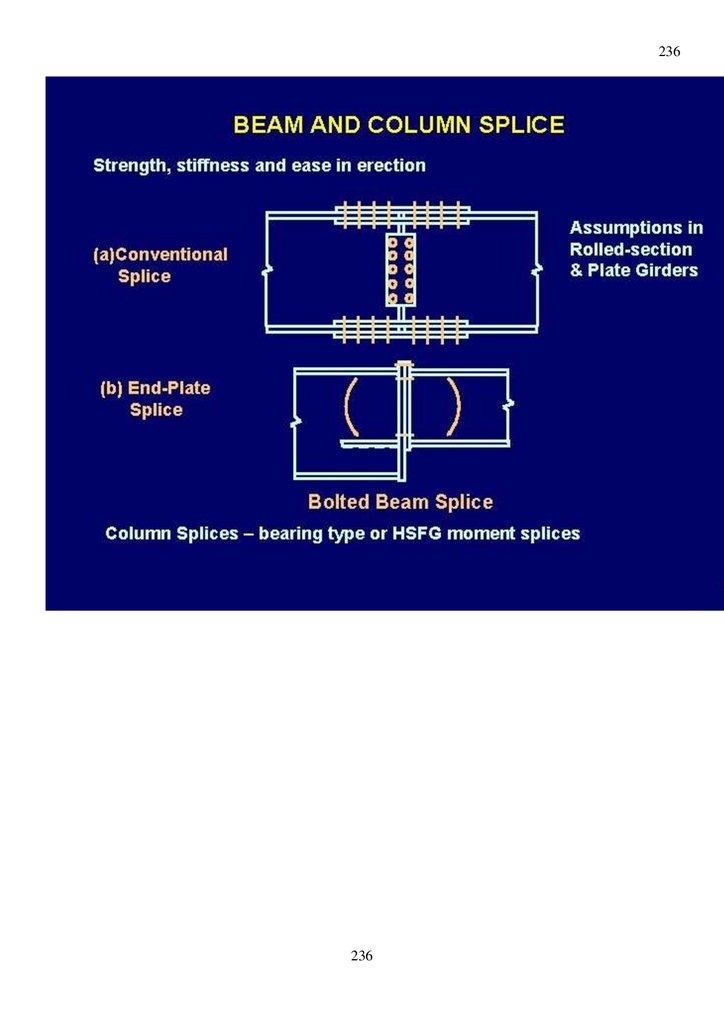
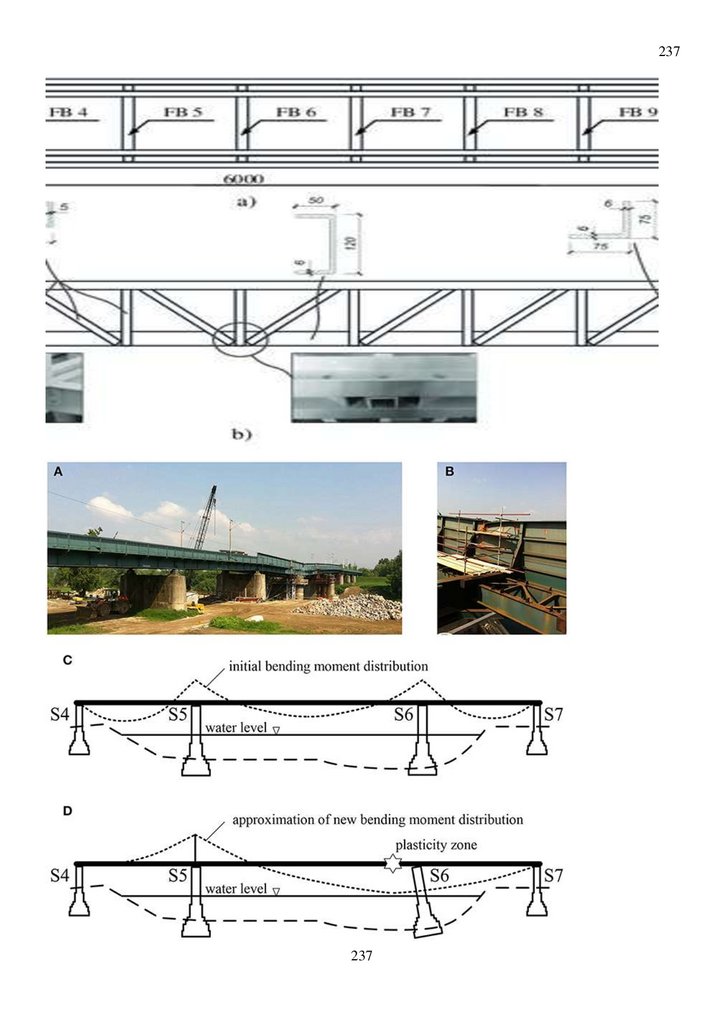





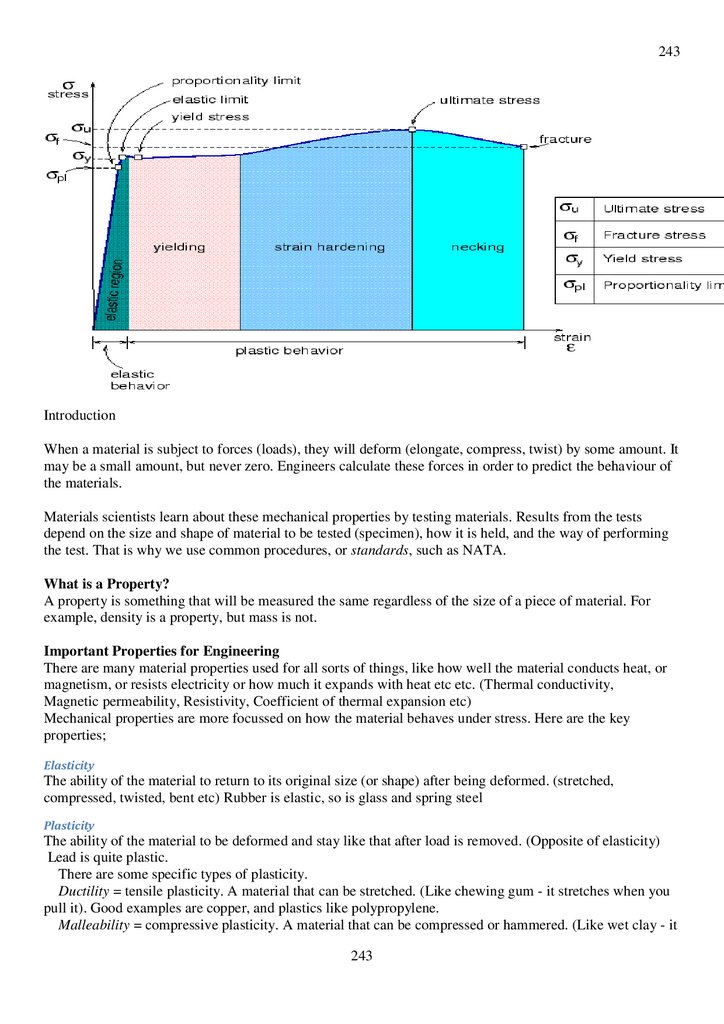

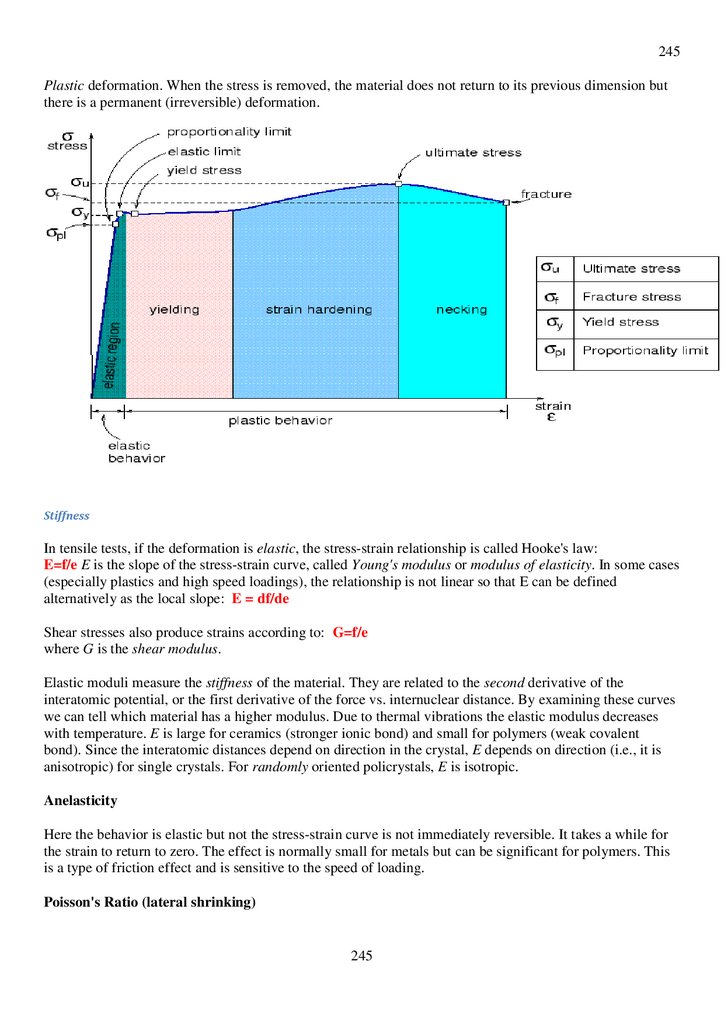
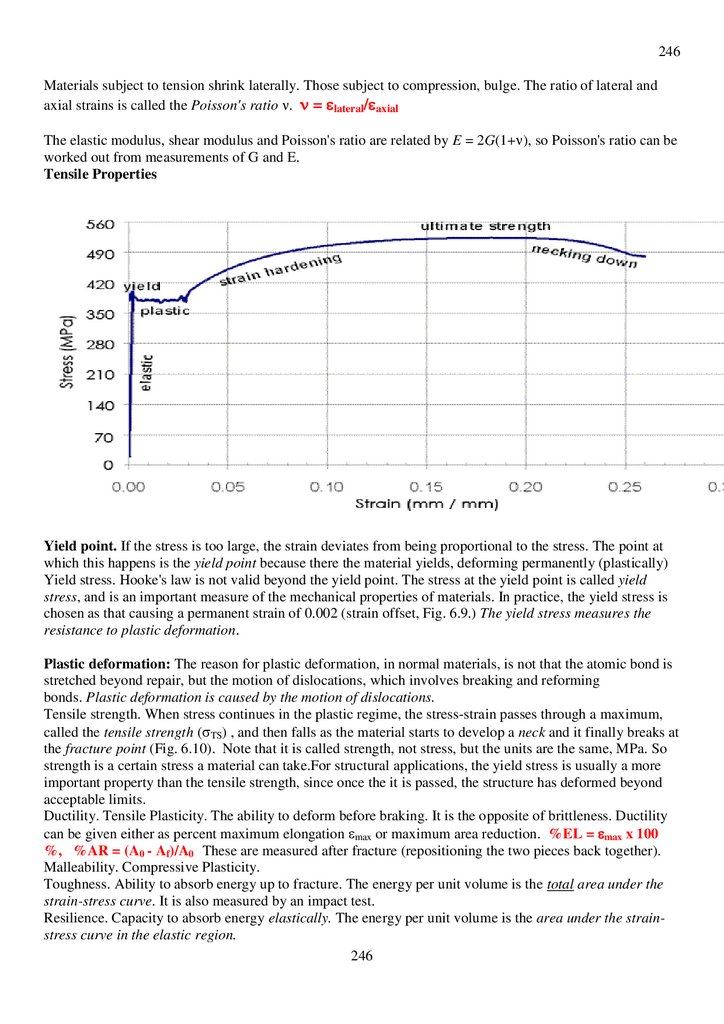

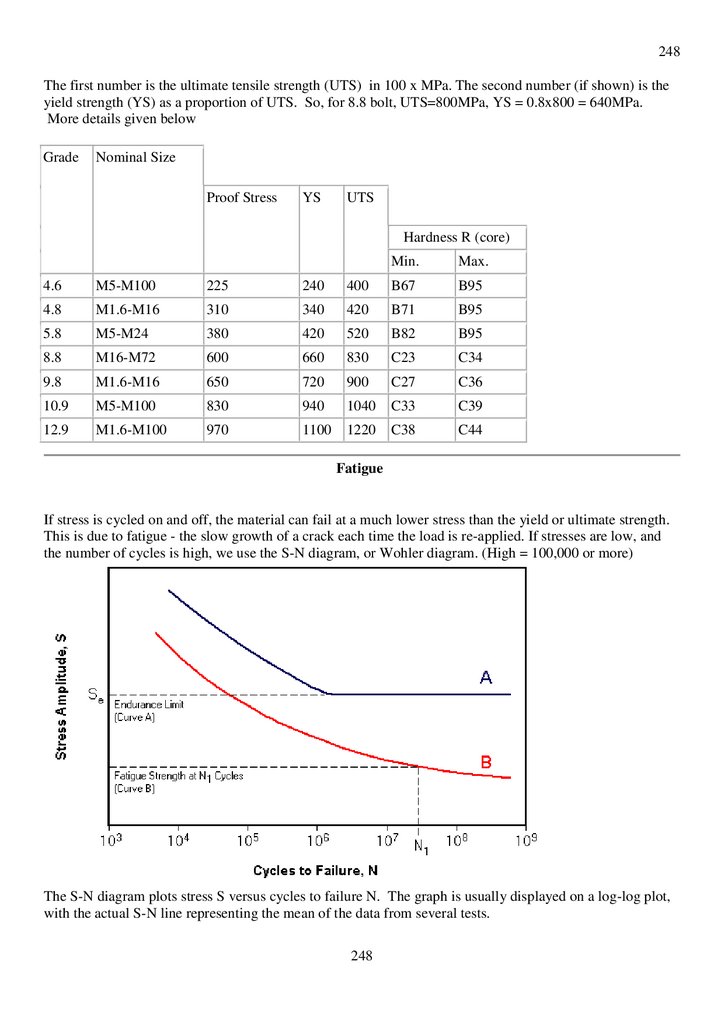

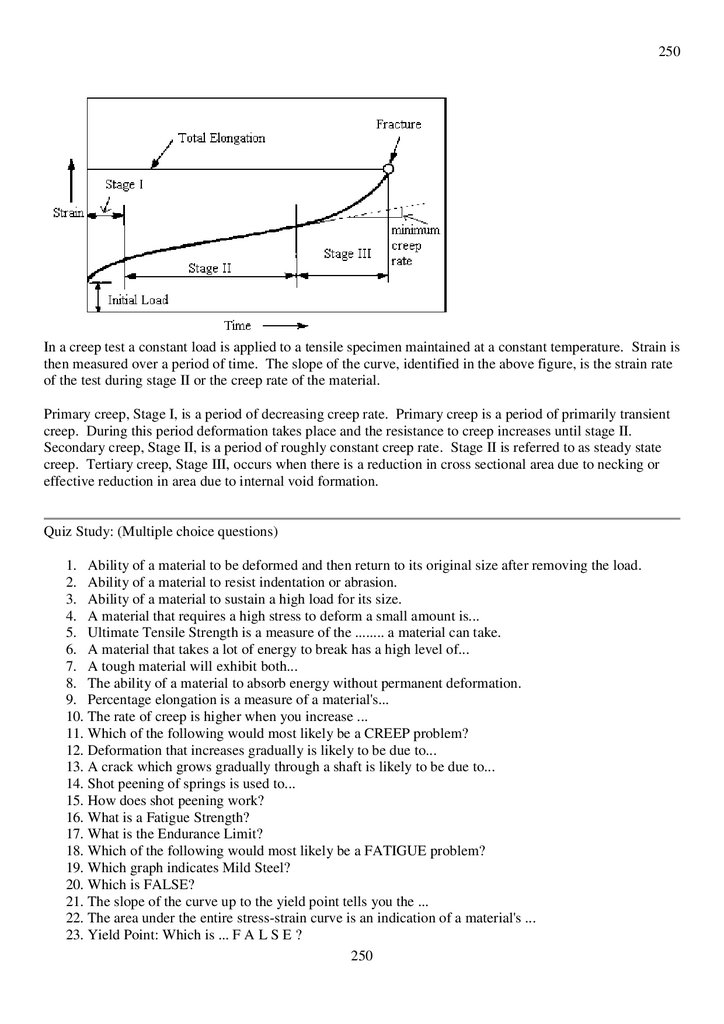

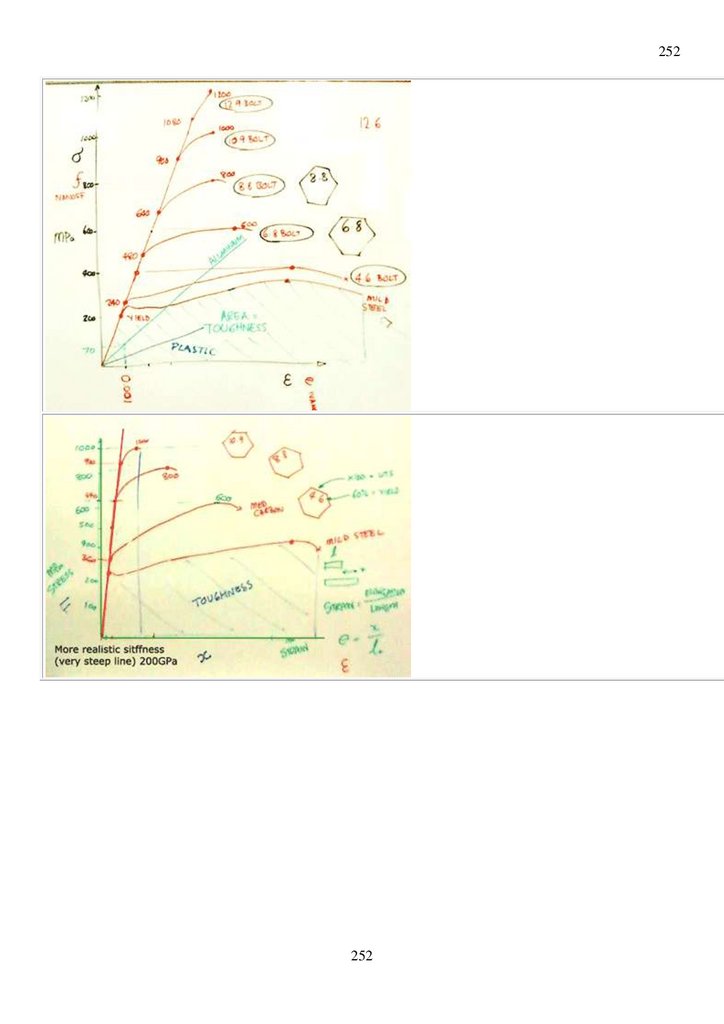
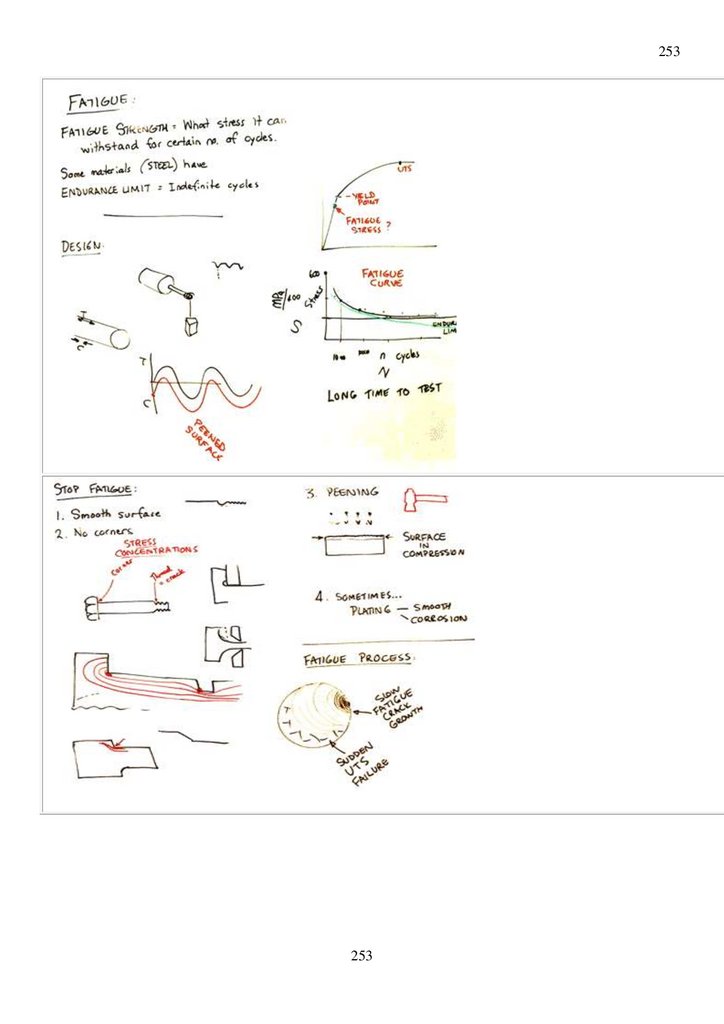

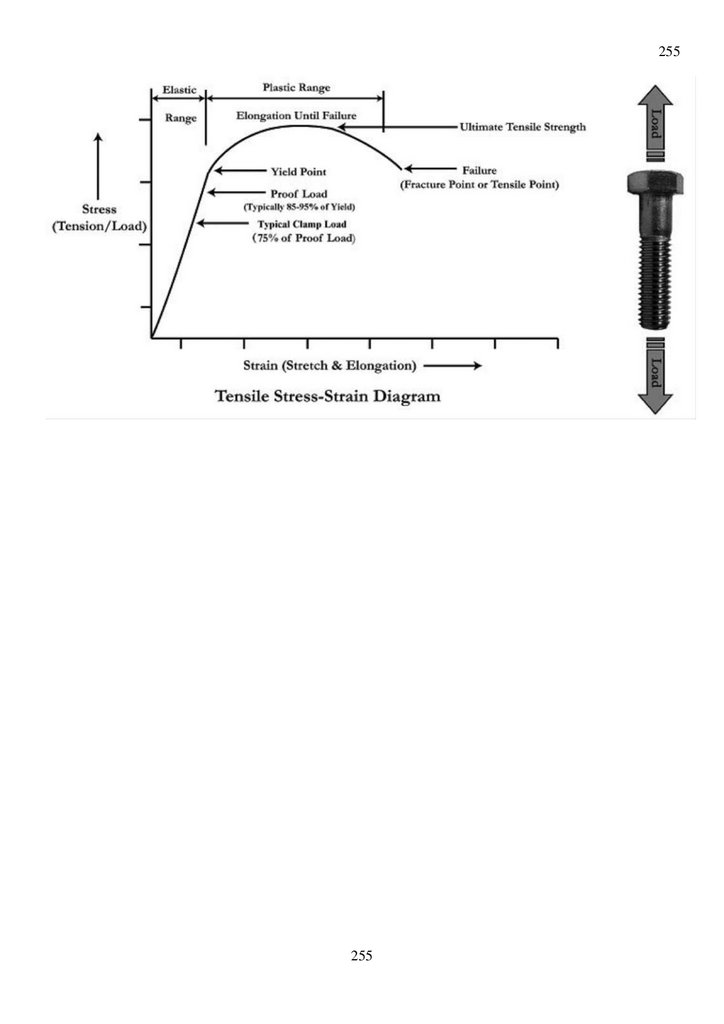
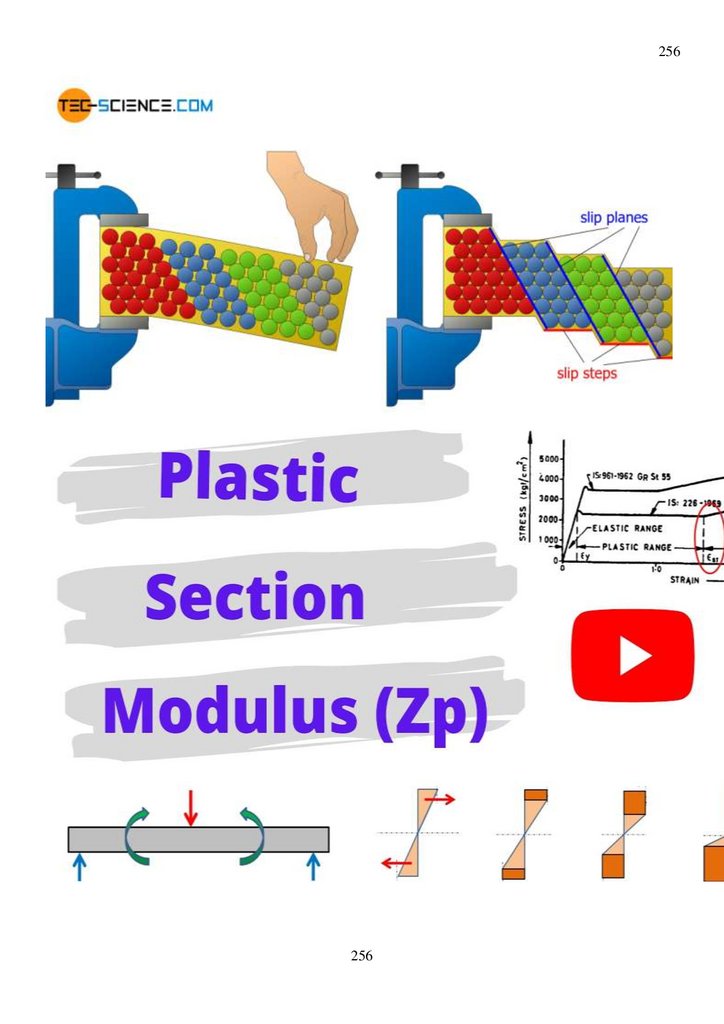
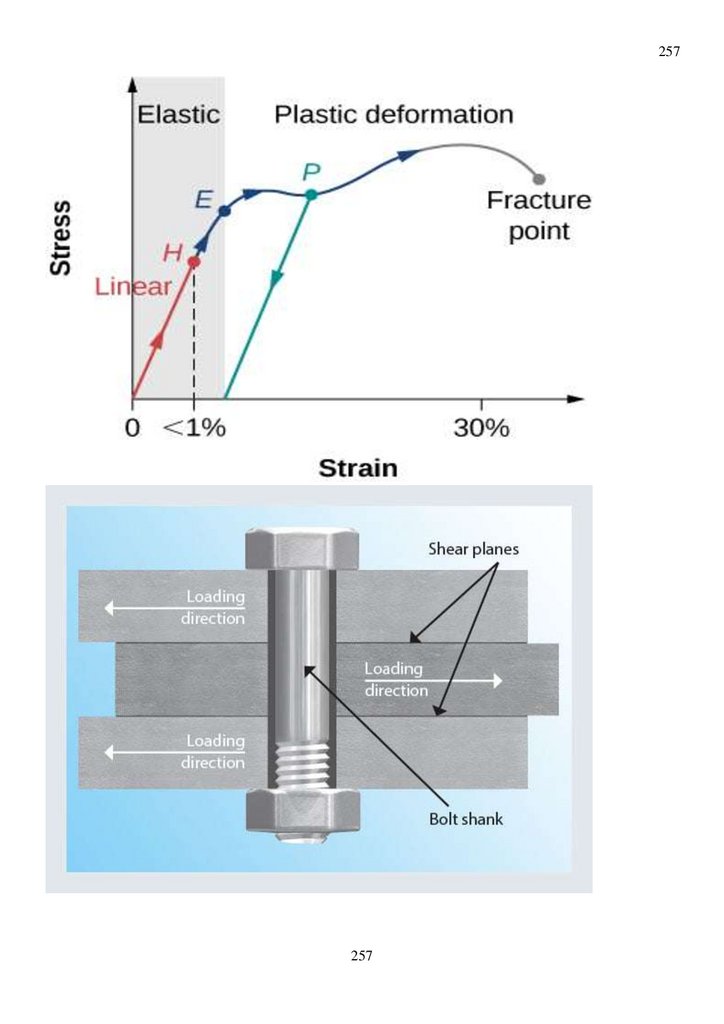
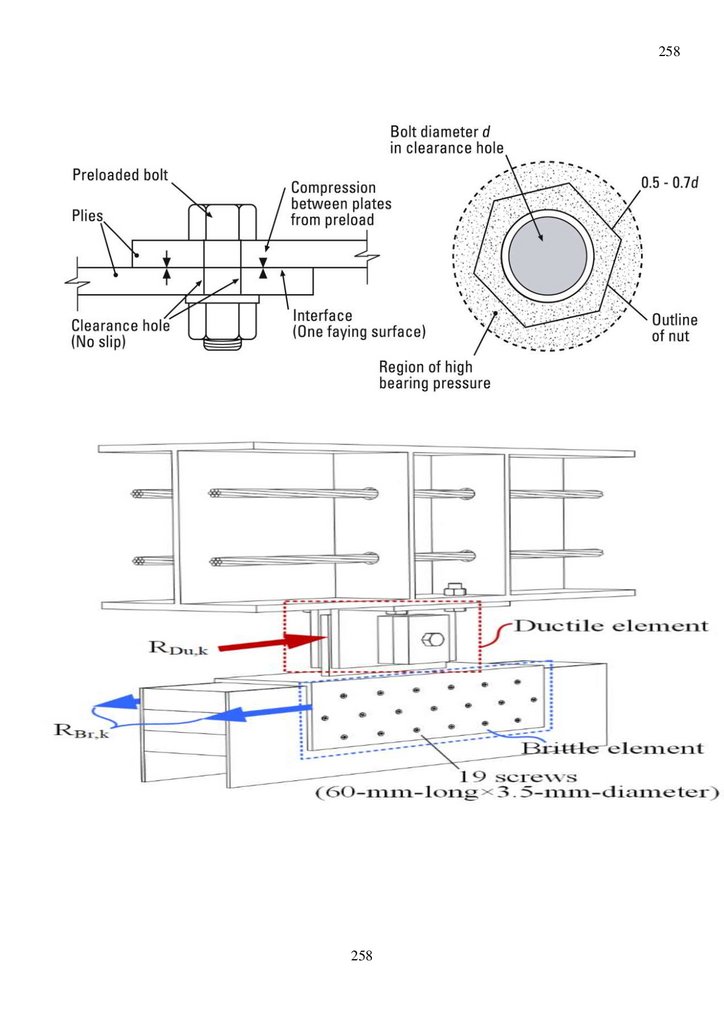
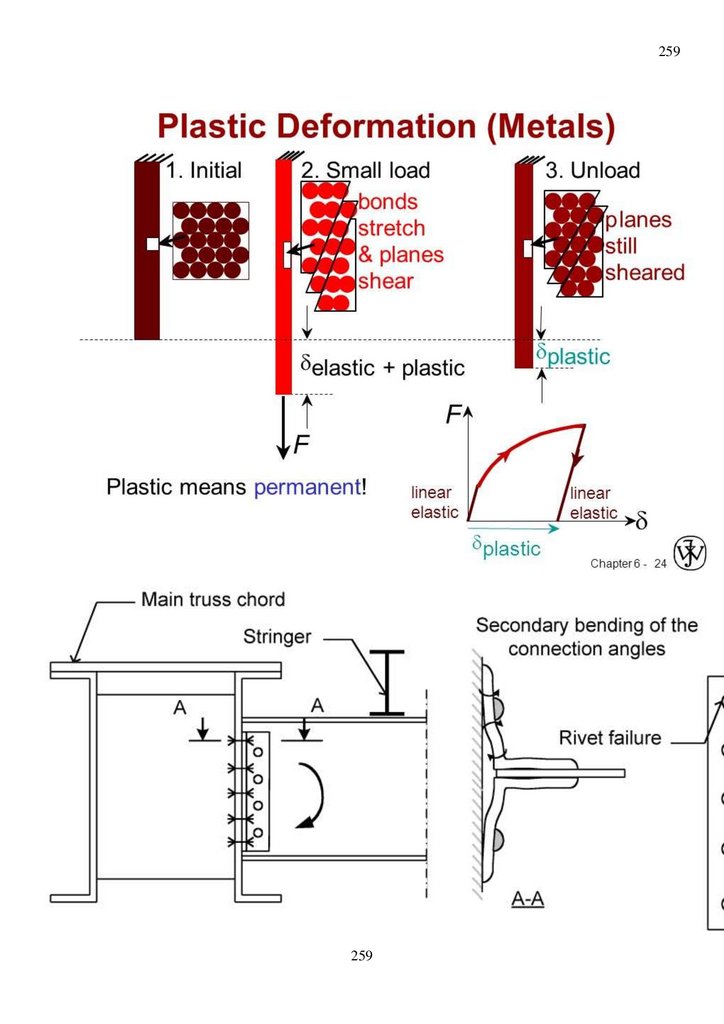
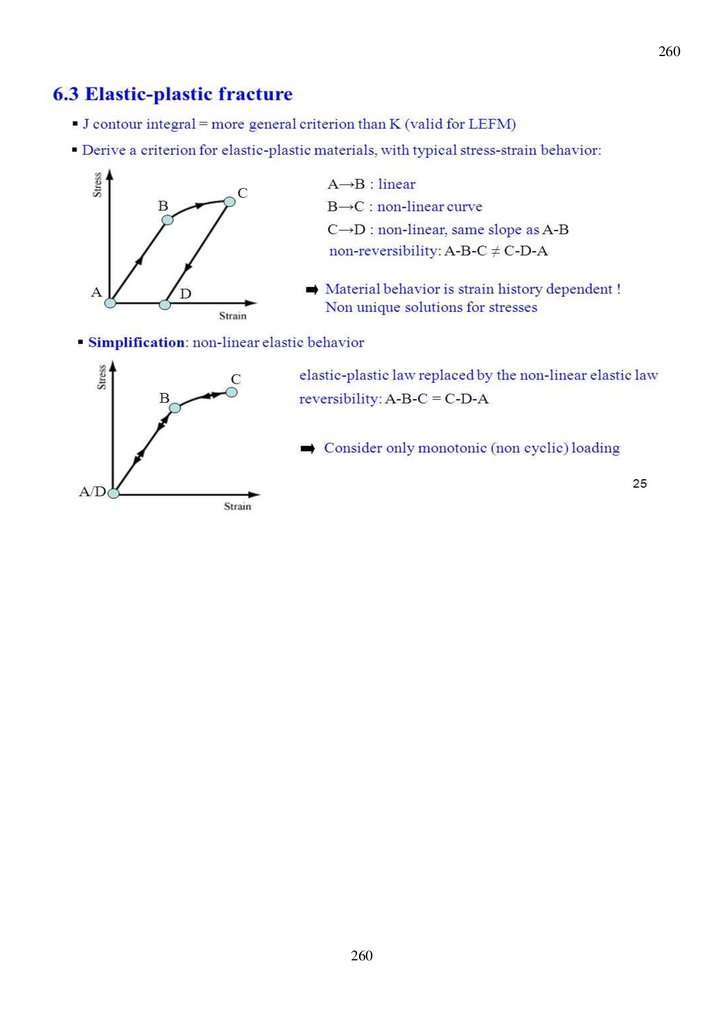
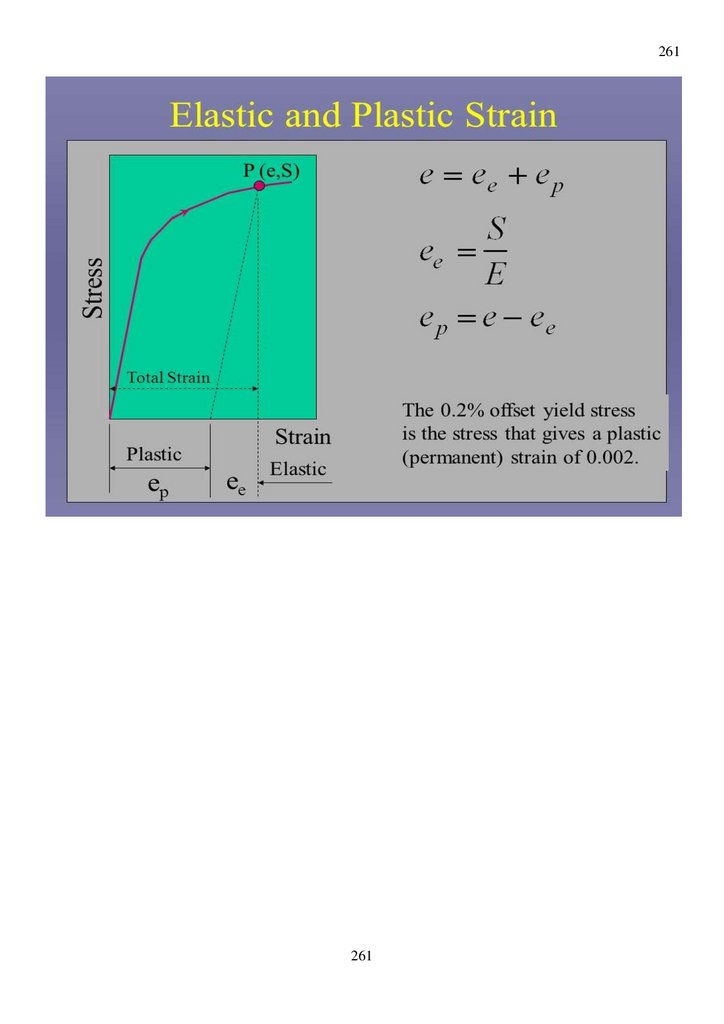
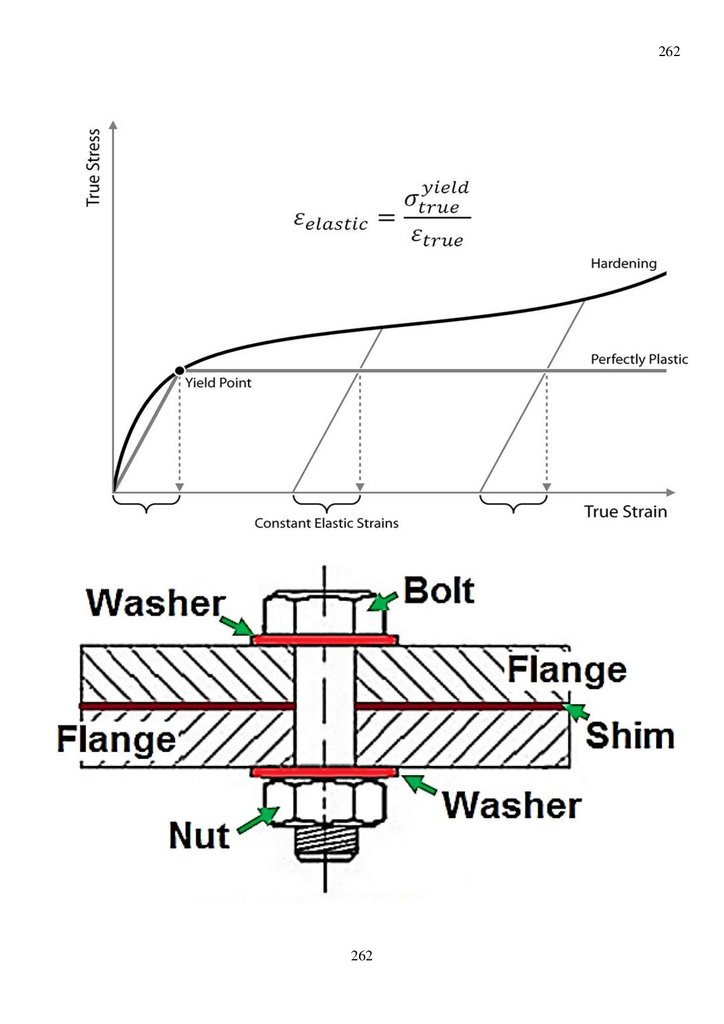
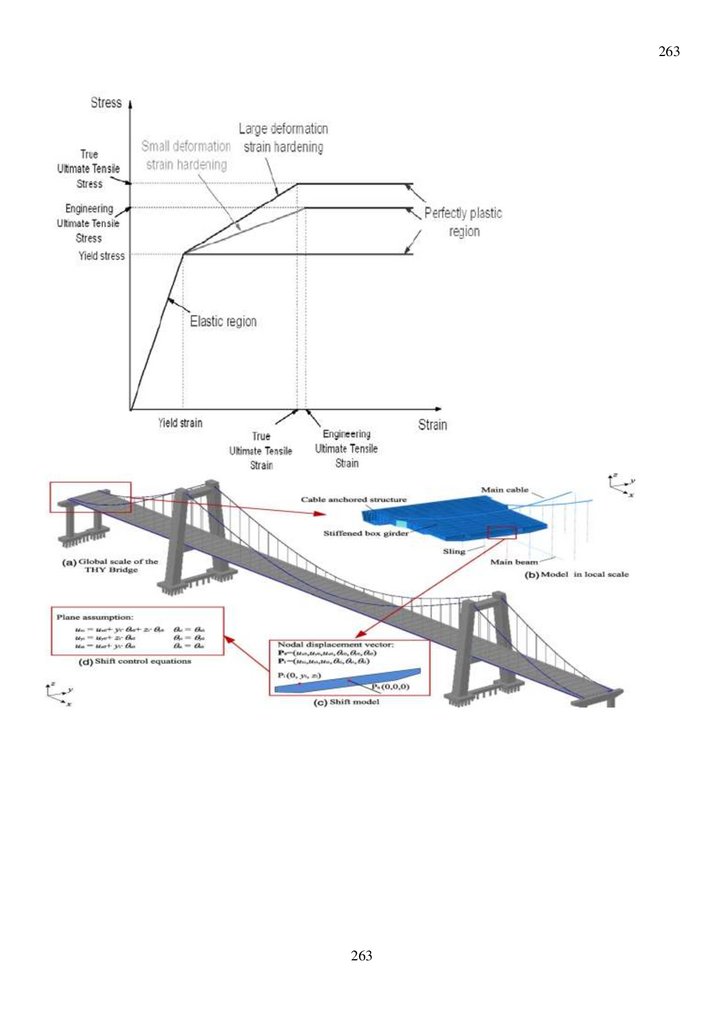
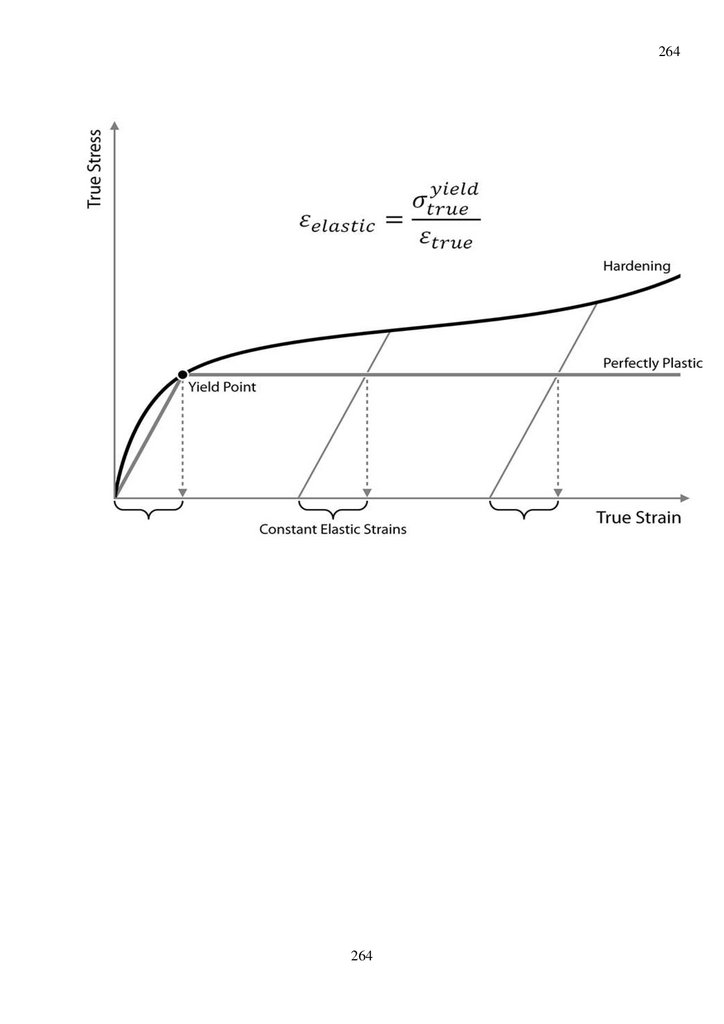


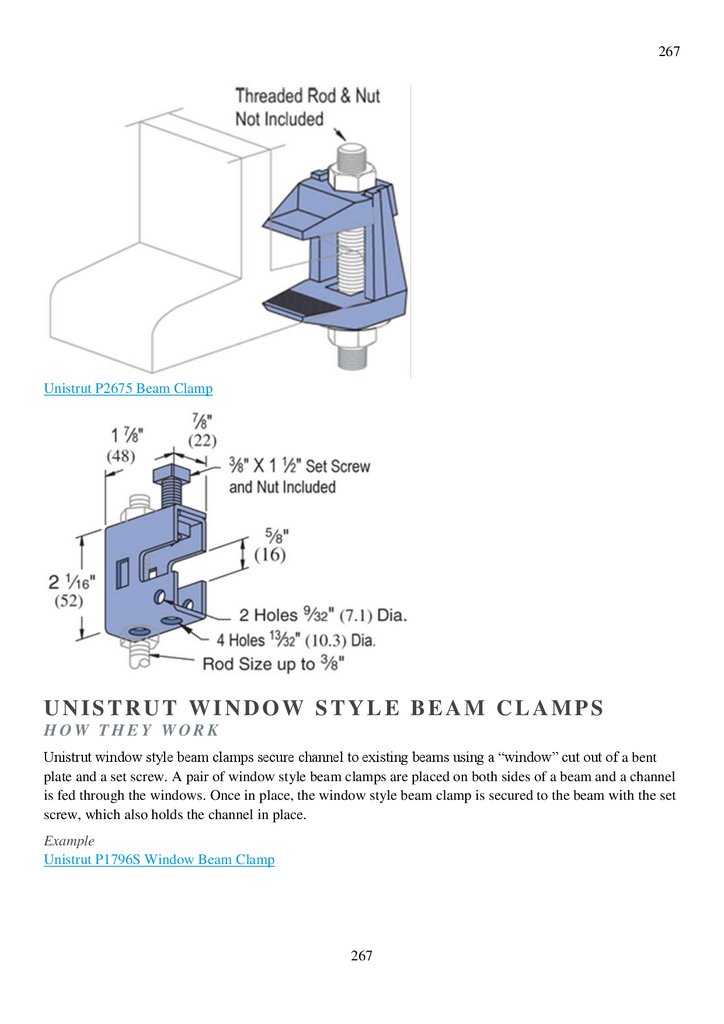

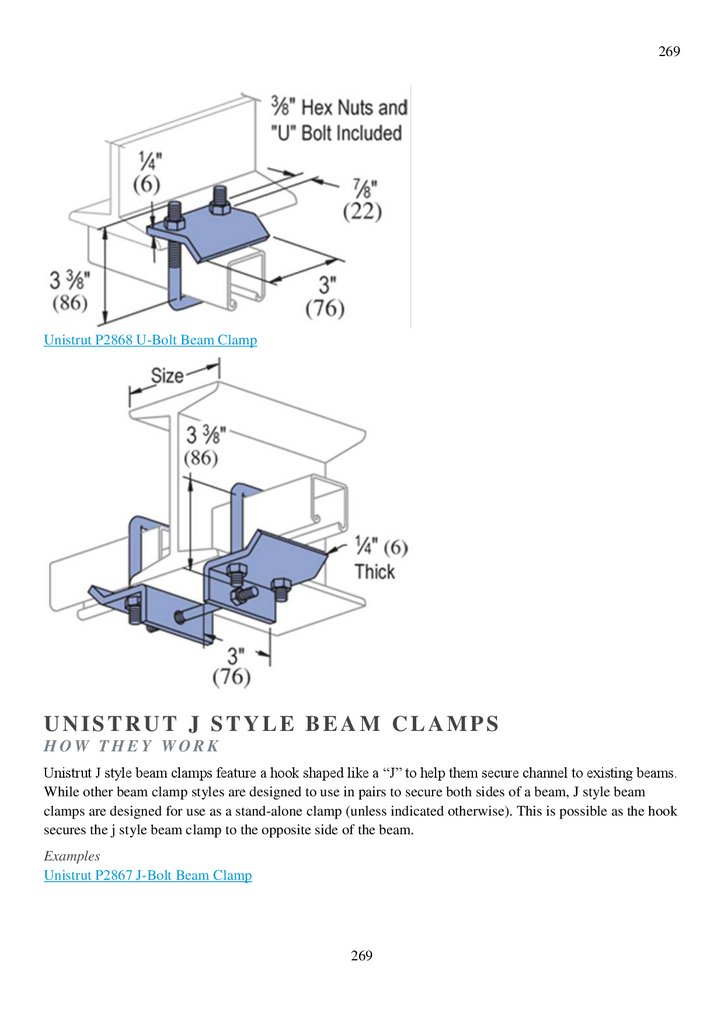
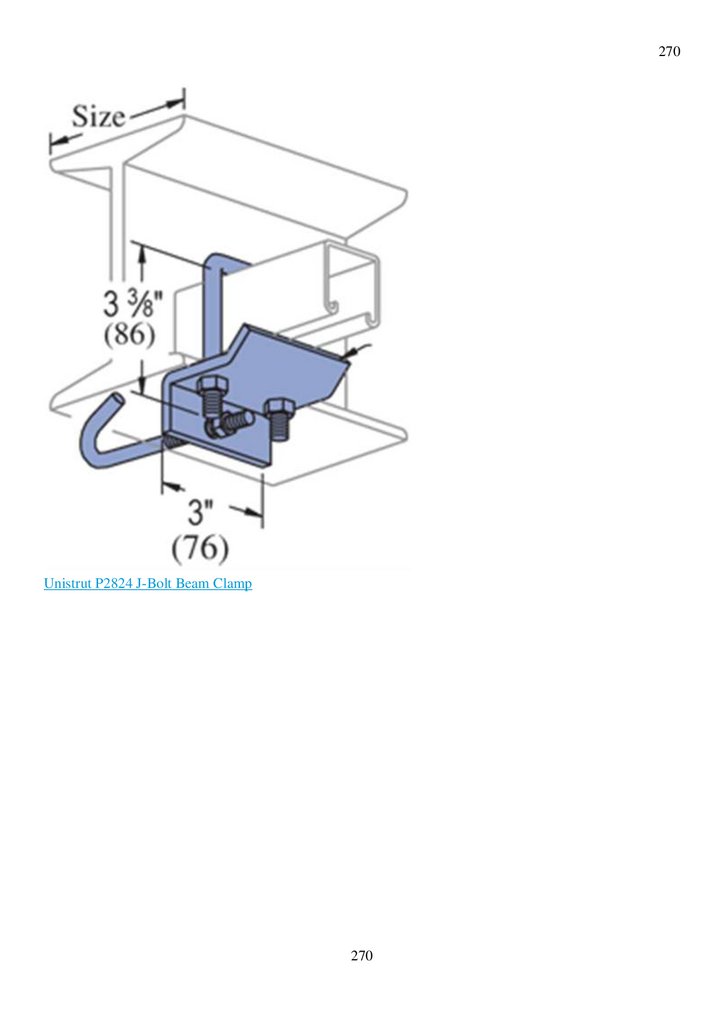



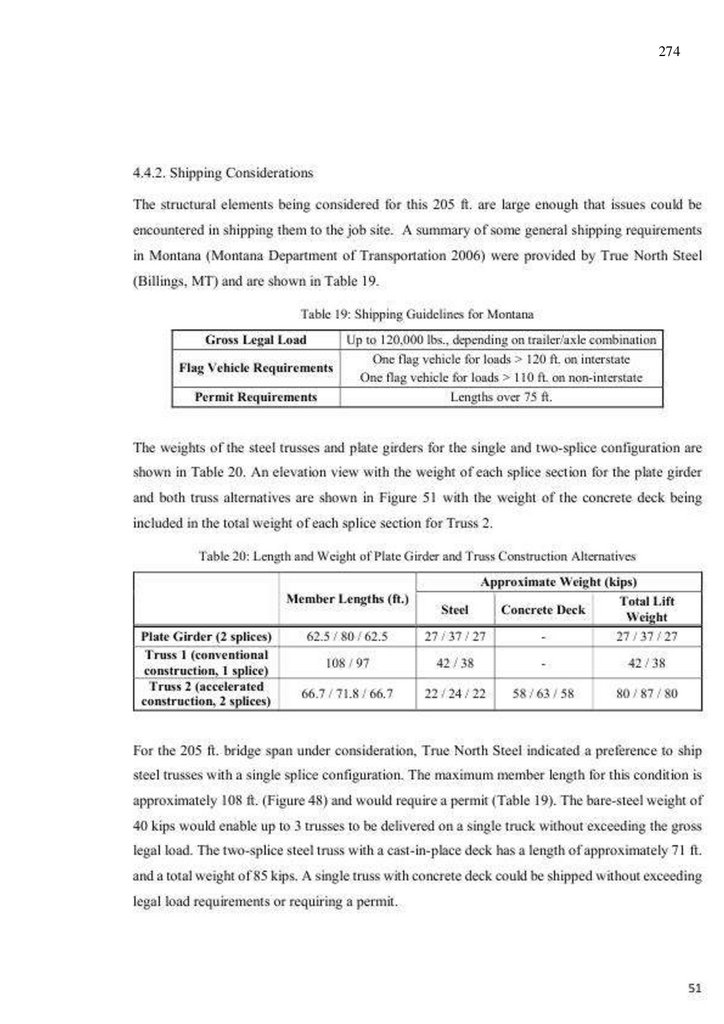


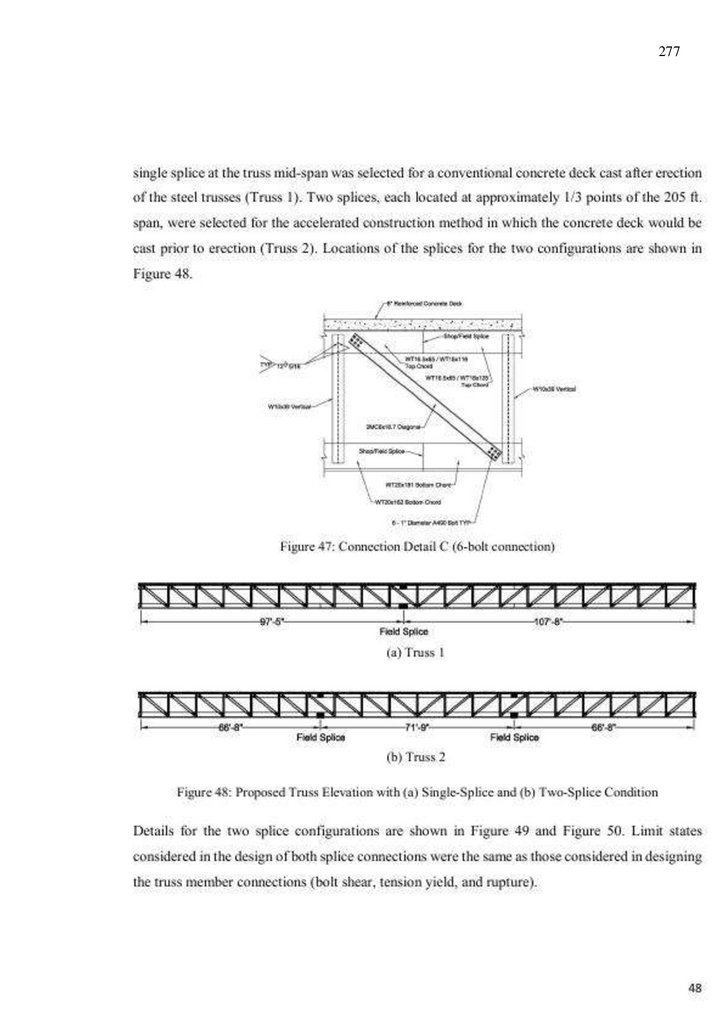
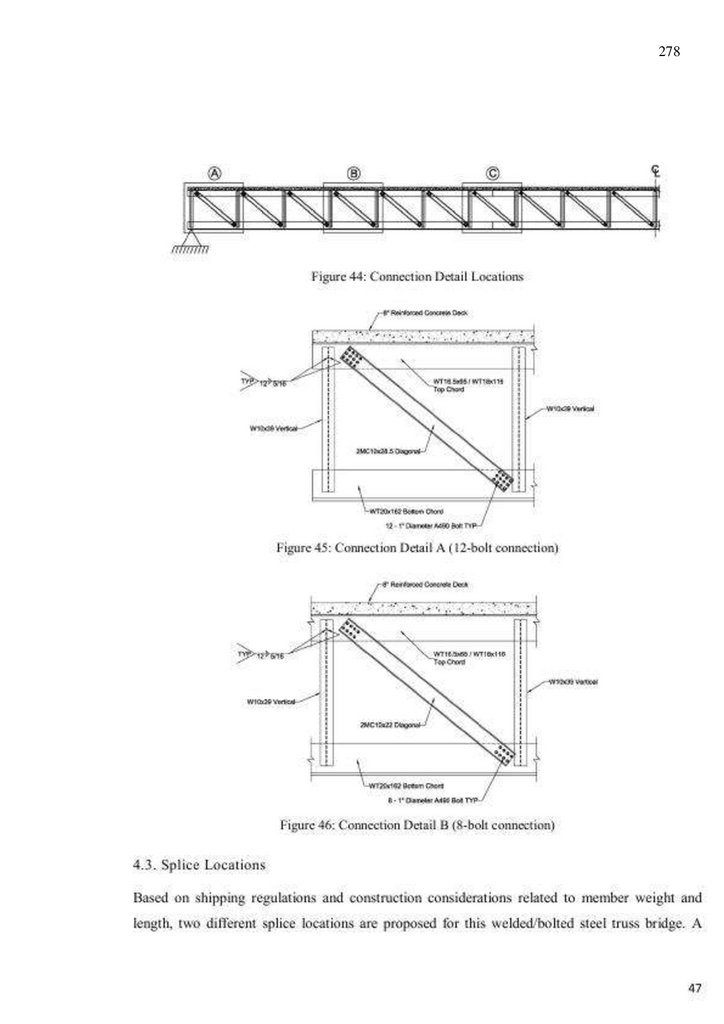
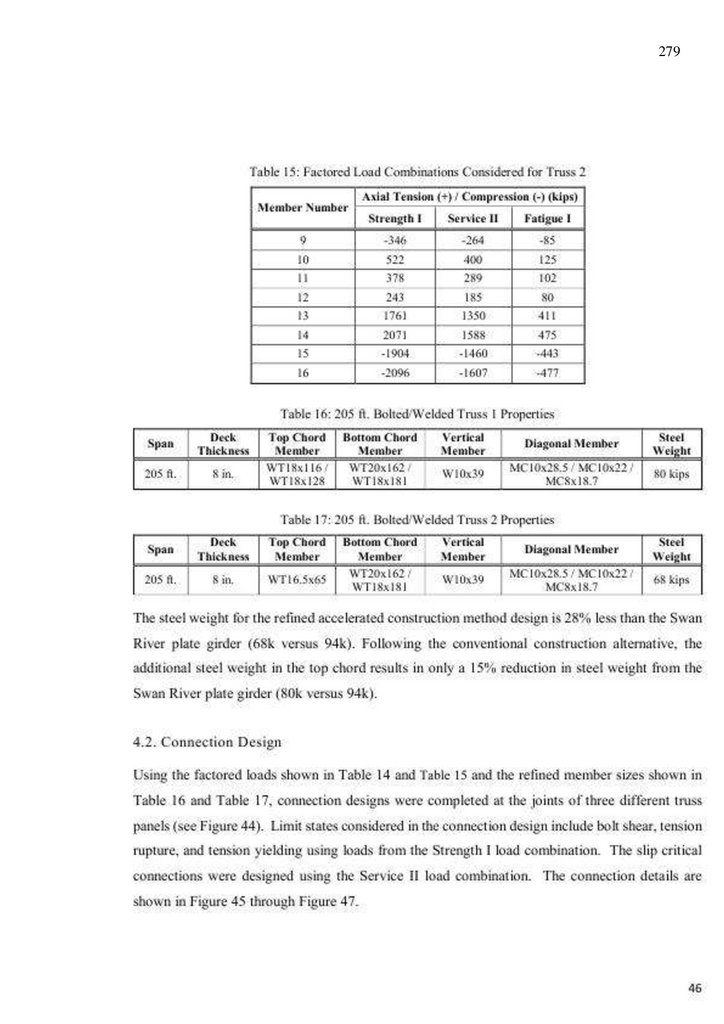
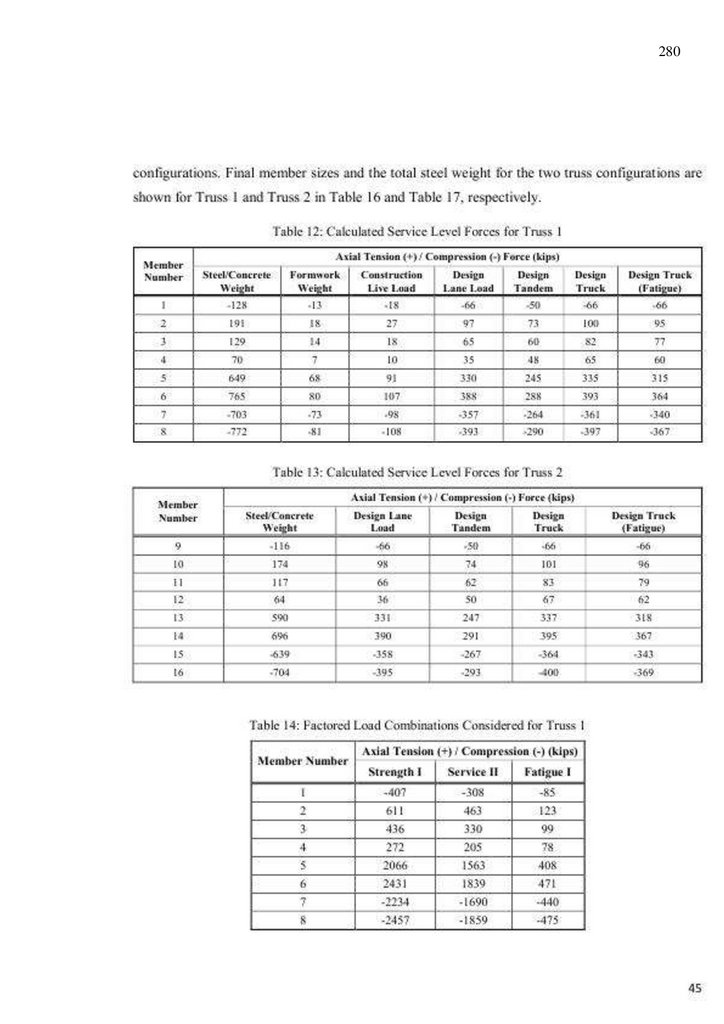



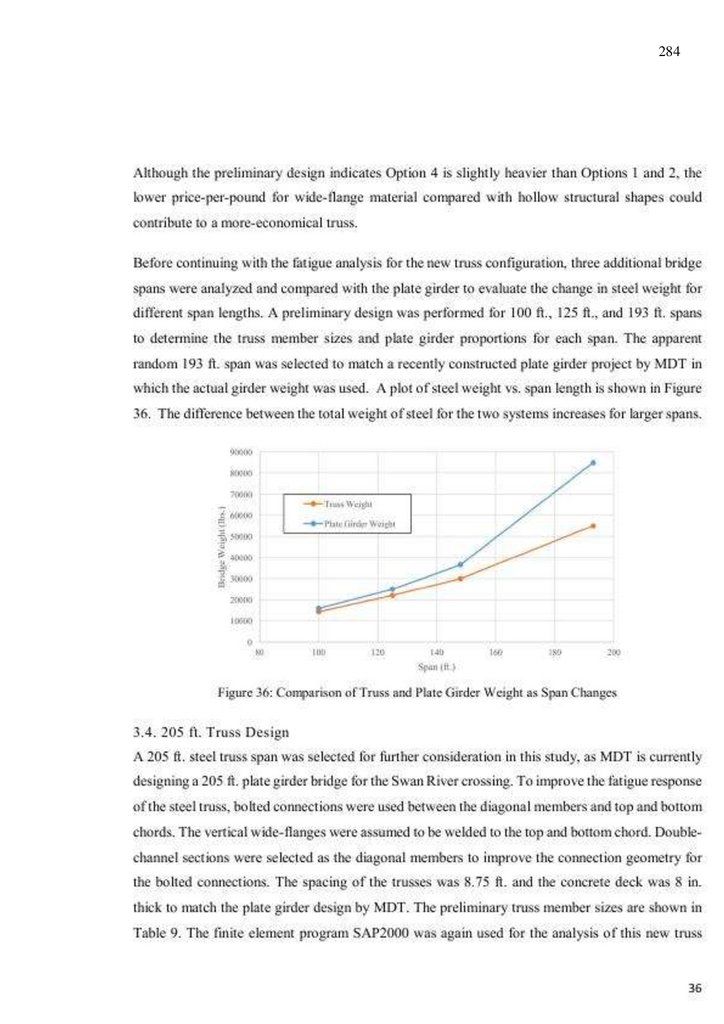


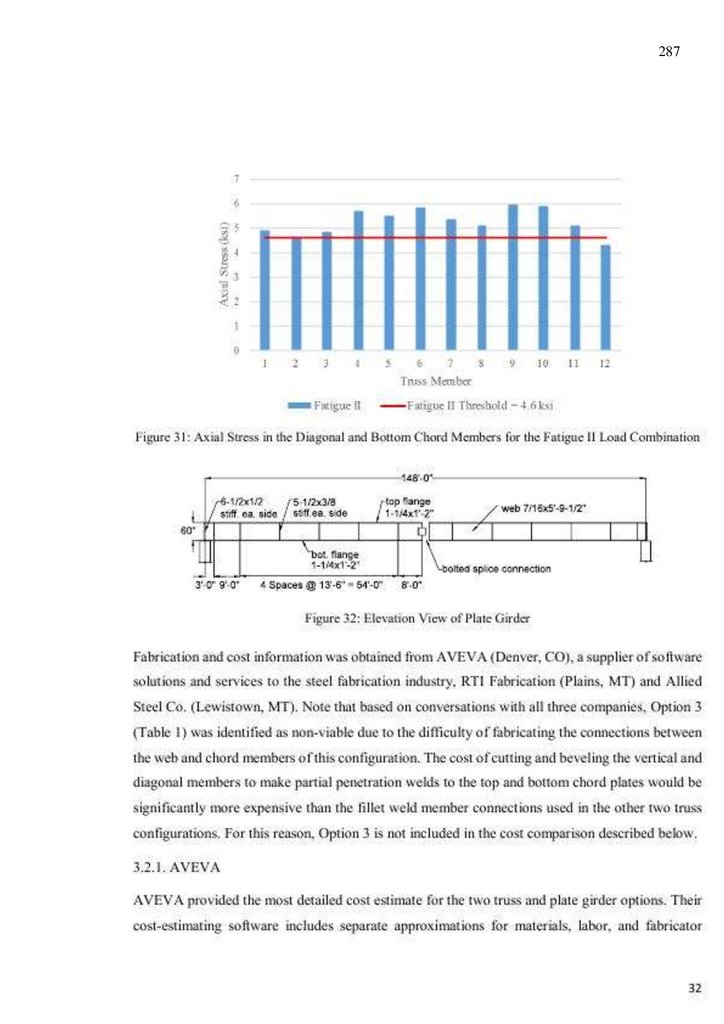






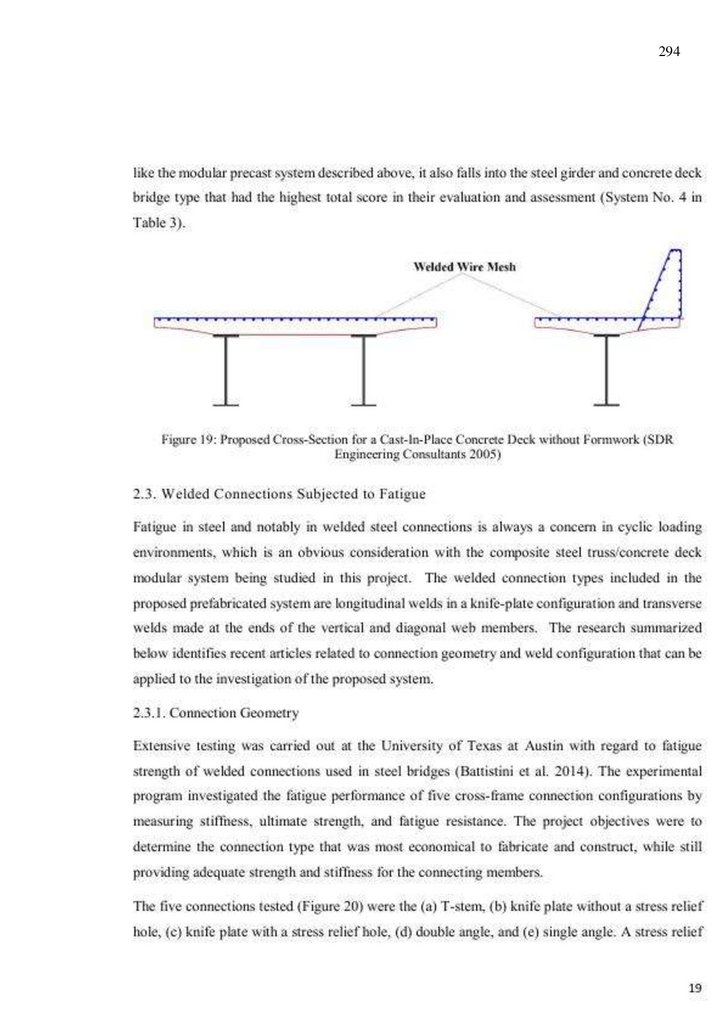


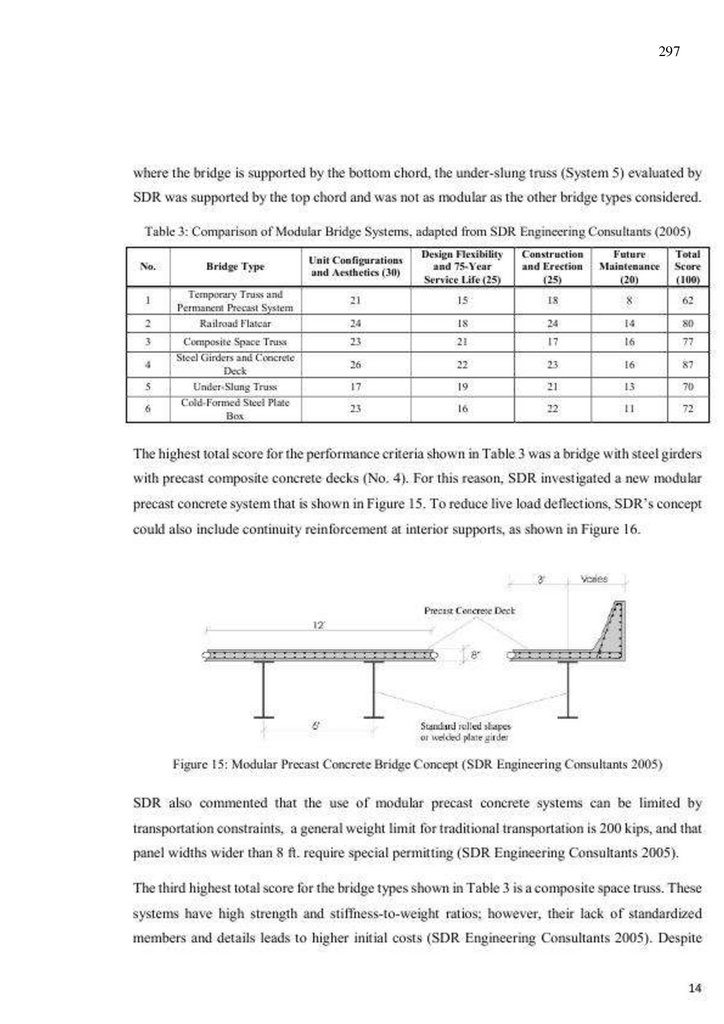







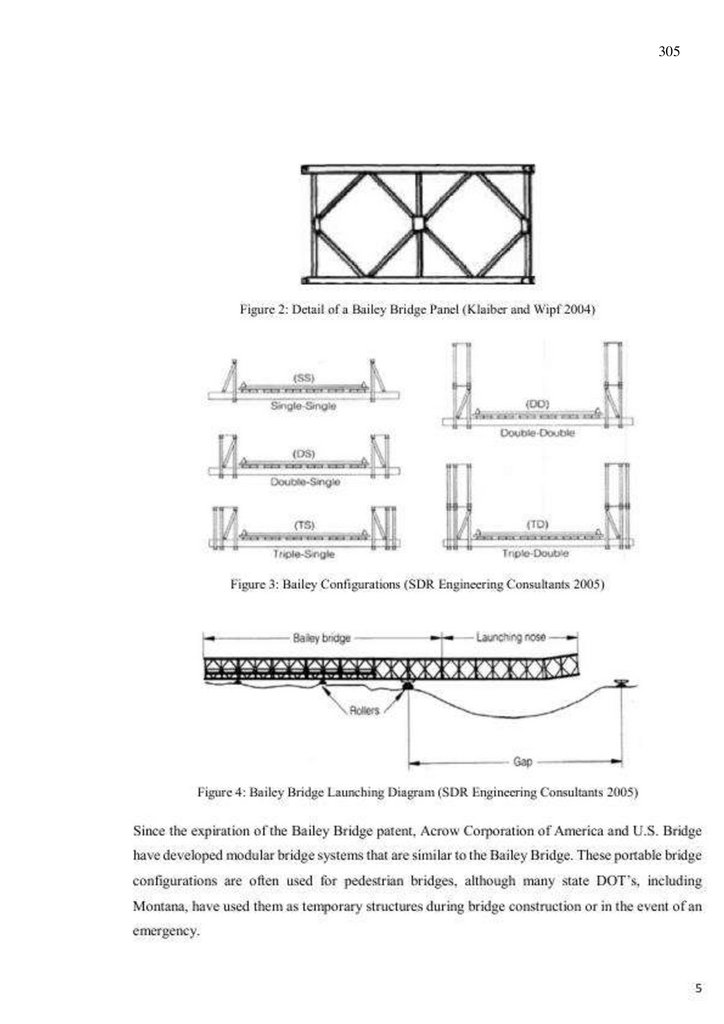





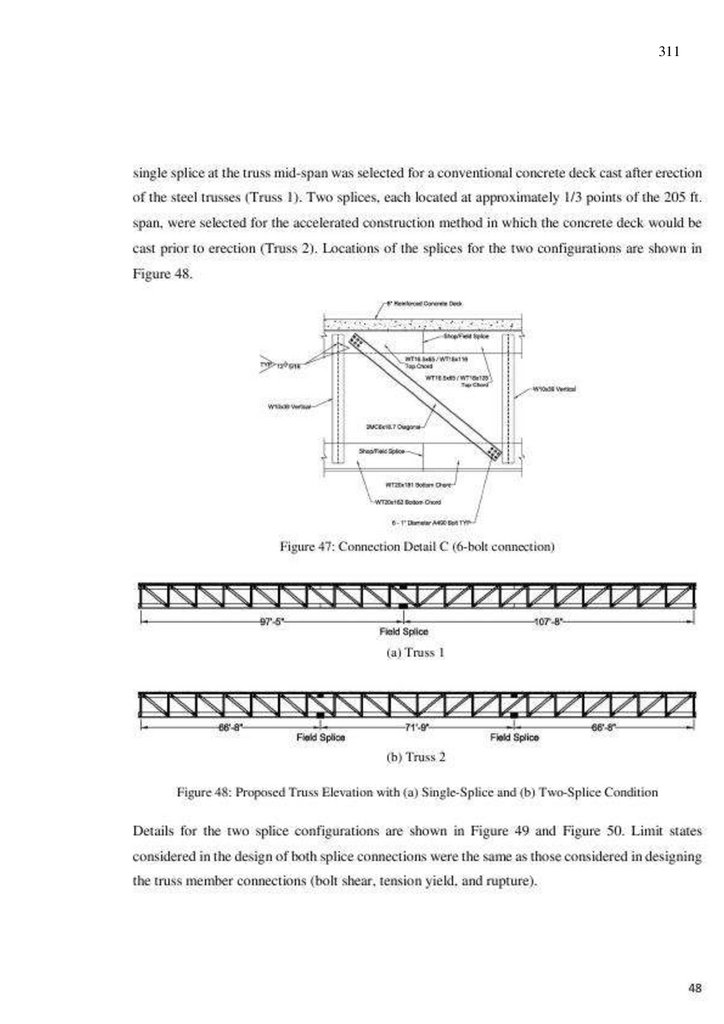
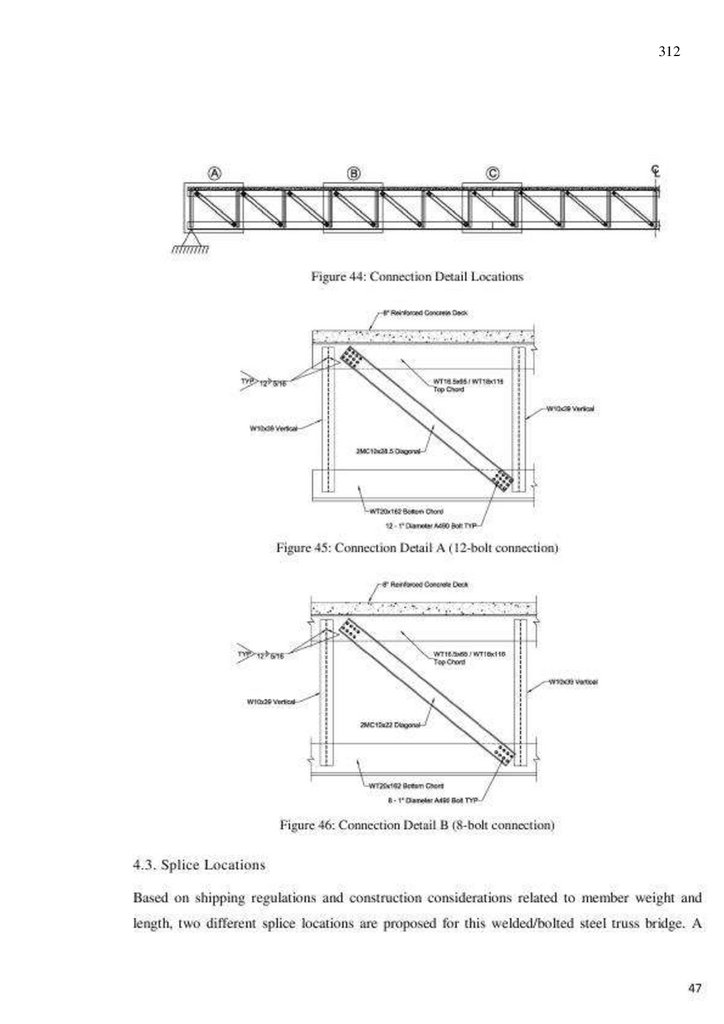
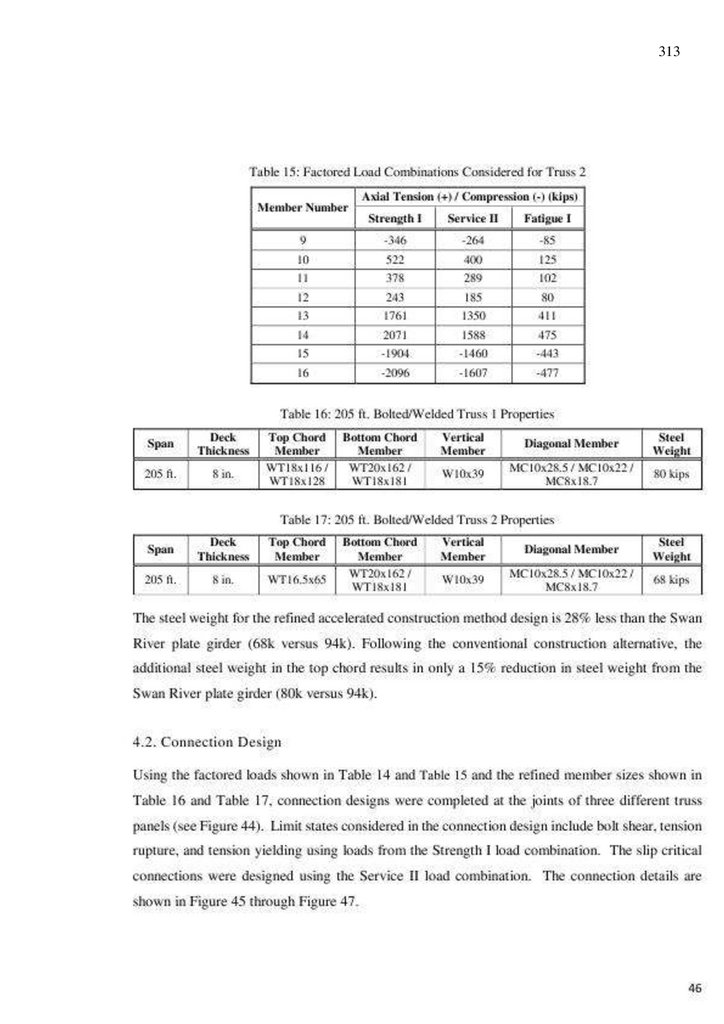
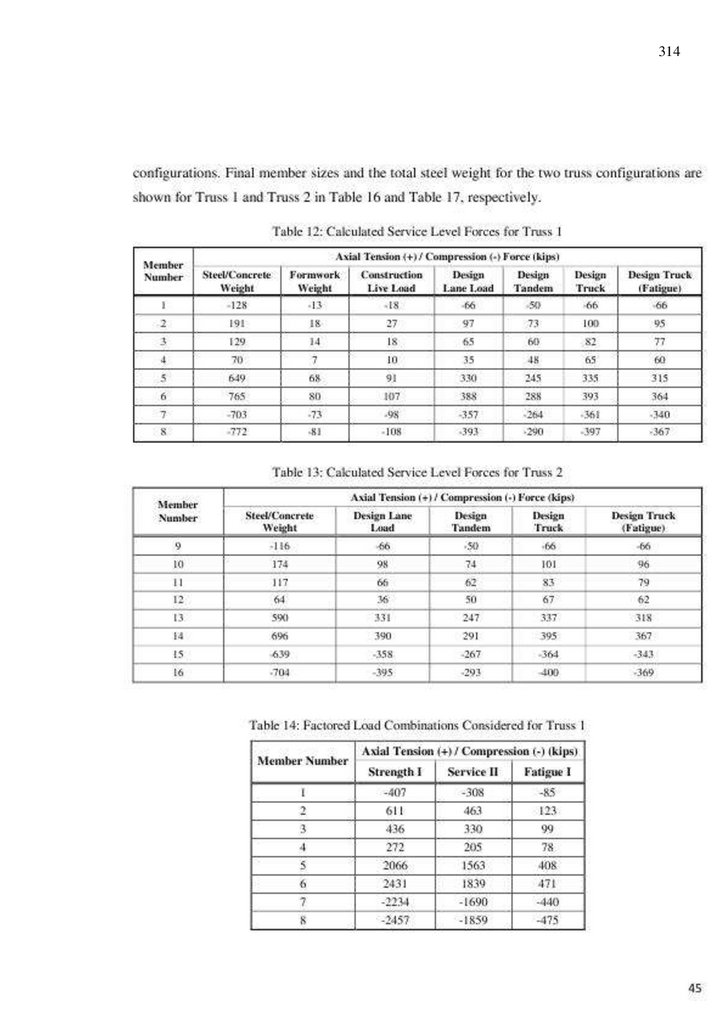



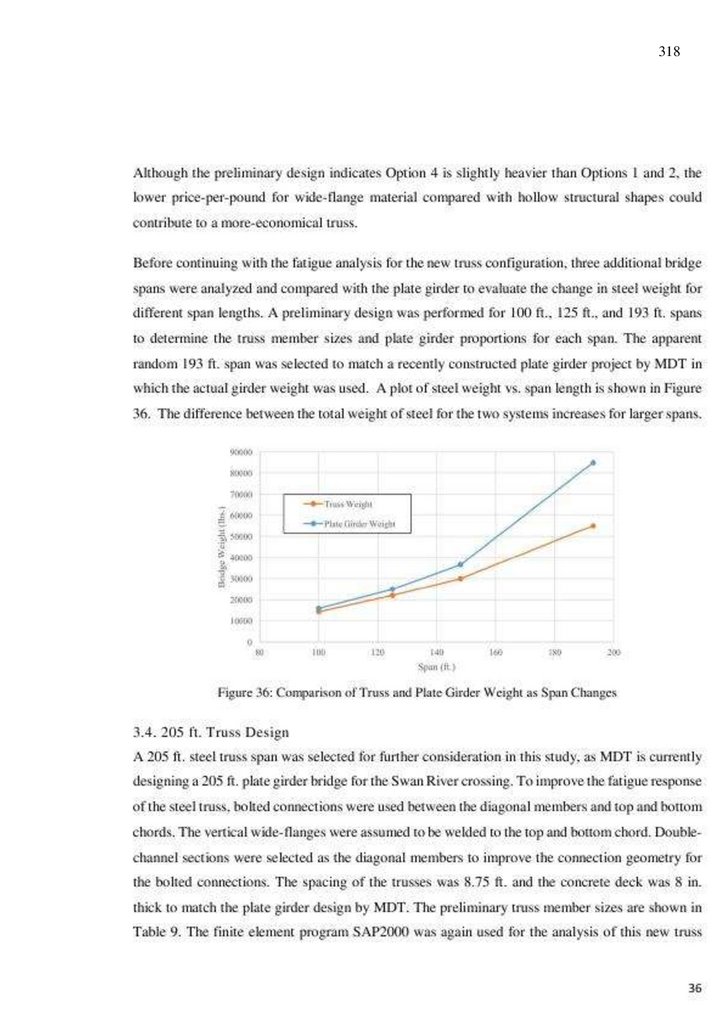


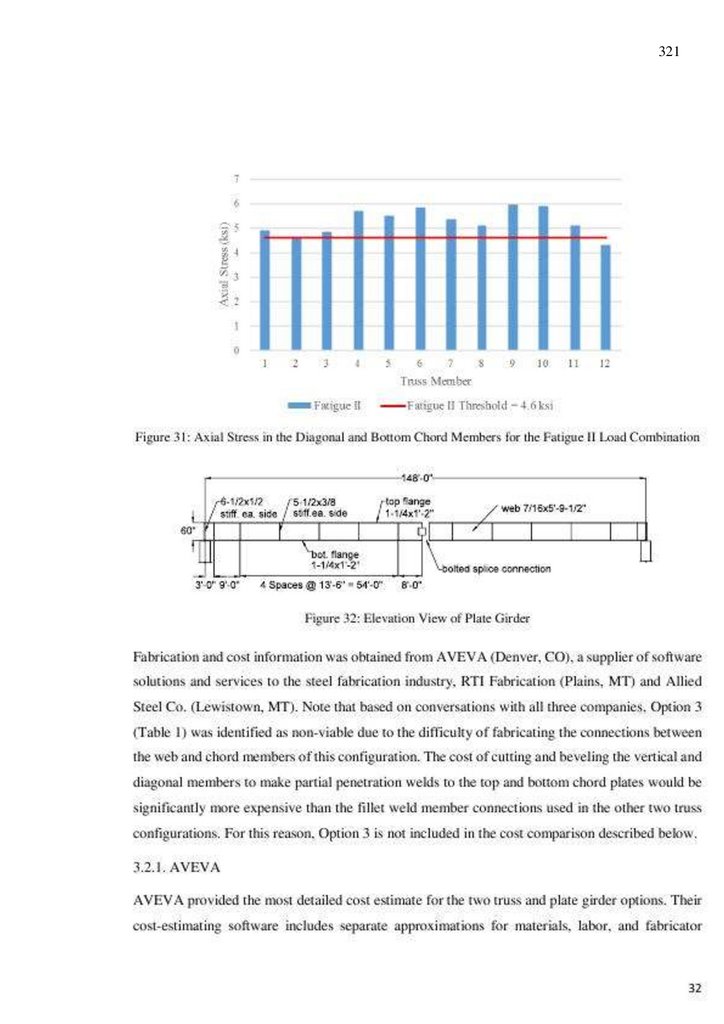






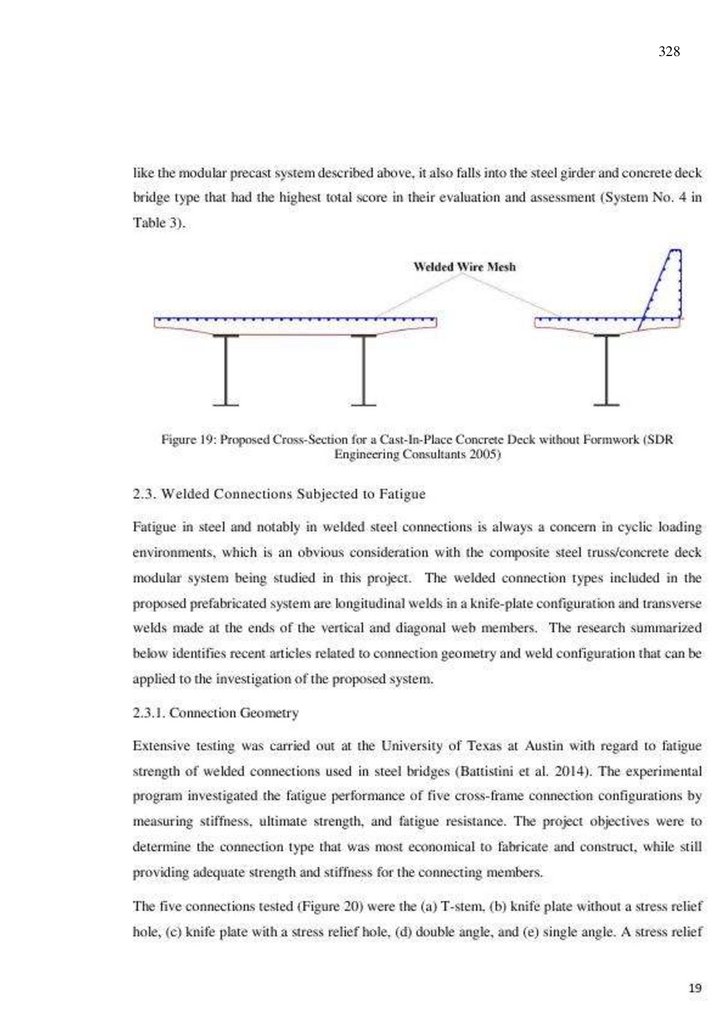


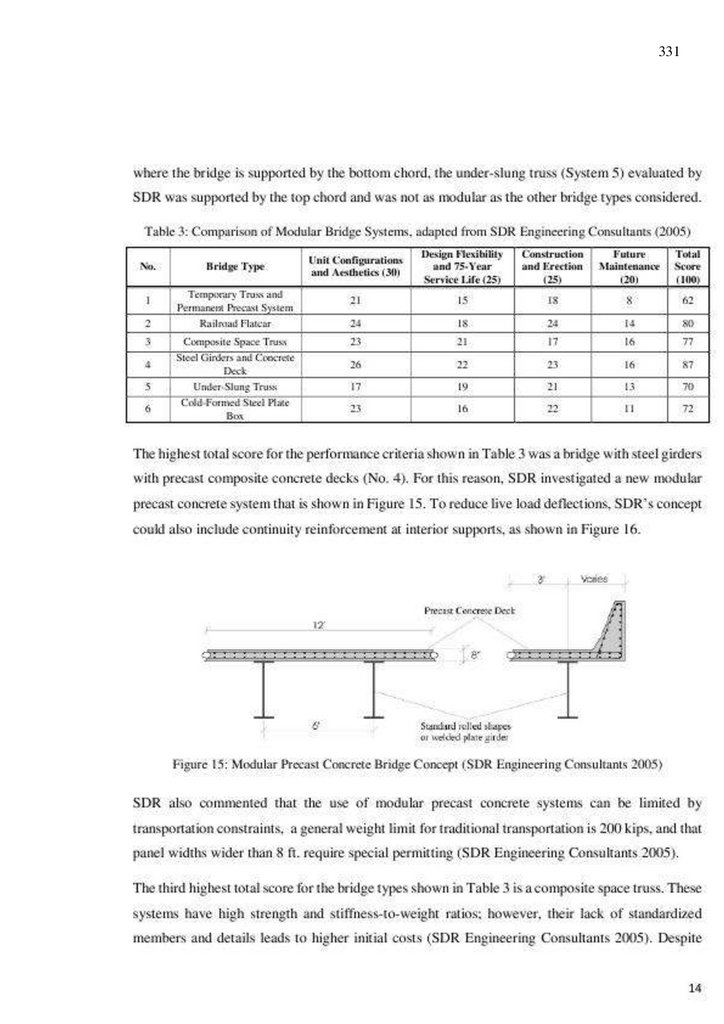







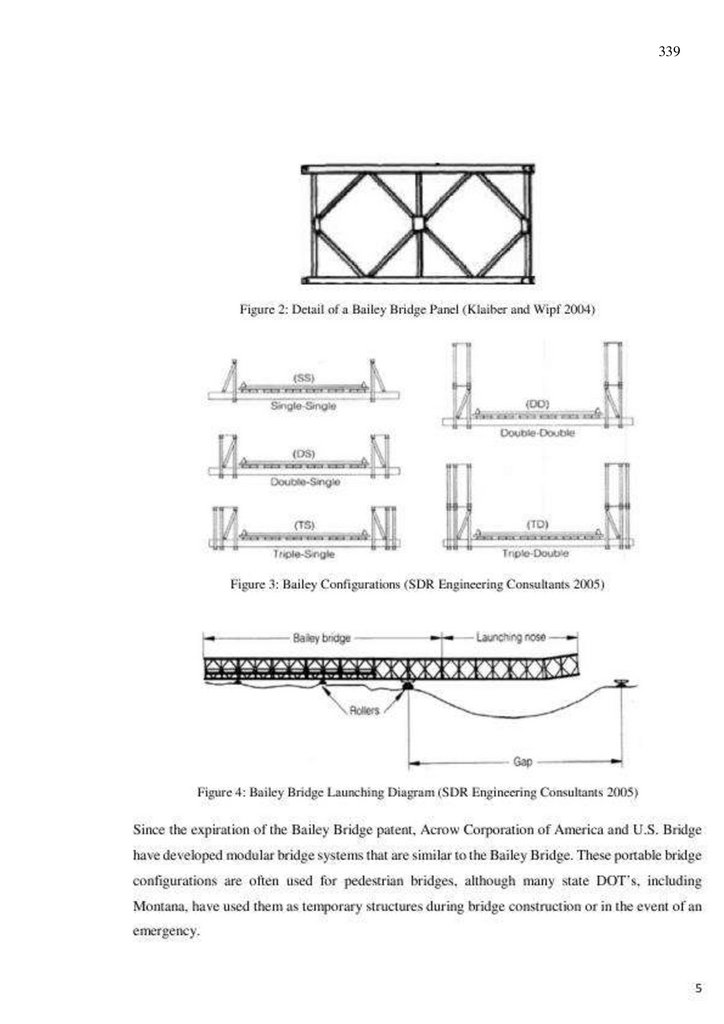




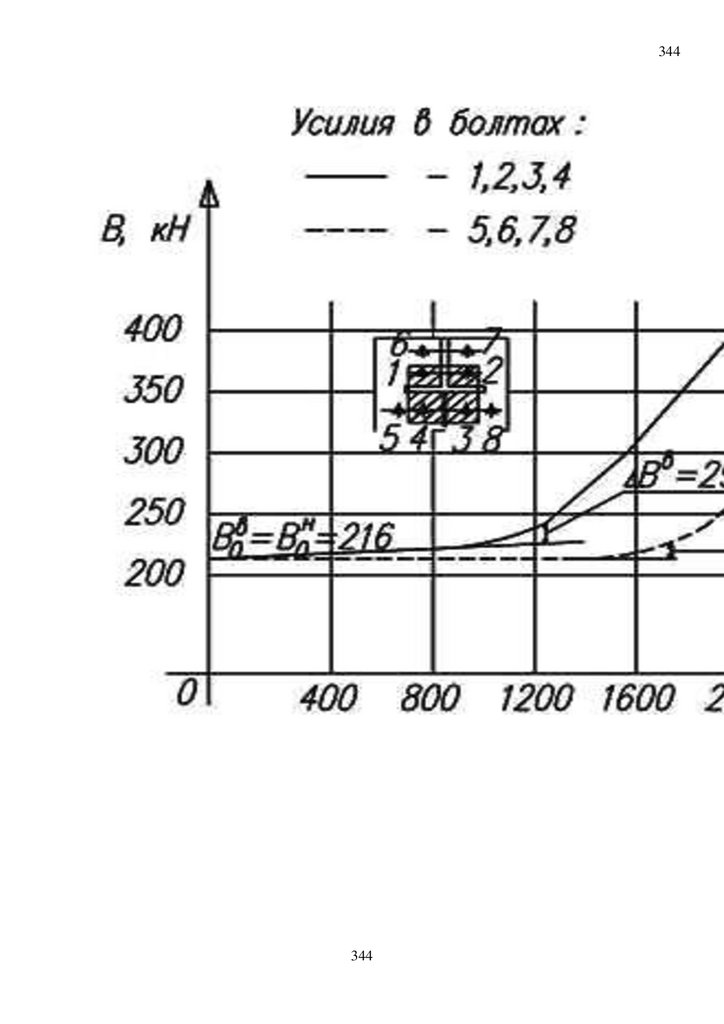
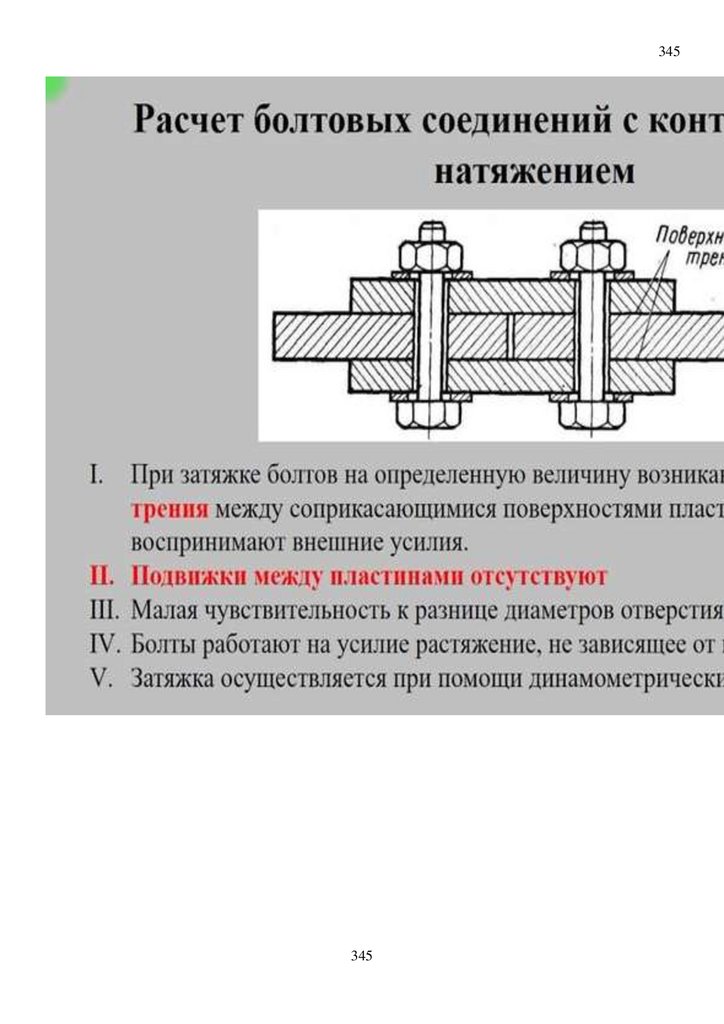
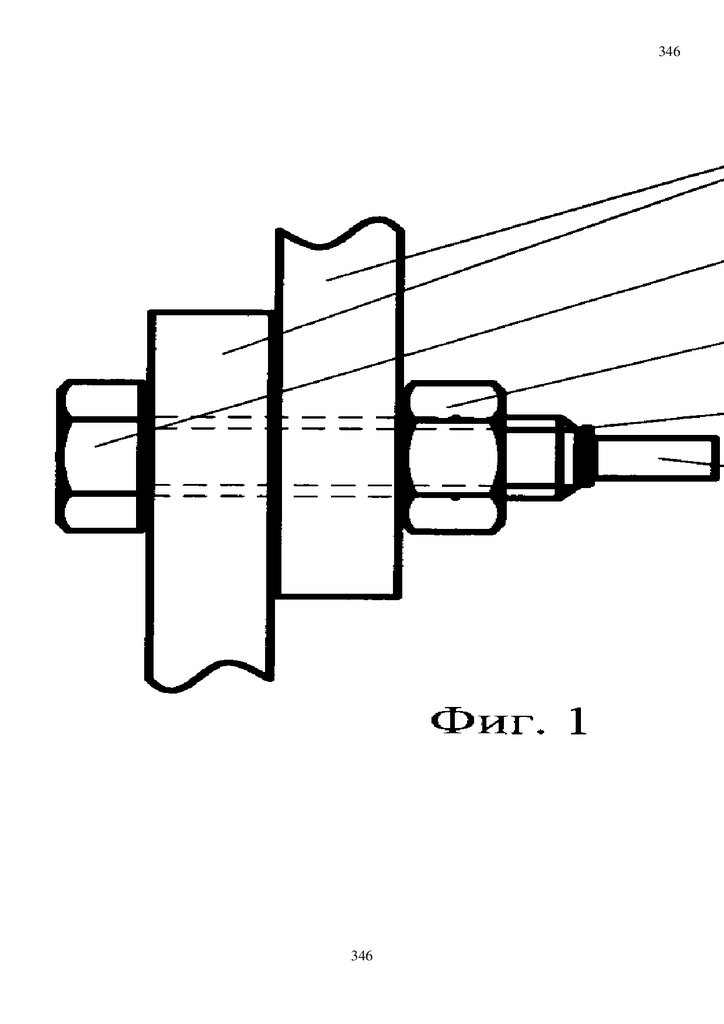
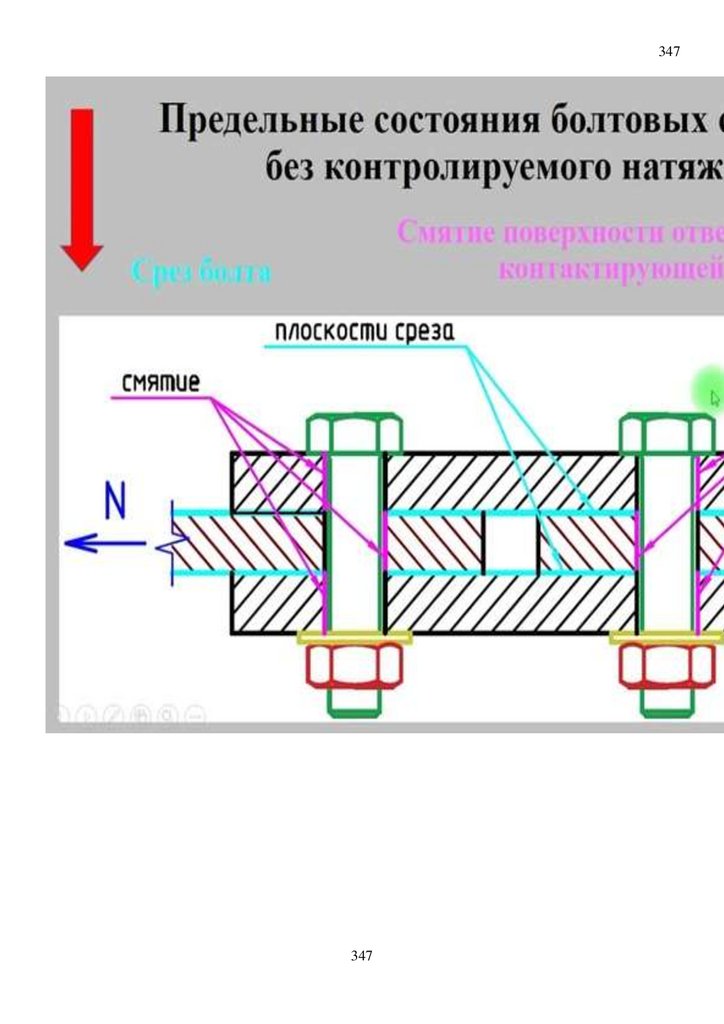
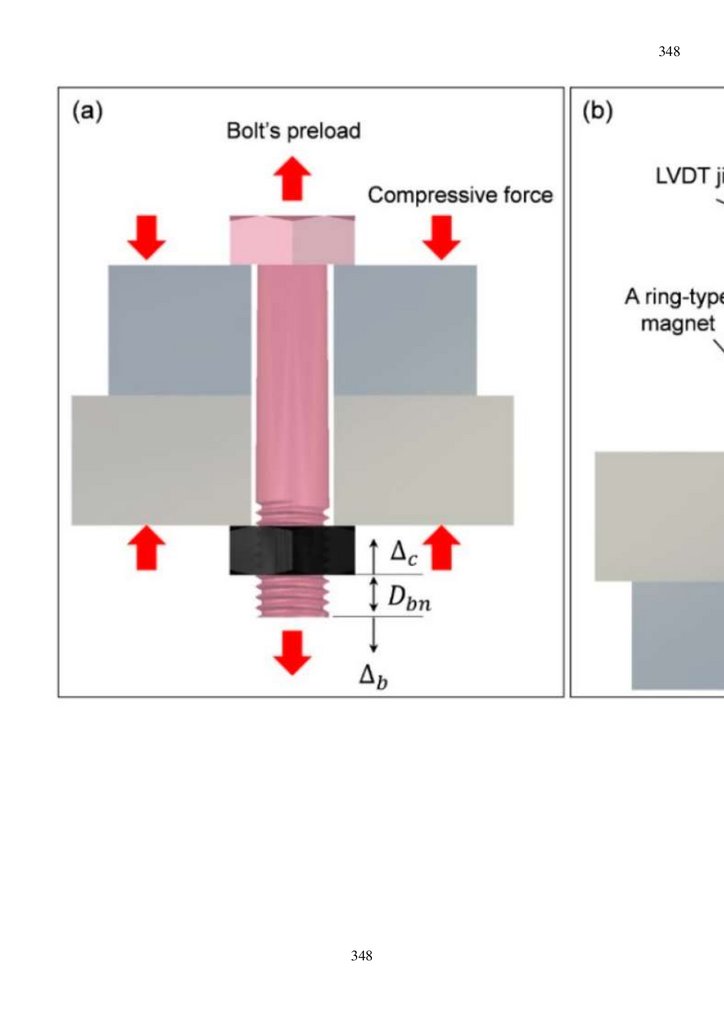
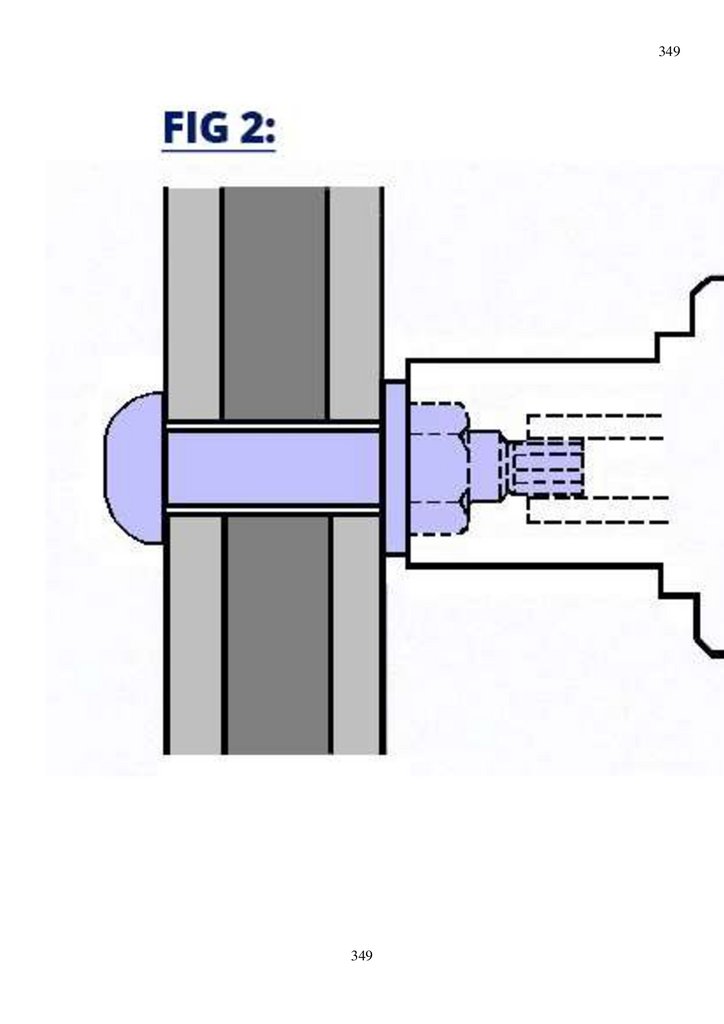
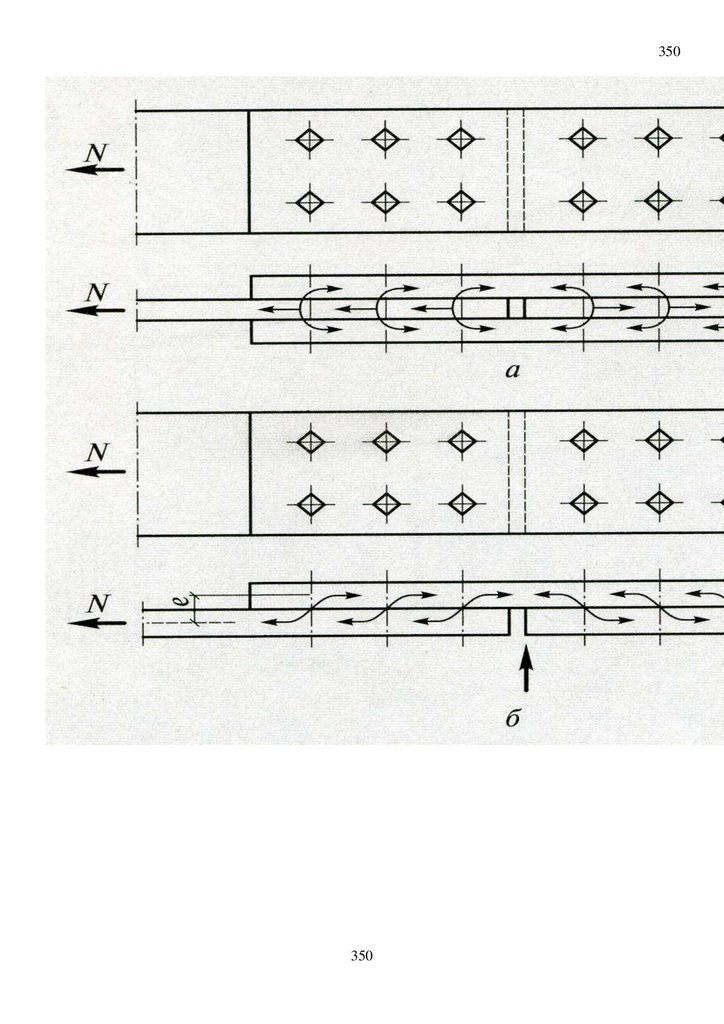
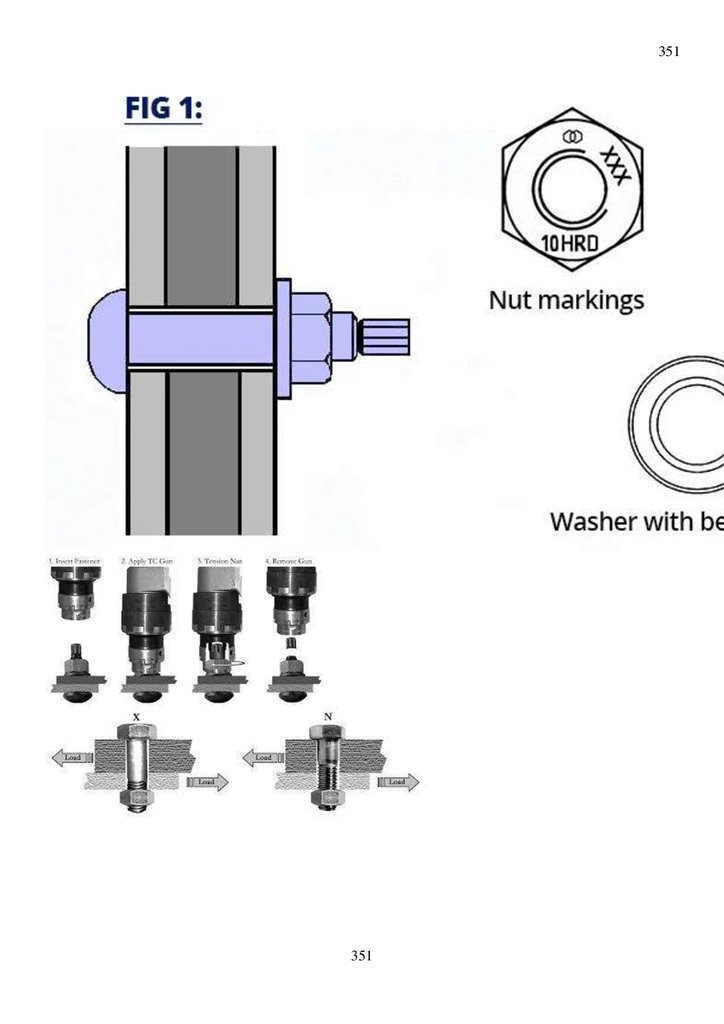




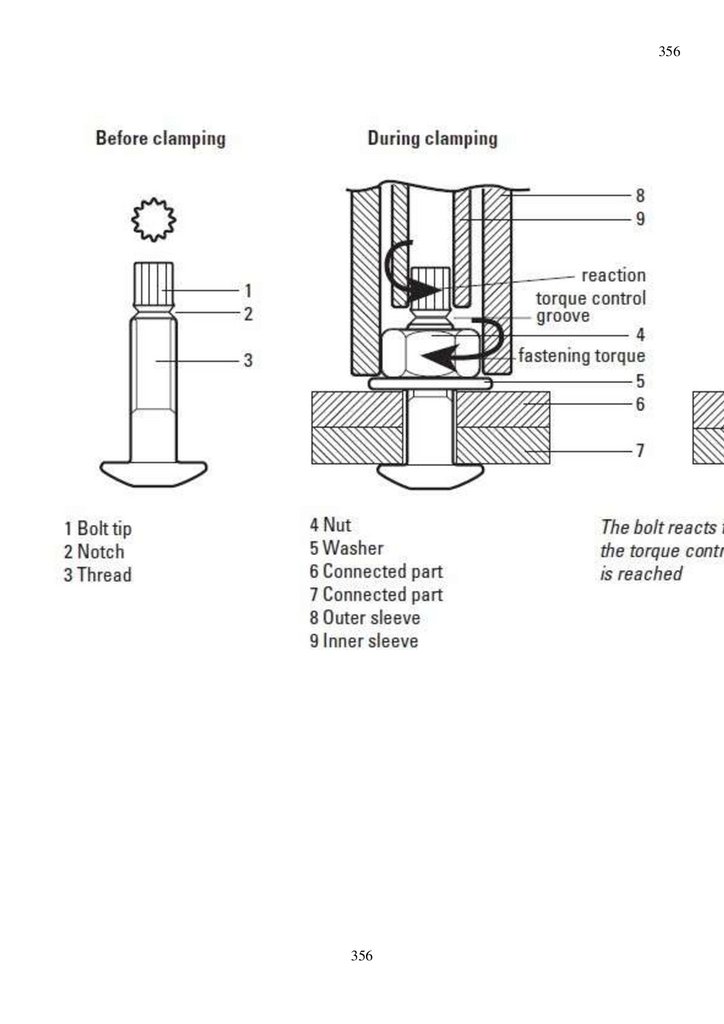
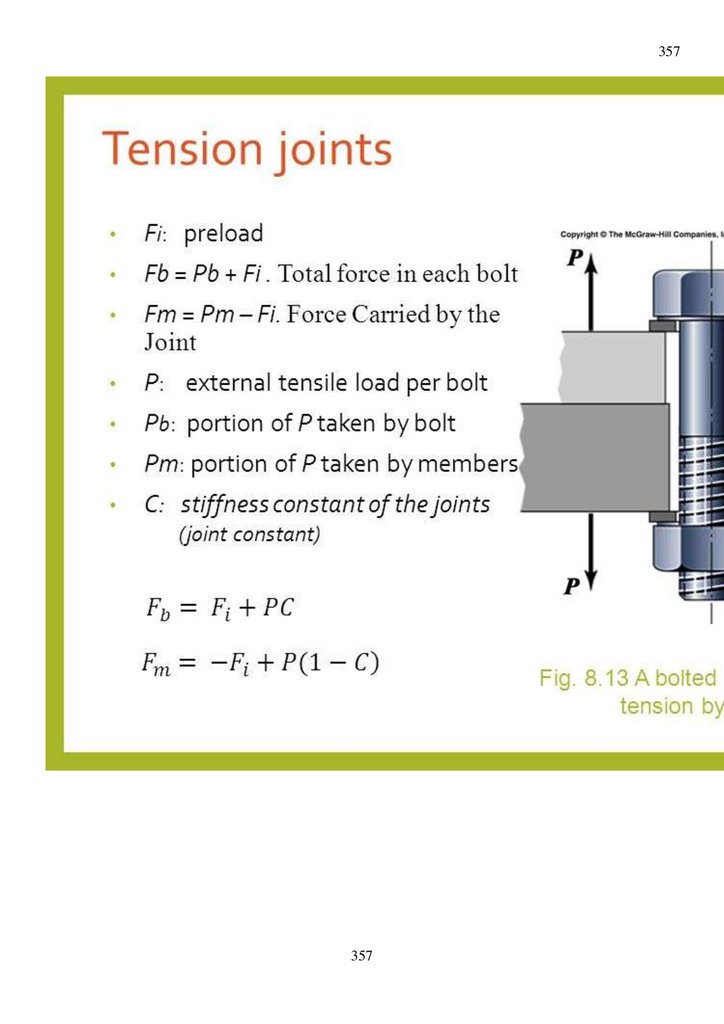

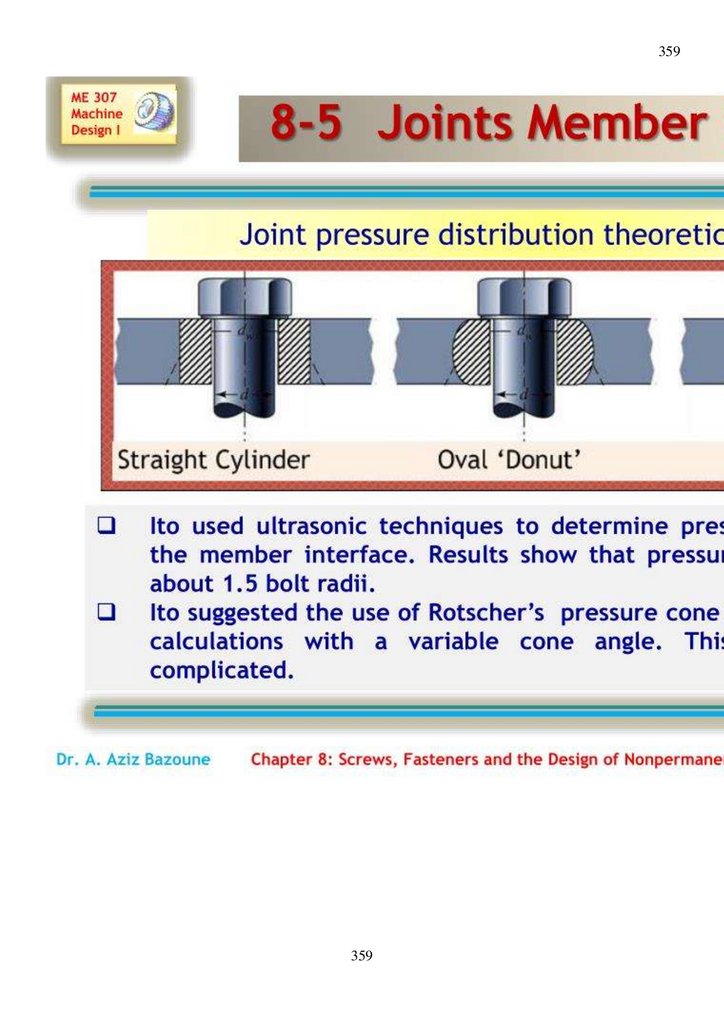
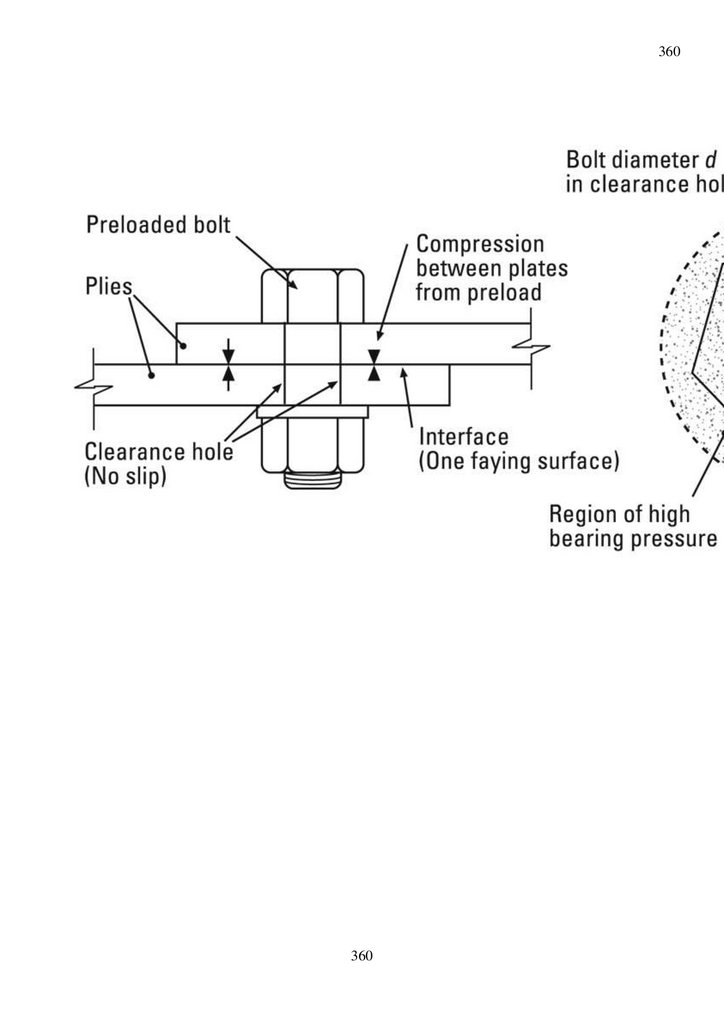

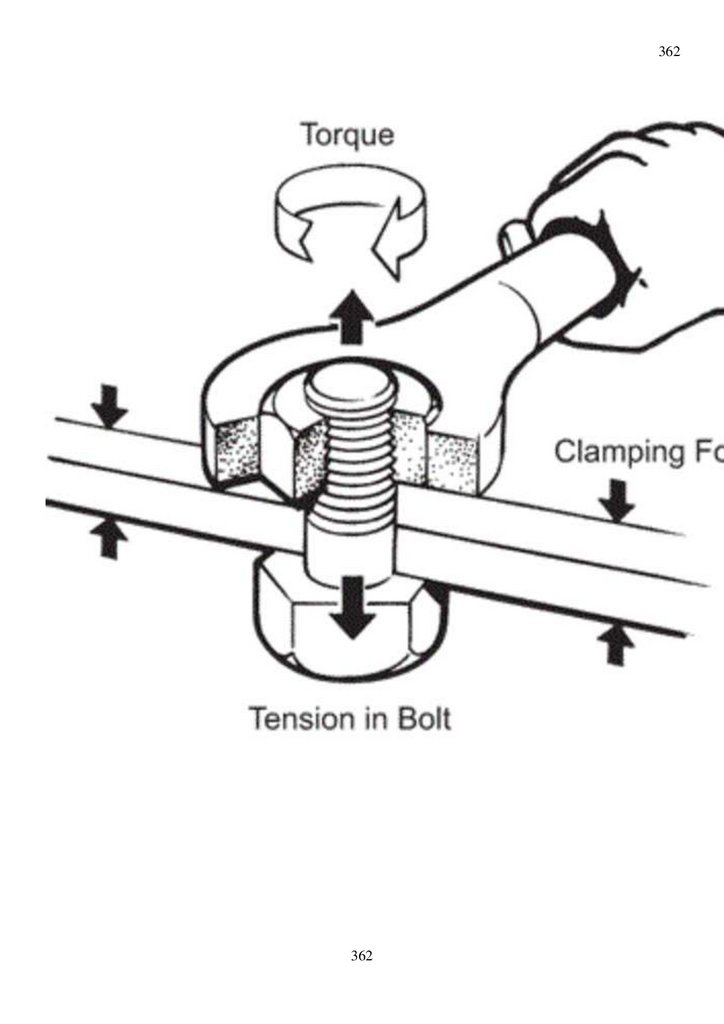
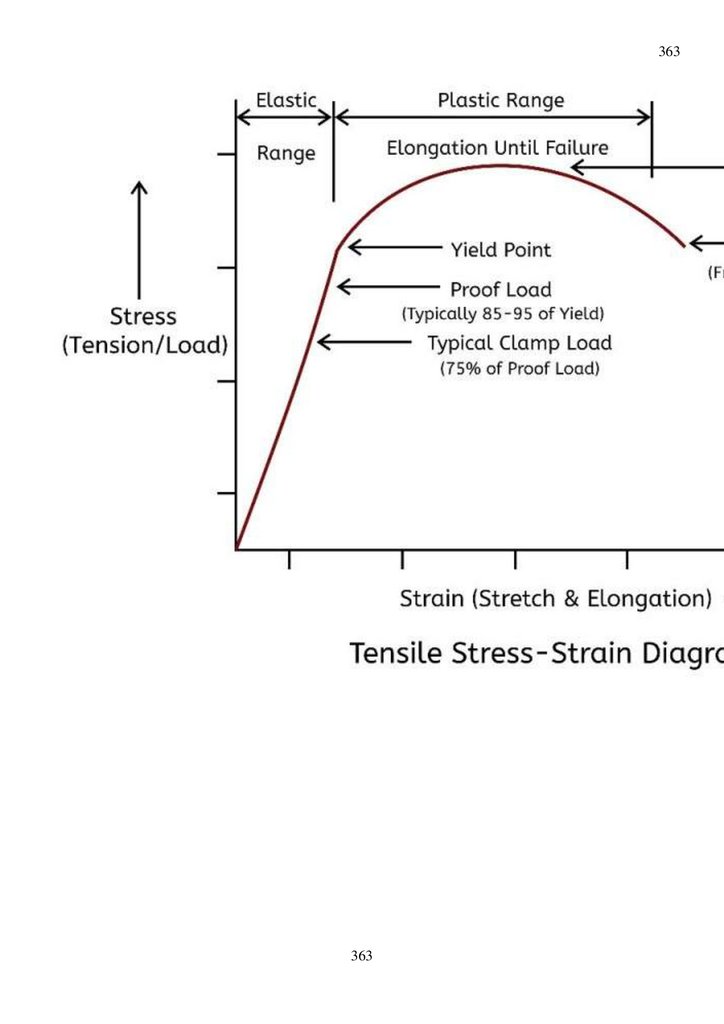
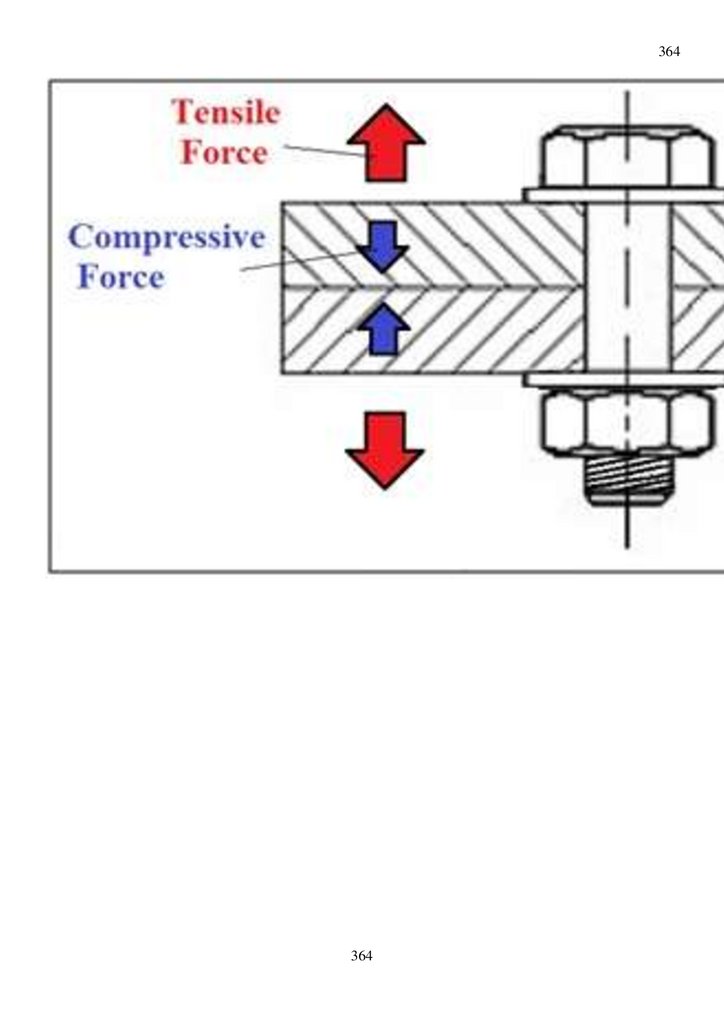
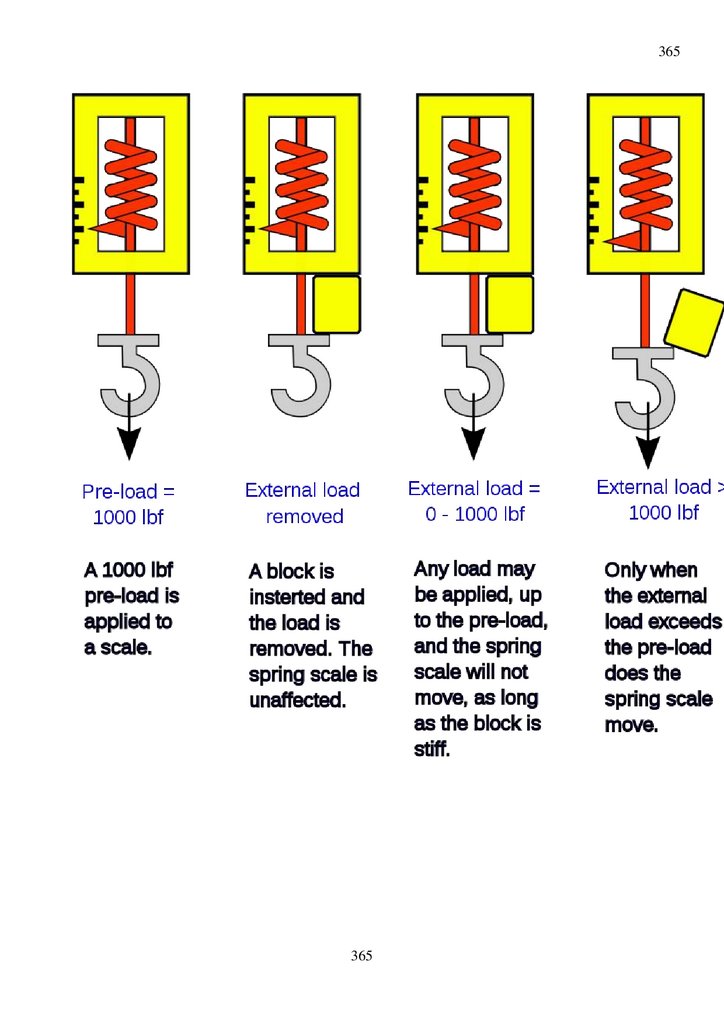
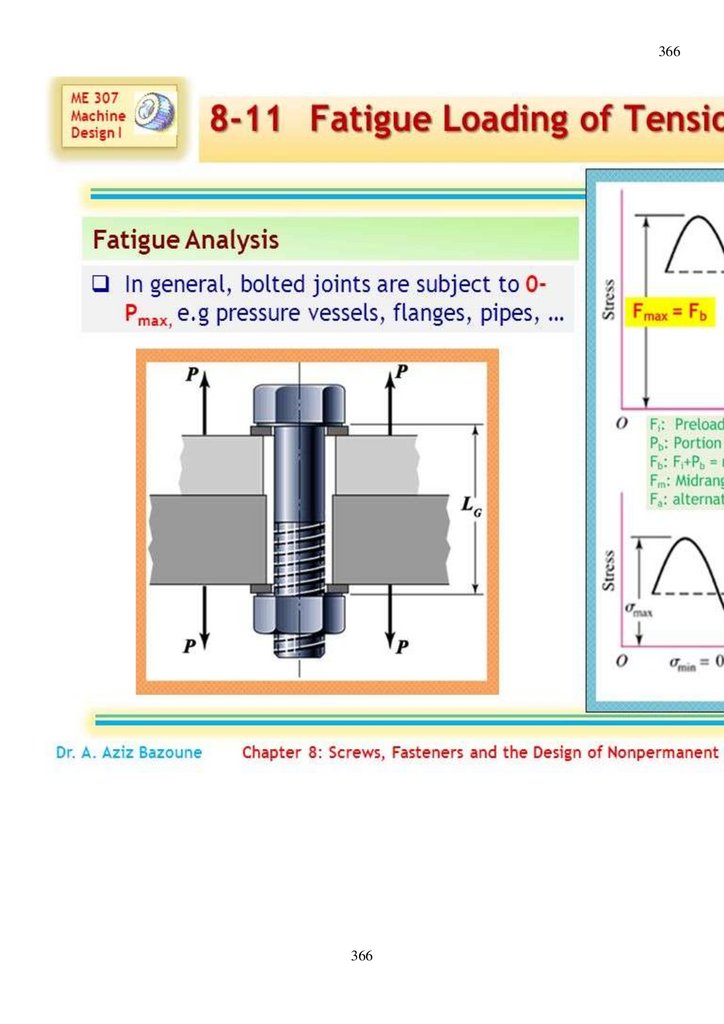


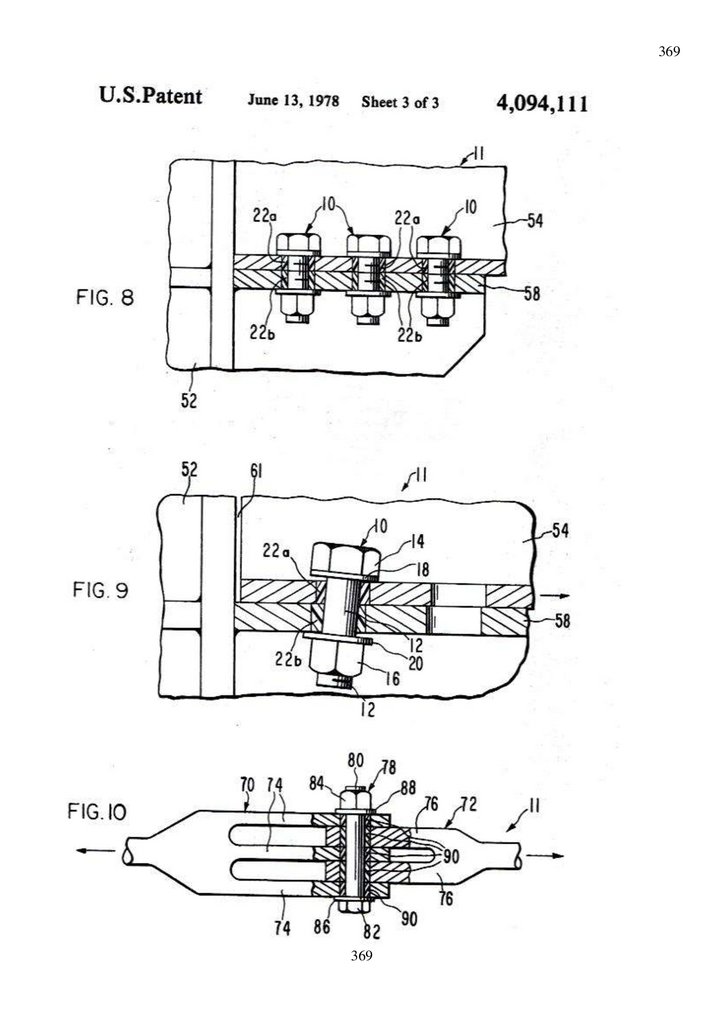
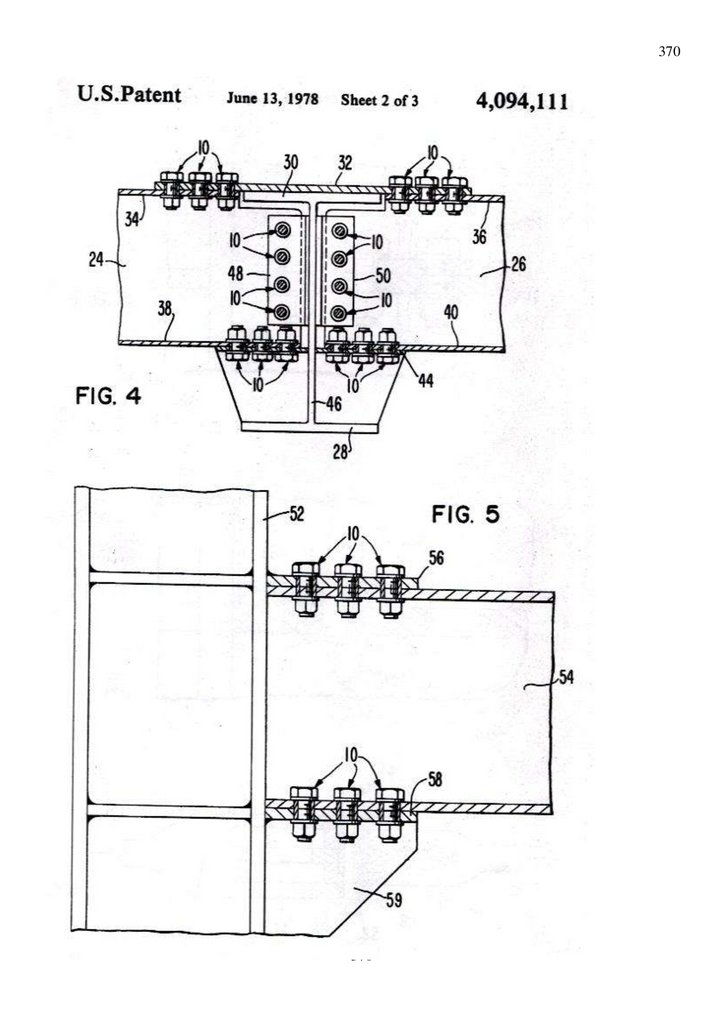
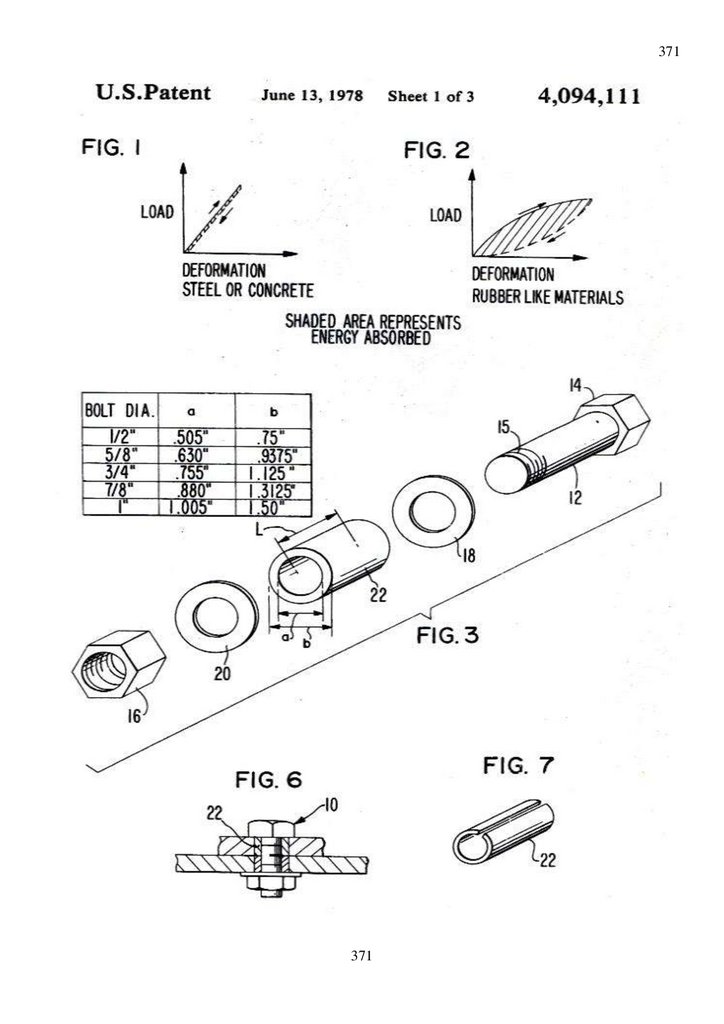
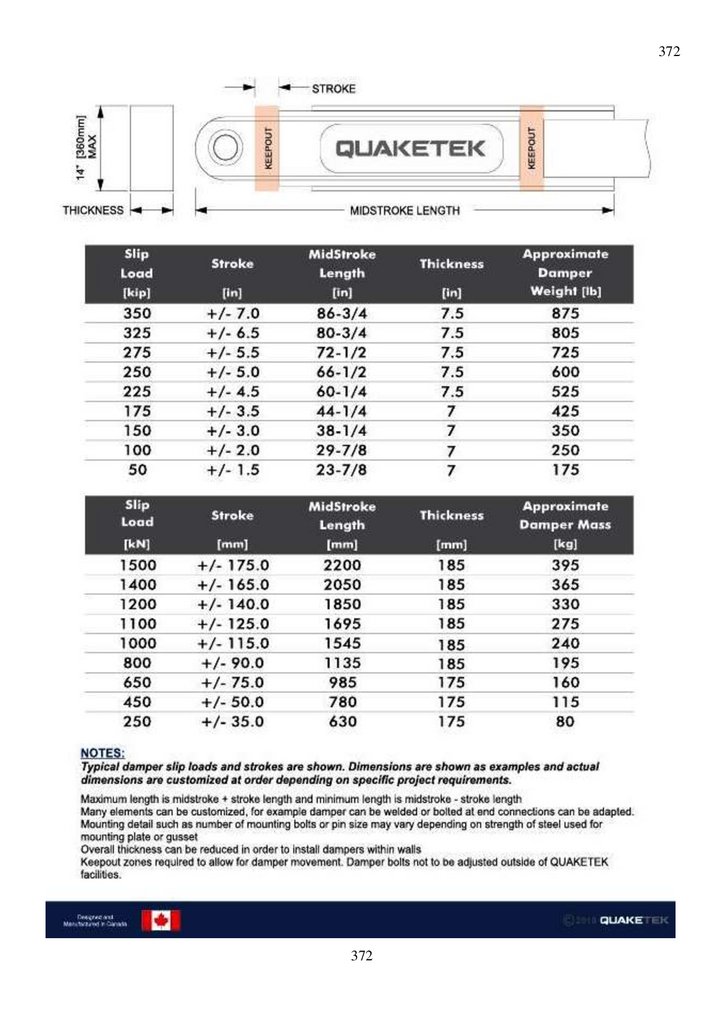







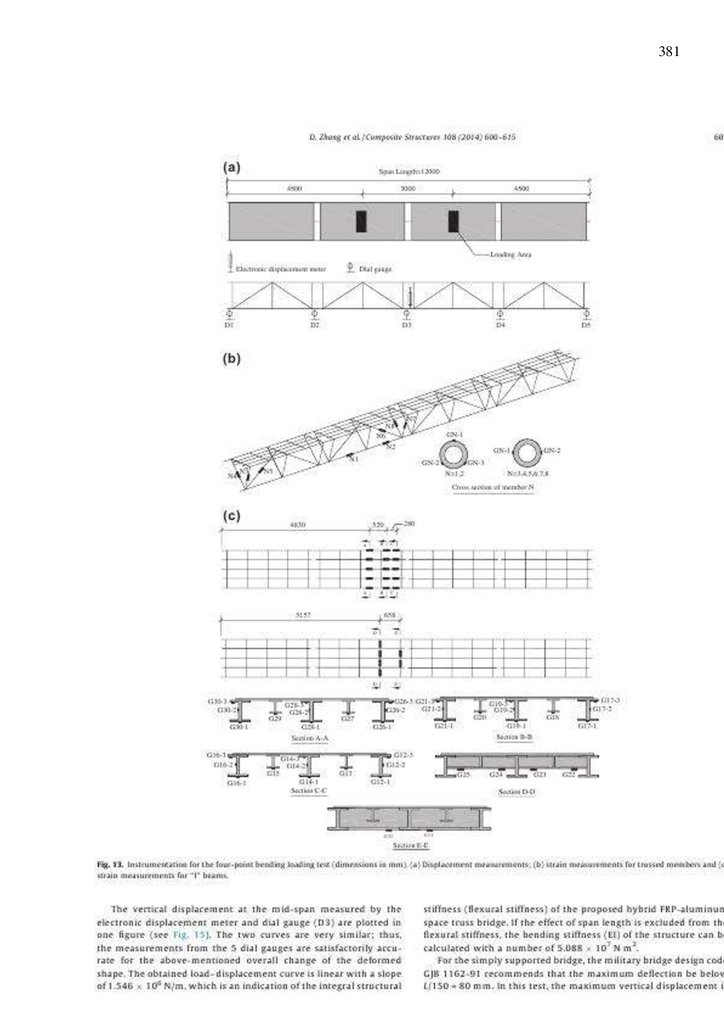
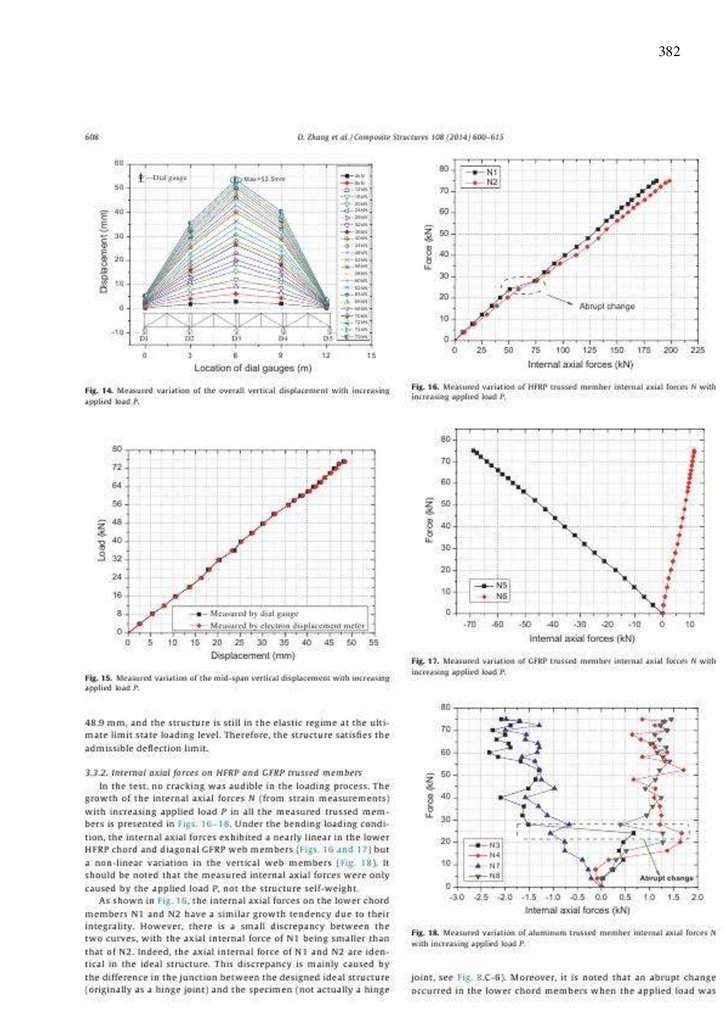



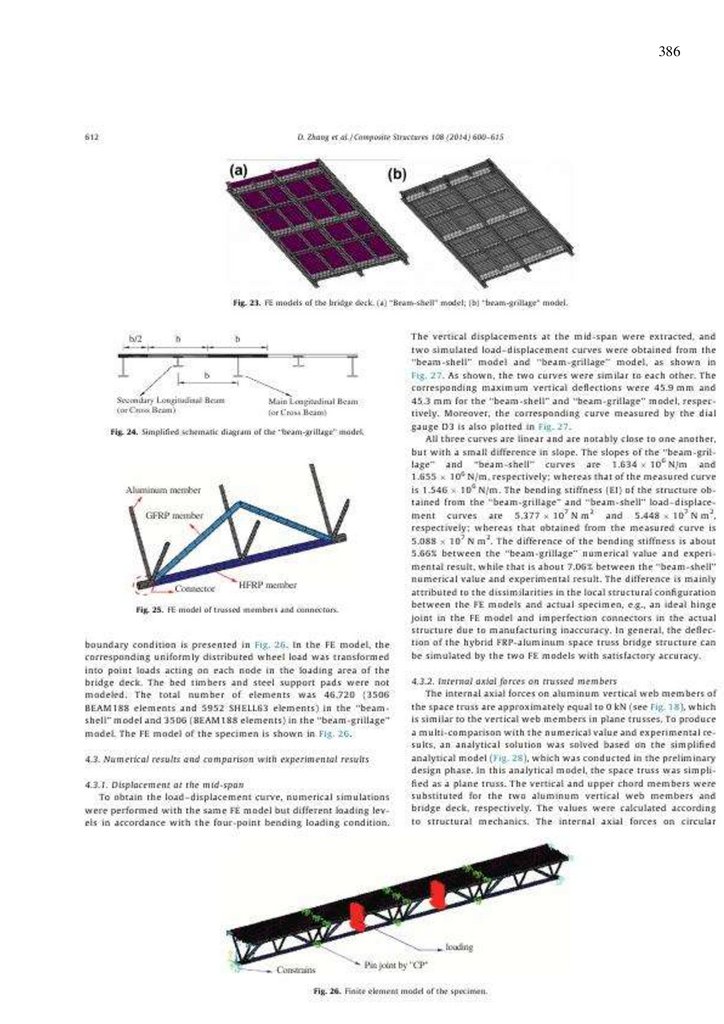
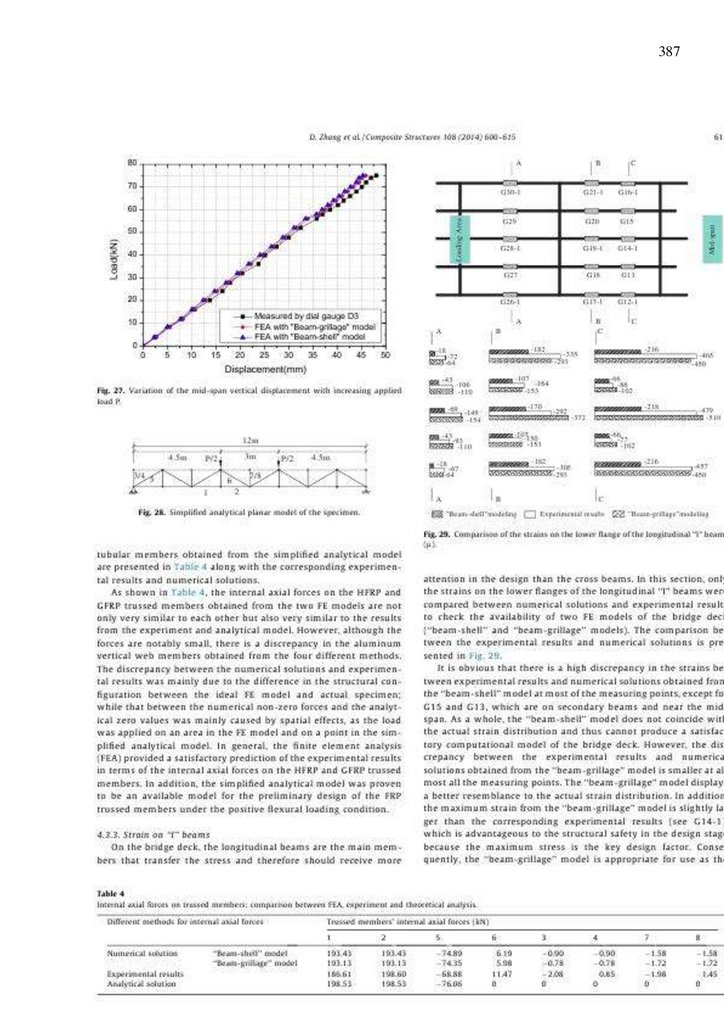




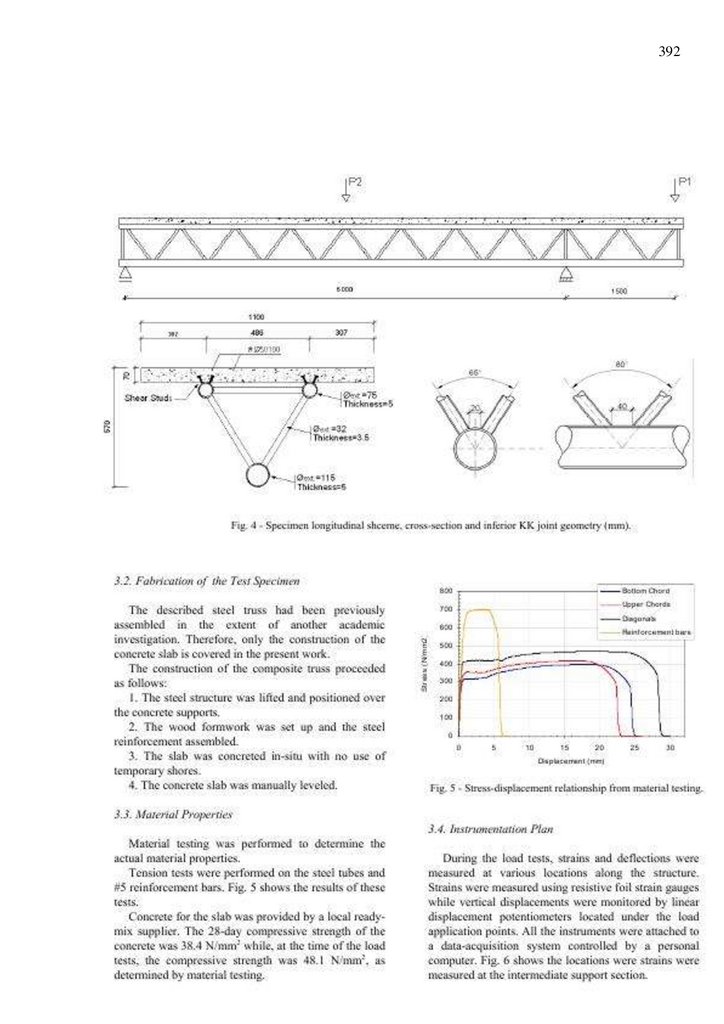

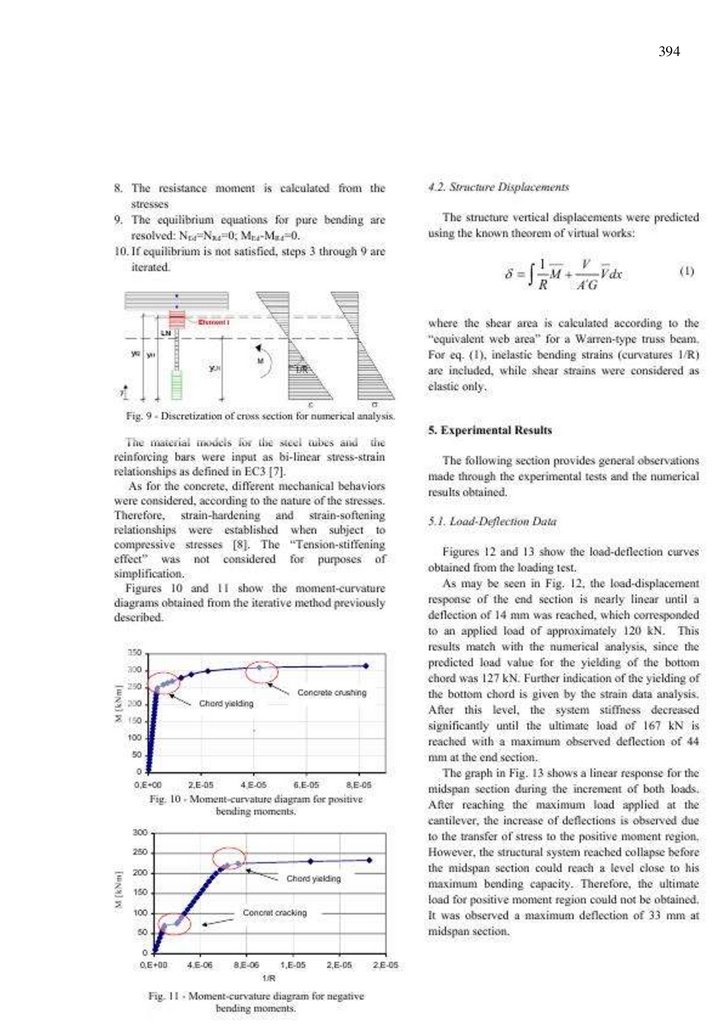
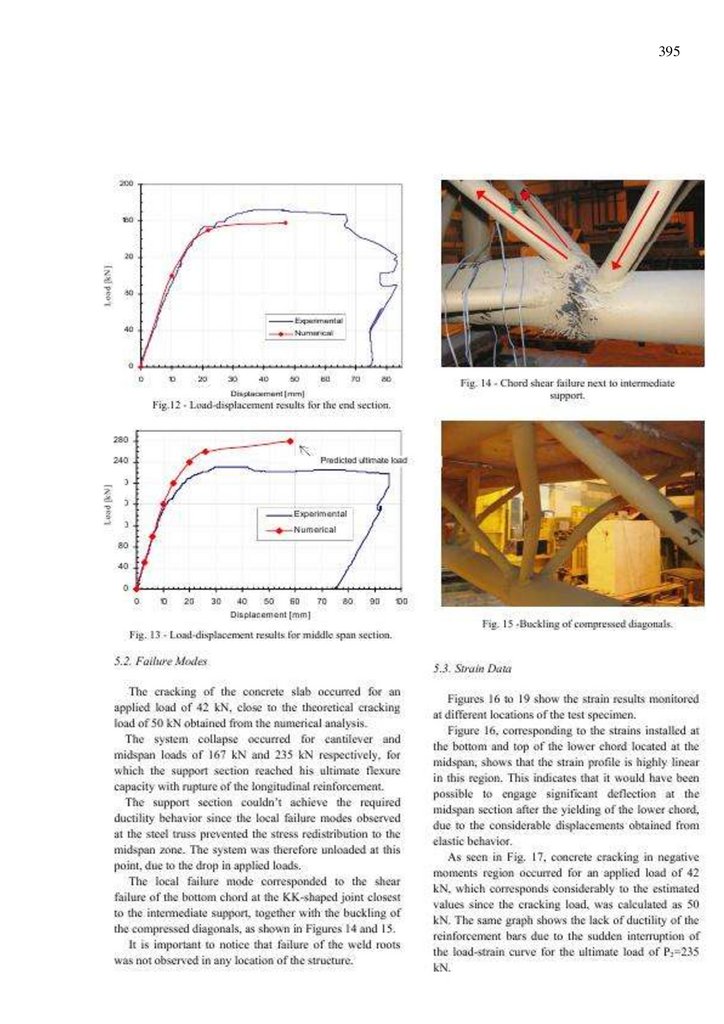
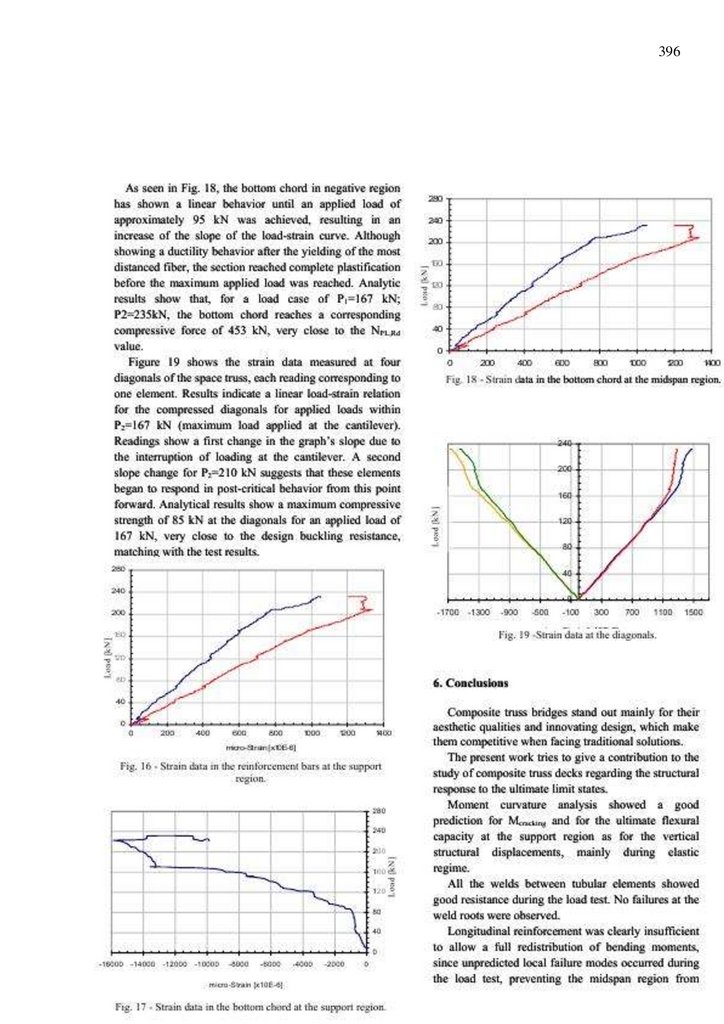








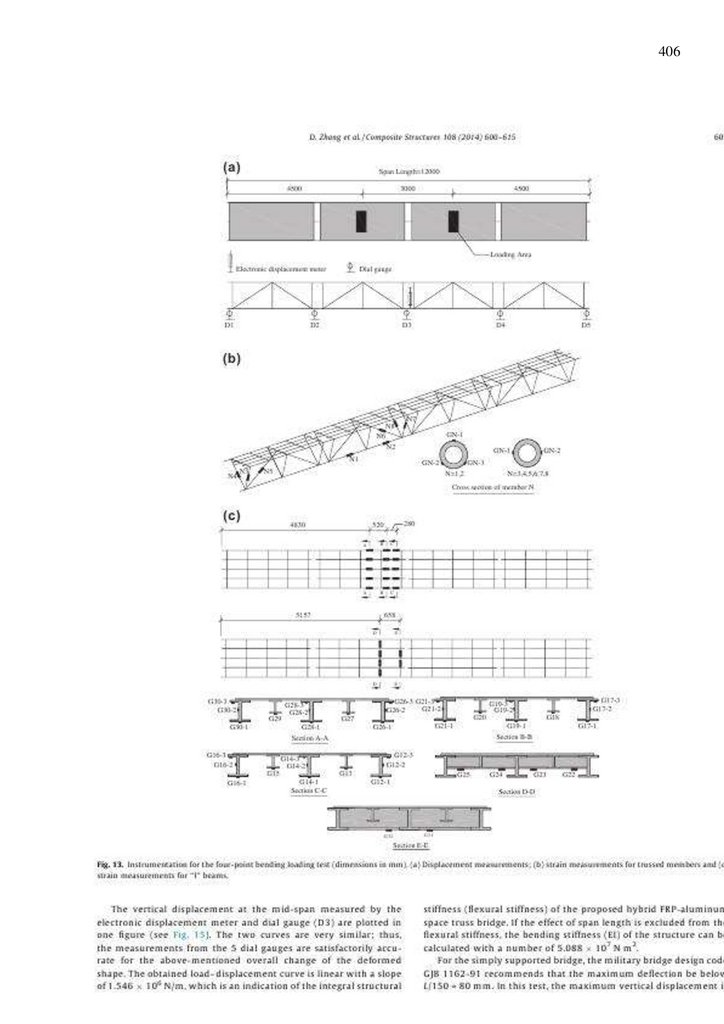
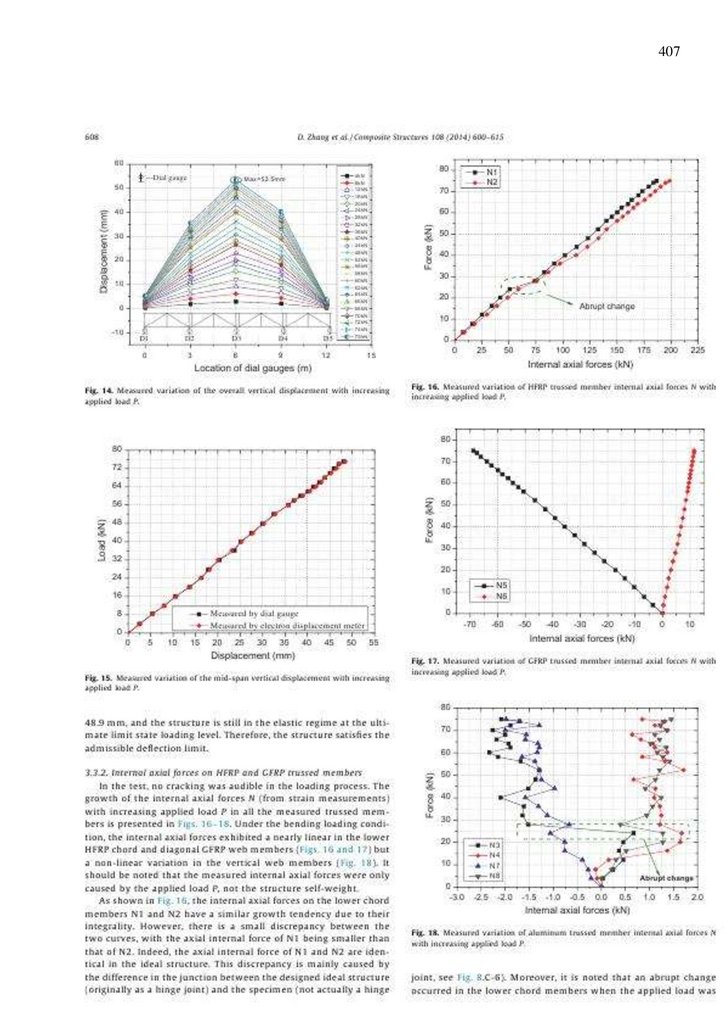



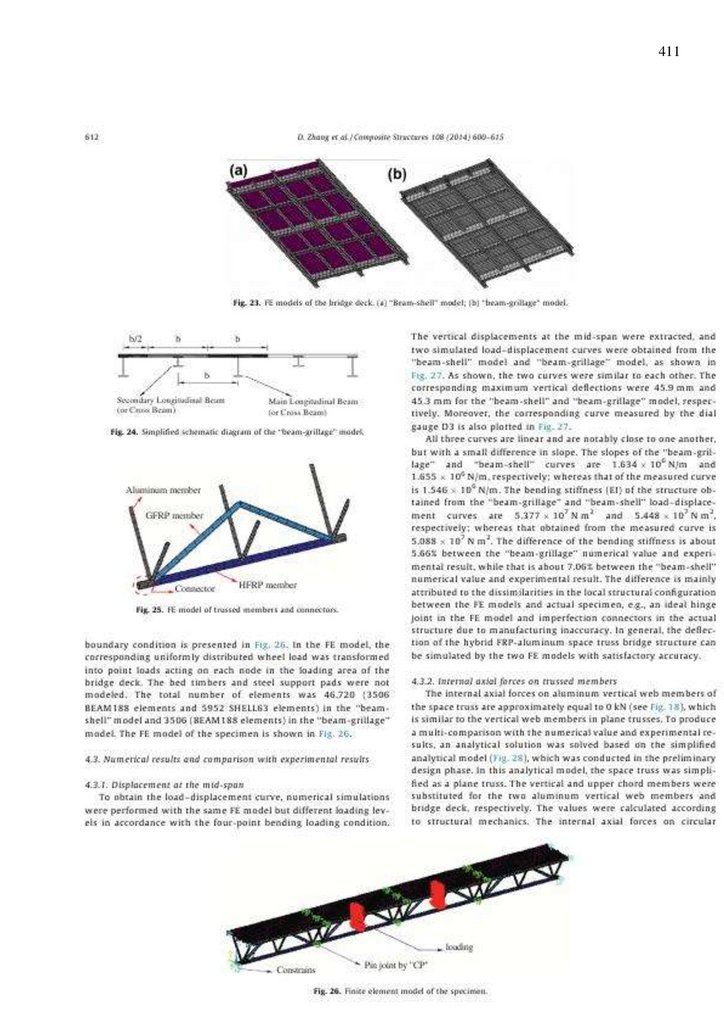
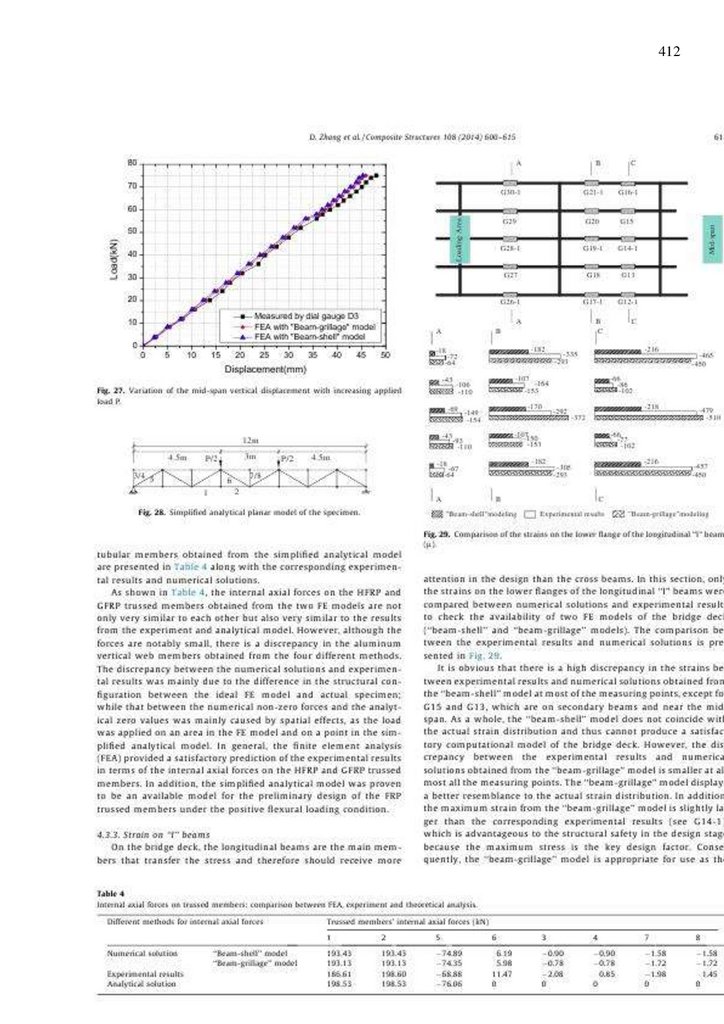




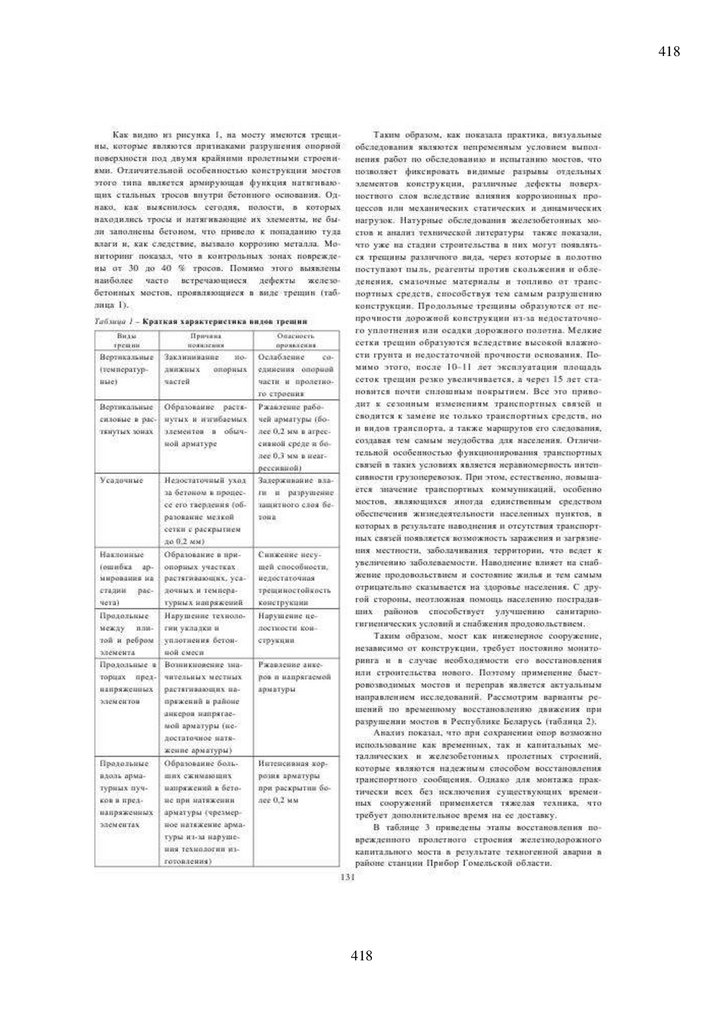


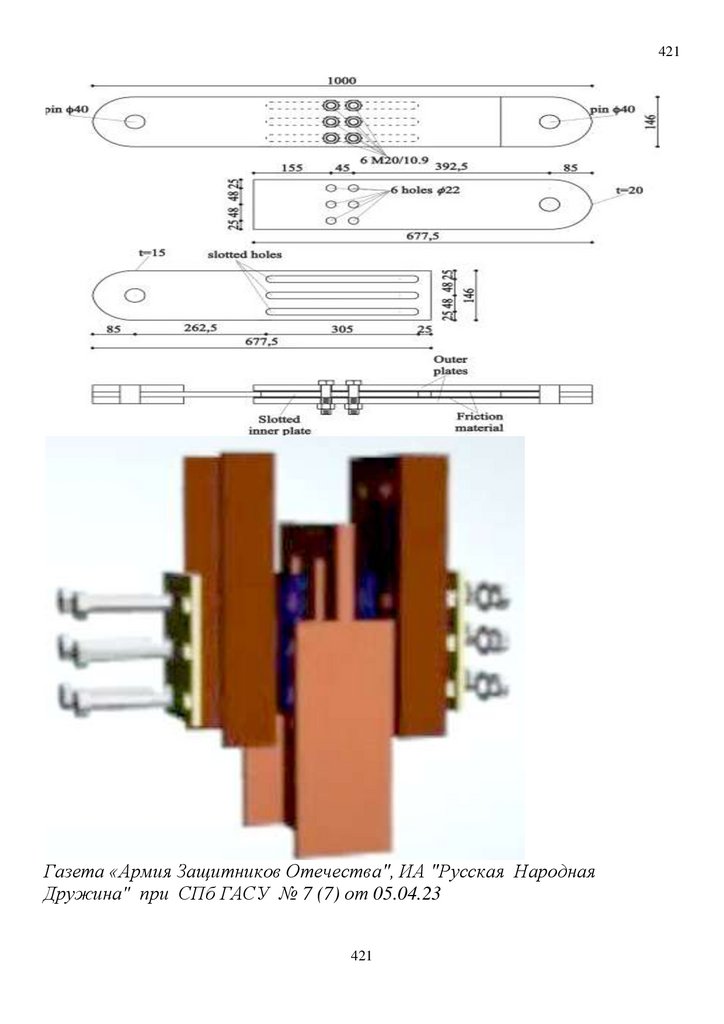

















 Construction
Construction








