Математическое описание детерминированных сигналов

1. ТЕМА 2 МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ДЕТЕРМИНИРОВАННЫХ СИГНАЛОВ

2. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ

Для
изучения
сигналов
необходимо
их
теоретическое описание с помощью моделей.
Одна из форм моделей – математическое описание
сигналов в виде функциональных зависимостей,
аргументом которых является время.
u(t)=U0cos(wt+j)
Другой
формой
может
быть
описание
в
спектральной
области,
когда
аргументом
функции является частота. Соответствие между
временнЫм
и
частотным
представлением
устанавливается
с
помощью
прямого
и
обратного преобразования Фурье.
Cигнал, описываемый одной функцией времени S(t)
- одномерный. Иначе - многомерный

3. ЭНЕРГЕТИЧЕСКИЕ ХАРАКТЕРИСТИКИ СИГНАЛОВ

Основными энергетическими характеристиками
вещественного сигнала s(t) являются его мощность и
энергия.
Мгновенная мощность определяется как квадрат мгновенного
значения s(t):
p (t) = s2(t).
Если s (t) — напряжение или ток, то р (t) есть мгновенная
мощность, выделяемая на сопротивлении в 1 Ом.
Энергия сигнала на интервале t2, t1 определяется как интеграл
от мгновенной мощности:
t2
t2
2
E p (t )dt s (t )dt
Отношение
t1
t1
t2
E
1
2
2
s (t )dt s (t )
t2 t1 t2 t1 t1
имеет смысл средней мощности сигнала на интервале t2 , t1.

4. ЭНЕРГЕТИЧЕСКИЕ ХАРАКТЕРИСТИКИ СИГНАЛОВ

Реальные сигналы имеют конечную
длительность и ограниченную по
величине мгновенную мощность. Энергия
таких сигналов конечна.
В теории сигналов часто рассматриваются
функции времени, заданные на всей оси
времени — < t < при конечной
величине средней мощности.
Говорить об энергии подобных сигналов,
обращающейся в бесконечно большую
величину, не имеет смысла.

5. ДИНАМИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ СИГНАЛОВ

Принцип динамического представления: реальный сигнал S(t)
приближенно описывается суммой некоторых элементарных
сигналов dn(t), возникающих в последовательные моменты
времени. Если длительность сигналов dn(t) -> 0, то получим в
пределе точное представление сигнала S(t).
2 способа представления: 1) dn(t) - ступенчатые функции (а); 2) dn(t) прямоугольные импульсы (б).
dn(t)
S(t)
S(t)
Sn
S2
d1(t)
S1
а
tn
S1
Sn
б
d1(t)
d0(t)
t
S0
0
t
2 t
n t
t
dn(t)
0
t1
tn = n t
t

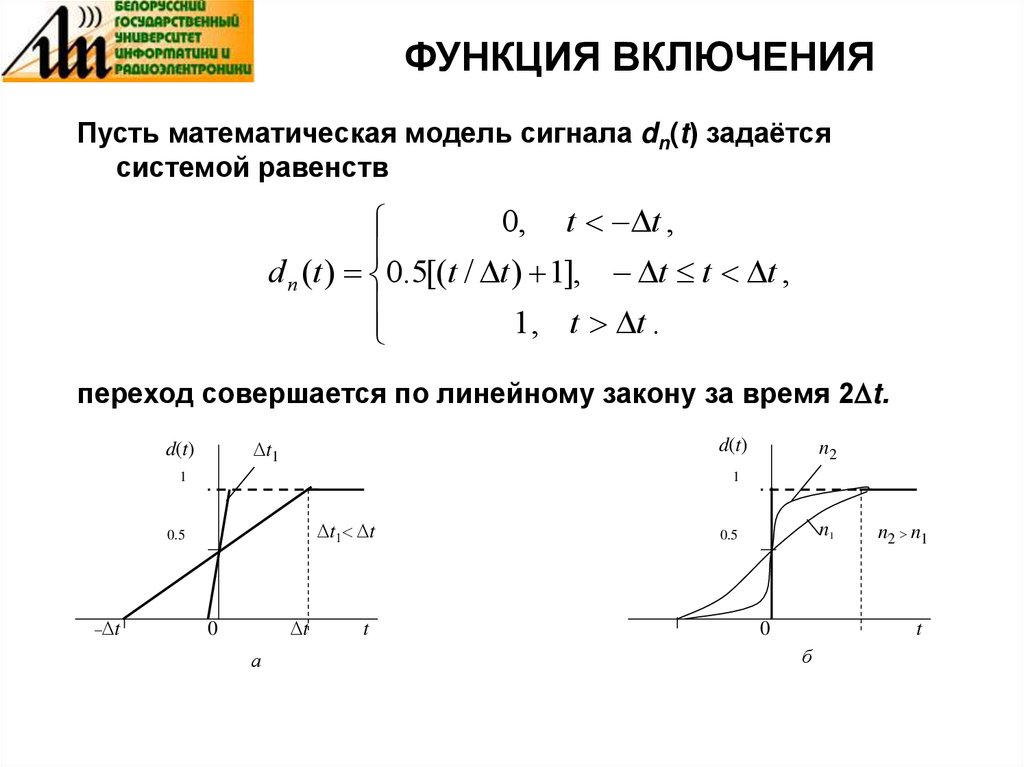
6. ФУНКЦИЯ ВКЛЮЧЕНИЯ

Пусть математическая модель сигнала dn(t) задаётся
системой равенств
0, t t ,
d n (t ) 0.5[(t / t ) 1], t t t ,
1, t t .
переход совершается по линейному закону за время 2 t.
t1
d(t)
d(t)
1
1
t1 t
0.5
– t
n2
t
0
а
t
n1
0.5
0
n2 n1
t
б

7. ФУНКЦИЯ ВКЛЮЧЕНИЯ

Пусть математическая модель сигнала dn(t) задаётся
системой равенств
0, t t ,
d n (t ) 0.5[(t / t ) 1], t t t ,
1, t t .
переход совершается по линейному закону за время 2 t.
t1
d(t)
1
t1 t
0.5
– t
0
а
t
d(t)
1
n2
0.5
n1
t
0
б
Другой вариант определения функции (рис. б):
1
d n (t )
1 exp( nt )
n2 n1
t

8. ФУНКЦИЯ ВКЛЮЧЕНИЯ

Если t устремить к нулю, то в пределе переход будет
совершаться мгновенно. Математическая модель этого
предельного сигнала g(t) - функция включения, или
функция Хевисайда, или единичный скачок:
0, t 0 ,
g (t ) 0.5, t 0 ,
1, t 0 .
С помощью функции включения g(t) удобно описывать, в
частности импульсные сигналы, а также разнообразные
процессы коммутации в электрических цепях.
В общем случае функция включения может быть смещена
относительно начала отсчёта времени на значение t0:
0, t t0 ,
g (t t0 ) 0.5, t t0 ,
1, t t .
0

9. ФУНКЦИЯ ВКЛЮЧЕНИЯ

Пример: сигнал S(t)=0 при t=0 и изменяется по закону S(t)=At2
при t>0 (парабола). Запишем динамическое представление
этого сигнала с помощью функций Хевисайда g(t).
Так как S0 = 0, а ds / d = 2A ,
S (t ) 2 A g (t )d
0
Смысл этой формулы в том, что высота элементарных
ступенек, из которых складывается сигнал, линейно
нарастает во времени.

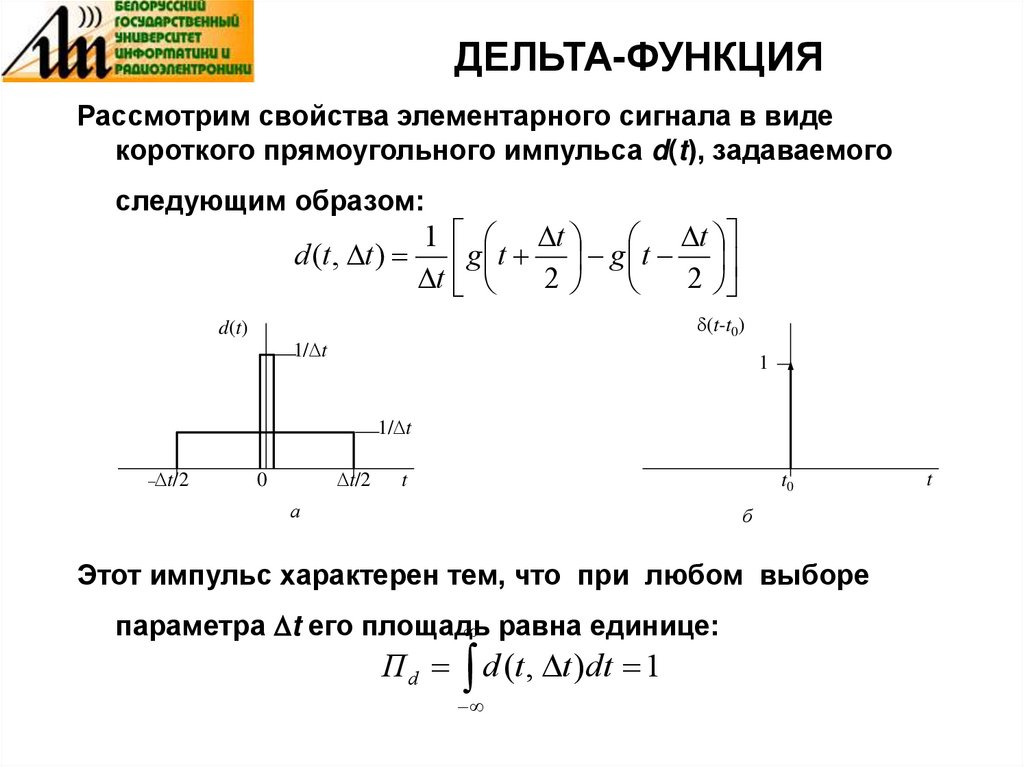
10. ДЕЛЬТА-ФУНКЦИЯ

Рассмотрим свойства элементарного сигнала в виде
короткого прямоугольного импульса d(t), задаваемого
следующим образом:
d (t , t )
1 t t
g t g t
t
2
2
(t-t0)
d(t)
1/ t
1
1/ t
– t/2
t/2
0
t
t0
а
б
Этот импульс характерен тем, что при любом выборе
параметра t его площадь
равна единице:
П d d (t , t )dt 1
t

11. ДЕЛЬТА-ФУНКЦИЯ

Например, если S(t) – напряжение, то Пd = 1 В с. Пусть t 0
Импульс, сокращаясь по длительности, сохраняет свою
площадь, поэтому его высота должна неограниченно
возрастать. Предел такой функции при t 0 носит
название дельта-функции или функции Дирака:
(t ) lim t 0 d (t , t )
Дельта-функция равна нулю всюду, за исключением точки t =
=0 (сосредоточена в этой точке), и обладает единичным
интегралом:
(t )dt 1
Дельта-функция - математическая модель короткого воздействия единичного импульса (площадь=1), смещённого от начала
отсчёта времени на значение t0, и записывается как
(t t0 )
Физическая размерность дельта-функции - размерность частоты.

12. ДЕЛЬТА-ФУНКЦИЯ

Рассмотрим аналоговый сигнала S(t), представляемый
суммой примыкающих друг к другу прямоугольных
импульсов. Если Sn – значение сигнала на n-м отсчёте, то
элементарный импульс с номером n представляется так:
dn (t ) = Sn[ (t tn ) (t tn t )]
По принципу динамического представления исходный сигнал
S(t) должен рассматриваться как сумма таких
элементарных слагаемых:
S (t ) d n (t )
n
Если перейти к пределу при t 0 (интегрированию по
формальной переменной = n t), получим формулу
динамического представления сигнала
S (t ) S ( ) (t )d

13. ДЕЛЬТА-ФУНКЦИЯ

• Если непрерывную функцию S(t) умножить на
дельта-функцию и произведение
проинтегрировать по времени, то результат
будет равен значению непрерывной функции
S(t = tn) в точке tn = n t, где сосредоточен импульс. В этом состоит фильтрующее свойство
дельта-функции.
S (t ) S ( ) (t )d

14. РАЗЛОЖЕНИЕ ФУНКЦИИ В РЯД ПО ОРТОГОНАЛЬНОЙ СИСТЕМЕ ФУНКЦИЙ

Для теории сигналов и их обработки важное значение имеет
разложение заданной функции f(х) по различным
ортогональным системам функций jn(х).
Бесконечная система действительных функций
j0 ( x), j1 ( x), j2 ( x),...jn ( x),....
называется ортогональной на отрезке [а, b], если
При этом
Т.е. никакая из функций рассматриваемой системы не равна
тождественно нулю.

15. РАЗЛОЖЕНИЕ ФУНКЦИИ В РЯД ПО ОРТОГОНАЛЬНОЙ СИСТЕМЕ ФУНКЦИЙ

Если выполняется условие
то функция jn(x) называется нормированной функцией, а система
ортогональных функций
j0 ( x), j1 ( x), j2 ( x),...jn ( x),....
называется ортонормированной.
Величина
называется нормой функции jn(x).

16. РАЗЛОЖЕНИЕ ФУНКЦИИ В РЯД ПО ОРТОГОНАЛЬНОЙ СИСТЕМЕ ФУНКЦИЙ

В математике доказывается, что если функции jn(x) непрерывны,
то произвольная кусочно-непрерывная функция f (x), для которой
выполняется условие
может быть представлена в виде суммы ряда
при этом коэффициенты сn определяются как
Такой ряд называется обобщенным рядом Фурье по данной системе
функций. Набор коэффициентов сn называется спектром сигнала
f(x) в данной системе функций и полностью определяет этот
сигнал.

17. СПЕКТР

Выше понятие спектра было дано как набор
коэффициентов сn. В более широком
смысле спектр (от лат. spectrum –
представление, образ, призрак) –
совокупность всех значений какой-либо
величины, характеризующей систему или
процесс. Чаще всего пользуются
понятием частотного спектра колебаний
(электромагнитных или акустических),
либо энергетического спектра (может
быть связан с частотным, поскольку
Е= ћw).

18. РЯД ФУРЬЕ В КОМПЛЕКСНОЙ ФОРМЕ

Если функции jn(x) принимают комплексные значения, то условие
ортогональности
Квадрат нормы функции
Коэффициенты Фурье
j*n(x) - функция, комплексно-сопряженная функции jn(x).

19. РЯД ФУРЬЕ ДЛЯ ФУНКЦИЙ ВРЕМЕНИ

Для функции времени s(t) ряд будем записывать в форме
Квадрат нормы функции
Таким образом, энергия сигнала
а при использовании ортонормированной системы функций

20. ВЫБОР ОРТОГОНАЛЬНОЙ СИСТЕМЫ ФУНКЦИЙ

Если задачей является точное разложение на
простейшие ортогональные функции, то
наибольшее распространение получила
ортогональная система основных
тригонометрических функций — синусов и
косинусов.
Причины:
1) гармоническое колебание - единственная функция
времени, сохраняющая свою форму при
прохождении через любую линейную цепь (с
постоянными параметрами). Изменяются лишь
амплитуда и фаза колебания.
2) Разложение сложного сигнала по синусам и
косинусам позволяет использовать
символический метод, разработанный для
анализа передачи гармонических колебаний через
линейные цепи.

21. ГАРМОНИЧЕСКИЙ АНАЛИЗ ПЕРИОДИЧЕСКИХ СИГНАЛОВ

При разложении в ряд Фурье периодического сигнала s(t) с периодом
Т по тригонометрическим функциям в качестве ортогональной
системы берут
либо
В первом случае получают ряд Фурье в тригонометрической форме,
во втором – в комплексной. Между ними есть простая связь.
Интервал ортогональности в обоих случаях равен периоду T=2p/w1
функции s(t).
Ряд Фурье в комплексной форме:
Совокупность коэффициентов сn называется частотным спектром
периодического сигнала.

22. ГАРМОНИЧЕСКИЙ АНАЛИЗ ПЕРИОДИЧЕСКИХ СИГНАЛОВ

Определим коэффициенты сn.
Таким образом,
Тогда коэффициенты ряда
Поскольку
получим
Т.е. коэффициенты сn имеют действительную (косинусную) часть сnс и
мнимую (синусную) часть сns .

23. ГАРМОНИЧЕСКИЙ АНАЛИЗ ПЕРИОДИЧЕСКИХ СИГНАЛОВ

Коэффициенты сn часто удобно записывать в виде
где
четная ф-ция отн. n
нечетная ф-ция отн. n.
Тогда ряд Фурье можно представить как
Если выделить из ряда пару слагаемых для заданного n (n=2) и
учесть, что
получим

24. ГАРМОНИЧЕСКИЙ АНАЛИЗ ПЕРИОДИЧЕСКИХ СИГНАЛОВ

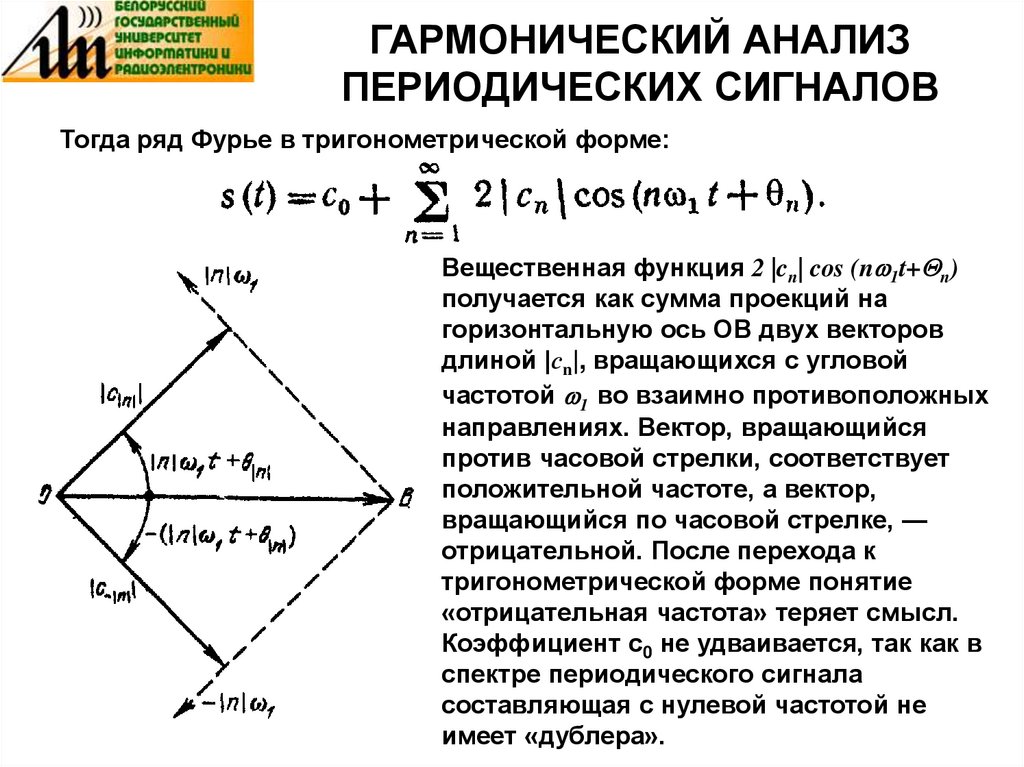
Тогда ряд Фурье в тригонометрической форме:
Вещественная функция 2 |cn| cos (nw1t+Qn)
получается как сумма проекций на
горизонтальную ось ОВ двух векторов
длиной |сn|, вращающихся с угловой
частотой w1 во взаимно противоположных
направлениях. Вектор, вращающийся
против часовой стрелки, соответствует
положительной частоте, а вектор,
вращающийся по часовой стрелке, —
отрицательной. После перехода к
тригонометрической форме понятие
«отрицательная частота» теряет смысл.
Коэффициент с0 не удваивается, так как в
спектре периодического сигнала
составляющая с нулевой частотой не
имеет «дублера».

25. ГАРМОНИЧЕСКИЙ АНАЛИЗ ПЕРИОДИЧЕСКИХ СИГНАЛОВ

Часто встречается другая форма записи выражения для ряда Фурье:
Амплитуда n-й гармоники Аn связана с коэффициентом |сn|
соотношением:
Таким образом, для всех n ≥ 0
Если сигнал – четная функция времени – в тригонометрической
записи остаются только косинусоидальные члены (bn=0), в
противном случае – только синусоидальные (an=0).

26. ГАРМОНИЧЕСКИЙ АНАЛИЗ ПЕРИОДИЧЕСКИХ СИГНАЛОВ

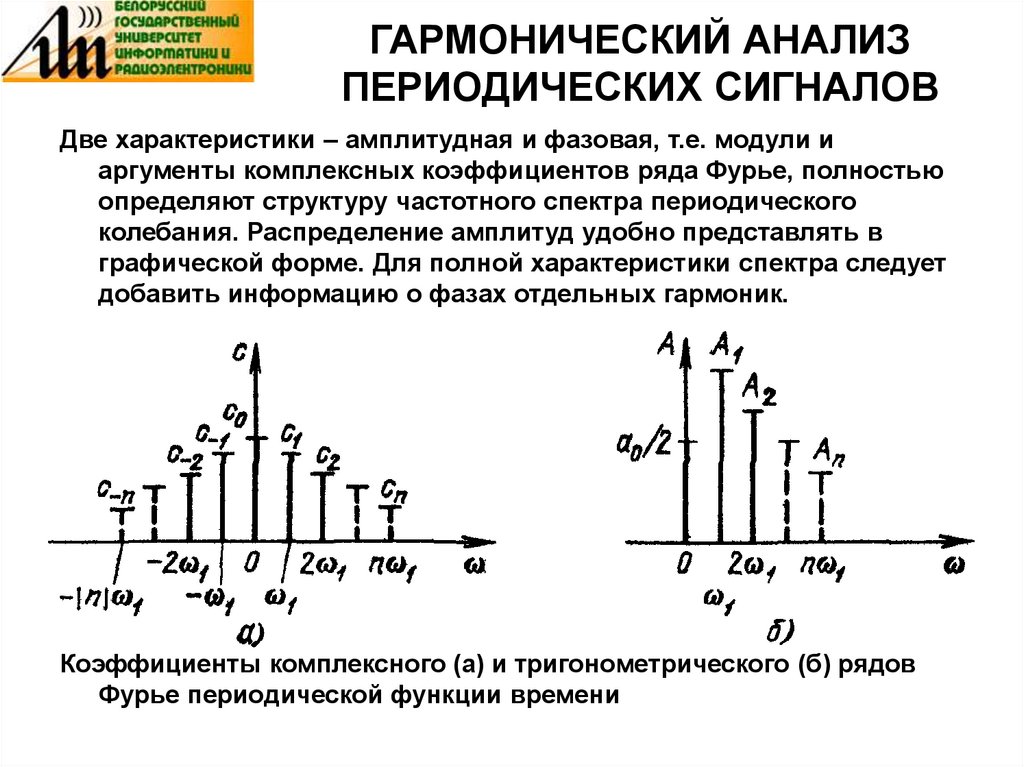
Две характеристики – амплитудная и фазовая, т.е. модули и
аргументы комплексных коэффициентов ряда Фурье, полностью
определяют структуру частотного спектра периодического
колебания. Распределение амплитуд удобно представлять в
графической форме. Для полной характеристики спектра следует
добавить информацию о фазах отдельных гармоник.
Коэффициенты комплексного (а) и тригонометрического (б) рядов
Фурье периодической функции времени

27. СПЕКТР ПЕРИОДИЧЕСКОГО СИГНАЛА

Спектр периодической функции является
линейчатым или дискретным, так как состоит из
отдельных линий, cоответствующих дискретным
частотам 0, w1, w2 = 2w1, w3 = 3w1 и т. д.
Использование для гармонического анализа
сложных периодических колебаний рядов Фурье в
сочетании с принципом наложения представляет
собой эффективное средство для изучения
влияния линейных цепей на прохождение
сигналов.

28. СПЕКТРЫ ПРОСТЕЙШИХ ПЕРИОДИЧЕСКИХ СИГНАЛОВ

ПРЯМОУГОЛЬНОЕ КОЛЕБАНИЕ (МЕАНДР)
Поскольку
, получим:
Начальные фазы всех гармоник равны –p/2.
Ряд Фурье в тригонометрической форме:

29. СПЕКТРЫ ПРОСТЕЙШИХ ПЕРИОДИЧЕСКИХ СИГНАЛОВ

ПРЯМОУГОЛЬНОЕ КОЛЕБАНИЕ (МЕАНДР)
Коэффициенты комплексного (а) и тригонометрического (б) ряда
Фурье для меандра.
Для случая четной функции:

30. СПЕКТРЫ ПРОСТЕЙШИХ ПЕРИОДИЧЕСКИХ СИГНАЛОВ

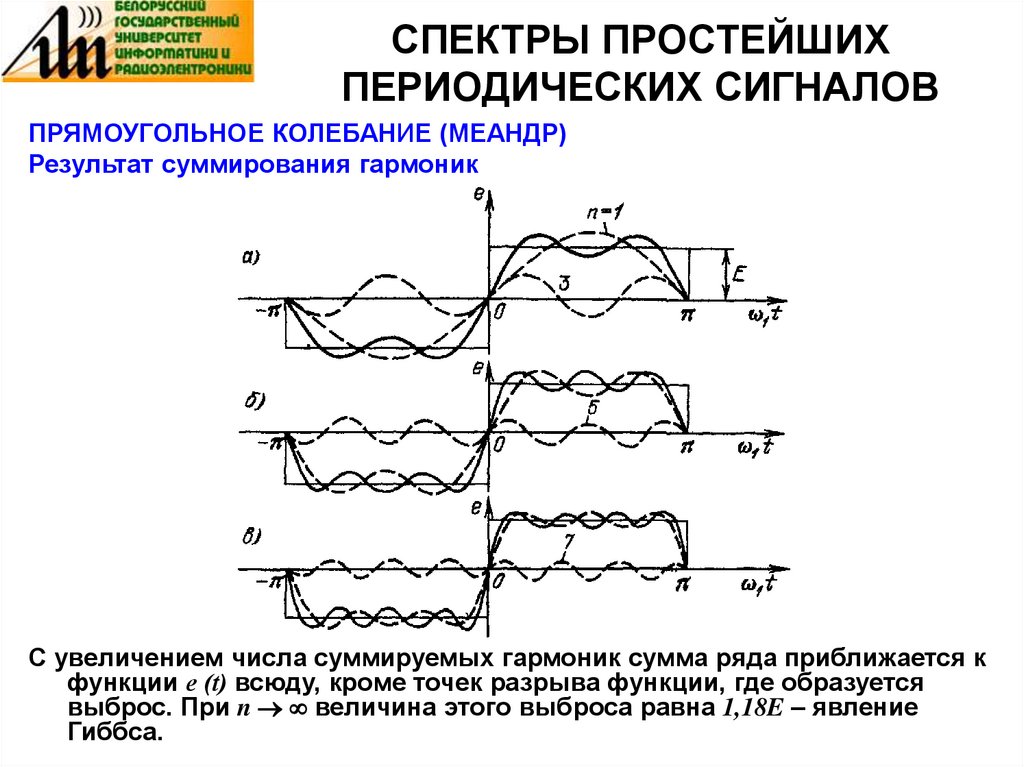
ПРЯМОУГОЛЬНОЕ КОЛЕБАНИЕ (МЕАНДР)
Результат суммирования гармоник
С увеличением числа суммируемых гармоник сумма ряда приближается к
функции е (t) всюду, кроме точек разрыва функции, где образуется
выброс. При n величина этого выброса равна 1,18E – явление
Гиббса.

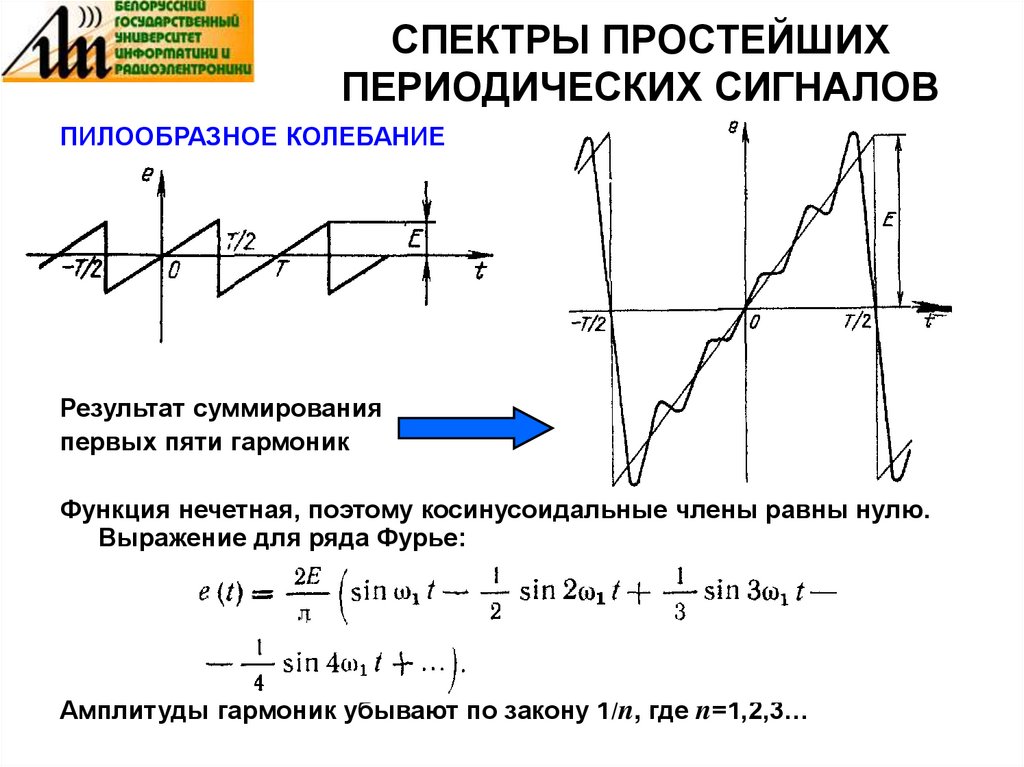
31. СПЕКТРЫ ПРОСТЕЙШИХ ПЕРИОДИЧЕСКИХ СИГНАЛОВ

ПИЛООБРАЗНОЕ КОЛЕБАНИЕ
Результат суммирования
первых пяти гармоник
Функция нечетная, поэтому косинусоидальные члены равны нулю.
Выражение для ряда Фурье:
Амплитуды гармоник убывают по закону 1/n, где n=1,2,3…

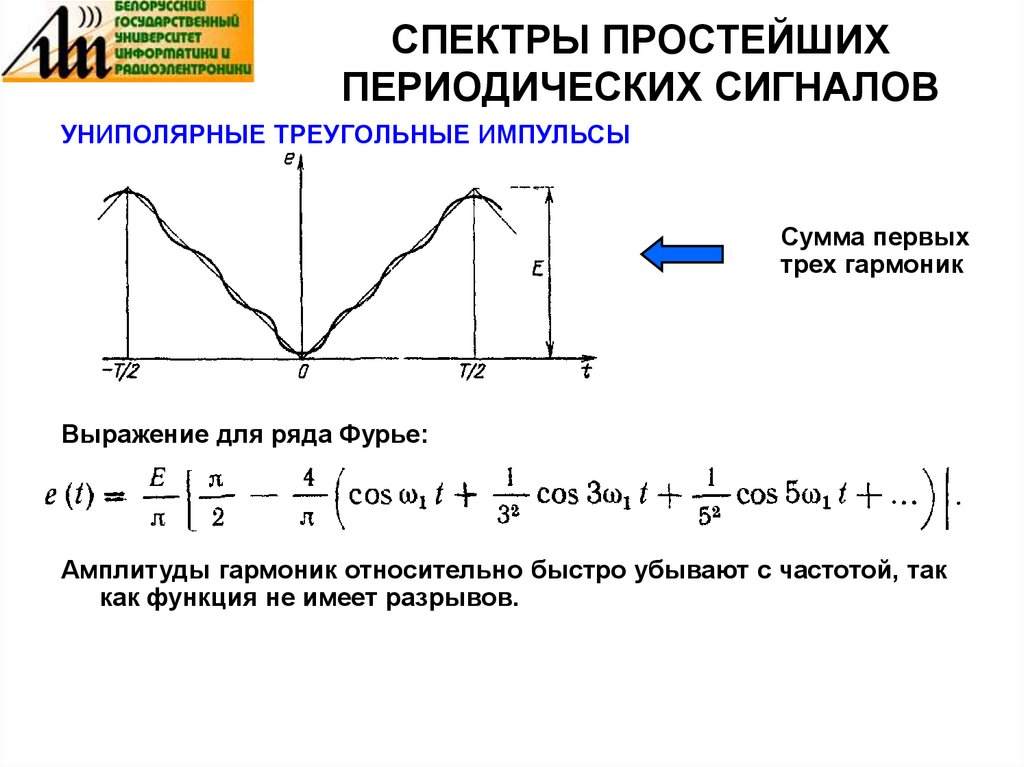
32. СПЕКТРЫ ПРОСТЕЙШИХ ПЕРИОДИЧЕСКИХ СИГНАЛОВ

УНИПОЛЯРНЫЕ ТРЕУГОЛЬНЫЕ ИМПУЛЬСЫ
Сумма первых
трех гармоник
Выражение для ряда Фурье:
Амплитуды гармоник относительно быстро убывают с частотой, так
как функция не имеет разрывов.

33. СПЕКТРЫ ПРОСТЕЙШИХ ПЕРИОДИЧЕСКИХ СИГНАЛОВ

УНИПОЛЯРНЫЕ ПРЯМОУГОЛЬНЫЕ ИМПУЛЬСЫ
Величина N=T/ и называется скважностью. Пусть N > 2.
Среднее значение
(постоянная составляющая):
Коэффициент n-й гармоники:
Выражение для ряда Фурье (ф-ция четная,
):

34. СПЕКТРЫ ПРОСТЕЙШИХ ПЕРИОДИЧЕСКИХ СИГНАЛОВ

УНИПОЛЯРНЫЕ ПРЯМОУГОЛЬНЫЕ ИМПУЛЬСЫ
СПЕКТР СИГНАЛА:
При больших значениях N спектр сигнала содержит очень большое
число медленно убывающих по амплитуде гармоник. Расстояние
между спектральными линиями очень мало, а амплитуды соседних
гармоник близки по величине.
Для малых n
Постоянная составляющая вдвое меньше
амплитуды первой
гармоники.

35. РАСПРЕДЕЛЕНИЕ МОЩНОСТИ В СПЕКТРЕ ПЕРИОДИЧЕСКОГО СИГНАЛА

Средняя мощность сигнала, рассматриваемого на всей оси
времени, совпадает со средней мощностью за период Т.
Средняя мощность периодического сигнала:
или
(с учетом того, что
)
Если s(t) представляет собой ток i(t), (то при прохождении его
через сопротивление R выделяется средняя мощность:
При этом I0 – постоянная составляющая, In – амплитуда n-й
гармоники тока.

36. РАСПРЕДЕЛЕНИЕ МОЩНОСТИ В СПЕКТРЕ ПЕРИОДИЧЕСКОГО СИГНАЛА

Итак, полная средняя мощность равна сумме
средних мощностей, выделяемых отдельно
постоянной составляющей I0 и гармониками с
амплитудами I1, I2, ... Это означает, что средняя
мощность не зависит от фаз отдельных гармоник.
Это вытекает из ортогональности спектральных
составляющих, в данном случае на интервале Т.

37. ИНТЕГРАЛЬНЫЕ ЗНАЧЕНИЯ ПЕРИОДИЧЕСКОГО СИГНАЛА

Периодический сигнал S(t) часто описывается
несколькими общепринятыми обобщающими
параметрами: амплитудным, средним,
средневыпрямленным и среднеквадратическим
значениями – называемыми интегральными.
Амплитудное (пиковое) значение Sm равно
максимальному мгновенному значению сигнала S(t) на
его периоде.
Среднее значение Scp определяется как
и характеризует постоянную составляющую сигнала.

38. ИНТЕГРАЛЬНЫЕ ЗНАЧЕНИЯ ПЕРИОДИЧЕСКОГО СИГНАЛА

Cредневыпрямленное значение:
используется для сигналов, не содержащих постоянную
составляющую.
Среднеквадратическое значение:
где An – среднеквадратическое (эффективное) значение n-й
гармоники сигнала S(t).
Большинство вольтметров проградуировано в среднеквадратических
значениях напряжения (RMS).

39. ИНТЕГРАЛЬНЫЕ ЗНАЧЕНИЯ ПЕРИОДИЧЕСКОГО СИГНАЛА

Связь между перечисленными параметрами
устанавливается с помощью следующих
трех коэффициентов:
Коэффициент формы kф = Sск / Sсв ,
Коэффициент амплитуды kа = Sm / Sск
Коэффициент усреднения kу = Sm / Sсв = kа kф.

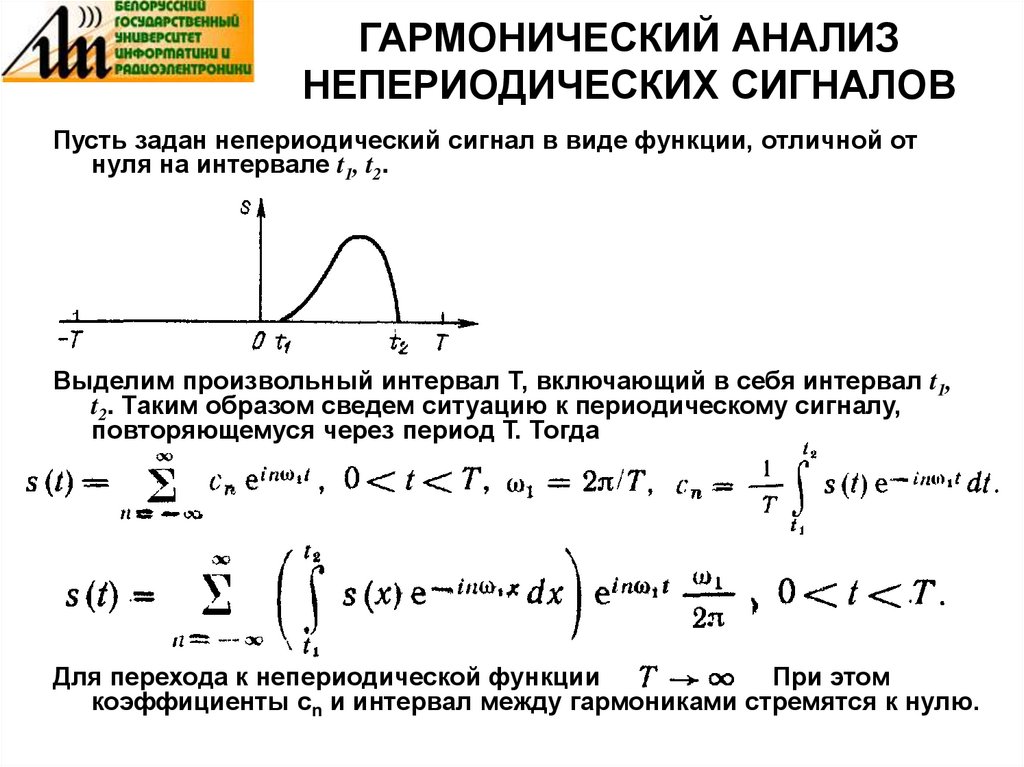
40. ГАРМОНИЧЕСКИЙ АНАЛИЗ НЕПЕРИОДИЧЕСКИХ СИГНАЛОВ

Пусть задан непериодический сигнал в виде функции, отличной от
нуля на интервале t1, t2.
Выделим произвольный интервал Т, включающий в себя интервал t1,
t2. Таким образом сведем ситуацию к периодическому сигналу,
повторяющемуся через период Т. Тогда
Для перехода к непериодической функции
При этом
коэффициенты сn и интервал между гармониками стремятся к нулю.

41. ГАРМОНИЧЕСКИЙ АНАЛИЗ НЕПЕРИОДИЧЕСКИХ СИГНАЛОВ

Число гармонических составляющих становится бесконечно большим,
расстояние между ними – бесконечно малым. Спектр становится
сплошным. Тогда от суммирования можно перейти к
интегрированию.
Переход w1 dw; nw1 w. Приходим к двойному интегралу Фурье:
Внутренний интеграл (функция w)
называется спектральной плотностью (или спектральной функцией,
или спектральной характеристикой, или Фурье-образом) функции
s(t). В общем случае неуточненных t1, t2 получаем выражения для
прямого и обратного преобразования Фурье:

42. ГАРМОНИЧЕСКИЙ АНАЛИЗ НЕПЕРИОДИЧЕСКИХ СИГНАЛОВ

По аналогии с рядом Фурье можно записать:
Модуль и аргумент функции спектральной плотности определяются
как
Первое выражение можно рассматривать как амплитудно-частотную
характеристику (АЧХ), а второе – как фазо-частотную
характеристику (ФЧХ) спектра непериодического сигнала.
Переход к тригонометрической форме:

43. ГАРМОНИЧЕСКИЙ АНАЛИЗ НЕПЕРИОДИЧЕСКИХ СИГНАЛОВ

Из четности модуля и нечетности фазы следует, что подынтегральная
функция в первом интеграле является четной, а во втором — нечетной
относительно w. Следовательно, второй интеграл равен нулю и
окончательно
При w=0
Спектральная плотность S(w) есть амплитуда напряжения (тока),
приходящаяся на 1 Гц в бесконечно узкой полосе частот, которая
включает в себя рассматриваемую частоту w.
Между сигналом s(t) и его спектром S(w) существует взаимнооднозначное соответствие.

44. ИНТЕГРАЛ ФУРЬЕ ДЛЯ ПРОИЗВЕДЕНИЯ СИГНАЛОВ

Пусть сигнал s(t) есть произведение двух функций времени f(t) и g(t).
Спектр сигнала:
Каждую функцию можно представить в виде интеграла Фурье:
Тогда
или

45. ИНТЕГРАЛ ФУРЬЕ ДЛЯ ПРОИЗВЕДЕНИЯ СИГНАЛОВ

Спектр произведения двух функций времени f(t) и g(t) равен с
коэффицентом 1/2p свертке их спектров F(w) и G(w).
При w=0 получим:
Тогда
- комплексно-сопряженная спектральная функция.
Аналогично для произведения двух спектров
- результат равен свертке двух функций времени f(t) и g(t) с
коэффицентом 2p .

46. ВЗАИМОЗАМЕНЯЕМОСТЬ w И t В ПРЕОБРАЗОВАНИЯХ ФУРЬЕ

Переменные w и t в преобразованиях Фурье взаимно заменимы; если
колебанию (четному) s (t) соответствует спектр S (w), то колебанию
S (t) соответствует спектр 2p s (w).

47. РАСПРЕДЕЛЕНИЕ ЭНЕРГИИ В СПЕКТРЕ НЕПЕРИОДИЧЕСКОГО СИГНАЛА

Если f(t) и g(t) представляют собой одно и то же колебание,
То полная энергия сигнала s(t) представляется как интеграл
Произведение спектральных плотностей G(w) и F*(w) можно привести к
виду
Тогда
Это равенство Парсеваля – соотношение между энергией сигнала и
модулем его спектральной плотности.
Величину |S (w)|2, имеющую смысл энергии, приходящейся на
частотный интервал в 1 Гц, можно рассматривать как спектральную
плотность энергии сигнала.

48. CООТНОШЕНИЕ МЕЖДУ ДЛИТЕЛЬНОСТЬЮ И ШИРИНОЙ СПЕКТРА СИГНАЛА

Чем меньше длительность сигнала, тем шире его спектр.
Определения длительности сигнала и ширины его спектра различны и
зависят от формы сигналов.
В некоторых случаях выбор является произвольным. Например:
- Ширину спектра прямоугольного импульса определяют либо как
основание главного лепестка либо на уровне 1/ 2 от максимального
значения спектральной плотности.
- Длительность колоколообразного импульса и ширину его спектра
иногда определяют на уровне 0,606 от максимального значения
соответственно s (t) или S (w).
- Часто пользуются энергетическим критерием, понимая под
шириной спектра полосу частот, содержащую заданную долю
полной энергии сигнала.
Для выявления предельных соотношений, связывающих
длительность сигнала и ширину спектра, в современной теории
сигналов большое распространение получил метод моментов.
Также широко используется такой параметр, как произведение
ПОЛОСА Х ДЛИТЕЛЬНОСТЬ.

49. CООТНОШЕНИЕ МЕЖДУ ДЛИТЕЛЬНОСТЬЮ И ШИРИНОЙ СПЕКТРА СИГНАЛА

Понятие длительности сигнала имеет ясный физический смысл
для импульсных сигналов (прямоугольный, треугольный и
др.), определённых на конечных интервалах времени.
Для сигналов, определённых на бесконечном или
полубесконечном интервале времени (например гауссов
или экспоненциальный импульсы), используют понятие
эквивалентной или эффективной длительности сигнала э
в одном из двух определений:
1)
под эффективной длительностью понимают конечную
величину э, определённую из решения уравнения
где (t2 – t1) = э, – коэффициент, численно определяющий
часть полной энергии сигнала, чаще всего принимаемый
= 0,9 и реже = 0,95 или 0,99.

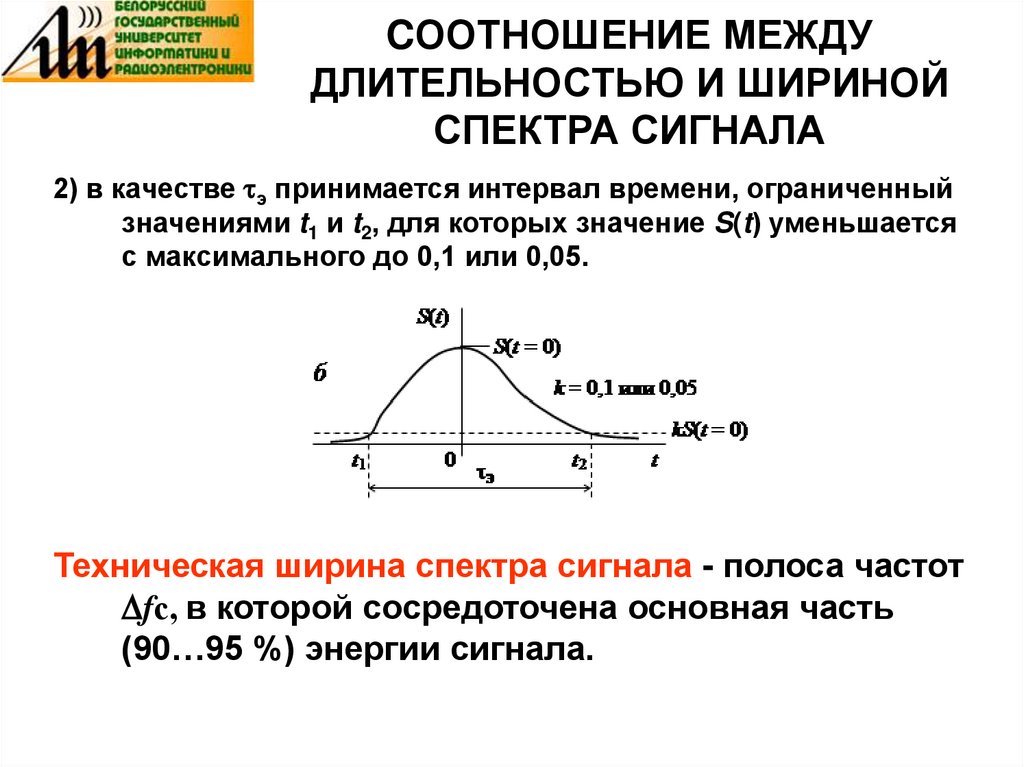
50. CООТНОШЕНИЕ МЕЖДУ ДЛИТЕЛЬНОСТЬЮ И ШИРИНОЙ СПЕКТРА СИГНАЛА

2) в качестве э принимается интервал времени, ограниченный
значениями t1 и t2, для которых значение S(t) уменьшается
с максимального до 0,1 или 0,05.
Техническая ширина спектра сигнала - полоса частот
fс, в которой сосредоточена основная часть
(90…95 %) энергии сигнала.

51. ОПРЕДЕЛЕНИЕ ПРОИЗВЕДЕНИЯ ПОЛОСА Х ДЛИТЕЛЬНОСТЬ

По аналогии с моментом инерции в механике эффективную
длительность сигнала Тэф можно определить как
где середина импульса t0 определяется из условия
Эффективная ширина спектра
определяется по аналогии:
Так как модуль спектра S (w) не зависит от смещения s (t) во времени,
можно положить t0 =0. Далее, сигнал s (t) можно нормировать таким
образом, чтобы его энергия Э равнялась единице.

52. ОПРЕДЕЛЕНИЕ ПРОИЗВЕДЕНИЯ ПОЛОСА Х ДЛИТЕЛЬНОСТЬ

Тогда получим:
В этих условиях
Тогда произведение полоса х длительность запишется как
‼ Полную длительность сигнала следует приравнять к 2Тэф, полную
щирину спектра – к 2 Wэф. Произведение Тэф Wэф зависит от формы
сигнала, однако оно не может быть меньше 1/2. Оказывается, что
наименьшее возможное значение Тэф Wэф = 1/2 соответствует
колоколообразному импульсу.

53. ТЕОРЕМЫ О СПЕКТРАХ СИГНАЛОВ

1 Теорема суммирования
Спектр суммы временных функций сигналов равен
сумме значений амплитудных и фазовых спектров
этих сигналов.
2 Теорема умножения на постоянное число
Изменение значений (амплитуды) функции сигнала в
«а» раз приводит к изменению в «а» раз значений
его амплитудного спектра без изменения его
ширины:

54. ТЕОРЕМЫ О СПЕКТРАХ СИГНАЛОВ

3 Теорема запаздывания (смещения по времени)
Сдвиг начала отсчёта функции сигнала на время
t0 приводит к изменению значений его фазового
спектра на величину
4 Теорема умножения на
(смещения по частоте)
Умножение функции сигнала на величину
вызывает смещение спектра на

55. ТЕОРЕМЫ О СПЕКТРАХ СИГНАЛОВ

5 Теорема подобия
Изменение временного масштаба функции сигнала в
«а» раз приводит к изменению в «а» раз значений
его амплитудного спектра, частоты гармоник и
ширины частотной полосы амплитудного и
фазового спектра:
При сжатии колебания в а раз на временной оси во
столько же раз расширяется его спектр на оси
частот. Модуль спектральной плотности при этом
уменьшается в а раз. При растягивании колебаний
во времени (а<1) получается сужение спектра и
увеличение модуля спектральной плотности.

56. ТЕОРЕМЫ О СПЕКТРАХ СИГНАЛОВ

6 Теорема дифференцирования
Дифференцирование функции сигнала адекватно умножению
его исходного спектра на величину jw, что приводит к
увеличению в «w» раз значений амплитудного спектра и
сдвигу на p / 2 значений фазового спектра:
7 Теорема интегрирования
Интегрирование функции сигнала адекватно делению его
исходного спектра на величину jw, что приводит к
уменьшению в «w» раз значений амплитудного спектра и
сдвигу на –p / 2 значений фазового спектра:

57. ТЕОРЕМЫ О СПЕКТРАХ СИГНАЛОВ

8 Теорема о свёртке двух сигналов
Спектр свёртки двух сигналов определяется
произведением их спектров
где
Свертка позволяет рассчитать сигнал на выходе
фильтра с импульсной характеристикой S2(t) при
подаче на него сигнала S1(t)

58. СВЕРТКА СИГНАЛОВ

Графическое представление свертки двух сигналов
1) два прямоугольных импульса
2)
Прямоугольный импульс и импульсная функция
с экспоненциальным затуханием

59. ТЕОРЕМЫ О СПЕКТРАХ СИГНАЛОВ

9 Теорема дуальности (взаимной обратимости
частоты и времени)
Если S(t) имеет спектр U(jw), то, рассматривая этот
спектр как функцию сигнала U(t), исходный сигнал
S(t), представленный в частотной области как S(–
jw), рассматривается в качестве спектра сигнала
U(t).