Механика ЭП

1.

1. Механика ЭП
1.1. Приведение сил, масс, моментов
Механическая часть электропривода может представлять
собой сложную кинематическую цепь с большим числом
движущихся
элементов
как
вращательного,
так
и
поступательного движения.
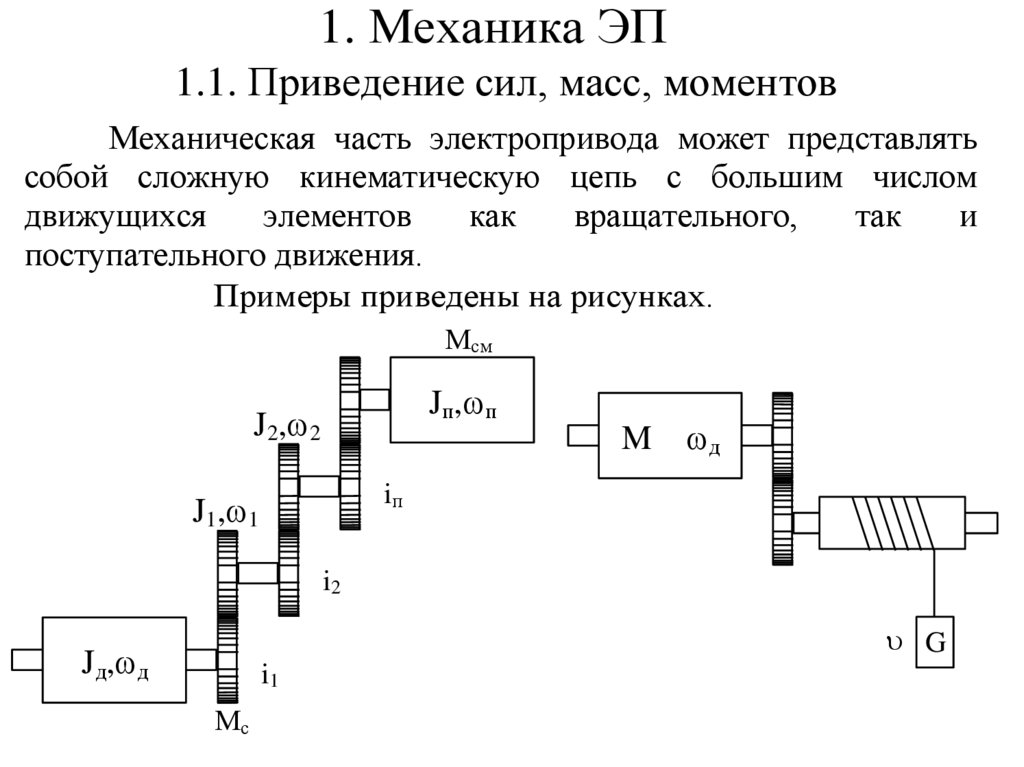
Примеры приведены на рисунках.
Мсм
Jп, п
J2, 2
M
д
iп
J1, 1
i2
G
Jд, д
i1
Мс

2.

Каждый из элементов этих цепей обладает упругостью, а в
соединениях имеются воздушные зазоры. Если учитывать эти
факторы, то расчетная схема получится весьма сложной и решается
только с использованием ЭВМ. Для практических инженерных
расчетов можно принять элементы системы абсолютно жесткими
без воздушных зазоров, тогда любая кинематическая цепь может
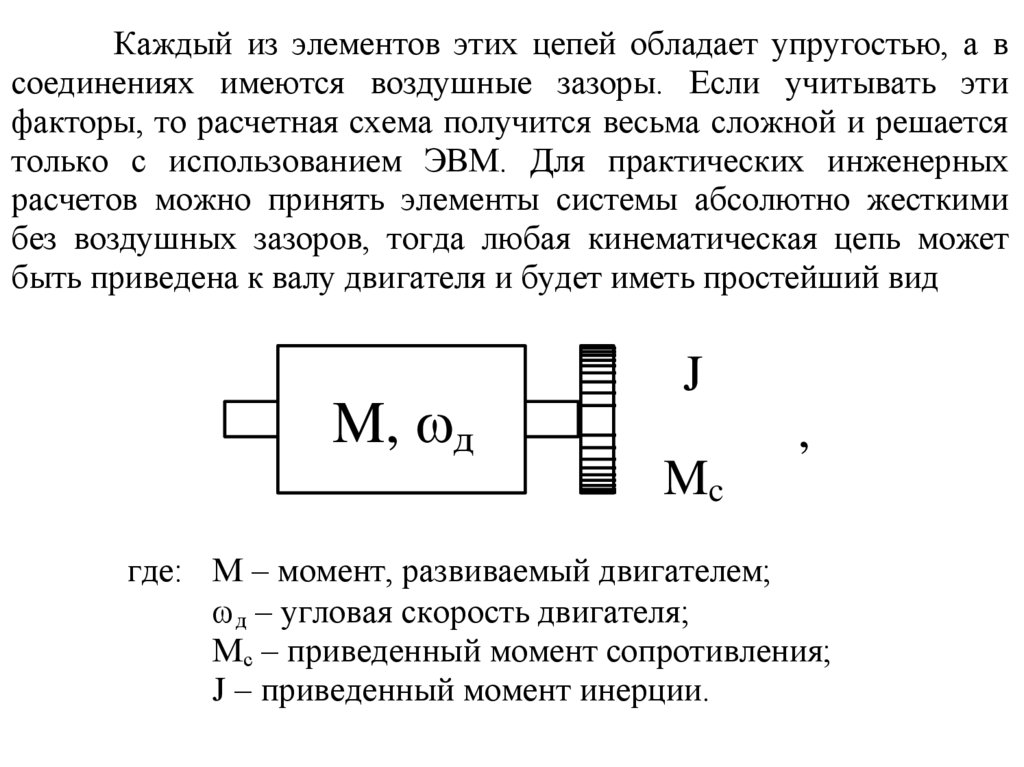
быть приведена к валу двигателя и будет иметь простейший вид
M, д
J
,
Mc
где: М – момент, развиваемый двигателем;
д – угловая скорость двигателя;
Мс – приведенный момент сопротивления;
J – приведенный момент инерции.

3.

Приведенный момент Мс определяется из условия равенства
мощностей приведенной и реальной систем
1
M с ωд M с.м ωп ;
ηп
ωп 1
M с M с.м ;
ω д ηп
д
где i п
– передаточное число;
п
1
1
M с M с.м
.
i1 i 2 ... i n η1 η2 ... ηn
(1)

4.

Из этого же условия приводятся силы поступательного
движения
M с ωд Fс.м υ
1
;
ηп
1 υ
M с Fс.м ;
ηп ω д
ω д ηп
Fс.м M с
.
υ
(2)

5.

Приведение моментов инерции осуществляется из условия
сохранения кинетических энергий систем
ω2д
ω2д
ω12
ω2n
J
Jд
J1 ... J n ;
2
2
2
2
1
1
1
J J д J1 2 J 2 2 2 ... J n 2 2
.
2
i1
i1 i 2
i1 i 2 ... i n
(3)

6.

Аналогично приводим массы элементов поступательного
движения
ω2д
mυ2
J ;
2
2
2
υ
ωд
J m ; m J .
υ
ωд
G
D
2
Напомним, что J mρ ; m ; ρ .
2
q
G D2
Отсюда J
q 4
2
(4)
или
4 q J G D2 ,
где G D 2– маховый момент.
(5)

7.

1.2. Уравнение движения ЭП
Для поступательного движения можем записать:
d
F Fс m
.
dt
Для вращательного движения:
d
М Мс J
.
(6)
dt
Возможны три варианта:
d
1. M > Mc;
> 0 – ускоряющееся движение;
dt
d
2. M < Mc;
< 0 – замедляющееся движение;
dt
d
3. M = Mc;
= 0 – равномерное движение либо
dt
неподвижное состояние.

8.

1.3. Время ускорения и замедления привода
Решив уравнение (6) относительно времени запишем:
2
d
d
или t 1, 2 J
.
dt J
M Mс
1 M M с
На первый взгляд интеграл прост, однако необходимо
помнить, что все входящие параметры могут оказаться
переменными во времени. Тогда решение может оказаться
достаточно сложным.
Допустим: М = const; Mc = const; J = const.
Тогда
2 1
t 1, 2 J
.
(7)
M Mс
Выражение (7) дает четкое представление о зависимости
времени переходного процесса от условий работы привода.

9.

Например:
1. Пуск двигателя:
при t = 0; M = Mп; 1 = 0; 2 = н.
Тогда
tп J
н
.
Mп Mс
(8)
2. Остановка (торможение) двигателя:
при t = 0; M = –Mт; 1 = н; 2 = 0.
Тогда
Сопоставьте
выражения (8) и (9) и
сделайте выводы:
н
.
tт J
Mт Mс
tт tп;
t1, 2 J;
t1, 2 ( 2 1 );
t1, 2
1
.
M Mс
(9)