Дискретные случайные величины

1.

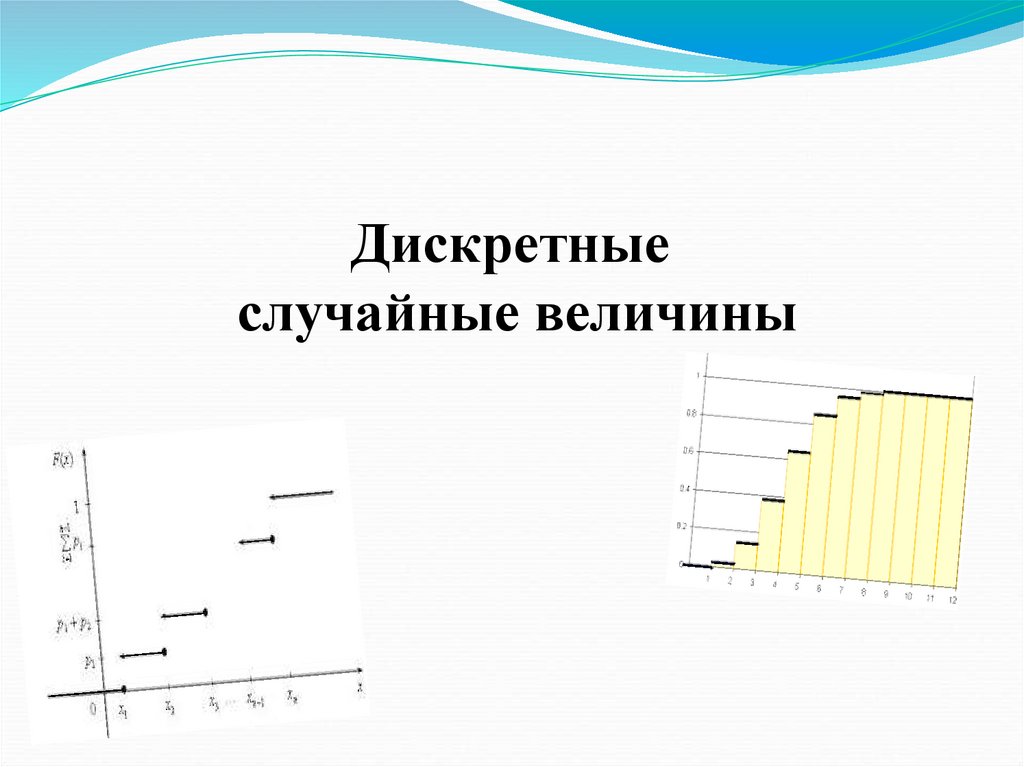
Дискретные
случайные величины

2.

Цели урока
Образовательные:
⚫ изучить дискретные случайные величины, закон и функцию
распределения дискретной случайной величины;
⚫ научить решать задачи на определение закона и функции
распределения дискретной случайной величины, на нахождение
вероятности попадания случайной величины в заданный интервал;
⚫ научить применять понятия теории вероятностей в реальных
ситуациях.
Воспитательные:
⚫ способствовать развитию знаний,;
⚫ формировать научное мировоззрение;
⚫ продолжать формировать умение самостоятельно работать с
различными источниками информации.
Развивающие:
⚫ способствовать развитию аналитического мышления, смысловой
памяти, внимания/

3.

Случайные величины
⚫Случайной называют величину, которая в результате
испытания примет одно и только одно числовое значение,
зависящее от случайных факторов .
⚫Случайные величины обозначают заглавными латинскими
буквами X,Y,Z,… , а их значения – маленькими буквами,
например,
.
⚫Cлучайные величины делятся на 2 группы:
⚫1) Дискретная случайная величина – принимает отдельно
взятые, изолированные значения. Количество этих
значений конечно либо бесконечно, но счётно.
⚫2) Непрерывная случайная величина – принимает
все числовые значения из некоторого конечного или
бесконечного промежутка.

4.

Дискретные случайные величины
⚫Закон распределения дискретной случайной величины –
это соответствие между возможными значениями этой
величины и их вероятностями.
⚫Чаще всего закон записывают таблицей:
xi
x1
x2
…
xn
pi
p1
p2
…
pn
⚫Т.к. случайная величина обязательно примет одно из
значений, то соответствующие события образуют полную
группу, и сумма вероятностей их наступления равна
единице:

5.

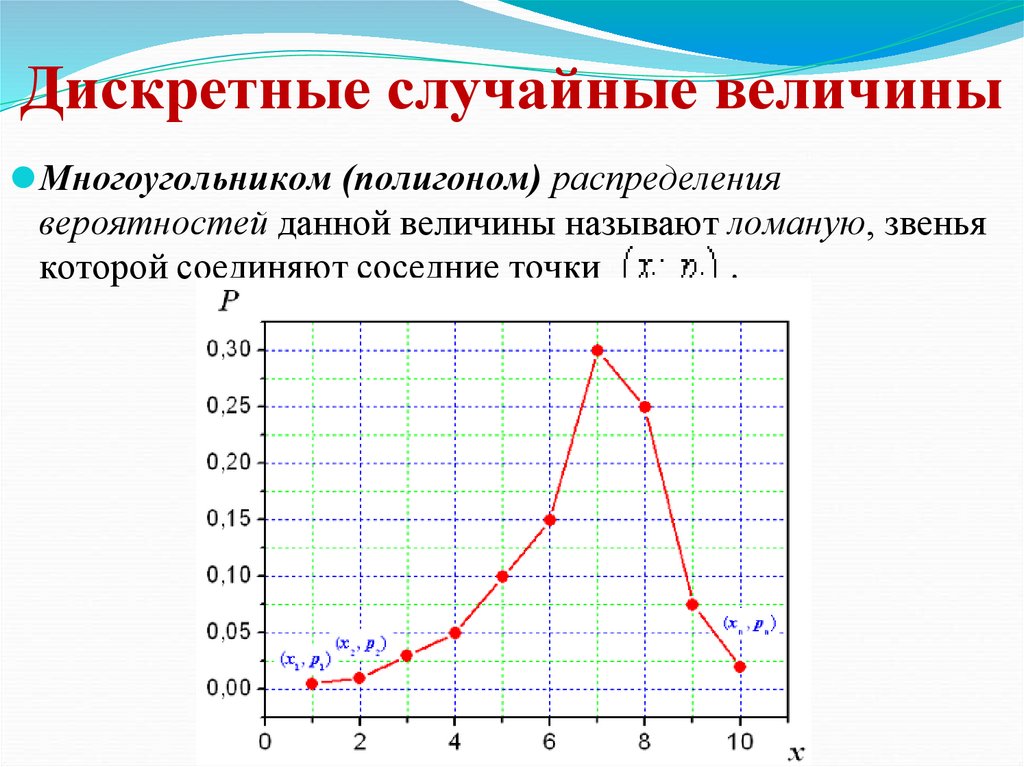
Дискретные случайные величины
⚫Многоугольником (полигоном) распределения
вероятностей данной величины называют ломаную, звенья
которой соединяют соседние точки
.

6.

Пример 1
⚫Написать закон распределения случайной величины —
числа очков, выпадающих при однократном бросании
игральной кости.
⚫Решение:
⚫Возможные значения — числа 1, 2, 3, 4, 5 и 6.
⚫При этом вероятность того, что примет любое из этих
значений, одна и та же и равна
.
⚫Закон распределения имеет вид
xi 1 2
pi
3
4
5
6

7.

Пример 2
⚫В коробке находятся 50 лотерейных билетов, среди
которых 12 выигрышных, причём 2 из них выигрывают
по 1000 рублей, а остальные – по 100 рублей. Составить
закон распределения случайной величины – размера
выигрыша, если из коробки наугад извлекается один
билет.

8.

Решение
⚫Рассмотрим возможные значения:
⚫Самый маленький выигрыш —0 рублей, х1=0
Таких билетов 50 – 12 = 38, и по классическому
определению
– вероятность того, что наудачу
извлечённый билет окажется безвыигрышным.
⚫ Вероятность выигрыша х2=100 рублей составляет:
⚫И для х3=1000
⚫ Закон распределения выигрыша имеет вид xi
xi
0
100
1000
pi
0,76
0,2
0,04

9.

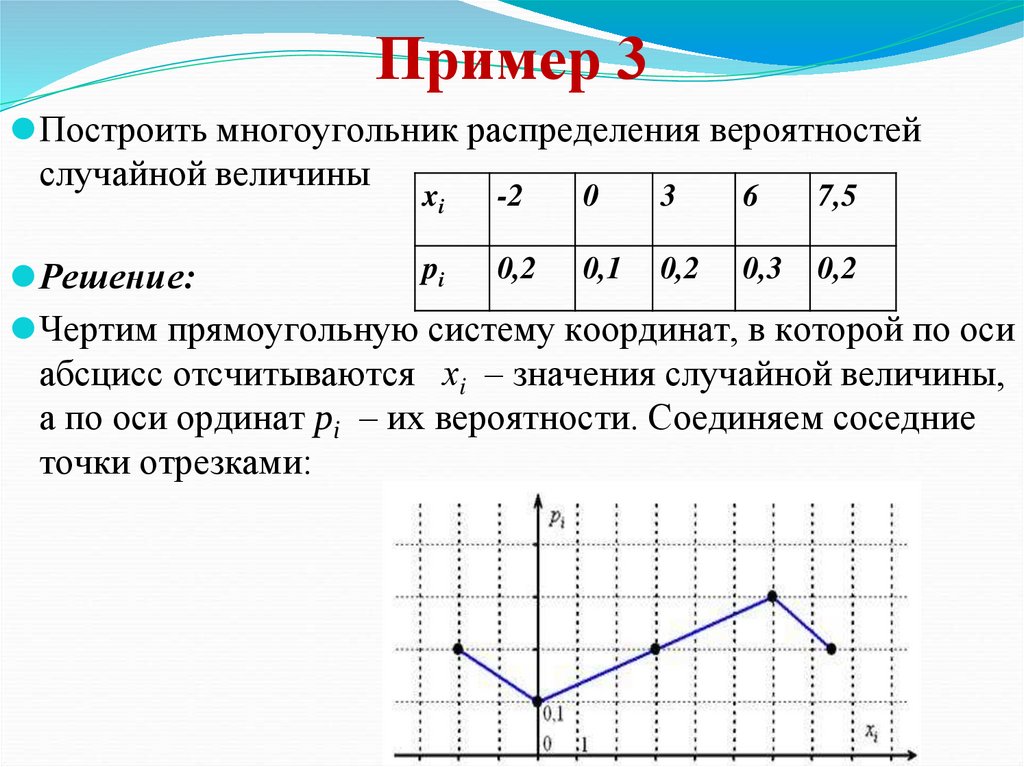
Пример 3
⚫Построить многоугольник распределения вероятностей
случайной величины
xi
-2
0
3
6
7,5
pi
0,2 0,1 0,2 0,3 0,2
⚫Решение:
⚫Чертим прямоугольную систему координат, в которой по оси
абсцисс отсчитываются хi – значения случайной величины,
а по оси ординат pi – их вероятности. Соединяем соседние
точки отрезками:

10.

Функция распределения
⚫Функцией распределения случайной величины Х
называется вероятность того, что случайная
величина Х примет значение, меньшее, чем переменная х,
которая «пробегает» все действительные значения.
F(x)=P(X<x)
Свойства функции распределения
⚫1) Функция распределения – неубывающая.
⚫2)
⚫3)
⚫Вероятность того, что дискретная случайная
величина примет одно из возможных значений xi, равна
скачку функции распределения в точке xi.

11.

Пример 4
⚫Найти функцию распределения и построить ее график для
случайной величины Х, заданной законом распределения
xi
-2
0
3
7
pi
0,4
0,1
0,2
0,3

12.

Выполнить задания
⚫1) Написать закон распределения случайной величины,
заданной своим многоугольником
⚫2) Составить функцию распределения, построить ее график
для дискретной случайной величины
xi
12
16
21
26
30
pi
0,2
0,4
0,1
0,2
0,1

13.

Домашнее задание
⚫ Производятся три выстрела по мишени. Вероятность поражения
мишени первым стрелком равна 0,4, вторым – 0,5, третьим – 0,6.
Случайная величина X – число поражений мишени. Составить
закон и функцию распределения . Построить полигон и график
функции случайной величины Х.