Алгоритмы иструктурыданных. Лекция 5

1.

Алгоритмы и
структуры
данных
• Лекция 5.
• Алгоритмы построения остовного дерева сети
en. Spanning tree
• Алгоритм Прима
• Алгоритм Краскала

2.

Задача построения остовного дерева
Допустим, есть n городов, которые
необходимо соединить дорогами, так, чтобы
можно было добраться из любого города в
любой другой (напрямую или через другие
города). Разрешается строить дороги между
заданными парами городов и известна
стоимость строительства каждой такой
дороги. Требуется решить, какие именно
дороги
нужно
строить,
чтобы
минимизировать
общую
стоимость
строительства.

3.

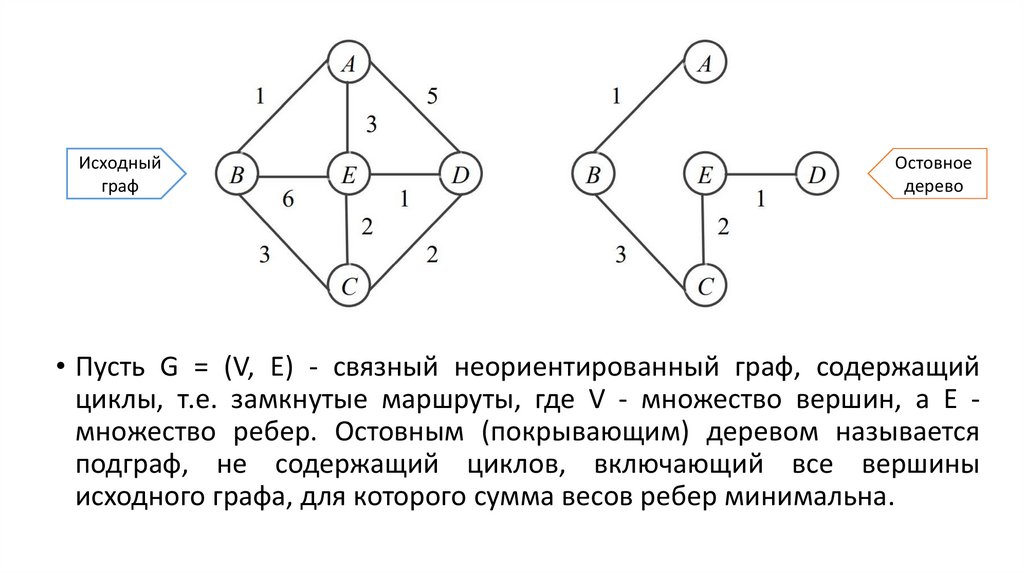
Исходный
граф
Остовное
дерево
• Пусть G = (V, E) - связный неориентированный граф, содержащий
циклы, т.е. замкнутые маршруты, где V - множество вершин, а E множество ребер. Остовным (покрывающим) деревом называется
подграф, не содержащий циклов, включающий все вершины
исходного графа, для которого сумма весов ребер минимальна.

4.

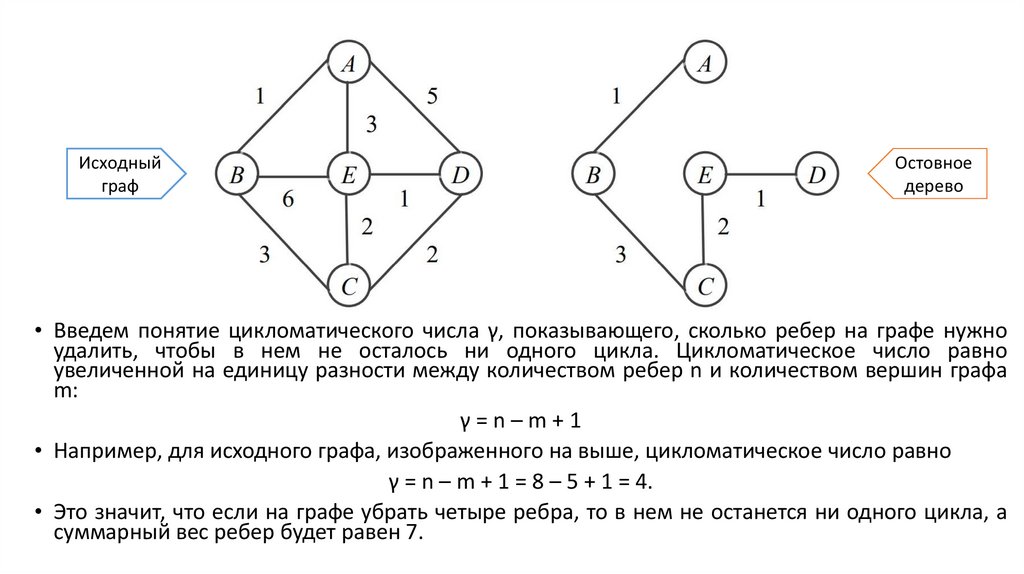
Исходный
граф
Остовное
дерево
• Введем понятие цикломатического числа γ, показывающего, сколько ребер на графе нужно
удалить, чтобы в нем не осталось ни одного цикла. Цикломатическое число равно
увеличенной на единицу разности между количеством ребер n и количеством вершин графа
m:
γ=n–m+1
• Например, для исходного графа, изображенного на выше, цикломатическое число равно
γ = n – m + 1 = 8 – 5 + 1 = 4.
• Это значит, что если на графе убрать четыре ребра, то в нем не останется ни одного цикла, а
суммарный вес ребер будет равен 7.

5.

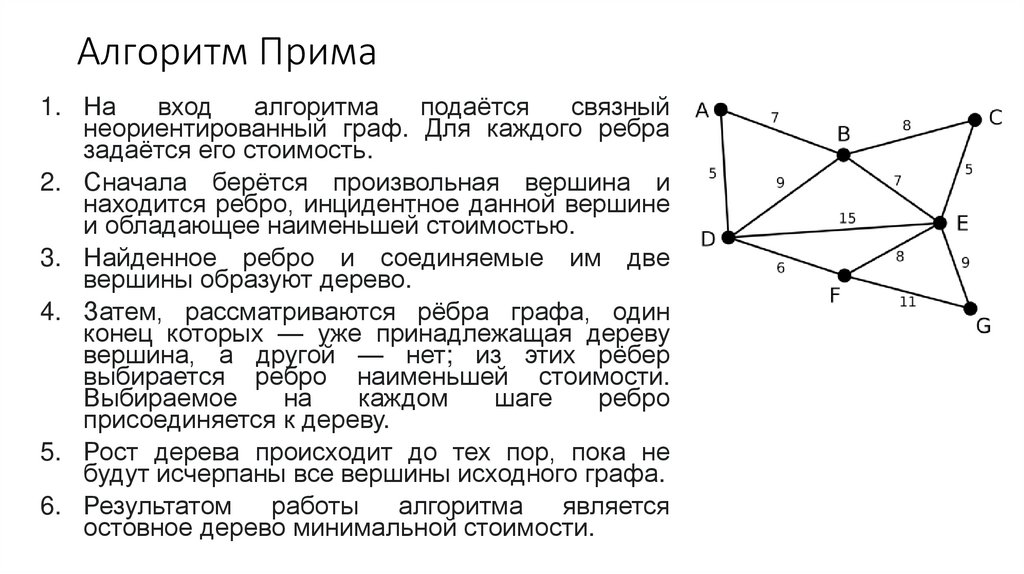
Алгоритм Прима
1. На
вход
алгоритма
подаётся
связный
неориентированный граф. Для каждого ребра
задаётся его стоимость.
2. Сначала берётся произвольная вершина и
находится ребро, инцидентное данной вершине
и обладающее наименьшей стоимостью.
3. Найденное ребро и соединяемые им две
вершины образуют дерево.
4. Затем, рассматриваются рёбра графа, один
конец которых — уже принадлежащая дереву
вершина, а другой — нет; из этих рёбер
выбирается ребро наименьшей стоимости.
Выбираемое
на
каждом
шаге
ребро
присоединяется к дереву.
5. Рост дерева происходит до тех пор, пока не
будут исчерпаны все вершины исходного графа.
6. Результатом
работы
алгоритма
является
остовное дерево минимальной стоимости.

6.

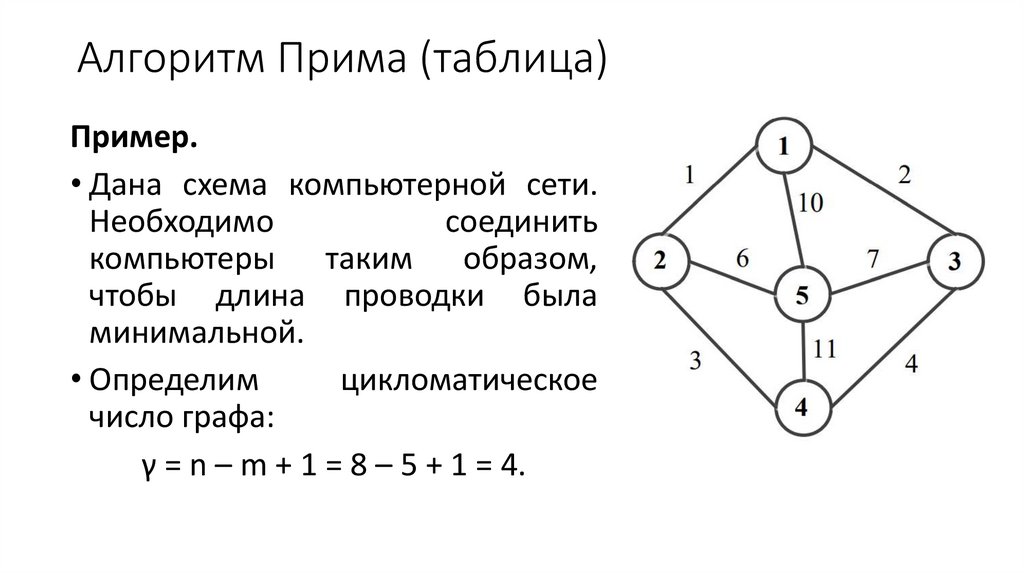
Алгоритм Прима (таблица)
Пример.
• Дана схема компьютерной сети.
Необходимо
соединить
компьютеры таким образом,
чтобы длина проводки была
минимальной.
• Определим
цикломатическое
число графа:
γ = n – m + 1 = 8 – 5 + 1 = 4.

7.

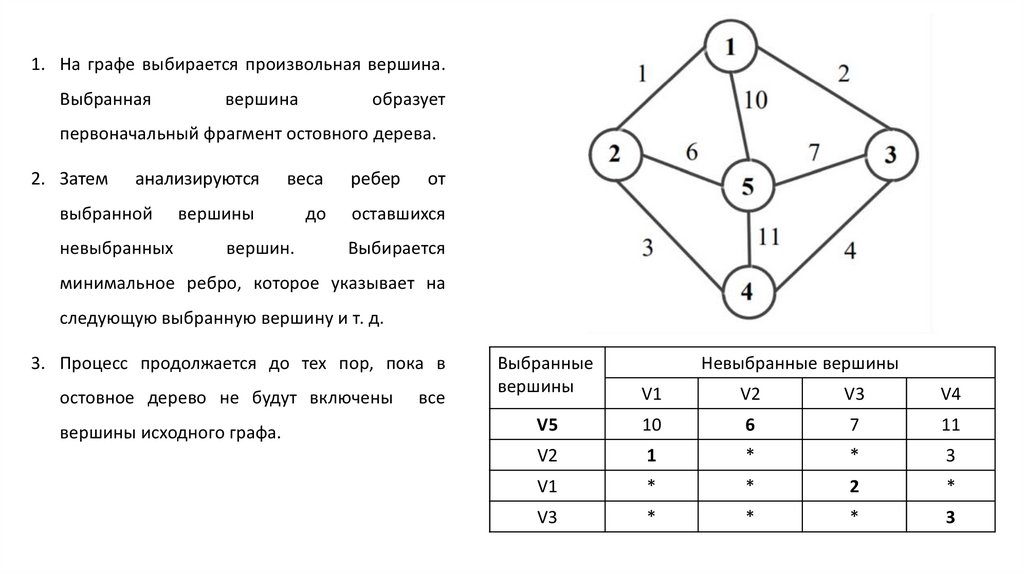
1. На графе выбирается произвольная вершина.
Выбранная
вершина
образует
первоначальный фрагмент остовного дерева.
2. Затем
анализируются
выбранной
невыбранных
веса
вершины
вершин.
до
ребер
от
оставшихся
Выбирается
минимальное ребро, которое указывает на
следующую выбранную вершину и т. д.
3. Процесс продолжается до тех пор, пока в
остовное дерево не будут включены
вершины исходного графа.
все
Выбранные
вершины
Невыбранные вершины
V1
V2
V3
V4
V5
10
6
7
11
V2
1
*
*
3
V1
*
*
2
*
V3
*
*
*
3

8.

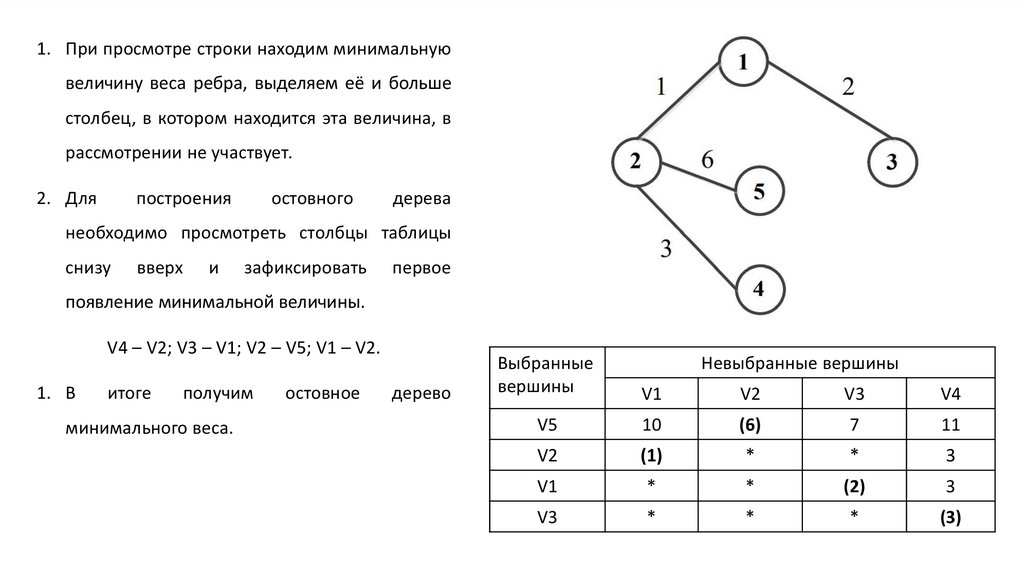
1. При просмотре строки находим минимальную
величину веса ребра, выделяем её и больше
столбец, в котором находится эта величина, в
рассмотрении не участвует.
2. Для
построения
остовного
дерева
необходимо просмотреть столбцы таблицы
снизу
вверх
и
зафиксировать
первое
появление минимальной величины.
V4 – V2; V3 – V1; V2 – V5; V1 – V2.
1. В
итоге
получим
минимального веса.
остовное
дерево
Выбранные
вершины
Невыбранные вершины
V1
V2
V3
V4
V5
10
(6)
7
11
V2
(1)
*
*
3
V1
*
*
(2)
3
V3
*
*
*
(3)

9.

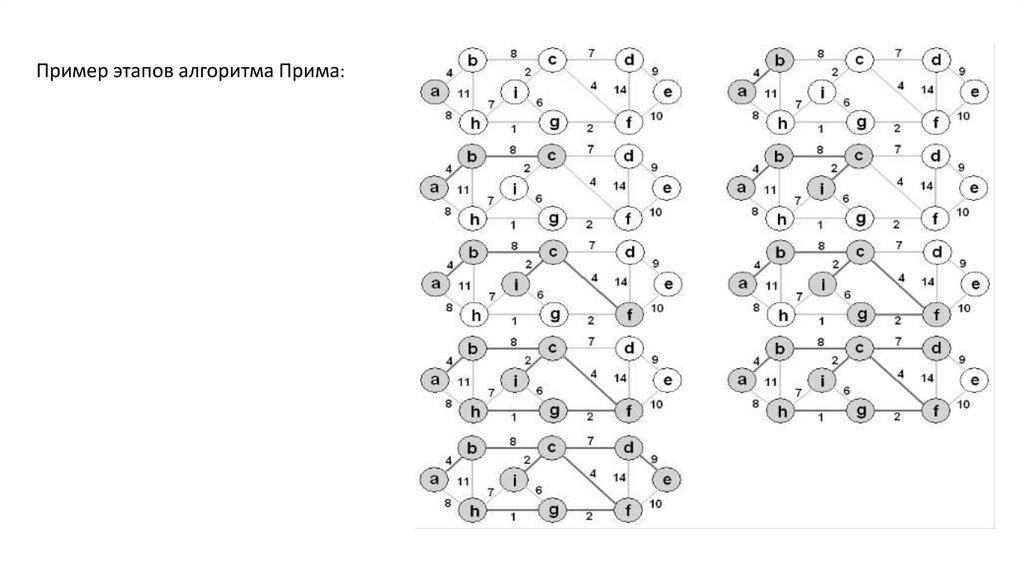
Пример этапов алгоритма Прима:

10.

11.

Сложность алгоритма Прима
Зависит от способа хранения графа и способа хранения вершин, не входящих в дерево:
Способ представления приоритетной очереди и графа
Сложность
Массив d, списки смежности (матрица смежности)
O(V2)
Бинарная пирамида, списки смежности
O((V+E)\log V)=O(E\log V)
Фибоначчиева пирамида, списки смежности
O(E+V\log V)

12.

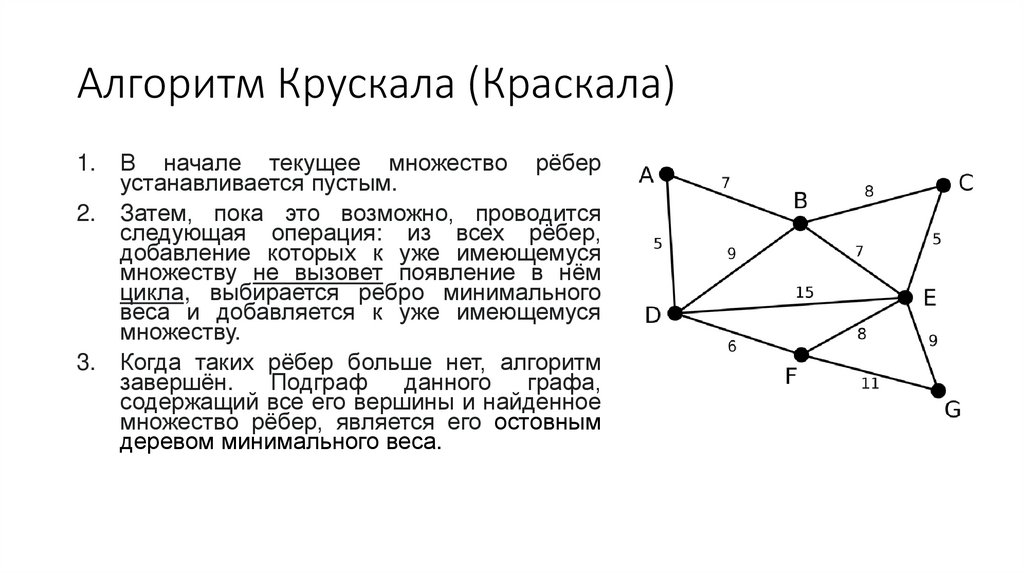
Алгоритм Крускала (Краскала)
1.
2.
3.
В начале текущее множество рёбер
устанавливается пустым.
Затем, пока это возможно, проводится
следующая операция: из всех рёбер,
добавление которых к уже имеющемуся
множеству не вызовет появление в нём
цикла, выбирается ребро минимального
веса и добавляется к уже имеющемуся
множеству.
Когда таких рёбер больше нет, алгоритм
завершён.
Подграф
данного
графа,
содержащий все его вершины и найденное
множество рёбер, является его остовным
деревом минимального веса.

13.

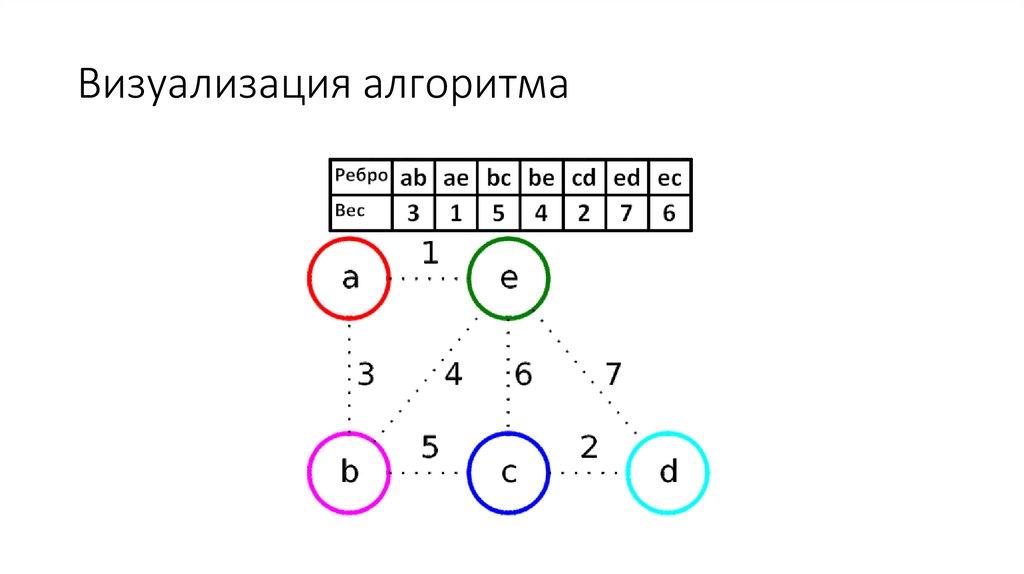
Визуализация алгоритма

14.

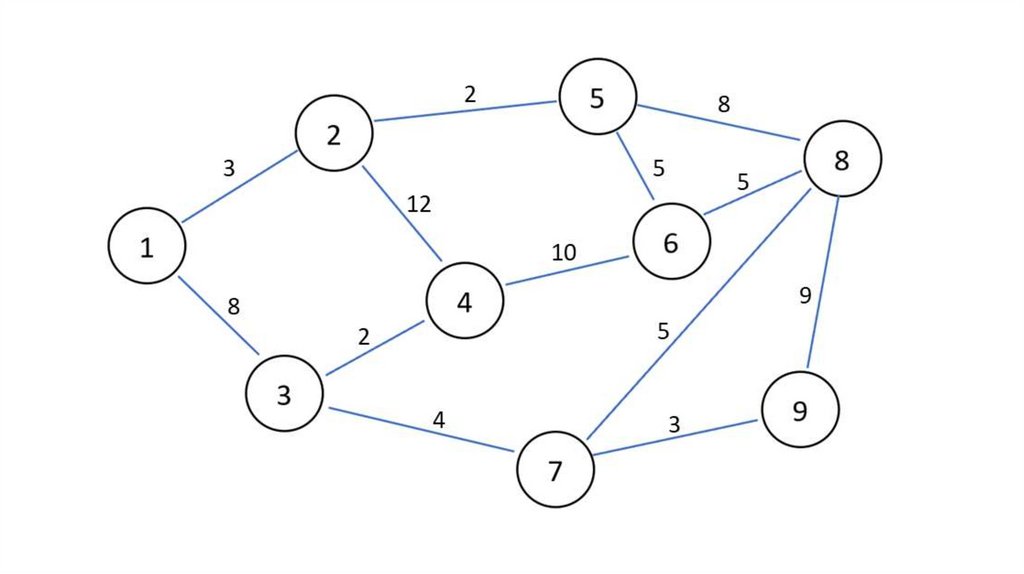
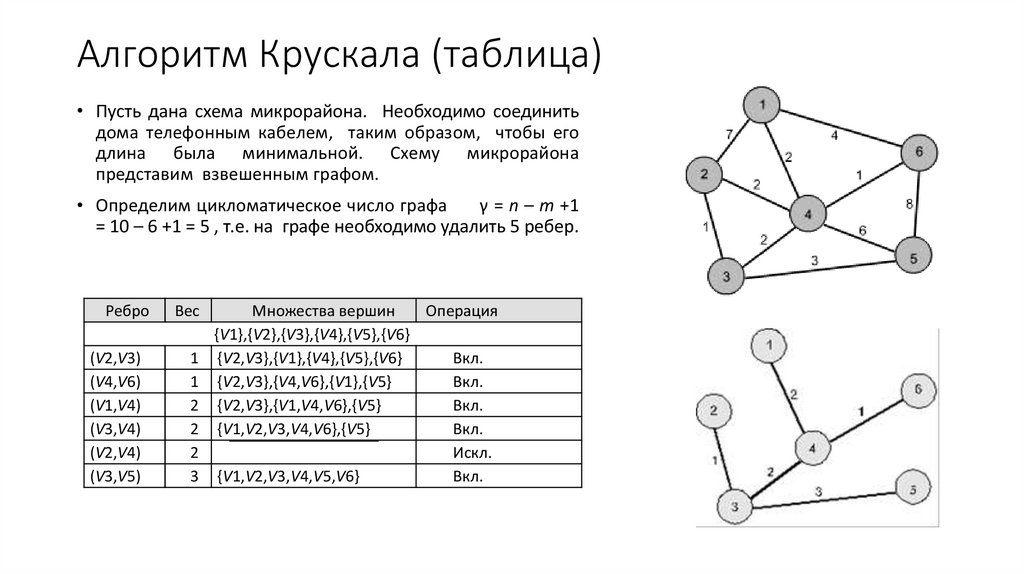
Алгоритм Крускала (таблица)
• Пусть дана схема микрорайона. Необходимо соединить
дома телефонным кабелем, таким образом, чтобы его
длина была минимальной. Схему микрорайона
представим взвешенным графом.
• Определим цикломатическое число графа
γ = n – m +1
= 10 – 6 +1 = 5 , т.е. на графе необходимо удалить 5 ребер.
Ребро
Вес
(V2,V3)
(V4,V6)
(V1,V4)
(V3,V4)
(V2,V4)
(V3,V5)
1
1
2
2
2
3
Множества вершин
Операция
{V1},{V2},{V3},{V4},{V5},{V6}
{V2,V3},{V1},{V4},{V5},{V6}
Вкл.
{V2,V3},{V4,V6},{V1},{V5}
Вкл.
{V2,V3},{V1,V4,V6},{V5}
Вкл.
{V1,V2,V3,V4,V6},{V5}
Вкл.
Искл.
{V1,V2,V3,V4,V5,V6}
Вкл.

15.

16.

Сложность алгоритма Крускала
• До начала работы алгоритма необходимо отсортировать
рёбра по весу, это требует O(E × log(E)) времени.
• После чего компоненты связности удобно хранить в
виде системы непересекающихся множеств. Все операции в
таком случае займут O(E × α(E, V)), где α — функция,
обратная к функции Аккермана.
• Поскольку для любых практических задач α(E, V) < 5, то
можно принять её за константу, таким образом, общее время
работы алгоритма Краскала можно принять за O(E * log(E)).

17.

Функция Акермана
Функция Аккермана — простой пример всюду
определённой вычислимой функции, которая
не является примитивно рекурсивной. Она
принимает два неотрицательных целых числа
в качестве параметров и возвращает
натуральное число, обозначается A(m,n). Эта
функция растёт очень быстро, например,
число A(4,4) настолько велико, что количество
цифр в порядке этого числа многократно
превосходит
количество
атомов
в
наблюдаемой части Вселенной.
Так как функция:
f(n)=A(n, n)
растёт очень быстро, обратная функция:
f-1(n)=min{k≥1 : A(k, k)≥n},
растёт очень медленно.