Задача о минимальном остовном дереве неориентированного графа

1.

ИСО
ЗАДАЧА О МИНИМАЛЬНОМ ОСТОВНОМ ДЕРЕВЕ НЕОРИЕНТИРОВАННОГО ГРАФА
Напомним, что дерево это ациклический связный граф.
Теорема 1. Для неориентированного графа G( V, E ), с числом вершин |V|= n, числом рёбер
| E | = m, следующие условия эквивалентны:
1. G – дерево;
2. Для любых две вершин графа G существует единственный соединяющий их путь;
3. Добавление в G ребра, соединяющего любую пару несмежных рёбер, приводит к
образованию ровно обного цикла;
4. G связный граф с n=m+1;
5. G ациклический граф с n=m+1;
6. G связный граф и каждое его ребро является мостом.
Подграф графа называется остовным, если он содержит все вершины исходного графа.

2.

ИСО
Пусть дан связный неориентированный граф G( V, E ), с числом вершин | V |= n, числом
рёбер | E | = m, и каждому его ребру e
E приписан некоторый вес w(e).
Вес подграфа G’(V ‘, E’) графа G( V, E ) определим как сумму весов его рёбер, то есть
w(G ' ) w(e)
.
Задача о минимальном остовном дереве состоит в поиске остовного дерева исходного
графа с минимальным весом.
Приведём базовые алгоритмы решения задачи. Обозначим через Ij совокупность рёбер,
e E '
включённое в искомое дерево на j-ой итерации алгоритма.
Алгоритм Крускала. Начальный шаг: j = 0, I0 =
.
Шаг 1. Упорядочиваем рёбра множества E в порядке неубывания их весов. Пусть
w(e1) ≤ w(e2) ≤…≤w(em).
Шаг 2.
I j e j , если I j e j не содержит цикла ,
I j 1
I j , в противном случае.
Шаг 3. Если | Ij+1 | = n-1, стоп. Ij+1 - совокупность рёбер искомого дерева. В противном случае
j := j+1, идём к шагу 2.
Алгоритм Краскала выполняет не более чем m итераций, сложность алгоритма O(m log m).

3.

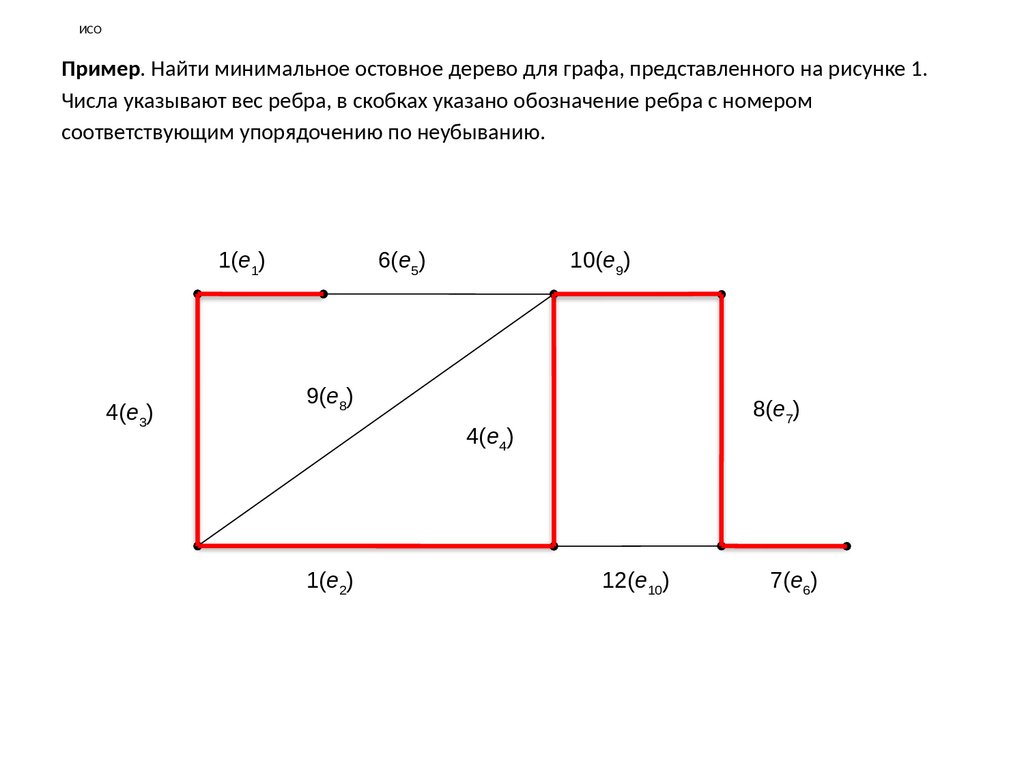
ИСО
Пример. Найти минимальное остовное дерево для графа, представленного на рисунке 1.
Числа указывают вес ребра, в скобках указано обозначение ребра с номером
соответствующим упорядочению по неубыванию.
1(e1)
4(e3)
6(e5)
10(e9)
9(e8)
8(e7)
4(e4)
1(e2)
12(e10)
7(e6)

4.

ИСО
Теорема 2. Алгоритм Крускала корректен.
Доказательство проведём от противного. Пусть K=(V,T) остовное дерево, построенное
алгоритмом Крускала и w(K) его вес. Предположим, что существуют остовные деревья с
меньшим весом. Среди всех таких деревьев выберем дерево K’=(V,T’), имеющее
минимальное число общих ребер с K. Пусть e’ – ребро минимального веса из рёбер
множества T’\T. Алгоритм Крускала не добавляет это ребро в решение T. Это означает, что
добавление e’ к рёбрам, выбранным алгоритмом и имеющим вес не больше w(e’), приводит
к образованию некоторого цикла C в исходном графе G. В цикл C должно входить ребро e из
T\T’, иначе K’ содержит цикл.
e
С
e’
Добавим к K’ ребро e’ и удалим e. Получим новое остовное дерево K’’=(V,T’’), у которого вес
w(K’’) ≤ w(K’), причём |T∩T’’| < |T∩T’|. Что противоречит выбору дерева K’=(V,T’), как дерева
имеющего минимальное число общих ребер с K.

5.

ИСО
Обозначим через Oe ( Ij ) множество рёбер из E \ Ij, в котором каждое ребро инцидентно с
некоторым ребром из Ij . Полагаем Oe (
) = E.
Алгоритм Прима. Начальный шаг: j = 0, I0 =
.
Шаг 1. Строим множество Oe ( Ij ) и упорядочиваем его рёбра по неубыванию весов. Пусть
Oe ( Ij ) = { } и .
Шаг 2.1. k = 1.
Шаг 2.2.
I j ekj , если I j ekj не содержит цикла ,
I j 1
I j , в противном случае.
Шаг 2.3. Если Ij+1 ≠ Ij , то идем к шагу 3. В противном случае k := k + 1 и возвращаемся
к шагу 2.2.
Шаг 3. Если | Ij+1 | = n-1, стоп. Ij+1 - совокупность рёбер искомого дерева. В противном случае
j := j+1, идём к шагу 1.
Cложность алгоритма Прима составляет O(m + n log n).

6.

ИСО
1(e1)
4(e3)
6(e5)
10(e9)
9(e8)
8(e7)
4(e4)
1(e2)
12(e10)
7(e6)

7.

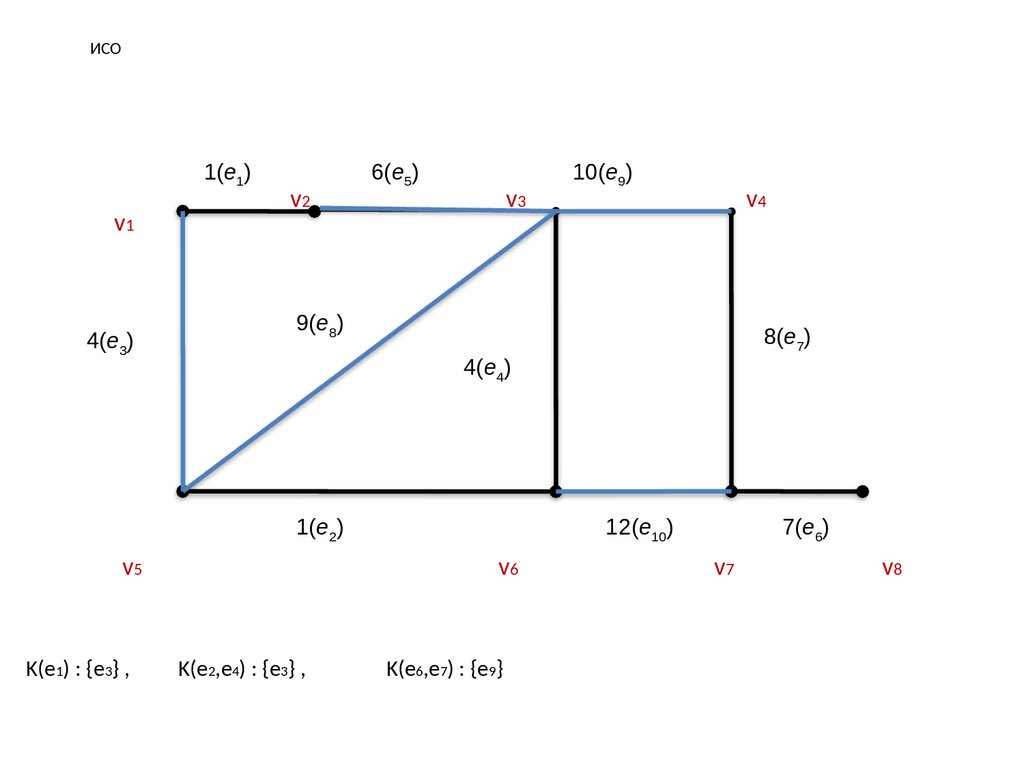
ИСО
Для подграфа G’(V ‘, E’) графа G( V, E ) обозначим через Ov (G’ ) множество рёбер из E \ E’
инцидентных ровно с одной вершиной множества V ‘. Через V( Ij ) обозначим множество
вершин графа G( V, E ) инцидентных рёбрам из Ij . При этом положим V(
) = V.
Алгоритм Борувки. Начальный шаг: j = 0, I0 =
.
Шаг 1. Упорядочиваем рёбра множества E в порядке неубывания их весов.
j
j
j
Шаг 2. Выделяем компоненты связности K1 , K 2 , ... , K p j подграфа G’(V( Ij ), Ij ),
образованного рёбрамиj Ij .
K i , i 1, p j
Шаг 3. Для
каждого
, находим первое в упорядочении, полученном на шаге
eij
O v K i j
w(eij ) min { w(e) | e Ov ( K i j ) }
1,
i 1, p
eij
ребро
из
. Очевидно, j
.
Шаг 4. Полагаем Ij+1 = Ij
{ ,
}.
Шаг 5. Если | Ij+1 | = n-1, стоп. Ij+1 - совокупность рёбер искомого дерева. В противном случае
j := j+1, идём к шагу 2.
Cложность алгоритма Борувки составляет O(m log n).
Пример. Схема алгоритма Борувки представлена на рисунке.
1(e1)
4(e3)
6(e5)
10(e9)
9(e8)
4(e4)
1(e2)
8(e7)
12(e10)
7(e6)
4(e3)
1(e1)
6(e5)
10(e9)
9(e8)
4(e4)
1(e2)
8(e7)
12(e10)
7(e6)

8.

ИСО
1(e1)
v1
4(e3)
v2
6(e5)
v3
v4
9(e8)
8(e7)
4(e4)
1(e2)
12(e10)
v5
K(v1):{e1} , K(v2):{e1} ,
10(e9)
v6
K(v3):{e4} ,
K(v4):{e7} ,
K(v5):{e2} , K(v6):{e2} ,
7(e6)
v7
v8
K(v7):{e6} ,
K(v8):{e6}

9.

ИСО
1(e1)
v1
4(e3)
v2
6(e5)
v3
v4
9(e8)
8(e7)
4(e4)
1(e2)
v5
K(e1) : {e3} ,
10(e9)
12(e10)
v6
K(e2,e4) : {e3} ,
K(e6,e7) : {e9}
7(e6)
v7
v8

10.

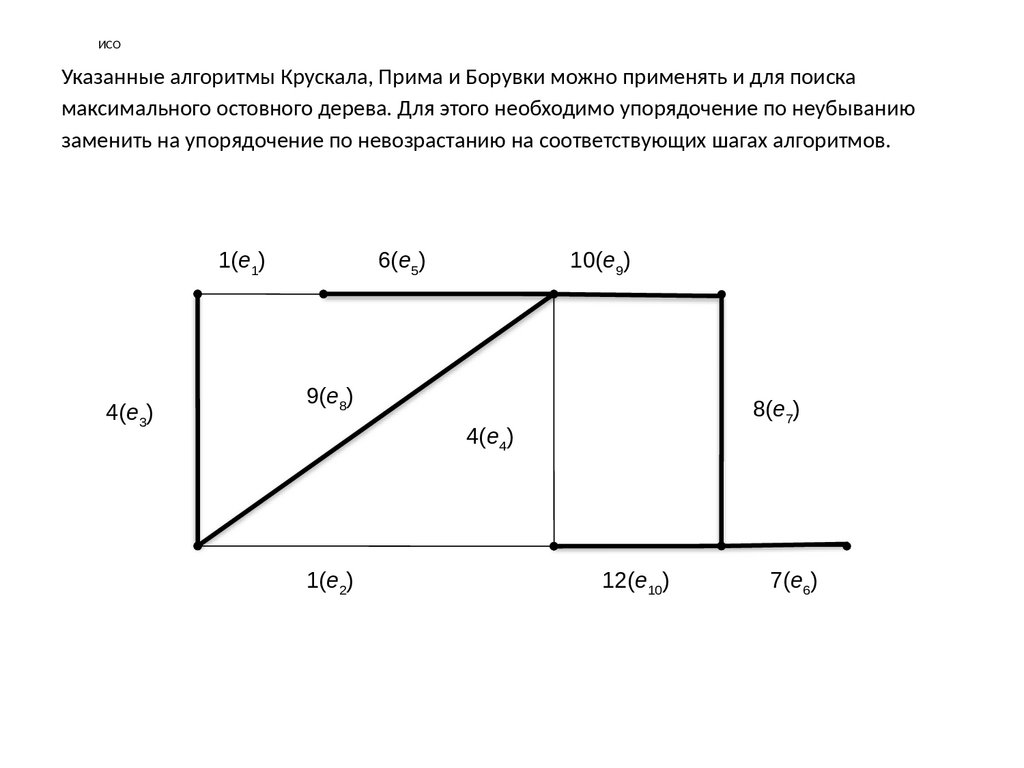
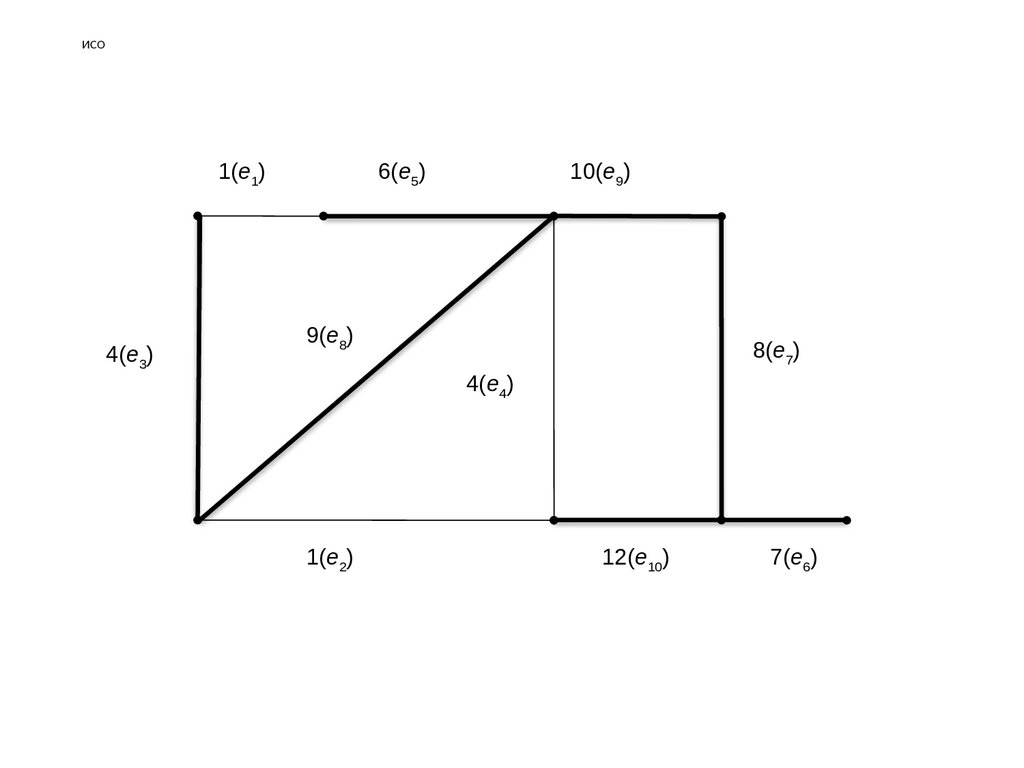
ИСО
Указанные алгоритмы Крускала, Прима и Борувки можно применять и для поиска
максимального остовного дерева. Для этого необходимо упорядочение по неубыванию
заменить на упорядочение по невозрастанию на соответствующих шагах алгоритмов.
1(e1)
4(e3)
6(e5)
10(e9)
9(e8)
8(e7)
4(e4)
1(e2)
12(e10)
7(e6)

11.

ИСО
1(e1)
4(e3)
6(e5)
10(e9)
9(e8)
8(e7)
4(e4)
1(e2)
12(e10)
7(e6)

12.

ИСО
1(e1)
4(e3)
6(e5)
10(e9)
9(e8)
8(e7)
4(e4)
1(e2)
12(e10)
7(e6)