Метод группировки данных. Закон нормального распределения

1. Практическая работа №2

«Метод группировки данных. Закон
нормального распределения»

2. Цель работы

Получение навыков работы с группировками в одномерной
статистической модели. Научится рассчитывать статистические
показатели центра распределения случайной величины в
группировке и научится проверке распределения на соответствие
закону нормального распределения.

3. Задачи

I.
Рассчитать расхождение значений коэффициента пористости Кп по
АК.
II. Провести группировку значений коэффициента пористости Кп (по
АК) по количеству образцов.
III. Определить среднее арифметическое значение, модальное и
медианное значения коэффициента пористости Кп (по группировке).
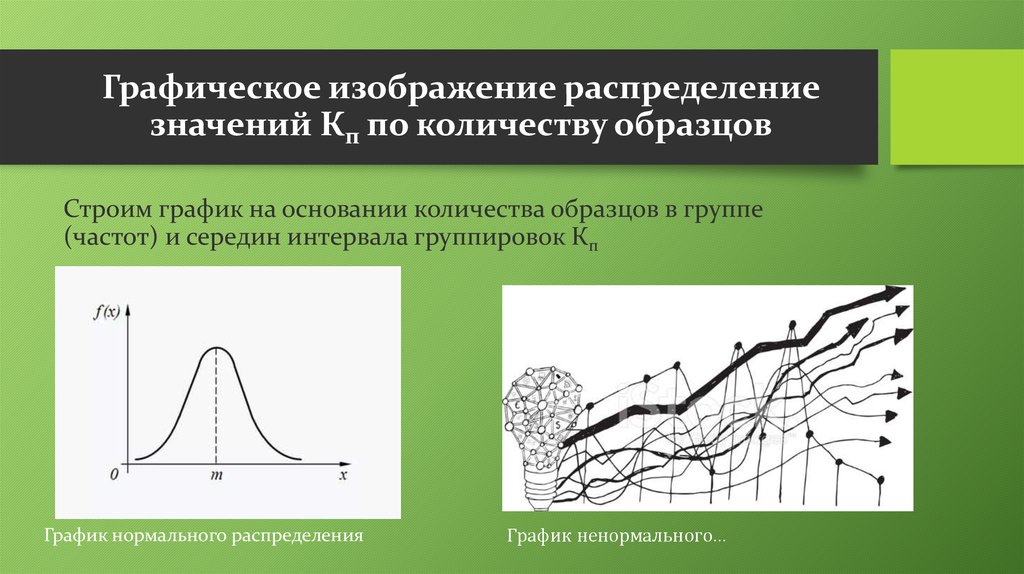
IV. Изобразить распределение значений Кп по количеству образцов.
V. Провести проверки на соответствие закону нормального
распределения.
VI. Сделать выводы.

4. Рассчитать расхождение значений коэффициента пористости Кп по АК

Абсолютное расхождение рассчитаем по следующей формуле:
Абс. = Кп АК − Кп СП ,
где Кп АК – коэффициент пористости по АК;
Кп СП – коэффициент пористости по СП.
Относительное расхождение рассчитаем по следующей формуле:
Абс.
Отн. =
∙ 100%
Кп СП

5. Группировка значений коэффициента пористости Кп (по АК) по количеству образцов

Для группировки необходимо рассчитать количество групп (n) размах (R)
и шаг интервала (h). Количество групп рассчитывается по методу
Стерджеса:
n 1 3,322 lg N
N – количество единиц в совокупности
Размах считается по формуле:
R = Хmax – Хmin
Xmax – максимальное значение признака в совокупности; Xmin –
минимально значение признака в совокупности.
Шаг считается по следующей формуле:
R
h
n

6. Определение среднего арифметического значения, модального и медианного значения коэффициента пористости Кп

Простое среднее арифметическое считается по следующей формуле: xi – значение i-того члена ряда; n –
количество членов в ряду.
x
x1 x2 ... xn
n
x
i
n
Средневзвешенное арифметическое считается по формуле:
x f
x
f
i
i
i
fi – значения параметра, по которому взвешиваем член ряда.
1
∗ σ