Логические схемы

1.

ЛОГИЧЕСКИЕ СХЕМЫ

2.

Пауль Эренфест (Paul Ehrenfest),
(1880—1933) — нидерландский
физик-теоретик.
Пауль Эренфест родился и вырос в
Вене, в еврейской семье,
происходившей из Моравии
(исторической область в Чехии).
Ученик Л. Больцмана. Окончил
Венский университет (1904), затем
вместе с женой — русским физиком Т.
А. Афанасьевой-Эренфест переехал в
Россию.
С 1912 профессор Лейденского
университета (Нидерланды). Оказал
большое влияние на развитие
теоретической физики в России и
СССР. Иностранный член АН СССР
(1924).

3.

Эренфест писал в 1910 году:
«…Пусть имеется проект схемы проводов
автоматической телефонной станции. Надо
определить: 1) будет ли она правильно
функционировать при любой комбинации, могущей
встретиться в ходе деятельности станции; 2) не
содержит ли она излишних усложнений.

4.

Каждая такая комбинация является посылкой,
каждый маленький коммутатор есть логическое
«или-или», воплощенное в эбоните и латуни; все
вместе – система чисто качественных … «посылок»,
ничего не оставляющих желать в отношении
сложности и запутанности … правда ли, что
несмотря на существование алгебры логики, своего
рода «алгебра распределительных схем» должна
считаться утопией?»

5.

Созданная позднее Михаил Александрович
Гавриловым (1903 -1979) теория релейно-контактных
схем показала, что вовсе не утопия.
Защита ученым докторской диссертации в самом
конце 40-х гг. вызвала эффект разорвавшейся бомбы,
хотя название работы "Теория релейных устройств“ не
давало повода для полемики.
Надо вспомнить, какие это были годы в истории
нашей страны. Кибернетика делала на Западе свои
первые шаги по пути интеграции различных научных
дисциплин, а у нас она считалась "буржуазной
лженаукой".
В это нелегкое время М. А. Гаврилов выдвинул
идею о том, что многие инженерные задачи
проектирования устройств релейной автоматики можно
решать формальными методами, используя для этого
аппарат математической логики.
Эта идея впервые промелькнула в работах советского физика В. И. Шестакова.
Американский исследователь К. Шеннон и японские ученые также приблизились к мысли
о том, что ряд инженерных задач синтеза допускает формальное математическое
решение. Но лишь Гаврилову удалось довести эту идею до практических методов синтеза
схем и устройств, в которых использовались контакты, управляемые реле. За эту
крамольную по тем временам идею М. А. Гаврилова обвинили в идеализме, в попытке
протащить в советскую науку чуждые ей идеи. И надо было обладать незаурядным
мужеством, уверенностью в правильности выбранного пути, чтобы упорно работать над
созданием нового научного направления, которое стало основой технической
кибернетики и способствовало возникновению теории автоматов, теории ЭВМ и многих
других дисциплин, без которых сейчас трудно было бы представить информатику.

6.

А
А
В
В
А

7.

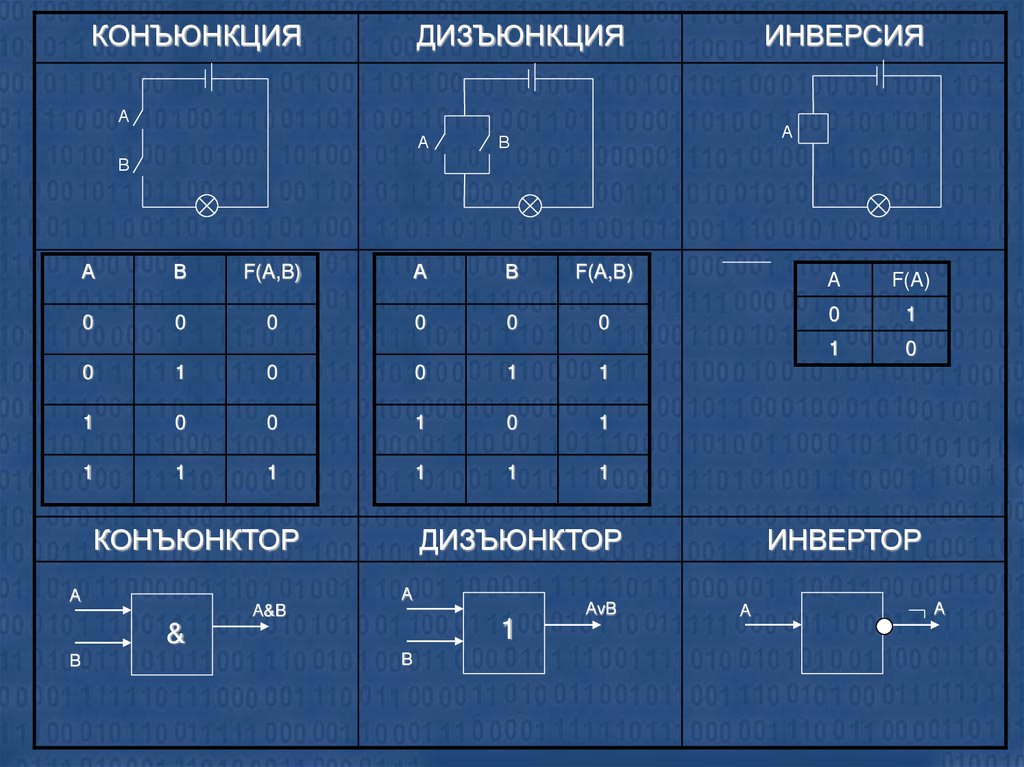
КОНЪЮНКЦИЯ
ДИЗЪЮНКЦИЯ
ИНВЕРСИЯ
А
А
В
А
В
А
В
F(A,B)
А
В
F(A,B)
A
F(A)
0
0
0
0
0
0
0
1
1
0
0
1
0
0
1
1
1
0
0
1
0
1
1
1
1
1
1
1
КОНЪЮНКТОР
А
А&B
&
В
ДИЗЪЮНКТОР
А
АvB
1
В
ИНВЕРТОР
А
А

8.

ПЕРЕКЛЮЧАТЕЛЬНЫЕ СХЕМЫ

9.

ПЕРЕКЛЮЧАТЕЛЬНАЯ СХЕМА — это схематическое изображение
некоторого устройства, состоящего из переключателей и
соединяющих их проводников, а также из входов и выходов, на
которые подаётся и с которых снимается электрический сигнал.
x
y
x
x
y

10.

Каждый переключатель имеет только два состояния: замкнутое и
разомкнутое. Переключателю Х поставим в соответствие логическую
переменную х, которая принимает значение 1 в том и только в том
случае, когда переключатель Х замкнут и схема проводит ток; если
же переключатель разомкнут, то х равен нулю.

11.

Будем считать, что два переключателя Х и Х связаны таким
образом, что когда Х замкнут, то Х разомкнут, и наоборот.
Следовательно, если переключателю Х поставлена в соответствие
логическая переменная х, то переключателю Х должна
соответствовать х переменная.
Всей переключательной схеме также можно поставить в
соответствие логическую переменную, равную 1, если схема
проводит ток, и равную 0 — если не проводит. Эта переменная
является функцией от переменных, соответствующих всем
переключателям схемы, и называется функцией проводимости.

12.

Найдем функции проводимости F некоторых переключательных схем:
a)
Схема не содержит переключателей и проводит ток всегда, следовательно F=1;
б)
Схема содержит один постоянно разомкнутый контакт, следовательно F=0;
x
в)
Схема проводит ток, когда переключатель х замкнут, и не проводит, когда х разомкнут,
следовательно, F(x) = x;
г)
x
Схема проводит ток, когда переключатель х разомкнут, и не проводит, когда х замкнут,
следовательно, F(x) = x ;
y
x
д)
Схема проводит ток, когда оба переключателя замкнуты, следовательно, F(x) = x ^ y;
е)
x
y
Схема проводит ток, когда хотя бы один из переключателей замкнут, следовательно,
F(x)=x v y;

13.

Две схемы называются РАВНОСИЛЬНЫМИ, если через одну из них
проходит ток тогда и только тогда, когда он проходит через другую
(при одном и том же входном сигнале).
Из двух равносильных схем более простой считается та схема,
функция проводимости которой содержит меньшее число логических
операций или переключателей.

14.

СИНТЕЗ СХЕМЫ по заданным условиям ее работы сводится к
следующим трём этапам:
1. Составлению функции проводимости по таблице истинности,
отражающей эти условия;
2. Упрощению этой функции;
3. Построению соответствующей схемы.
АНАЛИЗ СХЕМЫ сводится к:
1. Определению значений её функции проводимости при всех
возможных наборах входящих в эту функцию переменных;
2. Получению упрощённой формулы.