Решение неравенств. 9 класс

1.

20.04.2023
9 класс
Повторение по теме
«Решение неравенств»

2.

Число а больше числа b,
если разность а – b – положительное число
a > b, если а – b > 0
Число а меньше числа b,
если разность а – b – отрицательное число
a < b, если а – b < 0
Если а – b = 0, то а = b
На координатной прямой большее число
изображается точкой, лежащей правее, а меньшее
– точкой, лежащей левее.

3.

Свойства числовых неравенств:
Если a > b и b > с, то a > c
a
c
b
Если a > b, с любое число, то a+c > b+c
Если к обеим частям верного неравенства прибавить
одно и то же число, то получится верное неравенство
Если а > b и с- положительное число (c > 0), то ac > bc
Если обе части верного неравенства умножить или
разделить на одно и то же положительное число, то
получится верное неравенство
Если а > b и с - отрицательное число (c<0), то ac< bс
Если обе части верного неравенства умножить или разделить
на одно и то же отрицательное число, и изменить знак
неравенства на противоположный, то получится верное
неравенство

4.

Какие неравенства соответствуют
промежуткам?
0;
;5
3;5
; 5
х 5
х 5
х≥0
3 х 5

5.

Определения
1. Линейные неравенства – неравенства вида
ах+в>0 (<0, > 0, < 0), где х – переменная, а и
в – числа.
2. Квадратные неравенства – неравенства
вида ах2+вх+с>0 (<0, > 0, < 0), где х –
переменная, а, в и с – числа, а≠0.

6.

При решении неравенств
используются следующие свойства:
Свойство 1. Если из одной части неравенства
перенести в другую слагаемое с противоположным
знаком, то получится равносильное ему
неравенство.
ax b c
ax c b

7.

Свойство 2. Если обе части неравенства умножить
или разделить на одно и то же положительное
число, то получится равносильное ему неравенство.
ax b :а
a 0
b
x
a

8.

Если обе части неравенства умножить или
разделить на одно и то же отрицательное число,
изменив при этом знак неравенства на
противоположный, то получится равносильное
ему неравенство.
ax b :а
a 0
b
x
a

9.

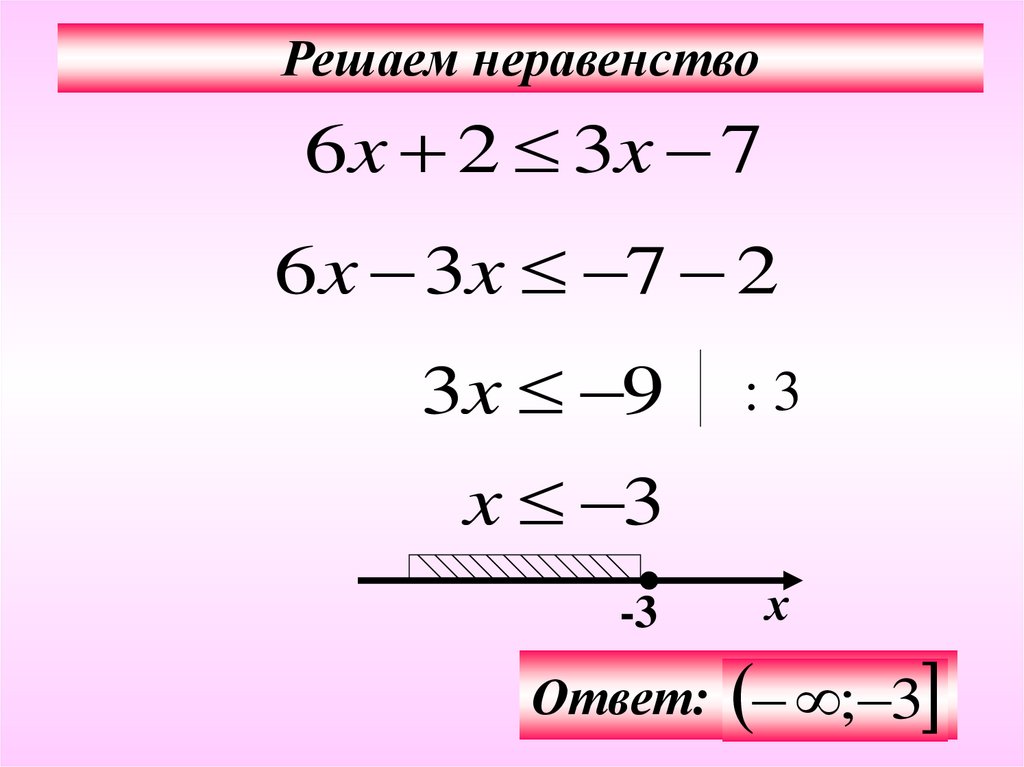
Решаем неравенство
6x 2 3x 7
6x 3x 7 2
3x 9
:3
x 3
-3
х
Ответ: ; 3

10. Решите неравенство

5(х – 1) + 7 ≤ 1 – 3(х + 2)
5х – 5 + 7 ≤ 1 – 3х – 6
5х + 3х ≤ 5 – 7 + 1 – 6
8х ≤ - 7
х≤- 7
8
7
Ответ: ( - ∞; - ]
8
вернуться

11.

Алгоритм решения квадратного
неравенства
1) Находят дискриминант квадратного
трехчлена ах2+вх+с и выясняют, имеет ли
трехчлен корни;
2
aх + bх + с = 0 D >0, два корня х1 и х2
2
D = b – 4ac
– b +- D
х 1, 2 =
2a
D=0, один корень х
D<0 корней нет

12.

2) Если трехчлен имеет корни, то отмечают
их на оси х и через отмеченные точки
проводят схематически параболу, ветви
которой направлены вверх при а > 0 или вниз
при а < 0; если трехчлен не имеет корней, то
схематически изображают параболу,
расположенную в верхней
Трехчленполуплоскости
не имеет корнейпри
> 0 0;
а<0
а > 0 или в нижней приа а<
х1
х2
х1
х2
х1
х2
х1
х2

13.

3) Находят на оси х промежутки, для
которых точки параболы расположены выше
оси х (если решают неравенство ах+вх+с>0)
2
или ниже оси х (если решают неравенство
2
ах+вх+с<0)
2
2
aх + bx + c < 0
aх + bx + c > 0
х1
х2
х1
х2

14. Устная работа

На рисунках изображен график функции у=ах²+вх+с, определите знаки
коэффициента a и дискриминанта D
у
1)
0 1
х
3
-1
а>0,
D >0
3)
4)
у
-3
0
у
2)
1
а<0,
D >0
х
а>0,
D =0
х
0
а < 0,
D <0
у
0
3
х

15.

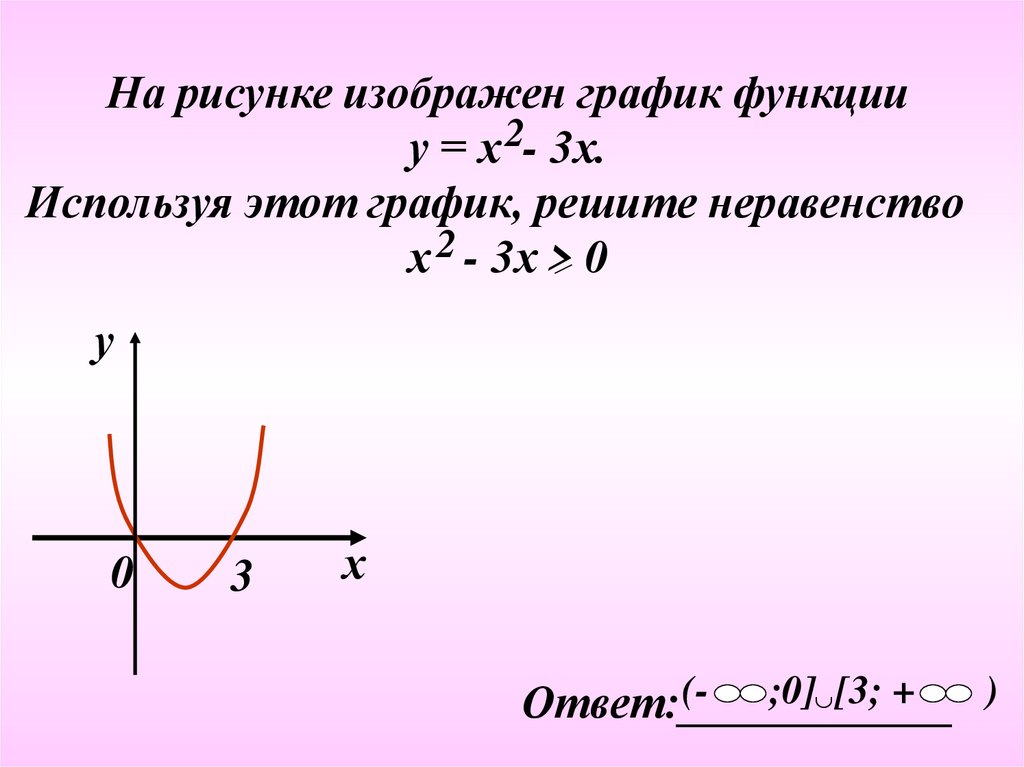
На рисунке изображен график функции
у = х 2- 3х.
Используя этот график, решите неравенство
х 2 - 3х > 0
у
0
3
х
(;0] [3; +
)
Ответ:____________

16.

Укажите неравенство, которое не имеет решений:

17. Решите неравенство:

х 8 х 15 0
2
а) ( 3; 5)
б) [ 3; 5 ]
в) (- ∞; 3) U (5; + ∞)
г) (- ∞; 3 ] U [ 5; + ∞)

18.

Решаем систему неравенств
2 х 7,
3 x 18
2 х 1 6,
5 3х 13
3,5
6
х 3,5,
x 6
Ответ: 3,5 x 6

19.

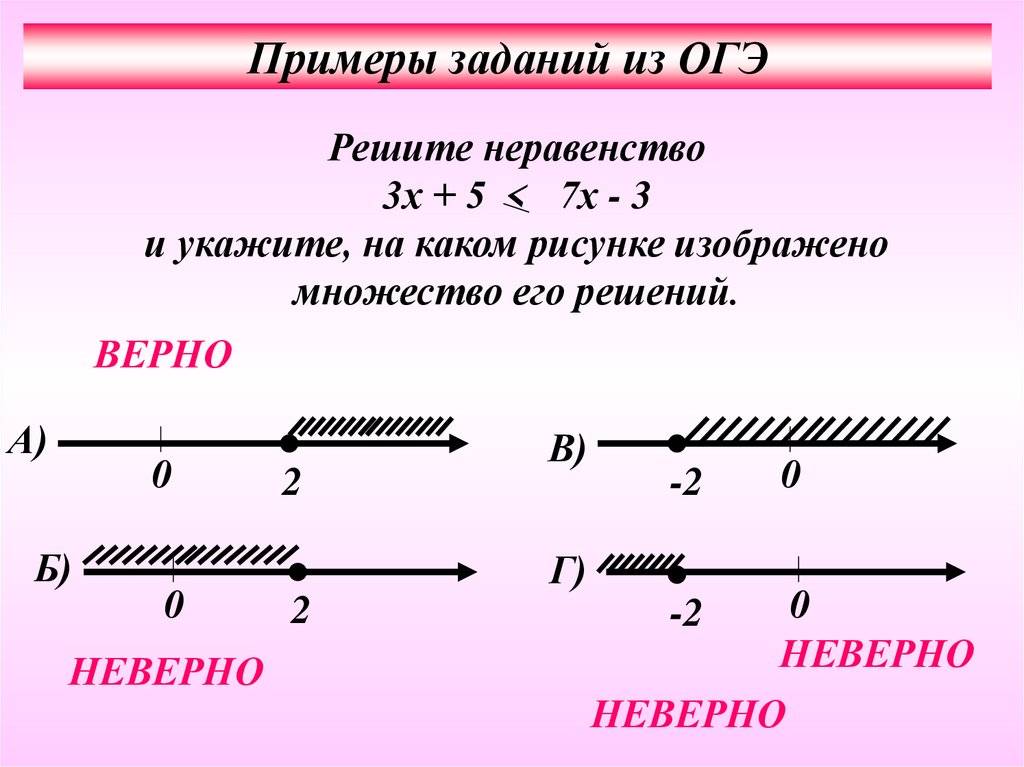
Примеры заданий из ОГЭ
Решите неравенство
3х + 5 < 7х - 3
и укажите, на каком рисунке изображено
множество его решений.
ВЕРНО
А)
0
Б)
0
НЕВЕРНО
2
В)
-2
0
-2
0
НЕВЕРНО
Г)
2
НЕВЕРНО

20.

Решите неравенство
5 х + 20 < 2(4х – 5)
А) (-10; +
Б) (-
)
НЕВЕРНО
; -10)
НЕВЕРНО
В) (10; +
Г) (-
; 10)
)
ВЕРНО
НЕВЕРНО

21.

Домашнее задание:
1. Решить неравенства:
17 ( x 2) 12 x 11 ;
5( x 10)(5 x 2)(1 x) 0
x 2 10 x 0 ;
3x 2 2 x 1 0 .
2. Решить двойное неравенство: 0 2x 4 14 ;
3. Решить системы неравенств:
1)
2 x 0
;
2 x 1 0
2)
x 2 4 0
2
x 5 x 6 0