Matrix form of the force method. Compliance Matrix. Lecture 12

1. Lecture 12 Matrix form of the force method. Compliance Matrix.

L X p 0
L
X
- is a matrix consisting of unit coefficients,
is a vector whose components are unknown
reactions of dropped bonds,
p is a vector whose components are the free
terms of the canonical equations.

2. Matrices of canonical equations of the force method for a 3-fold statically indeterminate system

11 12 13
L 21 22 23 ,
31 32 33
1 p
p 2p ,
3p
X1
X X2
X
3

3. Matrices of unit and freight movements

L L1 BL1 , C L1 B,
CL p ,
L
• 1 - a matrix whose elements are the ordinates of unit
diagrams of bending moments at fixed points ,
Mi ,
i 1,2,......n
L• 1 - transposed matrix, which is obtained from a direct matrix by
replacing rows with columns,
Lp
- a matrix whose elements are the ordinates of the load
diagram Мр at fixed points, i.e. ordinates of the diagram of
bending moments in the main system due to external influence
Р, В – system compliance matrix

4. System Compliance Matrix

B1
0
0
0
B
0
.
.
0
0
B2
0
0
0
.
.
0
0
0
B3
0
0
.
.
0
0
0
0
.
0
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
0
0
0
0
.
0
.
.
Bs
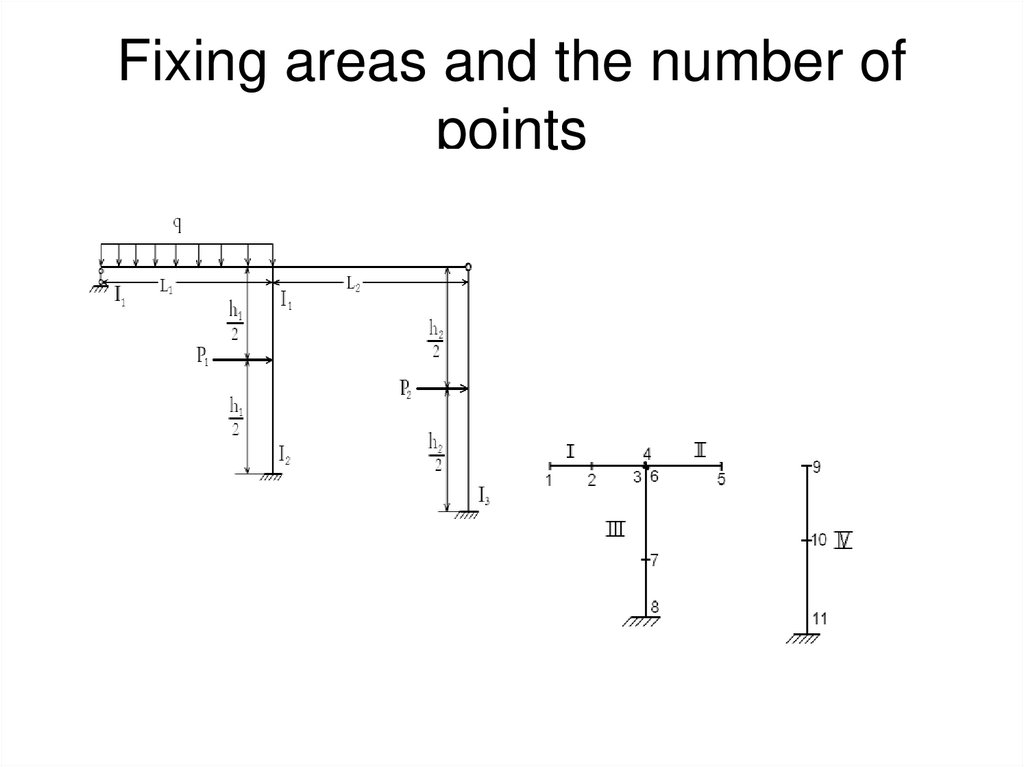
Вi is the compliance matrix in the i-th section,
s is the number of system sections

5. Compliance matrix B for a section with one fixed point

• 1. If one point is fixed on the site, then
l
B
6 EI
EI - bending stiffness of the section,
l - section length

6. Compliance matrix B for a section with two fixed points

l 2 1
B
6EI 1 2
EI–
bending stiffness of the section,
l - section length

7. Compliance matrix B in the section with a distributed load

• If three points are fixed on the section, then with
a distributed load of constant intensity, the
compliance matrix has the form:
1 0 0
l
B
0 4 0
6EI
0 0 1

8. Compliance matrix B for a section with a concentrated load

1 0,5 0
l
B
0,5 2 0,5
6EI
0
0
,
5
1

9. Compliance matrix B for a section with a concentrated force when two points are fixed

l 2 2 1
B
6EI 1 2 2

10. Solution of the canonical equations of the force method in vector form

1
X L ð
a~11
~
a 21
.
L 1
.
.
a~
n1
a~12
a~22
.
.
.
a~n 2
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
a~1n
~
a 2n
.
.
.
a~nn
i j
( 1)
~
aij
D
Dij

11. Inverse Matrix Check

Inverse
Matrix
1
L
1 0 . . 0
0 1 . . 0
1
L L E . . . . .
. . . . .
0 0 . . 1
Check

12. Bending moment and shear force vectors

M L1 X L p ,
dM
Q
K M
dx

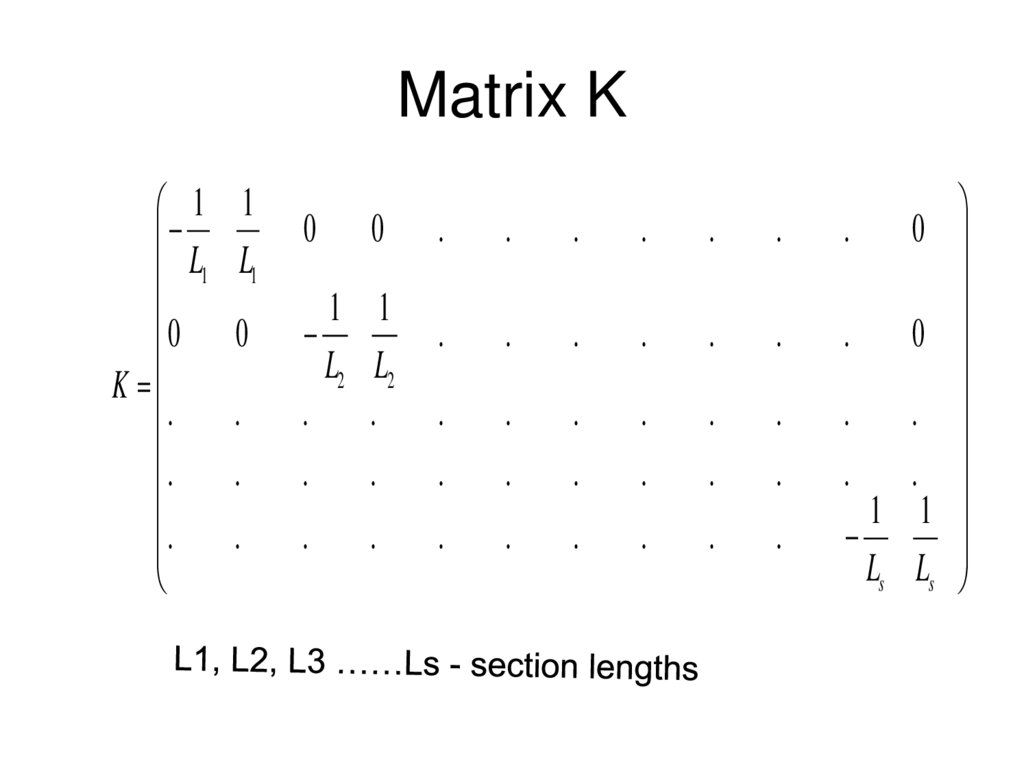
13. Matrix K

1 1
L1 L1
0 0
K
.
.
.
.
.
.
0
0
1 1
L2 L2
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
0
.
0
.
.
.
.
1 1
Ls Ls

14. Fixing areas and the number of points