Similar presentations:
Представление чисел в компьютере. Математические основы информатики. Информатика. 8 класс
1.
ПРЕДСТАВЛЕНИЕЧИСЕЛ В КОМПЬЮТЕРЕ
МАТЕМАТИЧЕСКИЕ ОСНОВЫ
ИНФОРМАТИКИ
2.
Ключевые слова• разряд
• беззнаковое представление целых
чисел
• представление целых чисел со
знаком
• представление вещественных чисел
3.
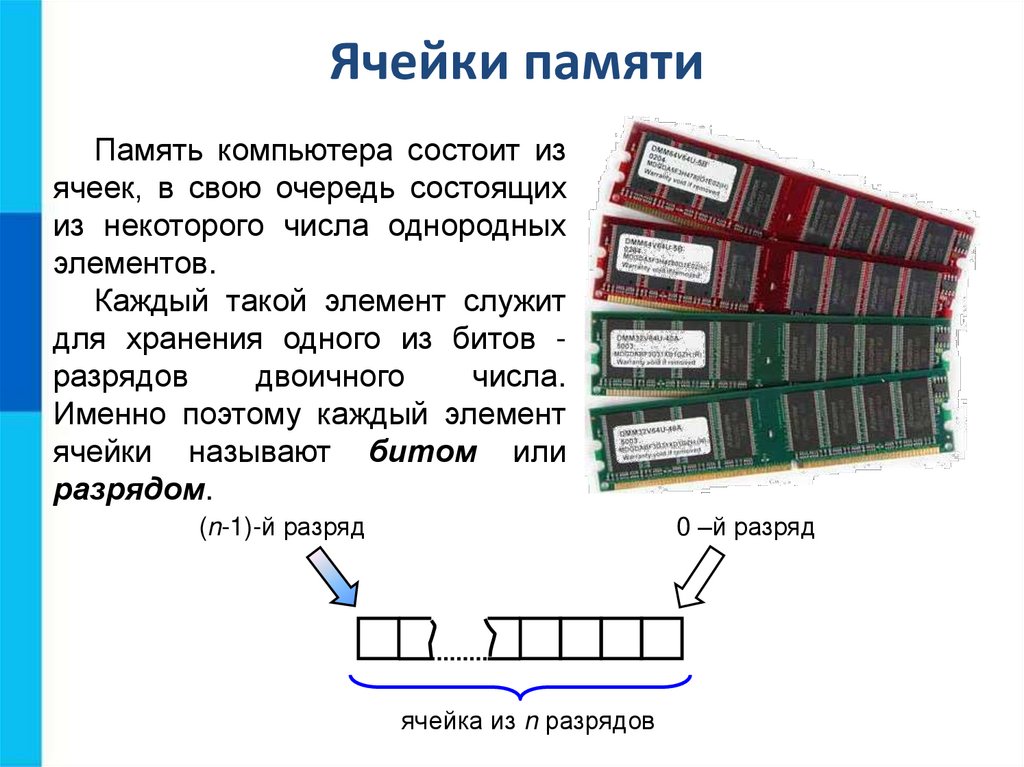
Ячейки памятиПамять компьютера состоит из
ячеек, в свою очередь состоящих
из некоторого числа однородных
элементов.
Каждый такой элемент служит
для хранения одного из битов разрядов
двоичного
числа.
Именно поэтому каждый элемент
ячейки называют битом или
разрядом.
(n-1)-й разряд
0 –й разряд
ячейка из n разрядов
4.
БАЙТБАЙТ
БАЙТ
БАЙТ
БАЙТ
5.
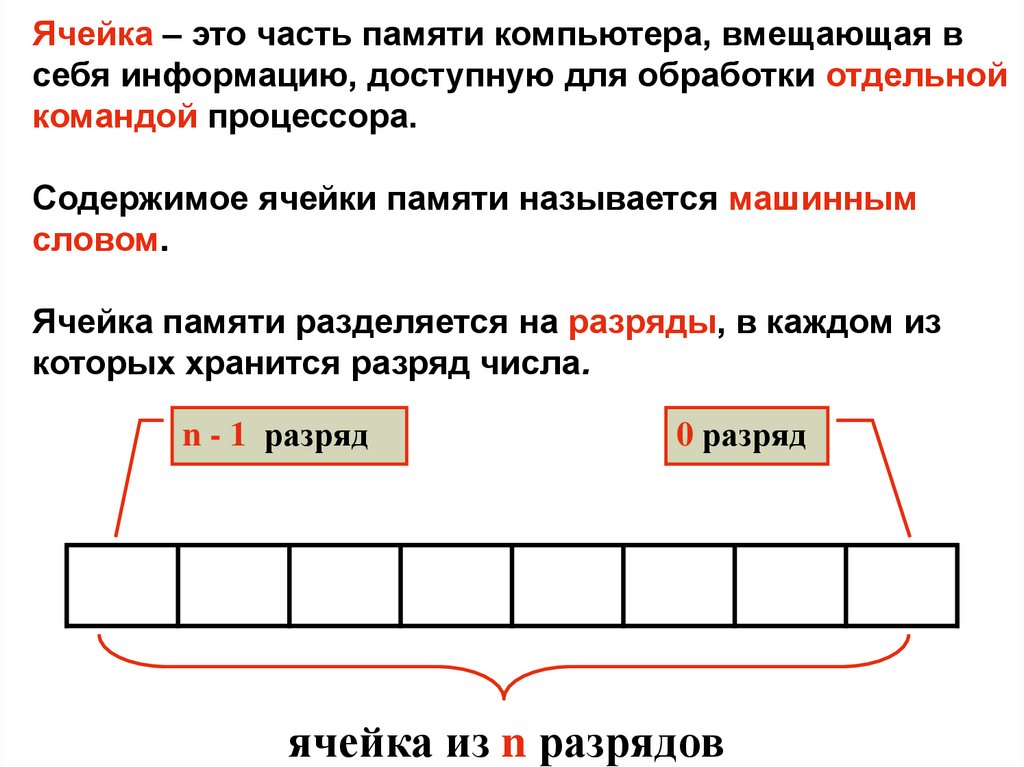
Ячейка – это часть памяти компьютера, вмещающая всебя информацию, доступную для обработки отдельной
командой процессора.
Содержимое ячейки памяти называется машинным
словом.
Ячейка памяти разделяется на разряды, в каждом из
которых хранится разряд числа.
n - 1 разряд
0 разряд
ячейка из n разрядов
6.
Единицы измерения объема информацииКоличество информации, хранящейся в ЭВМ,
измеряется её «объемом», который
выражается в битах
(от английского binary digit — двоичная цифра).
Элемент ячейки памяти ЭВМ
называют Битом (или разрядом).
7.
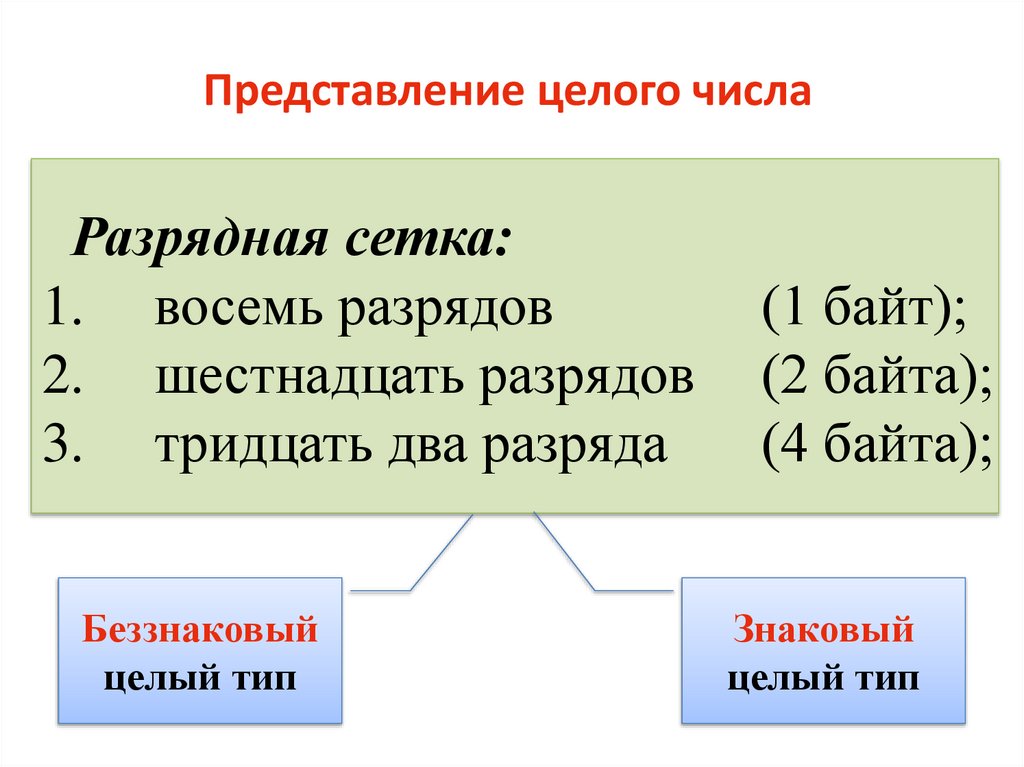
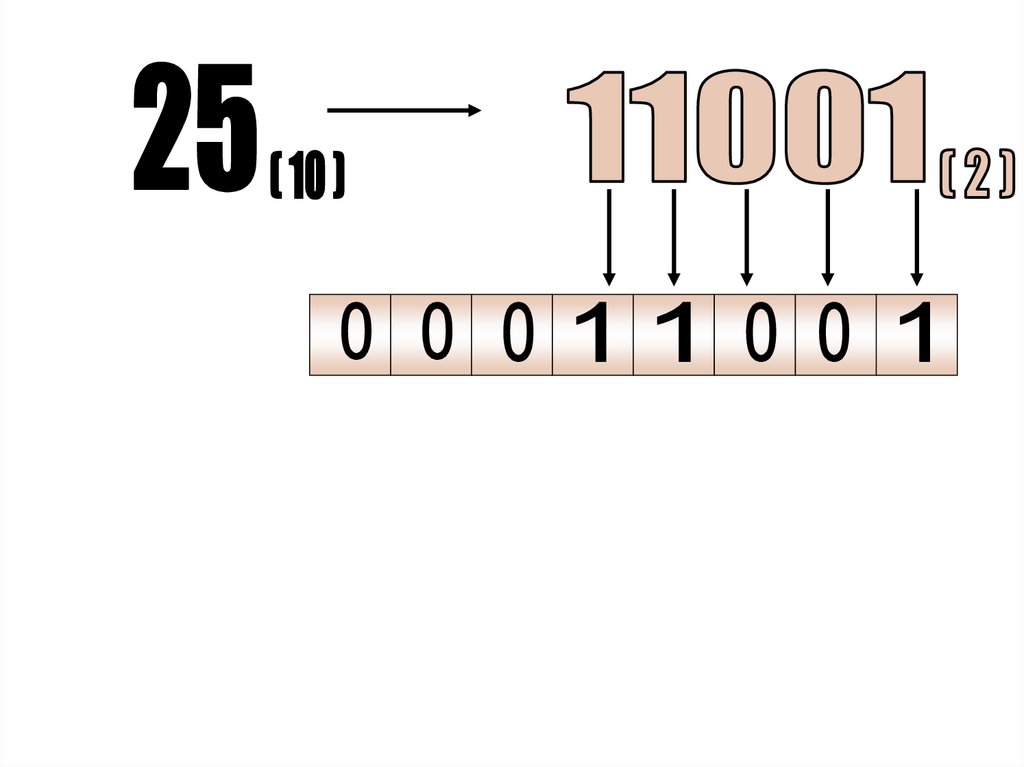
Представление целого числаРазрядная сетка:
1. восемь разрядов
2. шестнадцать разрядов
3. тридцать два разряда
Беззнаковый
целый тип
(1 байт);
(2 байта);
(4 байта);
Знаковый
целый тип
8. Беззнаковое представление используются для таких объектов:
• Адреса ячеек;• Счётчики;
• Числа, обозначающие дату и время;
• Числа, обозначающие размеры графических
изображений в пикселях.
9.
Двоичный код10.
11.
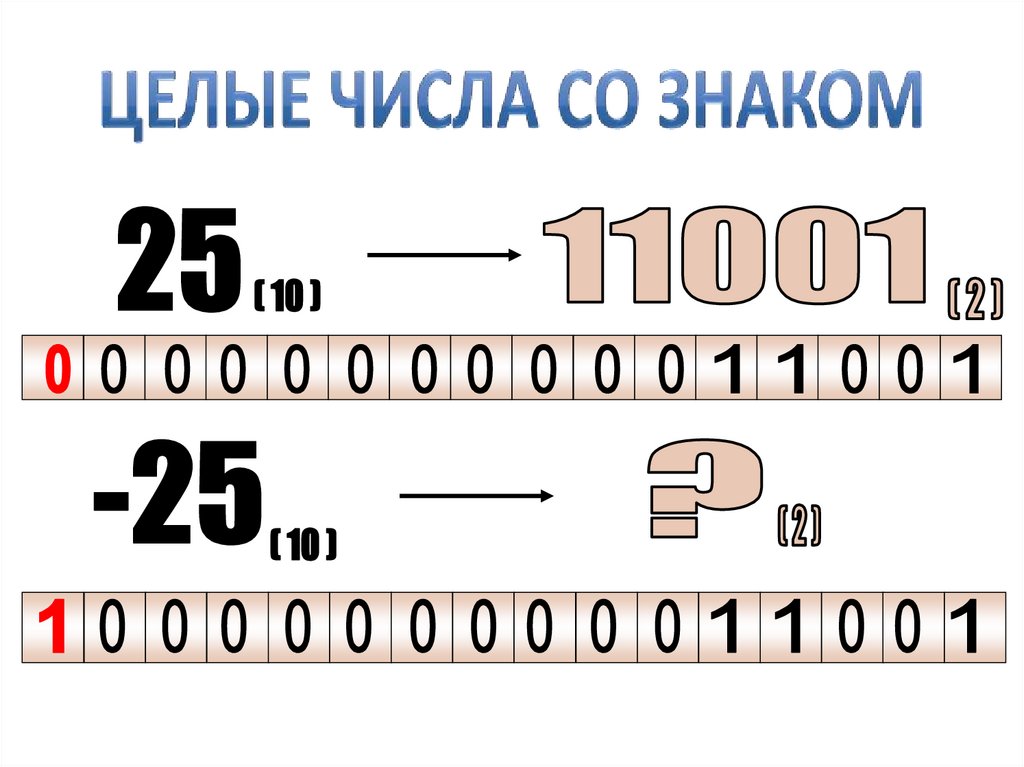
Целые числа со знаком«+»
0
«-»
1
12. Целые числа со знаком
• Разряды числа в коде жестко связаны сразрядной сеткой (8, 16, 32, 64 разряда);
• Для записи кода знака числа в разрядной
сетке отводится фиксированный разряд.
Знаковым разрядом является старший разряд
в разрядной сетке.
знаковый разряд
7
0
0
0
0
1
1
0
0
1
13.
14.
15.
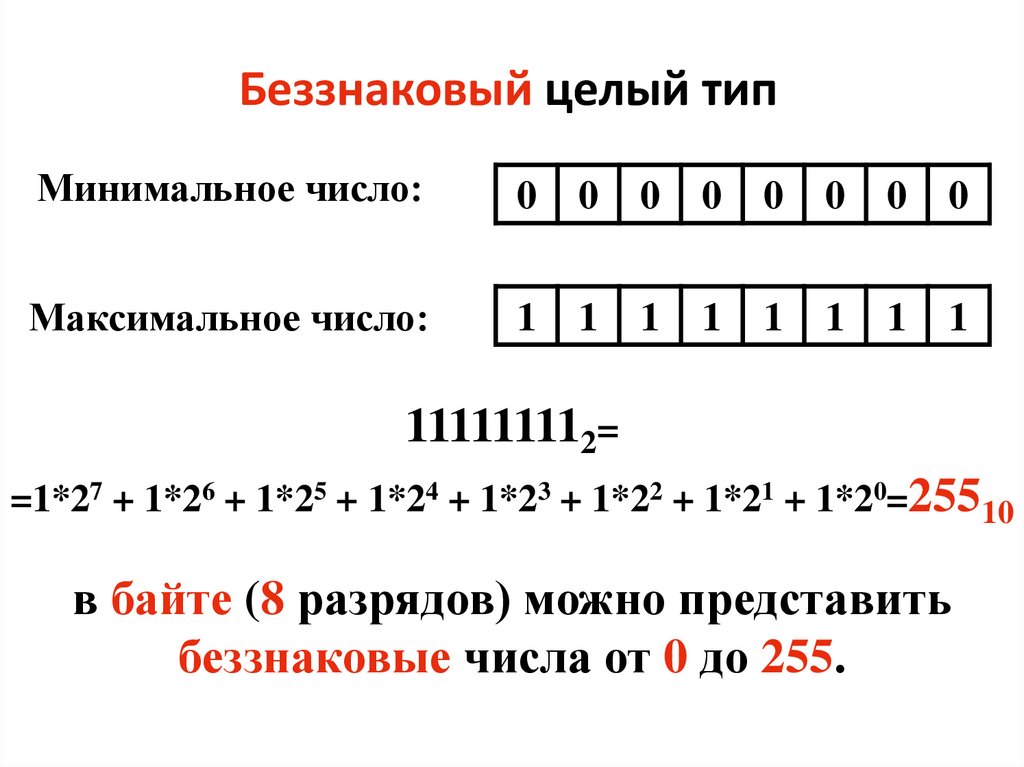
Беззнаковый целый типМинимальное число:
0
0
0
0
0
0
0
0
Максимальное число:
1
1
1
1
1
1
1
1
111111112=
=1*27 + 1*26 + 1*25 + 1*24 + 1*23 + 1*22 + 1*21 + 1*20=25510
в байте (8 разрядов) можно представить
беззнаковые числа от 0 до 255.
16.
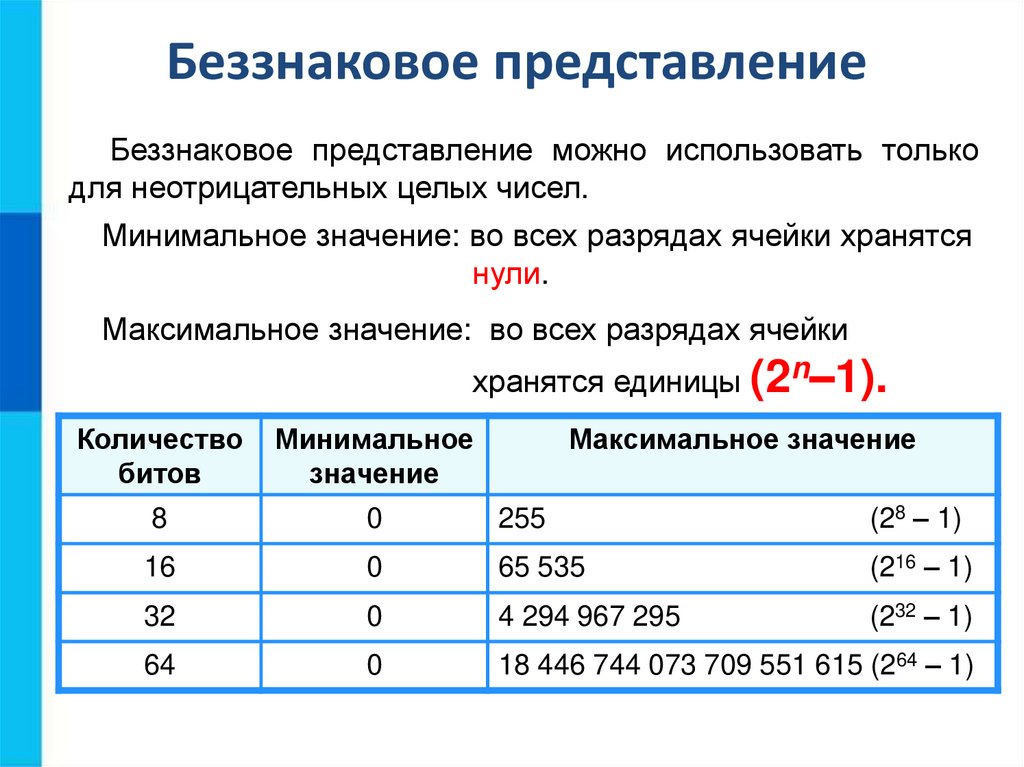
Беззнаковое представлениеБеззнаковое представление можно использовать только
для неотрицательных целых чисел.
Минимальное значение: во всех разрядах ячейки хранятся
нули.
Максимальное значение: во всех разрядах ячейки
хранятся единицы (2n–1).
Количество
битов
Минимальное
значение
Максимальное значение
8
0
255
(28 – 1)
16
0
65 535
(216 – 1)
32
0
4 294 967 295
(232 – 1)
64
0
18 446 744 073 709 551 615 (264 – 1)
17. Целые числа в памяти компьютера
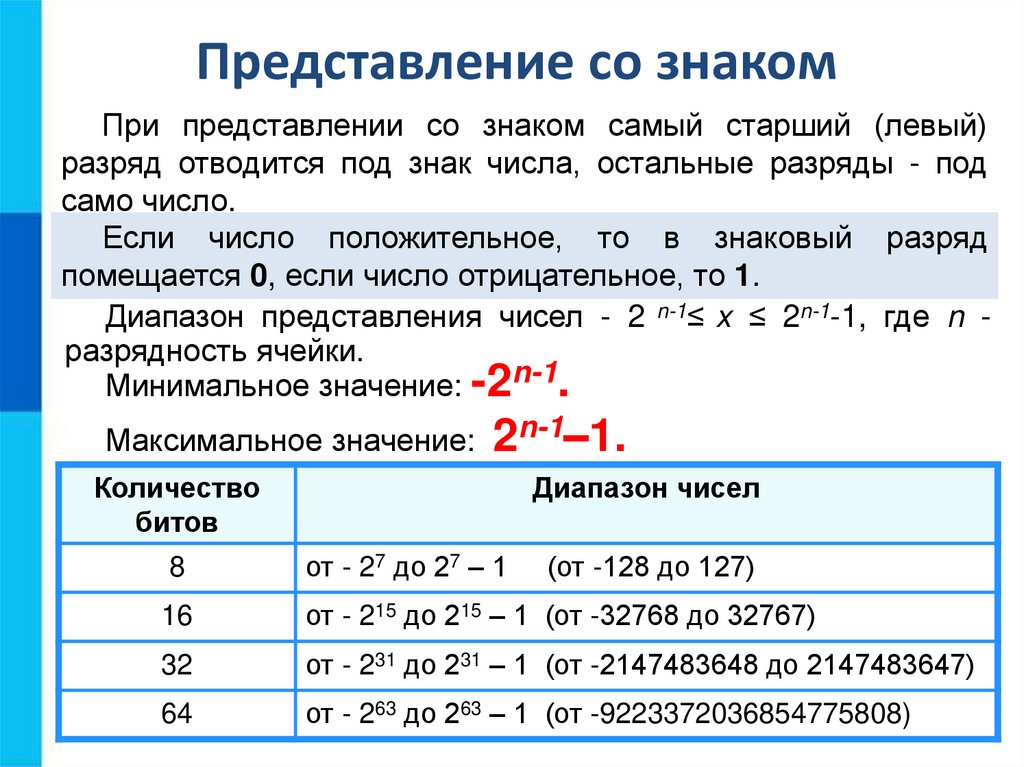
Представление со знакомПри представлении со знаком самый старший (левый)
разряд отводится под знак числа, остальные разряды - под
само число.
Если число положительное, то в знаковый разряд
помещается 0, если число отрицательное, то 1.
Диапазон представления чисел - 2 n-1≤ x ≤ 2n-1-1, где n разрядность ячейки.
Минимальное значение: -2n-1.
Максимальное значение: 2n-1–1.
Количество
битов
Диапазон чисел
8
от - 27 до 27 – 1
(от -128 до 127)
16
от - 215 до 215 – 1 (от -32768 до 32767)
32
от - 231 до 231 – 1 (от -2147483648 до 2147483647)
64
от - 263 до 263 – 1 (от -9223372036854775808)
18.
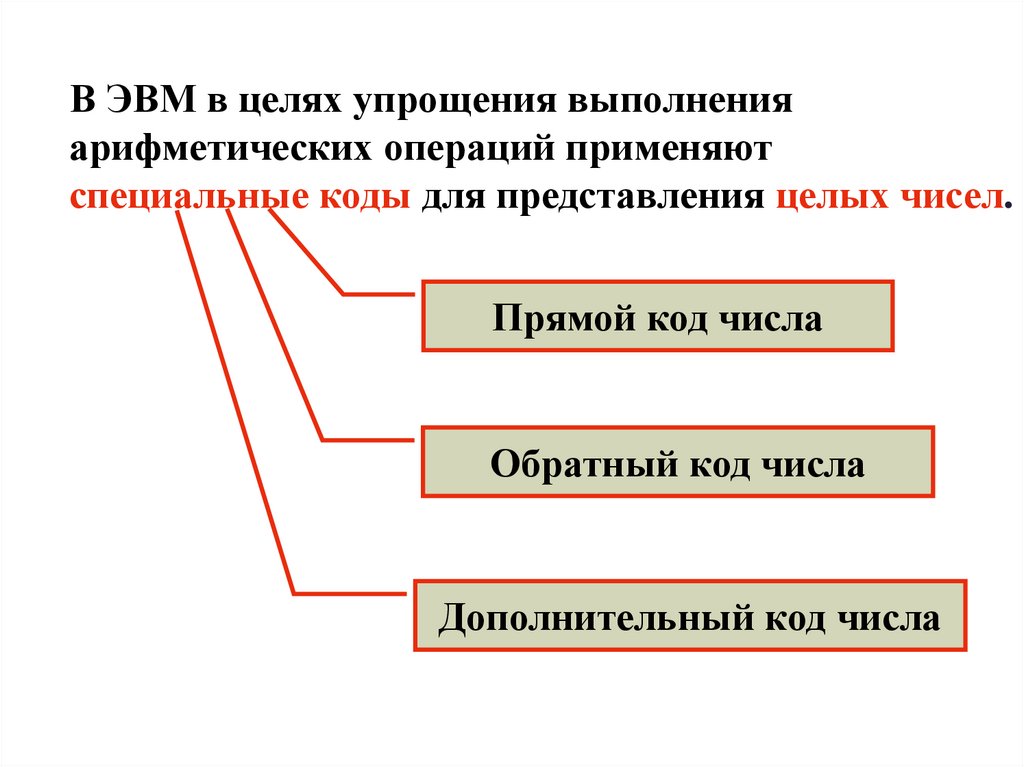
В ЭВМ в целях упрощения выполненияарифметических операций применяют
специальные коды для представления целых чисел.
Прямой код числа
Обратный код числа
Дополнительный код числа
19.
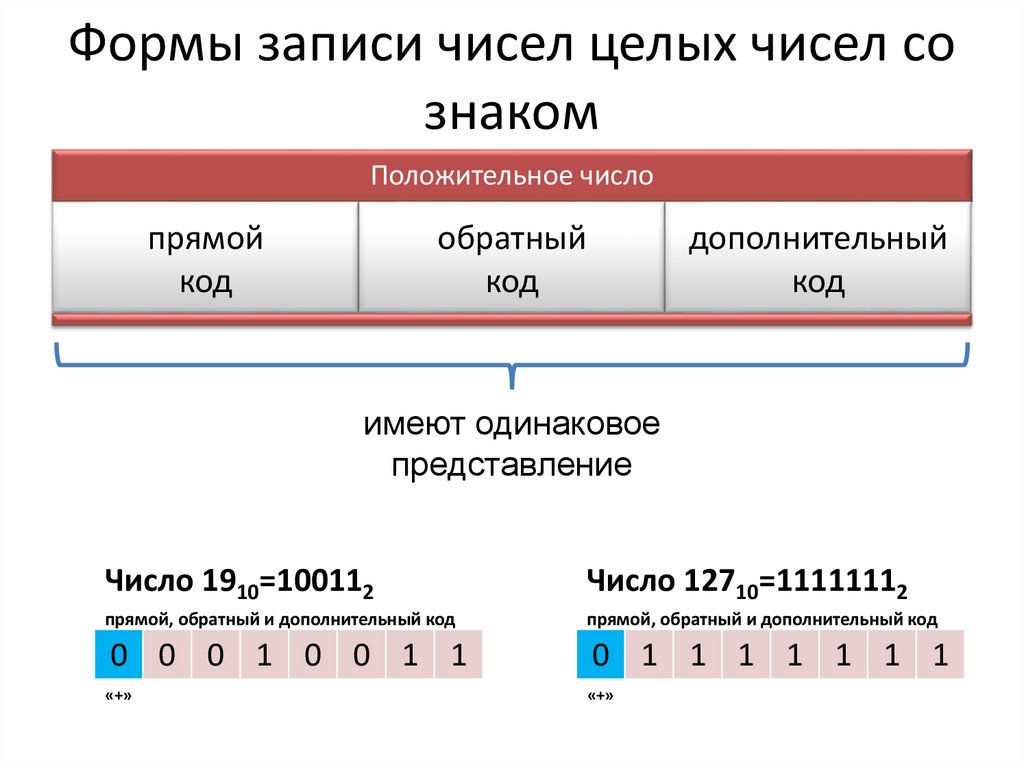
Формы записи чисел целых чисел сознаком
Положительное число
прямой
код
обратный
код
дополнительный
код
имеют одинаковое
представление
Число 1910=100112
Число 12710=11111112
прямой, обратный и дополнительный код
прямой, обратный и дополнительный код
0 0 0 1 0 0 1 1
0 1 1 1 1 1 1 1
«+»
«+»
20.
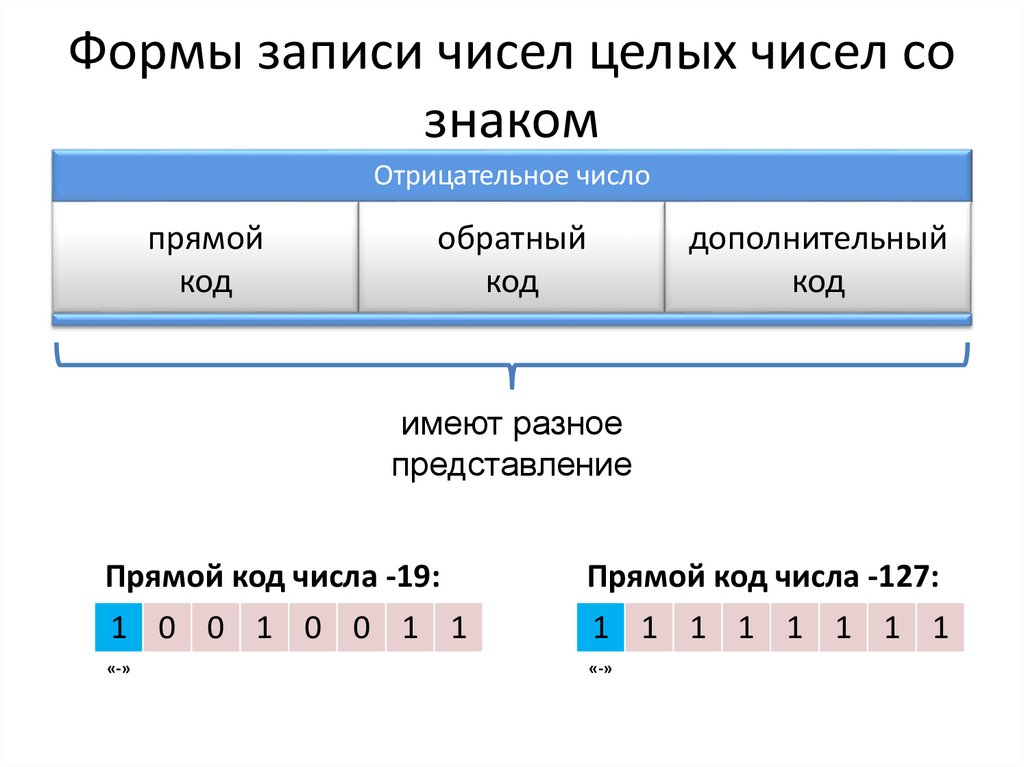
Формы записи чисел целых чисел сознаком
Отрицательное число
прямой
код
обратный
код
дополнительный
код
имеют разное
представление
Прямой код числа -19:
Прямой код числа -127:
1 0 0 1 0 0 1 1
1 1 1 1 1 1 1 1
«-»
«-»
21.
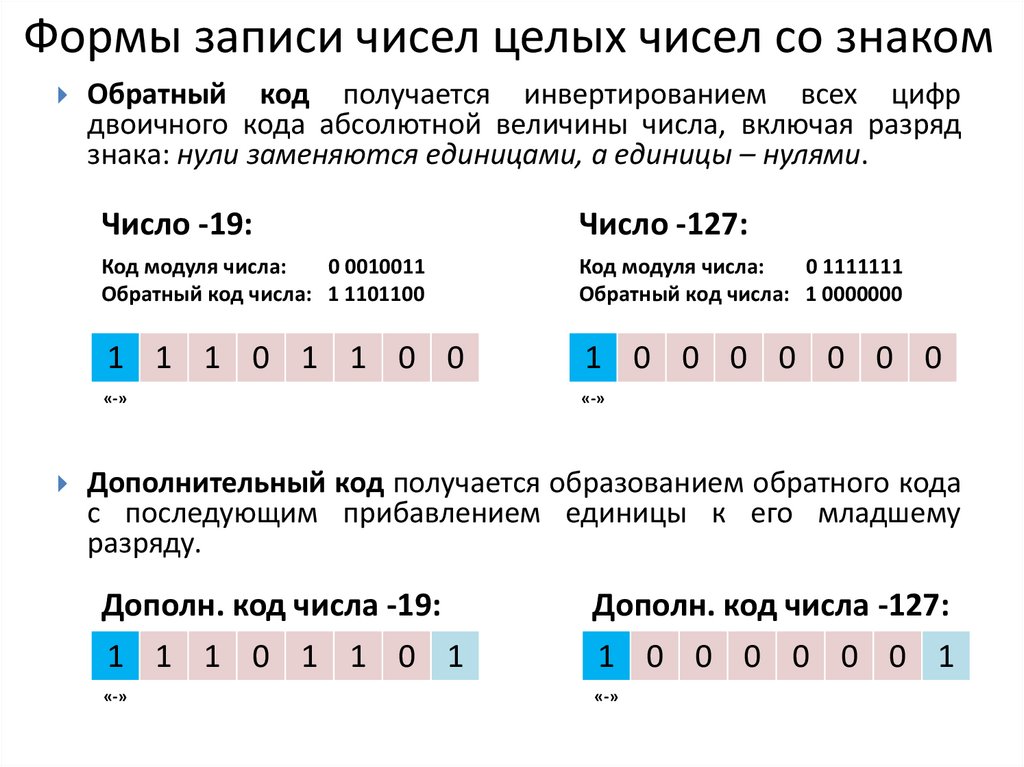
Формы записи чисел целых чисел со знакомОбратный код получается инвертированием всех цифр
двоичного кода абсолютной величины числа, включая разряд
знака: нули заменяются единицами, а единицы – нулями.
Число -19:
Число -127:
Код модуля числа:
0 0010011
Обратный код числа: 1 1101100
Код модуля числа:
0 1111111
Обратный код числа: 1 0000000
1 1 1 0 1 1 0 0
1 0 0 0 0 0 0 0
«-»
«-»
Дополнительный код получается образованием обратного кода
с последующим прибавлением единицы к его младшему
разряду.
Дополн. код числа -19:
Дополн. код числа -127:
1 1 1 0 1 1 0 1
1 0 0 0 0 0 0 1
«-»
«-»
22. Формы записи чисел целых чисел со знаком
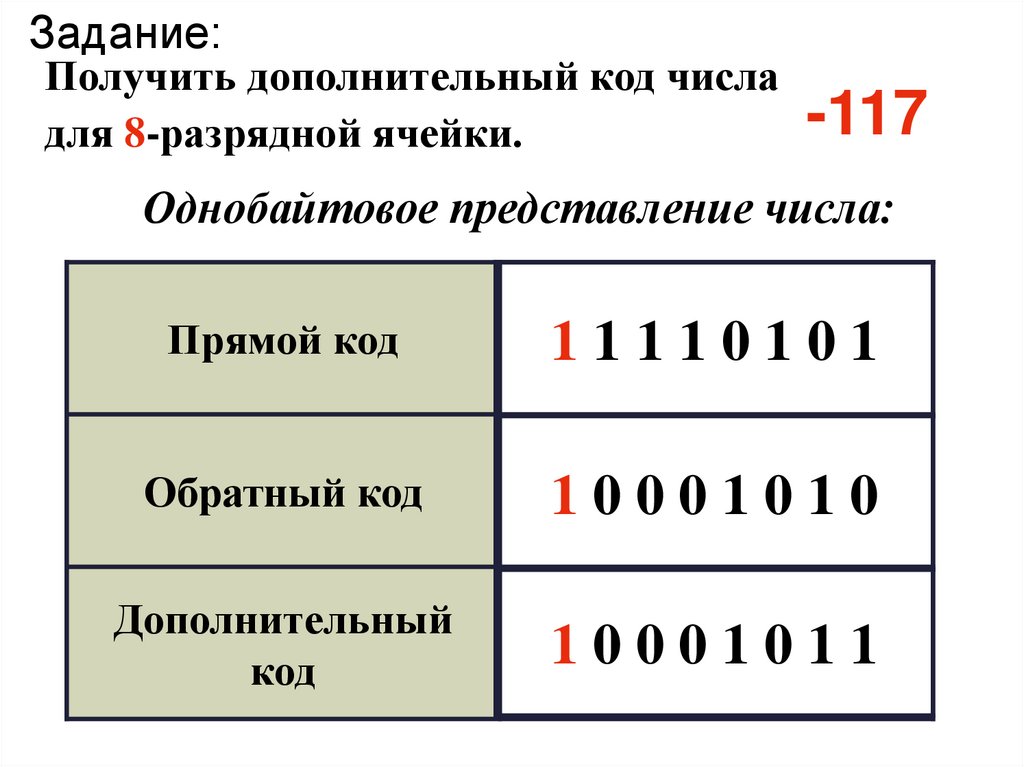
Задание:Получить дополнительный код числа
-117
для 8-разрядной ячейки.
Однобайтовое представление числа:
Прямой код
11110101
Обратный код
10001010
Дополнительный
код
10001011
23. Формы записи чисел целых чисел со знаком
Задание:Получить дополнительный код числа
-117
для 16-разрядной ячейки.
Двухбайтовое представление числа:
Прямой код
10000000 01110101
Обратный код
11111111 10001010
Дополнительный
код
11111111 10001011
24. Формы записи чисел целых чисел со знаком
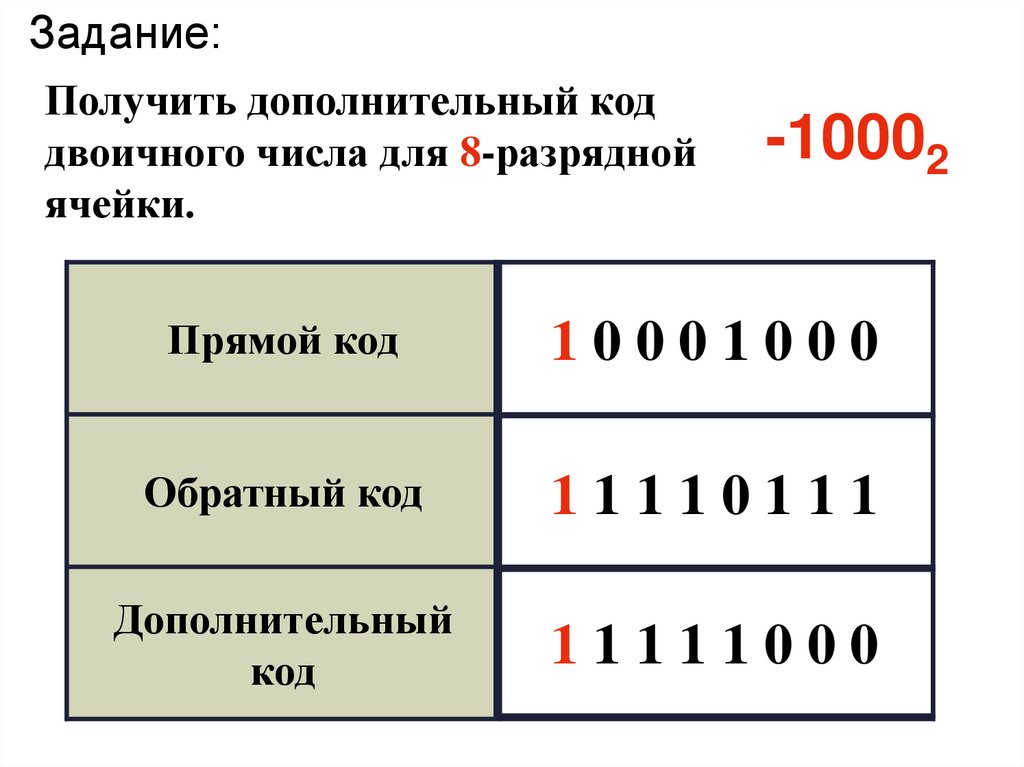
Задание:Получить дополнительный код
двоичного числа для 8-разрядной
ячейки.
-10002
Прямой код
10001000
Обратный код
11110111
Дополнительный
код
11111000
25.
Все целые отрицательные числав компьютере представляются
дополнительным кодом.
Прямой код
10001000
Обратный код
11110111
Дополнительный
код
11111000
26.
27.
28.
Представление вещественныхчисел
http://videouroki.net
29.
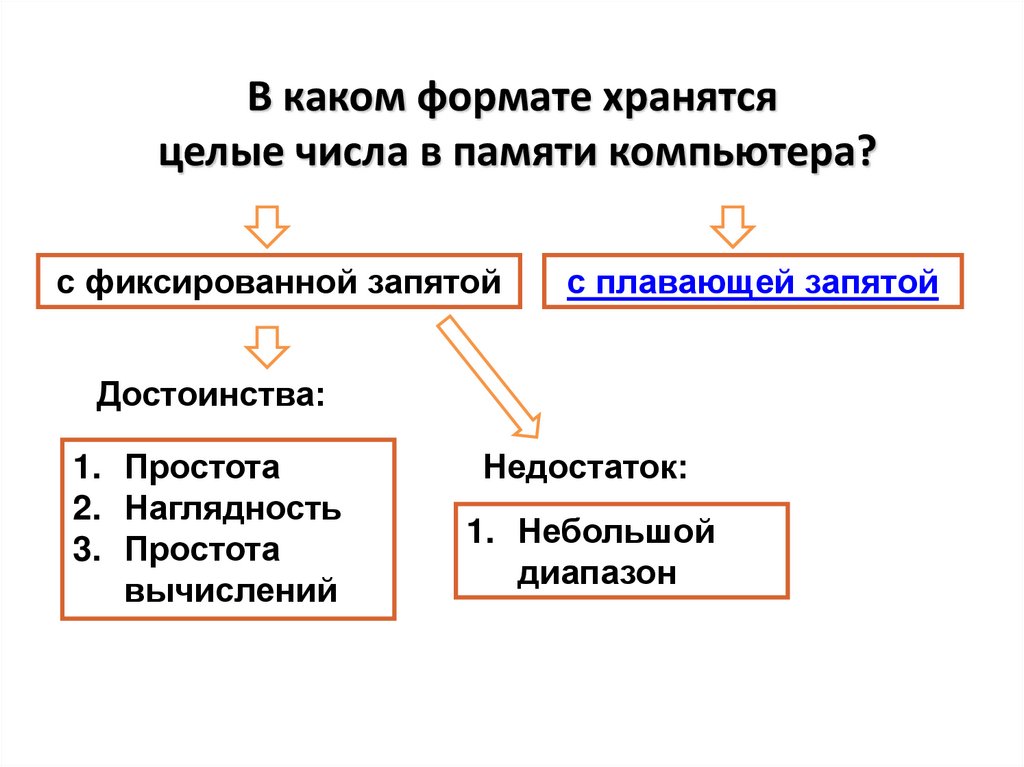
В каком формате хранятсяцелые числа в памяти компьютера?
с фиксированной запятой
с плавающей запятой
Достоинства:
1. Простота
2. Наглядность
3. Простота
вычислений
Недостаток:
1. Небольшой
диапазон
30.
2, = 0,2*101= 200,*10-2плавающая запятая
Число в формате с плавающей
запятой занимает
• 4 байта (число обычной точности);
• 8 байтов (число двойной точности).
31.
Представление вещественных чиселЛюбое вещественное число А может быть записано в
нормальной (научной, экспоненциальной) форме:
А =±m qp, где:
m - мантисса числа;
q - основание системы счисления;
p - порядок числа.
Пример. 472 000 000 может быть представлено так:
810
76 5
4,72
47,2
4720
472 10
10
10
Запятая «плавает» по мантиссе.
Такое
представление
числа
называется
представлением в формате с плавающей запятой.
Бывают записи вида: 4.72Е+8.
32. Представление вещественных чисел
Формат с плавающей запятойЧисло в формате с плавающей запятой может занимать в
памяти компьютера 32 или 64 разряда.
При этом выделяются разряды для хранения
знака порядка, порядок, знака мантиссы и мантисса.
0 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
Знак и порядок
Знак и мантисса
Диапазон
представления
вещественных
чисел
определяется количеством разрядов, отведённых для
хранения порядка числа, а точность - количеством разрядов,
отведённых для хранения мантиссы.
Числа в памяти компьютера
33. В каком формате хранятся целые числа в памяти компьютера?
34.
Арифметические действияВ большинстве компьютеров операция вычитания
не выполняется. Вместо неё производится
сложение уменьшаемого с обратным или
дополнительным кодом вычитаемого.
При сложении дополнительных кодов чисел А и В
имеют место четыре случая.
35.
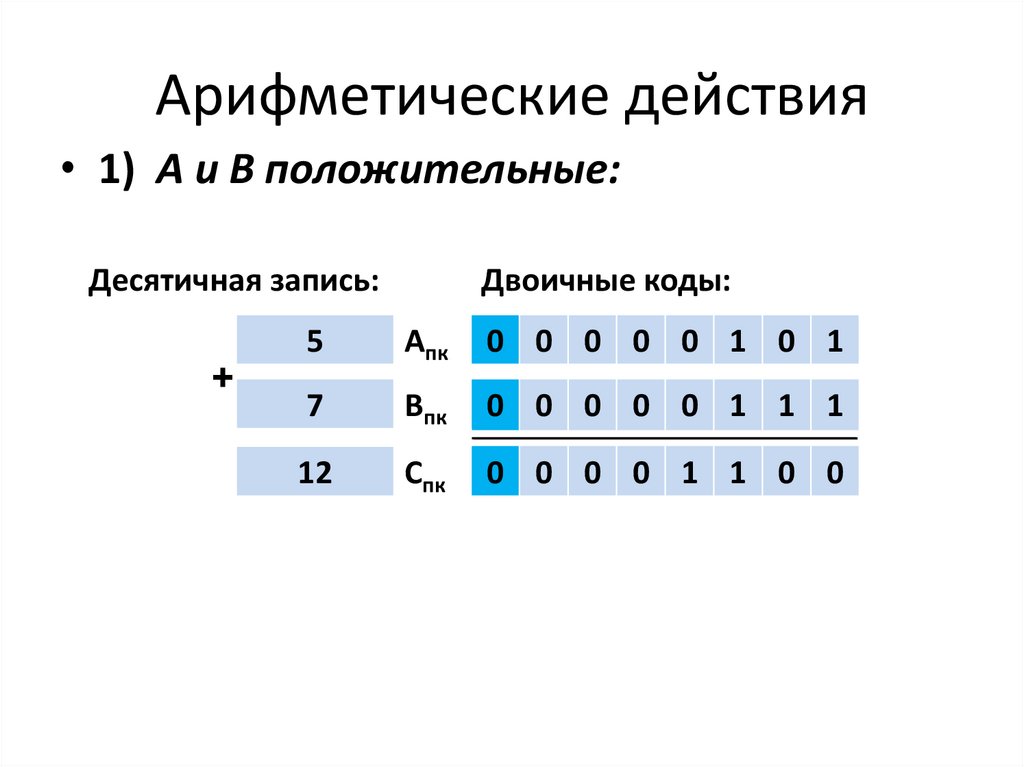
Арифметические действия• 1) А и В положительные:
Десятичная запись:
+
Двоичные коды:
5
Апк
0 0 0 0 0 1 0 1
7
Впк
0 0 0 0 0 1 1 1
12
Спк
0 0 0 0 1 1 0 0
36.
Арифметические действия• 2) А – положительное,
В – отрицательное,
Десятичная запись:
+
|B|>|A|
Двоичные коды:
5
Апк
0 0 0 0 0 1 0 1
-12
Вдк
1 1 1 1 0 1 0 0
-7
Сдк
1 1 1 1 1 0 0 1
При переводе в прямой код биты цифровой части результата
инвертируются и к младшему разряду прибавляется единица:
10000110 + 1 = 10000111= -710
37.
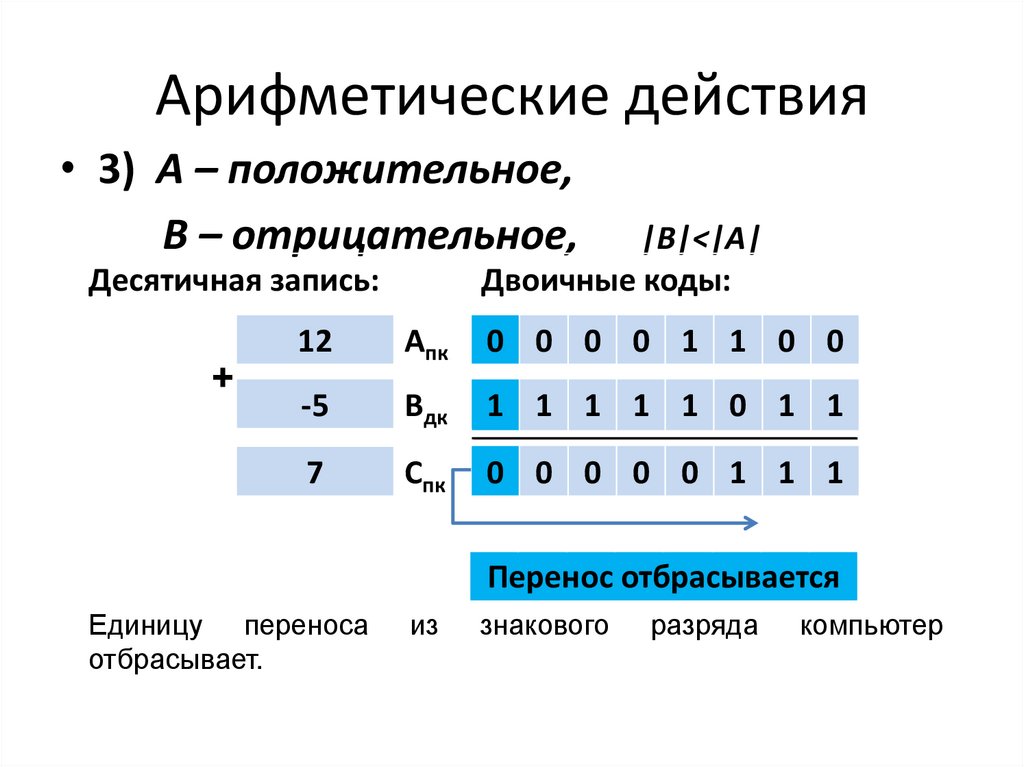
Арифметические действия• 3) А – положительное,
В – отрицательное,
|B|<|A|
Двоичные коды:
Десятичная запись:
+
12
Апк
0 0 0 0 1 1 0 0
-5
Вдк
1 1 1 1 1 0 1 1
7
Спк
0 0 0 0 0 1 1 1
Перенос отбрасывается
Единицу переноса
отбрасывает.
из
знакового
разряда
компьютер
38. Арифметические действия
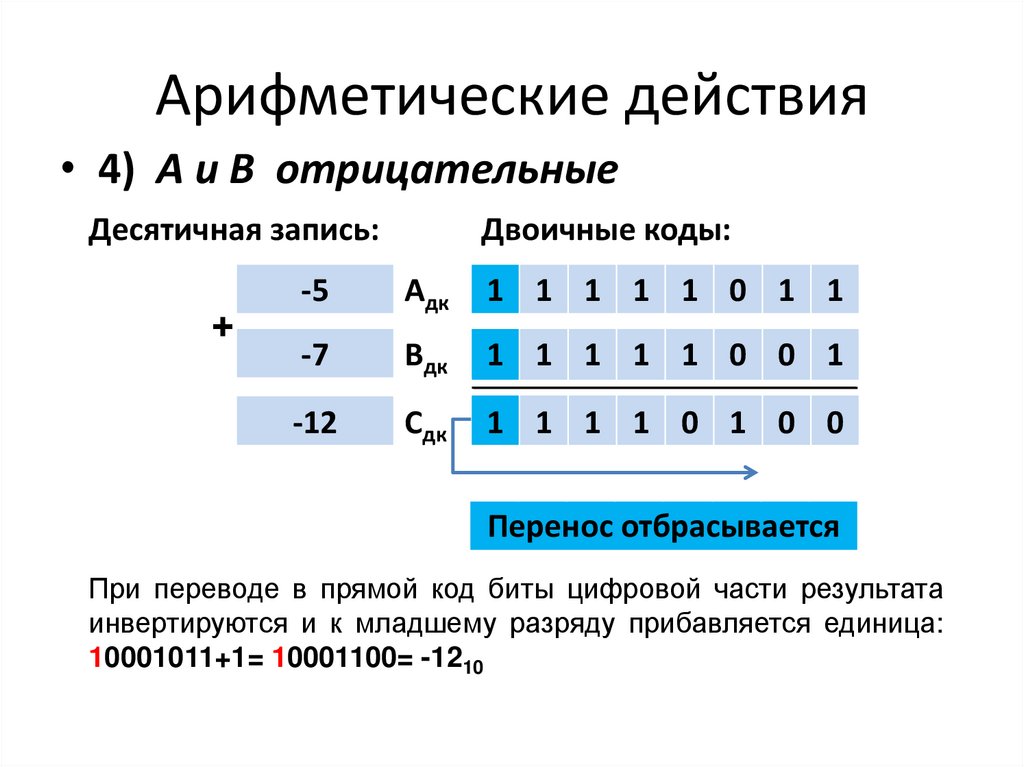
• 4) А и В отрицательныеДесятичная запись:
+
Двоичные коды:
-5
Адк
1 1 1 1 1 0 1 1
-7
Вдк
1 1 1 1 1 0 0 1
-12
Сдк
1 1 1 1 0 1 0 0
Перенос отбрасывается
При переводе в прямой код биты цифровой части результата
инвертируются и к младшему разряду прибавляется единица:
10001011+1= 10001100= -1210
39. Арифметические действия
Самое главноеДля компьютерного представления целых чисел используются
несколько различных способов, отличающихся друг от друга
количеством разрядов (8, 16, 32 или 64) и наличием или отсутствием
знакового разряда.
Для представления беззнакового целого числа его следует
перевести в двоичную систему счисления и дополнить полученный
результат слева нулями до стандартной разрядности.
При представлении со знаком самый старший разряд
отводится под знак числа, остальные разряды - под само число. Если
число положительное, то в знаковый разряд помещается 0, если
число отрицательное, то 1.
Вещественные числа в компьютере хранятся в формате с
плавающей запятой:
А = ±m qp, где:
m - мантисса числа;
q - основание системы счисления;
p - порядок числа.
40. Арифметические действия
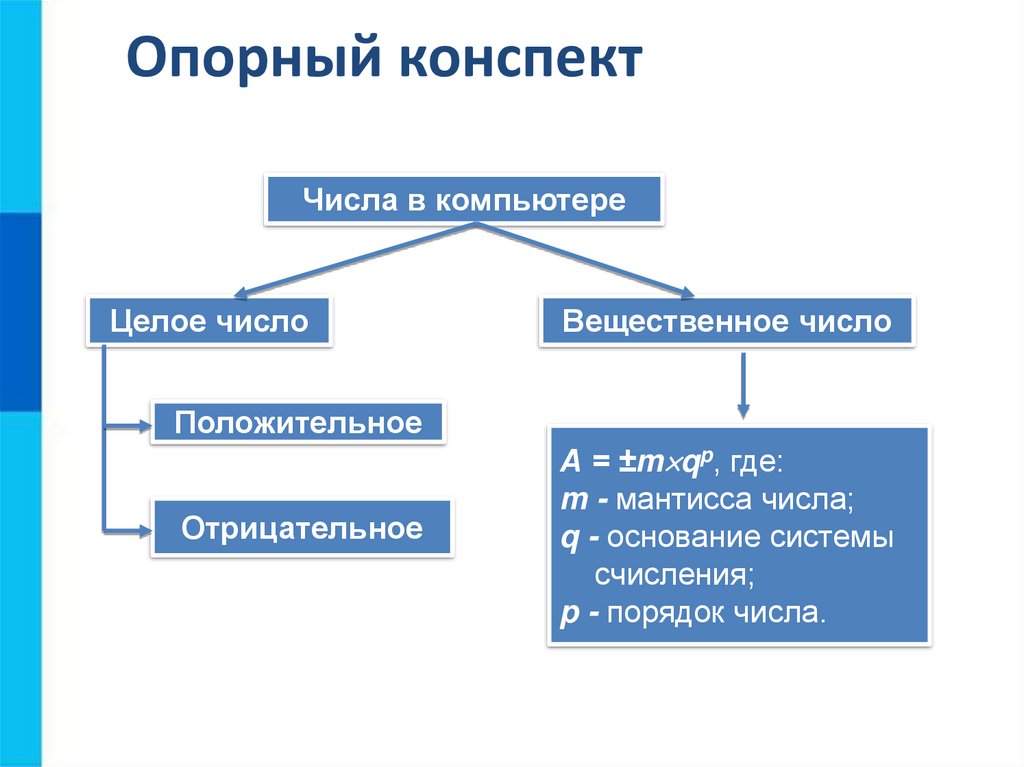
Опорный конспектЧисла в компьютере
Целое число
Положительное
Отрицательное
Вещественное число
А = ±m qp, где:
m - мантисса числа;
q - основание системы
счисления;
p - порядок числа.



















 informatics
informatics








