Similar presentations:
Функции нескольких переменных. Тема 7.1. ФНП и способы её задания
1.
2.
7. ФУНКЦИИ НЕСКОЛЬКИХПЕРЕМЕННЫХ
7.1 ФНП и способы её задания
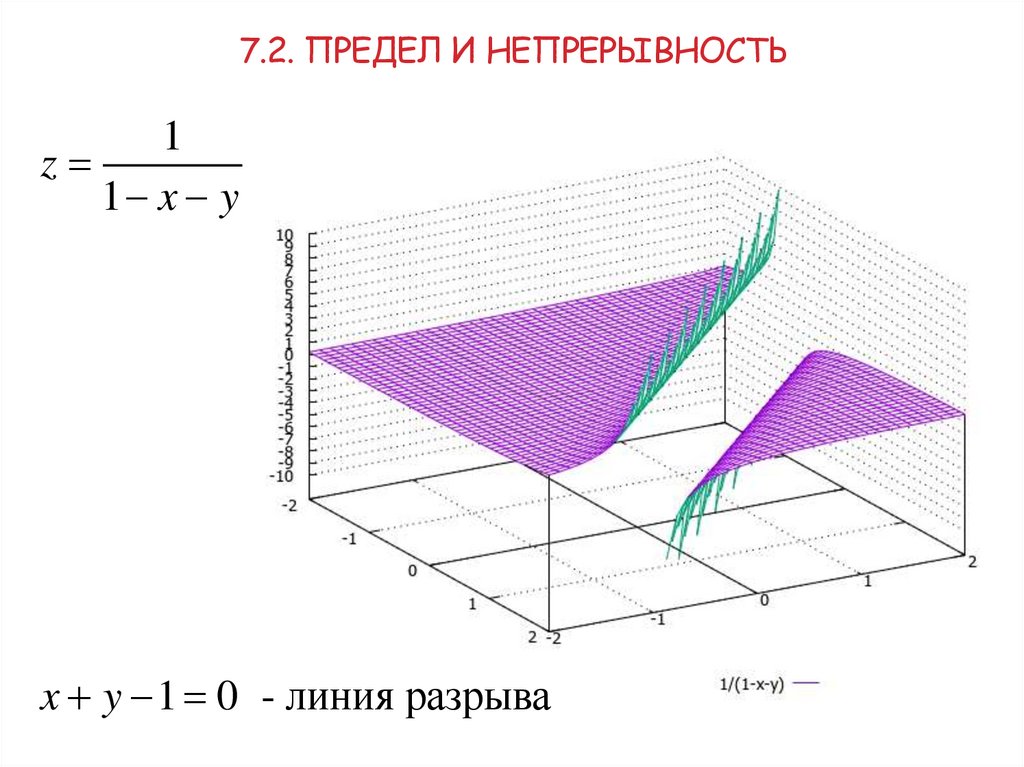
7.2. Предел и непрерывность
7.3. Частные производные 1-го порядка
7.4. Частные и смешанные производные различных порядков
7.5 Экстремум функции двух переменных
7.6 Полное приращение и полный дифференциал
7.7 Производная по направлению
7.8 Градиент
7.9 Касательная плоскость и нормаль к поверхности
3.
7.1 ФНП И СПОСОБЫ ЕЁ ЗАДАНИЯПусть имеется n переменных величин,
пусть каждому набору их значений x1 , x2 ,...xn
из некоторого множества Х соответствует определенное (единственное)
значение величины z.
Тогда говорят, что задана функция нескольких переменных
z f ( x1 , x2 ,...xn )
х1…хn
- независимые переменные
z
- зависимая переменная
множество Х - область определения функции
4.
7.1 ФНП И СПОСОБЫ ЕЁ ЗАДАНИЯПусть имеется две переменные величины,
пусть каждому набору их значений x, y
из некоторого множества D соответствует определенное (единственное)
значение величины z.
Тогда говорят, что задана функция двух переменных
z f ( x, y )
x, y
- независимые переменные (действительные числа)
z
- зависимая переменная (действительное число)
множество D(f) - область определения функции
множество E(f) - область изменения значений функции
Пример
z x12 x2
объем цилиндра как функция двух переменных:
х1 – радиус основания,
х2 – высота цилиндра.
5.
7.1 ФНП И СПОСОБЫ ЕЁ ЗАДАНИЯСпособы задания
1. Явный аналитический
z f ( x, y )
2. Неявный аналитический
F ( x, y , z ) 0
3. Графический
Пусть пары чисел (x,y) – это координаты точки М на плоскости.
Тогда каждой точке М(x,y) на плоскости соответствует единственная
точка N(x,y,z) в пространстве.
Совокупность всех таких точек образует некоторую поверхность, которая
геометрически изображает данную функцию двух переменных.
z = f(x,y) = f(M) – функция z как функция точки М
D(f) - область на плоскости Oxy
Графиком функции двух переменных является поверхность.
6.
7.1 ФНП И СПОСОБЫ ЕЁ ЗАДАНИЯДля построение графика функции z=f(x,y) полезно рассмотреть функции
одной переменной: z=f(x0,y) и z=f(x,y0)
которые есть сечения графика z=f(x,y) плоскостями, параллельными
координатным плоскостям Oxz и Oyz, т.е. плоскостями y=y0 и x=x0
Пример
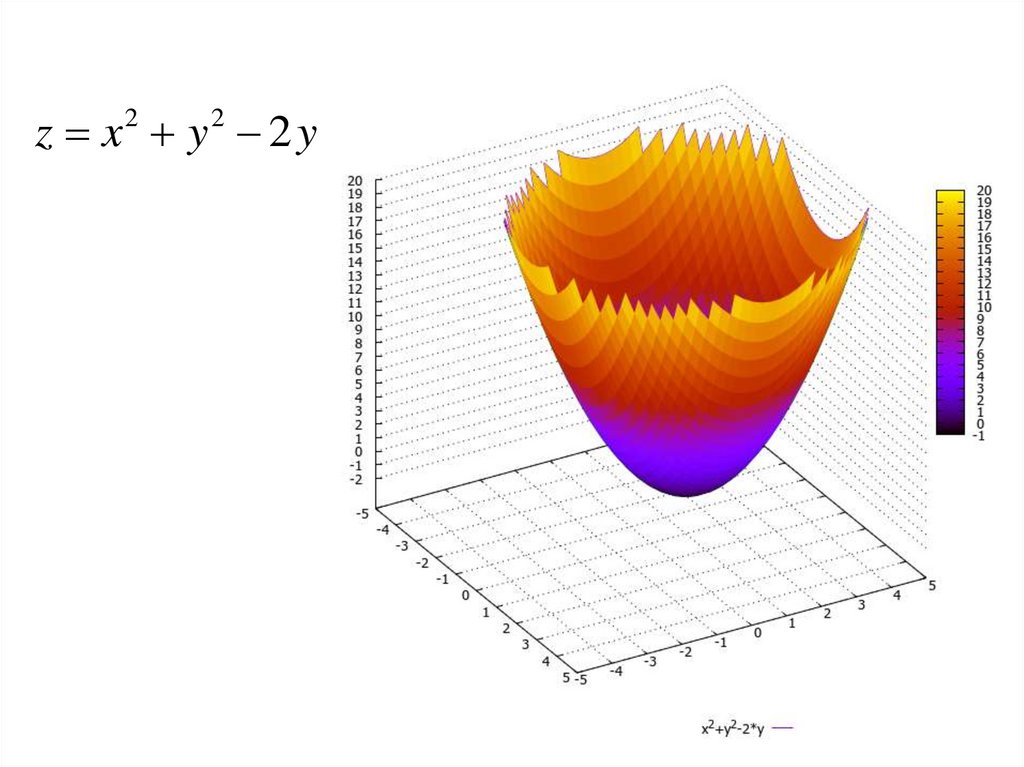
z x2 y2 2 y
Построить график функции
Найдем сечения поверхности плоскостями, параллельными координатным
плоскостям. Для этого преобразуем функцию к виду:
z x ( y 2 y 1) 1
2
2
z x 2 ( y 1) 2 1
7.
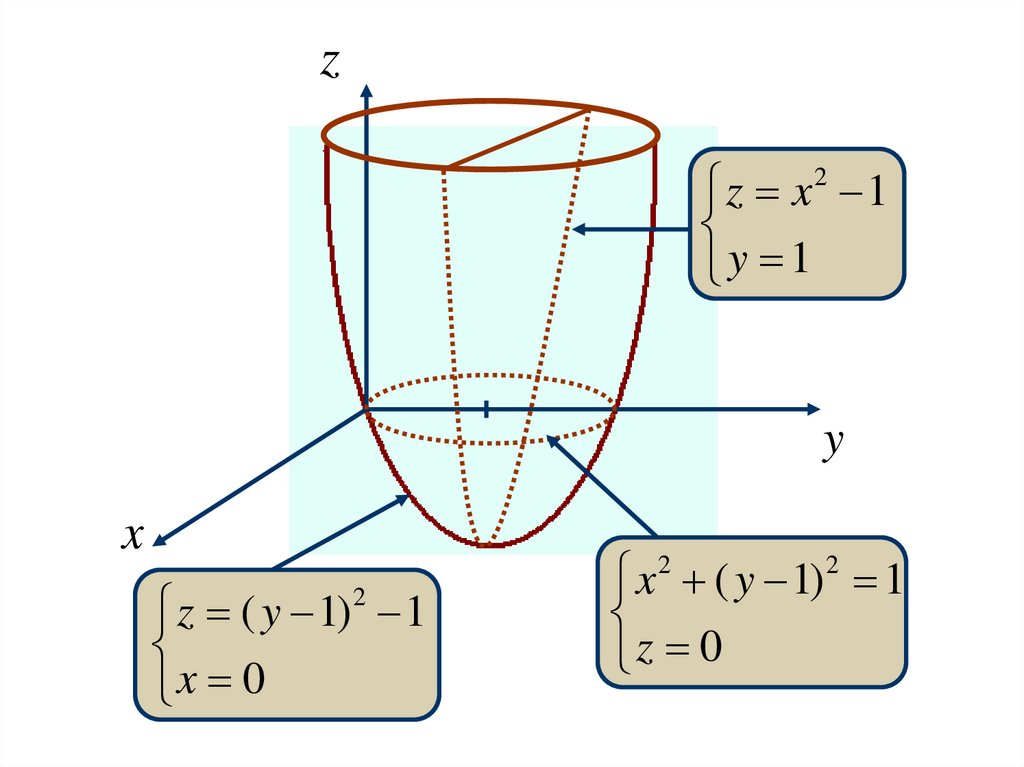
7.1 ФНП И СПОСОБЫ ЕЁ ЗАДАНИЯz x 2 ( y 1) 2 1
z x 2 - парабола
При у=0 (сечение плоскостью Oxz):
При х=0 (сечение плоскостью Oyz):
z ( y 1) 2 1
При z=0 (сечение плоскостью Oxy):
x 2 ( y 1) 2 1
- парабола
- окружность с центом в точке (0, 1).
Эта поверхность называется параболоидом.
8.
zz x2 1
y 1
y
x
z ( y 1) 2 1
x 0
x 2 ( y 1) 2 1
z 0
9.
z x2 y2 2 y10.
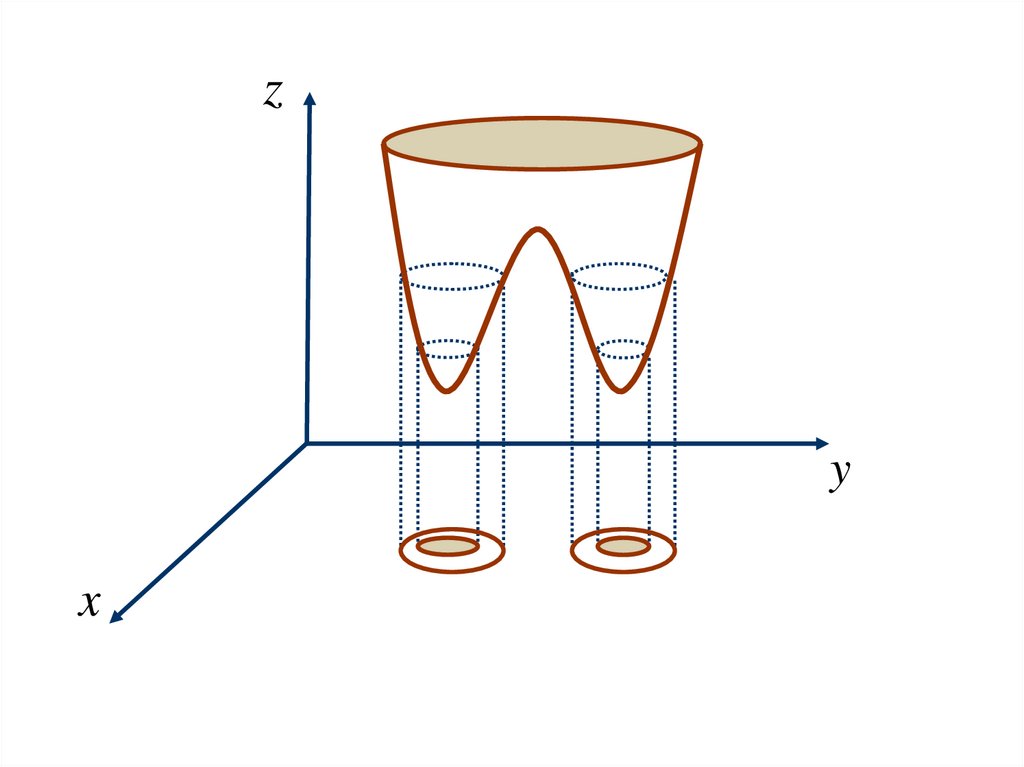
7.1 ФНП И СПОСОБЫ ЕЁ ЗАДАНИЯЛинией уровня функции двух переменных z=f(x,y) называется
множество точек на плоскости, таких что во всех этих точках
значение функции одно и то же и равно С (const).
Число С называется уровнем.
11.
zy
x
12.
7.1 ФНП И СПОСОБЫ ЕЁ ЗАДАНИЯПример
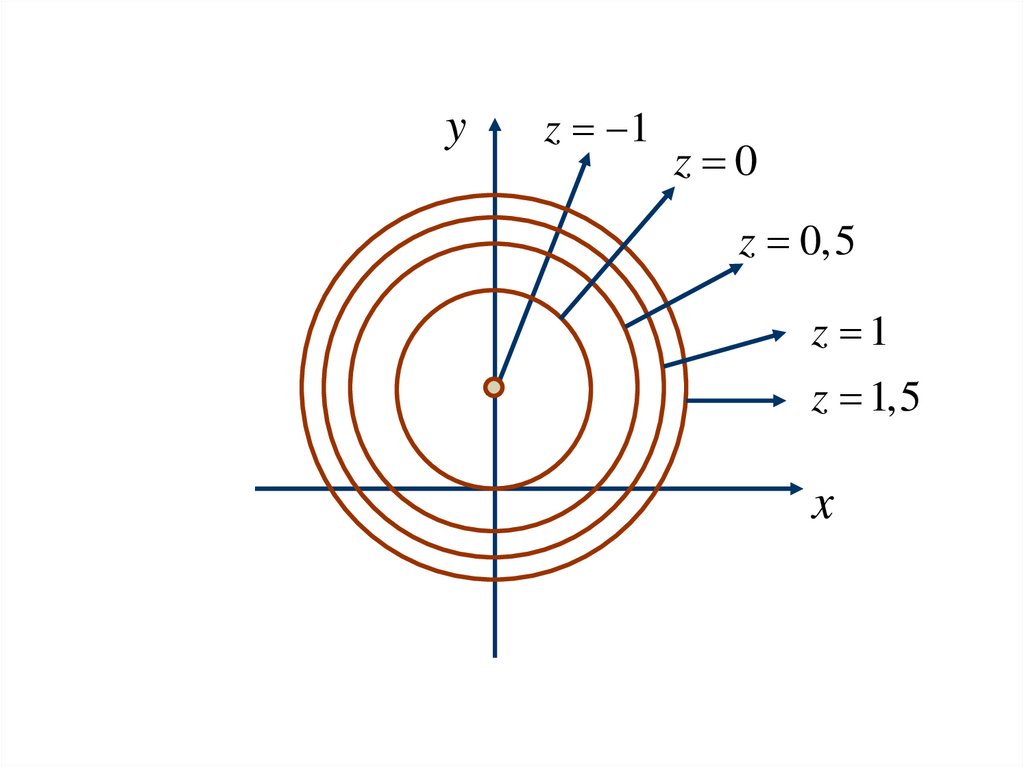
Построить линии уровня функции
z x2 y2 2 y
Линия уровня z = C – это кривая на плоскости Oxy, которая задается
2
2
уравнением
C x y 2y
C x 2 ( y 1) 2 1
x 2 ( y 1) 2 C 1
Получили окружность с центром в точке (0,1) и радиусом
R C 1
При С=-1 имеем точку (0,1).
При С=0 имеем окружность с радиусом
При С=0,5 имеем окружность с радиусом
При С=1 имеем окружность с радиусом
И так далее.
R 1
R 1,5 1, 22
R 2 1, 41
13.
yz 1
z 0
z 0,5
z 1
z 1,5
x
14.
7.2. ПРЕДЕЛ И НЕПРЕРЫВНОСТЬОкрестностью точки М0 (х0 ,у0 ), принадлежащей множеству D(f),
называется круг, содержащий точку М0 .
y
y0
M0
x0
x
15.
7.2. ПРЕДЕЛ И НЕПРЕРЫВНОСТЬδ-окрестностью точки М0 (х0 ,у0 ), принадлежащей множеству
D(f), называется круг с центром в точке М0 и радиусом δ.
U M 0 = M ( x, y ) : MM 0
y
y0
Если исключить из этого множества
саму точку М0 (х0 ,у0 ), то получим
проколотую δ-окрестность .
M0
M
x0
U 0 M 0 = M ( x, y ) : 0 MM 0
x
16.
7.2. ПРЕДЕЛ И НЕПРЕРЫВНОСТЬЧисло А называется пределом функции z=f(x,y) в точке М0 (х0 ,у0 )
( т. е. при
x x0
и
y y0), если
0
( )>0 :
если M U 0 M 0 ,
то
f M A
lim f ( x, y ) A
x x0
y y0
Замечания.
1. Точка М0 может не принадлежать области определения функции.
2. Число А должно быть пределом функции при любом способе
приближения М к М0. Если результат зависит от способа приближения,
то предел не существует.
17.
7.2. ПРЕДЕЛ И НЕПРЕРЫВНОСТЬПримеры
Вычислить пределы
2 3
xy 2
x kx
0
k
x
1) lim 2
y kx lim 2
lim 2
2
2
2
x 0 x y 2
x
0
x 0 x k x
0
x kx
y 0
2
k 2 x3
0
k 2x
lim 2
lim
0
2
2
x 0 x 1 k 2
x 0 1 k 1 k
(результат не зависит от k)
xy
0
x kx
kx 2
2) lim 2
y kx lim 2
lim 2
2
2 2
x 0 x y 2
x
0
x
0
0
x k x
x kx
y 0
k
kx 2
k
lim
lim 2
2
x 0 1 k 2
x 0 x 1 k 2
1 k
(результат зависит от k ,
значит предел не
существует)
18.
7.2. ПРЕДЕЛ И НЕПРЕРЫВНОСТЬФункция z=f(x,y) называется непрерывной в точке М0(х0 ,у0),
если она
1) Определена в точке М0(х0 ,у0)
2) Имеет конечный предел при
x x0
и
y y0
3) Этот предел равен значению функции в точке М0(х0 ,у0)
lim f ( x, y ) f ( x0 , y0 )
x x0
y y0
Замечания.
1. Точки, в которых не выполняется хотя бы одно из этих условий,
называются точками разрыва функции.
2. Функция может иметь множество точек разрыва. Если они составляют
линию, то она называется линией разрыва.
19.
7.2. ПРЕДЕЛ И НЕПРЕРЫВНОСТЬz
1
1 x y
2
2
x y 1 - линия разрыва
2
2
20.
7.2. ПРЕДЕЛ И НЕПРЕРЫВНОСТЬ1
z
1 x y
x y 1 0 - линия разрыва
21.
7.3. ЧАСТНЫЕ ПРОИЗВОДНЫЕ 1-ГО ПОРЯДКАПусть задана функция z=f(x,y).
Дадим аргументу х приращение Δх, а аргументу у приращение Δу.
Тогда функция z получит значение
f ( x x, y y )
Полное приращение функции z в точке (х,у) имеет вид
z f ( x x, y y ) f ( x, y )
Если задать только приращение х или у, то
x z f ( x x, y) f ( x, y)
- частное приращение функции z по аргументу х
y z f ( x, y y ) f ( x, y )
- частное приращение функции z по аргументу y
22.
7.3. ЧАСТНЫЕ ПРОИЗВОДНЫЕ 1-ГО ПОРЯДКАЕсли существует конечный предел
xz
lim
,
x 0 x
то он называется частной производной функции z=f(x,y) в точке М(x,y)
по переменной x.
xz
z
lim
z x f x
x 0 x
x
Если существует конечный предел
lim
y 0
yz
y
,
то он называется частной производной функции z=f(x,y) в точке М(x,y)
по переменной y.
yz
z
lim
z y f y
y 0 y
y
23.
7.3. ЧАСТНЫЕ ПРОИЗВОДНЫЕ 1-ГО ПОРЯДКАПравила вычисления.
1. Для нахождения производной z x нужно считать постоянной переменную у.
2. Для нахождения производной z y нужно считать постоянной переменную х.
3. При нахождении частных производных сохраняются известные ранее
правила дифференцирования.
(C ) 0
(C u ) C u
(u v) u v
(u v) u v u v
u u v u v
2
v
v
u u
C C
C C v
2
v
v
24.
7.3. ЧАСТНЫЕ ПРОИЗВОДНЫЕ 1-ГО ПОРЯДКАПримеры
Найти частные производные 1-го порядка
1) z 2 x3 3 y 2 4 xy 5 x 5 y 4 3
z x 2 x3 3 y 2 4 y x x 5 y 4 x 5 3 x
x
x
x
2 3 x 2 0 4 y 1 5 y 4 5 x 4 0 6 x 2 4 y 25 x 4 y 4
z y 2 x3 3 y 2 4 x y y 5 x 5 y 4 3 y
y
y
y
0 3 2 y 4 x 1 5 x 5 4 y 3 0 6 y 4 x 20 x 5 y 3
25.
7.3. ЧАСТНЫЕ ПРОИЗВОДНЫЕ 1-ГО ПОРЯДКАПримеры
Найти частные производные 1-го порядка
z x
Основание степени зависит от х, показатель
степени не зависит от х, значит будем
использовать производную степенной функции
также учтём, что функция сложная.
z x ln x
z y
2) z ln x
cos y
cos y ln x
x
cos y 1
x nx ,
n
z y ln x
ln x
cos y
y
ln x
cos y
ln ln x cos y y
ln ln x sin y
n 1
cos y 1 1
ln x x cos y ln x
x
Основание степени не зависит от у, показатель
степени зависит от у, значит будем
использовать производную показательной функции
также учтём, что функция сложная.
cos y
cos y
x
x
a
a
ln a,
26.
7.4. ЧАСТНЫЕ И СМЕШАННЫЕ ПРОИЗВОДНЫЕРАЗЛИЧНЫХ ПОРЯДКОВ
Если частные производные 1-го порядка сами являются
дифференцируемыми функциями, то можно найти их частные
производные, которые называются частными производными второго
порядка:
2
2
z
z xx z x x 2
x
z
z yy z y 2
y
y
Можно также определить смешанные производные второго порядка:
2
2
z
z xy z x y
x y
z
z yx z y
x
y x
Теорема
Если частные производные второго порядка функции z=f(x,y) непрерывны
в точке М0(х0,у0), то в этой точке смешанные производные равны:
f xy ( x0 , y0 ) f yx ( x0 , y0 )
27.
7.4. ЧАСТНЫЕ И СМЕШАННЫЕ ПРОИЗВОДНЫЕРАЗЛИЧНЫХ ПОРЯДКОВ
Примеры
Найти производные 2-го порядка функции
z 3x 2 x sin y в точке А(1;0).
z x 6 x sin y
z xx 6
z xx (1;0) 6
z y x cos y
z yy x sin y
z yy (1;0) 0
z xy cos y
z xy (1;0) 1
z yx cos y
z yx (1;0) 1
28.
7.4. ЧАСТНЫЕ И СМЕШАННЫЕ ПРОИЗВОДНЫЕРАЗЛИЧНЫХ ПОРЯДКОВ
Аналогичным образом вычисляются частные и смешанные производные
порядков выше второго.
4
z
z
4
xxxx z x x
x
x
x
4
z
z
2 2
xyxy z x y
x
y x y
7 z
z
xxyxxyx z xxxyxxy
5
2
x y
29.
7.4. ЧАСТНЫЕ И СМЕШАННЫЕ ПРОИЗВОДНЫЕРАЗЛИЧНЫХ ПОРЯДКОВ
Частные и смешанные производные для функции трёх переменных
вычисляются следующим образом:
u f ( x, y , z )
u
u x
x
u
u y
y
y, z const
u
u z
z
x, y const
x, z const
4u
u
xxyz u xzxy
2
x y z
30.
7.4. ЧАСТНЫЕ И СМЕШАННЫЕ ПРОИЗВОДНЫЕРАЗЛИЧНЫХ ПОРЯДКОВ
Пример (обычное решение)
4u
Найти производную
x y z 2
x
для функции u x y z sin .
y
2
3 4
1
x
x x
3 4
u x x y z cos 2 xy 3 z 4 cos
x
y
y
y y x
1
x 1
x
3
4
u xy 2 x y z cos cos
y
y y
y y
y y
2
1
x 1
x x
2 x 3 y z 2 cos sin
y y
y y y
y
2
6 xy 2 z 4
4
1
x x
x
1
x 1
x x
2 4
6
xy
z
cos
sin
cos
sin
y2
y y3
y
y2
y y
y y2
2
4
u
6
xy
z
0 0 6 xy 2 4 z 3 24 xy 2 z 3
xyz
z
2
2
2 2
u
xyzz 24 xy z z 24 xy 3 z 72 xy z
2
3
4u
x y z 2
31.
7.4. ЧАСТНЫЕ И СМЕШАННЫЕ ПРОИЗВОДНЫЕРАЗЛИЧНЫХ ПОРЯДКОВ
Пример (рациональное решение)
4u
x
2 3 4
Найти производную
для функции u x y z sin .
2
x y z
y
4u
u
xyzz по теореме u zzxy
2
x y z
u z x 2 y 3 z 4 0 x 2 y 3 4 z 3 4 x 2 y 3 z 3
z
u zz 4 x 2 y 3 z 3 4 x 2 y 3 3z 2 12 x 2 y 3 z 2
z
2
3 2
3 2
3 2
u
12
x
y
z
12
2
x
y
z
24
xy
z
zzx
x
4
u
3
2
2
2
2 2
u
24
x
y
z
24
x
3
y
z
72
xy
z
y
zzxy
x y z 2



























 mathematics
mathematics








