Similar presentations:
Математические основы функционального программирования. Лекция 2
1.
Лекция 2Математические основы функционального программирования
2.
Процедурный стильИзменение состояний программы от начального к конечному
Состояния модифицируются с помощью команд присваивания, ход выполнения
команд меняется условными операторами
3.
Функциональная парадигма•Не используется оператор присваивания для изменения состояний
•Не используются циклы
•Выполнение последовательности команд не имеет смысла, т.к. одна команда не
влияет на выполнение следующей
•Функции можно передавать в другие функции в качестве аргументов и
возвращать в качестве результата, результатом вычислений тоже может быть
функция
•Вместо циклов используется рекурсия
4.
Алонзо ЧёрчАлонзо Черч родился 14 июня 1903 года в городе
Вашингтон, США.
Известность пришла к Черчу после разработки
теории лямбда-исчислений. Данная теория
последовала за его знаменитой статьей 1936 года,
в которой показал существование так называемых
«неразрешимых задач».
Статья предшествовала знаменитому
исследованию Алана Тьюринга на тему проблемы
остановки, в котором также продемонстрировано
существование задач, неразрешимых
механическими способами.
Также Черчу принадлежит работа, в которой
доказал, что проблема для исчисления предикатов
неразрешима.
5.
Лямбда-исчисления•Формализация, которая может быть использована для написания программ
•Простая модель для рекурсии и вложенных сред
•Большинство конструкций процедурных языков может отображено в
конструкции лямба-исчислений
•Функциональные языки в основном являются удобной формой синтаксической
записи для конструкций различных вариантов лямбда-исчислений
6.
Лямбда-выражениеE –некоторое выражение, возможно, использующую переменную x
7.
λ-термы8.
Переменная9.
Комбинация10.
Абстракция11.
Свободные и связанные переменныеВхождение переменной V в выражение E свободно, если оно не принадлежит
области действия «λV» и связано в противном случае
В выражении подчеркнуты свободные переменные
12.
ПодстановкиE
V
V’ (где V≠V’)
E1E2
λV.E1
λV’.E1 (где V≠V’ и V’ ∉ FV(E’))
λV’.E1 (где V≠V’ и V’ ∉ FV(E’))
E[V:=E’]
E’
V’
E1[V:=E’] E2[V:=E’]
λV.E1
λV’.E1[V:=E’]
λV’’.E1[V’:=V’’][V:=E’], где V’’ –
переменная такая, что V’’ ∉ FV(E’)
и ∉ FV(E1)
13.
Конверсии14.
α-конверсияВспомогательный механизм для изменения имен связанных переменных ()
15.
β-конверсияВычисление значения функции от аргумента
16.
η-конверсияФормализованное правило введения и удаления формального параметра
17.
Пример18.
Обобщение определений19.
Равенство лямбда-выраженийДва выражения равны, если от одного к другому можно перейти за конечное
число конверсий
20.
Редукция лямбда-выраженийВыражение редуцирумо от одного к другому, если можно перейти от одного к
другому за конечное число последовательных конверсий.
















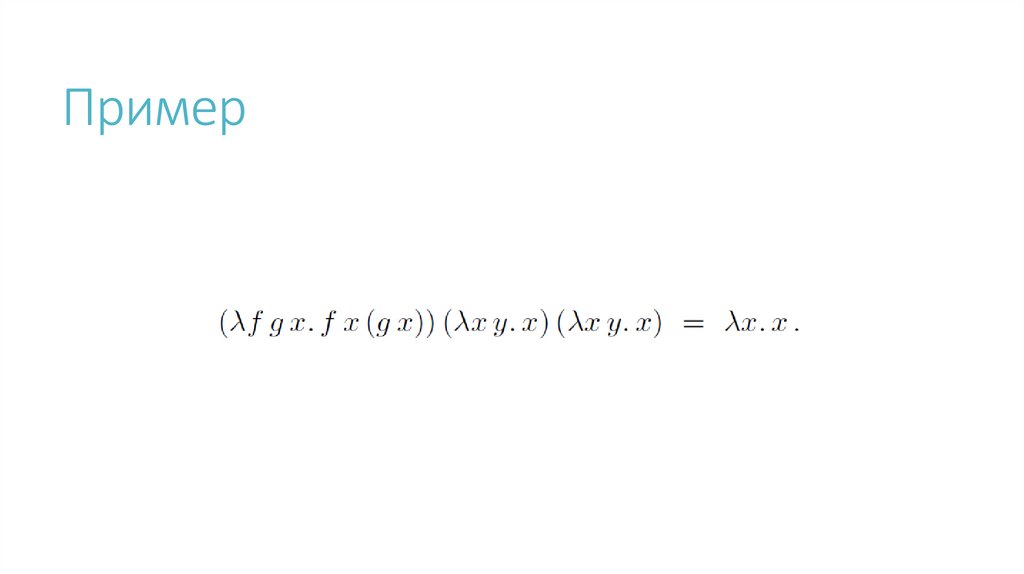





 mathematics
mathematics programming
programming








