Функциональное программирование. LISP

1. Функциональное программирование

LISP

2. Введение в декларативное программирование

1.
Введение в декларативное программирование
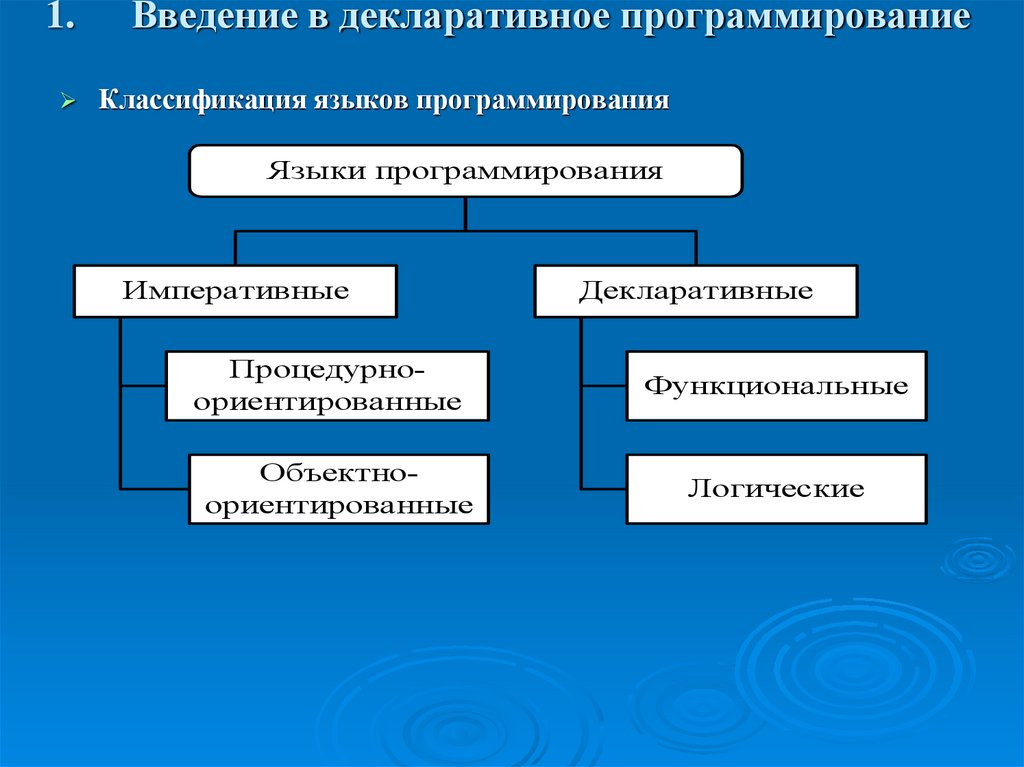
Классификация языков программирования
Языки программирования
Императивные
Декларативные
Процедурноориентированные
Функциональные
Объектноориентированные
Логические

3.

Императивные языки ориентированы на
реализацию конкретного алгоритма решения
задачи. С их точки зрения программа
представляет собой определяемую
алгоритмом последовательность операторов
и предложений, управляющих
последовательностью их исполнения. Основу
такой программы составляет вычисление и
присвоение переменным значений
выражений вплоть до получения нужного
значения. Первыми и наиболее
многочисленными представителями
императивной группы являются процедурноориентированные (процедурные) языки,
например, Ada, Basic, C, Fortran, Pascal и т.п.

4.

Концепции, объединяющие объектно-
ориентированные языки, возникли несколько
позже. В данном случае программа состоит
из объектов, взаимодействующих
посредством пересылки сообщений, а,
значит, в программу вносится модульность –
посредством абстрагирования данных и
наследования. Это позволяет избежать
дублирования и локализовать описания
механизмов работы с информацией. Одним
из первых языков такого типа стал Smalltalk.

5.

Декларативные языки ориентированы главным
образом на оптимальное представление знаний и
организацию работы с декларативной
(описательной) частью задачи. Подразделение
декларативных языков на группы определяется
доминирующей парадигмой программирования.
С точки зрения функциональной парадигмы
программа состоит из независимых функций, каждая
из которых определяет правило преобразования
своих аргументов в некоторый результат. Эти
функции определяются путём композиции системных
или определяемых программистом функций с
использованием структур типа альтернативы или
рекурсии. Наиболее известным языком,
реализующим функциональную парадигму, является
LISP.

6. Математические основы функционального программирования

Общее понятие функции
Математическая функция – это отображение (mapping)
элементов одного множества, называемого областью
определения (domain set), в другое множество, называемое
множеством значений (range set):
f: A B.
Отображение описывается выражением или таблично.
Функция может иметь и несколько параметров, но всегда
возвращает единственный результат.

7.

Функции более высокого порядка, или функциональные
формы (functional forms) в отличие от т.н. простых
функций получают функции в виде параметров, либо
возвращают некоторую функцию в качестве своего
результата. Можно выделить три основных вида
функциональных форм:
1) Композиция функций (function composition) является
наиболее распространённых из форм. Она имеет два
функциональных параметра. Результат композиции
функций – это функция, значения которой являются в
свою очередь, результатом применения первой функции–
параметра к результату работы второй функциипараметра.
Например, пусть заданы две функции f(x)=x+2 и g(x)=3*x,
и известно, что функция h является их композицией, то
есть h=f ◦ g. Её значения можно вычислить по следующей
формуле:
h(x) = f(g(x)) = (3*x) + 2.

8.

2) Конструкция (construction) – это функциональная
форма, получающая в качестве параметра список
функций. В результате применения к своему аргументу
конструкция формирует список, элементы которого
определяются результатом применения к этому аргументу
каждой из функций-параметров.
Например, пусть задана функция h(x)=x/2, а также
функции f(x) и g(x). Предположим, что функция s является
конструкцией следующего вида: s(x)=[f, g, h](x). Тогда
результатом вызова вида s(4) является значение (6, 12, 2).

9.

3) Функция ПРИМЕНИТЬ-КО-ВСЕМ (apply-to-all) – это
функциональная форма, имеющая в качестве параметров
одну функцию, а также список аргументов. В качестве
результата возвращается список, элементы которого
определяются результатом применения функциипараметра к каждому аргументу.
Например, пусть задана функция f(x). Предположим, что
функция s реализует принцип ПРИМЕНИТЬ-КО-ВСЕМ, а
её вызов имеет следующий вид: s= (f, (2, 3, 4)). Тогда
будет получен следующий результат (4, 5, 6).

10. . Лямбда-исчисление Чёрча

Ранние теоретические работы, посвящённые функциям,
отделяли задачу определения функции от задачи её
именования. Метод определения безымянных функций
реализуется с помощью лямбда-исчисления,
разработанного А.Чёрчем в 1932 году.
Параметры и результат функции, задаются -выражением
(lambda expression). Само -выражение является функцией
и записывается в виде
(x1, x2, …, xn).fn .
Здесь символы xi являются формальными параметрами
(formal parameter) определения, которые именуют
аргументы в описывающем вычисления теле (body)
функции fn. Формальность означает, что их можно
заменить любыми другими символами, и это не отразится
на процессе вычислений.
Телом функции является произвольная форма, значение
которой может вычислить интерпретатор Лиспа:
константа или вызов другой функции.

11.

Рассмотрим в качестве примера выражение (x).x*x*x.
Как было указано выше, перед вычислением функции её
параметр символизирует любой элемент из области
определения, но в процессе вычисления он связан с
конкретным элементом. При исчислении -выражения для
заданного параметра говорят, что выражение применяется
к данному параметру. Механизм такого применения такой
же, что и при вычислении любой функции. Применение
-выражения, называемое также -вызовом, обозначается
следующим образом:
(x).x*x*x (2).
Результат вычисления данного выражения равен восьми.
Теория -исчисления утверждает что всё то, что
вычисляемо может быть представлено этим формализмом.
Действительно, в этих терминах можно описать
«предопределённые» константы (например, числа),
структуры данных (списки, кортежи и т.п.), логические
значения и ветвление.

12. Рекурсивные определения функций.

Принципиальная возможность решить некоторую задачу с
помощью компьютера, называется вычислимостью.
Одной из основополагающих математических теорий,
изучающих проблемы вычислимости функций
(алгоритмов) является теория рекурсивных функций.
Существуют различные виды рекурсии. Будем описывать
соответствующие функции с помощью Лисп-конструкции
DEFUN (см. раздел 2.6.1).

13.

простая рекурсия – одиночный рекурсивный вызов
встречается в одной или нескольких ветвях тела функции
f:
( defun f … (f …) … (f …) … )
параллельная рекурсия – тело функции f содержит вызов
некоторой функции g, несколько аргументов которой
являются рекурсивными вызовами функции f:
( defun f … (g … (f …) … (f …) … ) … )
взаимная рекурсия – в теле функции f вызывается
некоторая функция g, которая в свою очередь содержит
вызов функции f:
( defun f … (g … ) … )
( defun g … (f … ) … )

14. Задержанные и смешанные вычисления

Императивная организация вычислений по принципу
немедленного и обязательного выполнения каждой
очередной команды не всегда эффективна. Рассмотрим
следующую ситуацию, программа A вычисляет свой
вывод, который используется как ввод, для программы B.
Традиционно, это можно осуществить, сохраняя вывод A
во временный файл. Проблема состоит в том, что
временный файл может занять слишком много памяти.
Существует много неимперативных моделей управления
процессами, позволяющих прерывать и откладывать
процессы, а потом восстанавливать их и запускать или
отменять. Организация такого управления, достаточного
для оптимизации и программирования параллельных
процессов, реализуется с помощью так называемых
отложенных или ленивых вычислений (lazy evaluation).

15.

Ленивые вычисления являются одним из самых
мощных средств модульного построения программ,
позволяя отделять генератор данных от селектора
этих данных (например, тело цикла от условия его
завершения). Реализация ленивых вычислений
повышает эффективность исполнения программ.
Однако в этом случае чрезвычайно сложно
реализовать средства отладки программ. Поэтому
далеко не всякий язык программирования
предоставляет такие возможности. Функциональные
языки в зависимости от данного признака делят на
«ленивые» (нестрогие, non-strict) и «энергичные»
(строгие, strict). К первым относятся, например,
Haskell и Miranda, а ко вторым – Scheme, Standard ML
и Caml.

16. Специфика реализации рекурсии и ленивых вычислений

Пример
fact(n) )=df n. IF(n=0,1,n*fact(n-1))
В отличие от итерационного способа программирования
выполнение рекурсивно определяемой программы
происходит в два этапа . На первом этапе осуществляется
построение рекурсивных соотношений и частичное
вычисление с задержкой выполнения действий , которые
не могут быть выполнены на данном этапе. Задержка
вычислений обусловливается тем , что в описании
рекурсивно определяемой функции всегда присутствует
явное или косвенное обращение к той же самой функции .
Первый этап завершается после выполнения так
называемого условия завершения рекурсии. На втором
этапе осуществляется полное завершение всех
задержанных действий путем последовательного
"сворачивания" Рекурсивных соотношений.

17.

Например , при реализации функции вычисления факториала
при n=4, результатом первого этапа является следующая
последовательность :
fact(4)=4*fact(3)
fact(3)=3*fact(2)
fact(2)=2*fact(1)
fact(1)=1*fact(0)
fact(0)=1 .
Условием завершения рекурсии здесь является n=0 .
Сворачивание рекурсивных соотношений на втором этапе
происходит путем выполнения соответствующих
подстановок , в результате чего получается соотношение :
fact(4)=4*3*2*1 .

18. Основы программирования на языке Лисп

Исходный базис Лиспа (LISP 1), разработанный Мак-Карти
предельно лаконичен. Помимо определения понятия
символьных выражений, на обработку которых он и был
ориентирован, так называемый элементарный или «чистый»
Лисп (pure LISP) содержит лишь несколько базовых функций и
функционалов, предназначенных для обработки (ATOM, EQ,
CAR, CDR, CONS) и управления обработкой выражений
(QUOTE, EVAL, COND, LAMBDA, LABEL).
Над базисом языка строятся формулы, синтаксически
неотличимые от простых символьных выражений. Все
остальные механизмы вычисления и преобразования формул
могут сводиться к базису, рассматриваться как его вариант или
расширение. Это позволило в последствии разработчикам без
особых усилий расширить Лисп, включив в его состав средства,
упрощающие процесс разработки программ, в том числе и
императивные.

19. Запись и вычисление выражений

Основу Лиспа составляют символьные выражения,
которые называются S-выражениями (symbolic expression)
и образуют область определения для функциональных
программ. Можно сказать, что S-выражения является
основной структурой данных в Лиспе. Любое Sвыражение – это либо атом, либо список.
Атомы (atom) являются простейшими объектами Лиспа (и
соответственно простейшими S-выражениями), из
которых строятся остальные структуры. Они бывают двух
типов – символьные и числовые.
Символьный атом (символ) – последовательность букв,
цифр и специальных символов, содержащая, по крайней
мере, один символ отличающий его от числа. Например:
Дмитрий АВ13 В54 10А

20.

Числовые атомы – это обыкновенные числа, например:
124
-344
4.5
3.055Е8
Список (list) – это последовательность элементов,
заключённых в скобки и разделённых пробелами.
Элементами списка могут быть любые атомы или списки.
Рассмотрим примеры:

21.

Таким образом, список можно охарактеризовать, как
многоуровневую (иерархическую) структуру данных, в
которой открывающиеся и закрывающиеся скобки
находятся в строгом соответствии.
Список, в котором нет ни одного элемента, называется
пустым списком и обозначается «( )» или символом NIL.
Он играет такую же важную роль в работе со списками,
что и ноль в арифметике.
В Лиспе определены два вида констант: числовые атомы и
логические константы. Существует только две логические
константы. Символ NIL обозначает в логических
выражениях константу «ложь» (false). Логическое «да»
(true) задаётся символом «Т».

22.

Одно из основных требований при разработке Лиспа
состояло в необходимости создания системы обозначений,
позволяющих выражать функцию тем же способом, что и
данные. Данную задачу авторы языка решили, во-первых,
выбрав для определения функций систему -обозначений,
описанную в разделе :
(LAMBDA (аргумент_1 … аргумент_N) выражение),
и, во-вторых, представив вызов функции ( -вызов) в виде
списочной структуры:(имя_функции аргумент_1 …
аргумент_N).Данная форма записи вызова функций
называется префиксной, в противовес инфиксной форме,
широко применяемой, например, в арифметике: запись в
инфиксной форме 5 + 7 =>> префиксная (+ 5 7).
Очевидно, что синтаксический анализ программ при
использовании польской записи значительно упрощается,
так как по первому символу текущего выражения система
уже знает, с какой структурой имеет дело: с данными или
с программой.

23.

Кроме того, появляются широкие возможности по
динамической («на лету») модификации кода программы:
можно создавать функции и тут же их исполнять. Для того
чтобы реализовать всё это, Мак-Карти разработал
универсальную функцию, способную вычислять любую
другую функцию. Эта функция получила название EVAL
и имела вид S-выражения.

24. Префиксная и постфиксная записи выражений.

Классическим способом представления выражений для
анализа перед генерацией кода являются префиксная и
постфиксная записи .
Для пояснения рассмотрим выражение вида a+b*c+d/e-f .
Такая запись выражения называется инфиксной , что
означает расположение знака бинарной операции между
операндами . Интерпретация и соответственно анализ
такого выражения в общем случае носит неоднозначный
характер . Для устранения неоднозначности используется
приоритет операций .

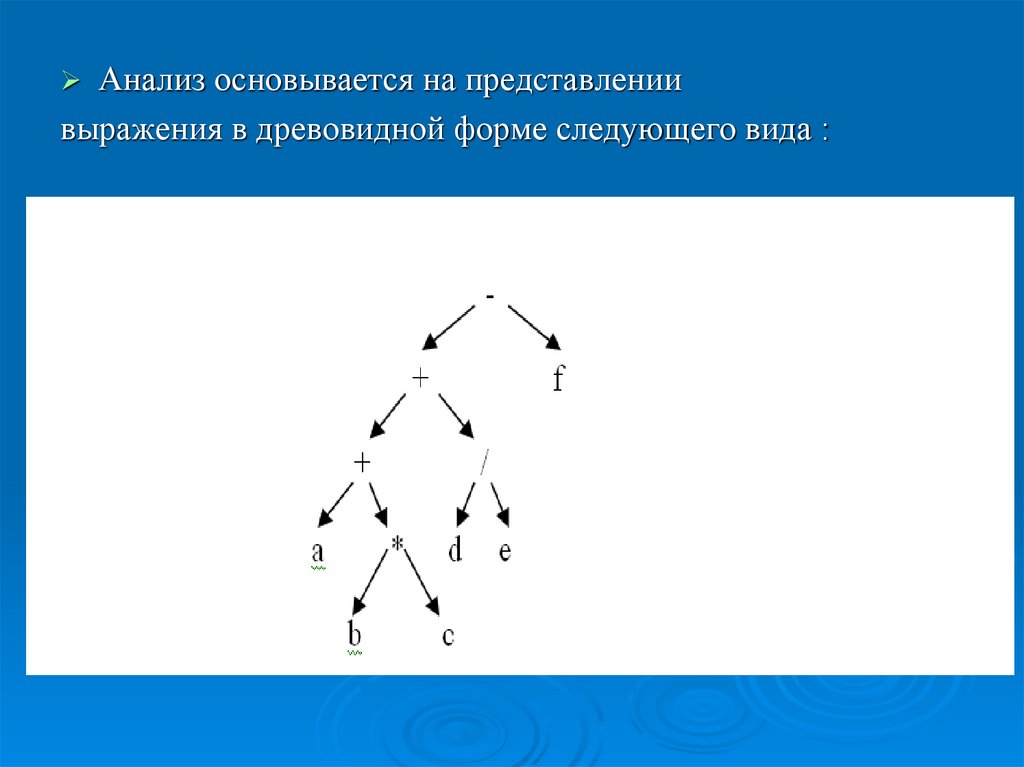
25.

Анализ основывается на представлении
выражения в древовидной форме следующего вида :

26.

Теперь, начиная с вершины (сверху вниз) и
придерживаясь лево-ориентированного пути ,
обойдем это дерево, попутно выписывая в
строку все встречающиеся символы. В
результате получим выражение вида - + + a * b c / d e f ,
представляющее префиксную запись.
Отличительная особенность префиксной
записи заключается в том, что каждый знак операции
предшествует своим операндам .
Например: + a b

27.

Постфиксная запись получается "зеркальным
отображением " соответствующей префиксной записи .
Таким образом для указанного выше выражения
постфиксная запись имеет вид f e d / c b * a + + - .
Отличительной особенностью постфиксной записи является
то , что каждый знак операции записывается после
операндов . Постфиксная запись является очень удобной для
вычисления выражений , поскольку в ней все знаки
выполняемых операций располагаются в порядке
убывания приоритетов. Последнее означает , что первая
встретившаяся операция при просмотре выражения слева
направо выполняется первой , вторая встретившаяся - второй
и т.п. . Для вычисления постфиксной записи используется
классический алгоритм с использованием стека . Алгоритм
основывается на просмотре символов выражения слева
направо и выполнении соответствующих действий в
зависимости от назначения символа (знак операции , символ
операнда или символ конца строки) .

28.

Таблица ниже иллюстрирует работу алгоритма на примере
постфиксной записи f e d / c b * a + + - , где символ определяет конец строки.
Считываемый символ Состояние
Содержимое стека
____________________________________________________________
f
1
Vf
e
1
Vf ,Ve
d
1
Vf ,Ve,Vd
/
2
Vf,Vd/e
c
1
Vf,Vd/e ,Vc
b
1
Vf,Vd/e ,Vc,Vb
*
2
Vf,Vd/e ,Vb*c
a
1
Vf,Vd/e ,Vb*c,Va
+
1
Vf,Vd/e ,Va+b*c
+
1
Vf,Va+b*c+d/e
1
Va+b*c+d/e-f
3
Va+b*c+d/e-f

29.

Таким образом алгоритм в процессе просмотра выражения
может находиться в одном из следующих состояний .
Считываемый символ является операндом (состояние 1).
В этом случае значение операнда заносится в стек.
Считываемый символ является знаком операции
(состояние2). Выполняется соответствующая
операция с операндами ,которые извлекаются из стека.
Извлеченные из стека операнды соответственно удаляются
из стека и в стек заносится результат выполнения операции.
Считываемый символ определяет конец строки
(состояние 3). Алгоритм завершает свою работу . В стеке
остается единственный элемент, определяющий результат
вычисления

30.

Здесь состояние 1 определяет Ve определяет значение
выражения e,а верх стека предполагается находящимся
справа . Приведенный выше алгоритм является
упрощенным , поскольку предполагается наличие только
односимвольных операндов . Если снять указанное
ограничение, то потребуется разделять элементы
постфиксной записи(например запятой). Приведенный выше
алгоритм является упрощенным , поскольку предполагается
наличие только односимвольных операндов . Если снять
указанное ограничение , то потребуется разделять элементы
постфиксной записи (например запятой).

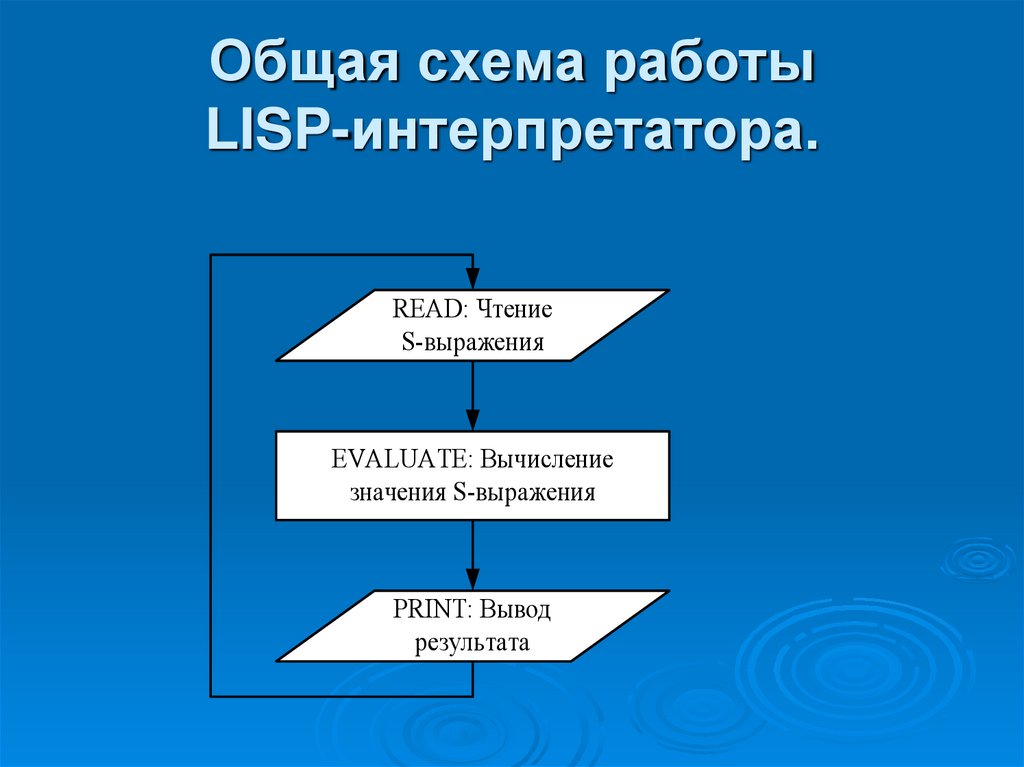
31. Общая схема работы LISP-интерпретатора.

READ: Чтение
S-выражения
EVALUATE: Вычисление
значения S-выражения
PRINT: Вывод
результата

32. Функция задержки вычислений

В некоторых случаях не требуется вычисления
значений выражений, а требуется само выражение.
Если прямо ввести с клавиатуры (+ 2 3), то в
качестве результата будет получено «5». Но данное
выражение можно понимать не только как функцию,
но и как список. Для этого необходимо
воспользоваться специальной функцией блокировки
QUOTE. Эта функция имеет один аргумент, который
и возвращает в качестве результата:
> (quote (+ 2 3))
(+ 2 3)
> (quote y)
y

33. Функция задержки вычислений

Блокировку QUOTE можно снять с помощью вызова
функции EVAL. Это универсальная функция Лиспа,
которая может вычислить любое правильно составленное
S-выражение. При этом вызов может производиться
внутри любого другого вычисляемого S-выражения.
> (eval (quote (+ 2 3)))
5
Рассмотрим взаимодействие функций EVAL и SETQ
> (setq x ' (1 2 3))
(1 2 3)
>x
(1 2 3)
>'x
x
> (eval ' x)
(1 2 3)

34. Функции обработки списков

Любой список может быть разбит на две части – голову, то есть первый
элемент списка, и хвост, список, взятый без своей головы (см. Рис. 8).
Голову любого списка позволяет извлечь функция CAR, а хвост –
функция CDR.
(A B C D)
Голова
(head)
Хвост
(tail)
Эти функции имеют по одному параметру типа «список». Применение
CAR либо CDR к атомам вызывает ошибку исполнения. Более того, в
первой версии Лиспа NIL-аргумент также приводил к ошибке, так как
NIL является атомом.
Имена функций CAR и CDR возникли по историческим причинам. Автор
Лиспа реализовывал свою первую систему на машине IBM 605. Для
хранения адреса головы списка использовался регистр CAR (contents of
address register), а для хранения адреса хвоста списка – регистр CDR
(contents of decrement register).
В ряде диалектов Лиспа вместо CAR и CDR можно использовать
более очевидные функции FIRST и REST, либо HEAD и TAIL.

35. Функции обработки списков. Примеры.

> (car ' (3 4 5))
3
> (car ' ((1 2) (3 4)) )
(1 2)
> (car NIL)
NIL
> (car ' (NIL 10))
NIL
> (cdr ' (3 4 5))
(4 5)
> (car ' ((1 2) (3 4)) )
((3 4))
> (cdr NIL)
NIL
> (cdr ' (10))
NIL

36. Пример определения функции обработки списков

Подсчитать сумму элементов числового списка:
(DEFUN sums (s) (IF (EQUAL (cdr s) NIL ) (car s) (+ (car s) (sums (cdr s))
))
)
(PRINT (sums '(1 2 3)))

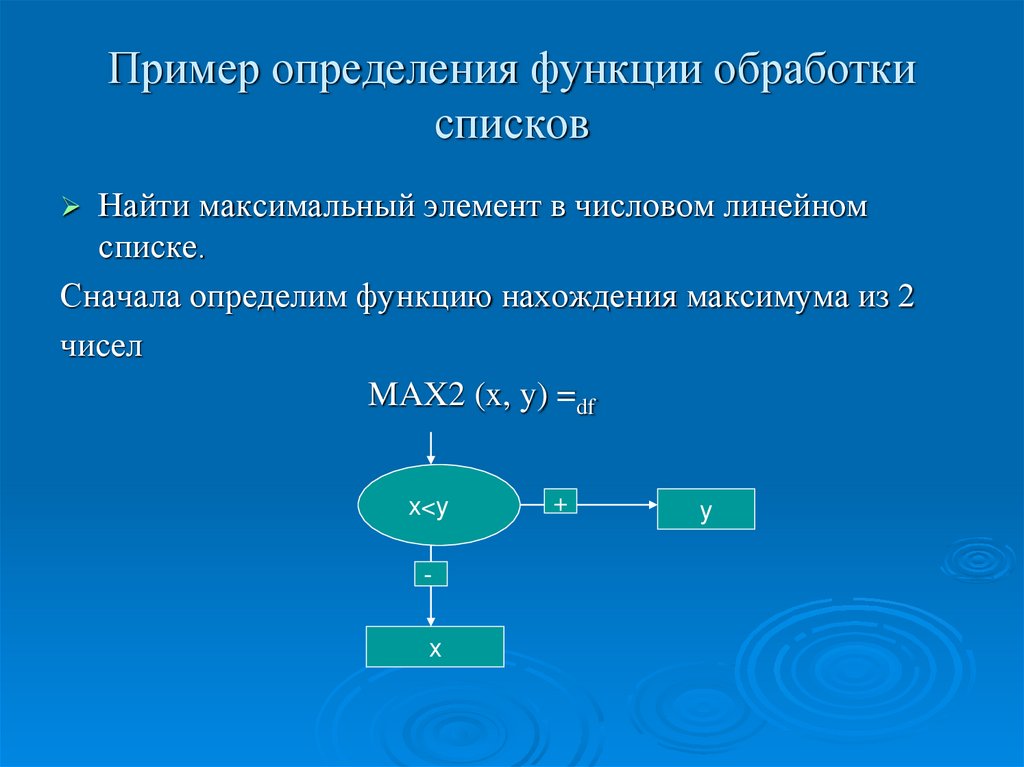
37. Пример определения функции обработки списков

Найти максимальный элемент в числовом линейном
списке.
Сначала определим функцию нахождения максимума из 2
чисел
MAX2 (x, y) =df
x<y
x
+
y

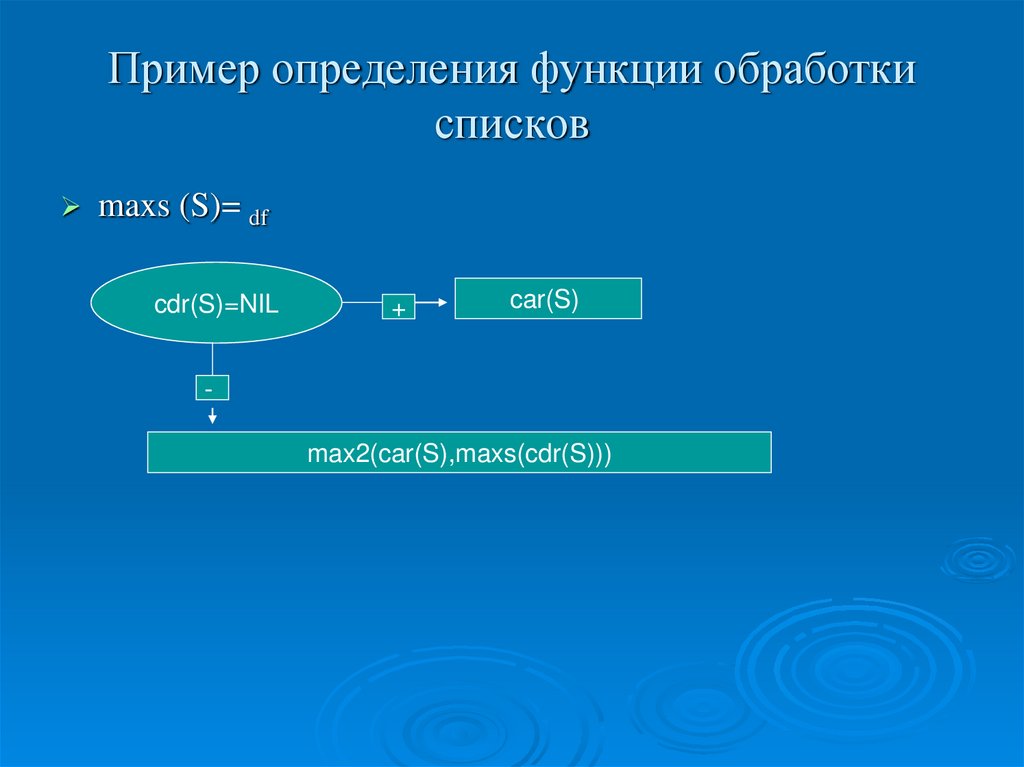
38. Пример определения функции обработки списков

maxs (S)= df
cdr(S)=NIL
+
car(S)
max2(car(S),maxs(cdr(S)))

39. Функции обработки списков. Функция CONS.

(CONS s-выражение список)
Данная функция строит новый список из своих аргументов
таким образом, что первый аргумент становится его головой,
а второй – хвостом.
> (cons ' a ' (b c))
(a b c)
> (cons ' (a b) ' (c d))
( (a b) c d)
Это даёт нам возможность вновь собрать список, разбитый
функциями CAR и CDR:
> (cons (car ' (a b c)) (cdr ' (a b c))
(a b c)
>

40. Функции обработки списков. Функция CONS.

(cons ' a ' (+ 1 2))
(a + 1 2)
Второй аргумент функции конструктора списков ВСЕГДА
должен быть списком, в противном случае будет получено
сообщение об ошибке:
> (cons ' a ' c)
ОШИБКА
Рассмотрим, как CONS работает с пустыми списками.
> (cons ' a NIL)
(a)
> (cons ' (a b) NIL)
( (a b) )
> (cons NIL ' (a b))
(NIL a b)
> (cons NIL NIL)
(NIL)

41. Функции обработки списков. Функция CONS. Пример.

Из числового линейного списка получить новый список,
включив в него только четные элементы исходного списка
Evenl(s) = df
+
s=NIL
NIL
-
mod(car(s),2)=0
evenl (cdr (s))
+
cons (car (s), evenl (cdr (s)))

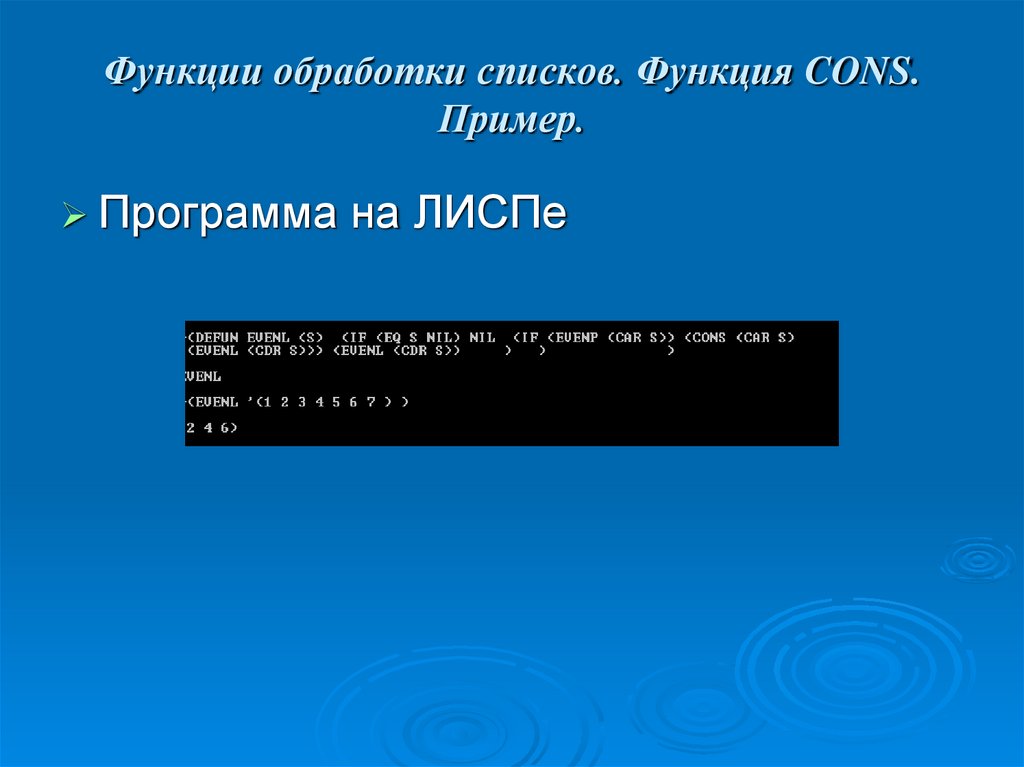
42. Функции обработки списков. Функция CONS. Пример.

Программа на ЛИСПе

43. Функции обработки списков. Примеры.

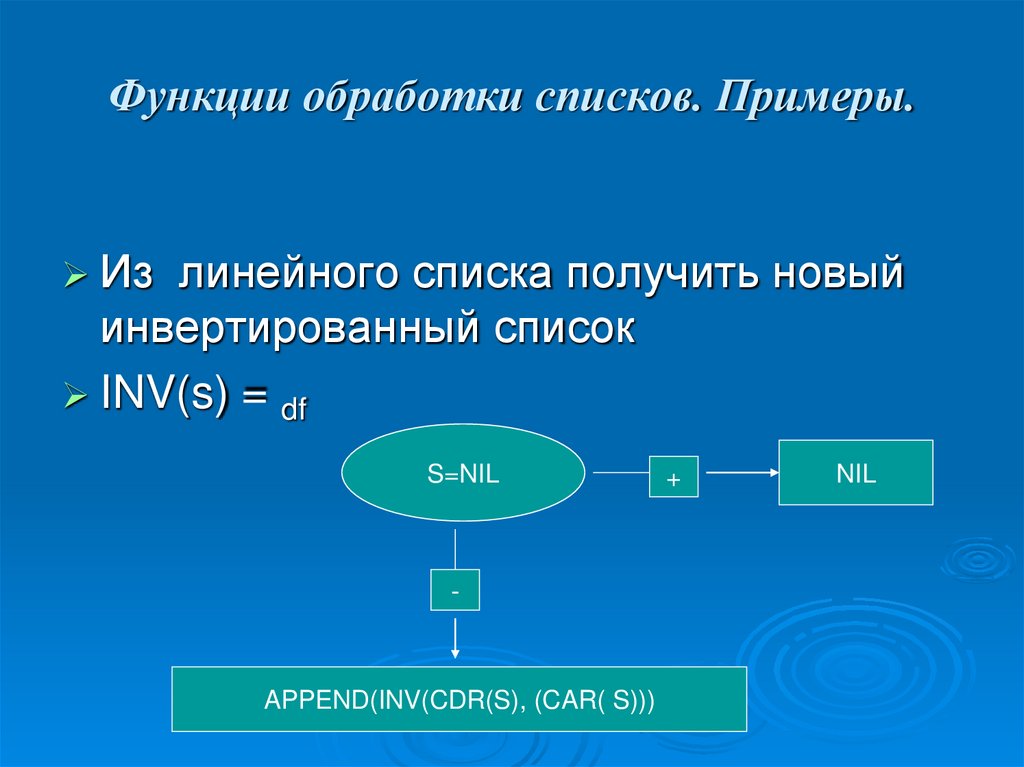
Из линейного списка получить новый
инвертированный список
INV(s) = df
S=NIL
-
APPEND(INV(CDR(S), (CAR( S)))
+
NIL

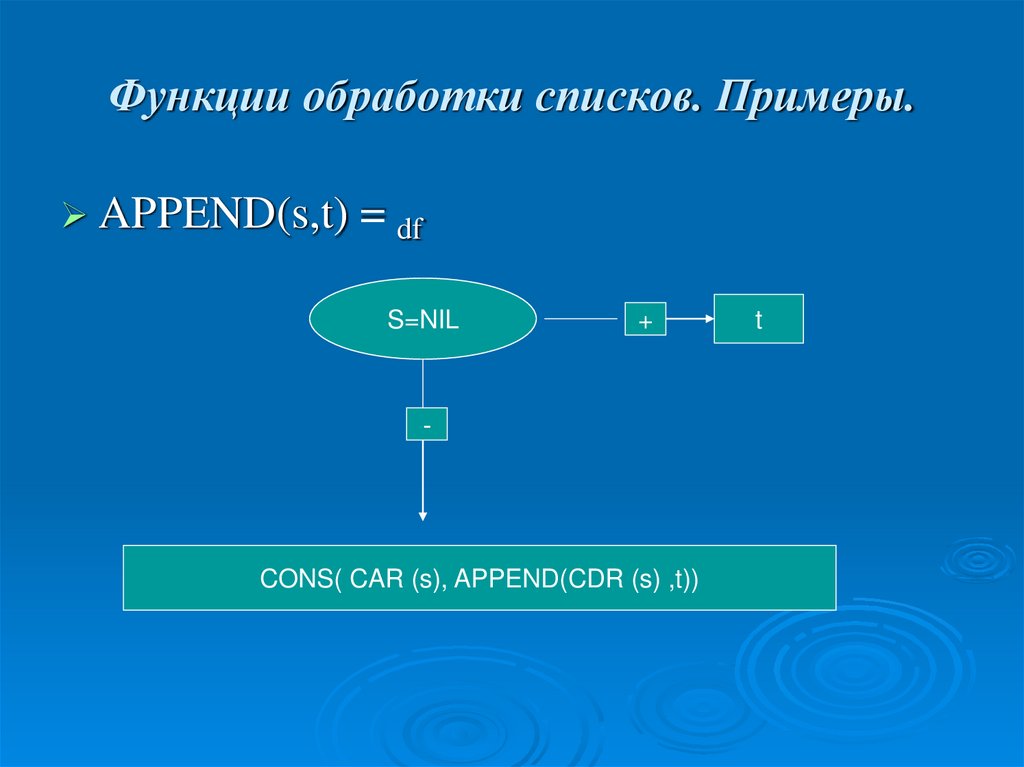
44. Функции обработки списков. Примеры.

APPEND(s,t) = df
S=NIL
+
-
CONS( CAR (s), APPEND(CDR (s) ,t))
t

45. Предикаты. Разветвление вычислений

Предикат в Лиспе – это функция, которая
определяет, обладает ли аргумент определённым
свойством, и в зависимости от результата
проверки возвращает в качестве значения T или
NIL.
В «чистом» Лиспе было предусмотрено только
два предиката: ATOM и EQ.

46. Предикат ATOM

Предикат ATOM возвращает значение T, если его аргумент
является атомом, и NIL в обратном случае. Формат вызова:
(ATOM s-выражение)
> (atom ' a)
T
> (atom ' (a b))
NIL
> (atom (car ' (a b) ) )
T
> (atom (cdr ' (a b) ) )
NIL

47. Предикат ATOM

Обратите внимание, как ATOM работает
с пустым списком:
> (atom ' NIL)
T
> (atom ' ( ) )
T

48. Предикат EQ

Предикат EQ сравнивает два символа и возвращает значение
Т, если они тождественны друг другу, и NIL в обратном
случае. Формат вызова:
(EQ аргумент1 аргумент2)
> (eq ' cat ' cat)
T
> (eq ' cat ' dog)
NIL
> (eq ' (cat) (car ' (cat dog) ) )
T
> (eq T NIL)
NIL

49. Предикат EQ

Предикат EQ можно применять к числам, если только они
представлены одним типом:
> (eq 10 10)
T
> (eq 10 10.0)
NIL
> (eq 350.0 3.5e2)
NIL
> (eq 3.14 3.14)
NIL
Поскольку предикат EQ определён только для атомов, то
перед его использованием необходимо проверить тип обоих
аргументов с помощью предиката ATOM.

50. Функция IF

(IF <условие> <то-форма> <иначе-форма>)
Пример
(IF (> X Y) X Y)

51. Функция COND

Проверка условий и последующее
разветвление вычислений выполняется с
помощью функции COND. Её структура
описывается следующим образом:
( COND ( <условие-1> <действие-1> )
( <условие-2> <действие-2> )
( <условие-N> <действие-N> ) )

52. Функция COND

Значение COND определяется следующим образом:
1.Выражения < условие-i >, выполняющие роль
предикатов, вычисляются
последовательно, слева направо, до тех пор, пока не
встретится выражение,
значением которого не является NIL.
2.Вычисляется результирующее выражение,
соответствующее этому
предикату, и полученное значение возвращается в
качестве значения
всего предложения COND.
3.Если истинного значения нет, то значением COND
будет NIL.

53. Функция COND

Значение COND определяется следующим образом:
1.Выражения < условие-i >, выполняющие роль
предикатов, вычисляются
последовательно, слева направо, до тех пор, пока не
встретится выражение,
значением которого не является NIL.
2.Вычисляется результирующее выражение,
соответствующее этому
предикату, и полученное значение возвращается в
качестве значения
всего предложения COND.
3.Если истинного значения нет, то значением COND
будет NIL.

54. Примеры задач на «COND»

if x>50 then 10 else if x > 20 then 30 else if x > 10 then 20
else 0;
(DEFUN pcond (x) (cond ((> x 50) 10)
((> x 20) 30)
((> x 10) 20)
(t 0)
))
(PRINT (pcond 42))

55. Примеры задач на «COND»

(defun fact (n)
(cond
((= n 0) 1)
(t (* (fact (- n 1)) n))))
(PRINT (fact 5))

56. Задачи на структурные списки

Структурный список – список ,
элементами которых являются списки.
Пример: ( a (b c) d)
Линеаризация структурного списка
lin (s):
Например: ( a (b c) d) lin (a b c d)
1.

57. Линеаризация структурного списка lin (s):

lin (s):
=df
S=NIL
+
NIL
+
cons (car (s), lin ( cdr (s)))
-
Atom (car (s) )
append ( lin (car (s)), lin ( cdr (s)))

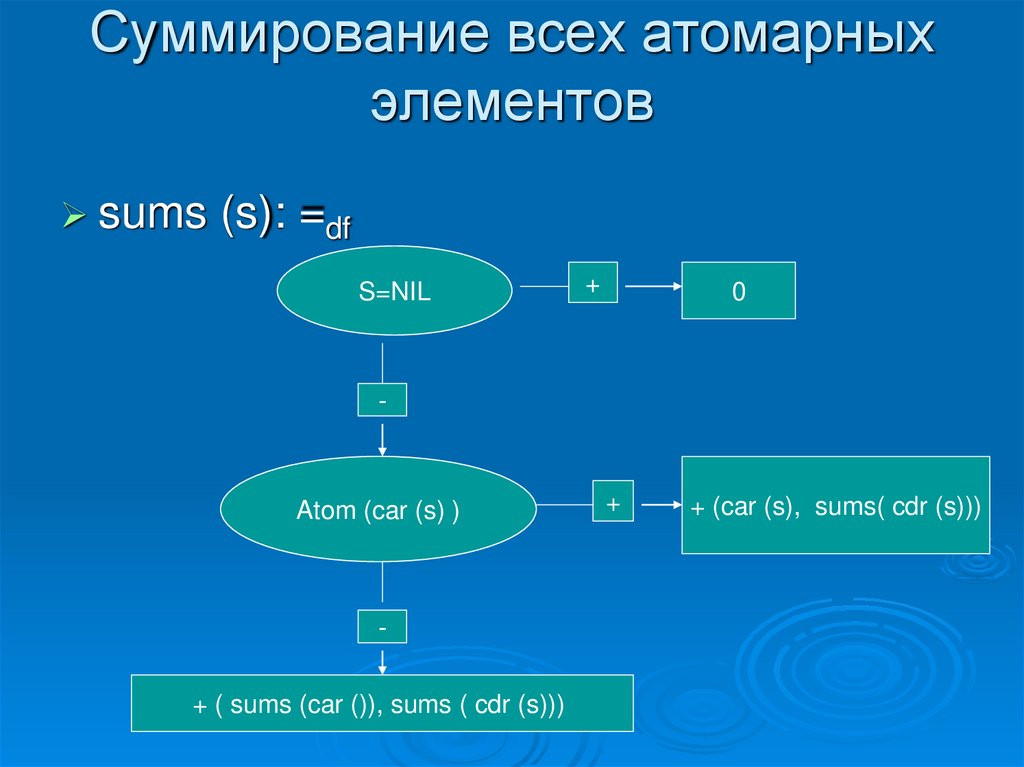
58. Суммирование всех атомарных элементов

sums (s): =df
S=NIL
+
0
-
Atom (car (s) )
-
+ ( sums (car ()), sums ( cdr (s)))
+
+ (car (s), sums( cdr (s)))

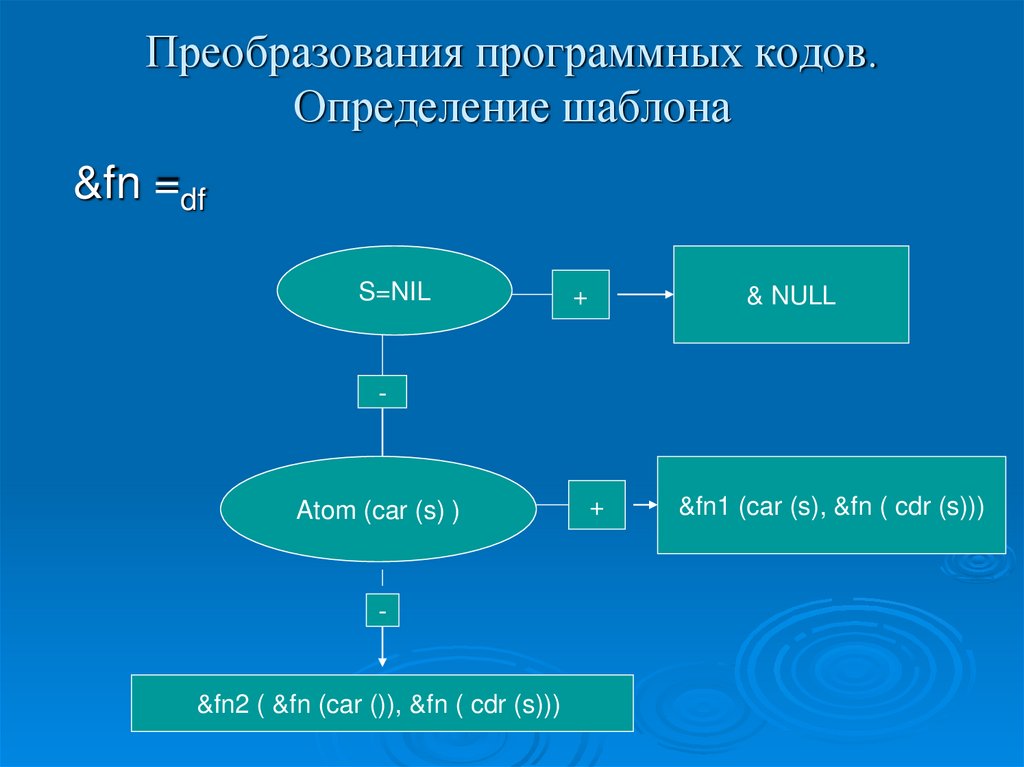
59. Преобразования программных кодов. Определение шаблона

&fn =df
S=NIL
+
& NULL
-
Atom (car (s) )
-
&fn2 ( &fn (car ()), &fn ( cdr (s)))
+
&fn1 (car (s), &fn ( cdr (s)))

60. Подстановки

fn ->lin
fn -> sums
NULL -> NIL
NULL -> 0
fn1 -> cons
fn1 -> +
fn2 -> append
fn2 -> +
Применяя
Применяя
указанные
подстановки мы
получим
определение
функции LIN
указанные
подстановки мы
получим
определение
функции SUMS

61. Использование переменных

Функциональные языки по определению не содержат
переменных и операторов присваивания. Однако с целью
повышения эффективности вычислительного процесса в
Лисп были введены аналогичные понятия. Изначально
символы в Лиспе не имеют значения. Значения имеют
только константы.
Для связывания символов используются специальные
функции: SET, SETQ.

62. Использование переменных

Функция SET связывает символ со значением,
предварительно вычисляя значения аргументов:
(SET аргумент1 аргумент2).
Параметр аргумент1 определяет символ, а аргумент2 – его
новое значение. В качестве значения функция возвращает
значение второго аргумента.
Если перед первым аргументом нет апострофа, то значение
будет присвоено значению этого аргумента. Рассмотрим
примеры:
> (set ' a ' (1 2 3))
(1 2 3)
>a
(1 2 3)

63. Использование переменных

> (set ' b ' c)
c
> (set b ' a)
a
>b
c
>c
a
>(eval c)
a
>(eval ' c)
(1 2 3)

64. Использование переменных

Функция SETQ аналогична SET, но не вычисляет
значение первого аргумента:
> (set m ' (3 4 5))
(3 4 5)

65. Арифметические операции

Изначально Лисп (pure LISP) был ориентирован только на работу со
списками, но достаточно скоро его дополнили возможностью
оперировать и числами. Системные арифметические функции могут
быть использованы с целыми или действительными (вещественными)
аргументами. Число аргументов у большинства из них может быть
разным.
(+ x1 x2 … xn) возвращает x1 + x2 + x3 + … + xn.
(– x1 x2 … xn) возвращает x1 – x2 – x3 – … – xn.
(* x1 x2 … xn) возвращает x1 * x2 * x3 * … * xn.
(/ x1 x2 … xn) возвращает x1 / x2 / x3 / … / xn.
Предусмотрены также две специальные функции для прибавления
(инкремент) и вычитания единицы (декремент): (1+ x) и (1– x).

66. Выделение элементов списка

Выделение элементов списка
может быть выполнено Функцией, выделяющей
n-ый элемент списка:(NTH n список).
Здесь n – номер элемента в списке; причём
индексация начинается с нуля.
> (nth 2 ' (1 2 3))
3
> (nth 3 ' (1 2 3))
NIL

67. Выделение элементов списка

Часто используются более наглядные имена FIRST, SECOND, THIRD,
FOURTH.
> (second ' (1 2 3))
2
> (fourth ' (1 2 3))
NIL
Последний элемент любого списка можно выделить с помощью
функции LAST:
> (last ' (1 2 3))
(3)
> (car (last ' (1 2 3) ) )
3
Можно сказать, что функция LAST удаляет из списка
все элементы кроме последнего.

68. Функция длины списка

Функция LENGTH возвращает в качестве значения длину
списка, то есть число элементов на верхнем уровне:
> (length ' (1 2 3 4 5))
5
> (length ' (1 (2 3 4) 5) )
3
Её также можно использовать для выделения последнего
элемента в списке:
> (setq x ' (a b c d) )
> (nth (1– (length x) ) x)
d

69. . Создание и модификация списков

Для создания новых списков можно использовать
функцию LIST:
(LIST аргумент1 аргумент2 аргумент3 … ),
которая возвращает список из своих аргументов. В качестве
аргумента может выступать любое s-выражение. Число
аргументов не ограничено.
> (list ' a ' b ' c))
(a b c)
> (list ' a ' (b c) )
(a (b c))
> (list (+ 1 2) (– 3 4) )
(3 -1)
> (list ' a NIL))
(a NIL)

70. Создание и модификация списков

Функция APPEND объединяет два и более списков в один:
(APPEND список1 список2 список3 … ).
> (append ' (a b) ' (c d) )
(a b c d)
> (append ' (a b) ' ((c d) e) )
(a b (c d) e)

71. Примеры на list и append

Построить список (1 2 ..N)
1) (DEFUN NAT (N) (IF (EQ N 0 ) NIL (append (NAT (- N 1)) (list N))))
(PRINT (NAT 3))
(1 2 3)
Инвертировать список s
2) (DEFUN INVERT (s) (IF (NULL s)NIL(append((invert (cdr s)) (list(car
s)))) ) )
(PRINT '(3 2 1))
(1 2 3)

72. Создание и модификация списков

Функция REVERSE изменяет порядок элементов в
аргументе-списке. Необходимо помнить, что REVERSE не
меняет порядок во вложенных списках (подсписках).
> (reverse ' (a b c) )
(c b a)
> (reverse ' (a (b c d) e) )
(e (b c d) a)

73. Создание и модификация списков

Удаление элементов из списка реализуется функцией
REMOVE:(REMOVE аргумент1 аргумент2).
Результирующий список формируется удалением из
списка аргумент2 всех вхождений атома аргумент1.
Вложенные списки при этом не проверяются.
> (remove ' a ' (a b a c a) )
(b c)
> (remove ' a ' (a b (a c) a) )
(b (a c))

74. Создание и модификация списков

Необходимо отметить, что большинство из
рассмотренных в данном разделе функций
можно свести к комбинации базовых функций.
Рассмотрим в качестве примера функцию LIST:
> (cons ' 2 NIL)
; эквивалентно (list ' 2)
> (cons ' 1 (cons ' 2 NIL) NIL) ; эквивалентно (list ' 1 ' 2)
Символ « ; » означает начало комментария. Текст
комментария интерпретатором Лиспа игнорируется.

75. Предикаты.Сравнение объектов

Предикат EQ, как уже было показано выше, может
правильно обрабатывать только символьные аргументы.
Это связано с тем, что он не проверяет логического
равенства сравниваемых объектов, а лишь смотрит,
представлены ли они в памяти вычислительной машины
физически одной структурой или нет. Одноимённые
символы представлены в одном и том же месте памяти (не
считая нескольких исключений), что позволяет EQ
сравнивать их «логически». Прочие же ЛИСП-объекты,
будучи внешне похожими, могут занимать физически
разные ячейки памяти

76. Предикаты.Сравнение объектов

Более общим является предикат
EQL. Он работает так же,
как и EQ, но дополнительно
позволяет сравнивать числа
одного типа:
> (eql 10 10)
T
> (eql 10 12)
NIL
> (eql 10 10.0)
NIL
> (eql 350.0 3.5e2)
T
> (eql 3.14 3.14)
T
> (eql ' (a b) ' (a b))
NIL

77. Обобщением EQL является предикат EQUAL. Он работает как EQL, но, кроме того, проверяет одинаковость двух списков:

> (equal 10 10)
T
> (equal 10 10.0)
NIL
> (equal 350.0 3.5e2)
T
> (equal ' x ' x)
T
> (equal ' (a b) ' (a b))
T
> (equal ' (a b c) ' (a (b c)) )
NIL

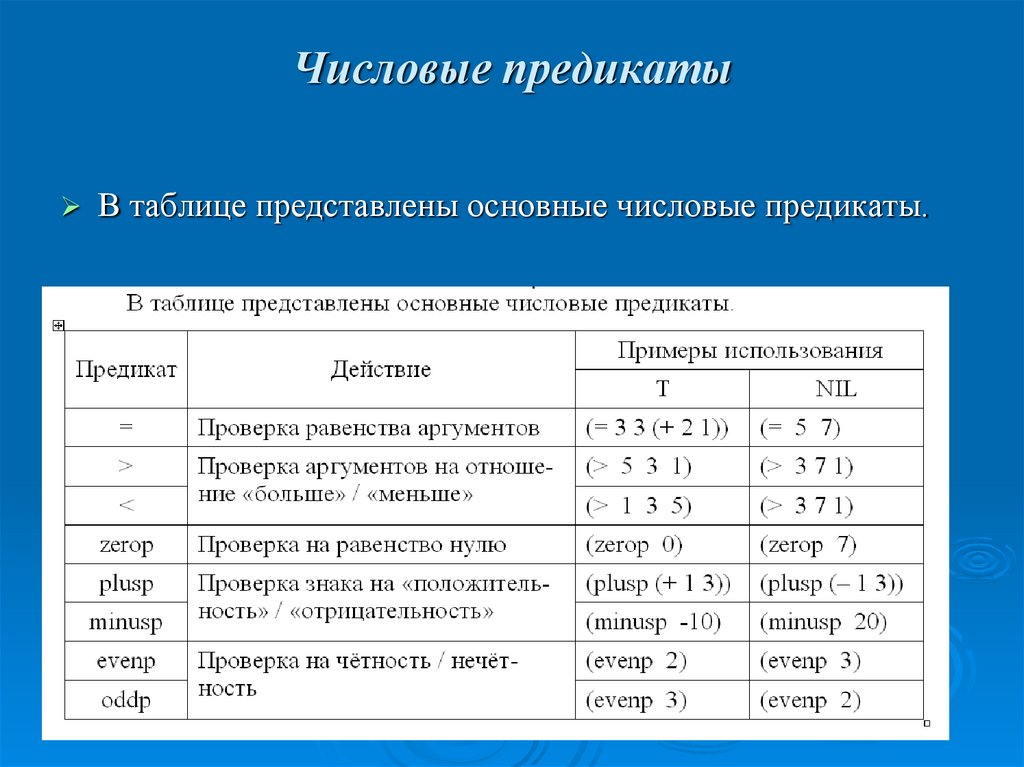
78. Числовые предикаты

С появлением в Лиспе стандартных функций для
арифметических операций, в его составе
появились и специальные предикаты,
оперирующие исключительно числами.

79. Числовые предикаты

В таблице представлены основные числовые предикаты.

80. Списковые предикаты

Предикат MEMBER имеет следующий формат:
(MEMBER s-выражение список)
и проверяет, находится ли первый аргумент внутри списка,
представленного вторым аргументом. При этом проверяются
только элементы первого уровня вложенности, подсписки не
просматриваются.
Если элемента в списке нет, MEMBER возвращает NIL.
В противном случае возвращается хвост второго
аргумента, начинающийся с этого элемента.
Таким образом, MEMBER в качестве истины
возвращает не Т, а величину не-NIL. В Лиспе для
предикатов значение не-NIL означает истину.

81. Списковые предикаты

> ( member ' b ' (c d b a) )
(b a)
> ( member ' c ' (a b (c)) )
NIL

82. Списковые предикаты

Предикат NULL проверяет, не является
ли указанное s-выражение пустым
списком:
> (null ' (a b) )
NIL
> (null ' ( ) )
T
> (null ' NIL)
T
> (null 10)
NIL

83. Контроль типов данных

Очень часто при разработке пользовательских
функций возникает необходимость в том, чтобы
аргументы имели конкретный тип. Поскольку
гарантировать, что ваша функция будет вызвана с
«правильными» аргументами, нельзя вы должны
сами выполнить их проверку. Лисп предоставляет
следующие предикаты для контроля типов
данных:

84. Контроль типов данных

85. Логические функции

Для объединения предикатов в сложные выражения и для
выделения элементов NIL используются логические
функции AND, OR и NOT.
> (not NIL)
T
> (not T)
NIL
> (not (zerop 10))
T
> (not ' (a b c))
NIL

86. Логические функции

Логическая функция OR принимает один или несколько
аргументов. Она выполняет (вычисляет) их слева направо и
возвращает значение первого аргумента, который не равен
NIL. Если все аргументы OR имеют значение NIL, то OR
возвращает NIL.
> (or NIL)
NIL
> (or NIL T NIL)
T
> (or (> 3 4) ' (a b c) )
(a b c)
> (or ' ( ))
NIL
Функцию OR можно использовать для выделения первого
непустого элемента в списке.

87. Логические функции

Логическая функция AND принимает один или несколько
аргументов. Она выполняет их слева направо. Если она
встречает аргумент, значение которого NIL, она
возвращает NIL, не продолжая вычисления остальных.
Если NIL- аргументов не встретилось, то возвращается
значение последнего аргумента.
> (and T)
T
> (and T NIL T)
NIL
> (and (> 3 4) ' (a b c) )
(a b c)
> (and ' ( ))
NIL
Функцию AND можно использовать для выделения
пустого элемента в списке.

88. Определение функций пользователя

(DEFUN имя _функции
список_ аргументов тело_
функции).
В качестве параметра имя_функции может использоваться
любой символ. Параметр список_аргументов называется
-списком и содержит перечень формальных аргументов
функции. Тело функции – это вычисляемая форма от
аргументов. Значение тела функции при заданных
аргументах образует значение функции.
> (defun double ( num ) (* 2 num) )
> (double 7)
14
Если функция не имеет аргументов, то при её создании в
функцию DEFUN нужно передать пустой список:
> (defun Pi_2 ( ) (* 3.14 3.14) )
> (Pi_2)
9.8596

89. Специальные формы языка Лисп

В любом императивном языке программирования
наряду с основными действиями есть
специальные механизмы для управления
вычислительным процессом. В Лиспе для этих
целей используются специальные разновидности
форм, которые мы будем называть
предложениями (clause). Внешне предложения
выглядят как функции, и так же, как они,
предложения возвращают значение (результат).
Однако функциями они не являются, и разные
предложения использую аргументы по-разному.

90. Специальные формы языка Лисп

Специальные формы предложения) можно
разбить на следующие группы:
1)управление контекстом;
2)последовательное исполнение;
3)разветвление вычислений;
4) итерации (циклические предложения);
5) передача управления;
6)динамическое управление вычислением.

91. Управление контекстом

Обычно различают три вида средств управления
контекстом:
блокировка вычислений;
вызов функции;
предложения LET и LET*.
Первые два из них были рассмотрены ранее.
Если говорить, немного упрощённо, то конструкция LET
предназначена для создания локальных переменных в
логически связанных вычислительных блоках.

92. Управление контекстом

В общем виде форма LET записывается так:
(LET ((перем-1 знач-1) (перем-2 знач-2) ... ) форма-1
форма-2 ... форма-N).
Вычисляется LET следующим образом:
1.Локальные переменные перем-1, перем-2, ...
одновременно связываются с соответствующими
значениями знач-1, знач-2, … Вместо списка вида (перем-i
знач-i) можно указать просто перем-i, в этом случае
переменная будет связана со значением NIL.
2.Последовательно вычисляются значения её аргументов
форма-1, форма-2, форма-N.
3.В качестве значения предложения LET возвращается
значение последнего аргумента форма-N.
4.После выхода из предложения связи переменных
перем-1, перем-2, ... ликвидируются и любые их
изменения не будут видны извне.

93. Управление контекстом

Форму LET удобно использовать, когда необходимо
временно сохранять промежуточные значения. В качестве
примера построим функцию rectangle, которая будет
иметь один аргумент – список из двух элементов,
задающих длину и ширину прямоугольника. Она должна
рассчитывать и выводить на экран площадь и периметр
прямоугольника, а в качестве результата возвращать– Ok.
(defun rectangle (dim)
(let ( (len (car dim)) (wid (cadr dim)) )
( print (list ' area (* len wid)) )
( print (list ' perimeter (* (+ len wid) 2)) )
' Ok))
Итак, вызовем данную функцию:
> (rectangle ' (4 5))
(area 20)
(perimetr 18)
Ok

94. Управление контекстом

Поскольку присвоение значений всем переменным формы
выполняется одновременно, то следующий вызов вызовет
ошибку:
>
(print (let ( (x 2) (y (* 3 x)) ) (list x y)))
Тип ошибки зависит от диалекта языка. Действительно, в
XLISP при вычислении значения переменной y символ x
будет связан со значением NIL, а в Common LISP его
значение не будет определено (unbound).
Подобных ошибок можно избежать, воспользовавшись
формой LET*, единственное отличие которой от формы
LET состоит в последовательном вычислении значений
переменных.
> (print (let* ( (x 2) (y (* 3 x)) ) (list x y)))
> (2 6)

95. Последовательное исполнение

Предложения PROGN, PROG1, PROG2
позволяют работать с несколькими
вычисляемыми формами:
(PROG1 форма1 форма2 ... формаN)
(PROG2 форма1 форма2 ... формаN)
(PROGN форма1 форма2 ... формаN)
Все они имеют переменное число аргументов,
которые последовательно вычисляются. В
качестве результата возвращается значение
первого (PROG1), второго (PROG2) или
последнего (PROGN) аргумента.

96. Последовательное исполнение

> (prog1
(setq x 2) (setq y (* 3 2)))
2
> (progn
(setq x 2) (setq y (* 3 2)))
6

97. Разветвление вычислений

(IF <условие> <то-форма> <иначе-форма>)
Пример
(IF (> X Y) X Y)

98. Разветвление вычислений

( CASE ключ
( список-ключей-1 форма-11 форма-12 … )
( список-ключей-2 форма-21 форма-22 … )
( список-ключей-N форма-N1 форма-N2 … )
[ ( T форма-T1 форма-T2 … ) ]
)

99. Разветвление вычислений

Вычисляется CASE следующим образом:
Вычисляется значение ключевой формы КЛЮЧ.
Значение ключа сравнивают с элементами списков список
-ключей-i, с которых начинаются альтернативы.
Когда в списке найдено значение ключевой формы,
начинают вычисляться соответствующие формы форма-i1,
форма-i2, …, значение последней из которых
возвращается в качестве результата CASE (неявный
PROGN).
Если ключевое значение не было найдено ни в одном из
списков ключей, но определено действие по умолчанию
(T), то начинают выполняться формы форма-T1, формаT2, …, значение последней из которых возвращается в
качестве результата CASE. Если же действие по
умолчанию не определено, то в качестве результата
формы CASE возвращается NIL.

100. Разветвление вычислений

В качестве примера рассмотрим функцию case_test:
(defun case_test (x)
(case x
( (1 2 3) ' (first case) )
( (4) ' (second case) )
( T ' (default case) )
)
)
Она будет порождать следующие результаты:
> (print (case_test 2))
(first case)
> (print (case_test 4))
(second case)
>(print (case_test 10))
(default case)
> (print (case_test NIL))
(default case)

101. Циклические предложения

Предложение LOOP реализует бесконечный цикл, в котором
формы, представленные в списке LOOP, вычисляются до
тех пор, пока не встретится явный оператор завершения
RETURN.
(LOOP форма1 форма2 … )
В качестве примера определим функцию, которая
принимает один аргумент n и возвращает сумму всех чисел
от 1 до n.
(defun add-integers (n)
(let ( (count 1) (total 1) )
(loop
( cond ((= count n) (return total)) )
( setq count (+ count 1) )
( setq total (+ total count) )
)
)
)

102. Циклические предложения

Построим функцию, принимающую список
чисел и возвращающую новый список, в
котором каждое число удвоено.
(defun double(lst)
(let ( (newlst nil) )
(loop
( cond ((null lst) (return newlst)) )
( setq newlst ( append newlst (list (* 2 (car
lst))) ) )
( setq lst (cdr lst) ) ) ) )
(print(double '(5 15 10 20)))

103. Циклические предложения

(defun double(lst)
(let ( (newlst nil) )
(loop
( cond ((null lst) (return newlst)) )
( setq newlst ( append newlst (list (* 2 (car lst))) ) )
( setq lst (cdr lst) ) ) ) )
(print(double '(5 15 10 20)))

104. Циклические предложения

В обоих примерах для организации цикла кроме самого
LOOP пришлось использовать формы LET и COND. Этого
можно было бы избежать, воспользовавшись другими
формами циклического вычисления. Самым общим
циклическим предложением является форма DO:
( DO (( перем-1 знач-1 шаг-1) (перем-2 знач-2
шаг-2) … )
( условие_окончания форма-11 форма-12 … )
форма-21 форма-22 …
)

105. Циклические предложения

Вычисляется DO следующим образом:
Локальным переменным перем-1, перем-2, …
присваиваются начальные значения знач-1, знач-2, …
Переменным, для которых не заданы начальные значения,
присваивается NIL.
Проверяется условие окончания, если оно выполняется,
вычисляются форма-11, форма-12, … В качестве
результата DO берётся значение последней из этих форм.
Если условие окончания не выполняется, то вычисляются
форма-21, форма-22, …
На следующем шаге цикла переменным перем-i
присваиваются одновременно новые значения,
определяемые формами шаг-i, и всё повторяется.
Значения переменных, для которых не задана форма шаг-i,
не изменяются.

106. Циклические предложения

Реализуем функцию add-integers с помощью цикла DO:
(defun add-integers (n)
(do ( (count 1) (total 1) )
( (= count n) total) ; эквивалентно ( (= count n) (return
total) )
( setq count (+ count 1) )
( setq total (+ total count) )
)
)
(PRINT (add-integers 4))
1+2+3+4
Аналогично LET* существует форма DO*, вычисляющая
значения локальных переменных последовательно, а не
одновременно.

107. Циклические предложения

Если вам нужно просто повторить некоторые вычисления
заданное количество раз, удобнее будет воспользоваться
функцией DOTIMES:
(DOTIMES (var num-форма return-форма) body-форма )
Вычисляется DOTIMES следующим образом:
Вычисляется num-форма, в результате чего получается
целое число count.
Локальная переменная-счётчик меняется от 0 до count-1, и
соответственно каждый раз вычисляется body-форма.
Последней вычисляется return-форма. Если она
отсутствует, то результатом DOTIMES будет NIL.

108. Циклические предложения

Реализуем функцию, которая выводит на экран
последовательность чисел от нуля до n:
(defun f_test (n)
( dotimes ( count (1+ n) NIL ) (print count) )
)
Для наглядности рассмотрим также функцию add-integers:
(defun add-integers (n)
(let ( (total 0) )
( dotimes ( count (1+ n) total ) ( setq total (+ total count) )
)
)
)

109. Ввод и вывод

Для ввода данных от пользователя используется
безаргументная псевдо - функция READ (собственно ввод
данных с клавиатуры и есть её побочный эффект).
Функция READ отличается от операторов ввода-вывода
других языков программирования тем, что обрабатывает
вводимое выражение целиком, а не как набор одиночных
элементов данных.
Как только интерпретатор встречает READ, вычисления
приостанавливаются до тех пор, пока пользователь не
введёт какой-либо символ или выражение. При этом
READ никак не указывает на ожидание информации.
Введённое оператором выражение становится результатом
функции READ. Если прочитанное выражение
необходимо для дальнейшего использования, то READ
должна быть аргументом какой-либо формы, которая
свяжет полученное выражение с конкретным символом:

110. Ввод и вывод. Пример.

> ( setq x (read) )
> (+ 1 2) вводимое выражение
> (print (eval x))
3

111. Ввод и вывод.

Для вывода выражений чаще всего используют функцию
PRINT. Она возвращает значение своего же аргумента, а в
качестве побочного эффекта выводит это значение на
монитор.
> (print (+ 2 3) )
5 печать выражения
5 значение
> (+ (print 2) 3)
2 печать выражения
5 значение
Выводимое выражение можно считывать функцией READ в
виде, логически тождественном первоначальному, либо
обрабатывать функцией EVAL:
> (eval (print (read) ) )
(* 2 3)
(* 2 3) печать выражения
6 значение

112. Функционалы

Стандартные функционалы языка Лисп можно разбить на две группы:
применяющие и
отображающие.
Применяющие (аппликативные) функционалы применяют функциональный
аргумент к его
параметрам. Так как применяющие функционалы вычисляют значение функции,
в этом
смысле они аналогичны функции EVAL, вычисляющей значение выражения.
Функционал APPLY имеет два аргумента: имя функции и список, и применяет
названную
функцию к элементам списка, как к аргументам функции.
Используя APPLY, можно в зависимости от функционального аргумента
осуществлять в
одной и той же точке
программы различные вычисления:
> (setq f ' +)
+
> (apply f ' (2 7))
9
> (setq f ' *)
*
> (apply f ' (2 7))
14

113. Функционалы

Построим функцию расчёта среднего значения списка чисел:
(defun list-mean (lis)
( / (apply '+ lis) (length lis) ) )
(print(list-mean ' (10 20 30 40)))
25
Применяющий функционал FUNCALL аналогичен APPLY, но
аргументы он принимает, не в списке, а по отдельности:
(setq add ' +)
(print(funcall add 2 7 1))
10
Таким образом появляется возможность использовать
синонимы имён функций.

114. Функционалы

Отображающие функционалы (МАР-функционалы) – это
функции, которые некоторым образом отображают список в
новый список.
Одним из основных MAP-функционалов является
MAPCAR:
(MAPCAR функция список1 список2 … списокN)
Число аргументов-списков должно быть равно числу
аргументов, принимаемых функцией, указываемой в
качестве первого аргумента.
Если при вызове MAPCAR указаны только два аргумента,
то функция, определённая первым аргументом,
применяется к каждому элементу списка, определённого
вторым аргументом. При этом результат помещается
(отображается) в новый список.

115. Функционалы

(defun case_test (x)
(case x
( (1 2 3) ' (first case) )
( (4) ' (second case) )
( T ' (default case) )
)
)
(print(mapcar
' case_test ' (2 4 6)))
((first case) (second case) (default case))
((first case) (second case) (default case))

116. Функционалы

( print (mapcar ' + ' (2 4 6 8) ' (10 20)))
(12 24)

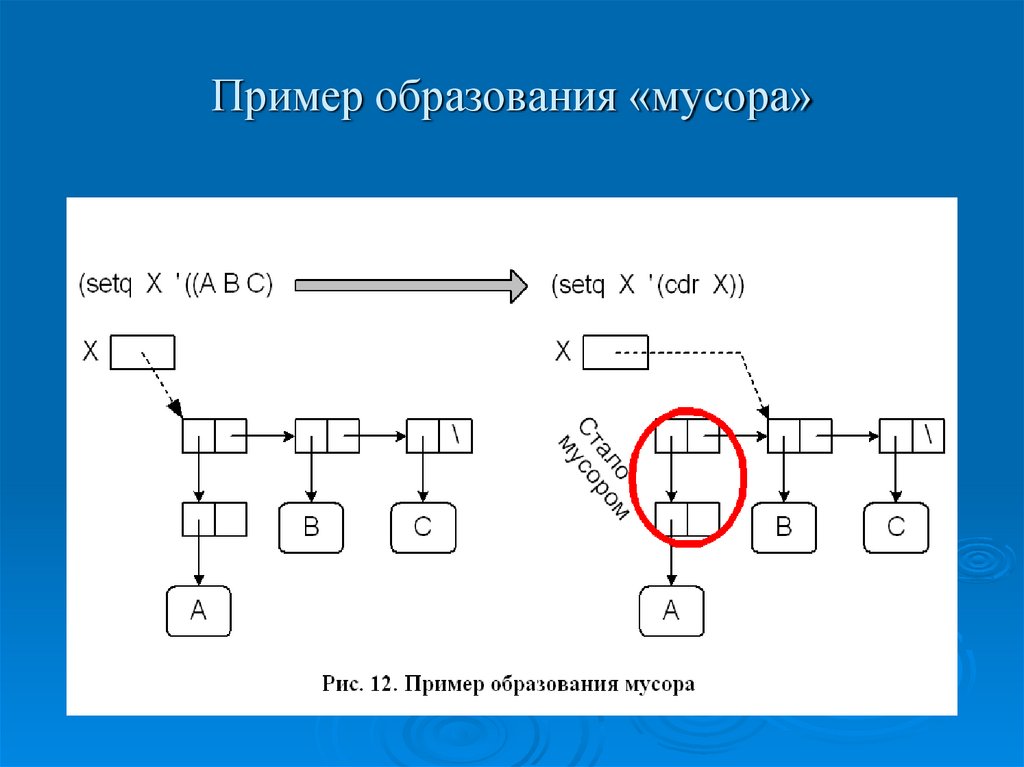
117. Чистка «мусора»

В результате вычислений в памяти могут
возникнуть структуры, на которые нельзя
сослаться. Это происходит, когда
вычисляемая структура не сохраняется с
помощью SETQ, или когда теряются ссылки
на старое значение. Такие ячейки памяти
называют мусором.

118. Пример образования «мусора»

119. Чистка «мусора»

Для повторного использования памяти, ставшей мусором,
в Лисп-системах предусмотрен специальный сборщик
мусора (garbage collector), который работает в фоновом
режиме либо запускается автоматически, когда в памяти
остается мало места. Сборщик мусора перебирает все
ячейки и собирает ставшие мусором ячейки в список
свободной памяти (free list).

120. Системные функции

Для упрощения работы оператора с Лисп-системой
используются специальные системные функции

121. ПРИМЕРЫ

(DEFUN DD (x) (* x x) )
(PRINT (DD 5) )
(DEFUN fact (n) (IF (EQ n 0)1 (* n (fact (- n 1) ))))
(PRINT (fact 5))

122. ПРИМЕРЫ

(DEFUN gcd (m n) (IF (EQ (mod m n)0 ) n (gcd n (mod m n) ) ) )
(PRINT (gcd 12 7))
DEFUN fxy (n) (IF (EQ n 0) NIL (cons 'x (fyx (- n 1) ) )
(DEFUN fyx (n) (IF (EQ n 0) NIL (cons 'y (fxy (- n 1) ) )
(PRINT (fxy 5)
) )
) )

123. Примеры программ на ЛИСПе

Следующий пример программы относится к классу программ
сортировки, а именно сортировке перестановкой. Идея, воплощенная
в этой программе, заключается в том, что вначале на первую позицию
списке перемещается минимальный элемент, а затем процедура
повторяется для оставшейся части списка:
;Сортировка перестановкой на Лиспе
;вспомогательная функция возвращает минимальное значение в
списке
(DEFUN MINS(X)
(COND
((NULL (CDR X)) (CAR X));В списке один элемент — он же min
((< (CAR X) (MINS (CDR X))) (CAR X)); рекурсия
(T (MINS (CDR X)))
19
)
)

124. Примеры программ на ЛИСПе

;вспомогательная функция удаляет первое вхождение элемента в
список
(DEFUN REMV (EL S)
(COND
((NULL S) NIL)
((EQ EL (CAR S)) (CDR S)); если первый — возвращается хвост
(T (CONS (CAR S) (REMV EL (CDR S))));рекурсия
)
)
;собственно функция сортировки списка по возрастанию
перестановкой
(DEFUN SORTS(X)
(COND
((NULL (CDR X)) X)
(T (CONS (MINS X) (SORTS (REMV (MINS X) X))))
)
)

125. Примеры программ на ЛИСПе

Еще один вариант программы сортировки основан на идее вставки, начиная с
первого, элемента в список на подобающее ему место в зависимости от
величины, своего рода выполнение команды «Равняйся!»:
;Сортировка вставкой на Лиспе
;вспомогательная функция вставки элемента
;в список на подобающее место
(DEFUN INS(X S)
(COND
((NULL S) (LIST X)); если был пустой список
((< X (CAR S)) (CONS X S) );если меньше первого, вставляется перед ним
(T (CONS (CAR S) (INS X (CDR S))))
)
)
;функция сортирует список по возрастанию
(DEFUN SORTS(X)
(COND
((NULL X) X)
(T (INS (CAR X) (SORTS (CDR X))))
)
)

126. Примеры программ на ЛИСПе

(DEFUN sumd (n) (IF (< n 10) n (+ (mod n
10) (sumd (floor n 10 ))) ) )
(Print (sumd 123))