Введение в функциональное программирование

1. ВВЕДЕНИЕ В ФУНКЦИОНАЛЬНОЕ ПРОГРАММИРОВАНИЕ

1

2.

Общие особенности ФП
Любая вычислительная операция это процесс, имеющий вход и выход.
Следовательно, она может быть описана функцией.
Математические функции также выражают связь между параметрами
(вход) и результатом (выход) некоторого процесса.
Функциональная программа представляет собой определения функций.
Функции могут определяться через другие функции или через самих себя
(рекурсивно).
Программируя на функциональном языке, программист не должен
описывать порядок вычислений. Ему необходимо просто описать желаемый
результат в виде системы функций, установить функциональную
зависимость между входами и выходом.
Простейший пример – таблица Microsoft Excel, в которых значения ячеек
задаются выражениями, а не командами, определяющими как вычислять
это значение. Нигде не задается порядок вычислений. Фактически вся
таблица представляет собой набор функций и констант, определенных
друг через друга. Другим функциональным языком является, как ни
странно, SQL основанный на реляционном исчислении.
2

3.

Общие особенности ФП
Функциональное программирование (ФП) – это способ составления
программ, в которых единственным действием является вызов функции,
единственным способом расчленения программы на части является
введение имени для функции и задание для этого имени выражения,
вычисляющего значение функции.
Чистое ФП не признает никаких ячеек памяти, присваивания, передач
управления, циклов и блок-схем. Повторные вычисления осуществляются
через рекурсию, являющуюся основным средством ФП.
3

4.

Аксиоматика ФП
Аксиоматическое понятие - понятие принимаемое как данность и не
сводимое к другим понятиям. Следовательно, аксиома не может иметь
строгого определения.
Исходным аксиоматическим понятием ФП является множество.
Множество не имеет строгого определения, однако может быть
охарактеризовано или описано в образных выражениях:
под «множеством» мы понимаем соединение в некое
целое M определённых хорошо различимых предметов m нашего
созерцания или нашего мышления (которые будут называться
«элементами» множества M) (Георг Кантор);
множество есть совокупность различных элементов, мыслимая как
единое целое (Бертран Рассел)
4

5.

Аксиоматика ФП
Корте́ж — это множество, состоящее из последовательного и конечного
числа элементов.
Основные отличия множества от кортежа:
Кортеж – это упорядоченный набор элементов. Каждый элемент
находится на своем порядковом месте. Поэтому иногда кортеж называют
вектором.
Кортеж это конечная последовательность элементов.
Каждый порядковый номер (положение элемента) уникальный.
5

6.

Аксиоматика ФП
Соответствие – предполагает наличие двух множеств, причем для каждого
элемента первого множества либо не указано соответствующих элементов
второго множества, либо такие элементы указаны.
Первое множество называется множеством отправления.
Второе множество – множеством прибытия.
Кроме этого должно быть указано множество пар (кортежей) <a,b>,
указывающих, какие элементы множества отправлений (а) соответствуют
каким элементам множества прибытия (b).
Таким образом, понятие соответствия задается (выражается) через
понятия множества и кортежа.
6

7.

Аксиоматика ФП
Функция.
Существует два основных подхода к пониманию функции:
1. Трактовка функции через переменные: «Функция – одно из основных
понятий математики, выражающая зависимость одних переменных
величин от других» [Большая Советская Энциклопедия].
1.1 Истолкование функции как переменной величины (то, чему
учат в средней школе): «Та переменная величина, числовые значения
которой изменяются от числовых значений другой величины, называется
зависимой переменной или функцией этой другой переменной величины».
1.2 Истолкование функции как закона, но также связанного с
понятием переменной величины: «Закон (правило), по которому
значениям независимых переменных соответствуют значения
рассматриваемой переменной называется функцией».
Недостаток первого подхода: расплывчатость формулировок, для
уточнения которых необходимо дать четкое понятие переменной
величины, изменению во времени и самому времени.
7

8.

Аксиоматика ФП
2. Отказ от переменных величин. Это более широкое понятие, поскольку
позволяет рассматривать функции не только от величин. Здесь можно
выделить три разновидности определения:
2.1 Определяется не сама функция, а «функциональная
ситуация». Пусть M и N два произвольных множества. Говорят, что на М
определена функция f, принимающая значения из N, если каждому
элементу x M поставлен в соответствие один и только один элемент из N.
Здесь вместо термина функция часто используется термин отображение.
Однако, что такое функция здесь не определяется. Например, какие две функции считать
одинаковыми?
2.2 Функция это правило (закон), посредством которого для
каждого элемента одного множества указывается некий элемент
другого.
Здесь проблема в том, что считать законом и как его записывать.
2.3 Рассмотрение функции как соответствия: Функция это
соответствие, в силу которого каждому элементу х некоторого множества
М отвечает единственный элемент (ровно один или не одного) множества
N.
8

9.

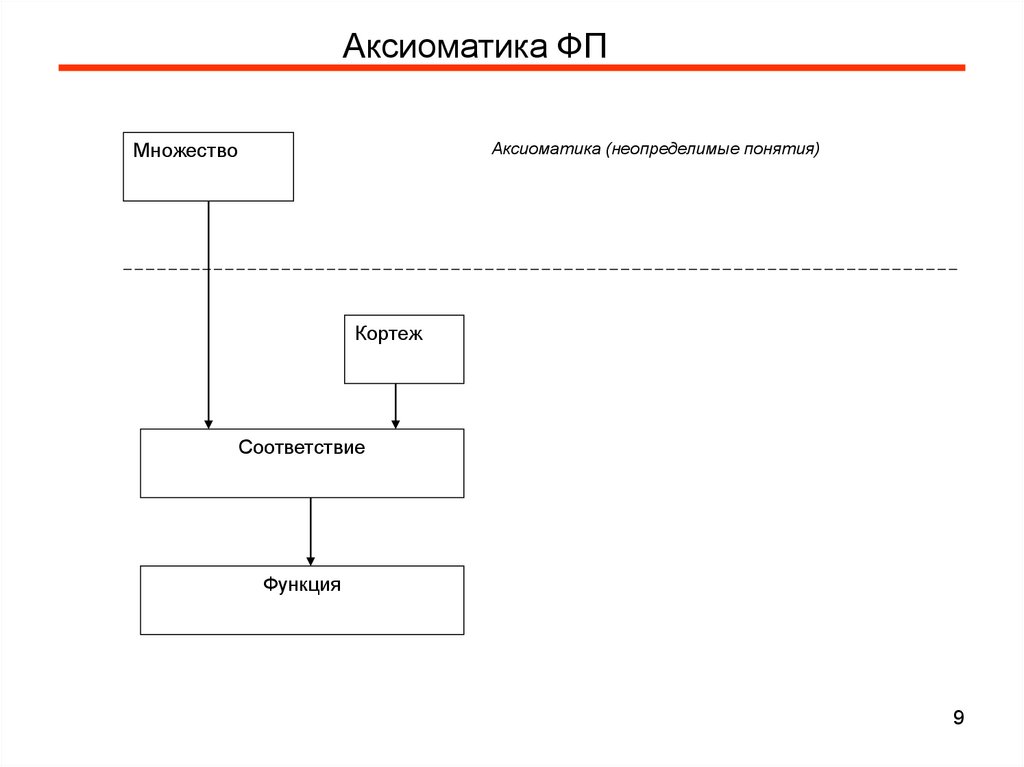
Аксиоматика ФП
Аксиоматика (неопределимые понятия)
Множество
Кортеж
Соответствие
Функция
9

10.

Программирование при помощи функций
Графическое представление функции f, для которой областью определения
является класс элементов {a,b,c,d} и областью значений – {p,q,r}.
Элементы области значений единственным образом определяются по
элементам из области определения.
Этот факт позволяет нам обозначить через f(x) тот элемент из области
значений, который функция f соотносит элементу x из области
определения этой функции.
Говорят также, что f отображает x в f(x) или что f(x) является образом x
относительно f.
10

11.

Программирование при помощи функций
Другие способы записи функций:
в виде последовательности пар-кортежей: (a,p),(b,q),(c,q),(d,r);
в виде таблицы:
в виде ряда равенств: f(a)=p, f(b)=q, f(c)=q, f(d)=r
Недостаток таких способов изображения в том, что их нельзя использовать
для больших и бесконечно больших областей определения.
Пример: Функция квадрат имеет областью определения класс всех целых
чисел (положительных, нуль, отрицательных), а областью значений – класс
всех неотрицательных чисел. Таким образом, мы, например, имеем:
квадрат(3)=9, квадрат(4)=16, квадрат (-4)=16. Но мы не в состоянии
перечислить все соответствия.
11

12.

Программирование при помощи функций
Определить все соответствия полностью можно следующим правилом
(определением):
квадрат(х)≡x*x
Здесь мы используем переменную x для обозначения любого элемента из
области определения и записали правило вычисления соответствующего
элемента из области значений. Такую переменную обычно называют
параметром определения.
В таком определении как квадрат, область определения и область
значений даны неявно и не всегда очевидны. То, что множество
определений – множество целых числе, можно выразить только в
дополнительных ограничениях. Для вещественных чисел, например,
функция квадрат имела бы тот же вид.
12

13.

Программирование при помощи функций
Зачастую, в качестве области определения и области значений задаются
множества более широкие, чем они есть фактически.
Говорят, что функция, для которой в качестве области определения задано
множество А, является частичной над А (или частично определенной в
множестве А), если в А существуют элементы, для которых образ
посредством этой функции не определен.
Функция, которая не является частичной над А, является всюду
определенной в А, или общей функцией.
13

14.

Программирование при помощи функций
Пусть имеется функция макс, выдающая максимальное значение из двух
чисел:
макс(1,3)=3, макс(1.7,-2.0)=1.7
Для такой функции правило вычисления удобно выражать через два
параметра:
Или более компактно:
макс(x,y) ≡ если x≥y то x иначе y
14

15.

Программирование при помощи функций
Программирование при помощи функций происходит следующим образом:
Определяется базовый набор полезных функций (таких как макс или
квадрат), которые являются, по существу, программами с аргументами на
входе и результатом на выходе.
Далее, если их не хватает для построения программы, то на их базе
конструируются более сложные функции.
Иными словами, новые функции должны ссылаться только на основные,
базовые функции. Это достигается построением иерархии определений.
Например: наиб(x,y,z) ≡макс(макс(x,y),z)
Такой подход называется методом композиции функций. Функции могут
вкладываться одна в другую на произвольную глубину и составлять, таким
образом, произвольно глубокие композиции:
Например: макс(наиб(a,b,c),наиб(d,e,f)) – функция, возвращающая
максимальное из шести аргументов.
15

16.

Программирование при помощи функций
Таким образом, чтобы программировать при помощи функций, необходимо
определить исходную библиотеку базовых функций.
В число основных функций, как правило, должны входить арифметические
операции: плюс(x,y) ≡x+y; минус(x,y) ≡x-y; умн(x,y) ≡x*y; дел(x,y) ≡x/y.
Например:
a+b*c -> плюс(a,умн(b,c))
(2*x+3*y)/(x-y) -> дел(плюс(умн(2,x), умн(3,y)), минус(x,y))
Такая запись математических выражений называется аппликативной
структурой выражений. Любое математическое выражение может быть
разбито на составные части, каждая из которых является либо операцией,
либо операндом.
Аппликативная структура имеет важное свойство: значение выражения
единственным образом определяется по значениям составляющих его
частей. То есть, если одно и то же выражение дважды встретилось в одном
и том же контексте, оно имеет одно и то же значение в обоих случаях.
Язык, в котором это свойство сохраняется для всех его выражений, обычно
называют аппликативным или строго функциональным.
16

17.

Программирование при помощи процедур
Пример:
int max(int x, int y)
{ if (x≥y) return x;
else return y;
}
//
( реализация1)
И далее эта функция может быть вызвана оператором присваивания:
M = max(max(a,b),c); // Максимальное из трех значений
Это классическая строгая функция. Отход от них начинается тогда,
когда процедура не выдает результат, а присваивает его одному из
своих параметров:
17

18.

Программирование при помощи процедур
void max (int x, int y, int m)
// (реализация 2)
{
if (x≥y) m=x;
else m=y;
return;
}
max(a,b,m); max (m,c,m); // Максимальное из трех значений
Еще дальше мы отходим от строгой функции, когда
void max(int x, int y) // (реализация 3)
{
if (x>y) x=y;
return;
}
max (a,b); max (a,c); // Максимальное из трех значений
Процедуры (2) и (3) обладают свойствами функций, но имеют побочный
эффект присваивания. При составлении программ на основе таких процедур
приходится думать в терминах нарастающих изменений значений
переменных.
18

19.

Программирование при помощи процедур
Более сильный пример побочного эффекта, когда изменяется значение, не
являющееся параметром:
int m;
void max(int x, int y) //реализация (4)
{
if (x≥y) m=x;
else m=y;
return;
}
max(a,b); max(m,c); // Максимальное из трех значений, результат в m
Два вызова функции max работают по-разному! В первом случае аргументы
неизменны, а во втором – аргумент m меняется.
19