Aniq integralning tatbiqlari

1.

Aniq integralning
tatbiqlari

2.

REJA
1. To’g’ri burchak koordinatalar sistemasida yuzalarni
hisoblash
2. Qutb koordinatalarda egri chiziqli sektorning yuzi
3. Egri chiziq yoyining uzunligi
4. Aniq integrallarni taqribiy hisoblash

3.

Agar [a, b] kesmada f ( x) 0 bo’lsa, u holda, y f ( x) egri chiziq, Ox o’q hamda x a , x b to’g’ri chiziqlar
bilan chegaralangan egri chiziqli trapetsiyaning yuzi
b
Q f ( x)dx
(1)
a
b
Agar f ( x) 0 [a, b] da bo’lsa, u holda f ( x)dx aniq integral ham 0 bo’ladi.
a
Absolyut qiymati jihatidan u mos egri chiziqli trapetsiyaning Q yuziga teng:
b
Q f ( x)dx
a
Agar f ( x) funksiya [a, b] kesmada chekli marta ishorasini o’zgartirsa, u holda butun [a, b] kesma bo’yicha
olingan intervali qism-qism kesmalar bo’yicha integrallar yig’indisiga ajratamiz. Integral f ( x) 0 bo’lgan joylarda
musbat va f ( x) 0 bo’lganda manfiy bo’ladi. Bunday holda
b
Q | f ( x) | dx
a
bo’ladi.

4.

Misol 1. y sin x sinusoid ava Ox o’q bilan 0 x 2 bo’lganda chegaralangan Q yuzani toping.
Yechish. 0 x da sin x 0 va x 2 da sin x 0 bo’lganligi uchun
2
2
0
0
Q sin xdx sin xdx | sin x | dx
sin
xdx
cos
x
|
0 (cos cos0) ( 1 1) 2
0
2
2
sin
xdx
cos
x
|
(cos2 cos ) 2
Demak, Q 2 | 2 | 4

5.

Agar y f1 ( x) , y f 2 ( x) egri chiziqlar va x a , x b ordinatalar bilan chegaralangan yuza f1 ( x) f 2 ( x) shart
bajarilganda
b
b
b
a
a
a
Q f1 ( x)dx f 2 ( x)dx [ f1 ( x) f 2 ( x)]dx (2)
bo’ladi.

6.

Misol 2. y x va y x2 egri chiziqlar bilan chegaralangan yuzani toping.
Yechish. Egri chiziqlarning kesishish nuqtasini topamiz:
yerdan x1 0 va x2 1 .
Demak,
1
Q
0
1
1
1
1
2 32
x3
2 1 1
2
2
xdx x dx ( x x )dx x
3 0 3 0 3 3 3
0
0
x x2 ; x x4 ,
bu

7.

Endi tenglamasi
x (t ) , y (t )
(3)
parametrik ko’rinishda bo’lgan egri chiziq bilan chegaralangan egri chiziqli trapetsiya yuzasini topamiz, bu yerda
t va ( ) a , ( ) b .
(3) tenglamalar [a, b] kesmada biror y f ( x) funksiyani aniqlash va demak egri chiziqli trapetsiyaning yuzi
b
b
a
a
Q f ( x)dx y dx
formula bilan hisoblanishi mumkin.
Bu integralda o’zgaruvchini almashtiramiz: x (t ) , dx '(t )dt . (3) tenglamalar asosida topamiz:
y f ( x) f [ (t )] (t )
Demak,
b
Q (t ) '(t )dt
(4)
a
Bu parametric ko’rinishda berilgan egri chiziq bilan chegaralangan egri chiziqli trapetsiyani yuzasini topish
formulasidir.

8.

Misol. Ellips bilan chegaralangan soha yuzini toping.
x a cos t , y b sin t
Yechish. Ellipsning yuqori yarmi yuzasini topamiz va a dan a gacha o’zgaradi,
demak, t dan 0 gacha o’zgaradi:
0
0
0
Q 2 (b sin t )( a sin tdt ) 2ab sin 2 t dt 2ab sin 2 t dt
1 cos 2t
t sin 2t
2ab
dt 2ab
ab
2
4 0
2
0

9.

2. Qutb koordinatalarda egri chiziqli sektorning yuzi
Qutb koordinatalar sistemasida egri chiziq
f ( )
tenglama bilan berilgan bo’lsin, bu yerda f ( ) - da uzluksiz funksiya.
f ( ) egri chiziq hamda , radius-vektolar bilan chegaralangan OAB sektorning yuzini topamiz.
Berilgan yuzani 0 , 1,..., n radius-vektorlar yordamida n qismlarga ajratamiz. O’tkazilgan radius-vektorlar
orasida burchaklari 1, 2 ,..., n bilan belgilaymiz.
i 1 va i orasida joylashgan qandaydir i burchakka mos kelgan radius-vektorning uzunligini i bilan belgilaymiz.

10.

1 2
Radiusi i va markaziy burchagi i bo’lgan doiraviy sektorni qaraymiz. Uning yuzasi Q i i i ga teng. Ushbu
2
1 n 2
1 n
Qn i i [ f ( i )]2 i
2 i 1
2 i 1
esa “zinasimon” sektorning yuzini beradi.
Bu yig’indi kesmada 2 [ f ( i )]2 funksiya uchun integral yig’indi bo’lganligi uchun uning max i 0 bo’lgandagi
limiti
1 2
d
2
aniq integral bo’ladi. U biz i burchakning ichida qaysi i radius-vektorni olishimizga bo’gliq emas.
Shunday qilib, OAB sektorning yuzi
1
Q 2 d
2
(1)
yoki
1
Q [ f ( i )]2 d
2
formula bilan topiladi.
(1’)

11.

Misol. a cos 20 lemniskata bilan chegaralangan yuzani toping.
Yechish. Agar burchak 0 dan
gacha o’zgarsa radius-vektor izlanayotgan yuzaning chorak
4
qismiga teng:
1
14 2
1 24
Q d a cos 20d
4
20
2 0
2
a sin 20 4 a 2
2 2 0
4
Demak, Q a 2 .

12.

3. Egri chiziq yoyini uzunligi
1.To’g’ri burchakli koordinatalarda egri chiziq yoyining uzunligi. Tekislikda to’g’ri burchakli
koordinatalarda egri chiziq y f ( x) tenglama bilan berilgan bo’lsin.
Bu egri chiziqning x a va x b vertical to’g’ri chiziqlar orasida joylashgan AB yoyining uzunligini
topamiz.
yoydan
nuqtalarni
A, M1, M 2 ,..., M i ,..., B
AB
x0 a, x1, x2 ,..., xi ,..., b xn bo’lsin. AM1, M1M 2 ,..., M n 1B
olamiz,
bu
nuqtalarning
absissalari
vatarlarni o’tkazamiz va bu vatarlarning
uzunliklarini mos ravishda s1, s2 ,..., sn bilan belgilaymiz. Bu holda AB yoyga ichki chizilgan
n
AM1M 2 ...M n 1B siniq chiziqqa ega bo’lamiz. Siniq chiziqning uzunligi sn si ga teng.
i 1

13.

AB yoyning s uzunligi deb
n
s lim
max si 0
s
i 1
i
(1)
limitga aytiladi. Yuqoridagi kabi mulohazalarni takrorlab topamiz:
b
s 1 [ f '( x)]2 dx
a
yoki
b
s 1 [
a
dy 2
] dx
dx
(2)

14.

Misol 1. x 2 y 2 r 2 aylana uzunligini toping.
Yechish. Avval aylana chorak qismining uzunligini topamiz. Bu holda AB quyidagicha:
y r 2 x 2 , bu yerdan
dy
x
dx
r 2 x2
Demak,
1
x2
r
x r
s 1 2
dx
dx
r
arcsin
|0 r
2
2
2
4
r x
r
2
r x
0
0
r
Butun aylananing uzunligi s 2 r ga teng.
r

15.

Endi egri chiziq parametric ko’rinishida
x (t ), y (t ) ( t )
berilganda yoy uzunlikligini topamiz, bu yerda (t ) va (t ) - hosilalari bilan uzluksiz
bo’lgan uzluksiz funksiyalar, bunda '(t ) berilgan uchastkada nolga teng emas. Bu holda
yoy uzunligi
s [ '(t )]2 [ '(t )]2 dt
formula bilan topiladi.
(5)

16.

Misol 2. x a cos3 t , y a sin 3 t giposikloidning uzunliklarini toping.
Yechish. Egri chiziq ikkala koordinata o’qlariga nisbatan simmetrik bo’lganligi uchun avval birinchi
chorakda qismining uzunligini topib olamiz:
dx
dy
3a cos 2 t sin t , 3a sin 2 t cos t
dt
dt
t parametr 0 dan
gacha o’zgaradi.
2
Demak,
2
2
1
2
4
2
2
4
2
s 9a cos t sin t 9a sin t cos tdt 3a sin 2 t cos 2 tdt
4
0
0
sin 2 t 2 3a
3a sin t cos tdt 3a
|0
2
2
0
2
s 6a

17.

x (t ), y (t ), z (t )
(6)
parametrik ko’rinishida berilgan fazoviy egri chiziqning
t bo’lgandagi uzunligi
s [ '(t )] [ '(t )] [ '(t )] dt
2
2
2
(7)

18.

Misol 3. x a cos t , y a sin t , z amt vint chiziqning t 0 dan 2 gacha
o’zgargandagi yoyi uzunligini toping.
Yechish.
dx a sin tdt , dy a cos tdt , dz amdt
(7) formulaga qo’yib, topamiz:
s a sin t a cos t a m dt a 1 m dt 2 a 1 m
2
2
2
2
2
2
2
2

19.

Qutb koordinatalarida berilgan egri chiziq yoyining uzunlgi.
Egri chiziq
f ( )
(8)
qutb koordinatalarda berilgan bo’lsin, bu yerda - qutb radiusi, - qutb burchagi.
(8) egri chiziqning qutb burchagi 1 dan 2 gacha o’zgargandagi yoyining uzunligi
1
s '2 2 d
0
formula bilan topiladi.

20.

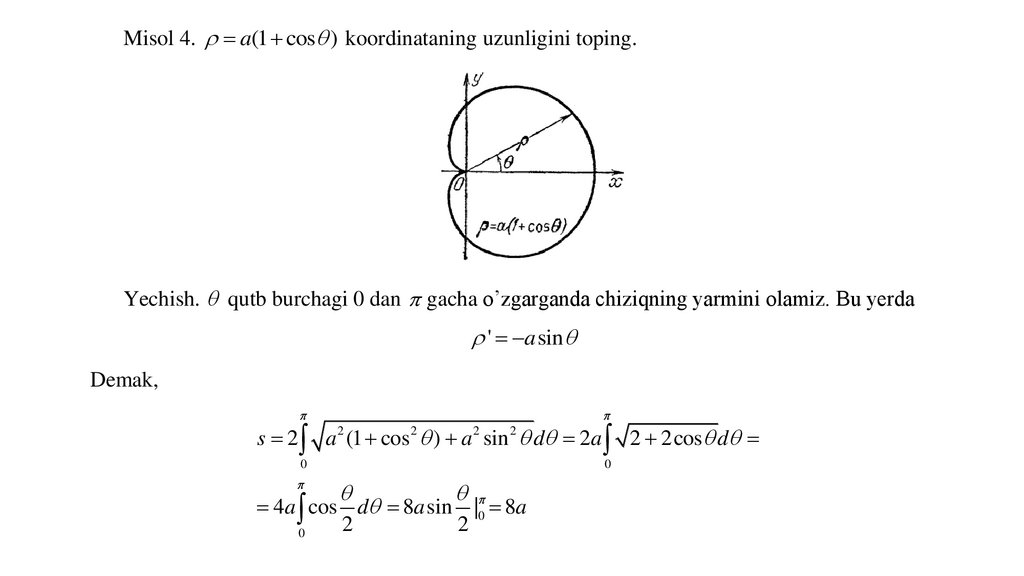
Misol 4. a(1 cos ) koordinataning uzunligini toping.
Yechish. qutb burchagi 0 dan gacha o’zgarganda chiziqning yarmini olamiz. Bu yerda
' a sin
Demak,
s 2 a (1 cos ) a sin d 2a 2 2cos d
2
2
2
2
0
0
4a cos d 8a sin | 0 8a
2
2
0

21.

4.Aniq integrallarni taqribiy hisoblash
Ma’lumki, [a, b] intervalda uzluksiz bo’lgan har qanday y f ( x)
funksiya shu intervalda boshlang’ichga ega, ya’ni F '( x) f ( x) tenglikni
qanoatlantiradigan F ( x) funksiya mavjuda. Ammo har qanday
boshlang’ich funksiya, hattoki u mavjud bo’lgan holda ham, elementar
funksiyalar orqali chekli ko’rinishda ifodalanmaydi. Bunday hollarda
aniq integrallarni Nyuton-Leybnits formulasi yordamida hisoblash ancha
mushkul ish va aniq integralni hisoblashning turli taqribiy usullar
qo’llaniladi. Hozir biz taqribiy integralning bir necha usullarini
keltiramiz.

22.

I.To’g’ri to’rtburchaklar formulasi [a, b] kesmada uzluksiz y f ( x) funksiya berilgan bo’lsin. Ushbu
b
f ( x)dx
a
aniq integralni hisoblash talab etiladi.
[a, b] kesmani a x0 , x1, x2 ,..., xn b nuqtalar yordamida uzlukligi x bo’lgan n ta teng qismlarga bo’lamiz:
b a
x
n
y0 , y1, y2 ,..., yn 1, yn bilan f ( x) funksiyaning x0 , x1, x2 ,..., xn nuqtalardagi qiymatlarini belgilaymiz:
y0 f ( x0 ), y1 f ( x1 ),..., yn f ( xn )
Endi
y0 x y1 x ... yn 1 x
y1 x y2 x ... yn x
yig’indilarni tuzamiz.

23.

Bu yig’indilardan har biri f ( x) funksiya uchun [a, b] kesmada integral yig’indi bo’ladi va shuning uchun
b
f ( x)dx
a
b
f ( x)dx
a
b a
y0 y1 y2 ... yn 1
n
(1)
b a
y1 y2 ... yn
n
(1’)
Mana shu to’g’ri to’rtburchaklar formulasidir. Rasmdan ko’rinib turibdiki, agar f ( x) - musbat va o’suvchi funksiya bo’lsa, u
holda (1) formula ichlaridan to’g’ri to’rtburchaklardan tuzilgan zinasimon figuraning yuzasini ifodalaydi. (1’) formula esa
tashqariga chiqib turgan zinasimon figurani yuzasini ifodalaydi.
b a
bo’lishi qadami qanchalik kichik bo’lsa) integralni to’g’ri to’rtburchaklar
n
formulasi yordamida hisoblashdagi hatolik shunchalik kam bo’ladi.
n soni qanchalik kata bo’lsa, (ya’ni x

24.

II.Trapetsiyalar formulasi. Agar berilgan y f ( x) egri chiziq o’rniga zinasimon funksiyani emas, balki ichki
chizilgan aniq chiziqni olsak (2-rasm) biz aniq integralning yanayam aniqroq qiymatini olamiz. Bu holda aABb
egri chiziqli trapetsiyaning yuzasi o’rniga yuqoridan AA1, A1 A2 ,..., An 1B vatarlar bilan chegralangan to’g’ri chiziqli
y0 y1
x ga
trapetsiyalar yuzalarining yig’indisini olamiz. Bu trapetsiyalardan birinchisining yuzasi
2
y y2
x g ava v.h.zga teng bo’lganligi uchun
ikkinchisiniki 1
2
y1 y2
yn 1 yn
y0 y1
f
(
x
)
dx
x
x
...
x
a
2
2
2
b
yoki
b
f ( x)dx
a
b a y0 y1
y1 y2 ... yn 1
n 2
(2)
Bu trapetsiyalar formulasidir. (2) formulaning o’ng tomonida turgan son (1) va (1’) formulalarning o’ng
tomonlarida turgan sonlarning o’rta arifmetigidir.
b a
qadam shunchalik kichik bo’ladi,
n
(2) taqribiy tenglikning o’ng tomonida turgan yig’indi integralning qiymatini shunchalik aniq beradi.
n soni ixtiyoriy tanlanadi. Bu son qanchalik kata bo’lsa, demakki, x

25.

III.Parabolalar formulasi (Simpson formulasi). [a, b] kesmani juft sondagi n 2m teng bo’laklarga
bo’lamiz. Dastlabki ikkita [ x0 , x1 ] va [ x1, x2 ] kesmalarga mos kelgan va berilgan y f ( x) egri chiziq
bilan chegaralangan egri chiziqli trapetsiyaning yuzasini M ( x0 , y0 ), M1 ( x1, y1 ), M 2 ( x2 , y2 ) uchta nuqtalar
bilan chegaralangan va Oy o’qqa parallel o’qqa ega bo’lgan egri chiziqli trapetsiya yuzasi bilan
almshtiramiz. Bunday egri chiziqli trapetsiya parabolic trapetsiya deyiladi.
O’qi Oy o’qqa parallel bo’lgan parabolaning tenglamasi
y Ax 2 Bx C
ko’rinishida bo’ladi.
A, B, C koeffitsientlar parabolaning berilgan uchta nuqtalardan o’tish shartidan topiladi.
Kesmalarning boshqa juftlari uchun ham shunga o’xshagan parabolalarni quramiz. Parabolic
trapetsiyalar yuzalarining yig’indisi integralning taqribiy qiymatini beradi.
Avvalo bitta parabolik trapetsiyaning yuzasini hisoblaymiz.

26.

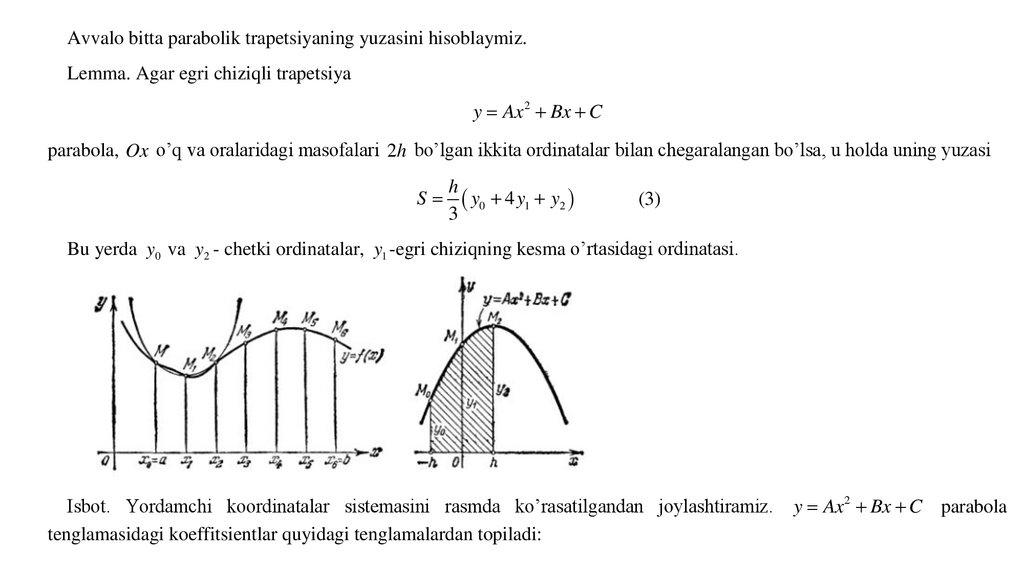
Avvalo bitta parabolik trapetsiyaning yuzasini hisoblaymiz.
Lemma. Agar egri chiziqli trapetsiya
y Ax 2 Bx C
parabola, Ox o’q va oralaridagi masofalari 2h bo’lgan ikkita ordinatalar bilan chegaralangan bo’lsa, u holda uning yuzasi
S
h
y0 4 y1 y2
3
(3)
Bu yerda y0 va y2 - chetki ordinatalar, y1 -egri chiziqning kesma o’rtasidagi ordinatasi.
Isbot. Yordamchi koordinatalar sistemasini rasmda ko’rasatilgandan joylashtiramiz.
tenglamasidagi koeffitsientlar quyidagi tenglamalardan topiladi:
y Ax 2 Bx C parabola

27.

Agar x0 h bo’lsa y0 Ah2 Bh C
Agar x1 0 bo’lsa y1 C
(4)
Agar x2 h bo’lsa y Ah2 Bh C
A, B, C koeffitsientlarni ma’lum deb hisoblab, parabolic trapetsiyaning yuzasini aniq integral yordamida topamiz:
h
Ax3 Bx 2
h
2
S Ax Bx C dx
Cx (2 Ah 2 6C )
2
3
h 3
h
h
Ammo (4) tenglikdan
y0 4 y1 y2 2 Ah2 6C
Kelib chiqadi. Shunday qilib
h
S (2 Ah 2 6C )
3
Shuni isbotlash talab etilgan edi.
Endi o’zimizning asosiy masalamizga qaytamiz. (3) formuladan foydalanib, biz quyidagi taqribiy tengliklarni
yozishimiz mumkin ( h x ):

28.

x2
f ( x)dx
a x0
x4
f ( x)dx
x2
x
( y0 4 y1 y2 )
3
x
( y2 4 y3 y4 )
3
.................................................
x2 m b
f ( x)dx
x2 m 2
x
( y2 m 2 4 y2 m 1 y2 m )
3
Chap va o’ng tomonlarni yig’ib, chap tomonda izlanayotgan integralni chap tomonda esa uning taqribiy qiymatini topamiz:
b
f ( x)dx
a
x
( y0 4 y1 2 y2 4 y3 ...
3
(5)
... 2 y2 m 2 4 y2 m 1 y2 m )
yoki
b
b a
f ( x)dx 6m ( y y 2[ y y ... 2 y
0
2m
2
4
2 m 2
]
a
4[ y1 y3 ... y2 m 1 ])
Bu Simpson formulasidir. Bu yerda 2m bo’linishlar soni ixtiyoriy, ammo bu son qanchalik kata bo’lsa, (5)ning o’ng tomonidagi
yig’indi integralning qiymatini shunchalik aniq beradi.

29.

Misol. Taqribiy hisoblang:
2
dx
x
1
ln 2
Yechish. [1,2] kesmani 10ta teng bo’laklarga bo’lamiz.
x
2 1
0.1
10
deb olib, integral ostidagi funksiyaning qiymatlari jadvalini tuzamiz:
x
x0 1,0
y 1/ x
y0 1,00000
x
x6 1,6
y 1/ x
y6 0,62500
x1 1,1
y1 0,90909
x7 1,7
y7 0,58824
x2 1,2
y2 0,83333
x8 1,8
y8 0,55556
x3 1,3
y3 0,76923
x9 1,9
y9 0,52632
x4 1,4
y4 0,71429
x10 2,0
y10 0,50000
x5 1,5
y5 0,66667

30.

1.To’g’ri to’rtburchaklar (1) formulasi bo’yicha topamiz:
2
dx
1 x 0,1( y0 y1 ... y9 ) 0,1 7,18773 0,71877
To’g’ri to’rtburchaklar (1’) formulasi bo’yicha
2
dx
1 x 0,1( y1 y2 ... y10 ) 0,1 6,68773 0,66877
Rasmdan bevosita kelib chiqadiki, bu holda birinchi formula integralning qiymatini ortig’i bilan, ikkinchisi esa
kami bilan beradi.
II.Trapetsiyalar (2) formulasi bo’yicha
dx
1 0,5
0,1(
6,18773) 0,69377
1 x
2
2
III.Simpson (5) formulasi bo’yicha
2
dx 0,1
1 x 3 [ y0 y10 2( y2 y4 y6 y8 ) 4( y1 y3 y5 y7 y9 )]
0,1
(1 0,5 2 2,72818 4 3,45955) 0,69315
3

31.

2
dx
Aslida ln 2 0,6931472 (7xona aniqlikda).
x
1
Shunday qilib [1,2] kesmani teng 10ta qismlarga bo’lganda Simpson
formulasi bo’yicha 5ta ishonchli raqamlarni; trapetsiyalar formulasi bo’yicha
3ta ishonchli raqamlarni; to’g’ri to’rtburchaklar formulasi bo’yicha faqat 1ta
ishonchli raqam oldik.