Integrallar. Kurs ishi

1.

TOSHKENT XALQARO MOLIYAVIY BOSHQARUVI
TEXNALOGIYALRI UNIVERSITETI
60610100 Kompyuter
ilmlari va dasturlash texnalogiyalari yo’nalishi ISKT 22/08 guruh
talabasi
Xamidov Ilhomjon
Matematik analiz fanidan
KURS ISHI
TOPSHIRDI: XAMIDOV I.
QABUL QILDI: BOTIROV I.
Toshkent 2023
1

2.

MUNDARIJA
Kirish
3
I. BOB. Birinchi tur egri chiziqli integrallar
4
1.1. Birinchi tur egri chiziqli integrallarning xossalari
8
1.2. Birinchi tur egri chiziqli integrallarni hisoblash
9
1.3. Birinchi tur egri chiziqli integrallarning ba’zi bir tadbiqlari
13
II. BOB. Ikkinchi tur egri chiziqli integrallar
14
2.1. Ikkinchi tur egri chiziqli integrallarning xossalari
22
2.2. Ikkinchi tur egri chiziqli integrallarni hisoblash
24
III. BOB. Egri chiziqli integrallarni hisoblashga oid masalalar
26
Xulosa
30
Foydalanilgan adabiyotlar
31
2

3.

KIRISH
Ushbu kurs ishi matematik analiz fanining “Egri chiziqli integrallar” bo’limi
bo’yicha tayyorlangan bo’lib, unda nazariy ma’lumotlar keltirilgan , misol va
masalarning izohli yechimlari bilan ko’rsatilgan. Bu yerda birinchi va ikkinchi tur
egri chiziqli integrallarning ta’riflari sodda tilda keltirilgan bo’lib, ba’zi egri chiziqli
integrallar ta’rif yordamida hisoblab ko’rsatilgan. Bu esa egri chiziqli integralni
yaxshi tushunishga , yechilgan misol va masalalarning mohiyatini anglashga xizmat
qiladi.
Integrallash
sohasi
biror
egri
chiziq
bo’lgan
aniq
integralning
umumlashtirilishi egri chiziqli integral deb ataladi. Ma’lumki , f funksiyadan
kesma bo’yicha olingan integralni , shu
kesma bilan ustma-ust tushuvchi
[a,b]
va chiziqli zichligi f funksiyaga teng bo’lgan o’zakning massasi deb hisoblash
mumkin.Endi bordiyu kesma bukilib, biror egri chiziqqa aylangan bo’lsa , u holda
bunday bukilgan o’zak massasini qanday topish mumkin?
Buning uchun xuddi kesma bo’yicha olingan aniq integral holidagidek ish
tutamiz. Chunonchi , bu egri chiziqni qismiy yoylarga bo’lamiz va har bir bo’lakni
taxminan birjinsli deb faraz qilib, barcha bo’laklar massasini yig’ib chiqamiz. Aynan
mana shu hosil bo’lgan kattalik bukilgan o’zakning taxminiy massasi bo’lib, uning
qiymati egri chiziqli integral tasavvurini beradi.
Biz quyida birinchi va ikkinchi tur egri chiziqli integrallar, xossalari va ularni
hisoblash formulalari bilan tanishamiz. Bundan tashqari egri chiziqli integrallarning
ba’zi bir tadbiqlari keltirilib o’tiladi.
3

4.

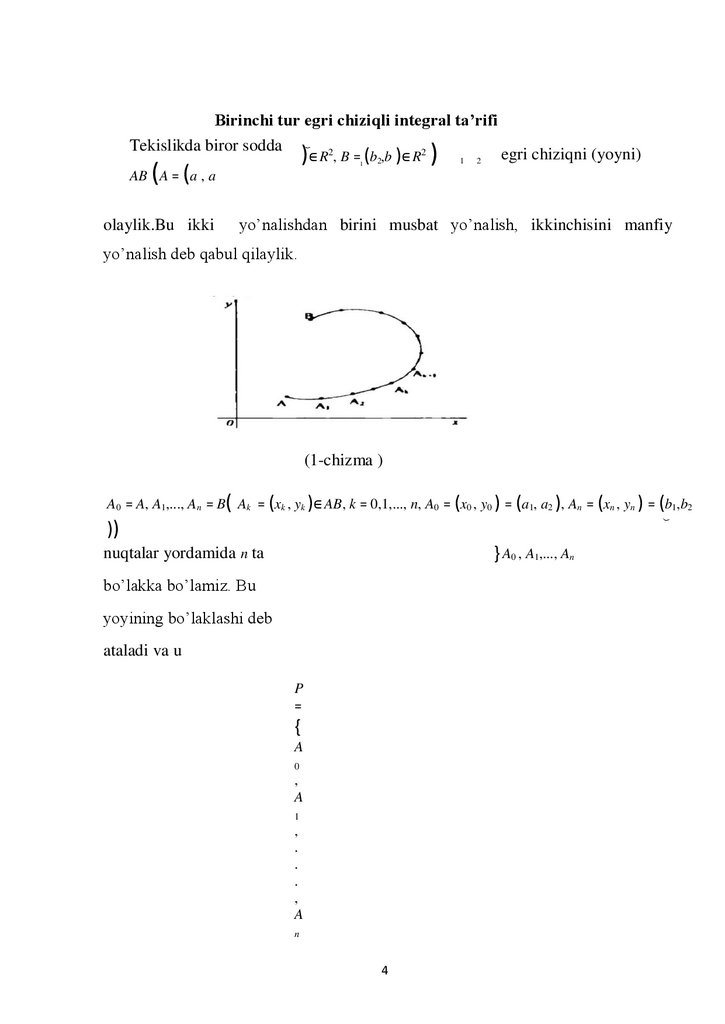
Birinchi tur egri chiziqli integral ta’rifi
Tekislikda biror sodda
)∈ R2, B = (b ,b )∈ R2 )
( (
1
2
1
2
egri chiziqni (yoyni)
AB A = a , a
olaylik.Bu ikki
yo’nalishdan birini musbat yo’nalish, ikkinchisini manfiy
yo’nalish deb qabul qilaylik.
(1-chizma )
A0 = A, A1,..., An = B( Ak = (xk , yk )∈ AB, k = 0,1,..., n, A0 = (x0 , y0 ) = (a1, a2 ), An = (xn , yn ) = (b1,b2
))
} A0 , A1,..., An
nuqtalar yordamida n ta
bo’lakka bo’lamiz. Bu
yoyining bo’laklashi deb
ataladi va u
P
=
{
A
0
,
A
1
,
.
.
.
,
A
n
4

5.

nuqtalar sistemasi AB
kabi belgilanadi.
AA
k
yoy ( bo’laklash
yoylari) uzunliklari
k +1
eng kattasi P bo’laklash diametri deyiladi
va u λp
ΔSk (k = 0,1, 2,..., n)
ning
bilan belgilanadi:
λp = max{ΔSk }
Ravshanki , AB egri chiziqni turli usullar bilan istalgan sonda bo’linishlarini tuzish
mumkin.
AB egri chiziqda
funksiya berilgan bo’lsin.
Bu egri chiziqning
f (x, y)
P ={A0, A1,..., An}
5

6.

bo’linishini
g
va
unin
har
bir
AA
k
(Qk = (ξk ,ηk )∈ Ak Ak +1, k = 0,1,
2,..., n)
nuqtadagi
f (ξk ,ηk )
yoyida
k +1
ixtiyoriy
nuqta olamiz.Berilgan
funksiyaning
qiymatini
AA
k
ning
k +1
Qk = (ξk ,ηk )
Qk = (ξk ,ηk )
ΔSk
uzunligiga
ko’paytirib
quyidagi
yig’indini tuzamiz:
n 1
σ = ∑ f (ξk
(0.1)
,ηk )⋅ ΔSk
k =0
Endi AB egri chiziqning
shunday
(0.2)
P1, P2,..., Pm ,...,
bo’linishlari ketma-ketligini qaraymizki, ularning mos diametrlaridan tashkil
topgan
λp , λp ,..., λp ,...,
1
Ketma-ketlik nolga intilsin: λ
2
m
→0
p
m
yig’indilarni tuzib, ushbu
bunday bo’linishlarga
nisbatan
kabi
σ1,σ2 ,...,σm ,...,
ketma-ketlikni
hosil qilamiz. Ravshanki bu
ketma-ketlikning
har bir hadi
Qk = (ξk ,ηk ) nuqtalarga bog’liq.
1.1-ta’rif. Agar AB egri chiziqning (1.2) ko’rinishdagi bo’linishlari ketma6

7.

ketligi {Pm} olinganda ham, unga mos yig’indilardan iborat
{σm}ketma-
ketlik
(ξk ,ηk ) tanlab olinishiga bog’liq bo’lmagan holda hamma vaqt bitta
I
soniga
intilsa, bu son σ yig’indining limiti deb ataladi va
n 1
lim σ = lim ∑ f (ξk ,ηk )⋅ ΔSk = I
λx→0
(0.3)
λx→0 k =0
kabi belgilanadi.
7

8.

1.2-ta’rif.
Agar∀ε > 0
chiziqning
son olinganda ham
shunday
δ>0
topilsaki, AB egri
λp ≤∂ bo’lgan har qanday P bo’linishi
uchun tuzilganσ
diametri
yig’indi ixtiyoriy (ξk ,ηk )∈ Ak Ak +1
nuqtalarda
σ−I<ε
Tengsizlik bajarilsa, I son
λp → 0
dagi limiti deb ataladi va
(1.3)
λp → 0
da σ yig’indi chekli
limitga ega
bo’lsa u holda
yig’indining kabi
belgilanadi.
1.3-ta’rif. Agar
f (x, y) funksiya c egri chiziq bo’yicha
f (x, y)
integrallanuvchi deyiladi. Bu limit
funksiyaning egri chiziq bo’yicha birinchi tur egri chiziqli integrali deb ataladi va
∫ f ( x, y)dS
AB
kabi belgilanadi.
Shunday qilib kiritilgan egri chiziqli integral tushunchasining o’ziga xosligi
qaralayotgan ikki argumentli funksiyaning berilish sohasi tekislikdagi biror AB egri
chiziq ekanligidir.
Uzluksiz funksiya birinchi tur egri chiziqli integralining mavjudligi
Faraz qilaylik ,
AB egri chiziq
ushbu
⎧⎪
x
=
x
8

9.

(s
)
⎨
0
(0.4)
s
S
⎪⎩
y
=
y
s
yoyning uzunligi
(Q = ( x, y )∈ AB), S
esa AB yoyning uzunligi.
f (x, y)
funksiya shu AB egri
chiziqda berilgan bo’lsin,
modomiki ,
x = x (s) x = x (s), y = y (s) (0 ≤ ekan, unda
sistema bilan berilgan
bo’lsin.
Bunda
s − AQ
s≤S)
(x, y) = f (x (s),
y (s))
bo’lib, natijada ushbu
f (x (s), y (s)) = F (s) (0 ≤ s ≤ S )
9

10.

funksiyaga ega bo’lamiz.
bo’linishini va har bir
AB egri
AA
k
chiziqning P
k +1
da
={A0, A1,..., An}
ixtiyoriy
uzunligi
Qk = (ξk ,ηk )
Ak nuqtaga mos
nuqtani
olaylik. Har
bir
keladigan
sk , har bir
ning
AAk
AQk ning
s* deylik.
uzunligi
Ravshanki,
AA
k
k +1
ning uzunligi
k
sk +1 − sk = sk bo’ladi.
Natijada P bo’linishga nisbatan tuzilgan
n 1
σ = ∑ f ( ξ k ,η k ) ⋅ s
k
k =0
yig’indi ushbu
n−1
f ξk ,η )⋅
k
s
k
k =0
n 1
fxs ,ys s
k
n 1
k
k =0
k
F s k
sk
s
Fs
k
k
k =0
ko’rinishga keladi. Demak
n−1
*
k =0
Bu
yig’indini [0,
F (s)
(0.5)
funksiyaning
yig’indisi
S ]oraliqdagi ekanligini
payqash qiyin emas.
Agar
f (x, y)
funksiya AB
F ( x)
egri
chiziqda
uzluksiz bo’lsa, u
holda
10
integral

11.

F (s) funksiya
funksiya [0, S ]da uzluksiz
[0, S ]da
bo’ladi.Demak
bu holda integrallanuvchi:
lim
∑ F (s* )⋅ s = F (s )ds
S
n 1
O
λp →0
k
k =0
k
∫
(0.6)
λp → 0 da σ yig’indining limiti
Shunday qilib,(1.5) va (1.6)
munosabatlardan mavjud bo’lishi va
11

12.

S
lim σ = F (s )ds
λp →0
O
ekanligini topamiz.Natijada quyidagi teoremaga kelamiz.
f (x, y)
1.1-teorema. Agar
bu funksiyaning
funksiya AB egri chiziqda
uzluksiz bo’lsa , u holda
AB egri chiziq bo’yicha
birinchi tur egri chiziqli integrali
mavjud bo’ladi va
S
∫ f ( x, y )ds = ∫ f (x (s ), y (s ))ds
AB
0
bo’ladi.
Bu teorema bir tomondan uzluksiz funksiya birinchi tur egri chiziqli integralining
mavjudligini
aniqlab
bersa
,
ikkinchi
tomondan
bu
integralning
aniq
integralga(Riman integraliga) kelishini ko’rsatadi.
Birinchi tur egri chiziqli integrallarning xossalari
Birinchi tur egri chiziqli integrallar ham Riman integrallari xossalari kabi
xossalarga ega bo’ladi.Shuni e’tiborga olib , egri chiziqli integrallarning asosiy
xossalarini sanab o’tish bilan kifoyalanamiz.
(1.4) sistema bilan aniqlangan
f (x, y) funksiya berilgan va
AB
egri
chiziqd
a uzluksiz.
1. Agar AB = AC + CB bo’lsa, u holda
x, y)ds
∫ f(
=
12
∫
AB
AC

13.

f ( x, y )ds +
f ( x, y )ds
∫
CB
bo’ladi.
2 . Ushbu
13

14.

f (x, y)ds
∫ cf ( x, y)ds = c ∫
c = const
tenglik o’rinli.
AB
AB
f (x, y) funksiya bilan
AB egri chiziqda
g ( x, y)funksiya ham
berilgan va uzluksiz.
3 . Quyidagi
∫ ⎡ ⎣ f (x, y) ± g (x, y)⎤ ⎦ ds = ∫ f (x, y)ds ± ∫ g
(x, y)ds
AB
AB
AB
formula o’rinli bo’ladi.
f (x, y) ≥ 0 bo’lsa , u holda
∀( x, y)∈ AB da
4 . Agar
∫ f ( x, y)ds ≥ 0
bo’ladi.
AB
5 . f ( x, y )
funksiya shu AB da integrallanuvchi va
f x,y ds f x,y ds
AB
AB
bo’ladi.
6. Shunday (c1, c2 )∈ AB nuqta topiladiki ,
∫ f (x, y)dsdx = f (c , c )⋅ S
1
14
2

15.

AB
bo’ladi, bunda S − AB
ning
teorema deb ataladi.
uzunligi.Ushbu
qiymat
xossa o’rta
haqidagi
Birinchi tur egri chiziqli integrallarni hisoblash
Birinchi tur egri chiziqli integrallar, asosan Riman integrallariga
keltirilib
hisoblanadi. Yuqorida keltirilgan 1.1-teoremaga ko’ra AB egri chiziq ushbu
15

16.

(0 ≤ s ≤ S )
⎧⎪x = x (s)
⎨
y = y (s)
f (x, y) shu uzluksiz
sistema bilan berilganda (bunda s
yoy
uzunligi) ga AB da
bo’lganda egri chiziqli integral Riman integraliga keldi.Demak, bu Riman integralini
hisoblash
natijasida
egri
chiziqli
integral
topiladi.
Endi AB egri chiziq ushbu
⎧⎪x = ϕ (t )
⎨
(0.7)
0
ϕ (t ),ψ (t ) funksiyalar
s
S
⎪⎩ y =ψ t
sistema bilan ( pa rametrik formada)
berilgan bo’lsin. Bunda
[α , β ] da ϕ '(t ),ψ '(t ) hosilalarga ega va bu hosilalar shu oraliqda uzluksiz hamda
(ϕ (α ),ψ (α )) = A
va
(ϕ (β ),ψ (β )) = B
Ravshanki, (1.7) sistema [α , β ]
bo’lsin.
oraliqni AB egri chiziqqa
akslantiradi.Bunda
[γ ,δ ] ⊂[α, β ] ning AB egri chiziqdagi Aγ Aδ aksining uzunligi
δ
t t dt
λ
'2
'2
bo’ladi.
f (x, y) funksiya AB da berilgan va uzluksiz
2-teorema. Agar
16

17.

bo’lsa, u holda
β
∫ f ( x,
ϕ'2 (t ) +ψ '2 (t )dt
y) ds =
∫ f (ϕ
(t ),ψ (t
))
AB
α
bo’ladi.
Isbot[α , β ]oraliqning
P ={t0,t1,...,tn} (α = t0 < t1 < ... < tn = β )
bo’linishini olaylik.Bu bo’linishning
bo’luvchi nuqtalari
tk (k = 0,1, 2..., n) ning AB
17
(0.8)

18.

Ak (k = 0,1, 2..., n)
dagi mos akslarini
nuqtalar
deylik.Ravshanki, bu Ak (k =
AB egri chiziqning
0,1, 2..., n)
{A0, A1,..., An}
bo’linishini
Ak = (ϕ (tk ),ψ (tk
h
(k = 0,1, 2,..., n)
va A A
k
))
ning
k +1
osil
qi
ladi. Bunda
uzunligi
tk +1
Δsk
=
∫ ϕ '2 (t ) +ψ '2 (t )dt
tk
bo’ladi.O’rta qiymat haqidagi teoremadan foydalanib quyidagilarni topamiz:
Δsk = ϕ '2 (τ ) +ψ '2 (τ )
ϕ '2 (τ ) +ψ '2 (τ ) ⋅
⋅ (t
k
tk ,
k
−t)=
k
bunda
k
k 1
k
ϕ (τk ) = ξk ,ψ (τk )
= ηk
tk < tτ < tk +1 .Endi
deb
olamiz.R
avshanki,
bo’ladi. AB egri chiziqning yuqorida
aytilgan
(ξk ,ηk )∈ Ak Ak+1 (k = 0,1, 2,..., n −1)
{A0, A1,..., An}
Ak Ak+1da (ξk ,ηk ) nuqtani olib,
bo’linishini va har bir
18

19.

n 1
σ = ∑ f (ξk ,ηk )⋅ s
k
k =0
yig’indini tuzamiz. Uni quyidagicha ham yozish mumkin:
n 1
σ = ∑ f ( ξ k , ηk
n 1
s
k
f , ' ' t
2
k =0
k
k
2
k
k
(0.9)
k
)⋅
k =0
Bu
tenglikning
tomonidagi
f (ϕ (t ),ψ (t ))⋅
o’ng
yig’indi
funksiyaning [α , β ] oraliqdagi
'2 t '2 t
Riman yig’indisidir.Shartga ko’ra f (x, y)
ϕ '(t ),ψ '(t ) funksiyalar uzluksiz.Murakkab funksiyaning
uzluksizligi
haqidagi
teoremadan kelib chiqadiki ushbu
funksiya [α , β ]
oraliqda uzluksiz. Demak, bu
funksiya [α , β ]
oraliqda integrallanuvchi bo’ladi.
19
va

20.

Ya’ni
n−1
)+,ψψ '2(τ(τ)))Δt
ϕ ='2 (τ )
σ ∑ f (ϕ (τ
lim
f (ϕ (t ),ψ (t ))
β
ϕ
)dt'2 (t ) +ψ '2 (t
∫
max{Δtk }→0
k =1
k
Modomiki,
x = ϕ (t ), y =ψ (t )
da uzluksiz ekan, unda
funksiyalar [α , β ]
max{Δtk } → 0
demak,
da Δxk → 0, Δyk → 0
Δsk → 0 . Bundan esa
k
α
k
λp → 0 bo’lishi kelib
chiqadi.(1.8)
munosabatdan foydalanib
β
lim σ =
λp →0
∫ f (ϕ (t ),ψ (t )) ϕ '2 (t ) +ψ '2 (t )dt
α
bo’lishini topamiz.Bu esa
β
∫ f ( x, y)ds = ∫ f (ϕ (t ),ψ
ϕ '2 (t ) +ψ '2 (t )dt
(t ))
AB
α
ekanini bildiradi.Teorema isbotlandi.
Bu teoramadan quyidagi natijalar kelib chiqadi.
1.1-natija. AB egri chiziq ushbu
y = y (x) (a ≤ x ≤ b, y (a) = A, y (b) = B)
tenglama bilan aniqlangan bo’lib, y = y (x)funksiya [a,b] da hosilaga egava uzluksiz
bo’lsa, u holda
b
20
k

21.

∫ f ( x, y)ds = ∫ f (x, y ( x)) 1+ y '2 ( x)dx
AB
bo’ladi.
1.2-natija. AB egri chiziq ushbu
ρ = ρ (θ )
(θ0 ≤ θ ≤ θ1 )
21
a

22.

tenglama bilan (qutb koordinata sistemasida) berilgan bo’lib, ρ (θ ) funksiya [θ0 ,θ1 ]
da hosilaga ega va uzluksiz bo’lsin.Agar
f (x, y) funksiya shu AB da berilgan va
uzluksiz bo’lsa, u holda
θ1
ρ 2 + ρ '2 dθ
∫ f ( x, y )ds = ∫ f (ρ
(0.10)
bo’ladi
cosθ , sinθ )
θ0
AB
Birinchi tur egri chiziqli integrallarning ba’zi bir tatbiqlari
Birinchi tur egri chiziqli integrallar yordamida yoy uzunligini,jismning
massasini, og’irlik markazlarini topish mumkin.Quyida biz birinchi tur egri chiziqli
integrallar yordamida yoy uzunligini hisoblashni ko’rsatamiz.
Tekislikda sodda AB egri chiziq berilgan
bo’lsin.Bu chiziqda
f (x, y) =1 funksiyani
qaraylik. Ravshanki, bu funksiya AB da
uzluksiz.
f (x, y) funksiyaning birinchi tur
egri chiziqli integrali ta’rifidan quyidagini
topamiz:
n−1
n−1
∫ f ( x, y)ds = lim ∑ f (ξ ,η )Δs = lim ∑Δs = S.
k
AB
k
k
λp →0 k =0
k
λp →0 k =0
AB
Demak,
S = ∫ ds
22

23.

(*)
Misol. Ushbu
⎧⎪x = x (t ) = a cos3 t
⎨
⎪ y = y (t ) = a sin3 t
Sistema bilan berilgan AB chiziqning uzunligi topilsin.Bu chiziq
astroidani ifodalaydi.(*) formulaga ko’ra astroidaning uzunligi
23

24.

π
2
2
2
π
2
2
2
2
2
∫ ds = 4∫ x ' (t ) + y ' (t )dt = 4∫ (−3a cos t dt =
sin t ) + (3a sin t cos t )
AB
=
0
0
2 ⎟2
⎠0
π
π
2
9a2 2
4 4 sin 2tdt = 6a∫sin 2t = 6a ⎜−
2
0
0
⎝
⎛ cos 2t ⎞
= 6a
Ikkinchi tur egri chiziqli
integral ta’rifi
f (x, y)
Tekislikda biror sodda AB egri
chiziqni qaraylik.Bu egri chiziqda
funksiya berilgan bo’lsin. AB egri
chiziqning
P
=
{
A
0
,
A
1
,
.
.
.
,
A
n
}
bo’linishini va uning har bir Ak Ak+1 (k = 0,1,..., n −1) yoyida ixtiyoriy
Qk = (ξk ,ηk
)
(Q = (ξ ,η )∈ A A , k = 0,1,..., n
−1)olaylik.
nuqtani
k
k
Berilgan
24
k
k
k +1

25.

funksiyaning
Qk = (ξk ,ηk )
f (ξk ,ηk )
nuqtadagi
qiymatini
ox (oy) o’qdagi
Ak Ak +1 ning
proyeksiyasiga ko’paytirib quyidagi yig’indini tuzamiz:
n−1
σ
⎛
=)⋅ Δx
n−1
k
σ '' = ∑
fξ
,η
k
k =0
k
⎜
⎝
)⋅ Δy ⎞.
f (ξ ,η
k
k =0
k
Δxk (Δyk )
k
⎟
⎠
Endi egri chiziqning
shunday
P1, P2,..., Pm ,...
(0.12)
bo’linishlari ketma-ketligini qaraymizki, ularning diametrlaridan tashkil topgan
mos
λp , λp ,..., λp ,...
1
2
m
ketma-ketlik nolga intilsin:
λpm → 0
25
(
0
.
1
1
)

26.

bunday bo’linishlarga nisbatan (1.11) kabi yig’indilarni tuzib ushbu
σ1 ' ,σ2 ' ,...,σ m' ,...(σ ''1 ,σ ''2 ,...,σ ''m,...)
ketma-ketlikni hosil qilamiz.Ravshanki,bu ketma-ketlikning har bir hadi, xususan
(ξk ,ηk ) nuqtalarga ham bog’liq.
AB egri chiziqning har qanday (1.12) ko’rinishdagi
1.4-ta’rif. Agar
bo’linishlari ketma-ketligi {Pm } olinganda ham, unga mos yig’indilardan iborat
) nuqtalarningk k ((ξ ,η
{σ ' } ({σ '' })
m
m
)k ∈ Ak A
)tanlab
kk 1
olinish
ketmaiga
ketlik
(ξ ,η
bog’liq bo’lmagan
ravishda hamma
vaqt bitta I '
songa intilsa, bu son
(I )
''
σ ' (σ '' )
yig’indining limiti
deyiladi va
n−1
l )⋅ Δx
i
m
σ
'
=I'
=
l
i
m
f
ξ
,
η
λp →0
λp →0
k
k =1 n−1
l
k
i
26
k
(0.13)
m

27.

σ
'' )⋅ Δy
= I ''
=
l
i
m
∑
f
(
ξ
,
η
λp →0
k
λp →0
k
k
k =1
kabi belgilanadi.
1.5-ta’rif. Agar
λ
p
da σ ' (σ '' ) yig’indi chekli
limitga ega bo’lsa, u holda
→0
m
f (x, y)
funksiya AB egri chiziq
bo’yicha integrallanuvchi
deyiladi.Bu limit
f (x, y)
funksiyaning AB egri chiziq bo’yicha ikkinchi tur egri chiziqli integrali deb ataladi
va u
⎛
∫
⎞
f ( x, y )dy ⎟
⎜∫
⎠
⎝AB
f
(
x,
y
)
d
x
AB
27

28.

kabi belgilanadi.Demak,
'
f=(lim
x, y∑)dxf (=ξ lim
,η σ )⋅ Δx n 1
∫
k
→0
λ →0
AB
p
p
k
k
k
k =0
f =( lim
x, y)∑dyf =(ξlim
,η σ
''
∫
k
λ
)⋅ Δy n 1
k
λ
→0
λ →0
AB
p
p
k =0
28

29.

f (x, y) funksiyadan ikkita ox o’qidagi
Shunday qilib, AB egri chiziqda berilgan
proyeksiyalar vositasida va oy o’qidagi proyeksiyalar vositasida olingan ikkinchi
tur egri chiziqli integral tushunchalari kiritildi.
Faraz qilaylik, AB
egri chiziqda ikkita
bo’lib,
P (x, y) va
Q(x, y) fuksiyalar berilgan
∫ P ( x, y)dx , ∫ Q ( x, y)dy
lar esa ularning ikkinchi tur
egri chiziqli integrallari
AB
AB
bo’lsin. Ushbu
∫ P ( x, y)dx + ∫ Q (x, y)dy
AB
AB
Yig’indi ikkinchi tur egri chiziqli integralning umumiy ko’rinishi deb ataladi va
∫ P ( x, y)dx + Q ( x, y)dy
AB
kabi yoziladi. Demak,
∫ P ( x, y)dx + Q (x, y)dy = ∫ P (x, y)dx + ∫ Q (x, y )dy
AB
AB
AB
Ikkinchi tur egri chiziqli integral ta’rifidan quyidagi natijalar kelib chiqadi.
1.3-natija. Ikkinchi tur egri chiziqli integral egri chiziqning yo’nalishiga
29

30.

bog’liq bo’ladi.
1.4-natija. AB egri chiziq ox (oy)
o’qiga perpendikular bo’lgan to’g’ri
chiziq kesmasidan iborat bo’lsin. f (x, y) funksiya shu chiziqda berilgan
bo’lsin. U holda
⎛
∫
f ( x,
⎞
f ( x, y)dy ⎟
⎜∫
⎠
⎝AB
y)dx
AB
mavjud bo’ladi va
30

31.

⎛
∫ f ( x,
⎞
f ( x, y )dy = 0⎟.
⎜∫
⎠
⎝AB
y)dx = 0
AB
Bu tenglik bevosita ikkinchi tur egri chiziqli integral ta’rifidan kelib chiqadi.
Endi AB -sodda yopiq egri chiziq bo’lsin, ya’ni A va B nuqtalar ustma-ust
tushsin.Bu yopiq chiziqni K deb belgilaylik.Bu sodda yopiq chiziqda ham ikki
yo’nalish bo’ladi. Ularning birini musbat yo’nalish, ikkinchisini manfiy yo’nalish
deb qabul qilaylik.Shunday yo’nalishni musbat deb qabul qilamizki, kuzatuvchi
yopiq chiziq bo’ylab harakat qilganda,
(2-chizma)
yopiq chiziq bilan chegaralangan soha unga nisbatan doim chap tomonda yotsin.
f (x, y) funksiya berilgan bo’lsin.Bu K
Faraz qilaylik, K sodda yopiq chiziqda
chiziqda ixtiyoriy ikkita turli nuqtalarni olib, ularni A va B bilan belgilaylik. AaB va
BbA chiziqlarga ajraladi (2-chizma).
Ushbu
∫
f ( x, y)dx +
∫
31
f ( x, y )dx

32.

AaB
BbA
Integral (agar mavjud bo’lsa )
f (x, y) funksiyaning K yopiq chiziq
bo’yicha
ikkinchi tur egri chiziqli integrali deb ataladi va
32

33.

yoki
∫ f ( x, y)dx
∫
K
f(
x,
y)
dx
K
kabi belgilanadi.Bunda K yopiq chiziqning musbat yo’nalishi olingan.Shunga
o’xshash
∫ f ( x, y)dy
K
hamda umumiy holda
∫ P ( x, y)dx + Q (x, y)dy
K
integrallar ta’rifilanadi.
AB fazoviy
egri
chiziq
bo’lib,bu
bo’lsin.Yuqoridagidek,
chiziqda f ( x, y, z )funksiya berilgan
f ( x, y, z )funksiyaning AB egri chiziq
bo’yicha ikkinchi tur
egri chiziqli integrallari ta’riflanadi va ular
∫ f ( x, y, z)dx , ∫ f (x, y, z )dy , ∫ f (x, y, z )dz
33

34.

AB
AB
kabi belgilanadi. Umumiy holda
AB
P(x, y, z),Q(x, y, z), R (x, y, z )funksiyalar
AB
da
berilgan bo’lib, ushbu
∫ P ( x, y, z)dx , ∫ Q (x, y, z )dy , ∫ R (x, y, z )dz
AB
AB
AB
Integrallar mavjud bo’lsa , u holda
∫ P (x, y, z)dx + ∫ Q (x, y, z )dy + ∫ R (x, y, z )dz
AB
AB
AB
Yig’indi ikkinchi tur egri chiziqli integralning umumiy ko’rinishi deb ataladi va u
∫ P ( x, y, z)dx + Q (x, y, z )dy + R (x, y, z )dz
AB
34

35.

kabi belgilanadi.Demak,
∫ P ( x, y, z)dx + Q (x, y, z )dy + R (x, y, z )dz ∫ P ( x, y, z)dx + ∫ Q (x, y, z )dy + ∫ R (x, y, z
=
)dz.
AB
AB
AB
AB
Uzluksiz funksiya ikkinchi tur egri chiziqli integrali
Endi ikkinchi tur egri chiziqli integralning mavjud bo’lishi taminlaydigan shartni
topish bilan shug’ullanamiz.
Faraz qilaylik AB egri
chiziq ushbu
(α⎧≤ t ≤ β )
(0.14)
⎪
x
=
ϕ
(
t
)
⎨
y
=
ψ
(
t
)
35

36.

Sistema bilan (parametric formada )berilgan bo’lsin.Bunda ϕ (t ) funksiya [α , β ]da
ϕ' (t ) hosilaga ega va bu hosila shu oraliqda uzluksiz, ψ (t ) funksiya ham [α , β ]da
(ϕ (α ),ψ (α )) = A
uzluksiz hamda
va (ϕ (β ),ψ (β )) = B
bo’lsin.
t paramer α dan β ga o’zgarganda ( x, y) = (ϕ (t ),ψ (t )) nuqta A dan B ga qarab AB ni
chiza borsin.
f (x, y) funksiya AB da berilgan va
1.3-teorema. Agar
uzluksiz bo’lsa, u
holda bu funksiya AB egri chiziq bo’yicha ikkinchi tur egri chiziqli integrali
∫ f ( x, y)dx
AB
mavjud va
β
∫ f ( x, y)dx = ∫ f (ϕ (t ),ψ (t ))ϕ (t )dt
'
AB
α
bo’ladi.
Isboti. [α , β ] oraliqning
36

37.

P ={t0,t1,...,tn}
(α = t0 < t1 < ... < tn = β )
bo’linishni olaylik. Bu bo’linishning
bo’luvchi nuqtalari
tk (k = 0,1,..., n) ning AB
(k = 0,1,..., n)
dagi mos akslarini
Ak deylik
chiziqning
.Ravshanki,
bu
Ak nuqtalar
AB egri
{A0, A1,..., An}
Ak = (ϕ (tk ),ψ (tk )) (k = 0,1,..., n) bo’ladi.
bo’linishini hosil qiladi. Bundan
Bu bo’linishga nisbatan (1.11) yig’indini
n−1
σ '=
f ξ ,η ) ⋅ Δx
k
k
k
k =0
tuzamiz.
Keyingi
Δxk = xk+1 − xk = ϕ (tk+1 ) −ϕ (tk ) ga
tenglikda
tengdir.La
teoremasidan foydalanib topamiz:
granj
ϕ (tk 1 ) −ϕ (tk ) = ϕ ' (kθ )(k 1
t − tk ) = ϕ ' (θk )Δtk
(θk ∈[tk ,tk +1 ])
Ma’lumki , (ξk ,ηk )∈ Ak Ak+1 , (k = 0,1, 2,..., n −1) .Agar bu (ξk ,ηk ) nuqtaga akslantiruvchi
nuqtani
rk (rk ∈[tk , tk +1 ])
deyilsa, unda
ξk = ϕ (rk ), ηk =ψ (rk )
bo’ladi. Natijada, σ ' yig’indi quyidagi ko’rinishga keladi
n 1
σ ' = ∑ f (ϕ (r ),ψ (r
) Δt
))ϕ ' (θ
k
k =0
37
k
k
k

38.

endi λ' = max{Δt } → 0 da σ ' yig’indining limitini topish maqsadida uning ifodasini
p
k
o’zgartirib quyidagicha yozamiz:
n 1
σ ' = ∑ f (ϕ (r ),ψ (r
+ ∑ f (ϕ (r ),ψ (r ))
) Δt
))ϕ ' (θ
) −ϕ ' (r )⎤ ⎦ Δt
⎡ ⎣ ϕ ' (θ
n 1
k
k =0
k
k
k
k
k
k
k
k =0
38
k

39.

Bu tenglikning o’ng tomonidagi ikkinchi qo’shiluvchi baholaymiz:
n 1
∑ f (ϕ (r ),ψ (r ))⎡ ⎣ ϕ (θ ) −ϕ (r )⎤ ⎦ Δt ≤
'
'
k
k
k
k
k
k =0
≤
n−1
f (ϕ (r ),ψ (r )) ϕ ' (θ
k
) − ϕ ' (r ) Δt ≤
k
k
k
k
k =0
≤ M
n−1
ϕ ' θk
k
) − ϕ ' (r )Δt
k
k =0
bunda
f (ϕ (t ),ψ (t ))
M = maxα ≤t ≤β
ϕ' (t ) funksiya [α , β ]
da uzluksiz. U holda Kantor teoremasining
natijasiga ko’ra,
δ > 0 topiladiki, [α , β
]oraliqning diametri
∀ε > 0 olinganda ham
shunday
'
<δ
p
bo’lgan harqanday P bo’linish uchun
ε
ϕ' (θ ) −ϕ' (r ) <
k
k
M ( β −α )
bo’ladi. Unda
n 1
∑ f (ϕ (r ),ψ (r ))⎡ ⎣ ϕ (θ ) −ϕ (r )⎤ ⎦ Δt <
'
'
k
k
k =0
M n−1
k=0 M
ε
t
=
(β −α )
39
ε
n−1
Δt = ε
k
k
k

40.

k
β −α k =0
k
demak,
n 1
lim ∑ f (ϕ (r ),ψ (r )) ⎡ ⎣ ϕ ' (θ ) − ϕ ' (r )⎤ ⎦ Δt = 0
λp →0
k
k
k
k =0
k
k
bo’ladi. Bu munosabatni hisobga olib, λp → 0 limitga o’tib quyidagini topamiz:
= β f (ϕ (t ),ψ (t ))ϕ' (t )dt
'
'
lim
)Δt σ = lim n 1 f (ϕ (r ),ψ (r ))ϕ (r
∑
λ →0
p
p
λ →0
k
α
k =0
40
k
k
k
∫

41.

demak,
β
∫ f ( x, y)dx = ∫ f (ϕ (t ),ψ (t ))ϕ (t )dt.
'
α
AB
teorema isbotlandi.
Ikkinchi tur egri chiziqli integrallarning xossalari
P (x, y) funksiya AB yoy bo’ylab
1. Agar
integrallanuvchi bo’lsa,
∫ kP (x, y)dx = k ∫ P (x, y)dx
AB
AB
tenglik o’rinli.
P1 ( x, y)va
2 . Agar
P2 ( x, y)
funksiyalar AB yoy
bo’ylab
integrallanuvchi
bo’lsa,
∫ (P ( x, y) ± P (x, y))dx = ∫ P (x, y)dx ± ∫ P (x, y)dx
1
AB
2
1
AB
2
AB
tenglik o’rinli.
3 .(Additivlik xossasi)Agar AB yoy biror C nuqta orqali AC va CB yoylarga
ajratilgan bo’lib, P (x, y)
funksiya AC
va
integrallanuvchi bo’lsa,
CB
biri
41
yoylarning har
bo’ylab

42.

∫ P ( x, y)dx = ∫ P ( x, y )dx + ∫ P ( x, y )dx
AB
AC
CB
tenglik o’rinli bo’ladi.
4 . Agar
∫
egri chiziqli integral ham mavjud bo’lsa,
P ( x, y)dx
AB
∫ P ( x, y) dx =− ∫ P ( x, y ) dx
AB
BA
42

43.

tenglik o’rinli bo’ladi.
.
5 Agar funksiya L yopiq kontur bo’ylab integrallanuvchi bo’lsa, u holda
P x,y dx
L
U holda egri chiziqli integralning qiymati L konturdagi qaysi nuqtani boshlang’ich
nuqta (bu nuqta ham bo’ladi) deb olinishiga bog’liq emas.
lar teng bo’lmagan ixtiyoriy nuqtalar
bo’lsin.
Isboti. A va A1
( 3-chizma)
A nuqtani boshlang’ich nuqta deb, egri chiziqli integralni ko’rsatilgan yo’nalish
bo’yicha hisoblasak
∫ P ( x, y )dx = ∫ P ( x, y )dx + ∫ P ( x, y )dx
AmA1nA
AmA1
A1nA
tenglikka ega bo’lamiz.
Agar nuqtani boshlang’ich nuqta deb hisoblasak, u holda
∫ P ( x, y )dx = ∫ P ( x, y )dx + ∫ P ( x, y )dx
AnA1mA
AnA1
A1mA
tenglikka ega bo’lamiz.
43

44.

Bu tengliklarning o’ng tomonlari bir xil qo’shiluvchilardan iborat.Shuning
uchun chap tomonlari ham teng bo’ladi.Demak, xossa isbotlandi.
Ikkinchi tur egri chiziqli integrallarni hisoblash
44

45.

Ikkinchi
tur egri chiziqli integrallar ham asosan Riman integrallariga
keltirilib hisoblanadi:
β
(0.15)
∫ f ( x, y)dx = ∫ f
(ϕ (t ),ψ (t ))ϕ' (t
)dt
α
AB
β
(0.16)
∫ f ( x, y)dy = ∫ f
(ϕ (t ),ψ (t ))ψ ' (t
)dt
α
AB
β
∫ P ( x, y)dx + Q ( x, y)dy = ∫ ⎡ ⎣ P
(0.17)
(ϕ (t ),ψ (t ))ϕ' (t ) + Q (ϕ (t ),ψ (t
))ψ ' (t )⎤ ⎦ dt
A
B
Xususan AB egri
chiziq
α
y = y (x) (a < x < b)
tenglama bilan aniqlangan
bo’lib,
y = y (x)funksiya [a,b] da hosilaga ega va uzluksiz bo’lsa (1.15)va (1.17) formulalar
quyidagi
45

46.

b
(0.18)
∫ f ( x, y )dx =
∫ f (x, y (
x))dx
AB
a
b
∫ P ( x, y )dx + Q ( x, y ) dy = ∫ ⎡ ⎣ P (x, y ( x)) + Q (x, y ( x )) y' ( x )⎤ ⎦ dx
AB
a
ko’rinishga keladi.
x = x ( y) (c < y < d ) tenglama bilan
Shuningdek, AB egri chiziq
aniqlangan
bo’lib, x ( y) funksiya [c, d ]oraliqda hosilaga ega va uzluksiz bo’lsa (1.16) va (1.17)
tenglamalar quyidagi
d
(0.19)
∫ f ( x, y )dy =
∫ f (x ( y ), y
)dy
AB
c
(x ( y ), y )⎤ ⎦ dy
d
∫ P ( x, y )dx + Q ( x, y ) dy =
∫ ⎡ ⎣ P (x ( y ), y ) x' ( y ) + Q
46
AB
c

47.

(0.20)
ko’rinishga keladi.
47

48.

va Q(x, y) funksiyalar uchun
Agar P (x, y)
∂Q = ∂P
∂x
∂y
funksiyaning to’la
P (x, y)dx + Q(x, y)dy ifoda
Shart bajarilsa, u holda
biror U ( x, y)
differensiali bo’ladi va
∫ P ( x, y)dx + Q (x, y)dy
AB
integral integrallash yo’liga bog’liq bo’lmaydi, faqat
A
va
B
nuqtalarning berilishi bilan birqiymatli aniqlanadi.To’la differensial bo’yicha
funksiyaning o’zi
x
U ( x, y) =
y
∫ P (t, y0 )dt + ∫ Q ( x,t )dt + C
x0
y0
formula bo’yicha topiladi.
Ikki karrali va egri chiziqli integrallarni bog’lovchi
∫ P ( x, y )dx + Q ( x, y ) dy = ∫∫⎛∂Q − ∂P ⎞
⎜
∂x
(0.21)
∂y ⎟dxdy
∂D
D
⎝
⎠
formula Grin formulasi deyiladi.Grin formulasidan D sohaning yuzasini hisoblash
uchun ushbu
S = xdy, xdy ydx
S ydx
S=
∂D
2
∂D
48
1

49.

(0.22)
(0.23)
formulalar kelib chiqadi.
Egri chiziqli integrallarni hisoblashga oid misollar
1- masala. Quyidagi x = 2 cos t , y = 2sin t , 0 ≤ t ≤ π
yarim aylana
integralni bo’yicha
hisoblang
49

50.

∫ ydl.
L
Yechish.Birinchi tur egri chiziqli integralni ta’rif yordamida hisoblash
uchun berilgan yarim aylanani n ta bo’laklarga bo’lib olamiz.(4-chizma)
(4-chizma)
⎛
π
A0 (2, 0), A1 ⎜2 cos n , 2sin
n ⎟, A2 ⎜2 cos
n , 2sin
A=
⎝
A
⎠
⎛
2cos
π⎞
⎛
2π
2π ⎞
n ⎟,...,
⎝
⎠
(n −1)π , 2sin (n −1)π ⎞, B = A (2, 4).
n−1
⎝
⎜
n
n
⎟
n
⎠
Berilgan yarim aylananing uzunligi 2π ga, demak har bir bo’lakchaning uzunligi
2π
ga teng ekanligi
AA
i
(i = 0,1, 2,...,)
i+1
bo’lakchalardagi ixtiyoriy Mi
ravshan.Endi
n
nuqtalar sifatida har bir bo’lakchaning boshidagi nuqtani olib integral yig’indini
50

51.

tuzamiz.
n 1
∑ f (Mi )σ
= 0⋅
i
2π
+ 2sin
(n
π 2π
2π 2π
⋅
+ 2sin
⋅
+... + 2sin
−1)π ⋅ 2π =
n
nn
nn
n
n
i=0
=
4π ⎛
sin
n
⎜
⎝
π
n
+ sin
2π
n
+... + sin
(n −1)π ⎞= 4π ⎛sin π + sin 2π +... + sin (n −1)π + sin πn ⎞=
n
⎟
⎠
n
⎜
⎝
51
n
n
n
n
⎟
⎠

52.

=
sin n +1 ⋅ π
4π
2 n
⋅
⋅ sin
= 8⋅
sin π (n +1)
2n .
⋅
π
nπ
n
sin
π
2n
2n
sin
2n
π
2n
Demak,
π sin π (n +1)
n
∫ ydl = lim ∑ f (Mi )σi = lim 8⋅
L
⋅
n→∞
maxσi →0 i=1
2n
= 8.
2n
sin
π
2n
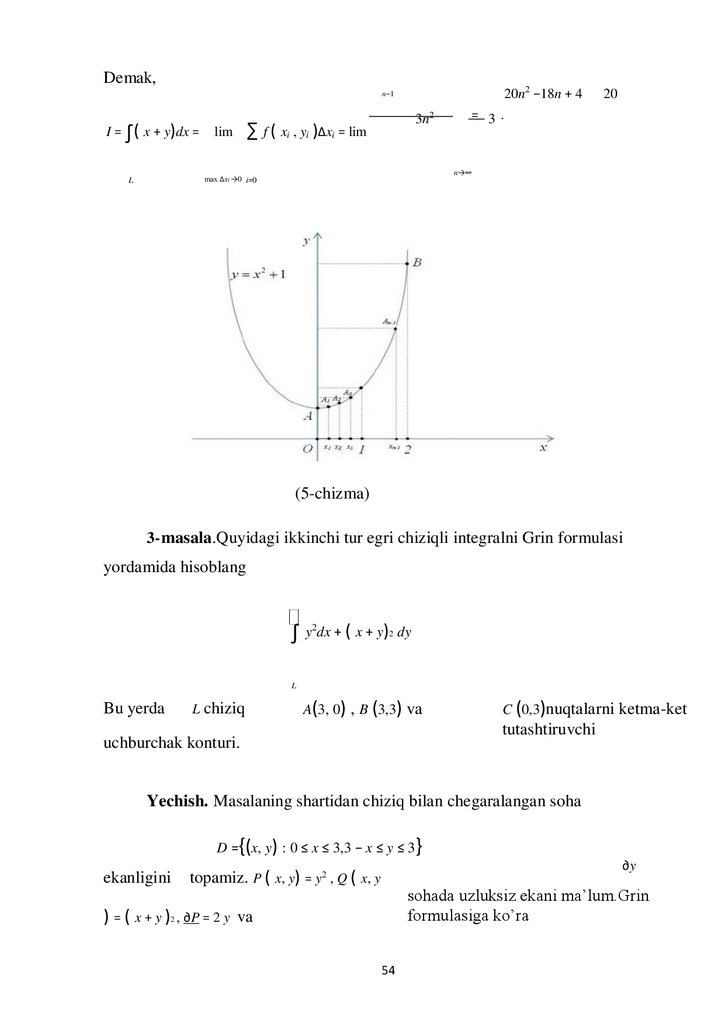
2- masala.Qu
parabolaning
y = x2 +1
A(0,1)
yidagi
integralni
B (2,5)
va
nuqtalaridan o’tuvchi AB yoy bo’yicha hisoblang.
I=
∫( x + y)dx
L
Yechish. Ikkinchi tur egri chiziqli integralni hisoblash uchun AB yoyni n ta
bo’lakchalarga bo’lib olamiz (5-chizma)
⎛2 4
⎞
⎛4 16
⎞
⎛6 36
⎞
A = A 0(0,1), A 1 ⎜ , 2+1 ,⎟
A 2 ⎜, 2+1 ,⎟A 3 ⎜ , 2 +1 ,...,
⎟
n n
n n
n n
⎝
⎠ ⎝
⎠ ⎝
⎠
A ⎛2(n −1) , 4(n −1) + ⎞
n−1
⎜
n
1⎟, B = An (2,5).
n2
52

53.

⎝
⎠
Endi har bir
AA
i
bo’lakchalardagi Mi nuqta sifatida
ixtiyoriy
shu
i+1
bo’lakchaning boshidagi nuqtani olib integral yig’indi tuzamiz
⎛
n−1
2 ⎛2 4
⎞
4 2 ⎛
16 ⎞ 2
2(n −1)
4(n −1)2
∑ f (Mi )Δxi = 1⋅
+
+
2
+1⎟⋅
+
+⎜
2 +1⎟⋅
⎜
n
i=0
=
⎝n
⎠n
n
+ ... + ⎜
⎝n n
⎝
⎠n
(
+1⎟⋅
2
⎜
nn
⎟
⎠
)
2 ⎡
2
4
⎤ =
⋅ n + ⋅ (1+ 2 + ... + (n −1)) +
⋅ 1+ 4 + ... + (n −1)2
n
⎢⎣
n
n2
2 ⎡
2 n (n −1)
⋅
n2⎢ n + n ⋅ 26 +⎥ =
⎣
=
⎥⎦
4 n (n −1)(2n −1)⎤
3n2
⎦
53
.
⎞
20n2 −18n + 4
n
2
=

54.

Demak,
20n2 −18n + 4
n−1
I=
∫( x + y)dx =
lim
3n2
∑ f ( xi , yi )Δxi = lim
= 3.
n→∞
max Δxi →0 i=0
L
20
(5-chizma)
3- masala.Quyidagi ikkinchi tur egri chiziqli integralni Grin formulasi
yordamida hisoblang
∫ y2dx + ( x + y) dy
2
L
Bu yerda
L chiziq
A(3, 0) , B (3,3) va
C (0,3)nuqtalarni ketma-ket
tutashtiruvchi
uchburchak konturi.
Yechish. Masalaning shartidan chiziq bilan chegaralangan soha
D ={(x, y) : 0 ≤ x ≤ 3,3 − x ≤ y ≤ 3}
ekanligini
∂y
topamiz. P ( x, y) = y2 , Q ( x, y
sohada uzluksiz ekani ma’lum.Grin
formulasiga ko’ra
) = ( x + y )2 , ∂P = 2 y va
54

55.

∂Q
∫ y dx + ( x + y) dy = ∫∫(2( x + y ) − 2 y
2
2
∂x
)dxdy = ∫∫ 2xdxdy =
L
D
D
55
= 2 ( x + y ) lar D

56.

3 3
3
3
⎞
⎛3
⎛
⎞
3
3
2
3
= 18.
=
∫ ∫ 2xdxdy =∫⎜∫ 2xdy ⎟dx
⎟dx =
∫ 2x dx = x
2
3
∫
= ⎜2xy
0
0 3−x
⎝3−x
⎠
0
⎝
3−x⎠
0
3
0
aylana bo’yicha hisoblang
x2 + y2 = 2x
4- masala. Quyidagi
integralni
x y dl.
I=
L
2
Yechish.
2
aylananing
parametrik
tenglamasi
x + y = 2x
ko’rinishda bo’lganligi uchun (1.8) formulaga ko’ra
2π
I=
2
2
x y dl (1+ cos t − sin t )⋅ (−sin t ) + (cos t ) dt =
L
0
=
2π
2π
∫ (1+ cos t − sin t )dt = (t + sin t +
0
cos t )
0
56
= 2π
x = 1+ cos t , y = sin t

57.

XULOSA
Ushbu kurs ishi orqali men matematik analiz fanida “Egri chiziqli integrallar”
mavzusini yanada mustahkamladim va menda yangi bilim va ko’nikmalar hosil
bo’ldi.Egri chiziqli integallar nazariyasida egri chiziqlarning muhimligini
e’tiborga olib, ular haqida ba’zi ma’lumotlarni keltirishni lozim topdim. Ayni
paytda ushbu kurs ishi orqali birinchi va ikkinchi tur egri chiziqli integrallarning
xossalari, yechilish usullari va ularning ba’zi tadbiqlarini o’rgandim. Qolaversa ,
egri chiziqli integrallarning geometrik va fizik ma’nolari haqida tushunchaga ega
bo’ldim. Birinchi tur egri chiziqli integrallar yordamida yoy uzunligini, jism
massasini, og’irlik markazlarini topish mumkin. Ikkinchi tur egri chiziqli
inegrallar asosan fizika fanida qo’laniladi. Ya’ni fizika fanida ikkinchi tur egri
chiziqli integrali tekis kuch maydonining bajarilgan ishini hisoblashda
qo’llaniladi.Egri chiziqli integrallarning bu kabi fanlarga tadbiqlarida umuman
olganda matematik usullar yordamida fizik masalalarda matematik analiz
fanining o’rni naqadar muhim ekanligini anglashimiz mumkin.Xulosa qilib
aytganda, ushbu kurs ishida o’rganilgan egri chiziqli integrallar nazariyasi mavzusi
amaliy ahamiyatga ega bo’lgan, matematik analiz fanidagi muhim mavzulardan
bo’lib, hayotda ko’pgina sohalarda qo’llaniladi.
57

58.

FOYDALANILGAN ADABIYOTLAR:
1. T.Azlarov,
H.Mansurov.
Matematik
analiz
asoslari 2-qism.
Toshkent
“o’qituvchi” 1994y.
2. Sh.R.Xurramov. Oliy matematika.Barcha texnik yo’nalishlar uchun darslik. 2qism.Toshkent “Tafakkur” nashriyoti , 2018y.
3. Sh.Alimov, R.Ashurov. Matematik analiz 2-qism.Toshkent
“Mumtoz so’z”
2018y.
4. B.A.Shoimqulov, T.T.To’ychiyev, D.X.Djumaboyev, Matematik analizdan
mustaqil ishlar. Toshkent 2008y
5. Yo.U.Soatov. Oliy matematika 3-jild.Toshkent “O’zbekiston” 1996y
6. G.Xudoyberganov, A.K.Vorisov, T.X.Mansurov, A.B.Shoimqulov. Matematik
analizdan ma’ruzalar, 2-qism.Toshkent “Voris-nashriyot” 2010 y
7. Минорский В. П. Сборник задач по высшей математике. Москва “Наука”
1987.
8. Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления.
Том III. Москва: «ФИЗМАТГИЗ» 1960.
9. Shokirova X.R. Karrali va egri сhiziqli integrallar. Toshkent ”O`qituvсhi”
1992y.
58