Similar presentations:
Теоремы сложения и умножения вероятностей. Формула полной вероятности
1.
2 Mavzu . Ehtimolliklarni qo'shish vako'paytirish teoremalari. To'liq ehtimollik
formulasi. Bayes formulalari
Тема 2. Теоремы сложения и умножения вероятностей.
Формула полной вероятности. Формулы Байеса
2.
Классическое определение вероятности3.
Статистическое определение вероятностиКлассическое определение вероятности применимо только для
очень узкого класса задач, где все возможные исходы опыта можно
свести к схеме случаев. В большинстве реальных задач эта схема
неприменима. В таких ситуациях требуется определять вероятность
события иным образом.
Ehtimollikning statistik ta’rifi
Ehtimollikning klassik ta'rifi faqat juda tor vazifalar sinfiga
taalluqlidir, bu erda tajribaning barcha mumkin bo'lgan natijalari holatlar
sxemasiga qisqartirilishi mumkin. Ko'pgina haqiqiy vazifalarda ushbu sxema
qo'llanilmaydi. Bunday vaziyatlarda voqea ehtimolini boshqacha aniqlash
talab qilinadi.
4.
Статистическое определение вероятности5.
Статистическое определение вероятностиСтатистической вероятностью события
относительную частоту или число, близкое к ней.
считают
его
Ehtimollikning statistik ta’rifi
Hodisaning statistik ehtimoli uning nisbiy chastotasi yoki unga
yaqin bo'lgan raqam deb hisoblanadi.
Пример. Если в задаче задается вероятность попадания в
мишень для данного стрелка (скажем, р = 0,7), то эта величина
получена в результате изучения статистики большого количества
серий выстрелов, в которых этот стрелок попадал в мишень около
семидесяти раз из каждой сотни выстрелов.
6.
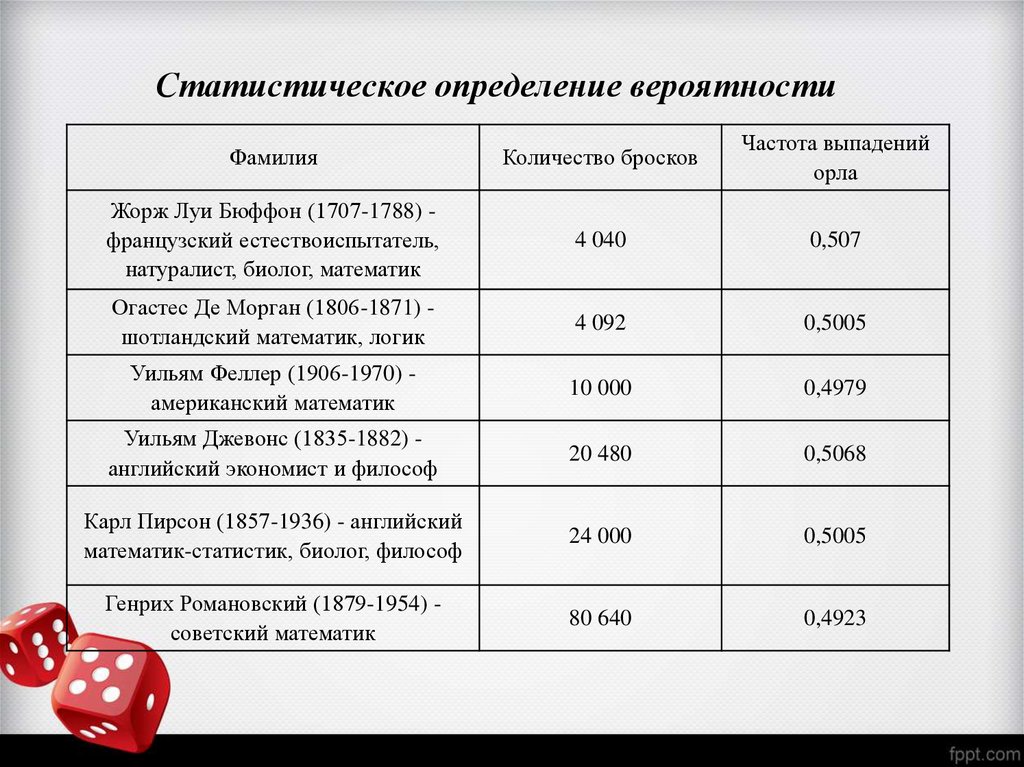
Статистическое определение вероятностиФамилия
Количество бросков
Частота выпадений
орла
Жорж Луи Бюффон (1707-1788) французский естествоиспытатель,
натуралист, биолог, математик
4 040
0,507
Огастес Де Морган (1806-1871) шотландский математик, логик
4 092
0,5005
Уильям Феллер (1906-1970) американский математик
10 000
0,4979
Уильям Джевонс (1835-1882) английский экономист и философ
20 480
0,5068
Карл Пирсон (1857-1936) - английский
математик-статистик, биолог, философ
24 000
0,5005
Генрих Романовский (1879-1954) советский математик
80 640
0,4923
7.
Сложение событийСуммой событий А и В называется событие А + В,
которое наступает тогда и только тогда, когда наступает
хотя бы одно из событий: А или В.
Ҳодисаларнинг йиғиндиси
А ва В ҳодисаларнинг йиғиндиси А + В ҳодисаси
деб аталади, бу ҳодисалардан камида биттаси содир
бўлганда содир бўлади: А ёки В.
8.
Теорема сложения вероятностейТеорема сложения вероятностей: Вероятность
появления одного из двух несовместных событий равна
сумме вероятностей этих событий.
Эҳтимолларни қўшиш теоремаси
1-chi Ehtimollarni qo'shish teoremasi: mos
kelmaydigan ikkita hodisadan birining paydo bo'lish ehtimoli
ushbu hodisalarning ehtimolliklari yig'indisiga teng.
9.
Теорема сложения вероятностейЭҳтимолларни қўшиш теоремаси
Сформулированная теорема
несовместных событий:
справедлива
для
любого
числа
Если случайные события
образуют полную группу независимых событий, то
Ushbu teorema har qanday mos kelmaydigan hodisalar uchun amal qiladi:
Agar tasodifiy hodisalar
tashkil etsa, unda:
mustaqil hodisalarning to'liq guruhini
10.
Произведением событий А и В называется событиеАВ, которое наступает тогда и только тогда, когда
наступают оба события: А и В одновременно. Случайные
события А и B называются совместными, если при
данном испытании могут произойти оба эти события.
A va B hodisalarining ko'paytmasi AB hodisasi deb
ataladi, u faqat ikkala voqea sodir bo'lganda sodir bo'ladi: A
va B bir vaqtning o'zida. Tasodifiy hodisalar A va B agar
ushbu sinovda ikkala hodisa ham sodir bo'lishi mumkin
bo'lsa, qo'shma deyiladi.
11.
Теорема сложения вероятностей 2. Вероятностьсуммы совместных событий вычисляется по формуле
2-chi ehtimollarni qo'shish teoremasi. Qo'shma
hodisalar yig'indisi ehtimoli formula bo'yicha hisoblanadi
12.
События А и В называются независимыми, еслипоявление одного из них не меняет вероятности
появления другого. Событие А называется зависимым от
события В, если вероятность события А меняется в
зависимости от того, произошло событие В или нет.
A va B hodisalar mustaqil hodisalar deb nomlanadi,
agar ulardan birining paydo bo'lishi boshqasining paydo
bo'lish ehtimolini o'zgartirmasa. Aks holda, ular qaram deb
ataladi.
13.
Теорема умножения вероятностейТеорема умножения вероятностей: Вероятность
произведения независимых событий А и В вычисляется по
формуле:
Вероятность произведения зависимых событий
вычисляется по формуле условной вероятности.
Ehtimollarni ko'paytirish teoremasi: A va B mustaqil
hodisalarni hosil qilish ehtimoli formula bo'yicha hisoblanadi:
Bog'liq hodisalarni hosil qilish
ehtimollik formulasi bo'yicha hisoblanadi.
ehtimoli
shartli
14.
Задача 1. Студент разыскивает нужную ему формулу в трехсправочниках. Вероятности того, что формула содержится в первом,
втором и третьем справочниках равны 0,6; 0,7 и 0,8. Найти вероятности
того, что формула содержится 1) только в одном справочнике; 2) только в
двух справочниках; 3) во всех трех справочниках.
Решение. А – формула содержится в первом справочнике; В –
формула содержится во втором справочнике; С – формула содержится в
третьем справочнике. Воспользуемся теоремами сложения и умножения
вероятностей.
1)
2)
3)
15.
Задача 2. Студент сдает в сессию три экзамена. Вероятностьвоспользоваться шпаргалкой на первом, втором и третьем экзамене
равна соответственно, 0.4, 0.5, 0.7. Найти вероятность того, что на всех
экзаменах студенту удастся списать.
Решение: Пусть событие А1 состоит в том, что студенту удалось
списать на первом экзамене, А2 - на втором экзамене, А3 - на третьем
экзамене. Эти события будут независимыми. Событие А, состоящее в
том, что студент спишет на всех трех экзаменах, выразится как
произведение событий А1, А2 и А3 :
А=А1А2А3
Тогда по теореме об умножении вероятностей
Р(А)=Р(А1)Р(А2)Р(А3),
где Р(А1)=0.4, Р(А2)=0.5, Р(А3)=0.7
Следовательно,
Р(А)=0.4*0.5*0.7=0.14
16.
Условная вероятностьСлучайное событие определено как событие, которое при
осуществлении совокупности условий эксперимента может
произойти или не произойти. Если при вычислении вероятности
события никаких других ограничений, кроме условий эксперимента,
не налагается, то такую вероятность называют безусловной; если же
налагаются и другие дополнительные условия, то вероятность
события называют условной. Например, часто вычисляют
вероятность события В при дополнительном условии, что
произошло событие А.
Условной вероятностью
называют вероятность события В, вычисленную в предположении,
что событие А уже наступило.
17.
Вероятностьсовместного
появления
двух
зависимых событий равна произведению вероятности
одного из них на условную вероятность второго,
вычисленную при условии, что первое событие
произошло, т.е.
В частности отсюда получаем:
18.
Задача 2. В урне находятся 3 белых шара и 2черных. Из урны вынимается один шар, а затем второй.
Событие В – появление белого шара при первом
вынимании. Событие А – появление белого шара при
втором вынимании.
Решение: Очевидно, что вероятность события А,
если событие В произошло, будет
Вероятность события А при условии, что событие В не
произошло, будет
19.
Теорема умножения вероятностей(для зависимых событий)
Р(А1 А2 А3 ... Аn) =
Р(А1) Р(А2/А1) Р(А3/А1 А2) …
Р(Аn/А1 А2 А3 ... Аn-1).
20.
Задача 3:Студент знает ответы на 20 из 25 вопросов.
Какова вероятность того, что он ответит на два
выбранных наудачу вопроса?
20
21.
Решение:Рассмотрим события:
А- студент знает ответ на первый вопрос,
В- студент знает ответ на второй вопрос.
Найдем Р(А В).
20 19 19
Р(А В) = Р(А) Р(В/А) =
25 24
30
21
22.
Задача 4:Два студента выполняют независимо друг от
друга задание. Вероятность того, что задание
будет выполнено первым студентом 0,6;
для второго студента эта вероятность равна 0,8.
Найти вероятность того, что
оба студента выполнят задание;
только один из них выполнит задание;
хотя бы один из них выполнит задание.
22
23.
Решение:События: А- задание выполнит первый студент,
В- задание выполнит второй студент.
По условию Р(А) = р1 = 0,6; Р(В)=р2 = 0,8; следовательно,
Р( А ) = 1-p1 = q1 = 1-0,6 = 0,4; P(B ) = 1-p2 = q2 = 1-0,8 = 0,2.
Р(А В) = /события А и В - независимые события /
= Р(А) Р(В) = р1 р2 =0,6 0,8 = 0,48.
Р(А B + А B) = / A B и А B - несовместные
события /= Р(А B ) + Р(А В) = Р(А) Р( B ) +
Р( А ) Р(В) = p1 q2+q1 p2 = 0,6 0,2 + 0,4 0,8 = 0,44.
P(A+B)=/ А и В-совместные события /=
Р(А)+Р(В)-Р(А В)=0,6+0,8-0,48=0,92
или т.к. А+В и А B противоположные события, то
Р(А+В)=1-Р(А B)= 1 - Р( А ) Р(B ) = 1-q1 q2 = 1-0,4 0,2 =
1-0,08 = 0,92.
23
24.
Задача 5:Для получения кредита предприятие обратилось к трем
банкам. Статистические исследования показали, что
вероятности
выделения
кредита
этими
банками
соответственно равны р1=0,5, р2=0,4 и р3=0,9. Банки выделяют
кредит независимо друг от друга и, если примут решение о
его выделении, то в размере: первый банк-160 тыс. руб.,
второй-40 тыс. руб., третий-200 тыс. руб.
Найти вероятности того, что предприятие получит
кредит:
а) в размере 200 тыс. руб.,
б) не менее 240 тыс. руб.
с) в любом размере.
24
25.
Решение:События:
А - первый банк выделит кредит,
В - второй банк выделит кредит,
С - третий банк выделит кредит,
D - предприятие получит кредит в размере 200 тыс. руб.,
E - предприятие получит кредит в размере не менее 240
тыс. руб.,
F – получит кредит.
25
26.
а) Т.к. D = A B C ABC,
то P(D) = 0,5 0,4 (1 - 0,9) + (1 - 0,5) (1 - 0,4) 0,9 = 0,02 +
0,27 = 0,29.
б)Т.к.E=A B C A B C A B C
,
то P(E)=0,5 (1-0,4) 0,9+(1-0,5) 0,4 0,9+0,5 0,4 0,9=0,63.
с) F A B C , то P(F) = 1 – P( F ) = 1 – 0 ,5 0,6 0,1=
0,97.
26
27.
Формула полной вероятностиПусть в результате опыта может появиться какое-либо
из несовместных событий Н1,Н2,...,Нn, образующих полную
группу. Событие А может появиться только вместе с одним из
этих событий. События Н1, Н2,..., Нn называются гипотезами.
Если известны вероятности гипотез Р(Нi) и условные
вероятности Р(А/Нi), где i =1, n , то
n
P( A) P( H i ) P( A / H i )
i 1
27
28.
Задача 6:На стройку поступают блоки с трех баз, причем 50% с
первой базы,30% со второй базы, остальные с третьей базы.
Вероятность того, что блок c первой базы бракованный - 0,09;
со второй - 0,1; с третьей - 0,08. Найти вероятность того, что
взятый наудачу на стройке блок окажется бракованным.
Решение:
Рассмотрим гипотезы:
Н1 -взятый наудачу блок поступил с первой базы,
Н2 -взятый наудачу блок поступил со второй базы,
Н3 -взятый наудачу блок поступил с третьей базы.
Событие А -взятый наудачу на стройке блок окажется
бракованным.
28
29.
По условиюР(Н1)=50/100=0,5;
Р(Н2)=30/100=0,3;
Р(Н3)=(100-50-30)/100 = 0,2.
.Р(А/Н1)=0,09;
Р(А/Н2)=0,1;
Р(А/Н3)=0,08.
Следовательно, по формуле полной вероятности
Р(А)=0,5 0,09+0,3 0,1+0,2 0,08=0,091.
Имеет место равенство:
n
P( H ) 1.
i 1
i
29
30.
Формула Байеса(теорема переоценки гипотез)
Пусть в условиях предыдущей теоремы событие А
наступило и мы нашли вероятность Р(А). Спросим, как
изменились вероятности гипотез в связи с появлением
события А, т.е. найдем Р(Нi/А), где i=1,2,...,n.
По
формуле
полной
вероятности:
Р(А Нi)=P(A) P(Hi/A)=P(Hi) P(A/Hi), откуда
.
P( H i ) P( A / H i )
P( H i / A)
P( A)
30
31.
Задача 7:В предыдущем примере событие А наступило, т.е. взятый
наудачу на стройке блок оказался бракованным.
Определить вероятность того, что этот блок поступил со
второй базы.
Решение:
P( H 2 ) P( А / H 2 ) 0,3 0,1 30
0,33.
Р(Н2/А) =
P( А)
0,091 91
31































 mathematics
mathematics

