Обнаружение когерентных сигналов со случайными параметрами. Лекция №8

1.

Военно-инженерный институт
Учебный военный центр
Отдел «Радиолокационного вооружения РТВ ВВС»
Дисциплина
«ОСНОВЫ ТЕОРИИ
РАДИОЛОКАЦИОННЫХ СИСТЕМ И
КОМПЛЕКСОВ»
Обнаружение когерентных сигналов
со случайными параметрами

2.

1

3.

2
1.Методы вычисления отношения правдоподобия.
Общие соотношения.
2. Обнаружение сигнала со случайной начальной
фазой.
3. Обнаружение сигналов со случайными начальной
фазой и амплитудой.

4.

3 1.Методы вычисления отношения правдоподобия. Общие
соотношения
Пусть на входе приемного устройства наблюдается смесь
сигнала со случайным параметром и помехи
y(t ) x(t ,β) n(t ).
Для вычисления отношения правдоподобия введем совместную
плотность распределения реализации сигнала и случайного
параметра
Pсп Y ,β Pсп Y P β Y P β Pсп Y β .
Интегрируя (1) по , получим
l Y
Pсп Y
Pп Y
Pсп Y P β Pсп Y β dβ.
β
P β l Y β dβ,
β
(1)

5.

Перейдем от многомерных реализаций Y к непрерывным y(t).
Тогда получим:
4
l y t P β l y (t ) β ,
β
Pсп Y β
частное отношение правдоподобия
l y (t ) β lim
t 0 P Y
при фиксированном значении .
п
Поскольку при фиксированном
Э β
2 Z β сигнал полностью известен, то
l y (t ) β e
N0
e
N0
(2)
где Z( ), Э( ) - частные значения корреляционного интеграла и
энергии сигнала
Таким
образом,
усредняя
частное
правдоподобия по случайному
z x t ,β y t dt , отношение
параметру , можем определить отношение
Э β x 2 t ,β dt.
(3)
правдоподобия l[y(t)] для сигналов со
случайными параметрами и использовать его
при
решении
задачи
оптимального
обнаружения.

6.

2. Обнаружение сигнала со случайной начальной
фазой
5
Рассмотрим модель когерентного сигнала со случайной
начальной фазой:
x t ,β X t cos ω0t φ t β ,
где (t) - закон фазовой модуляции;
(4)
Х(t) - закон амплитудной модуляции.
Преобразуем (4) с использованием формулы косинуса разности
двух углов к виду
x t ,β X t cos ω0t φ t cosβ X t sin ω0t φ t sinβ
x1 t cosβ x2 t sinβ,
где
cos
x1,2 t X t
ω0t φ t .
sin
Тогда частное
приводится к виду
значение
корреляционного
интеграла
(3)

7.

6
Z y(t ) β Z1 cosβ Z 2 sinβ Z cos θ - β ,
Z1,2 x1,2 t y t dt ;
Z1
cosθ ;
Z
Z Z12 Z 22 ;
Z2
sin θ .
Z
Значение энергии сигнала, содержащего
периодов колебаний,
не зависит от и равно
большое
Э β Э X t dt.
число
2
(6)
В соответствии с выражениями (5) и (6) частное отношение
правдоподобия будет равно:
l y(t ) β e
Э
N0
e
2
Z cos θ-β
N0
.
(7)

8.

7 Полагая P( )=1/2 и усредняя l[y(t)/ ] по , получим
следующий результат
l y t e
где
Э
N0
2Z
I0
N0
(8)
2 Z
I0
- функция Бесселя первого рода нулевого порядка;
N0
Z - модульное значение корреляционного интеграла.
Анализ полученного выражения показывает, что ввиду
монотонности функции I0(x) отношение правдоподобия является
монотонной функцией модульного значения корреляционного
интеграла .
Следовательно, алгоритм обнаружения сигнала со случайной
начальной фазой реализует следующее правило
1 z z0,
A опт y t
0, z z0,

9.

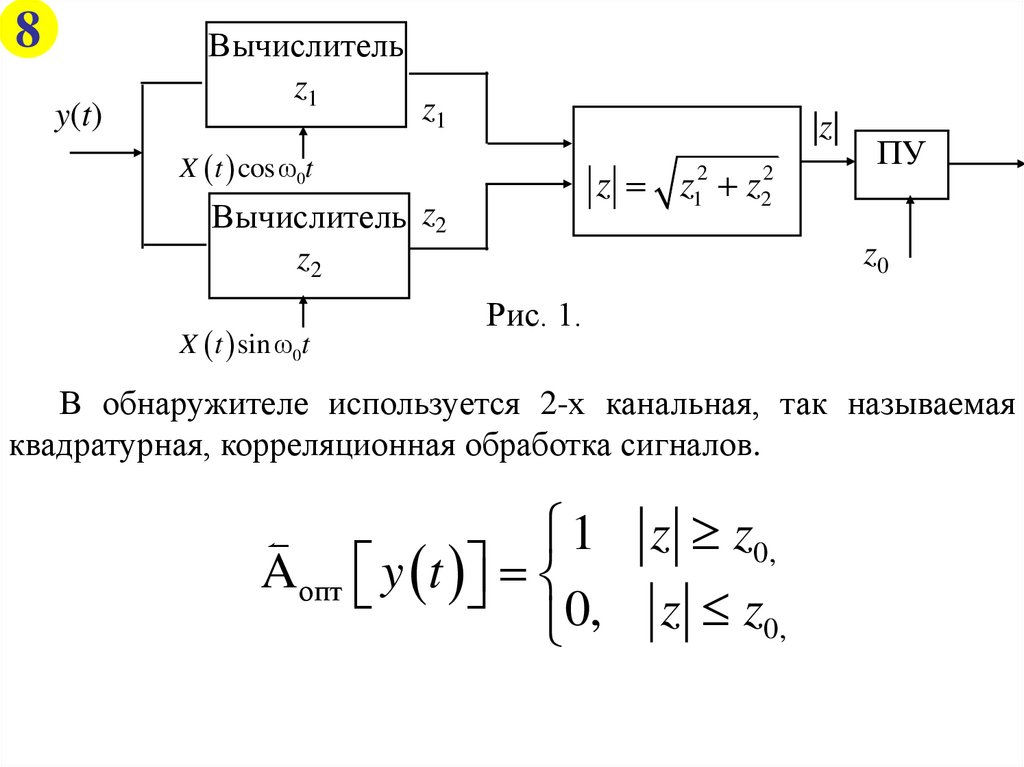
8
y(t)
Вычислитель
z1
z1
|z|
X t cosω0t
z1122 z222
zz z z
Вычислитель z2
z2
X t sin ω0t
ПУ
z0
Рис. 1.
В обнаружителе используется 2-х канальная, так называемая
квадратурная, корреляционная обработка сигналов.
1 z z0,
A опт y t
0, z z0,

10.

9
3.ОБНАРУЖЕНИЕ СИГНАЛОВ СО СЛУЧАЙНОЙ
НАЧАЛЬНОЙ ФАЗОЙ И АМПЛИТУДОЙ
а) Отношение правдоподобия и алгоритм обнаружения сигналов
со случайной амплитудой и начальной фазой
Модель сигнала описывается выражением
x t , , b bX t cos ω0t φ t β ,
Используя (7), при фиксированном значении b для рассматриваемого сигнала
можно записать следующее выражение частного отношения правдоподобия
где b - случайная величина, принимающая значения от 0 до 1.
b
l y (t ) b e
2 Z b
I0
N0
2
Z b b Z , Э b b Э;
N0
,
Э и - энергия и модульное значение корреляционного интеграла при
b =1.
Величина энергии Э выбирается при этом равной средней
энергии

11.

10
Задаваясь релеевским распределением амплитуд
P b 2b e
b2
и усредняя частное отношение правдоподобия, получим
2
N0
l y t P b l y (t ) b db
e
Э N0
Z
N0 Э N0
(8)
1, Z Z 0 ,
А опт y t
0, Z Z 0 .
Структурная схема обнаружителя сигналов со случайными начальной
фазой и амплитудой идентична структурной схеме обнаружителя сигналов со
случайной начальной фазой, рассмотренной выше.
Таким образом, алгоритм обнаружения для сигналов со случайными
параметрами сводится к следующему:
1. По принятой реализации y(t) вычисляются частные значения отношения
правдоподобия или корреляционного интеграла.
2. Производится усреднение частного значения отношения правдоподобия
по случайным параметрам и сравнивается с порогом или берется модуль
корреляционного интеграла и сравнивается с порогом Z0.
3. Принимается соответствующее решение Â

12.

11

13.

12

14.

13

15.

14

16.

15

17.

16

18.

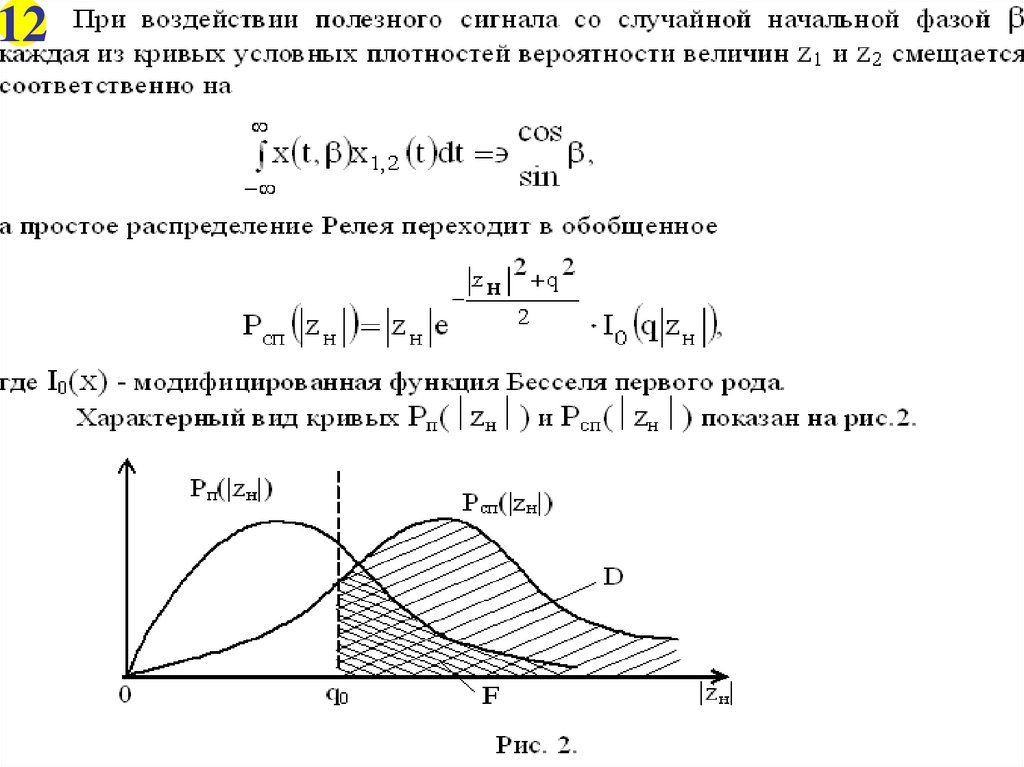
17
Кривые обнаружения для сигналов:
с полностью известными параметрами (штрих-пунктир);
со случайной начальной фазой (пунктир);
со случайными амплитудой и начальной фазой (сплошные линии).

19.

18
3. Заключительная часть
1. Отношение правдоподобия для сигналов со
случайной начальной фазой, либо случайными начальной
фазой
и
амплитудой
пропорционально
модулю
корреляционного интеграла.
2. Кривые обнаружения для сигнала со случайными
неинформативными
параметрами
сдвигаются
по
сравнению с кривыми с полностью известными
параметрами вправо.
3. Параметр обнаружения когерентного сигнала
заданного вида зависит только от энергии сигнала и
спектральной плотности шума.

20.

19
Задание на самостоятельную подготовку:
Отработать материал лекции
рекомендованной литературой.
Л 1/о с. 90-100;
Л 1/д с. 165-167;
в
соответствии
с