Флаттер консольно - защемленной лопасти несущего винта легкого многоцелевого вертолета

1.

Выпускная-квалификационная работа на тему:
Флаттер консольно-защемленной лопасти
несущего винта легкого многоцелевого
вертолета
Студент Тихонова А.Ю.
Группы 1260

Цели и задачи
Цель работы:
• Расчет флаттера лопасти несущего винта
Задачи:
• Определение собственных форм и частот изгибно-крутильных
колебаний лопасти;
• Расчет критической скорости флаттера;
• Преобразование дифференциальных уравнений возмущенного
движения лопасти в горизонтальном полете вертолета;
• Определение границ устойчивости колебаний лопасти несущего
винта.
©©2023
защищены
2019АО
АОВертолеты
Вертолеты России,
России, все права
права защищены
2

3.

Явление флаттера
©©2023
защищены
2019АО
АОВертолеты
Вертолеты России,
России, все права
права защищены
3

4.

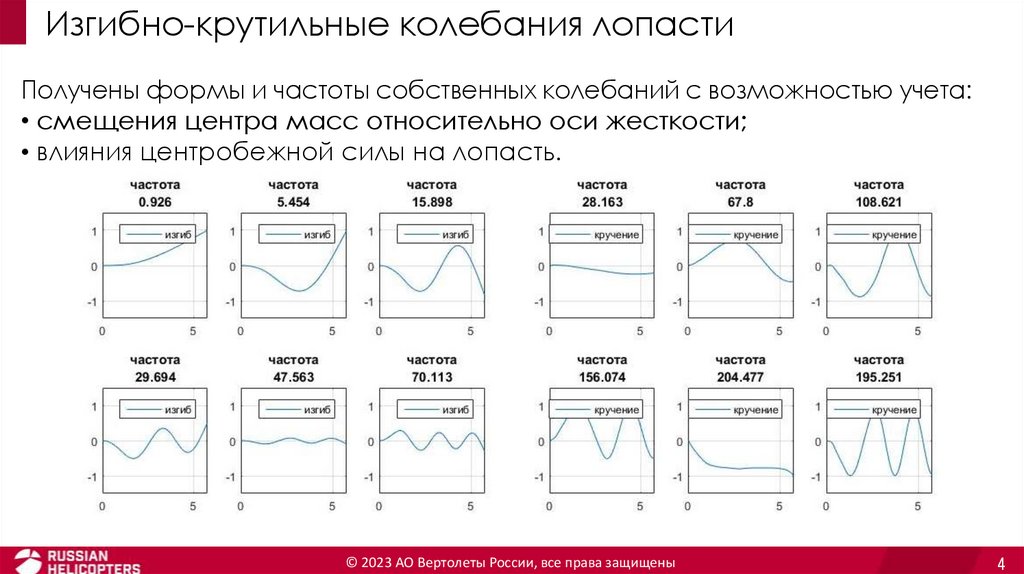
Изгибно-крутильные колебания лопасти
Получены формы и частоты собственных колебаний с возможностью учета:
• смещения центра масс относительно оси жесткости;
• влияния центробежной силы на лопасть.
©©2023
защищены
2019АО
АОВертолеты
Вертолеты России,
России, все права
права защищены
4

5.

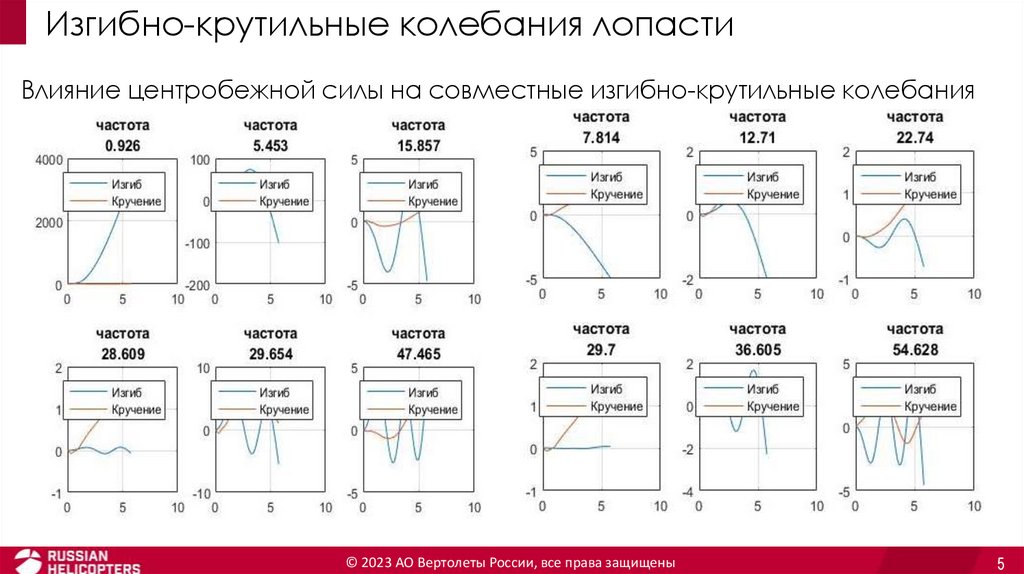
Изгибно-крутильные колебания лопасти
Влияние центробежной силы на совместные изгибно-крутильные колебания
©©2023
защищены
2019АО
АОВертолеты
Вертолеты России,
России, все права
права защищены
5

6.

Критическая скорость флаттера
©©2023
защищены
2019АО
АОВертолеты
Вертолеты России,
России, все права
права защищены
6

7.

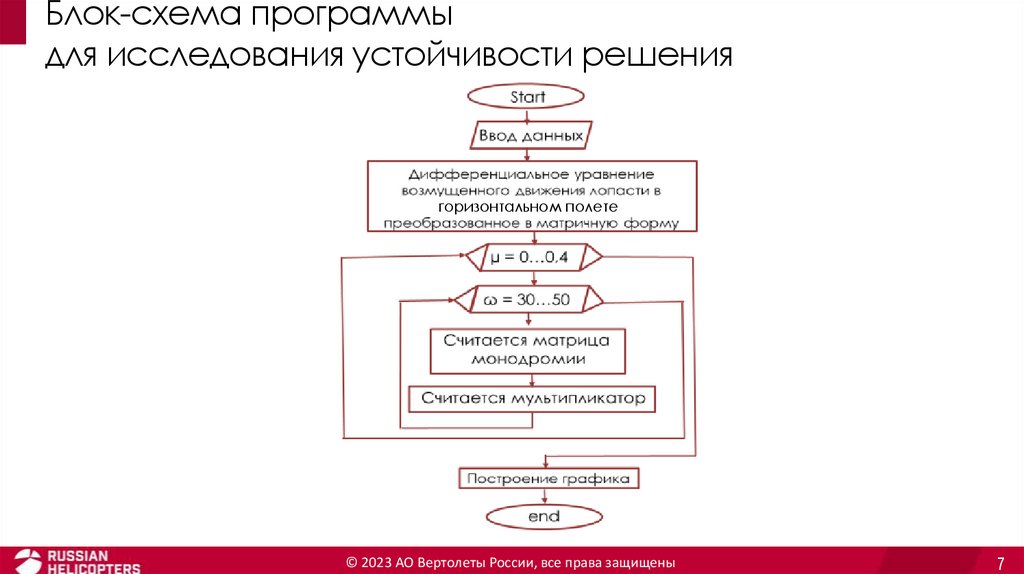
Блок-схема программы
для исследования устойчивости решения
горизонтальном полете
©©2023
защищены
2019АО
АОВертолеты
Вертолеты России,
России, все права
права защищены
7

8.

Дифференциальные уравнения возмущенного
движения лопасти в горизонтальном полете
d11 R b sin 1 R b11I cos R 2 2 b11II sin 2 2 pвз
I
11
1
2
1
c12 d12 R d sin b12 2 R b11I sin R 2 2 b11II 1 cos 2 2 0
2
I
12
2
d 22 R d sin b22 2 R b22I sin R 2 2 b22II 1 cos 2 2 pкр
I
22
1
2
1
2
c21 d 21 R b sin c21 R b22I cos R 2 2 b22II sin 2 2 pкр
0
2
I
22
©©2023
защищены
2019АО
АОВертолеты
Вертолеты России,
России, все права
права защищены
8

9.

Дифференциальные уравнения возмущенного
движения лопасти в горизонтальном полете
Совершаем замену:
После замены получаем:
©©2023
защищены
2019АО
АОВертолеты
Вертолеты России,
России, все права
права защищены
9

10.

Дифференциальные уравнения возмущенного
движения лопасти в горизонтальном полете
Представление уравнений в матричной форме
©©2023
защищены
2019АО
АОВертолеты
Вертолеты России,
России, все права
права защищены
10

11.

Определение устойчивости решения
Нахождение матрицы монодромии и
for i_mu = [0:10]
мультипликаторов уравнения
mu = 0.4/10*i_mu;
for i_omega = [30:50]
omega = i_omega;
t1 =2*pi/omega;
t,z]=ode23('dannie2',[t0 t1],[1 0 0 0]);
Y1 = z(end,:)';
[t,z]=ode23('dannie2',[t0 t1],[0 1 0 0]);
Y2 = z(end,:)';
[t,z]=ode23('dannie2',[t0 t1],[0 0 1 0]);
Y3 = z(end,:)';
[t,z]=ode23('dannie2',[t0 t1],[0 0 0 1]);
Y4 = z(end,:)';
YY = [Y1 Y2 Y3 Y4];
XX = eig(YY);
Max(i_mu+1,i_omega-29) = max(abs(XX));
end
Заменяя t на t+T в уравнении и
учитывая периодичность
коэффициентов a(t), b(t) получаем
end
©©2023
защищены
2019АО
АОВертолеты
Вертолеты России,
России, все права
права защищены
11

12.

Устойчивость решения
Зависимость между ω и µ записана в таблицу
Условие возникновение флаттера: ω(µ)>1 – возникновение явления флаттера;
ω(µ)<1 – отсутствие флаттера;
µ\
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
0
0.304 0.331 0.363 0.402 0.449 0.507 0.579 0.667 0.776 0.909 1.067 1.252 1.464 1.701 1.960 2.238 2.529 2.829 3.135 3.441 3.744
0,04
0.296 0.315 0.339 0.366 0.399 0.438 0.484 0.541 0.609 0.692 0.791 0.910 1.048 1.208 1.387 1.586 1.800 2.028 2.265 2.507 2.754
0,08
0.295 0.310 0.327 0.347 0.371 0.398 0.429 0.467 0.511 0.563 0.625 0.699 0.786 0.888 1.006 1.139 1.288 1.450 1.625 1.809 2.001
0,12
0.300 0.312 0.325 0.341 0.358 0.377 0.399 0.425 0.455 0.489 0.529 0.576 0.630 0.694 0.767 0.852 0.949 1.058 1.178 1.309 1.449
0,16
0.311 0.320 0.331 0.343 0.356 0.370 0.387 0.405 0.426 0.449 0.476 0.506 0.541 0.581 0.627 0.680 0.740 0.809 0.886 0.973 1.068
0,20
0.327 0.335 0.343 0.352 0.362 0.374 0.386 0.399 0.414 0.431 0.449 0.470 0.493 0.519 0.549 0.582 0.620 0.663 0.711 0.765 0.825
0,24
0.348 0.354 0.361 0.369 0.377 0.385 0.395 0.405 0.416 0.428 0.441 0.456 0.472 0.490 0.510 0.531 0.556 0.583 0.613 0.647 0.684
0,28
0.375 0.380 0.385 0.391 0.398 0.404 0.412 0.420 0.428 0.437 0.447 0.458 0.469 0.482 0.496 0.510 0.527 0.545 0.564 0.586 0.609
0,32
0.407 0.411 0.415 0.420 0.425 0.431 0.436 0.443 0.449 0.456 0.464 0.472 0.480 0.490 0.499 0.510 0.521 0.533 0.547 0.561 0.576
0,36
0.444 0.448 0.452 0.456 0.460 0.464 0.469 0.474 0.479 0.484 0.490 0.496 0.503 0.510 0.517 0.524 0.533 0.541 0.551 0.560 0.571
0,40
0.489 0.492 0.495 0.498 0.502 0.505 0.509 0.513 0.517 0.521 0.525 0.530 0.535 0.540 0.546 0.552 0.558 0.564 0.571 0.578 0.585
©©2023
защищены
2019АО
АОВертолеты
Вертолеты России,
России, все права
права защищены
- Отсутствие
флаттера
- Возникновение
явления
флаттера
12

13.

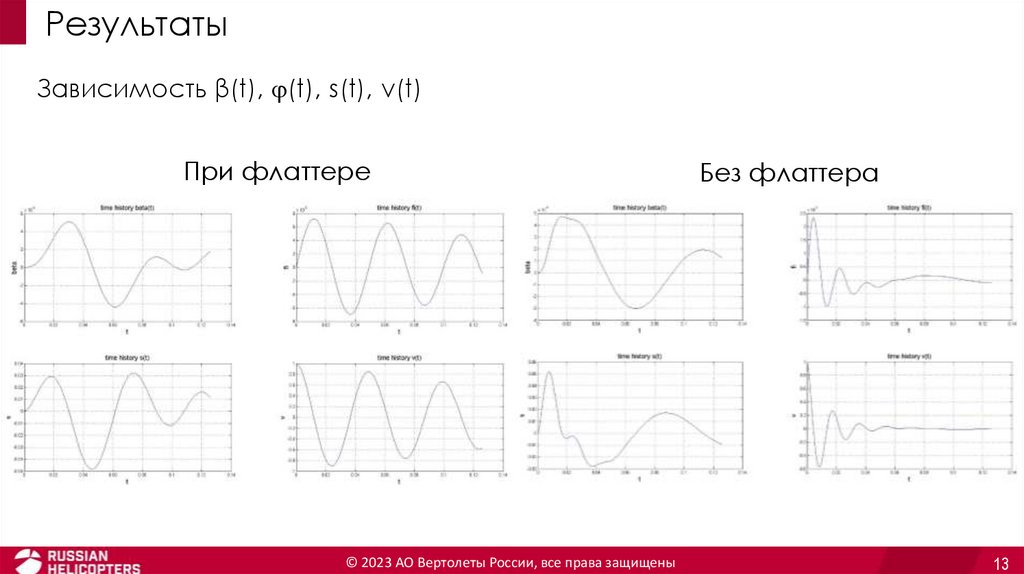
Результаты
Зависимость β(t), (t), s(t), v(t)
При флаттере
©©2023
защищены
2019АО
АОВертолеты
Вертолеты России,
России, все права
права защищены
Без флаттера
13

14.

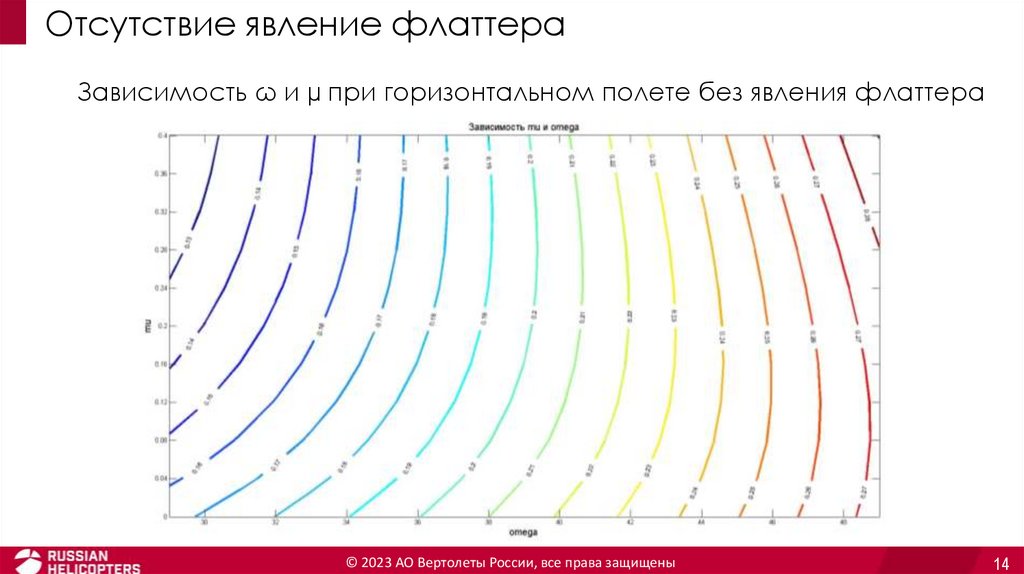
Отсутствие явление флаттера
Зависимость ω и µ при горизонтальном полете без явления флаттера
©©2023
защищены
2019АО
АОВертолеты
Вертолеты России,
России, все права
права защищены
14

15.

Явление флаттера
Зависимость ω и µ при горизонтальном полете при флаттере
©©2023
защищены
2019АО
АОВертолеты
Вертолеты России,
России, все права
права защищены
15

16.

Выводы
• В ходе работы были выражены и решены уравнения для расчета
совместных изгибно-крутильных колебаний с учетом центробежной силы
и жесткости системы управления;
• Определена критическая скорость флаттера лопасти несущего винта;
• Проведено преобразование расчета дифференциальных уравнений
возмущенного движения лопасти в горизонтальном полете;
• Создана программа в математическом пакете для расчета в которой
можно определить при каких значениях появляется флаттер лопасти
несущего винта вертолета;
• Изучен метод Флоке-Ляпунова для систем дифференциальных
уравнений с периодическими коэффициентами.
©©2023
защищены
2019АО
АОВертолеты
Вертолеты России,
России, все права
права защищены
16

17.

English Русский Rules