Геометрия. Способы решения задачи

1.

Задача
Через точку P, лежащую на
медиане CC1 треугольника ABC, проведены
прямые AA1 и BB1 (точки A1 и B1 лежат на
сторонах BC и CA соответственно). Докажите,
что A1B1 || AB.
-
Необходимо:
Предложить три способа решения данной задачи
Соотнести каждый из способов по методам
решения
Создать алгоритм решения по каждому из способов

2.

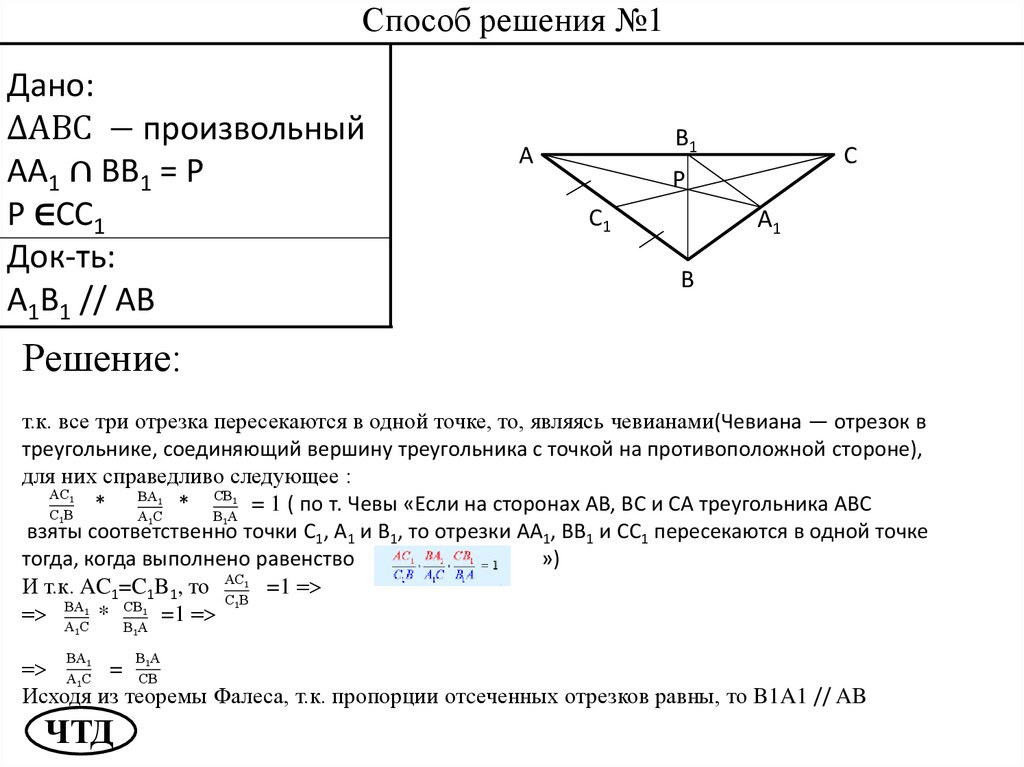
Способ решения №1
Дано:
∆ABC − произвольный
AA1 ∩ BB1 = P
P ∈СС1
Док-ть:
A1B1 // AB
B1
A
C
P
C1
A1
B
Решение:
т.к. все три отрезка пересекаются в одной точке, то, являясь чевианами(Чевиана — отрезок в
треугольнике, соединяющий вершину треугольника с точкой на противоположной стороне),
для них справедливо следующее :
AC1
CB1
BA1
*
*
= 1 ( по т. Чевы «Если на сторонах AB, BC и CA треугольника ABC
C1B
B1A
A1C
взяты соответственно точки С1, A1 и B1, то отрезки AA1, BB1 и CC1 пересекаются в одной точке
тогда, когда выполнено равенство
»)
AC1
И т.к. AC1=C1B1, то C B =1
1
CB1
1
BA
*
=1
AC
BA
1
BA
1
BA
1
A1C1 = CB
Исходя из теоремы Фалеса, т.к. пропорции отcеченных отрезков равны, то B1A1 // AB
ЧТД

3.

Алгоритм решения задачи №1:
АС1 ВА1 СВ1
*
*
= 1 (по теореме Чевы)
С1В А1С В1А
АС1
2)
=1 (АС1 = С1В)
С1В
ВА1 СВ1
ВА1 В1А
3)
*
=1 =>
=
А1С В1А
А1С
СВ1
1)
4) А1В1 ‖ АВ (по т.Фалеса)
Ч.Т.Д.

4.

Метод решения задачи №1:
При первом способе решения задачи
использовалась теорема Чевы

5.

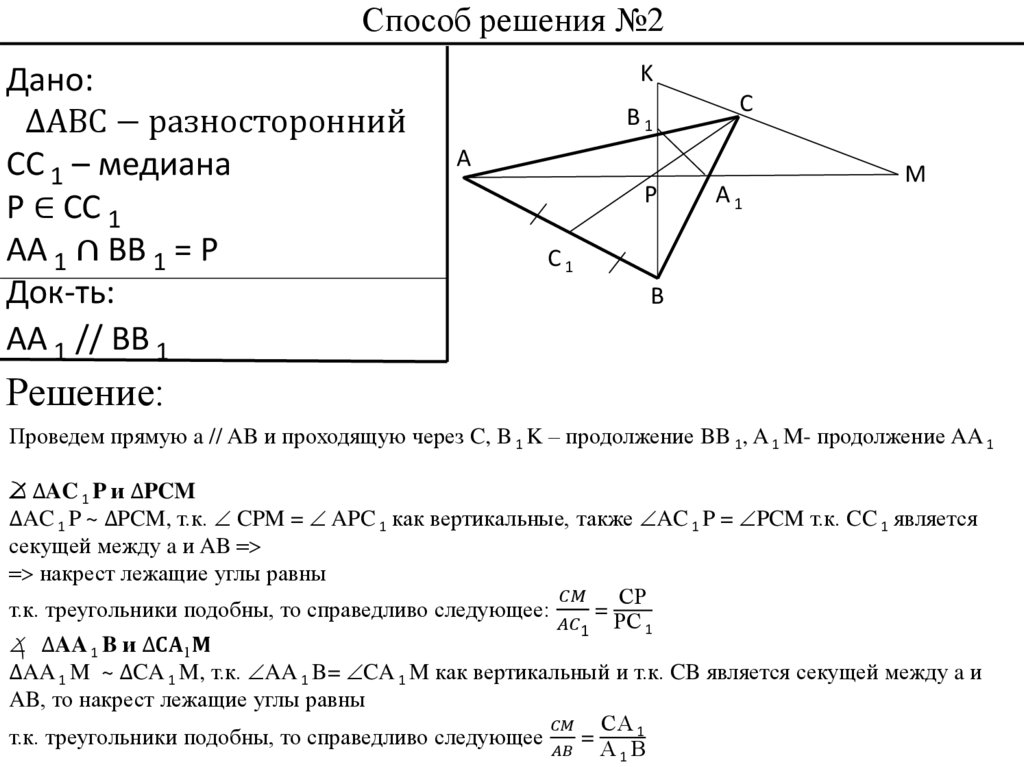
Способ решения №2
Дано:
∆ABC − разносторонний
СС 1 – медиана
P ∈ CC 1
AA 1 ∩ BB 1 = P
Док-ть:
AA 1 // BB 1
K
B1
C
A
P
A1
M
C1
B
Решение:
Проведем прямую a // AB и проходящую через C, B 1 K – продолжение BB 1, A 1 M- продолжение AA 1
∆AC 1 P и ∆PCM
∆AC 1 P ~ ∆PCM, т.к. CPM = APC 1 как вертикальные, также AC 1 P = PCM т.к. CC 1 является
секущей между a и AB
накрест лежащие углы равны