Задачи на обобщение изученного материала

1.

Упражнение 1

2.

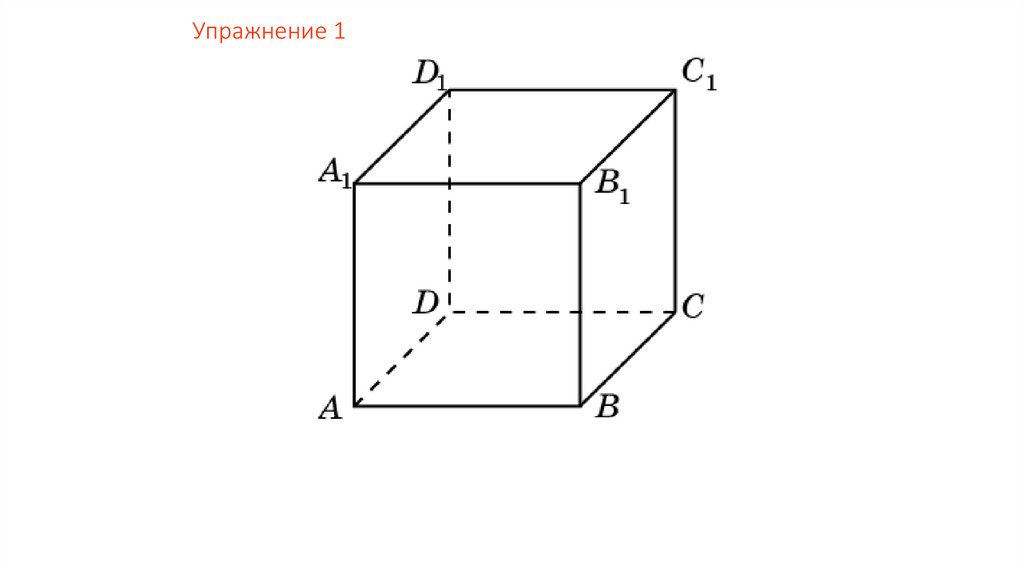
Упражнение 2
В кубе A…D1 укажите плоскости, проходящие через
вершины куба, параллельные прямой: а) AA1; б) AB1;
в) AC1.
Ответ: а) BCC1, CDD1, BDD1;
б) CDD1, DA1C1, BDC1;
в) нет.

3.

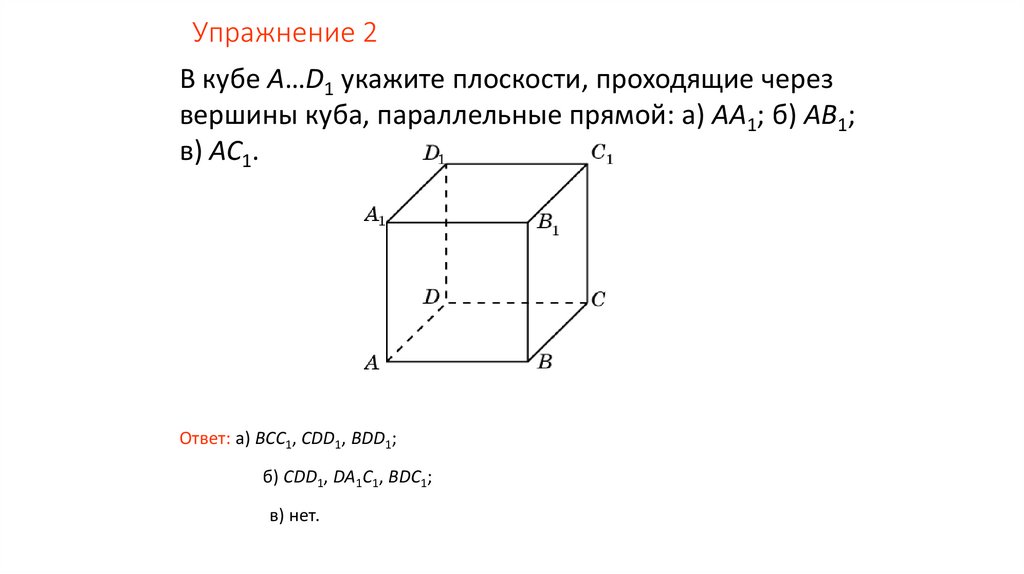
Упражнение 3
Докажите, что для куба ABCDA1B1C1D1 прямая AA1
параллельна плоскости BCC1.
Доказательство: Прямая AA1 параллельна прямой BB1,
лежащей в плоскости BCC1. Следовательно, прямая AA1
параллельна плоскости BCC1.

4.

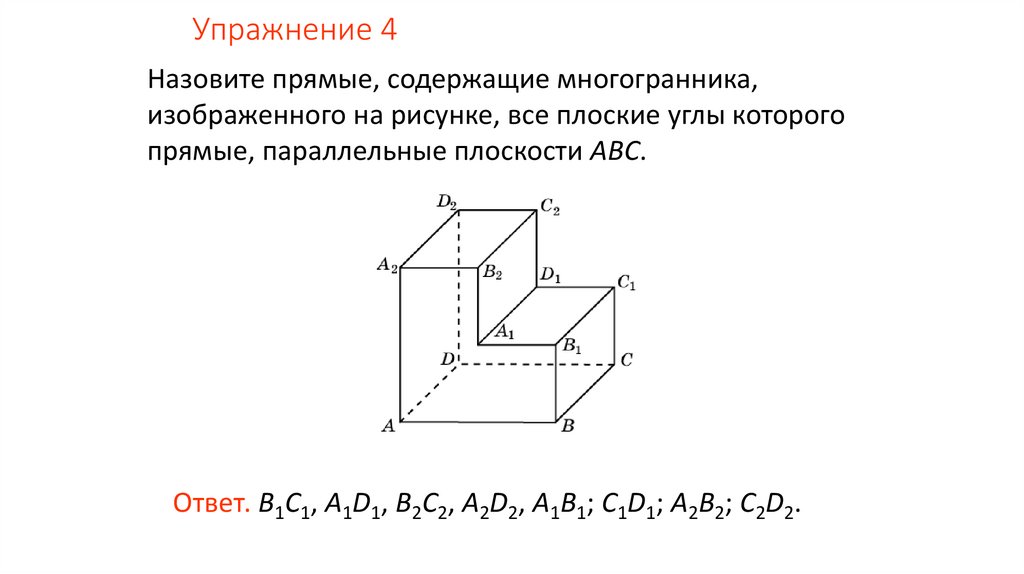
Упражнение 4
Назовите прямые, содержащие многогранника,
изображенного на рисунке, все плоские углы которого
прямые, параллельные плоскости ABC.
Ответ. B1C1, A1D1, B2C2, A2D2, A1B1; C1D1; A2B2; C2D2.

5.

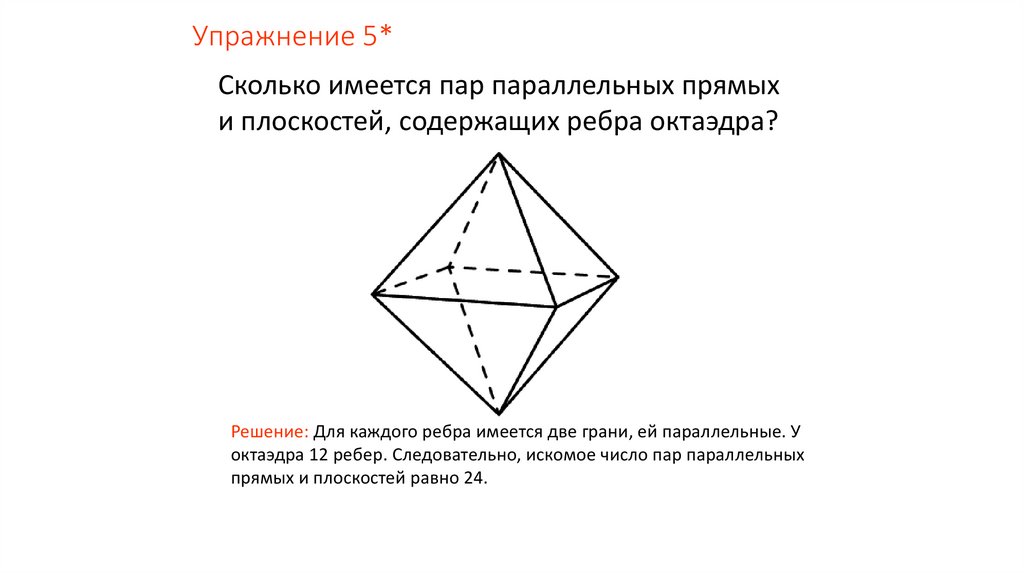
Упражнение 5*
Сколько имеется пар параллельных прямых
и плоскостей, содержащих ребра октаэдра?
Решение: Для каждого ребра имеется две грани, ей параллельные. У
октаэдра 12 ребер. Следовательно, искомое число пар параллельных
прямых и плоскостей равно 24.

6.

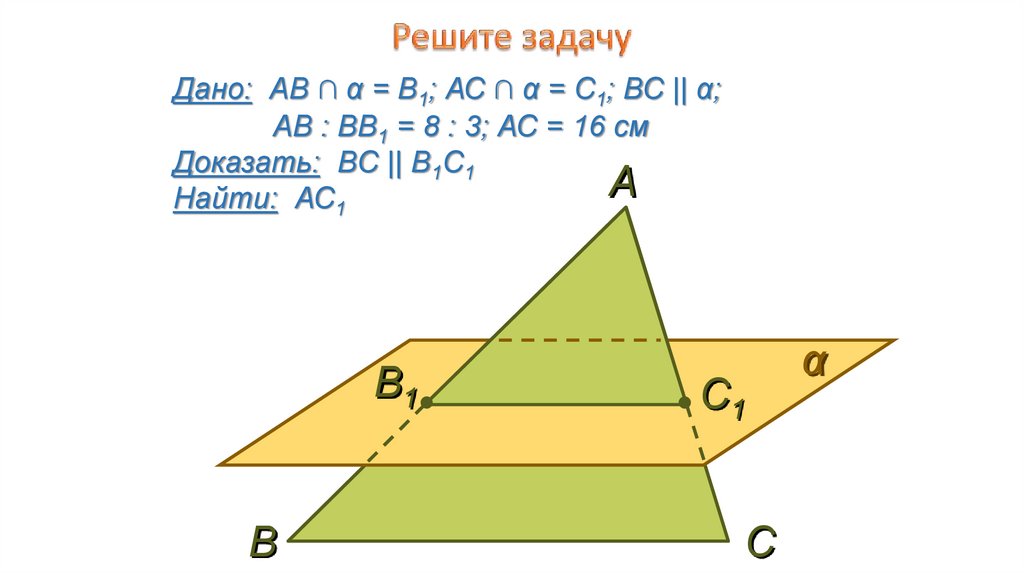
Дано: АВ ∩ α = В1; АС ∩ α = С1; ВС || α;
АВ : ВВ1 = 8 : 3; АС = 16 см
Доказать: ВC || B1С1
А
Найти: АС1
В1
В
С1
С
α

7.

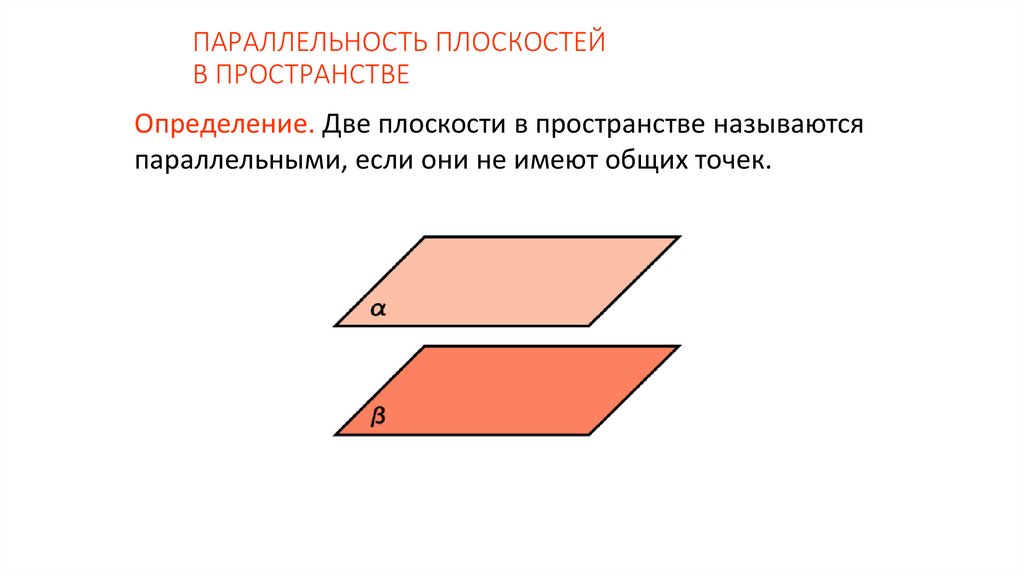
ПАРАЛЛЕЛЬНОСТЬ ПЛОСКОСТЕЙ
В ПРОСТРАНСТВЕ
Определение. Две плоскости в пространстве называются
параллельными, если они не имеют общих точек.

8.

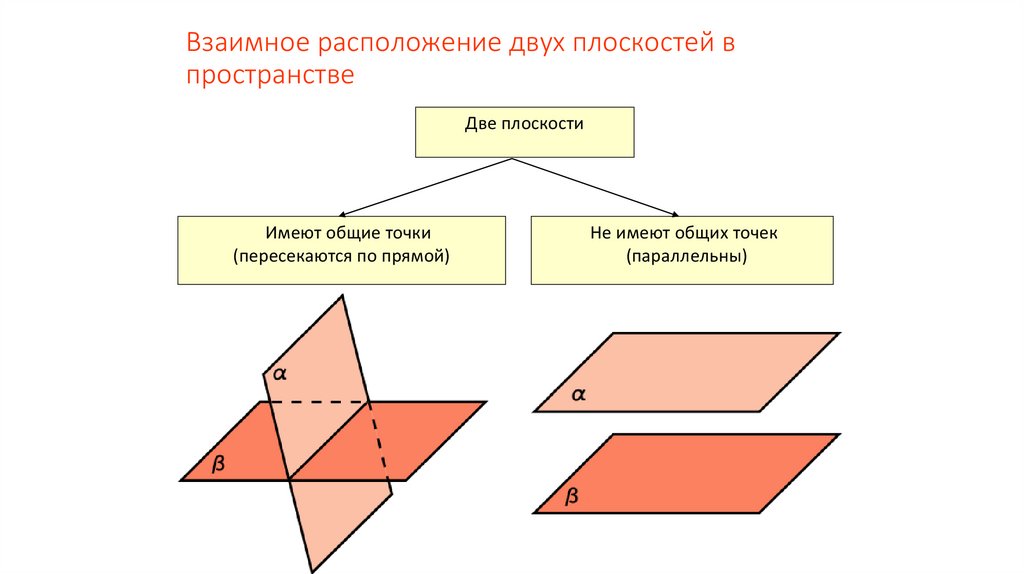
Взаимное расположение двух плоскостей в
пространстве
Две плоскости
Имеют общие точки
(пересекаются по прямой)
Не имеют общих точек
(параллельны)

9.

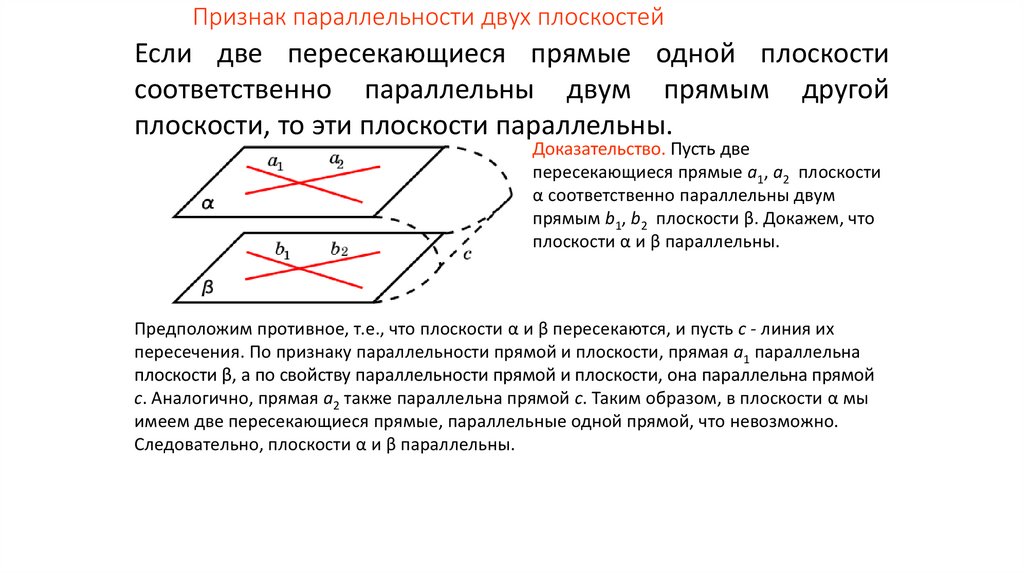
Признак параллельности двух плоскостей
Если две пересекающиеся прямые одной плоскости
соответственно параллельны двум прямым другой
плоскости, то эти плоскости параллельны.
Доказательство. Пусть две
пересекающиеся прямые a1, a2 плоскости
α соответственно параллельны двум
прямым b1, b2 плоскости β. Докажем, что
плоскости α и β параллельны.
Предположим противное, т.е., что плоскости α и β пересекаются, и пусть c - линия их
пересечения. По признаку параллельности прямой и плоскости, прямая a1 параллельна
плоскости β, а по свойству параллельности прямой и плоскости, она параллельна прямой
c. Аналогично, прямая a2 также параллельна прямой c. Таким образом, в плоскости α мы
имеем две пересекающиеся прямые, параллельные одной прямой, что невозможно.
Следовательно, плоскости α и β параллельны.

10.

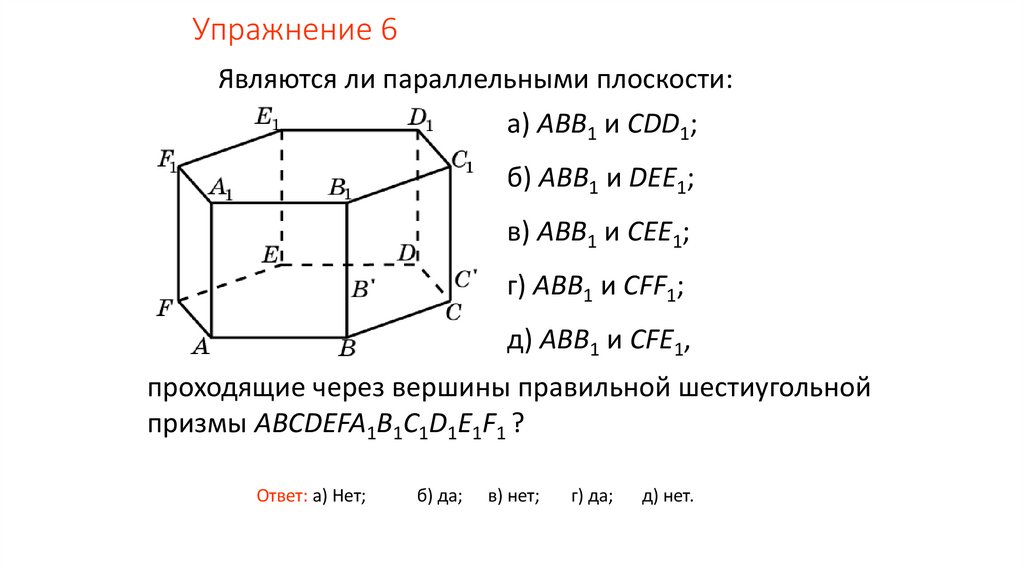
Упражнение 6
Являются ли параллельными плоскости:
а) ABB1 и CDD1;
б) ABB1 и DEE1;
в) ABB1 и CEE1;
г) ABB1 и CFF1;
д) ABB1 и CFE1,
проходящие через вершины правильной шестиугольной
призмы ABCDEFA1B1C1D1E1F1 ?
Ответ: а) Нет;
б) да;
в) нет;
г) да;
д) нет.

11.

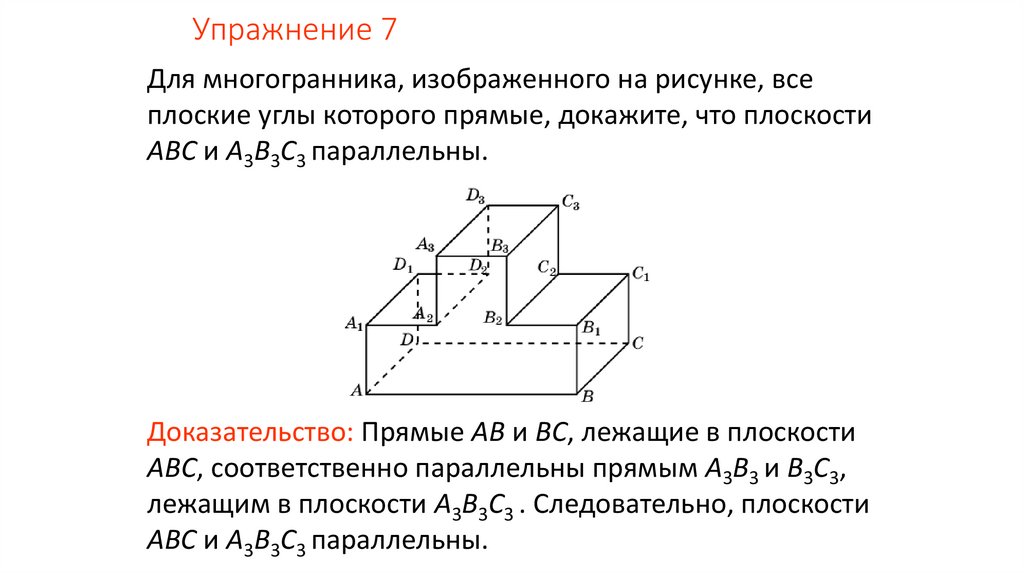
Упражнение 7
Для многогранника, изображенного на рисунке, все
плоские углы которого прямые, докажите, что плоскости
ABC и A3B3C3 параллельны.
Доказательство: Прямые AB и BC, лежащие в плоскости
ABC, соответственно параллельны прямым A3B3 и B3C3,
лежащим в плоскости A3B3C3 . Следовательно, плоскости
ABC и A3B3C3 параллельны.