Построение сечения. Решение задачи

1.

ЗАДАЧА
Текст задачи
Дано
Построение сечения
Решение задачи
Теоретическое обоснование

2.

Основанием прямой призмы является
прямоугольный треугольник с острым
углом φ. Через катет, противолежащий
этому углу, и через противоположную
этому катету вершину основания
проведено сечение, составляющее угол
с плоскостью основания. Найти
отношение площади боковой поверхности
призмы к площади сечения.
В начало

3.

B1
A1
C1
B
A
Дано:
ABCA1B1C1 – прямая призма
∆ABC – прямоугольный
‫ے‬ACB=90ْ
‫ے‬ABC=φ
‫(ے‬плоскостью сеч., (ABC))=θ
Сечение плоскостью α через
катет, противолежащий углу
φ, и через противоположную
этому катету вершину
Найти: Sбок.пов.пр/Sсеч
C
В начало

4.

B1
A1
C1
B
A
C
Какое сечение нам надо
построить? (Нам надо
построить сечение
плоскостью α через катет,
противолежащий углу φ, и
через противоположную
этому катету вершину.
‫ے‬ABC=φ, поэтому
сечение будет проходить
через катет AC.
Противолежащая катету
AC вершина - B1.
Следовательно, нам надо
провести сечение через
катет AC и вершину B1)
В начало

5.

B1
A1
C1
B
A
Посмотрите на чертеж. Есть
ли грань, которой
принадлежат две точки
сечения? (Да, в плоскости
(CC1B) расположены точки
сечения C и B1). Мы их
можем соединить? (Да).
Еще есть такие грани? (Да, в
плоскости (AA1B) тоже две
точки сечения: A и B1. Их
можно соединить).
Почему сечение AB1C –
искомое? (так как катет AC
и вершина B лежат в
плоскости сечения).
C
В начало

6.

B1
A1
C1
B
A
C
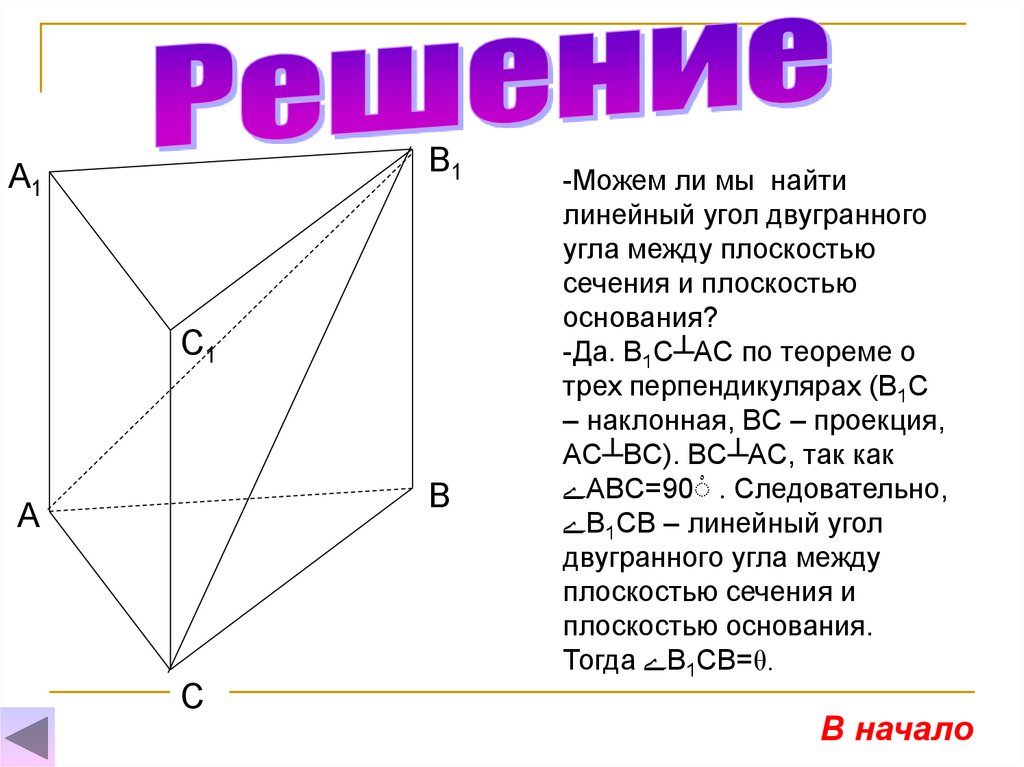
-Можем ли мы найти
линейный угол двугранного
угла между плоскостью
сечения и плоскостью
основания?
-Да. B1C┴AC по теореме о
трех перпендикулярах (B1C
– наклонная, BC – проекция,
AC┴BC). BC┴AC, так как
‫ے‬ABC=90ْ . Следовательно,
‫ے‬B1CB – линейный угол
двугранного угла между
плоскостью сечения и
плоскостью основания.
Тогда ‫ے‬B1CB=θ.
В начало

7.

B1
A1
C1
B
A
C
-Как мы можем найти площадь
сечения?
-Можно найти площадь
ортогональной проекции и
разделить ее на косинус угла
между проекцией и сечением.
-Нам что-нибудь из этого
известно?
-Да, нам известен угол между
проекцией и сечением, так как
∆ABC – ортогональная
проекция ∆AB1C.
-Что мы можем найти?
-Если принять сторону BC за x,
то можем найти площадь
∆AB1C.
В начало

8.

B1
A1
C1
B
A
C
-Как найти площадь ∆ABC?
-Так как ∆ABC – прямоугольный,
то AC=BC*tg‫ے‬ABC=x*tgφ. Тогда:
S∆ABC=1/2*AC*BC=1/2*x*x*tgφ
S∆ABC=1/2*x2*tgφ.
-Теперь мы можем найти
площадь сечения?
-Да.
Sсеч=S∆ABC/cosθ
Sсеч =1/2*x2*tgφ/cosθ
-Чему равна площадь боковой
поверхности призмы?
-Сумме площадей всех ее
боковых граней.
-Мы можем найти площадь
боковой поверхности призмы?
-Да.
В начало

9.

B1 Sб.пов.пр.=SAA C C+SAA B B+SCC B B=
1
A1
C1
B
A
C
1
1 1
1 1
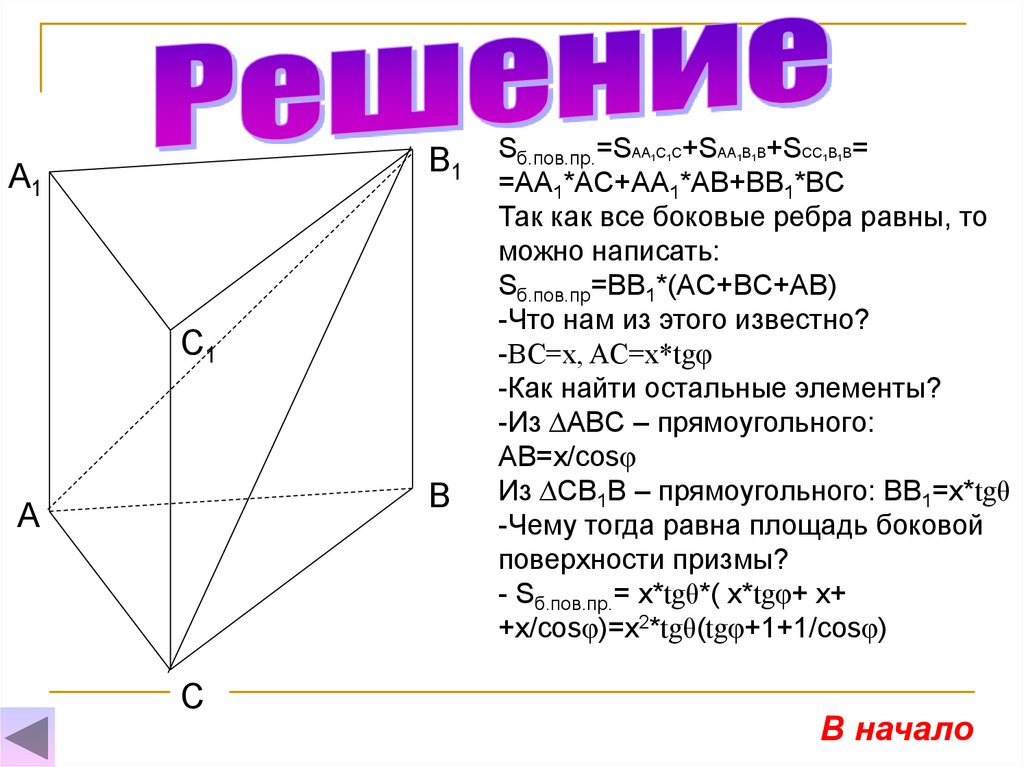
=AA1*AC+AA1*AB+BB1*BC
Так как все боковые ребра равны, то
можно написать:
Sб.пов.пр=BB1*(AC+BC+AB)
-Что нам из этого известно?
-BC=x, AC=x*tgφ
-Как найти остальные элементы?
-Из ∆ABC – прямоугольного:
AB=x/cosφ
Из ∆CB1B – прямоугольного: BB1=x*tgθ
-Чему тогда равна площадь боковой
поверхности призмы?
- Sб.пов.пр.= x*tgθ*( x*tgφ+ x+
+x/cosφ)=x2*tgθ(tgφ+1+1/cosφ)
В начало

10.

B1
A1
C1
B
A
C
-Чему тогда равно
отношение площади
боковой поверхности
призмы к площади сечения?
-Sб.пов.пр./Sсеч=(x2*tgθ*(tgφ+1+
+1/cosφ)*cosθ)/(1/2*x2*tgφ)=
=2*sinθ*(1+1/tgφ+1/sinφ)=
=2*sinθ*(1+ctgφ+1/sinφ)=
=2*sinθ*(sinφ+cosφ+1)/sinφ
-Что напишем в ответе?
-Ответ:
Sб.пов.пр./Sсеч=2*sinθ*(sinφ+
+cosφ+1)/sinφ
В начало

11.

1) Через любые две точки можно провести
прямую и притом только одну.
2) Если две различные плоскости имеют общую
точку, то они пересекаются по прямой,
проходящей через эту точку.
В начало