Similar presentations:
Тела вращения. Сфера и шар
1. Тела вращения Сфера и шар
2.
Сфера – бесконечное множество точек пространства, равноудалённых от заданнойточки на заданное расстояние. Заданная точка – центр сферы, заданное расстояние –
радиус сферы.
Шар – бесконечное множество точек пространства, удалённых от заданной точки на
расстояние, не превышающее заданного. Заданная точка – центр шара, заданное
расстояние – радиус шара.
О
Точка О – центр сферы(шара), R – радиус сферы(шара).
3.
Радиусом называется любой отрезок,соединяющий центр шара с точкой шаровой
поверхности.
O
Диаметром называется отрезок,
соединяющий две точки шаровой
поверхности и проходящий через
центр шара.
Концы любого диаметра называются
диаметрально противоположными
точками шара.
Хордой называется отрезок, соединяющий
две точки шаровой поверхности.
4.
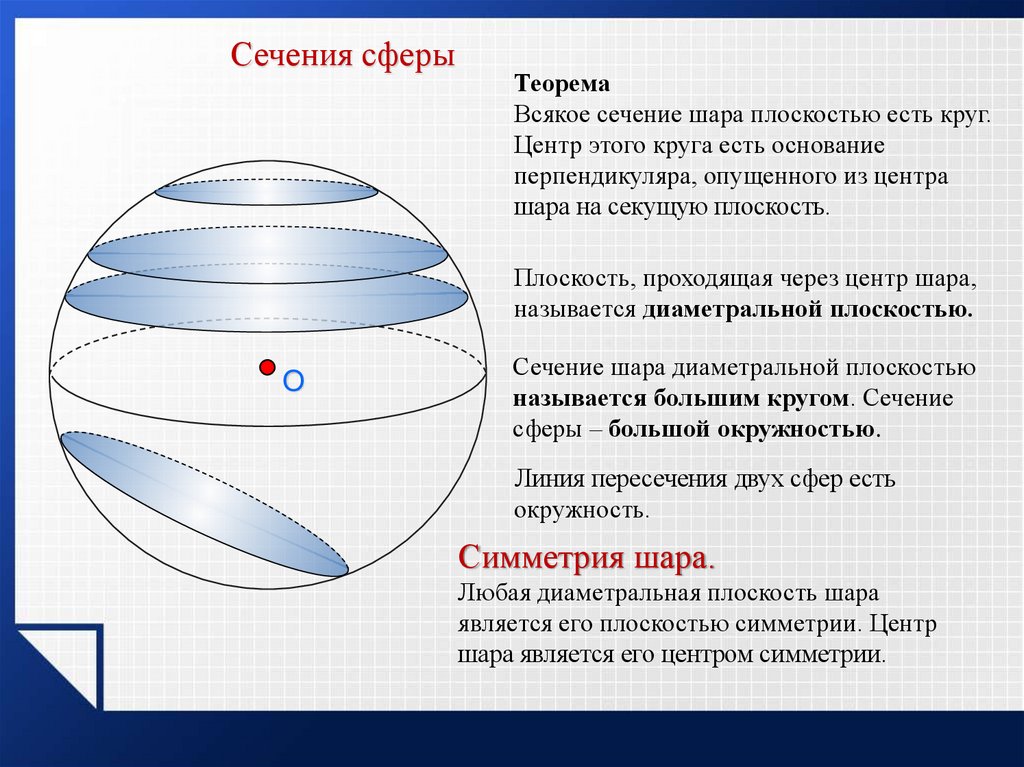
Сечения сферыТеорема
Всякое сечение шара плоскостью есть круг.
Центр этого круга есть основание
перпендикуляра, опущенного из центра
шара на секущую плоскость.
Плоскость, проходящая через центр шара,
называется диаметральной плоскостью.
O
Сечение шара диаметральной плоскостью
называется большим кругом. Сечение
сферы – большой окружностью.
Линия пересечения двух сфер есть
окружность.
Симметрия шара.
Любая диаметральная плоскость шара
является его плоскостью симметрии. Центр
шара является его центром симметрии.
5.
Для изображения сферы(шара) нужно: 1) начертить окружность;2) показать центральное сечение (больший круг);
A
O
B
6.
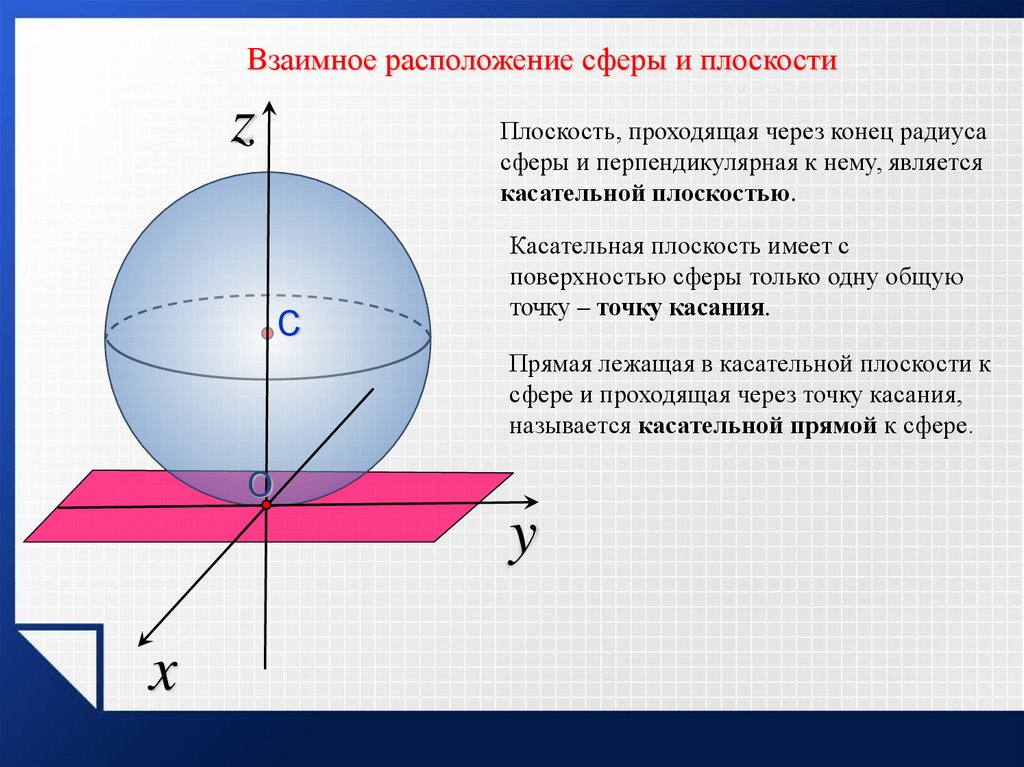
Взаимное расположение сферы и плоскостиz
Плоскость, проходящая через конец радиуса
сферы и перпендикулярная к нему, является
касательной плоскостью.
С
Касательная плоскость имеет с
поверхностью сферы только одну общую
точку – точку касания.
Прямая лежащая в касательной плоскости к
сфере и проходящая через точку касания,
называется касательной прямой к сфере.
О
y
x
7.
ПланиметрияСтереометрия
Свойство касательной.
В
А
r
О
А
r
О
АВ - касат ельная
АВ r
касательная пл.
r
Касательная к окружности
перпендикулярна к радиусу,
проведенному в точку касания.
Радиус сферы, проведенный в
точку касания сферы и плоскости,
перпендикулярен к касательной
плоскости.
8.
ПланиметрияСтереометрия
Признак касательной.
А касательная
В
r
О
А
касательная пл.
r
О
АВ r
АВ - касат ельная
r
касательная пл.
Если прямая проходит через конец
радиуса, лежащий на окружности, и
перпендикулярна к этому радиусу, то
она является касательной.
Если радиус сферы перпендикулярен
к плоскости, проходящей через его
конец, лежащий на сфере, то эта
плоскость является касательно к
сфере.
9. Описанные и вписанные шары
10. Описанные шары
Шар называется описанным околомногогранника, а многогранник
вписанным в этот шар, если все
вершины многогранника лежат на
поверхности шара.
Чтобы около многогранника можно
было описать сферу, необходимо и
достаточно,
чтобы каждая его грань была
многоугольником, около которого
можно было описать окружность.
11. Многогранники, вписанные в шар
Центр описанного около многогранника шараесть точка, равноудаленная от всех его вершин.
Геометрическое место точек, равноудаленных
от всех вершин какой-либо грани, есть прямая,
перпендикулярная к плоскости грани и
проходящая через центр описанной около нее
окружности.
Геометрическое место точек, равноудаленных
от концов какой-либо ребра, есть плоскость,
перпендикулярная ребру и проходящая через
его середину. Значит, центр шара принадлежит
одновременно двум указанным
геометрическим
местам
12.
Многогранники и тела вращения,вписанные в шар
13. Вписанные шары
Шар называетсявписанным в
многогранник, а
многогранник- описанным
вокруг шара,
если плоскости всех
граней касаются шара.
14. Вписанные шары
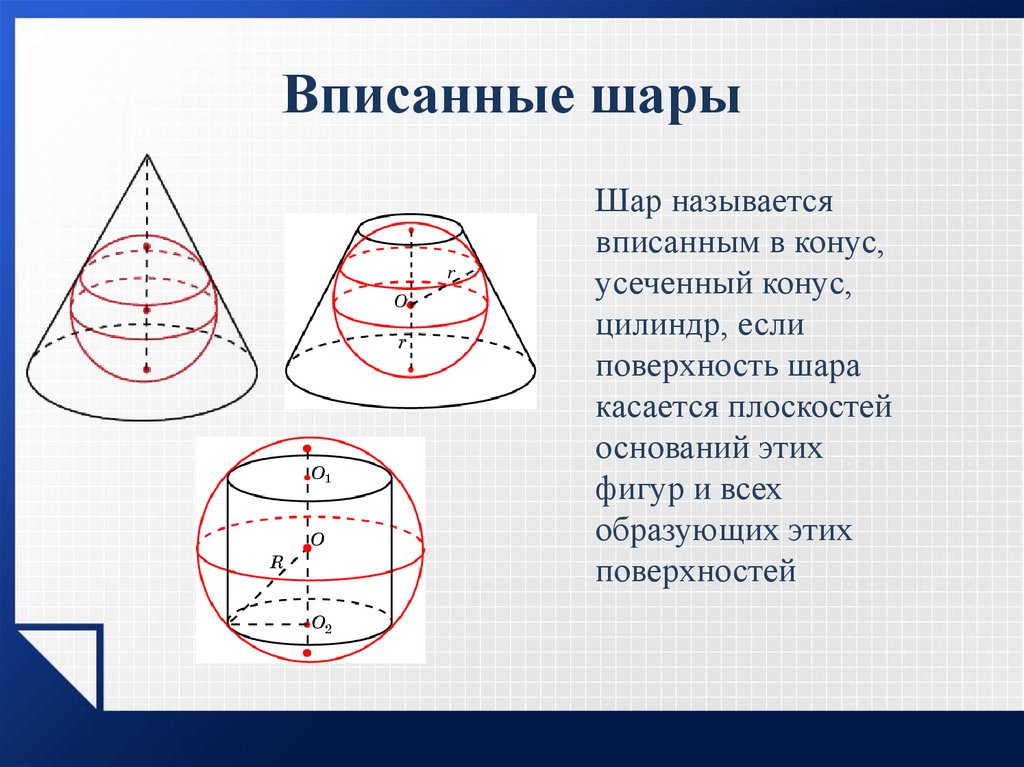
Шар называетсявписанным в конус,
усеченный конус,
цилиндр, если
поверхность шара
касается плоскостей
оснований этих
фигур и всех
образующих этих
поверхностей
15. Части сферы и шара.
17 февраля 2023 г.16.
Шаровой(сферический) сегмент.Шаровым сегментом называется часть шара, отсекаемая от него
плоскостью.
17.
Шаровой сегмент ограничен:1) частью сферы, которая называется сегментной поверхностью;
2)кругом, который называется основанием шарового сегмента.
18.
Радиус основания шаровогосегмента (сегментной поверхности)
Высота шарового сегмента
(сегментной поверхности)
Высотой шарового сегмента (сегментной поверхности) называется отрезок
радиуса шара (сферы) перпендикулярного основанию сегмента, принадлежащий
шаровому сегменту.
19.
Шаровой(сферический) слой(пояс).Часть шара, расположенная между двумя параллельными плоскостями,
пересекающими шар, называется шаровым поясом (слоем).
Часть сферы, ограниченная этими плоскостями, называется сферическим
поясом (слоем).
20.
Поверхность шарового слоя состоит из двух кругов (оснований) и сферическогопояса.
Высотой шарового слоя называется отрезок диаметра сферы, перпендикулярного
основаниям, заключенный между этими основаниями.
Высотой сферического пояса называется высота соответствующего
шарового слоя.
21.
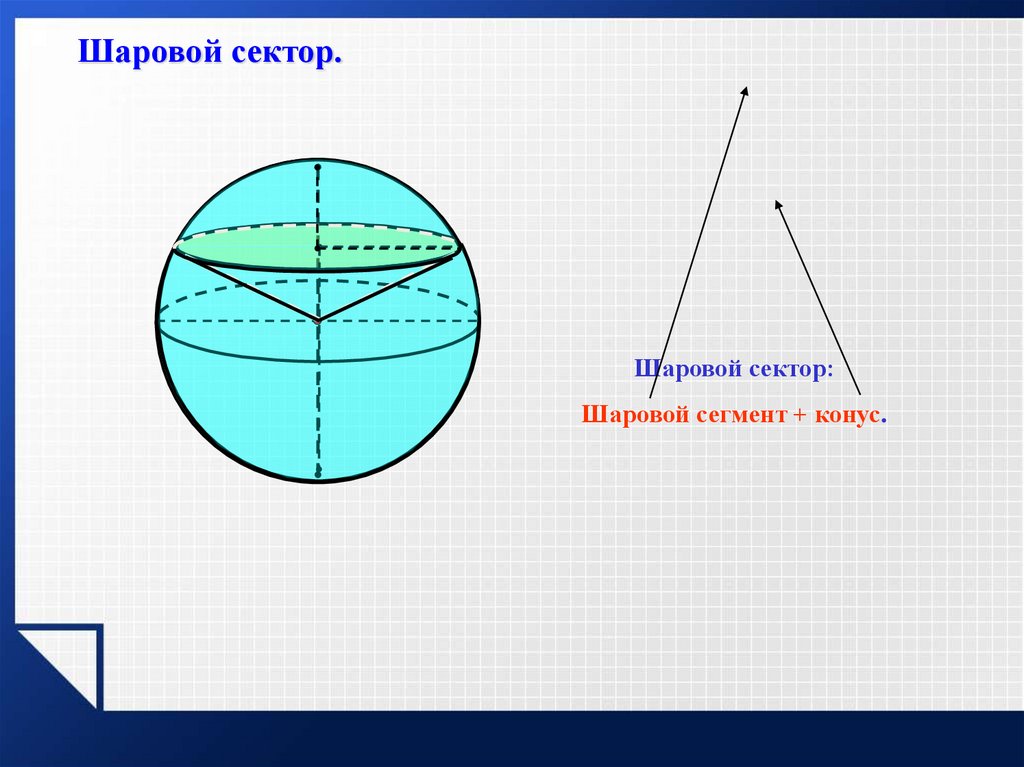
Шаровой сектор.Шаровой сектор:
Шаровой сегмент + конус.
22.
Шаровым сектором называется фигура, полученная при вращении круговогосектора с острым углом вокруг прямой, содержащий один из ограничивающий
сектор радиусов.
23.
Шаршар
R – радиус сферы (шара)
шаровой сегмент
R – радиус шара,
h – высота шарового сегмента.
шаровой сектор
R – радиус шара,
h – высота шарового сегмента
r – радиус основания
шарового сегмента



















 mathematics
mathematics








