Длины дуг кривых

1.

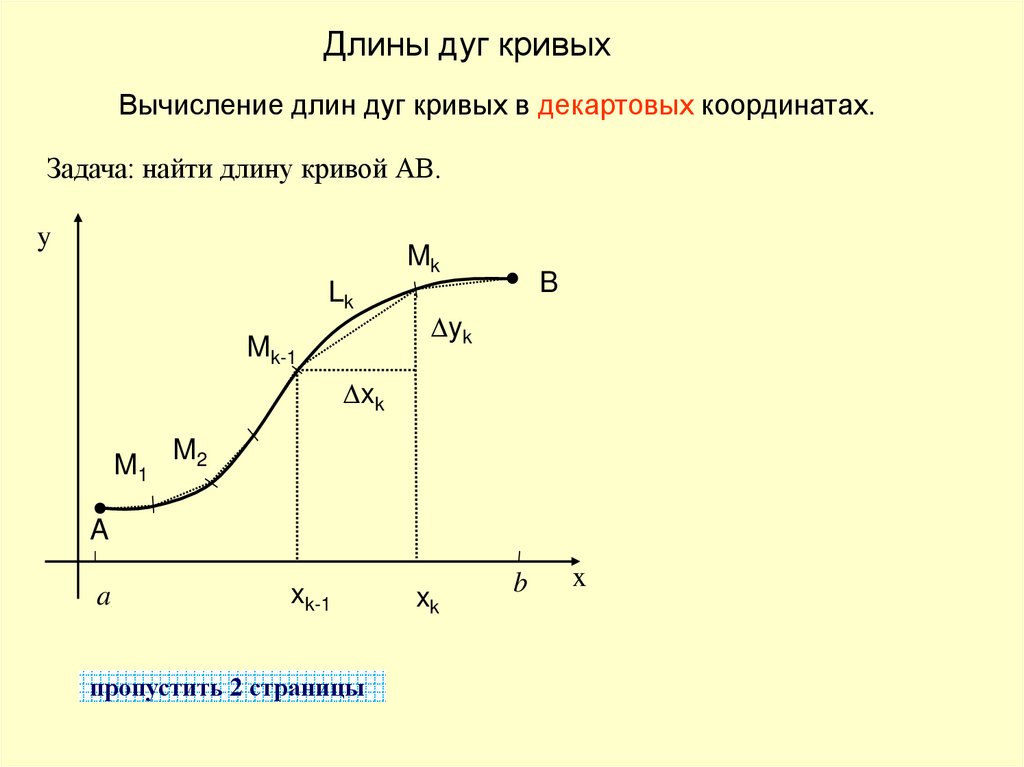
Длины дуг кривых
Вычисление длин дуг кривых в декартовых координатах.
Задача: найти длину кривой АВ.
y
Mk
Lk
Mk-1
B
Dyk
Dxk
M1
M2
A
a
xk-1
пропустить 2 страницы
xk
b
x

2.

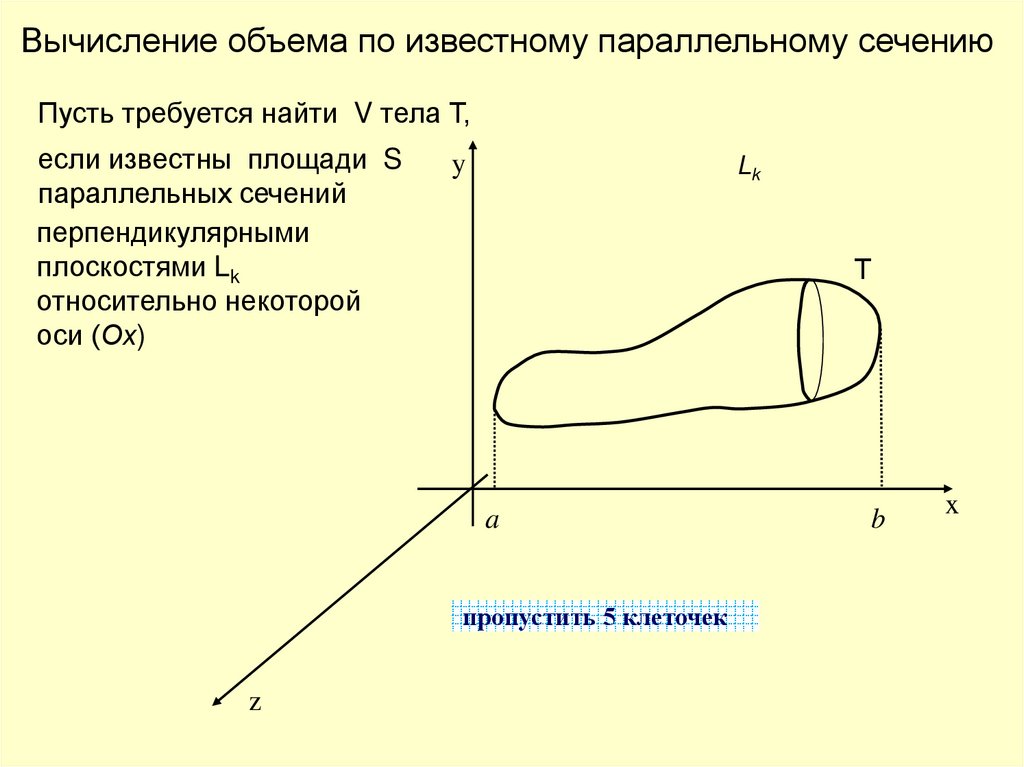
Вычисление объема по известному параллельному сечению
Пусть требуется найти V тела Т,
если известны площади S
параллельных сечений
перпендикулярными
плоскостями Lk
относительно некоторой
оси (Ох)
y
Lk
Т
a
пропустить 5 клеточек
z
b
x

3.

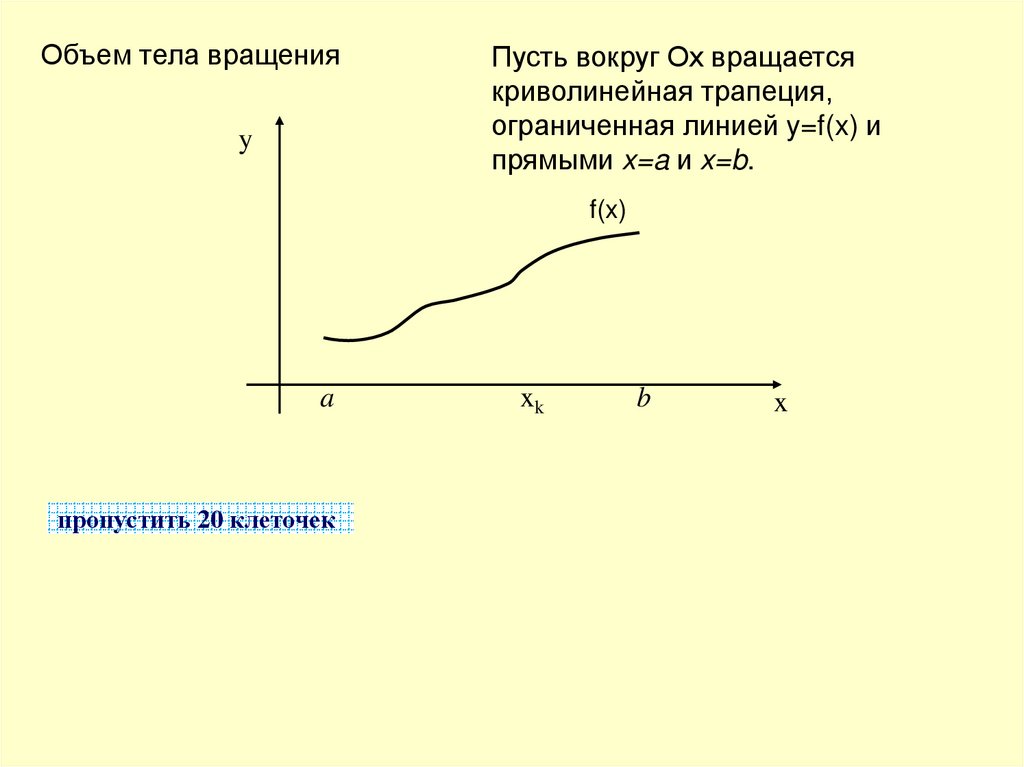
Объем тела вращения
y
Пусть вокруг Ох вращается
криволинейная трапеция,
ограниченная линией y=f(x) и
прямыми x=a и x=b.
f(x)
a
пропустить 20 клеточек
xk
b
x

4.

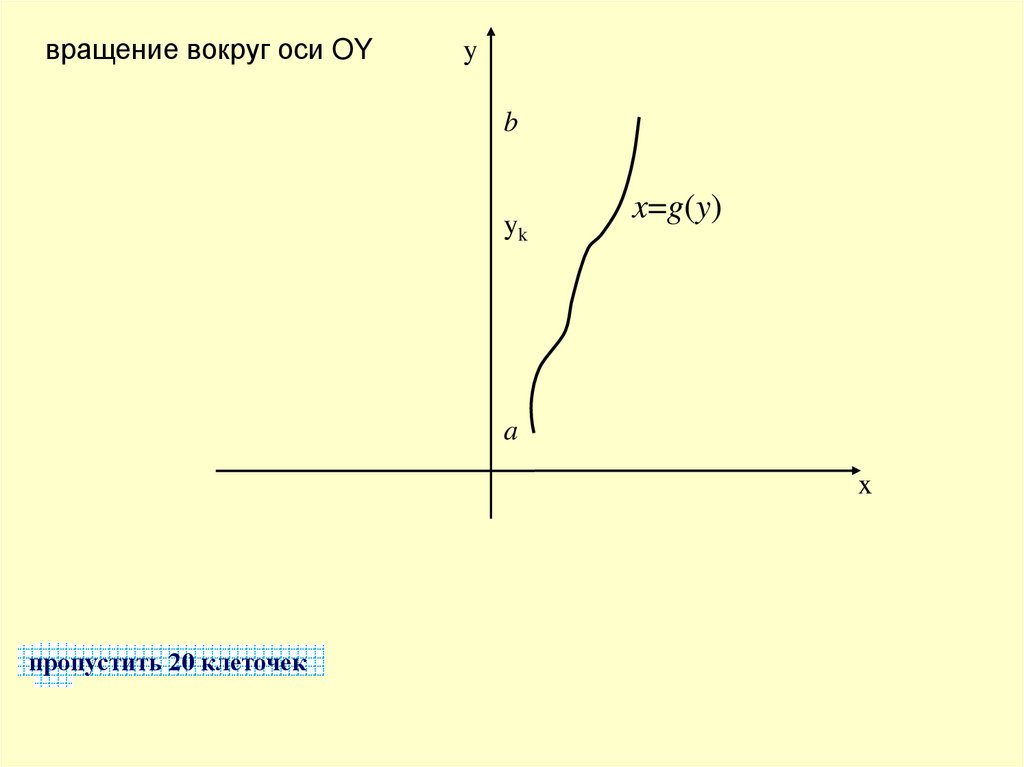
вращение вокруг оси OY
y
b
yk
x=g(y)
a
x
пропустить 20 клеточек

5.

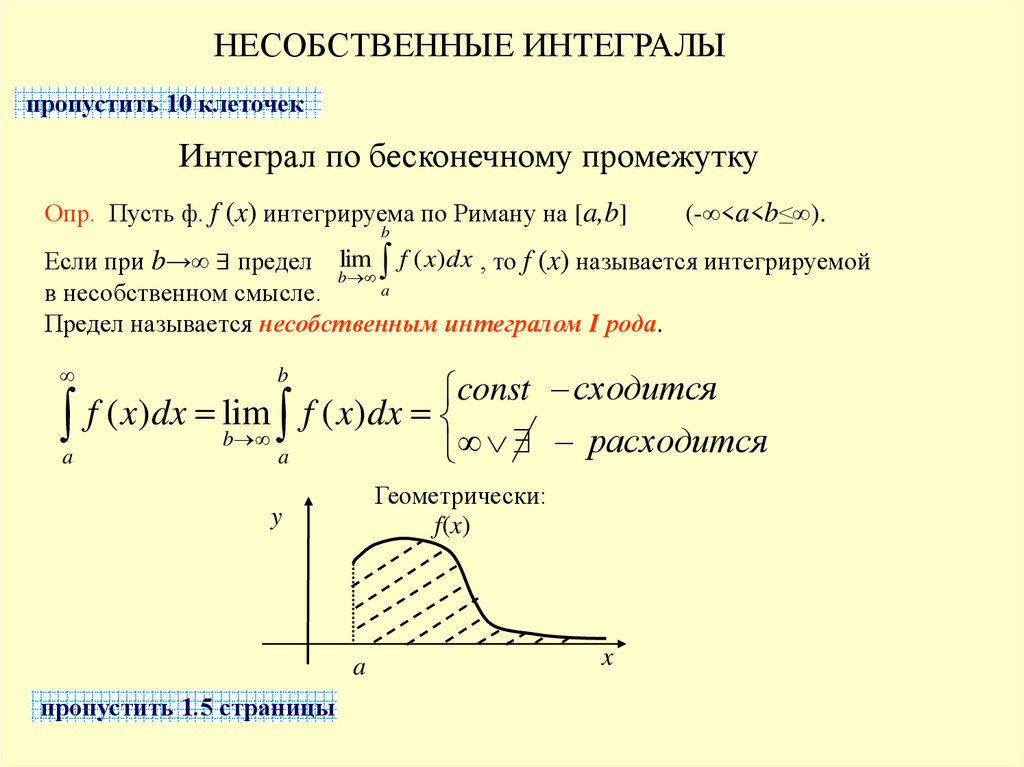
НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
пропустить 10 клеточек
Интеграл по бесконечному промежутку
Опр. Пусть ф. f (x) интегрируема по Риману на [a,b]
b
(-∞<a<b≤∞).
Если при b→∞ ∃ предел lim f ( x)dx , то f (x) называется интегрируемой
b
a
в несобственном смысле.
Предел называется несобственным интегралом I рода.
const сходится
f ( x)dx
a f ( x)dx lim
b
расходится
a
b
Геометрически:
f(x)
y
a
пропустить 1.5 страницы
x

6.

Теорема . (Признак сравнения)
Пусть функции f(x) и g(x) интегрируемы на [a, ∞)
и 0 ≤ f(x) ≤ g(x) ∀ x ∈ [a, ∞). Тогда
а) если
g ( x)dx – сходится, то
f ( x)dx
a
a
б) если
тоже сходится.
f ( x)dx – расходится, то
a
пропустить 1 страницу
a
g ( x)dx
тоже расходится.

7.

Теорема . (Предельный признак сравнения)
Пусть функции
f(x) и g(x) неотрицательны и интегрируемы на [a,∞),
g(x) ≠ 0 ∀x ∈ [a, ∞) и
а) если
f ( x)
lim
k . Тогда
x g ( x)
g ( x)dx сходится и 0 ≤ k < ∞,
то
a
тоже
сходится.
a
б) если
f ( x)dx
g ( x)dx расходится и 0 < k ≤ ∞,
a
в) если f(x) ~ g(x) при x→∞, то
то
g ( x)dxи
f ( x)dx тоже
a
f ( x)dx
a
a
ведут себя одинаково в смысле сходимости. (без доказательства)
расходится