Similar presentations:
Теория оптимального приема сигналов
1.
Теория оптимального приема сигналовПриемники сигналов, обеспечивающие минимальные искажения сообщения
при приеме сигналов в условиях помех, называются оптимальными или
идеальными.
В зависимости от назначения приемника критерии оптимальности и количественные характеристики искажений могут быть разными.
В теории оптимального приема обобщенным критерием качества является
критерий «среднего риска» R.
R I ( , ) ( , )d d min
,
(1)
I ( , ) - функция потерь (цена за ошибку)
( , ) - совместная плотность распределения вероятностей ,
( , ) ( ) ( / ) (2)
( ) - плотность распределения вероятностей (ПРВ) оценки сообщения
( / ) - условная плотность распределения вероятностей сообщения
2
2. Теория оптимального приема сигналов
Правило оценки принятого сообщения может быть регулярным илинерегулярным.
Регулярный прием – это такое решение, при котором каждой принятой
.
реализации y (t ) соответствует определенное решение
Нерегулярное решение – это такое решение, при котором оценка
связана с y (t ) статистической зависимостью, т.е. оценка сообщения
происходит с определенной вероятностью.
R I ( , ) ( y ) ( / y )dyd (3)
y ,
Rус I ( , ) ( / y )d - условный риск
(4)
R Rус ( y )dy
(5)
y
( y ) - априорная плотность распределения вероятностей y
( / y ) - апостериорная плотность распределения вероятностей
3
3.
Упрощенная структурная схема оптимального приемникаy (t )
( / y )
ОФУ
РУ
ОФУ – оптимальное
фильтрующее устройство
РУ – решающее устройство
Алгоритм разработки структурной схемы оптимального приемника:
1) выбор функции потерь (для непрерывных сообщений – это минимум ( )
для дискретных – это минимум вероятности ошибки;
2) вычисление апостериорной плотности распределения вероятностей (АПРВ)
для определения максимума ( / y ) ,т.е. наиболее вероятного значения;
3) разработка алгоритма работы решающего устройства.
Основная задача оптимального приемника – вычисление ( / y ) для всех
переданных сообщений и принятие решения в соответствии с выбранной
функцией потерь.
4
2
4.
Определение АПРВ1
( / y )
( ) ( y / )
( y)
(6)
( y ) , ( ) - априорные плотности распределения
вероятностей соответственно входного сигнала
и сообщения.
( y / )
- функция правдоподобия.
ПРВ входного сигнала и сообщения распределены по равномерному закону.
1
( y)
y
y
1
( )
- динамический диапазон изменения сообщения.
- динамический диапазон изменения входного
сигнала.
( / y ) K ( y / )
(7)
5
5.
Многомерная функция правдоподобия полностью известных сигналов(n)
y (t ) S ( , t ) n(t )
(8)
- многомерная плотность распределения вероятностей помехи
(гауссовский закон).
( y / ) n [ y(t ) S ( , t )]
(9)
T - интервал времени существования сигнала;
t
1
- интервал дискретизации входного сигнала;
2 Fэ
H
T
- количество выборок.
t
n (nh )
h
n2 N 0 2 Fэ
2
n
1
exp( h 2 )
2 n
2 n2
(11)
- дисперсия помехи.
nh yh Sh ( )
(10)
(12)
6
6.
77.
Определение ФРВДля одномерной ФРВ
P(t1 ) [ X (t1 ) x1 ]
Для многомерной ФРВ
P(t1 ) [ X (t1 ) x2 ]
P X (t1 ) x1 ; X (t 2 ) x2 ,.... X (t n ) xn
P(t1 ) [ X (t1 ) xn ]
Значения x1 , x2 ,.......xn меняются во всем диапазоне
изменений случайного процесса (флуктуационнойX (t )
n(t )сигнала
помехи
или первичного
).
(t )
8
8.
2n
( y / ) nh [ y h S h ( )] (
) H exp( h 2 ) (13)
2 n
h 1
h 1
2 n2
H
1
H
exp суммы = произведению exp (после
подстановки (14) в (13) получили (15))
2
(14)
h
h
nh2 [ y h S h ( )] 2 y h2 2 y h S ( ) S ( )
y h2
y h S h ( )
S h2 ( )
( y / ) K1 exp( 2 ) exp(
) exp(
) (15)
2
2
2 n
n
2 n
h 1
H
произведение exp = exp суммы (см. (16)
К2
H
( y / ) K 2 exp(
h 1
y h S h ( )
2
n
H
) K 2 exp (
h 1
( y / ) K 2 exp q( )
n ( y / ) nK 2 q( )
y h S h ( )
2
n
) (16)
(17)
(18)
9
9.
Структурная схема оптимального (корреляционного) приемникаразличения дискретных сигналов (полностью известных)
t
q( 1 )
0
S1 (t )
y (t )
t
q( 2 )
РУ
0
S 2 (t )
Оценка сообщения
t
q ( n )
дмЗ
0
S n (t )
n - количество сообщений или первичных сигналов (позиционность кода);
t
- длительность элементарного импульса.
10
10.
Коэффициент взаимной корреляцииq ( )
1
2
n
H
H
h 1
h 1
q ( )
[ S h ( ) S oh ( ) nh S oh ( )] g ( ) h( ) (19)
При непрерывном наблюдении выражение для
t
случайная
функция
q ( ) изменится:
t
2
q ( )
[ S ( , t ) S ( 0 , t )dt n(t ) S ( 0 , t )dt ] g ( ) h( )(20)
неслучайная
N0 0
0
функция
E
2 E
2
2
(22)
g ( )
rc ( , 0 ) 2 rc ( , 0 ) (21)
на входе пр-ка N 0
N0
t
t
1
rc ( , 0 )
S ( , t ) S ( 0 , t )dt (24)
E S 2 ( , t )dt (23)
E 0
0
2
вых
g 2 ( ) max
h2
(2 )
2
2
2 2
2 2
(25)
11
11.
Параметры сигналов-переносчиковПараметры сигналов-переносчиков делятся на
информационные и неинформационные.
Информационные параметры: амплитуда синусоидального
сигнала (АМн); частота синусоидального сигнала (ЧМн); фаза
синусоидального сигнала (ФМн, ОФМн).
Неинформационные параметры делятся на существенные и
несущественные.
Существенные неинформационные параметры синусоидального
сигнала: частота сигнала (АМн, ФМн, ОФМн); время прихода
элементарного импульса и его длительность; начальная фаза для
когерентного приема (ЧМн).
Несущественные неинформационные параметры
синусоидального сигнала: амплитуда (ЧМн, ФМн, ОФМн);
начальная фаза для некогерентного приема (АМн, ЧМн, ОФМн).
Для приема сигналов со случайными несущественными
параметрами используется квадратурный приемник. Для приема
сигналов со случайными существенными параметрами
используется приемник с синхронизацией: высокочастотной и
тактовой.
12
12.
Оптимальные приемники классифицируются в зависимости отрешаемых задач.
Оптимальный приемник решает одну из следующих задач:
1) различение сигналов;
2) обнаружение сигналов;
3) фильтрация сигналов от помех;
4) оценка параметров сигналов (для определения дальности, скорости,
условных координат);
5) одновременное обнаружение, различение и оценка параметров
сигналов.
Для каждой задачи выбирается критерий оптимальности.
Обобщенным критерием является критерий «среднего риска».
Если все ошибки приема являются равноценными, то критерий
«среднего риска» называется критерием «идеального наблюдателя».
13
13.
Лекция №2Оптимальный приемник для сигналов-переносчиков
со случайной амплитудой и начальной фазой
S ( , t , Ac , ) Ac (t ) cos[ 0 t c ( , t ) (t )]
y (t ) S ( , t , Ac , ) n(t )
(1)
(2)
Ac (t ) - огибающая радиосигнала (почти не меняется за время длительности сигнала).
с ( , t ) - медленно меняющаяся функция, обусловленная частотной или фазовой
модуляцией.
(t ) - случайная начальная фаза.
( )
1/ 2
Значения
Ac , ,
Равномерный закон
плотности распределения
вероятностей начальной
фазы
( )
являются статистически независимыми.
14
14.
Закон Рэлея( Ac ) 2h 2 Acexp( h 2 Aс2 )
( Ac )
1
h2
h 2
(3)
4
4 A2c
( Ac ) - плотность распределения
Ac
вероятностей амплитуды сигналапереносчика
- наиболее вероятное значение (мода)
15
15.
Выражение АПРВ для приемника полностью известных сигналов1
( / y )
( ) ( y / )
( y)
(4)
см. (6) лекция №1
Выражение АПРВ для приемника со случайными амплитудой и
начальной фазой
( , Ас , / y )
1
( , Ac , ) ( y / , Ac , )
( y)
(5)
( y ) - априорная ПРВ входного сигнала;
( , Ac , ) ( ) ( Ac ) ( ) - совместная ПРВ случайных
, Ас , ;
величин
( ) - априорная ПРВ случайной величины ;
(6)
( y / , Ac , ) - функция правдоподобия.
16
16.
( , Ас , / y) ( / y)Операция усреднения по случайным величинам
Ас ,
( / y) ( , Ac , / y) ( Ac , )dAc d
(7)
0
На основании статистической независимости случайных величин
( Ас , ) ( Ас ) ( )
Ас , :
(8)
После преобразований выражения ( 7 ) получим формулу ( 9 ):
0
( / y) ( Ac )[ ( , Ac , / y) ( )d ]dAc (9)
17
17.
Выражение АПРВ для сигналов со случайными несущественныминеинформационными параметрами ( Ас , ) после операции
усреднения по начальной фазе
( , Ac / y) k ( , Ac ) I 0 [| q( ) |]
(10)
1
АПРВ для полностью известных сигналов
k
( / y) k ( ) K 2 exp q( )
( y)
I 0 [| q( ) |] - модифицированная функция Бесселя нулевого порядка
Лекция №1
Модуль комплексной функции взаимной корреляции
| q ( ) | Ac q ( ) q ( )
2
1
Ac 1 ;
q1, 2 ( )
2
2
(11)
- квадратурные составляющие
q ( )
2
q1, 2 ( )
y(t ) S1, 20 ( , t )dt
N0 0
S1, 20 ( , t ) - квадратурные опорные сигналы
(12)
18
18.
Структурная схема квадратурного приемника0
q1 ( )
y (t )
q12 ( ) q 22 ( )
S10 ( , t ) U m cos 0 t
| q ( ) |
q2 ( )
0
S 20 ( , t ) U m sin 0 t
19
19.
Оптимальный приемник сигналов со случайными существенныминеинформационными параметрами
Цель: сформировать опорные сигналы с учетом оценок случайных параметров
сигнала-переносчика для использования в системах синхронизации СС
(высокочастотной СВС и тактовой СТС). СС работает по информационным или
специальным сигналам.
СВС предназначена для отслеживания несущего сигнала по частоте и начальной
фазе и формирования опорных сигналов.
СТС предназначена для отслеживания временных границ элементарных символов
и формирования коротких тактовых импульсов.
y (t )
t
0
РУ
t
0
СВС
СТС
СС
20
20.
Система фазовой автоподстройки частоты ФАПЧФазовый демодулятор
Входной
сигнал
Г
ФНЧ
Г
УЭ
- генератор сигналов
ФНЧ - фильтр нижних частот
УЭ - управляющий элемент
Обеспечивает автоматическое изменение
одного из параметров генератора (частоты,
фазы) за счет управляющего элемента в
соответствии с изменением параметра
входного сигнала с помощью
формирования на выходе фазового
демодулятора сигнала ошибки.
21
21.
Лекция №3Оптимальный приемник сигналов при воздействии негауссовской помехи
В основе оптимального приемника лежит алгоритм нахождения max АПРВ,
который сводится к вычислению max функции правдоподобия и max q ( ) .
Алгоритм справедлив, если ПРВ помехи имеет экспоненциальный характер, как у
закона Гаусса .
H
H
q( ) n ( y / ) n{ п [ y h S h ( )]} n n [ y h S h ( )] (1)
см. (18) лек.№1
h 1
см. (13) лек.№1
Z 0 [ y h S h ( )] n n [ y h S h ( )] (2)
h 1
логарифм произведения = сумме логарифмов
- характеристика оптимального блока
нелинейных преобразований ОБНП
H
y h S h ( ) n h
ОБНП
-
h 1
S h ( 1 )
H
ОБНП
S h ( 0 )
РУ
h 1
Опорные сигналы S h ( 1 ) и S h ( 0 )
22
должны формироваться с точностью до амплитуды.
22.
Асимптотически оптимальный приемникПреобразование функции n ( y / ) с помощью разложения в ряд Тейлора
S h ( ) nh
(справедливо для широкополосных приемников
Выражение для
членов ряда не выше
первого порядка
f ( y S ) f ( y) S f 1 ( y) (3)
Исходное выражение для разложения в ряд Тейлора
S S h ( )
d n п ( y h )
Z ao ( y h )
dy
при условии
f 1 ( y)
S y
H
n [ y S ( )]
h 1
f ( y S ) n n [ y h S h ( )]
f ( y) n п ( y h )
)
n
h
h
см. (1) лек. №3
d n n ( y h )
dy
(4) - характеристика блока нелинейного
преобразования (БНП)
Выражение для реализации схемы асимптотически оптимального приемника
H
H
n [ y S ( )] Z ( y ) S ( )
h 1
n
п ( y)
h
h
h 1
ao
h
h
(5)
S h ( ) и не влияет на
- функция не зависит от сигнала
схему приемника (поиск максимума коэффициента корреляции).
23.
Структурная схема асимптотически оптимального приемника при воздействиинегауссовских помех
yh
БНП
q( 1 )
H
h 1
РУ
S h ( 1 )
q ( 0 )
H
h 1
S h ( 0 )
2
2
2
2
выхнг
выхг
ао
2 2 ао
ао
2
ао
1
Е
N0
2
(см. (22), (23) лек. №1)
- коэффициент подавления негауссовской помехи
2
ао
1 для гауссовской помехи
24
24.
Лекция №4Основы теории обнаружения сигналов
Задача обнаружения состоит в формировании наибольшего пикового отношения сигнал/шум и
сравнении выходного напряжения
с порогом q ( ) .
H
Схема оптимального приемника обнаружения для полностью известных сигналов
у (t )
с
q ( )
ПУ
q( ) H
0
Выбор порога
H зависит от критерия оптимальности приемника:
1. Критерий среднего риска (известны априорные вероятности).
2. Критерий идеального наблюдателя (известны априорные вероятности, все
ошибки одинаково опасны).
3. Критерий Неймана-Пирсона (априорные вероятности неизвестны).
25.
Варианты результатов работы приемника обнаружения1
0
Р(0 / 1)
вероятность пропуска сигнала
Р (1 / 1)
вероятность правильного обнаружения
Р(1 / 0)
вероятность ложного обнаружения
Р (0 / 0) вероятность правильного необнаружения
Рош Р(0 / 1) Р(1 / 0) вероятность суммарной ошибки по
критерию идеального наблюдателя
Алгоритм выбора порога приемника (критерий Неймана-Пирсона):
1. Задается вероятность ложного обнаружения
Р(1./ 0)
Р(1 / 0) определяется величина порога H .
Р (1 / 1) ,
Р(0 / 1.) .
3. По значению порога вычисляются вероятности
2. По вероятности
26
26.
HОпределение порога
2 c
y(t ) S o (t )dt g ( ) h( ) (1)
q ( )
N0 0
y (t ) S (t ) n(t )
Сигнал присутствует, на выходе коррелятора - случайная величина
1.
с параметрами
М [q сп ] 2 ;2
q cп
D[q сп ] 2 2 .
В результате линейного преобразования гауссовского шума закон ПРВ
случайной величины
cп остается гауссовским (нормальным).
q
2.
(2)
Сигнал отсутствует, на выходе коррелятора - случайная величина
с параметрами гауссовского распределения
п (q)
2 с
[ S (t ) n(t )] S o (t )dt H
N0 0
cп (q)
qп
. 2
M [q п ] ; 0 D[q п ] 2
Сигнал есть
Отношение правдоподобия
2 c
n(t ) S o (t )dt H
N0 0
Сигнала нет
27
27.
ПРВ п (q ) (сигнала нет) и ПРВ cп (q ) (сигнал есть) распределены погауссовскому закону и нормальному закону
п (q)
cп (q)
H
Р (1 / 0) п (q ) dq
M [q сп ] 2 2
q
H
(3)
P(0 / 1) сп (q )dq
(4)
Пропуск сигнала
H
Ложная тревога
Р(1 / 1) 1 Р(0 / 1)
Правильное обнаружение
п (q)
cп (q)
q
28
28.
Вычисление вероятностей и порогаV [H ]
1
H
2
exp(
z
/ 2)dz
2 H
P(1 / 0) V [ H / 2 2 ]
(6)
(5)
Табличный интеграл (дополнение к
интегралу вероятностей)
Задаем значение вероятности ложной тревоги и
определяем по таблице порог
H .
Р[1 / 1] V [ H / 2 2 2 2 ]
(7)
Р(0 / 1) 1 V [ H / 2 2 2 2 ]
(8)
Р(0 / 0) 1 V [ H / 2 2 ]
Рош V [ H / 2 2 ] (1 V [ H / 2 2 2 2 ])
(9)
По критерию идеального наблюдателя
29
29.
Лекция №5Оптимальная линейная фильтрация непрерывных случайных сигналов
Выделение полезного сигнала (t ) из аддитивной смеси сигнала и помехи:
y (t ) (t ) n(t )
Для гауссовских случайных процессов оптимальными являются линейные фильтры.
y (t )
Wф ( j )
(t )
Критериями оптимальности фильтрации являются: 1) минимум среднеквадратической
погрешности , обеспечивает наилучшее воспроизведение формы
непрерывного сигнала (фильтрация второго рода); 2) отношение максимального
значения сигнала к среднеквадратическому отклонению помехи 2 , обеспечивает
надежную фиксацию факта наличия сигнала (фильтрация первого рода).
К фильтрам первого рода относятся согласованные и корреляционные фильтры.
Решение задачи оптимальной фильтрации (фильтрации второго рода) осуществляется
при непрерывном или дискретном наблюдении во временной или частотной областях.
Наиболее простой является расчетная модель линейной фильтрации в частотной
области при непрерывном времени.
30.
Расчетная модель линейной оптимальной фильтрации второго рода(t ) и n(t ) - независимые эргодические случайные процессы с гауссовским законом
ПРВ и известными функции СПМ
S ( ) и S п ( )
Wид ( j ) 1
2
(t ) (t ) (t )
(t )
(t )
2
На основании принципа
суперпозиции получим
выражения (1,2).
S ( ) S ( ) Wф ( j ) S п ( ) Wф ( j ) S ( ) Wид ( j )
S п S п ( ) Wф ( j )
2
S д S ( ) 1 Wф ( j )
(1)
(t )
Wф ( j )
-
(t )
y (t )
n(t )
Текущая погрешность
2 min
Критерий оптимальности
2
(2)
- помеховая составляющая текущей погрешности
2
- динамическая составляющая текущей погрешности
31.
2 д2 п2 (3) S ( ) S ( ) 1 W ( j ) 2 S ( ) W ( j ) 2 (4)ф
п
ф
2
2
1
1
2
S ( ) 1 Wф ( j ) d
S п ( ) Wф ( j ) d (5)
2
2
d 2
0
dWф ( j )
dS ( )
0
dWф ( j )
(6)
Фазовый сдвиг (время задержки) между входным и выходным сигналами фильтра не влияет на
текущую погрешность. Поэтому можно перейти от W
Уравнение (6) решаем относительно
ф
( j ) к
Wф ( . )
Wф ( ) .
Характеристика оптимального фильтра
Wф ( ) опт
Wф ( ) опт
S ( )
S ( ) S п ( )
(7)
32.
После подстановки формулы (7) в выражение (5) получим:S ( ) S п ( )
1
2
d
2 S ( ) S п ( )
(8)
Для физически реализуемых фильтров интегрирование имеет смысл в пределах от 0 до
.
Формула (8) показывает потенциальные возможности оптимальной фильтрации.
Если
S п ( ) S ( )
, то
Если
S п ( ) S ( )
,
Wф ( ) опт
то
S ( )
S п ( )
Wф ( ) опт 1
В полосе частот, где спектры сигнала и помехи не пересекаются, т.е.
2 2 .
,
,
2 п2
.
S ( ) S п ( ) 0 ,
Wф ( ) опт 1 . На участках, где спектры сигнала и помехи пересекаются, АЧХ фильтра тем
меньше, чем меньше соотношение между спектральными составляющими сигнала и помехи.
Wф ( ) опт
S ( )
S п ( )
1
33
33.
Пример передаточной функции физически реализуемого оптимальногофильтра
для
S п ( ) N 0
(белого шума)
и
S ( )
рациональной функции, стремящейся к нулю, например, экспоненциального типа.
N0
1 W ( j )
N 0 S ( )
2
2
min
S ( )
N0
n 1
d
2
N0
в виде
34.
Лекция №6Помехоустойчивость оптимального приемника дискретных сигналов
В качестве основного показателя помехоустойчивости приемника дискретных сигналов
используется вероятность ошибки при приеме элементарного символа
Р.
ош
Рош N ош
N пер
при
N пер
Pi
Pi / j
(1)
0
- апостериорные вероятности
Рош
Пример аналитического расчета
0 ( Р0 ); 1 (
- априорные вероятности
Р1 ); 2 ( Р2 ); 3 ( Р3 )
P1 / 0
Р2 / 0
Р3 / 0
Р0 / 0
Рош (а 1) Рi / j (4)
а=4
(позиционность кода)
3
Рош0 Рi / 0 (2)
i 1
Операция усреднения с помощью
априорных вероятностей
Pi
Рош Р0 Рош0 Р1 Рош1 Р2 Рош2 Р3 Рош3
a
a 1
Рош Pi Pi / j
i
j i
(3)
j
для случая равенства апостериорных вероятностей и
1
Pi
равенства априорных вероятностей
а
35
35.
Помехоустойчивость оптимального и асимптотически оптимального приемникаразличения полностью известных сигналов
у (t ) S ( , t ) n(t ) (1)
На входе приемника
х
х
S (t ) - ортогональные сигналы с
одинаковой энергией
n(t ) - гауссовская помеха
РУ
y (t )
Выражение коэффициента корреляции на выходе приемника в канале с копией входного
сигнала:
i j
q ( ) g ( ) h( ) 2 2 h H
(2)
Случай «свой-свой»
i, j
Закон распределения ПРВ
параметрами:
величины
сп (qслучайной
)
M [q сп ] 2 2
q сп- нормальный с
D[q сп ] 2 2
(3)
Выражение коэффициента корреляции на выходе приемника в канале без копии входного сигнала:
Случай «свой-чужой»
i j
q i , j ( ) 0 h ( ) h
п (qслучайной
)
Закон распределения ПРВ
величины
параметрами:
M [q п ] 0
q п - гауссовский с
D[q п ] 2 2
Вероятность превышения значения
h
величины
P1 (h H ) п (q )dq
(4)
(5)
H
(6)
H
36
36.
1 P1 (h H )Вероятность отсутствия ошибки:
(7)
Вероятность отсутствия ошибки во всех каналах, где нет копии входного сигнала:
[1 Р1 (h H )] a 1 (8)
Вероятность правильного приема:
Рправ.пр. [1 P (h H )] a 1 сп ( H )dH
Вероятность ошибки:
Выражение
Выражение
сп ( H ) сп (q)
а 1 Рош 0,1
2
для сигналов с неизвестной начальной фазой:
Рош [( а 1) / 2] exp( 2 / 2)
Выражение
(10)
Рош 1 Рправ.пр. (11)
Рош для ортогональных сигналов при условии
Рош (а 1) V ( ) (12)
Рош
(9)
(13)
- отношение мощностей
сигнала и шума на один
элементарный импульс
квадратурный прием
Рош для канала с негауссовской помехой:
Рош ( а 1) V [ , ао , 1 qi , j ( )]
i j
(14)
37
37.
Лекция №7Помехоустойчивость цифровых систем передачи непрерывных сообщений
2
Оценка помехоустойчивости – приведенная дисперсия суммарной
погрешности:
2 и2 ф ( кв2 ан2 )
и2 - погрешность интерполяции
(1)
и2 кв2 ан2
и2 0
ф - коэффициент фильтрации помех интерполяционным
фильтром
2
кв - погрешность квантования
2
- аномальная погрешность
ан
2
Причина погрешности:
2
кв
(2)
2
ан
ф 1
(3)
кв2 - операция квантования;
ан2 -
действие внешних помех.
38
38.
Оценка погрешности квантования в цифровых системах с ИКМПогрешность квантования – неустранимая погрешность, возникает вследствие
замены истинного значения сообщения
разрешенным
(t к )
квантованным уровнем
. кв
кв кв (tк )
кв - случайная величина, ПРВ
(4)
кв зависит от способа разбивки шкалы,
способа отождествления истинного значения с квантованным уровнем (шаг
квантования, число уровней квантования, основание кода), ПРВ сообщения.
( ) 1 / оптимальным (по
При равномерном распределении ПРВ сообщения
критерию минимума среднеквадратичной погрешности квантования) является равномерное
квантование.
АИМ-сигнал
кв
max min
Lкв 1
Lкв 1
(5)
кв
- шаг квантования
Lкв
- число уровней квантования
- динамический диапазон сообщения
Lкв а к
а
- позиционность кода
кв
к - разрядность кода
39
39.
Погрешность квантования( кв )
1
кв
в интервале
кв
кв / 2 кв кв / 2 (6)
в вне интервала ПРВ равна 0
М [ кв ] 0
кв / 2
3
2
2
D[ кв ] кв2 кв2 ( кв )d кв кв 2 2кв / 12
2
2
3
12
(
L
1
)
12
L
кв
кв
кв
2
/ 2
кв
кв
кв
( )
( кв )
1 / кв
-
6
36
2
2
(8)
-
- кв / 2
кв
кв / 2
кв
40
(7)
40.
кв2 ИКМПриведенная дисперсия погрешности квантования для ИКМ
2
2
36
3
3
2
кв
квИКМ 2
2 2к
2 2
12( Lкв 1)
Lкв а
2
кв ИКМ
(9)
зависит от шага квантования, количества уровней квантования,
позиционности кода, числа разрядов в кодовой комбинации, ПРВ
сообщения.
Приведенная дисперсия погрешности квантования для ДИКМ
кв2 ДИКМ
2р
12 L
6 р р
2
кв р
(11)
2
36 р2
12 L
2
кв р
2
3 р2
а
2к р
По аналогии с формулой (8)
2
р
2
р 2 1 (13)
2
(10)
2 р 36 р2 (12)
2
квДИКМ
квИКМ
(14)
41
41.
АИМ- сигнал(t k 1 ) (t k )
конечная разность первого порядка
р
(1) (t k ) (t k 1 )
р
кв const
Lкв р Lкв
при
кр к
при
а соnst
42
42.
Аномальные погрешности при ИКМВ результате действия помех в канале связи дискретные сигналы искажаются, происходит
ошибочный прием (вместо одного символа фиксируется другой).
Последовательность видеоимпульсов (огибающая радиоимпульсов)
1
0
1
1
1 2 0 0 21 1 2 2 1 2 3 13
1 2 0 0 21 1 2 2 0 2 3 5
1
0
1
0
ан 5 13 8
к 1
ан к а 0 а 1 а 2 а ... а
i
0
1
2
к 1
i 0
i
- разрядная цифра, случайная величина, принимающая значения:
правильно;
, если
1произошла ошибка для
i
ан кв ан
(16)
ан - аномальная ошибка в единицах измерения
амплитуды.
,
Lкв Lкв (15)
i , если
0 символ принят
а 2
а
- основание кода.
аномальная ошибка,
ан -выраженная
в количестве
разрядов.
43
43.
Дисперсия аномальной погрешностик 1
к 1
i 0
i 0
D( ан ) D( i a i ) (а i ) 2 D( ) (17)
- дисперсия
ан
D( ) - дисперсия случайной величины
(зависит от вероятности
ошибки Рош
и позиционности кода )
Дисперсия аномальной погрешности в единицах измерения амплитуды
k 1
D( ан ) a 2i D( )
2
кв
(18)
- дисперсия
i 0
ан
Приведенная дисперсия аномальной погрешности
2
ан
D( ан ) / 12 Pош (19)
2
для гауссовского сообщения
Аномальная погрешность характеризует достоверность передачи сообщений.
В качестве достоверности используют также вероятность появления
аномальной погрешности
.
Р
ан
44
44.
РанОценка вероятности появления аномальной погрешности
ксимволов, может быть искажено от одного
до всех к символов.
В кодовой комбинации, состоящей из
Р- ан
Вероятность появления аномальной погрешности
это вероятность того, что кодовая
Ран
комбинация будет принята хотя бы с одной ошибкой. Величина
зависит от вероятности
ошибочного приема элементарного символа
и характера распределения
Рош ошибок в
канале связи.
Допущения:
В канале действует белый гауссовский шум (все ошибки при приеме кодового слова независимые события). Значения вероятности ошибки в любом разряде кодового слова одинаковы
Рош i имеют
constодинаковые энергии и коэффициенты взаимной корреляции.
. Сигналы-переносчики
Вероятность того, что в кодовой комбинации из
символов, определяется
по формуле Бернулли:
l
ксимволов будут искажены
l
Рошк (l ) Ckl Pош
(1 Pош ) к l
C k! / l!(k l )! (21)
l
k
- число сочетаний из
(20)
к по l
45
45.
Расчет вероятности аномальной ошибкиРан
Вероятность хотя бы одной ошибки в кодовой комбинации
k
k
l
Ран Pошк (l ) C kl Pош
(1 Pош ) k l
l 1
(22)
l 1
При качественной передаче цифровых сигналов в кодовых комбинациях
возникают преимущественно одиночные ошибки и значение
Ран
рассчитывается по упрощенной формуле:
Ран 1 (1 Рош ) к к Рош (23)
где
(1 Рош ) к
(25)
к Рош 0,1 (24)
- вероятность того, что ошибки не будет
ни в одном из
к символов.
Ран зависит от основания кода, метода манипуляции,
Вероятность
коэффициента взаимной корреляции несущих сигналов, метода приема, вида
2 приемника.
помех, отношения мощностей сигнала к шуму
на входе
46
46.
2анр
Оценка
и
Ранр
при дифференциально-импульсно-кодовой
модуляции (ДИКМ)
2
Методика расчетов
и
Ранр при ДИКМ такая же, как для
анр
ИКМ.
р ДИКМ
Учитывая, что динамический диапазон изменений сигнала
при
(конечные разности первого порядка) значительно меньше динамического
диапазона
при ИКМ, можно записать следующие соотношения:
р
Lкв р Lкв
кв const
кр к
а соnst
2
анр
12 Рош р2
Ранр к р Рош
(26)
(27)
2
р
2
р 2 1
по аналогии с формулами
(19); (23)
При одинаковом качестве канала передачи, определяемом
,Р
в ош
2
системе с ДИКМ обеспечивается в
раз меньшее значение
р
и в ( к / к р ) раз меньшее значение
Ран
.
ан2
47
47.
Расчет суммарной погрешности при ИКМЯвление порога
При передаче непрерывных сигналов с помощью ИКМ с гауссовским законом ПРВ
помехи приведенная дисперсия суммарной погрешности определяется по формуле:
2
2
кв
3
2 к 12 Рош
а
2
ан
(28)
Если передача ведется с помощью ИКМ-ЧМ, то вероятность ошибки
равна:
См. лек.№6 формула (13) для
12
а 1
Рош
ехр( ) (29) квадратурного приема.
2
2
к - отношение мощности,
2
12 - отношение мощностей
элементарного импульса и помехи.
2
1
затраченной на передачу
кодового слова, к
мощности помехи.
3
2
2 к 6 (а 1) ехр( )
2к
а
2
(30)
48
48.
2 f (к , Lкв )2
2 const
Lкв а к
d 2
0
dк
Индекс модуляции
к опт
Области зависимости
f ( )
2
подпороговая,
2
:
2
к1
M опт а к опт
к, Lкв
к2
2 f ( 2 )
k const
к1 к 2
пороговая,
надпороговая.
2
пор
- рабочее значение
2
2
Чем больше число разрядов, тем больше вероятность аномальной ошибки, тем
резче проявляется порог. Чем больше индекс модуляции, тем больше полоса
частот сигнала, тем выше качество передачи.
49
49.
Расчет приведенной суммарной погрешности при ДИКМ2
3
2
2р кв2 р анр
[ 2 к 6 (а 1) ехр(
а
р
2к р
)] р2
(31)
р2 1
M р а кр
По сравнению с ИКМ при одинаковых условиях ДИКМ обеспечивает
меньшую погрешность квантования
погрешности
кв2и меньшие значения аномальной
ан2 и вероятности аномальной погрешности
Р,анявляясь
более помехоустойчивой системой передачи сигналов.
Недостаток ДИКМ (процесс накопления и размножения аномальных ошибок)
устраняется с помощью различных технических методов.
50
50.
Лекция №8Многоканальные системы передачи информации (МКС)
В основе МКС лежит принцип уплотнения линий связи (одновременная передача
нескольких модулированных сигналов-переносчиков), который повышает пропускную
способность, а также экономическую эффективность использования линий связи. В основе
уплотнения лежит принцип ортогональности (различимости) сигналов-переносчиков.
Методы уплотнения основываются на формуле Шеннона для определения информационного объема
канала (линии) связи
:
Vк
Vк Tк Fк Dк
Коэффициент корреляции для
ортогональных сигналов
1
C, i j
r ( Si , S j ) Si (t ) S j (t )dt
Е0
0, i j
Tк - время передачи сигналов
Fк - полоса частот канала (линии связи)
Dк - динамический диапазон канала (линии связи)
t
Классификация методов уплотнения:
1) временное разделение каналов (ВРК): на отдельные временные интервалы (тайм-слоты) делится
T
к
2) частотное разделение
каналов (ЧРК): на отдельные частотные полосы делится
;
Fк
3) кодовое разделение каналов или по форме сигнала переносчика (КРК): для разделения сигналов
используется ресурс
.
Dк
51
51.
DkВременное разделение
каналов (линии связи)
Частотное разделение
каналов (линии связи)
Tk
Dk
Fk
Vк Tк Fк Dк
Tk
Fk
52.
Особенности методов уплотненияВРК
Сигналы-переносчики – импульсные последовательности (кодовые комбинации),
которые передаются для каждого сообщения в отведенные временные интервалы (таймслоты), занимают всю полосу частот линии , требуют временной синхронизации
Fк
(точного совпадения начала и конца временных каналов на передающей и приемной
сторонах).
ЧРК
Сигналы-переносчики –синусоидальные сигналы, амплитудно-модулированные,
которые передаются в разных частотных полосах линии связи, существуют в одно и то
Tк одновременно), требуют частотной синхронизации (точного
же время
(передаются
совпадения спектра модулированного сигнала с выделенной полосой частотного канала
на передающей и приемной сторонах).
КРК
Сигналы-переносчики – дискретные ортогональные последовательности в виде
прямоугольных импульсов различной длительности и полярности («прямоугольной
волны» функций Уолша, Радемахера или прямоугольного синуса, Чебышева и т.д.),
требуют точного совпадения начала и конца интервалов ортогональности (тактовых
интервалов) на передающей и приемной сторонах, передаются одновременно и
Fк
занимают одну и ту же полосу частот линии связи
.
53
53.
Принципы временного уплотнения АИМ-сигналов в системе с ВРКАИМ-импульсы
В t АИМ может
учитываться
t АИМ
Период опроса
N
Т о 1 / 2 f эф
- число временных
каналов в системе с
ВРК
N
f эф
Tо
t АИМ
межканальный
интервал
- эффективная полоса
частот сообщения
54
54.
Структурная схема передающей аппаратуры системы с ВРК1 (t )
2 (t )
n (t )
ФНЧ
ФНЧ
ФНЧ
Кл
Кл
Кл
ФСИ
ГИ
АМн,
ЧМн,
ФМн,
ОФМн
АИМ
ИКМ
Гн
Кл
Распределитель
управляющих импульсов (РИ)
РИ состоит из линий задержки на
ФСИ - формирователь синхроимпульса
Коммутационная система КС=РИ+Кл
Мн
Под действием УИ
замыкается Кл и
формируется
выборка АИМ
t АИМ
Электронный ключ
(Кл)
Управляющий
импульс (УИ)
Длительность УИ =
t АИМ 55
55.
АМн, ЧМн,ФМн, ОФМн
ДМ
Структурная схема приемной аппаратуры системы с ВРК
ИКМ
Кл
Корреляционн
ый приемник
АИМ
ИКМ
Кл
АИМ
Кл
ИКМ
АИМ
Декодирующие
ВСИ
ГИ+РС
ФНЧ
ФНЧ
ФНЧ
1 (t )
2 (t )
n (t )
ИНТЕРПОЛЯЦИОННЫЕ
ФИЛЬТРЫ
устройства
ВСИ - выделитель синхроимпульса (СИ) для запуска генератора управляющих
импульсов и распределительной системы. СИ отличаются от импульсов АИМ
большей амплитудой и большей длительностью. Кл каждого временного канала
на передающей и приемной сторонах должны работать синхронно (замыкаться и
размыкаться).
56
56.
Принципы частотного уплотнения в системе с ЧРКАЧХ линии связи и спектры уплотняемых сигналов
(t )
(t )
АМ
ПФ1
ОМ
ОМсигнал
Частотная полоса ПФ
f
f н1
f н1
Преобразователь
(Пр)
f
f н1
4 кГц
Пр=АМ+ПФ
Частотная полоса уплотняемой линии связи
Число уплотняемых каналов
F
N
F
f
57
57.
Приемо-передающая аппаратура системы с ЧРКS1 ( , t )
1 (t )
S1 ( , t )
S 2 ( , t )
S 2 ( , t )
f н1
2 (t )
n (t )
f нn
1 (t )
S n ( , t )
f н2
Мод Гр
ЧМ,
ФМ
ДемодГ
р
S n ( , t )
Ген
ПФ1
ПФ2
f н1
2 (t )
f н2
n (t )
f нn
S1 ( , t )
ПФ1
S 2 ( , t )
ПФ2
S n ( , t )
ПФn
ПФn
58
58.
Принцип кодового уплотнения в системе с КРКФункции Уолша
Амп.
База шумоподобного сигнала ШПС
64 ортогональных комбинаций
В
Т
1
t
1
2
t
3
t
4
t
Т
- период ортогональности
59
59.
Принцип модуляции с помощьюШПС
Амп.
Т
- период опроса сообщений
1
Мод
1 функция
2
Мод
2 функция
3
Мод
3 функция
1
2
АИМсигнал
3
(t ) 1
t
1
2
2
3
3
Т
поступают на модуляторы
одновременно
60
60.
Модулированные сигналы (64 комбинации ШПС) складываются и поступают намодулятор ЧМ (ФМ). На одной несущей частоте могут одновременно
обслуживаться 64 абонента (на практике используют 32 комбинации для
уменьшения «шумов ортогональности», возникающих за счет отсутствия
возможности синхронизации периодов ортогональности ШПС, например, в
системах сотовой связи).
Структурная схема системы передачи сигналов ШПС
1 (t )
х
2 (t )
х
n (t )
х
Мод
Демод
ЧМ,ФМ
ЧМ,ФМ
СФ1
1 (t )
СФ2
2 (t )
n (t )
СФn
Чем больше база ШПС, тем меньше длительность элементарного импульса, тем
больше ширина полосы частот, занимаемая системой КРК, тем сильнее спектр
ШПС приближается к спектру белого шума, тем меньше «шумы ортогональности»
(выше качество связи). Свойство квазиортогональности ШПС и использование их без синхронизации
есть преимущество ШПС перед системой ортогональных синусоидальных сигналов.
На приемной стороне используются согласованные фильтры, настроенные на
прием определенной комбинации импульсов (функций Уолша). В основе
согласованных фильтров (СФ) – линии задержки на время длительности
элементарного импульса. На выходе СФ формируется метка по аналогии с
оптимальным приемником, пропорциональная амплитуде АИМ (сообщения) на
передающей стороне.
61
61.
Лекция №1I часть
Теория передачи сигналов (ТПС)
В курсе ТПС изучаются способы передачи информации от источника к потребителю.
Основные понятия курса: информация, сообщение, сигнал, система связи.
Информация – совокупность сведений о каких-либо событиях, явлениях или предметах.
Сообщение – форма представления информации в виде совокупности букв, цифр, знаков,
символов.
Сигнал – материальный носитель сообщения в виде физического процесса (звуковой или
электромагнитной волны, электрического тока).
Система связи – совокупность технических средств, предназначенных для передачи
сообщений в виде электрических или оптических сигналов по линиям связи.
Система связи состоит из передающего и приемного устройств, линейных сооружений
(электрического или оптического кабеля, воздушных линий, а также усилительных и
регенерационных устройств).
62
62.
Структурная схема системы связи(t )
Источник
сигналов
Передающее
устройство
S ( , t )
(t )
y (t )
Линия связи
n(t )
Приемное
устройство
Получатель
информации
y (t ) S ( , t ) n(t )
Источник
помех
Передающее устройство – предназначено для преобразования сообщения в сигнал-переносчик,
способный распространяться по линии связи.
Приемное устройство - предназначено для обратного преобразования сигнала-переносчика в
сообщение.
Линия связи – физическая среда, по которой распространяется сигнал-переносчик (электрический
или оптический кабель, воздушная линия связи, электромагнитная волна или радиоканал).
Важнейшими параметрами системы связи являются: энергия, затраченная на передачу сигналапереносчика; полоса частот канала связи, которые выбираются, исходя из заданного качества
передачи.
63
63. Структурная схема системы связи
Основы теории немодулированных сигналовНемодулированные сигналы – это сигналы, параметры которых не изменяются в
зависимости от других сигналов.
Модулированные сигналы – это сигналы, параметры которых изменяются под
действием других сигналов.
Немодулированные сигналы подразделяются на две группы: детерминированные сигналы,
случайные сигналы.
Детерминированные сигналы и их характеристики
Детерминированные сигналы подчиняются определенным функциям времени и при
известных параметрах этих функций могут быть определены точно на сколь угодно
большом промежутке времени.
S (t ) U m cos( o t o )
Например,
Um
,
o
,
o
- известные параметры синусоидальной функции
Детерминированные сигналы делятся на 1) периодические
2) непериодические
S (t ) S (t T0 )
S (t ) S (t T0 )
64
64. Основы теории немодулированных сигналов
Основные характеристики детерминированных сигналов:мощность, энергия, корреляционная функция, амплитудно-частотный спектр.
P(t ) S 2 (t )
- мгновенная мощность сигнала
T
- энергия сигнала
E S 2 (t )dt
0
T - длительность сигнала
T
1
E
2
Pср S (t )dt
T0
T
- средняя мощность сигнала
Т0
U m2 T0
Е (U m cos 0 t ) dt
2
0
2
А
t
Т0
Е U m2
Рср
Т0
2
для синусоидального сигнала
65
65.
Корреляционные характеристики детерминированных сигналовАвтокорреляционная функция сигналов с
конечной энергией
Т
Rав ( ) S (t ) S (t )dt
0
Т
1
R ав ( ) im S (t ) S (t )dt
T0
1
Автокорреляционная функция сигналов с бесконечно
большой энергией
T
T
RS1S2 ( ) S1 (t ) S 2 (t )dt
0
T
1
RS1S2 ( ) im S1 (t ) S 2 (t )dt
T0
Функция взаимной корреляции сигналов с
конечной энергией
Функция взаимной корреляции сигналов с
бесконечно большой энергией
T
T
RS1S2 (0) S1 (t ) S 2 (t )dt
0
при
S1 (t ) S 2 (t )
при
S1 (t ) S 2 (t )
Корреляция определяет зависимость между
двумя значениями сигнала (сигналов),
отстоящих друг от друга на временной
промежуток
Временной сдвиг между значениями сигналов
Определение
ортогональности
сигналов
66
66. Корреляционные характеристики детерминированных сигналов
Автокорреляционная функция прямоугольного импульсаи
Аим п
Т
Rав ( ) S (t ) S (t )dt
t
0
А
t
и
2
Е S 2 (t )dt Аимп
и
Rав ( )
0
Е Rав (0)
и
и
67
67.
Лекция №2Случайные сигналы и их характеристики
Случайные сигнал (процесс) изменяется случайным образом и не может быть точно определен
во времени.
t1
Случайный процесс
случайного сигнала
t2
tn
X (t )характеризуется совокупностью реализаций
x1 (t ), x2 (t )....xn (t )
.
Случайный процесс в фиксированный момент времени
величина.
t
есть
n случайная
x1 (t ), x2 (t )....xn (t )в
Совокупность случайных величин реализаций
момент времени
есть сечение случайного процесса.
n
t
xк (t )
68
68.
Определение ФРВДля одномерной ФРВ
P(t1 ) [ X (t1 ) x1 ]
Для многомерной ФРВ
P(t1 ) [ X (t1 ) x2 ]
P X (t1 ) x1 ; X (t 2 ) x2 ,.... X (t n ) xn
P(t1 ) [ X (t1 ) xn ]
Значения x1 , x2 ,.......xn меняются во всем диапазоне
изменений случайного процесса (флуктуационнойX (t )
n(t )сигнала
помехи
или первичного
).
(t )
69
69.
Функция распределения вероятностей случайного процесса ФРВ(интегральный закон)
F ( x1 , x2 ,.....xn ; t1 , t 2 ,....t n )
Случайный процесс
X (t )полностью задан, если для любого набора моментов времени
t1 , t 2 ,....t n
x1 , x2 ,.......xможно
и любых значений сигнала
вычислить вероятность
n
того, что в указанные моменты времени случайный сигнал
значения, не
Xпринимает
(t )
x1 , x2 ,.......xn , а именно:
превышающие
F ( x1 , x2 ,.....xn ; t1 , t 2 ,....t n ) Р X (t1 ) x1 , X (t 2 ) x2 ,...... X (t n ) xn
Р X (t1 ) x1 , X (t 2 ) x2 ,...... X (t n ) xn
совместная вероятность события,
определяющая многомерную ФРВ
Плотность распределения вероятностей случайного процесса ПРВ (дифференциальный
закон)
n F ( x1 , x 2 ,....x n , t1 , t 2 ,.....t n )
( x1 , x2 ,....xn , t1 , t 2 ,....t n )
x1 x 2 ...... xn
70
70.
Свойства ФРВ (одномерной)1.
F ( x, t ) 0
2.
0 F ( x, t ) 1
Свойства ПРВ (одномерной)
1.
( x, t ) 0
2.
( x, t )dx 1
x
F ( x, t ) ( x, t )dx
71
71.
ПРВФРВ
ФРВ
72
72.
Классификация случайных процессов1.Стационарные и нестационарные случайные процессы.
Случайный процесс, у которого вероятностные характеристики не изменяются во времени,
называется стационарным.
Случайный процесс, у которого вероятностные характеристики изменяются во времени,
называется нестационарным.
Стационарные процессы разделяются на стационарные в узком смысле, когда не изменяются во
времени законы распределения вероятностей, и в широком смысле, когда от времени не зависят
только числовые характеристики: математическое ожидание, дисперсия, корреляционная
функция (зависит только от
).
Стационарные случайные процессы в узком смысле стационарны и в широком смысле, но не
наоборот.
Эргодический случайный процесс относится к стационарным, у которого каждая достаточно
продолжительная реализация может характеризовать весь случайный процесс.
Эргодический случайный процесс
73
73.
7474.
Продолжение классификации случайных процессов2. Классификация по характеру зависимости текущего значения случайного процесса от
предыдущих значений:
2а) абсолютно случайные, т.е. непредсказуемые (например, белый шум), характеризуются
одномерной ПРВ, имеют корреляционную функцию в виде дельта-функции и
равномерную спектральную плотность мощности (СПМ).
X (t )
t
S x ( )
Rx ( )
N0
0
75
75.
2б. Марковский случайный процесс: текущие значения случайного процесса зависяттолько от одного предыдущего значения, характеризуется одномерной ПРВ и ПРВ
перехода из одного состояния в другое.
2в. Немарковские случайные процессы: текущие значения случайного процесса
зависят от двух и более предыдущих значений.
3. Классификация случайных процессов по виду закона распределения плотности
вероятностей:
3а. Гауссовские и негауссовские случайные процессы.
4. Классификация случайных процессов по виду корреляционной функции.
Закон Гаусса (ПРВ)
x(t ) m1 (t )
( x, t )
exp
2
2
2
2 x (t )
x (t )
1
2
x1
F ( x, t ) ( x, t )dx
Многомерная ПРВ гауссовского процесса определяется одномерной ПРВ и корреляционной
функцией. Некоррелированные сечения гауссовского процесса являются независимыми
случайными величинами.
76
76.
7777.
Лекция №3Моментные функции -
это среднее значение случайного процесса порядка
статистическим путем.
mk (t ) x k (t ) ( x, t )dx
m1 (t ) M [ x(t )] x(t ) ( x, t )dx
к, полученное
Усреднение по
множеству реализаций
к 1
0
x(t ) M [ x(t )] x(t )
2
D[ x(t )] x(t ) ( x, t )dx
0
к 2
T
Для стационарных и
эргодических случайных
процессов
M (x) D(x) (x )
1
M ( x) im x(t )dt
T0
T
Усреднение по времени
T
1 02
D( x) im x (t )dt
T0
T
78
78.
Среднее значение случайного процесса79.
mkk
x
k 1
k 3
k 4
(x)
- коэффициенты, характеризующие вид функции ПРВ
- коэффициент вариации, является мерой случайности
(стационарного случайного процесса)
- коэффициент характеризует степень несимметричности
функции ПРВ
- характеризует степень остроконечности функции ПРВ
( С 2, C 2 - обобщенный гауссовский закон,
гауссовский закон )
С 2
С
С 2
x
m4
x4
С 2 -
Среднеквадратическое
отклонение
x D[x]
80
80.
Корреляционная функция случайного процессаКорреляционная функция устанавливает взаимосвязь между двумя
значениями случайного процесса, соответствующими двум моментам
времени.
R x (t1 , t 2 ) x(t1 ) x(t 2 ) ( x1 , x 2 ; t1 , t 2 )dx1 dx 2
Для стационарных случайных процессов
(t 2 t1 )
R x ( ) x1 (t ) x 2 (t ) ( x1 , x 2 , )dx1 dx 2
Нормированная функция корреляции
R x ( 0) D ( x )
2
x
Rx ( )
rx ( )
Rx (0)
к rx ( )d интервал
корреляции
0
rx ( )
Rx ( )
1.
Rx ( ) Rx ( )
2
2. R x ( ) R (0) x
3. imR x ( ) 0
81
Свойства
81.
Нормированная функция корреляции стационарногослучайного процесса
к rx ( )d
0
интервал корреляции
1
к
Rx ( )d
Rx (0) 0
82.
Спектральная плотность мощности (СПМ)S x ( )
СПМ – энергетическая характеристика стационарного случайного процесса.
СПМ – это зависимость
частот шириной в 1 Гц.
S x ( средней
)
мощности случайного процесса от полосы
СПМ однозначно связана с корреляционной функцией преобразованиями
Винера-Хинчина.
Преобразования Винера-Хинчина:
1
j
R x ( )
S
(
)
e
d
x
2
S x ( ) R x ( ) e j d
Для четных функций и положительных значений аргументов:
S x ( ) 2 Rx ( ) cos( )d
Rx ( )
1
S ( ) cos( )d
x
0
0
Эффективная полоса частот случайного сигнала
1
эф
S x ( )d
S x (0) 0
83.
Примеры случайных процессовt
эф
к
Rx (0)
S x (0)
84
84.
Спектральная плотность мощности речевого сигналаформанты
2 (1Гц )
Частота
основного
тона
2 (1Гц )
85.
МоделиS x ( )
речевого сигнала
Полиномы Баттерворта
2 x2
sin( / 2k )
S x ( )
/ 2k
x [1 ( / x ) 2 k ]
эф
86.
Лекция №4Дискретное представление случайных процессов
- это преобразование функции непрерывного времени в функцию дискретного времени.
S (t ) может быть точно или приближенно
Случайный сигнал
представлен в виде линейного
функционального ряда в виде оценки
S:(t )
Nk
S (t ) S k Wk (t )
k 0
Sk
- весовые коэффициенты
Wk (t )
- базисные функции
Nk
N k конечно
S (t ) S (t )
S (t ) S (t ) (t )
- погрешность восстановления
T
S k S (t ) Vk (t )dt
Vk (t ) - весовые функции
0
87
87.
Классификация дискретных представленийОбобщенное дискретное представление в виде разложения в обобщенный ряд
Фурье с последующей аппроксимацией (восстановление непрерывного сигнала).
Vk (t ) Wk (t )
Дискретное представление в виде отдельных отсчетов (выборок)
с
S (t k )
последующей интерполяцией (восстановление непрерывного сигнала). Этот вид
дискретного представления лежит в основе импульсно-кодовой модуляции ИКМ.
Vk (t ) (t t k )
Разностное дискретное представление в виде конечных разностей с
последующей интерполяцией (лежит в основе дифференциально-импульсно-кодовой модуляции
ДИКМ) .
Весовая функция
Vk (t )есть линейная комбинация отсчетов
S (t. k )
88
88.
Обобщенные дискретные представления ортогональным рядом (ОДП)(разложение сигналов в обобщенный ряд Фурье)
Система ортогональных функций:
С
0 Wi (t ) Wk (t )dt 0
T
при
при
k i
k i
Т
2
W
k (t )dt 0
Функции не равны тождественно нулю.
0
T
2
W
k (t )dt 1
Система ортонормированных
функций
0
В качестве системы ортонормированных функций используются различные полиномы:
Лежандра, Чебышева, Уолша, Хаара, тригонометрические и др.
89
89.
Пример разложения сигнала в ряд Фурье с помощью тригонометрических функций90.
Пример формирования координатКоординаты
t
Временной промежуток
для передачи координат
других сигналов
00 1 0 0 11 00
91.
Структурная схема системы передачи сигналов с ОДПТ
х
S0
S0
х
Л. С.
0
W0 (t )
Т
х
S (t )
W0 (t )
S1
MUX
S1
DEMUX
х
0
W1 (t )
W1 (t )
Т
х
Sk
S (t )
Sk
х
0
Wk (t )
Wk (t )
92
92.
Лекция №5Текущая погрешность
(t ) (t ) (t )
2
(t )
2
2
Приведенная дисперсия
текущей погрешности
93
93.
Дискретизация по выборкам и интерполяцияВ качестве координат используются мгновенные значения сигнала, взятые в определенные
моменты времени. Представление непрерывного сигнала в виде отдельных отсчетов
называется процессом дискретизации.
k
S (t k ) S (kT0 ) S (t ) (t kT0 )
k
T0 const
- регулярная дискретизация
T0 const
- нерегулярная дискретизация
T0
- период опроса
94
94.
На приемной стороне осуществляется обратный процесс восстановления непрерывного сигналаиз отдельных выборок (интерполяция).
Nk
S (t ) S (kT0 ) Wи (t kT0 )
Wи (t kT0 ) - интерполирующий полином
k 0
S (t )
Квадратичная
интерполяция
Ступенчатая
интерполяция
t
T0
S (t )
Линейная
интерполяция
T0
t
t з T0
T0
t
95
95.
Теорема КотельниковаЛюбая непрерывная функция может быть восстановлена точно по своим
незашумленным выборкам только при следующих условиях:
T
1) процесс восстановления стремится к бесконечности
2) дискретизируемая функция должна иметь ограниченный спектр
3) частота опроса должна быть равна
сигнала)
F0 2F(c
[0 Fс ]
F-сграничная частота
4) интерполятором должен быть идеальный фильтр нижних частот ФНЧ:
Wи (t kT0 )
sin[ 2 Fc (t kT0 )]
2 Fc (t kT0 )
Теорема Котельникова определяет потенциальные возможности дискретизации по выборкам,
которые достижимы только теоретически:
1. Идеальные ФНЧ физически не реализуемы.
2. Бесконечное время наблюдения (восстановления) невозможно в случае практической
реализации.
Следовательно, в реальных условиях всегда имеет место интерполяционная
погрешность
и2 , которая является функцией СПМ дискретизируемого сигнала,
частоты опроса и метода интерполяции.
96
96.
Расчет интерполяционной погрешностиНепрерывные сигналы, представленные выборками, должны восстанавливаться с заданной
и2
интерполяционной погрешностью. Расчет
и определение
являются F
важными
0
задачами, возникающими при проектировании и эксплуатации цифровых систем передачи
информации.
При использовании частотной методики процесс интерполяции трактуется как процесс фильтрации
спектра исходной функции
из спектраSпоследовательности
выборок
(t )
S (kT0 ) .
Исходные данные:
S ( )
S ( ) СПМ исходного сигнала
S (t ) и период опроса
СПМ
S * ( )
есть сумма СПМ сигнала
смещенных составляющих
T0
выборок S (kT0 )
S ( ) и СПМ
S см ( )
2 Fc c
1
1
1
S ( )
S
(
k
)
[
S
(
)
S
(
k
)]
[ S ( ) S см ( )]
0
0
T0 k
T0
T0
k
*
k 0
97
97.
Интерполяция идеальным ФНЧS (t )
S * ( )
1
T0
F0
2 F0 0
2 Fc c
искажения
98
98.
Выделяют два случая фильтрации исходного сигнала в зависимости от ширины СПМ ипериода опроса:
1. СПМ сигнала ограничена
F0 2Fc ( спектры не перекрываются и с помощью
идеального ФНЧ выделяется сигнал без искажений.
2. СПМ сигнала не ограничена или не соблюдается условие
F0 2F(спектры
c
перекрываются и сигнал выделяется с искажением, т.е. интерполяционной
погрешностью
и2 ).
Интерполяционная погрешность состоит из двух статистически независимых
составляющих: динамической
ид2 , возникающей из-за того, что часть СПМ
S ( ) не пропускается через интерполяционных фильтр;
помеховой
ип2 , возникающей из-за того, что в полосу частот пропускания
S см.( )
интерполирующего фильтра попадает часть смещенных СПМ
сигнала
2
и
2
ид
2
ип
2 дисперсия сигнала
2
и2 и2
приведенная дисперсия
интерполяционной погрешности
99
99.
2ид
2
1
S ( ) 1 Wи ( j ) d
2
2
ип
1
2
S см ( ) Wи ( j ) d
2
Wи ( j )
комплексный коэффициент передачи
интерполирующего фильтра
Коэффициент фильтрации интерполирующего фильтра по отношению к внешним помехам
приблизительно равен единице.
100
100.
Лекция №6Дискретные разностные представления
Алгоритм формирования дискретных разностных представлений:
1. Формирование мгновенных отсчетов сигнала.
N гоотсчета
S пр (t kна) основании
2. Предсказание очередного
предыдущих ( N 1) отсчетов с учетом вероятностных свойств сигнала.
3. Сравнение предсказанного значения
с действительным значением
S
(
t
k)
текущего отсчета
и формированиепрразности
предсказания
S (t k )
порядка.
N го
( N ) S (t k ) S пр (t k )
В частном случае разностное представление первого порядка имеет вид:
S пр (t k ) S (t k 1 )
(1) S (t k ) S (t k 1 )
)
В линию связи посылается
В результате уменьшается динамический диапазон сигнала
( Nразность.
(сообщения), повышается помехоустойчивость, устраняется информационная избыточность сигнала, за
счет временного уплотнения повышается пропускная способность каналов связи. После дискретизации
сигнала по времени и формирования разности осуществляется процесс квантования по уровню и(1)
кодирование.
101
101.
Дельта-модуляцияПри увеличении частоты опроса разность между соседними отсчетами может быть
достаточно малой и квантоваться на два уровня:
1) если
( N ) S (t k ) 0
, то в линию связи передается единица,
2) если
( N ) S (t k ) 0
, то в линию связи передается ноль.
Структурная схема передающего и приемного устройств систем передачи сигналов с
дискретным разностным представлением
S (t )
дискретизатор
(1)
Прогнозирующее
устройство
Линия задержки на
(1)
T0
S (t к )
Канал связи
к интерполятору
Прогнозирующее устройство
Линия задержки на
T0
102
102.
На передающем сторонеS (t ) S (t k )
дискретизация
S (t k ) ( N ) S пр (t k )
S пр (t k ) S (t k 1 )
На приемной стороне
S (t k ) ( N ) S пр (t k )
S пр (t k ) S (t k 1 )
S (t k ) S (t )
интерполяция
103
103.
Дискретизация, квантование, кодированиеИмпульснокодовая
модуляция ИКМ
S (t k )
Уровни
квантования
икм
256 уровней
1)дискретизация
2)квантование
3
2
1
0
3)кодирование
t
кодирование
Динамические диапазоны
икм
00000110
(N )
дикм
Дифференциальноимпульсно-кодовая
модуляция ДИКМ
1)дискретизация
Уровни
квантования
3
дикм
0
t
2
1
16 уровней
2)вычисление конечных
разностей
3)квантование
4)кодирование
кодирование
0011
104
104.
Лекция №7Теория модулированных сигналов
Модуляция – управление параметрами несущего сигнала по закону передаваемого
сообщения.
Назначение модуляции:
1) преобразование первичного сигнала в высокочастотное колебание для передачи
информации по линии связи;
2) устранение информационной избыточности в первичном сигнале.
Классификация видов модуляции
сообщение
несущий сигнал
шумоподобные
непрерывные
дискретные
гармонические
импульсные
аналоговые виды
АМ,ЧМ,ФМ
аналоговые импульсные
АИМ,ШИМ,ФИМ,ЧИМ
дискретные виды
АМн,ЧМн,ФМн,ОФМн
цифровые виды
ИКМ,ДИКМ
105.
АМ – амплитудная модуляция (амплитуда синусоидального сигнала-переносчика изменяется по законуизменения амплитуды непрерывного сообщения).
ЧМ – частотная модуляция (частота синусоидального сигнала-переносчика изменяется по закону
изменения амплитуды непрерывного сообщения).
ФМ – фазовая модуляция (фаза синусоидального сигнала изменяется по закону изменения амплитуды
непрерывного сообщения).
АМн – амплитудная манипуляция (амплитуда синусоидального сигнала-переносчика изменяется по закону
изменения амплитуды дискретного сообщения).
ЧМн – частотная манипуляция (частота синусоидального сигнала-переносчика изменяется по закону
изменения амплитуды дискретного сообщения).
ФМн- фазовая манипуляция (фаза синусоидального сигнала-переносчика по закону изменения амплитуды
дискретного сообщения).
ОФМн – относительно фазовая манипуляция (фаза синусоидального сигнала-переносчика по закону
изменения амплитуды дискретного сообщения).
АИМ – амплитудно- импульсная модуляция (амплитуда импульса импульсного сигнала-переносчика
изменяется по закону изменения амплитуды непрерывного сообщения).
ШИМ – широтно-импульсная модуляция (длительность импульса импульсного сигнала-переносчика
изменяется по закону изменения амплитуды непрерывного сообщения).
ФИМ – фазо-импульсная модуляция ( фаза импульса импульсного сигнала-переносчика изменяется по
закону амплитуды непрерывного сообщения).
ЧИМ – частотно-импульсная модуляция (частота импульсов импульсного сигнала-переносчика изменяется
по закону амплитуды непрерывного сообщения).
ИКМ – импульсно-кодовая модуляция, ДИКМ – дифференциально-импульсно-кодовая модуляция,
ДМ – дельта-модуляция.
106
106.
(t )Дискретная модуляция (манипуляция)
107
107.
Модулятор ФМн(t )
S ( , t )
X
S (t )
f эф
101001
1
эл
СПМ –
бесконечна
0
При 180
несущая
подавлена
108
108.
Демодулятор ФМнФД
S ( , t )
ФНЧ
S(t)
(t )
УмЧ
ФВ
Ф2
ДЧ
Ф1
ВОК
109
109.
Манипулятор ОФМн(t )
ОФМн
2
ФМ
Л.З.
S (t )
Демодулятор ОФМн
ОФМн
ВОК
ФНЧ
2
(t )
Л.З.
110
110.
Частотный манипуляторАвтогенератор
Кв1
Выход
Кл
Кв2
Частотный демодулятор огибающей
Ф1
АД1
+
В
1
РУ
_
Ф2
0
АД2
f эф
2
эл
111
111.
Амплитудный манипулятор(t )
Кл
S ( , t )
АМн
Ген
S (t )
+
Кл
_
t
Детектор огибающей
(t )
+_
t
112
112.
Детектор огибающейf эф
1
эл
113
113.
Лекция №8Амплитудно-импульсно модулированный сигнал (АИМ)
Т0
эл
114
114.
U АИМ U 0 U m cos c t U 0 (1 M АИМ cos c t )M АИМ U m /U 0
(t ) U m cos( c t )
S ( , t ) (1 M АИМ cos c t ) S и (t t k )
k 1
U0
- амплитуда импульса
Um
- амплитуда первичного сигнала
с
- круговая частота первичного сигнала
M АИМ 1
- индекс модуляции АИМ
S и (t t k )
- функция, описывающая форму импульса
115
115.
Спектр АИМ - сигнала для(t ) U m cos( c t )
S ( )
0
0 c
c
2 0
3 0
2 0 c 3 0 c
0 c
2 0 c
3 0 c
f эф
1
им п
116
116.
Модулятор АИМU АИМ
(t )
t
АИМ сигнал
Демодулятор АИМ
АИМ-сигнал
ФНЧ
(t )
интерполятор
117
117.
Аналого-импульсные виды модуляции118
118.
Широтно-импульсная модуляция (ШИМ)изменяется по закону
Ширина импульса
(t ) U m sin .c t
0
0 sin c t
0
- среднее значение ширины (длительности) импульса
-- девиация ширины импульса
c
f эф
S ( )
-- круговая частота первичного сигнала
1
им п
- эффективная полоса частот ШИМ-сигнала
0 l c
0 l c
к 0 l c
c
0
2 0
3 0
119
119.
Модулятор ШИМ (мультивибратор Роера МР)(t )
Модулятор
ШИМ
T0
МР
t
Демодулятор ШИМ
ШИМ-сигнал
ФНЧ
(t )
120
120.
Фазо-импульсная модуляция (ФИМ)Аналитическое выражение ФИМ-сигнала
S ( , t ) U 0 S и (t k д k )
k 1
- амплитуда измерительного импульса
U0
- функция огибающей измерительного импульса
S и (t )
д Т0 / 2
T0
- период опроса
к (t k )
f эф
- девиация временного положения импульса
1
им п
t
- значение нормированного сообщения в момент опроса k
- эффективная полоса частот ФИМ-сигнала
121
121.
(t )t
tk
(t )
Модулятор ФИМ-сигнала
T0
t k T0
tk
ДУ
Мод.
ШИМ
дифференцирующ
ее устройство
tk
ОВ
Однополупериодный
выпрямитель
tk
Од
Одновибратор
восстанавливает
форму импульса
ФИМсигнал
Демодулятор ФИМ-сигнала
ФИМсигнал
РУ
ФНЧ
(t )
122
122.
АИМ-ЧМи
АИМ-ЧМ
ФИМ-АМ
f эф 2 f эфАИМ ( М 1) 2
1
им п
( М 1)
ФИМ-АМ
f эф 2 f эфФИМ
2
им п
123
123.
Лекция №9Аналоговые непрерывные системы модуляции
Амплитудная модуляция (АМ)
амплитуда несущего сигнала
(tизменяется
)
По закону передаваемого сообщения
.
S (t ) U cos( t )
0
АМ-сигнал:
0
0
S АМ (t ) U 0 [1 M АМ (t )] cos( 0 t 0 )
М АМ
Um
U0
индекс АМ модуляции
Выражение АМ-сигнала для
С учетом формулы
(t ) U m sin c t
М АМ 1
при
0 0
cos cos (1 / 2) cos( ) (1 / 2) cos( )
S ( , t ) U 0 [cos 0 t (1 / 2) M АМ cos( 0 c )t (1 / 2) M АМ cos( 0 c )t ]
f эф 2 Fc
для
f АМ 2 Fc
(t ) U m sin c t
Fc - ширина полосы частот (t )
124
124.
(t ) U m sin c t(t )
S ( )
0 c
c
S (t )
S ( )
0
0 c
S ( , t )
2 Fc
0
125.
(t )ПФ
Спектр
S ( )
Формирование АМ-сигнала (модулятор)
0 c
S ( , t )
2 0
2 c
S (t )
0
c
(t )
0 c
S ( , t )
I Вых
S (t )
i a0 a1u a2u 2 ...
u U 0 cos 0 t U m cos c t
Вх U
126
126.
Балансная модуляцияS ( )
2 Fc
f АМ 2 Fc
Однополосная амплитудная модуляция
S ( )
2 Fc
2 Fc
127
127.
Демодулятор АМ-сигналовS ( , t )
ФНЧ
(t )
S (t )
(t )
S ( , t )
S ( )
0 c
2 0 c
S (t )
2 0
c
2 c
0
0 c
2( 0 c )
2 0 c
2( 0 c )
128
128.
Угловая модуляция (УМ)SУМ U 0 cos[ 0 t ( , t ) 0 ]
( , t ) M ФМ (t )
ФМ
M
- индеск ФМ модуляции
(максимальное
ФМ 1 отклонение фазы)
t
ЧМ
( , t ) д (t )dt
д
0
(t ) cos c t
д
M ЧМ
с
0 c
М ЧМ 1
0 c
0 3 с
0 3 с
0
0 2 с
f эфУМ 2Fс (М УМ 1)
М УМ 1
М УМ 1
- девиация частоты
- индеск ЧМ
модуляции
(максимальное
отклонение
фазы)
0 2 с
f эфЧМ 2 Fд
f эфУМ 2 Fc
f эфФМ 2 М ФМ Fc
129
129.
Изменения частоты несущего сигнала при фазовой и частотной модуляциях(t ) at
S ( , t )
0 M ФМ a
1 const
(t ) at b
0 M ФМ а
2 const
t
t
( , t ) M ФМ (t )
ФМ
d ( , t )
M ФМ a
dt
S ( , t )
t
t
ЧМ
( , t ) д (t )dt
0
0 д аt
0 д ( at b)
d ( , t )
д (t )
dt
130
130.
Мгновенный спектрS ( )
2 2 Fc
N0
Pш N 0 f эф
f эфУМ 2 Fc
( f эф1 / f эф2 )
2 Fc ( M 1)
M 1
2 Fc
Система ФАПЧ
S ( , t )
ФНЧ
ЧМГ
0 2Fc
ФНЧ
(t )
0 Fc
131
131.
Модулятор ЧМ(t )
Демодуляция ЧМ
Колебательный
контур
Детектор
огибающей
t
132
t
132.
Лекция №10Основы теории кодирования
Преобразование дискретных сообщений в сигнал осуществляется с помощью двух операций:
кодирование и модуляция.
Кодирование – преобразование дискретных сообщений в последовательность некоторых символов.
Каждому элементу сообщения присваивается определенная совокупность кодовых символов,
которая называется кодовой комбинацией.
Правило, по которому устанавливается однозначное соответствие между сообщением и кодовой
комбинацией, называется кодом.
Код известен на передающей и приемной сторонах.
Для этого существует специальные кодовые таблицы, в которых размещают алфавит кодирования.
Классификация кодов
1) двухпозиционные
и многопозиционные
а 2
а 2
а - основание кода
2) равномерные
n
n const
и неравномерные
n var
- длина кодовой комбинации
3) по назначению: первичные, статистические, корректирующие
133
133.
Основные параметры кодова 0 2 0 а1 21 а 2 2 2 а3 2 3 а 4 2 4 а5 2 5 а 6 2 6 а 7 2 7
1)
а
2)
n
n k r s
информационные, проверочные, служебные
. Это число ненулевых элементов в комбинации,
3) вес кодовой комбинации
для двоичных кодов – число единиц в комбинации.
v1 01110
1 3
v2 01010
2 2
4) кодовое расстояние между двумя комбинациями
d . Это количество
элементов, в которых одна комбинация отличается от другой. Для двоичных кодов – это
вес суммы по модулю 2.
d (vi , v j ) (vi v j ) mod 2
(01101 00110) mod 2 01011( 3), d (vi , v j ) 3
+
=
01101
00110
01011
Минимальное кодовое расстояние (расстояние Хемминга) по множеству
комбинаций характеризует все множество кодовых комбинаций.
d min 1
- простые коды,
d min 2
- корректирующие коды
134
134.
Выполнение алгебраических операций над кодовыми комбинациями10011001 1 x 7 0 x 6 0 x 5 1 x 4 1 x 3 0 x 2 0 x1 1 x 0
A( x) x 7 x 4 x 3 1
Все операции выполняются по законам двоичной алгебры.
( x i x i ) mod 2 0
xn 1
7
4
3
[ A( x) B( x)] mod 2 [ A( x) x x x 1
B( x) x 6 x 4 1 ] mod 2
+
x7 x4 x3 1 x6 x4 1 x7 x6 x3
A( x) B( x) ( x 7 x 4 x 3 1)( x 6 x 4 1) x13 x10 x 9 x 6 x11 x 8 x 7 x 4 x 7 x 4 x 3 1
x6 x5 x 2 x
13-8=5
---
1
---
-
-
1 2 7 1 2 6 1 2 5 0 2 4 0 2 3 1 2 2 1 21 0 2 0
135
135.
Первичные (линейные) кодыПервичные коды (ПК) служат для согласования сформированной последовательности двоичных
сигналов с параметрами линии связи и обеспечения определенной синхронизации между передающей
и приемной сторонами. Первичный сигнал должен содержать тактовую частоту,
ПК должен иметь узкую полосу частот, не должен содержать постоянную составляющую (длинных
нулевых посылок) из-за присутствия в тракте передачи согласующих трансформаторов и усилителей,
не пропускающих низкочастотные составляющие (что вызывает искажения импульсов). Основная
часть энергии линейного сигнала должна быть сосредоточена в среднем диапазоне частот. От выбора
линейного кода зависят длина регенерационного участка и гарантированное выделение тактовой
частоты, качество передачи и возможность совместной работы различных систем передачи.
Искажения сигнала за счет
несоответствия полосе частот
л.св.
136
136.
12
1
2
1
2
1
2
Код
Манчестера
1 10
0 01
Квазитроичный
1b2b
Уменьшается вероятность длительных последовательностей единиц и нулей .
137
137.
Корректирующие коды (КК)КК – служат для повышения помехоустойчивости и достоверности передачи
информации в условиях помех. Это достигается введением в простые коды
избыточных разрядов.
Избыточные символы формируются по определенным правилам и называются
проверочными или контрольными.
d (vk ) 2
N0
- общее число комбинаций, делится на две части:
Nр
N0 N р
- разрешенные и
неразрешенные
d 1
d 2 1
- кратность обнаруживаемых
ошибок
-- кратность исправляемых
ошибок
1
d 2
1
d 3
138
138.
Классификациякорректирующих
Классификация
корректирующие
кодов
кодов
Блочные
Непрерывные
Разделимые
Неразделимые
Древовидный
Линейные
Нелинейные
Код с проверкой на четность (линейный, разделимый, блочный)
Обнаруживает все ошибки нечетной кратности (четной кратности не
обнаруживает)
k 01010
k 01011
r 0
r 1
139
139.
Код с постоянным весом (блочный, неразделимый)const
N 0 2 5 32
N р Сn
N р С53 10
N з 32 10 22
Код обнаруживается все ошибки нечетной кратности и часть ошибок четной кратности.
11100
1-группа
11101
10111
10101
11001
2-группа
3-группа
10001
11000
10001
11011
10011
Nр
00011
00001
Среди блочных линейных кодов самые перспективные - цикличные коды.
140
140.
Признаком принадлежности какой-либо комбинации к подмножеству разрешенныхкомбинаций является деление ее без остатка на некоторый многочлен
степени
g (x ) образующим.
r nВид
k многочлена определяет схему и порядок работы
, который называется
кодера и декодера.
g ( x) x 3 x 2 1
r 3
A( x) x 3 x 2 x
x
Пример:
x x x
5
5
4
x3 x
3
x4 x3
A( x) x 6 x 5 x 4 x
x x x
4
A( x) x x x
6
( x 3 x 2 1)
(x6 x5 x4 )
6
3
3
x
R( x) x
На приемной стороне комбинация
остатка на образующий многочлен
A(xбудет
)
делиться без
g (x.)
141
141.
Статистические кодыСлужат для уменьшения информационной избыточности в передаваемой
цифровой последовательности.
Количество информации определяется вероятностью появления сообщения
(буквы).
Каждая буква появляется с разной вероятностью и несет разное количество
информации.
Для повышения скорости передачи информации каждое сообщение должно
нести одно и то же количество информации. Для этого требуется
перекодирование сообщений, чтобы все сообщения были равновероятными.
Для этого часто встречающиеся буквы должны составлять короткие кодовые
комбинации. Реже встречающиеся буквы длинные кодовые комбинации.
Главное, чтобы короткие комбинации не совпадали с началом длинных
комбинаций.
Статистическое кодирование предложил К. Шеннон, правило кодирования
предложил Р. Фено. Статистические коды называются кодами ФеноШеннона.
142
142.
Лекция №11Модели сообщений, сигналов-переносчиков, помех
Сообщения
Импульсные
Дискретные
Непрерывные
Сигналыпереносчики
Синусоидальные
Импульсные
Шумоподобные
143
143.
Принцип кодового уплотнения в системе с КРКФункции Уолша
Амп.
База шумоподобного сигнала ШПС
64 ортогональных комбинаций
В
Т
1
t
1
2
t
3
t
4
t
Т
- период ортогональности
144
144.
S ( , t ) U m cos[ 0 t ( , t ) 0 ]Известны все параметры
Неизвестна
0
Неизвестны
0 U m
Неизвестны
0 U m 0
145
145.
Модели помехКлассификация помех
1. Флуктуационные
1. Внутренние
2. Импульсные
2. Внешние
3. Синусоидальные
1. Аддитивные
2. Мультипликативные
146
146.
Виды погрешностейПогрешности
1. Методические
1. Нормальные
2. Аппаратурные
2. Аномальные
3. Помеховые
147
147.
Показатели качестваНепрерывных
Дискретных
сигналов
сигналов
Приведенная
дисперсия текущей
погрешности
Вероятность
2 f ( Pс / Рш )
Рош f ( Рс / Рш )
ошибки
148
148.
Лекция №12Элементы количественной теории информации
Свойства количественной меры информации
1. Количество информации должно быть аддитивной мерой.
2. Количество информации в сообщении о достоверном событии равно нулю.
3. Количество информации не должно зависеть от качественного содержания.
i(a) k log 2 P(a)
а – дискретное
сообщение
k 1
1
i(a) log 2 [
]
P( a )
Энтропия дискретного источника сообщений
1
Н ( А) М [i (a)] М [log 2 (
)]
P(a)
K
H ( A) P (ai ) log 2 [
i 1
1
]
P(ai )
1
i(a) log 2 ( ) 1бит
0,5
149
149.
Свойства энтропии1. Энтропия неотрицательна
2. Энтропия аддитивна
3.
H ( A) log 2 K
32
1
1
H ( A) log 2 (
) 5бит
1 / 32
1 32
Избыточность источника информации
log 2 K H ( A)
log 2 K
150
150.
Взаимная информацияСовместная энтропия
H ( A / B) M {log 2
Условная энтропия
n
1
H ( A, B) M {log 2
}
P(a k , bi )
m
H ( A / B) P(ak / bi ) log 2 [
k 1 i 1
1
P (a k / bi )
}
1
]
P(ak / bi
P(a, b) P(a) P(b / a) P(b) P(a / b)
H ( A, B) H ( A) H ( B / A) H ( B) H ( A / B)
Теорема
умножения
вероятностей
Свойства условной энтропии
0 H ( A / B ) H ( A)
H ( A / B) H ( A)
151
151.
Взаимная информацияP(ak / bi )
1
1
I ( A, B) H ( A) H ( A / B) M [log 2
] M [log 2
] M [log 2
]
P ( ak )
P(ak / bi )
P ( ak )
P (ak , bi )
I ( A / B ) M [log 2
]
P (ak ) P (bi )
Выражение
симметрии взаимной
информации
Свойства взаимной информации
I ( A, B ) 0
1.
3.
5.
2.
I ( A, B ) H ( A)
I ( A, B) I ( B, A)
4.
I ( A, B ) H ( B )
I ( A, A) H ( A)
I ( A, B) H ( A) H ( A / B) H ( B) H ( B / A)
Потери информации
H ( A) I ( A, B) H ( A / B)
152
152.
Скорость передачи информацииI ( A, B )
I ( A, B )
T
Производительность источника сообщений
H ( A)
H ( A)
T
I ( A, B)
H (A)
H ( A / B)
H (B)
H ( B / A)
153
153.
Эффективное кодированиеИсточник
дискретных
сообщений
Кодирующее
устройство
I ( A, B)
H (A)
H (B)
Для эффективного кодирования (без учета помех) необходимо:
I ( A, B) H ( A)
Из свойства взаимной информации имеем неравенство:
I ( A, B) H ( B)
Отсюда,
Т с / Т к H ( A) / H ( B)
H ( A) H ( B)
H ( B) / Т к H ( A) / Т с
H ( A) log 2 256 8бит
Т с / Т к 8 /1
H ( B) log 2 2 1бит
154.
Дискретизация, квантование, кодированиеИмпульснокодовая
модуляция ИКМ
S (t k )
Уровни
квантования
икм
256 уровней
1)дискретизация
2)квантование
3
2
1
0
3)кодирование
t
кодирование
Динамические диапазоны
икм
00000110
(N )
дикм
Дифференциальноимпульсно-кодовая
модуляция ДИКМ
1)дискретизация
Уровни
квантования
3
дикм
0
t
2
1
16 уровней
2)вычисление конечных
разностей
3)квантование
4)кодирование
кодирование
0011
155
155.
Теоремы ШеннонаПервая теорема: если пропускная способность канала больше или равна
производительности источника дискретных сигналов, то имеются кодирующие и
декодирующие устройства, которые обеспечивают передачу информацию по
каналу связи без ошибок, в противном случае передача без ошибок невозможна.
Простое кодирование.
Вторая теорема: среди кодов и кодирующих устройств, обеспечивающих
выполнение условий первой теоремы, имеются коды, которые обеспечивают
максимальную производительность источника дискретных сигналов.
Статистическое кодирование.
156.
Лекция № 13Пропускная способность дискретного канала
При передаче каждого символа в среднем по каналу проходит следующее
количество информации:
I ( A, B) H ( A) H ( A / B) H ( B) H ( B / A)
Максимальное количество информации, взятое по всем возможным
источникам, характеризует канал и называется пропускной способностью
канала (в расчете на символ):
С max I ( A, B)
Ссим max I ( A, B)
Р( А)
Пример:
Р( А)
С VCсим
бит/ с
Дискретный канал (симметричный без памяти): может передать каждый
Рошошибки
символ с вероятностью ошибки
и без
(1 Рош )
157
157.
Условная вероятность того, что вместо переданноголюбой другой из ансамбля
:
K
Р(b j / ai ) 1 Pош , i j
Р(b j / ai ) Pош /( K 1), i j
Допустим:
К 3
i
-го символа может быть принят
Передали 9 раз букву a , приняли 3 раза а, 3 раза b, 3
раза с.
a
b
c
P (b / a ) 1 / 3
Рош 2 / 3
a
Ссим max[ H ( B) H ( B / A)]
H ( B) log 2 K *
1
K 1
1
H [ B / A] M [log 2
] Рош log 2
(1 Рош ) log 2
P(b j / ai )
Pош
(1 Pош )
K
1
1
Cсим log 2 K Рош log 2
(1 Рош ) log 2
Pош
(1 Pош )
158
158.
K 2С V [1 Pош log 2 Pош (1 Рош ) log 2 (1 Pош )]
C /V
1
Pош
1
1/2
Pош 1 / 2
С 0
инверсия
159
159.
Информация в непрерывных сигналах( )
к
Р( к к ) ( к )
log 2 1 / Р( к к ) log 2
H ( ) lim M [log 2
0
1
( к )
1
1
1
1
1
1
1
] lim M [log 2
log 2
] lim M [log 2
] lim M [log 2
] M [log 2
] lim M [log 2
]
( )
( )
( )
( )
0
0
0
0
160
160.
Лекция №14Дифференциальная энтропия
h( ) M [log 2
1
1
] ( )[log 2
]d
( )
( )
Количество взаимной информации в непрерывном сообщении
I ( , ) lim M [log 2
( , )
( , )
] M [log 2
]
( ) ( )
( ) ( )
0
0
На основании теоремы умножения вероятностей:
I ( , ) h ( ) h ( / ) h ( ) h ( / )
161
161.
Дифференциальная энтропия гауссовской случайной величины( x a) 2
( x)
exp[
]
2
2 x
2 x2
1
(x )
h( x) log 2 2 e
2
x
Максимальна, не зависит
от м.о., растет
пропорционально
дисперсии
x
162
162.
Пропускная способность непрерывного канала(t )
1
T0
2 Fc
- период
опроса
t
Cот max I ( , ) max[ h( ) h( / )]
( )
( )
Пропускная способность непрерывного канала с шириной полосы частот
может быть
взятой
F определена в виде суммы значений
,
С отпо всем
отсчетам за единицу времени 1 сек.
С 2 FCот
(t k ) - сообщение на выходе канала
163
163.
Непрерывный канал без памяти с аддитивным белым гауссовским шумом.(tk ) - входной сигнал с мощностью
с помехой мощностью
Рсв канале шириной полосы частот
Рш
.
Гауссовские распределения
(n)
n
F
( / )
n
n
t
t
t
164
164.
Cот max I ( , ) max[ h( ) h( / )]( )
( )
max h( ) log 2 2 e( Pс Рш )
h( x) log 2 2 e x2
h( / ) log 2 2 ePш
Условная энтропия:
Сот log 2 2 e( Pс Рш ) log 2
Pс Рш
1
2 ePш log 2 (
)
2
Рш
С 2 FCот
Формула Шеннона
С F log 2 (1
Pс
P
) Vк Т к Fк log 2 (1 с ) Т к Fк Dк
Рш
Рш
165
165.
DkВременное разделение
каналов (линии связи)
Частотное разделение
каналов (линии связи)
Tk
Dk
Fk
Vк Tк Fк Dк
Tk
Fk
166.
Эпсилон-энтропияКоличество информации в непрерывном сообщении равно бесконечности.
Для воспроизведения непрерывных сообщений не требуется абсолютная точность.
Допустимую неточность воспроизведения можно измерить с помощью малого
параметра
(эпсилон).
Минимальное количество информации, которое требуется передать по каналу связи,
чтобы обеспечить допустимую неточность, называется эпсилон-энтропией.
1
h ( B) log 2
2
2
B
2
167






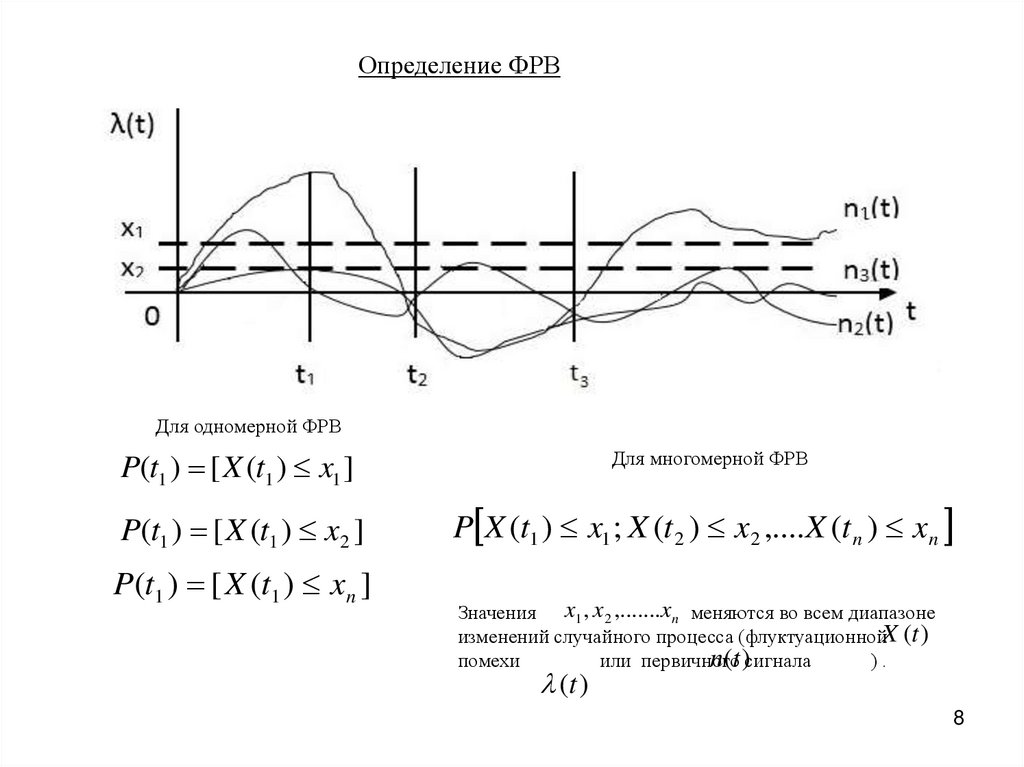

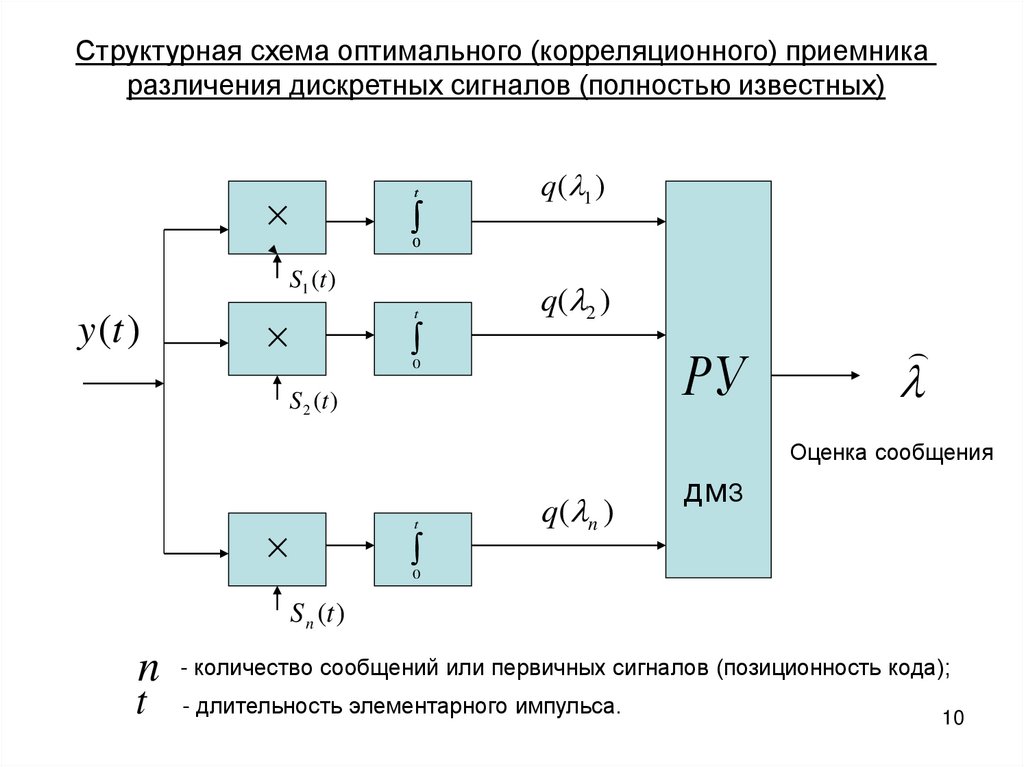



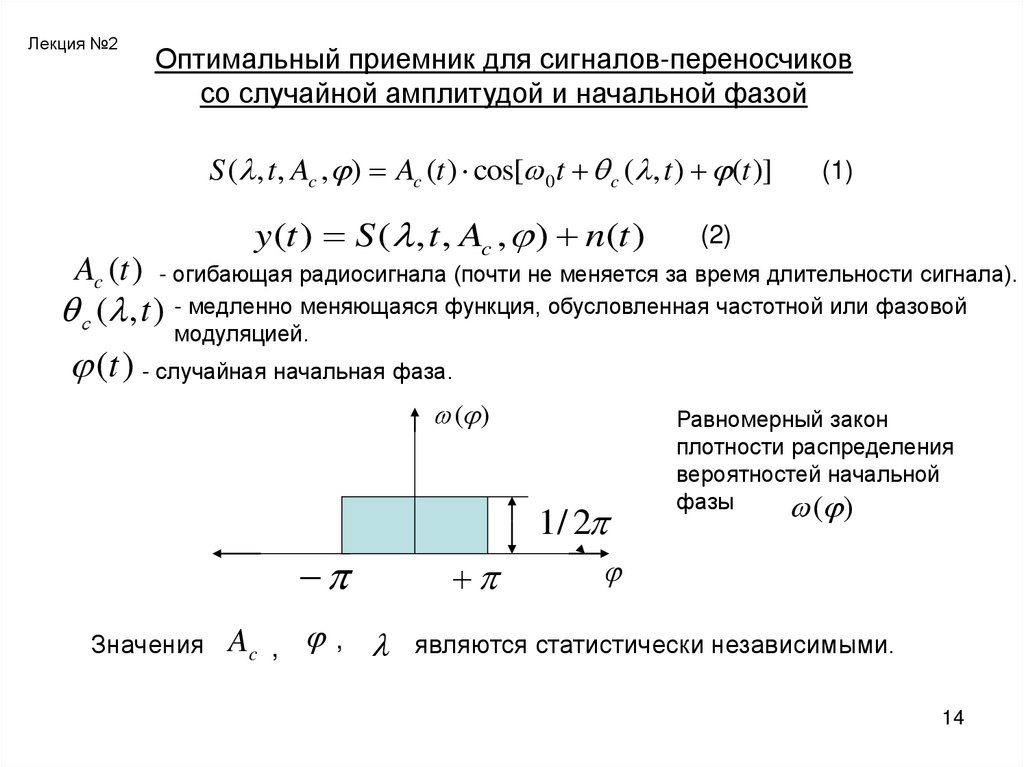




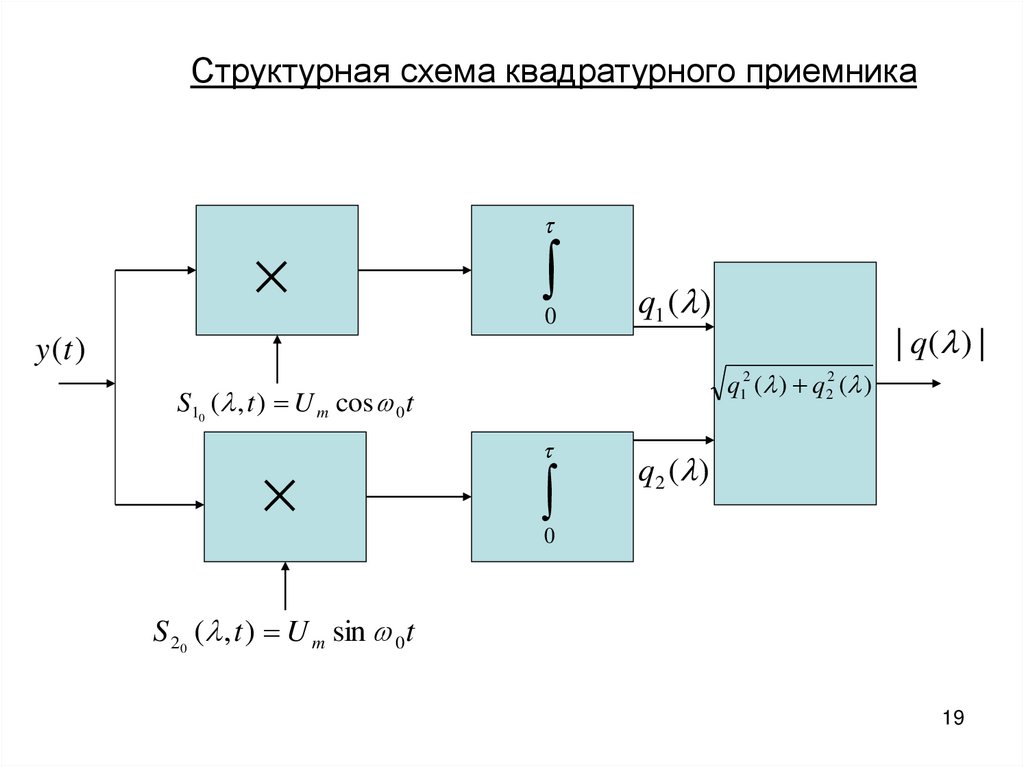
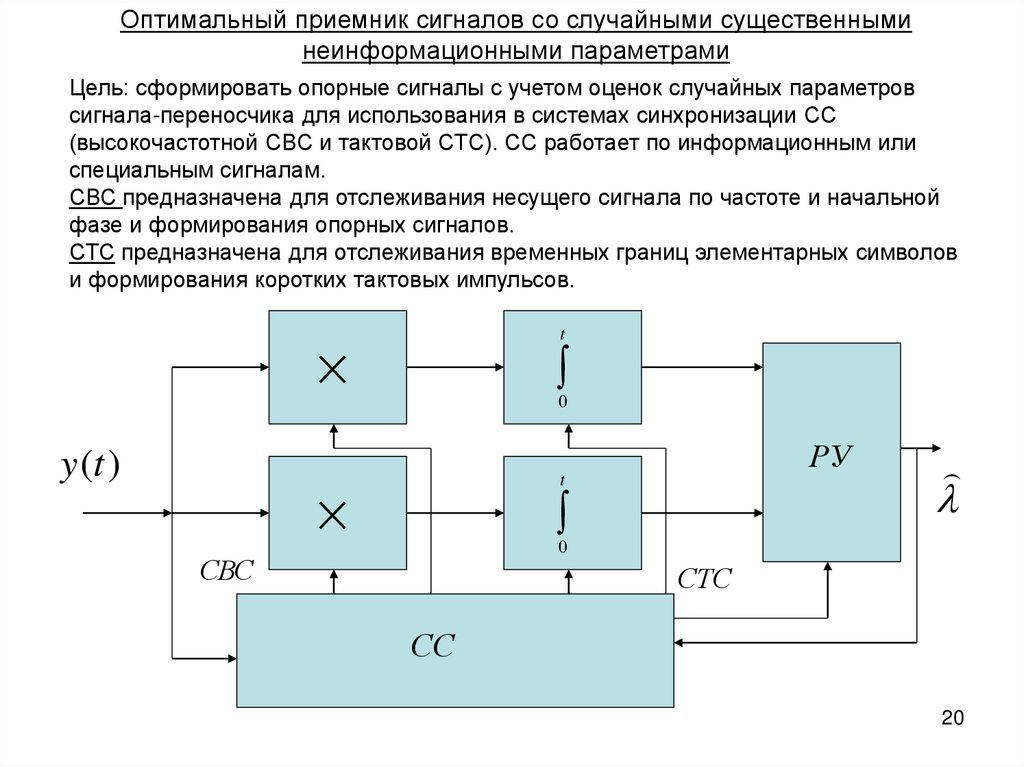

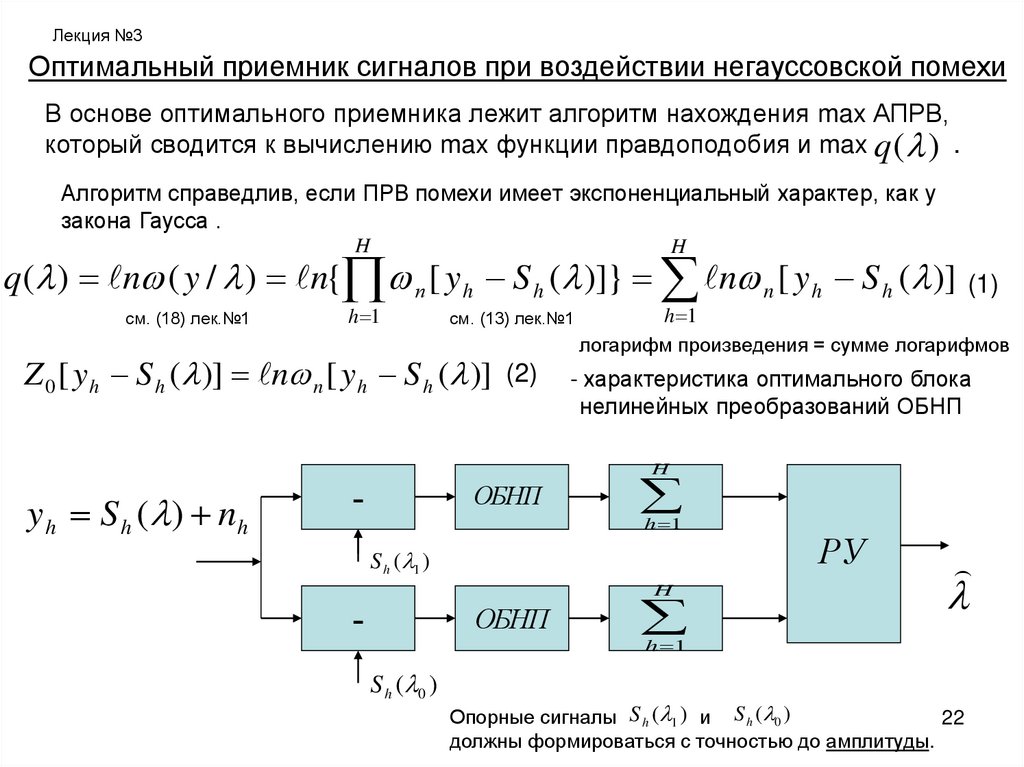

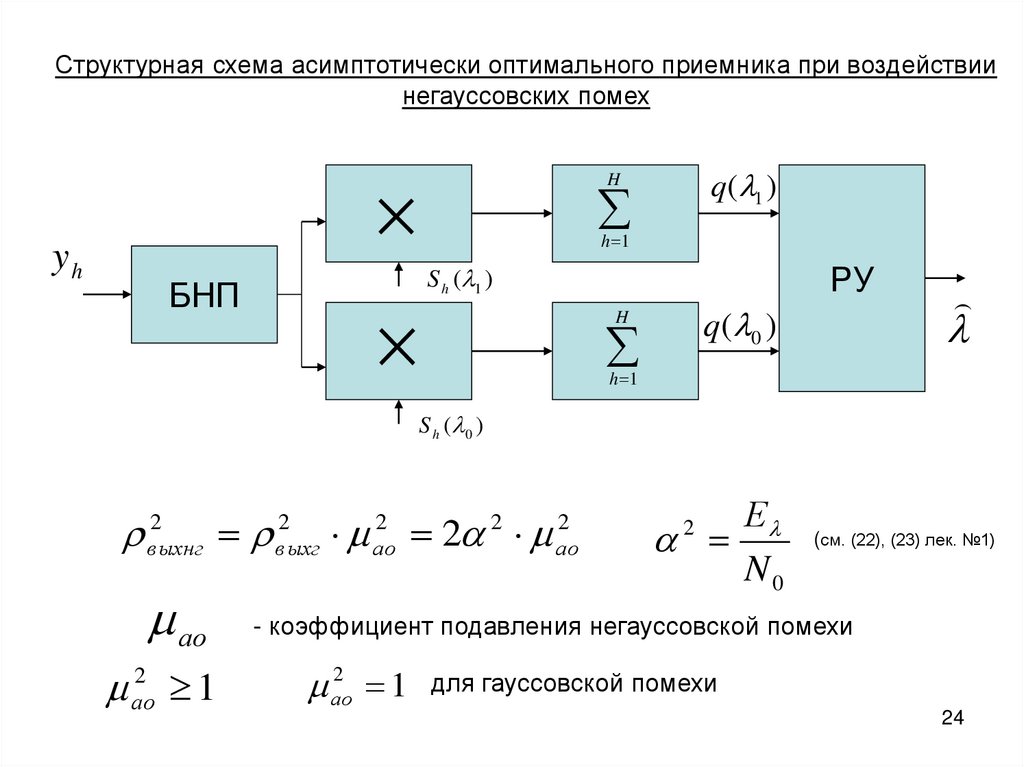
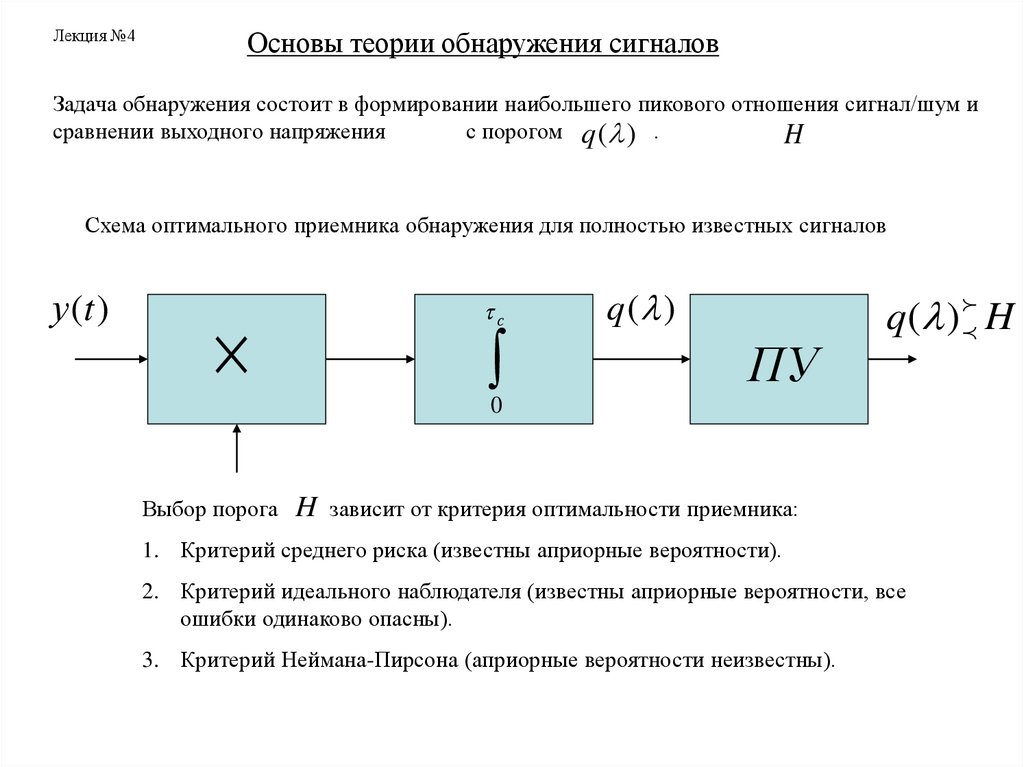


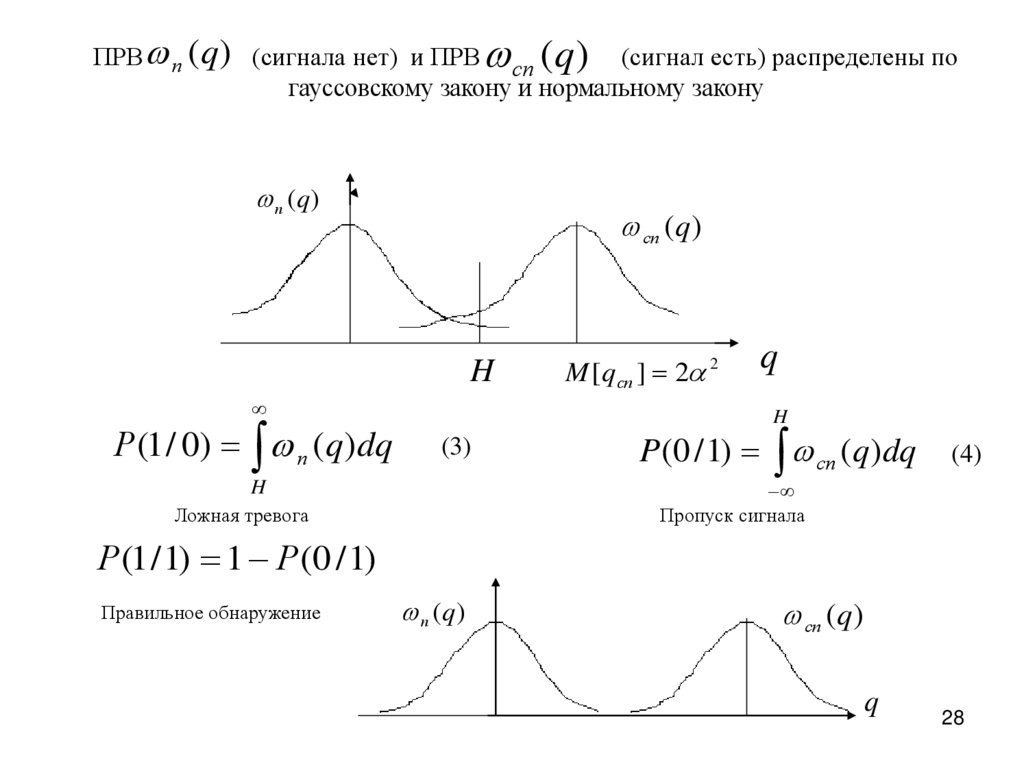











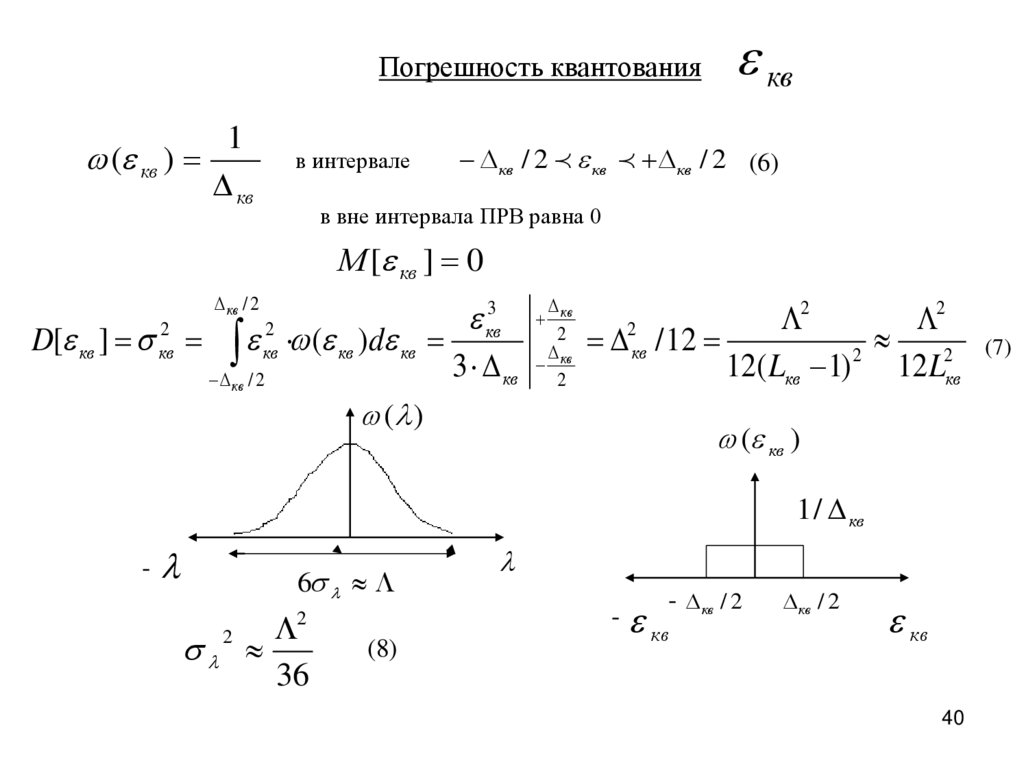

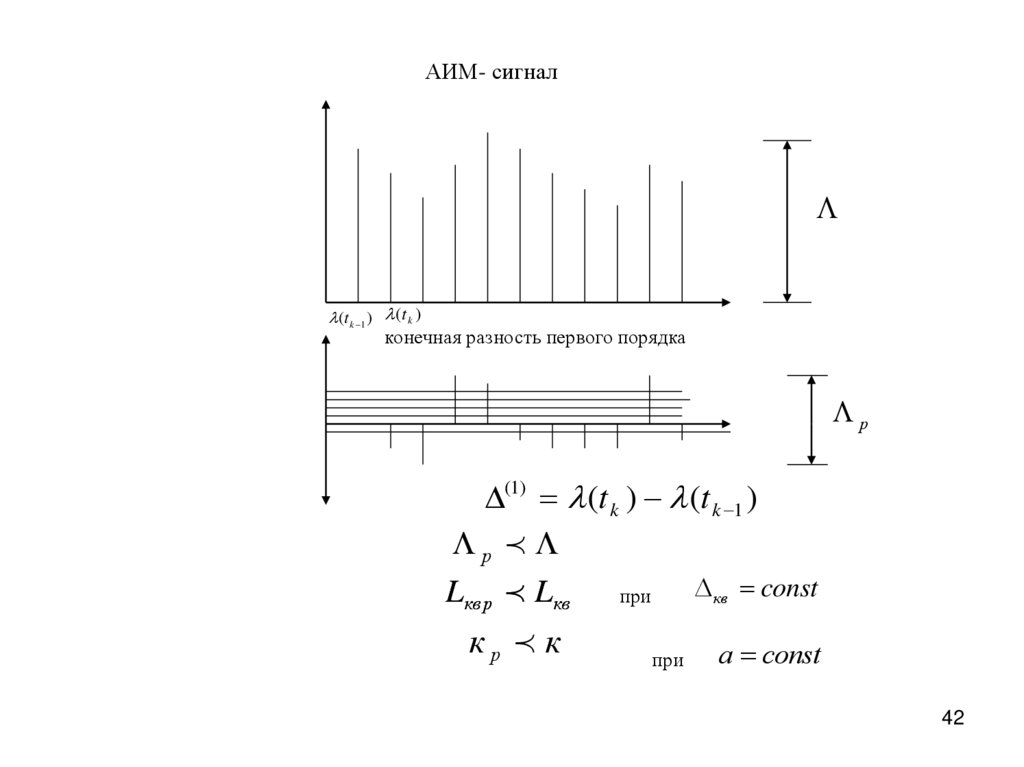






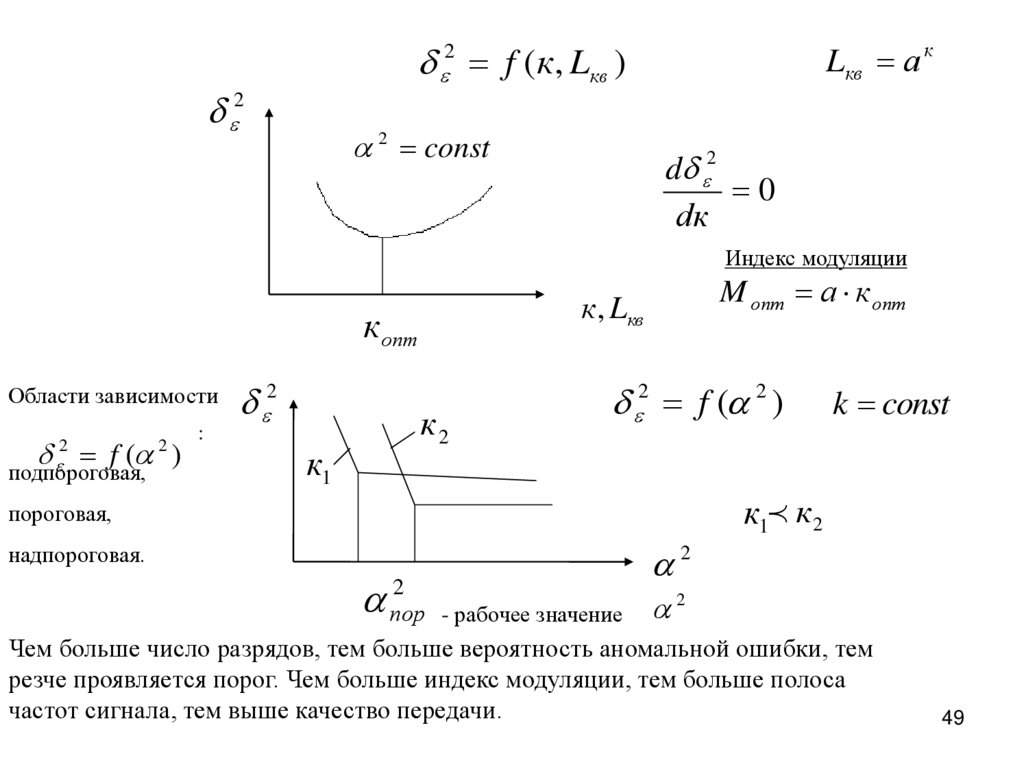


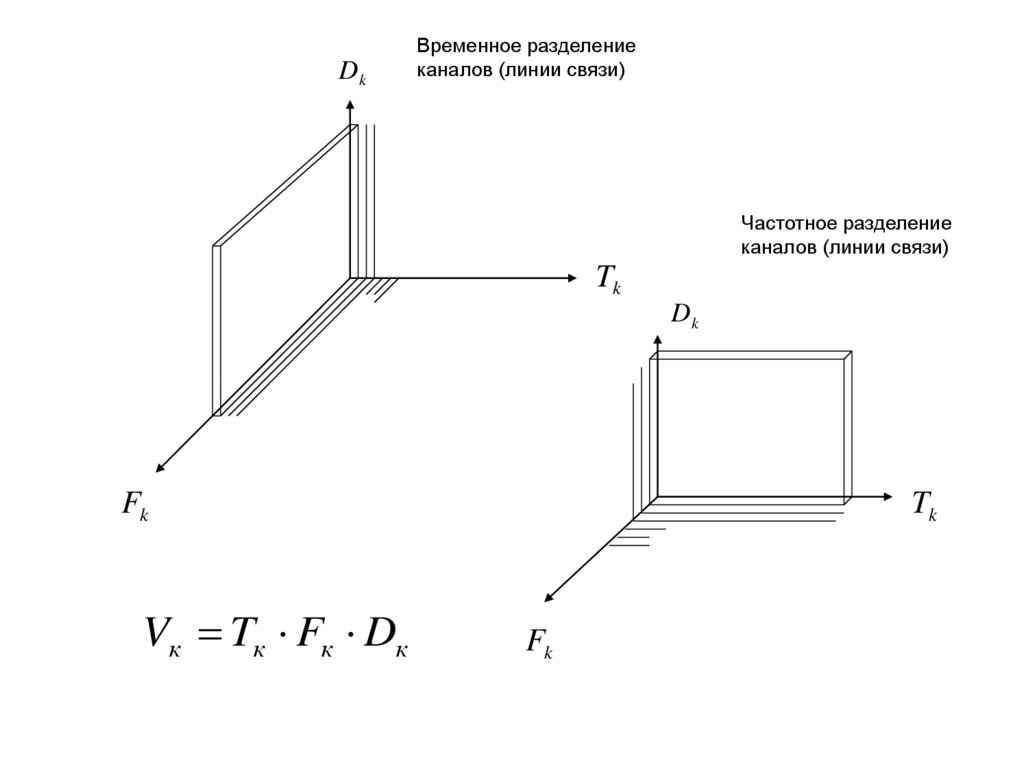

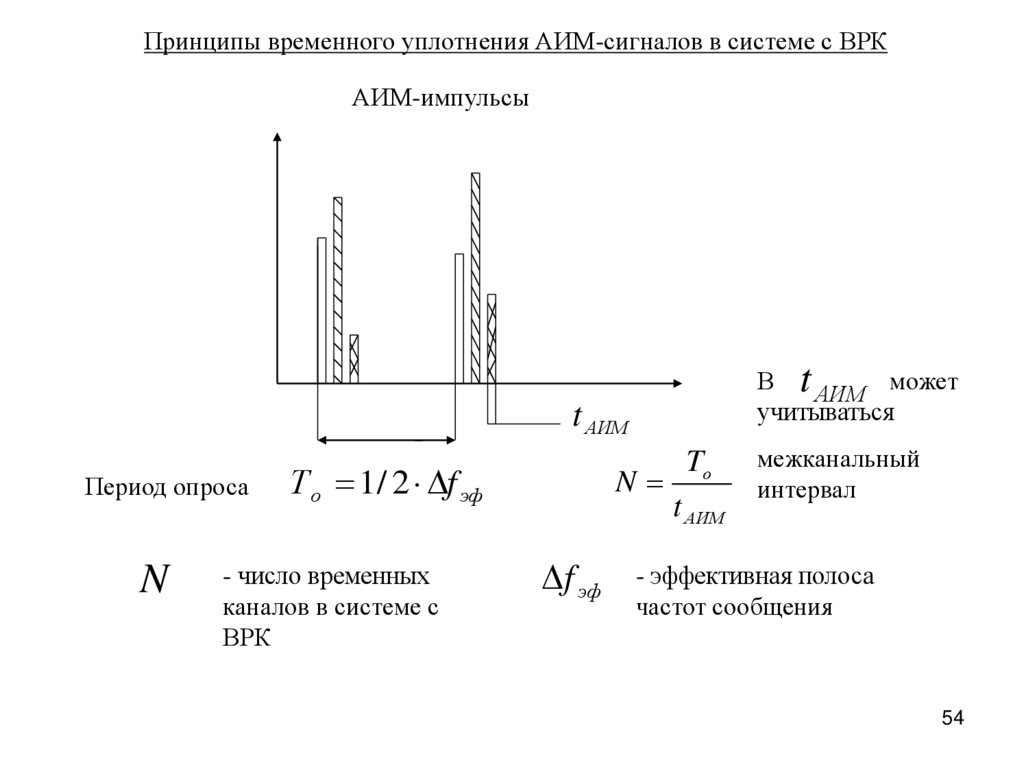
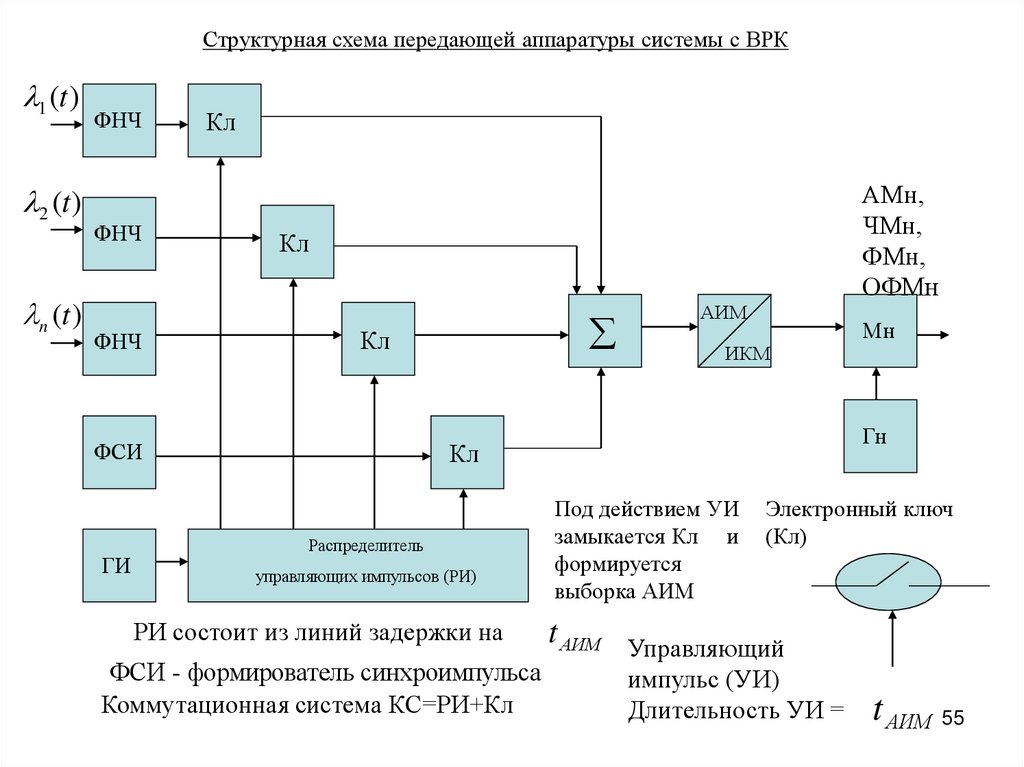
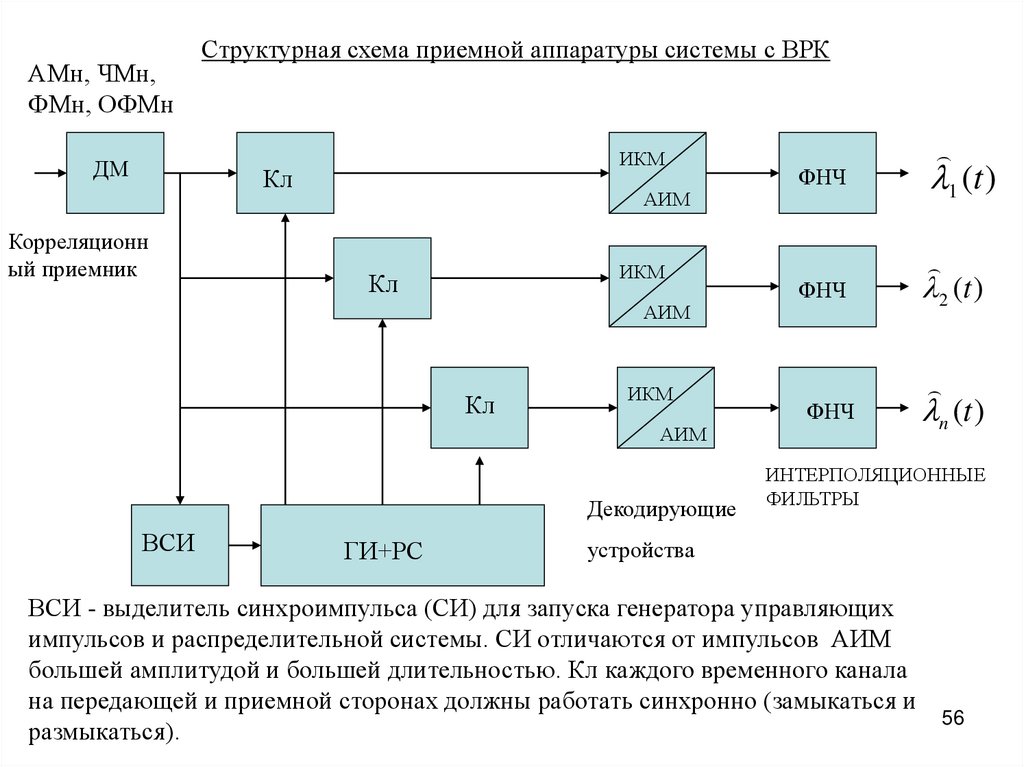
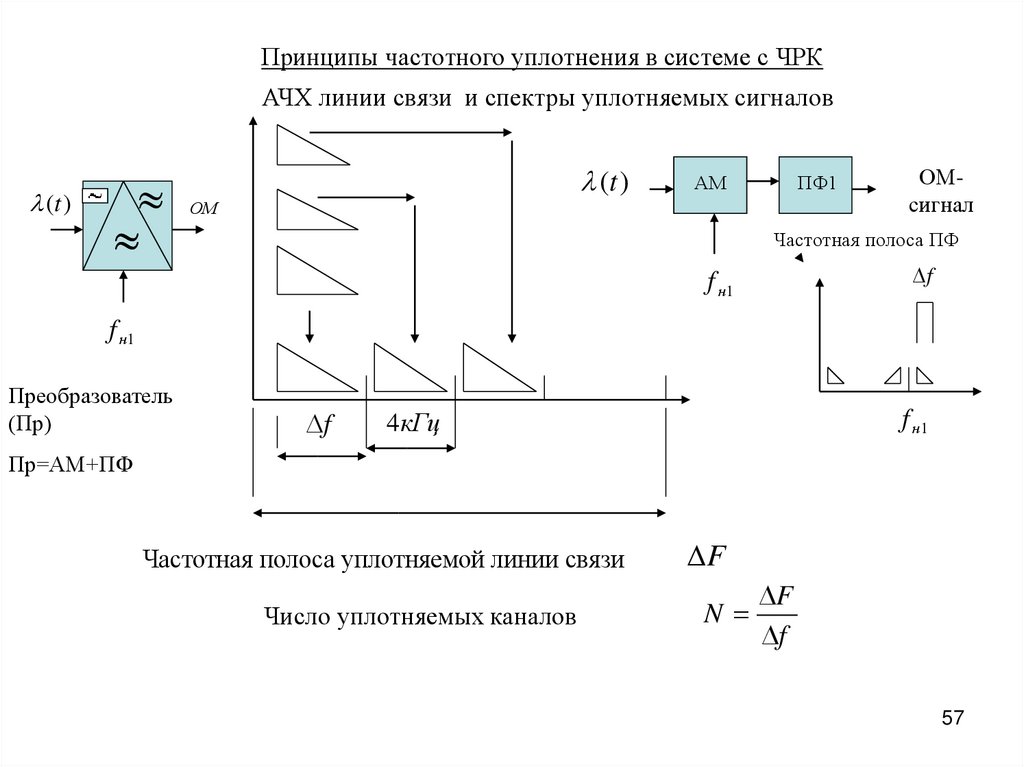
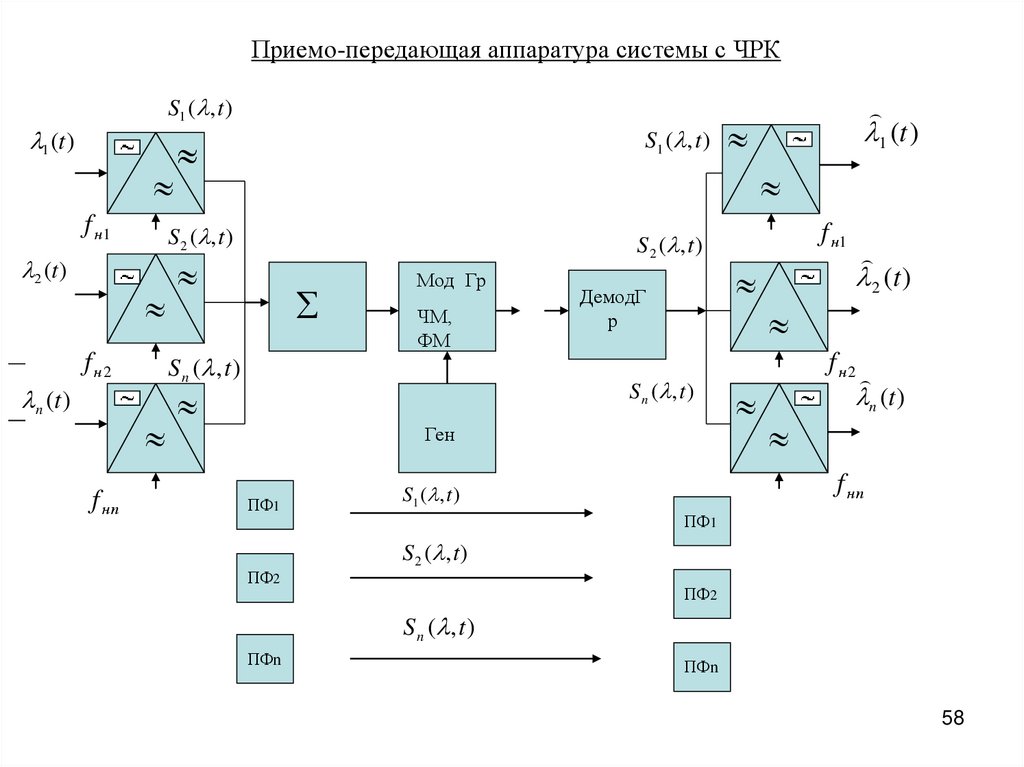
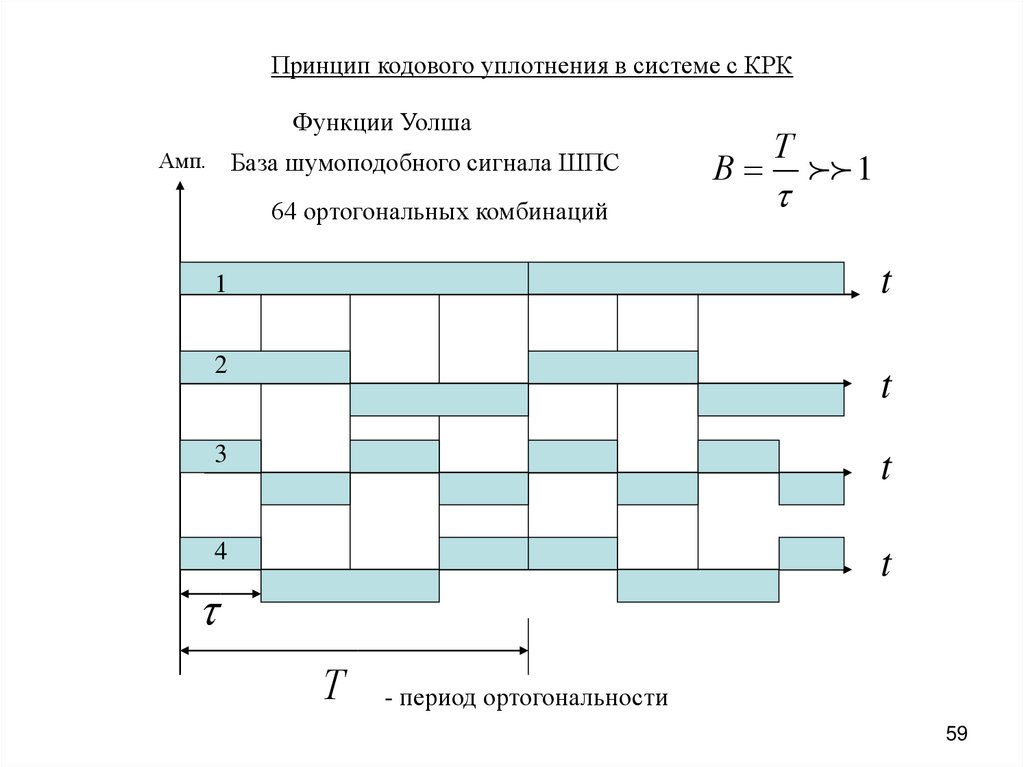

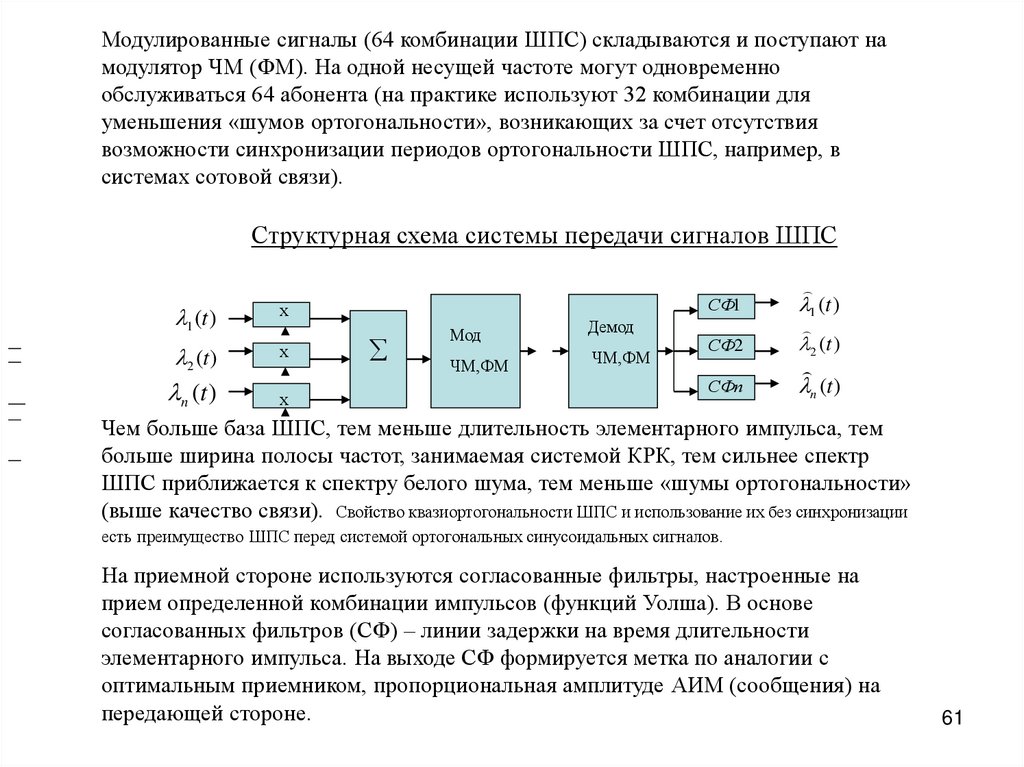

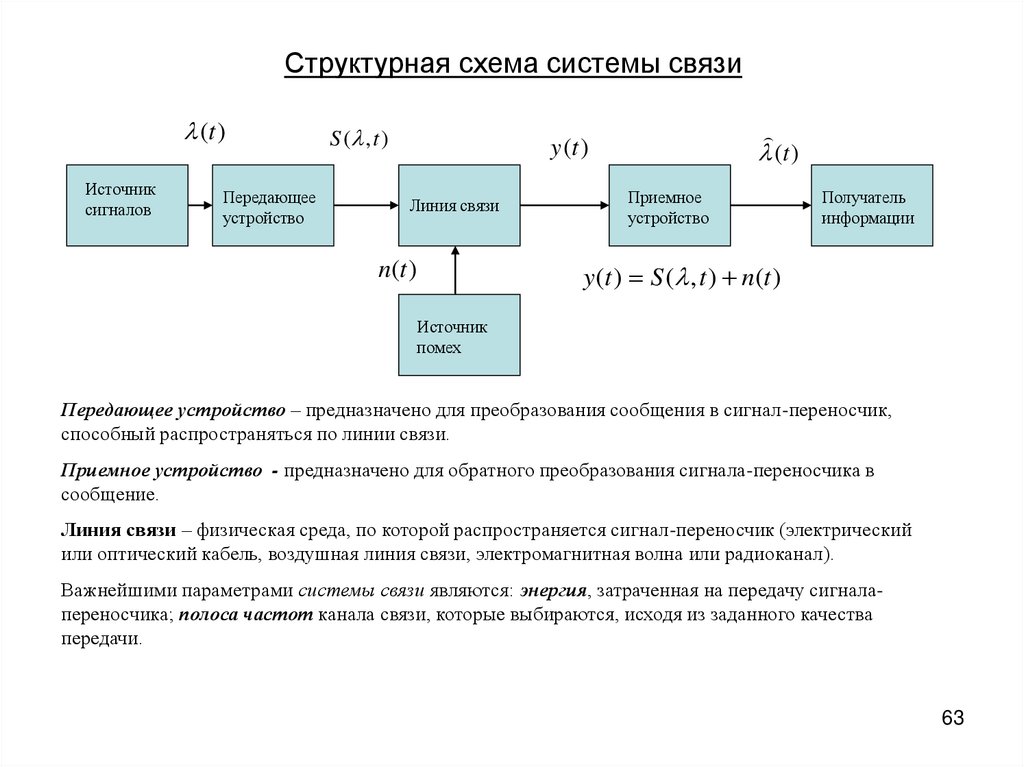



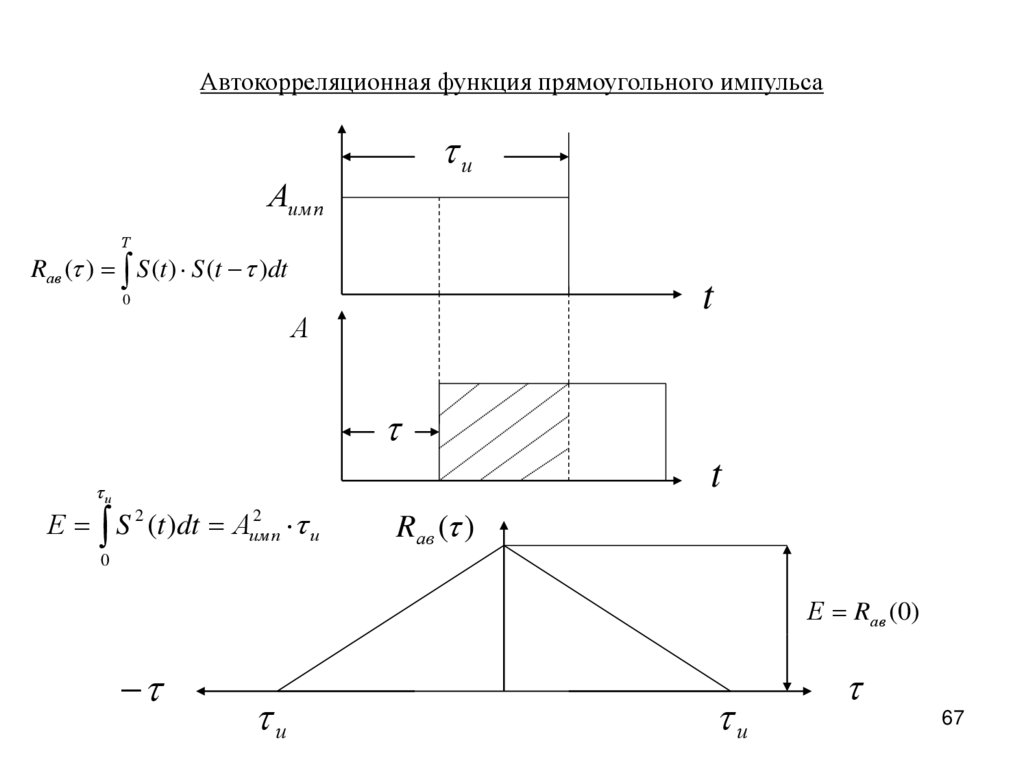

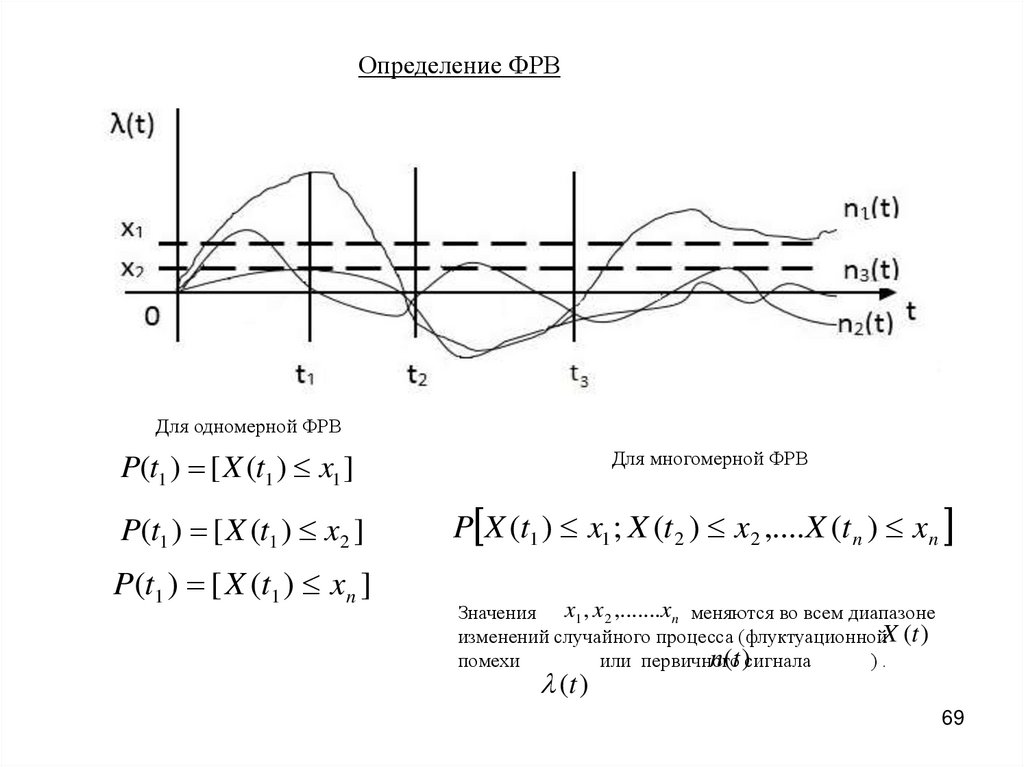







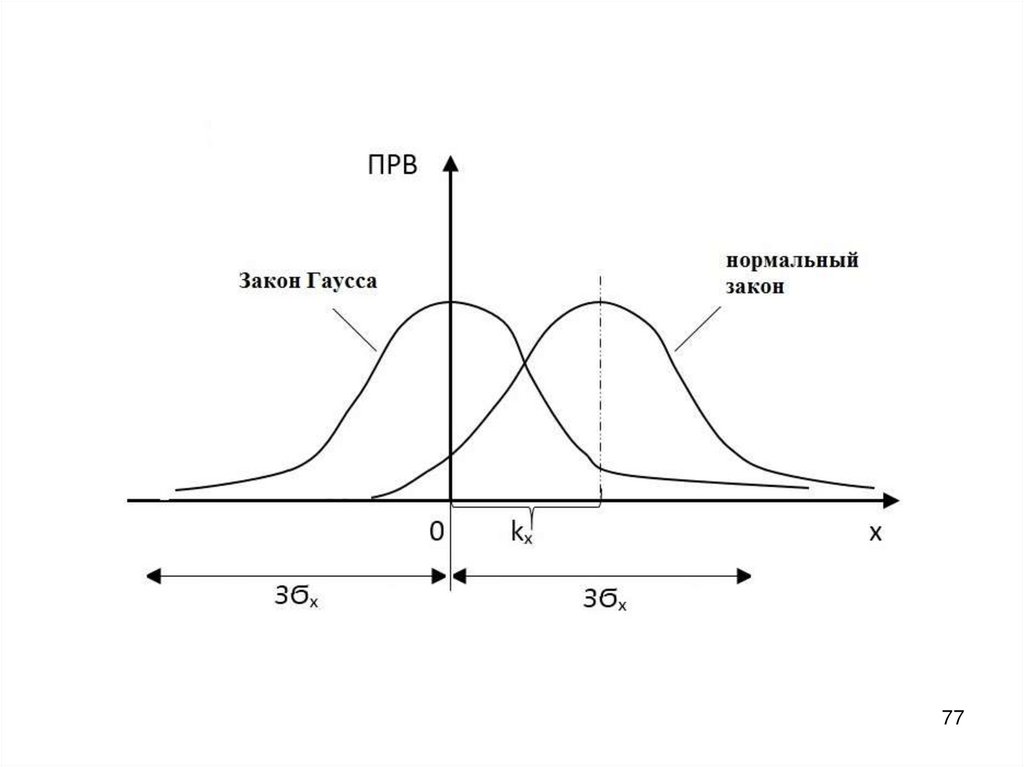

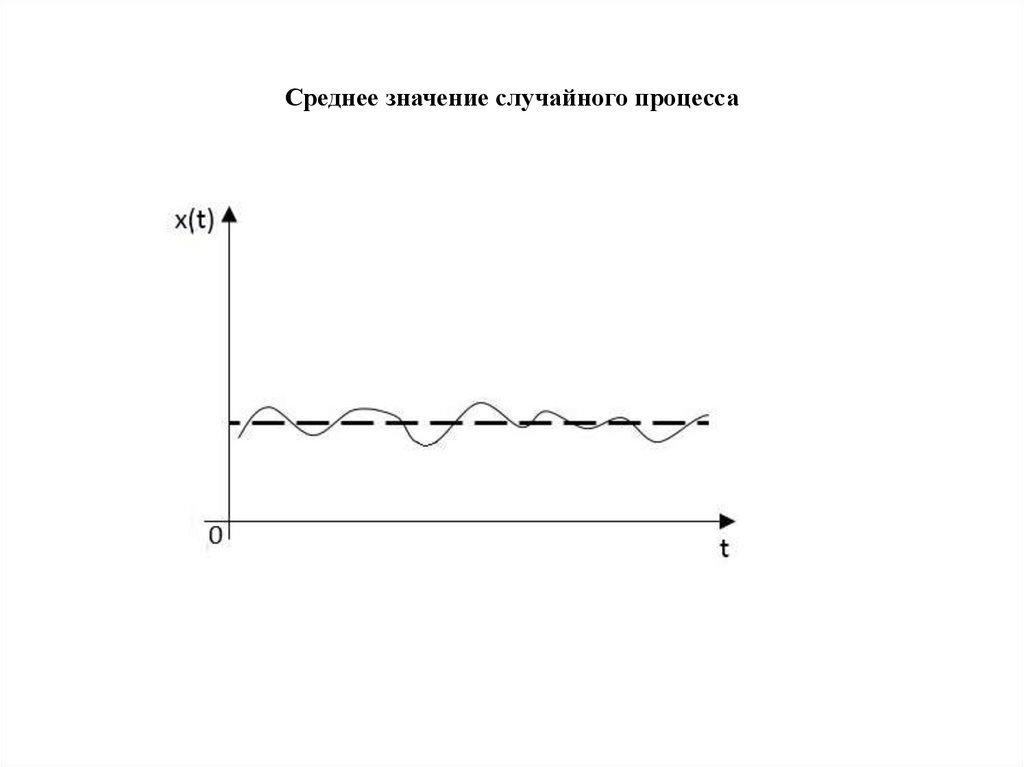


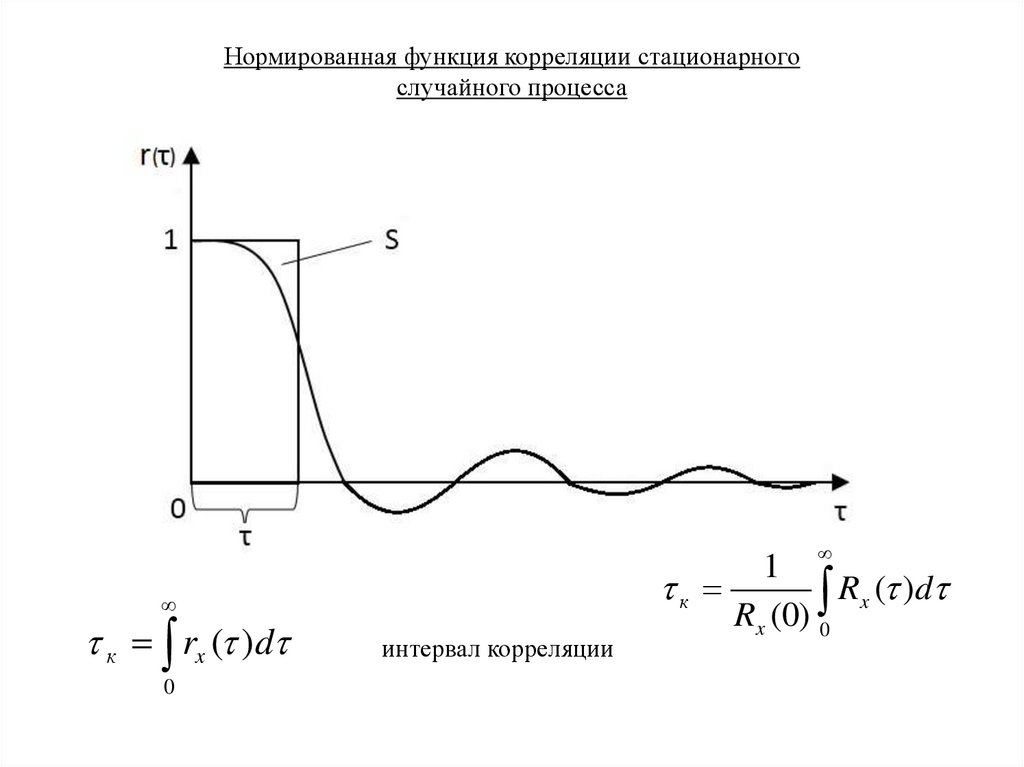

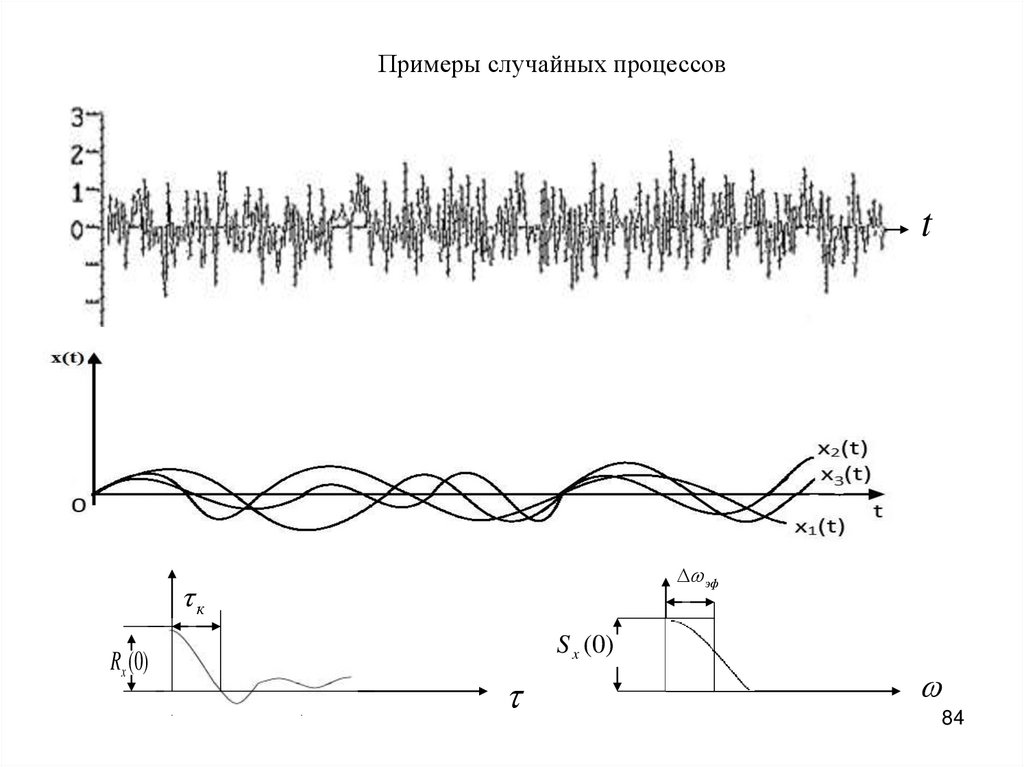
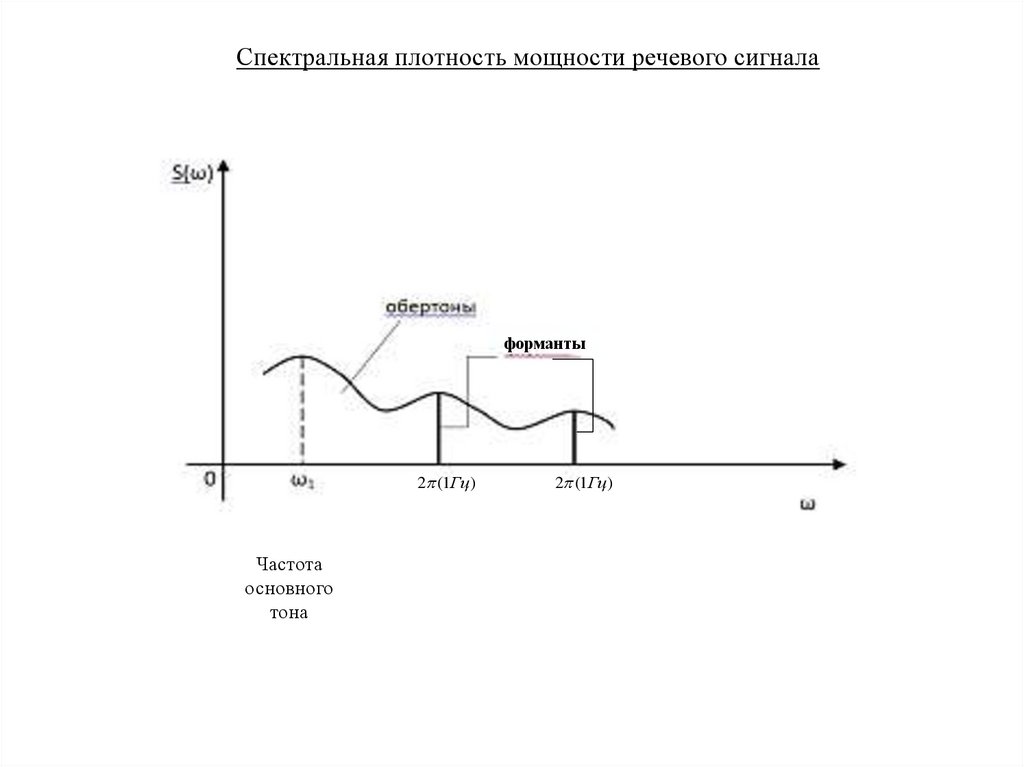




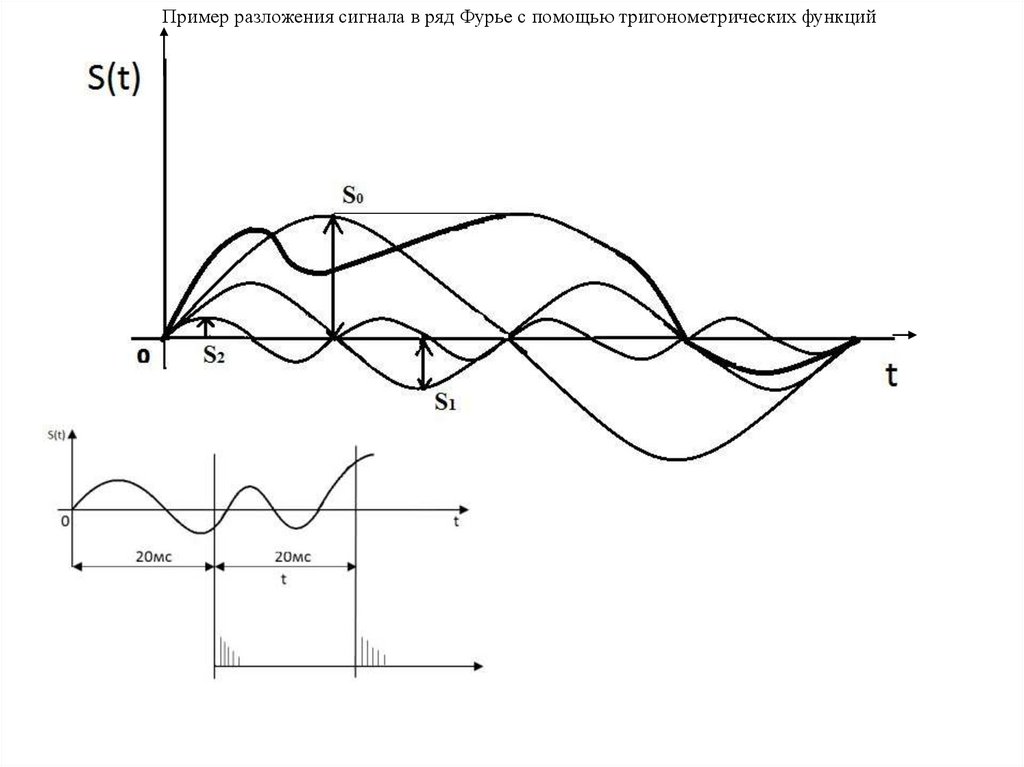

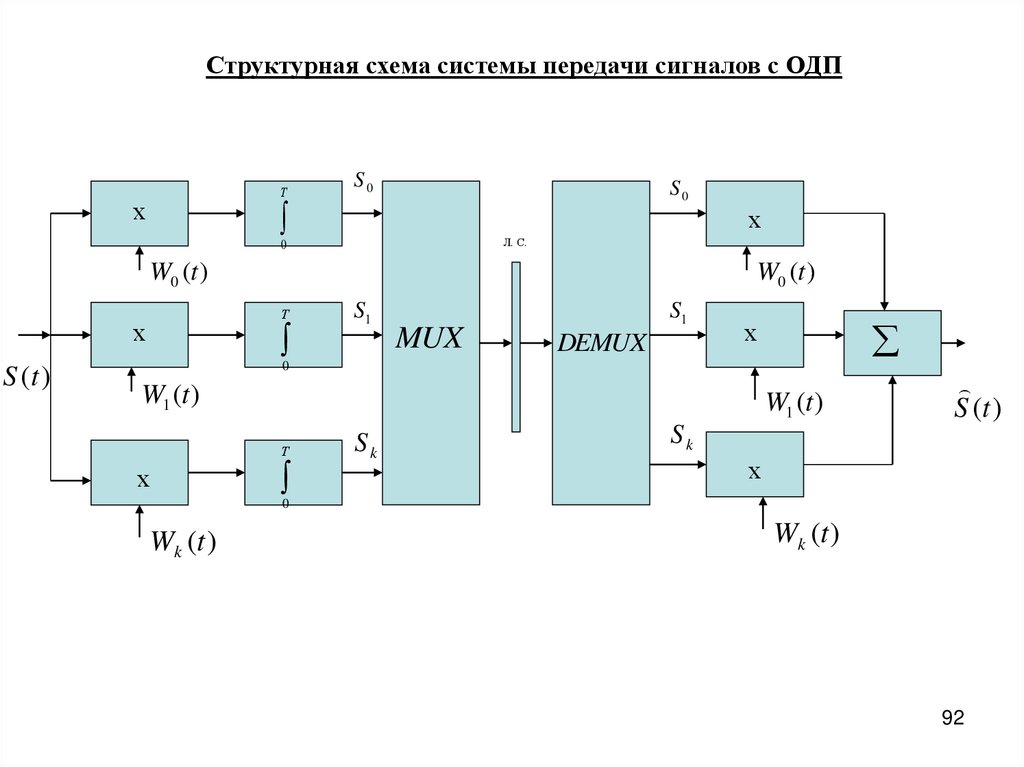
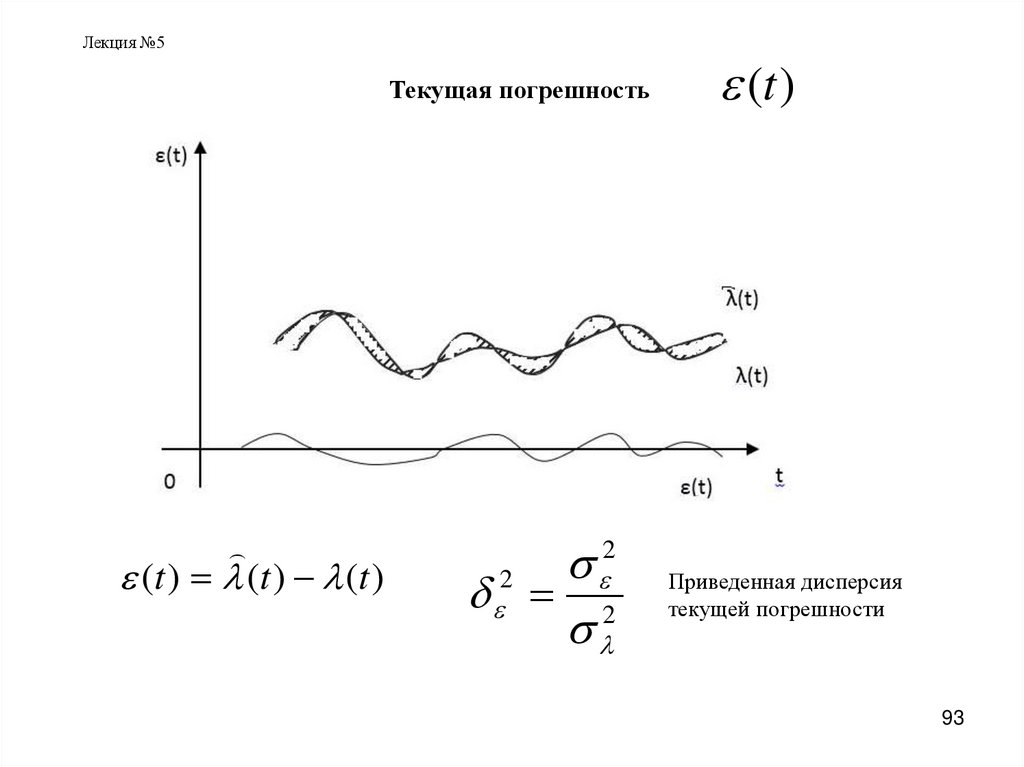
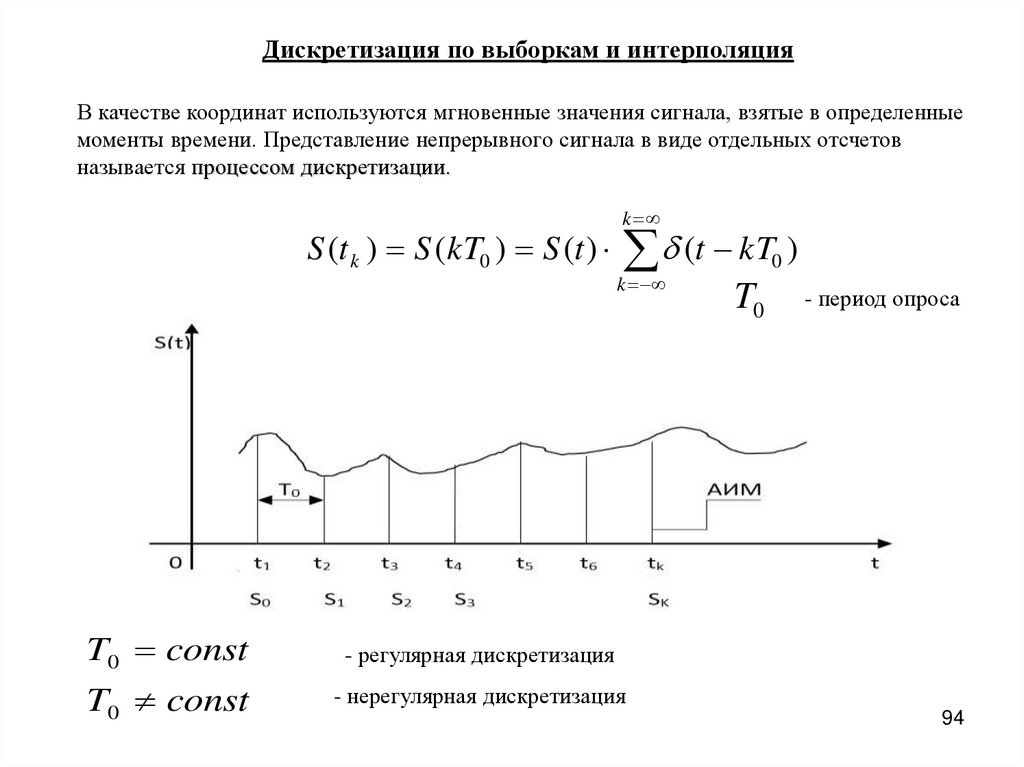
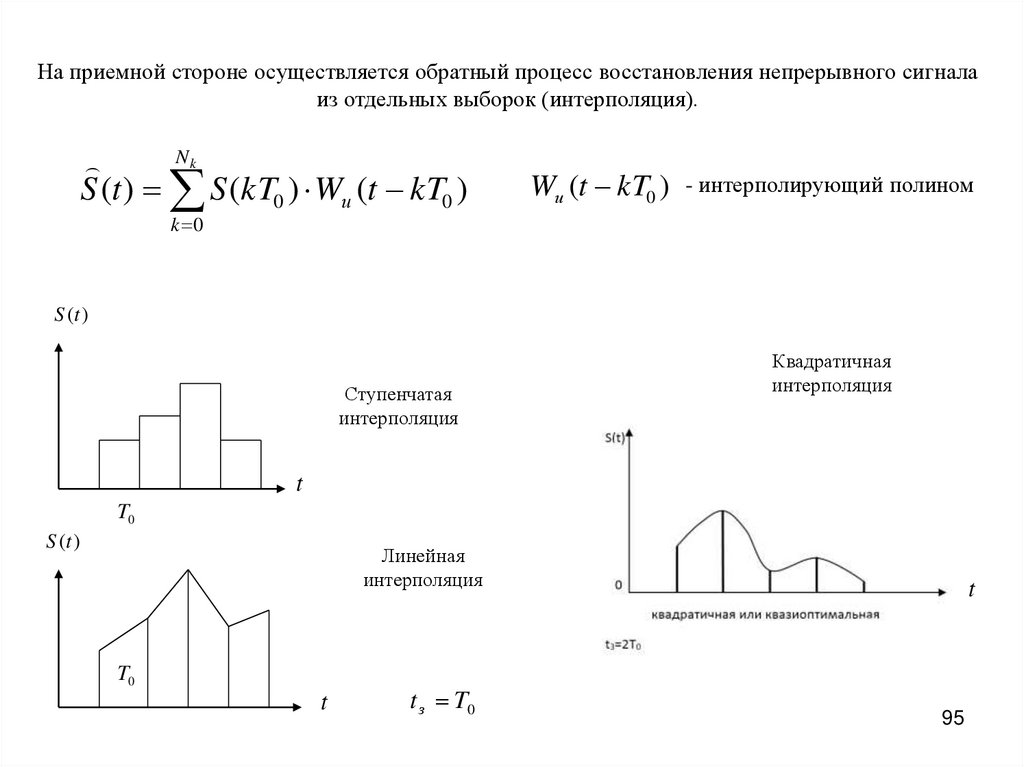






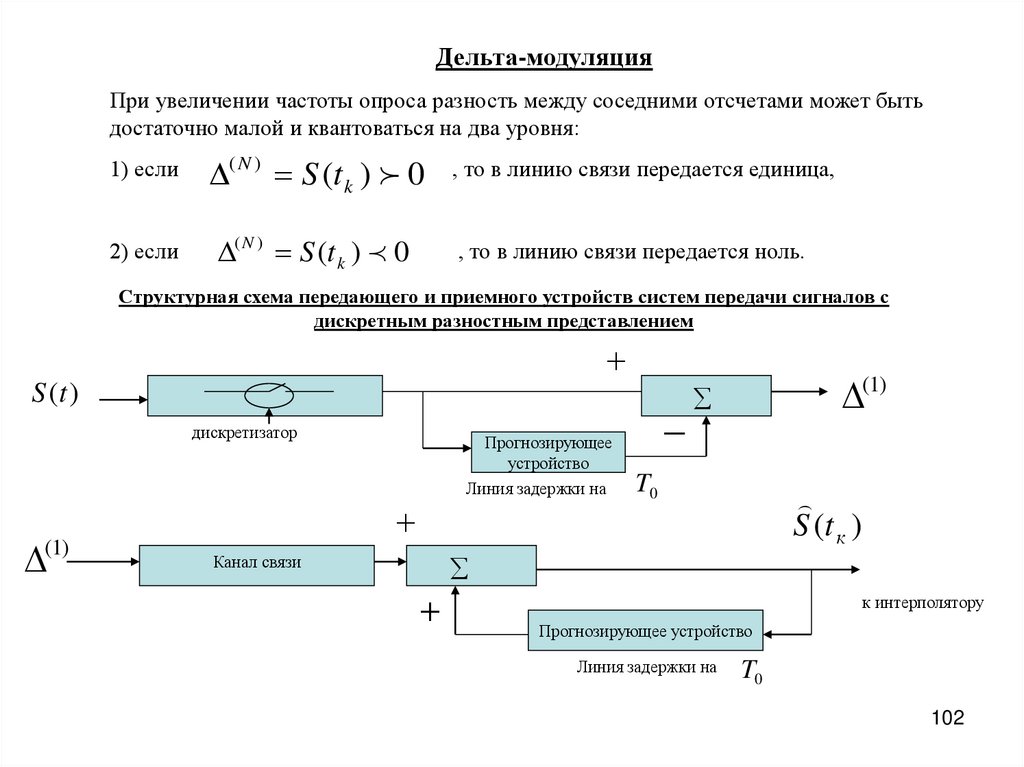

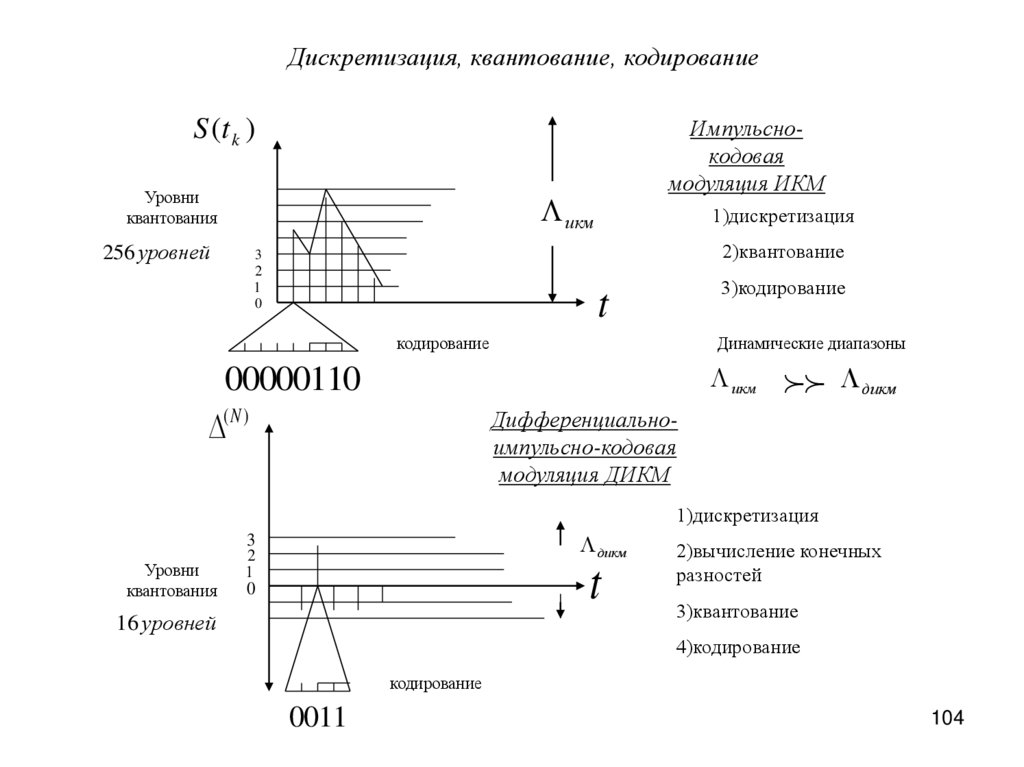




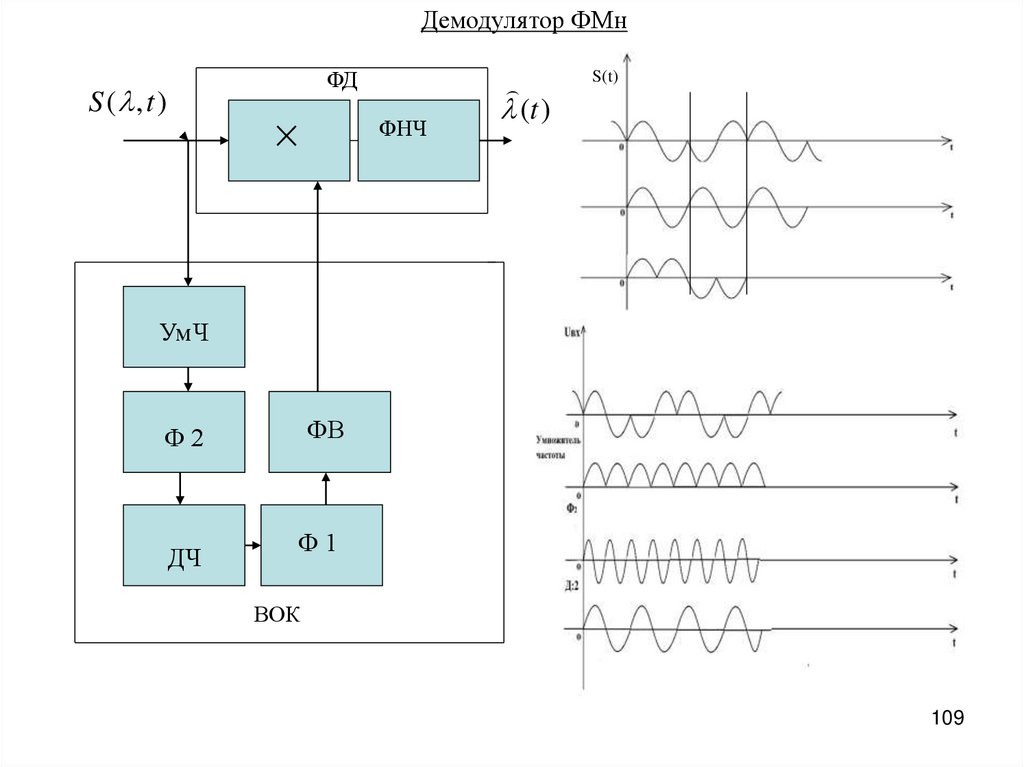
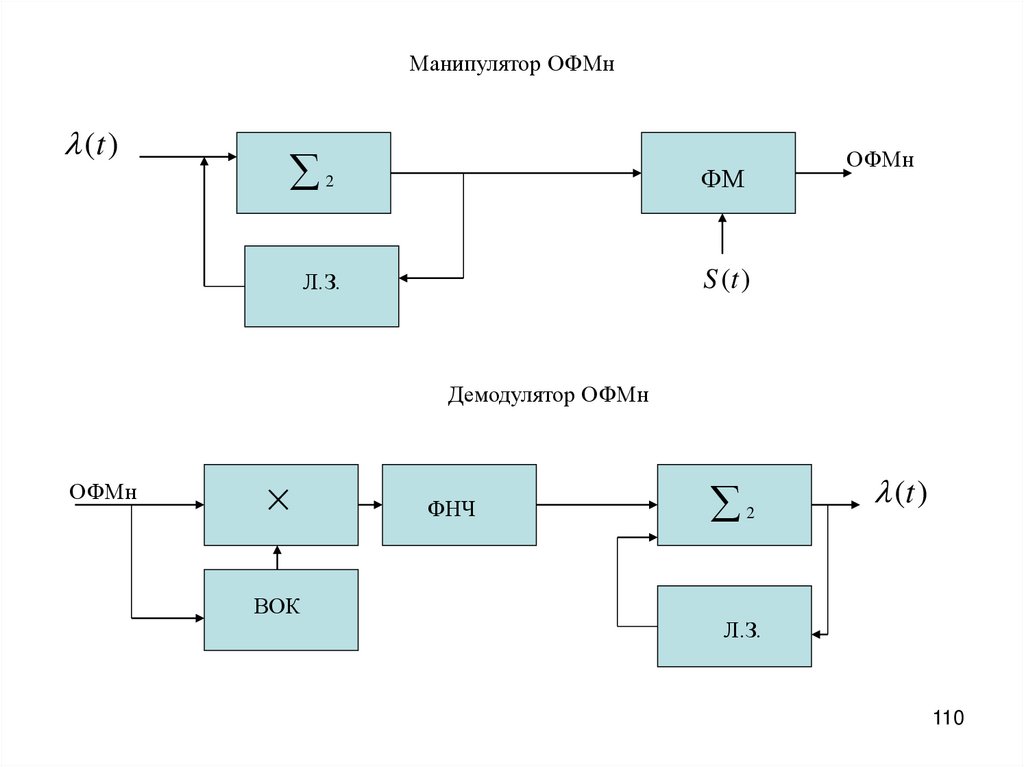
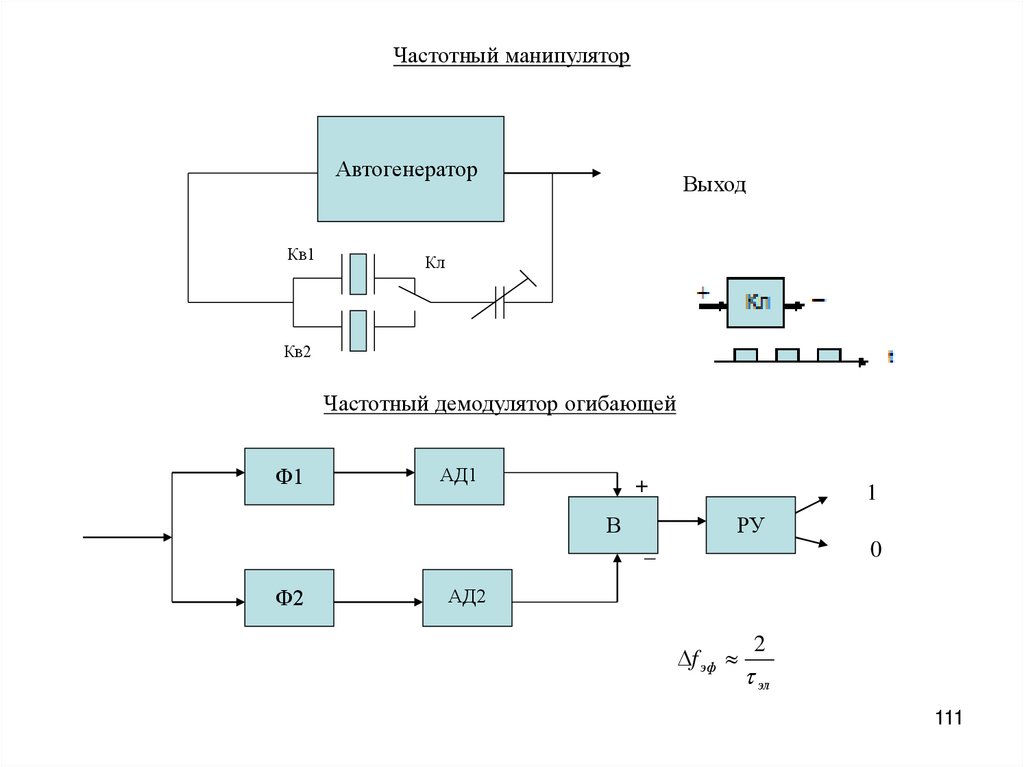

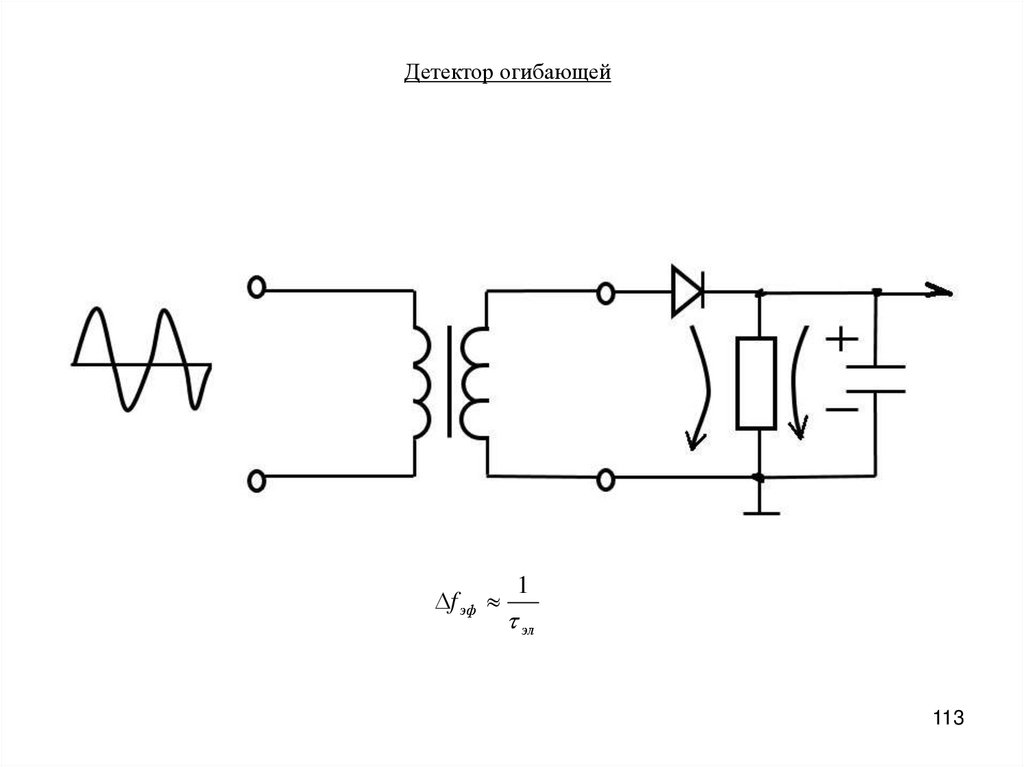
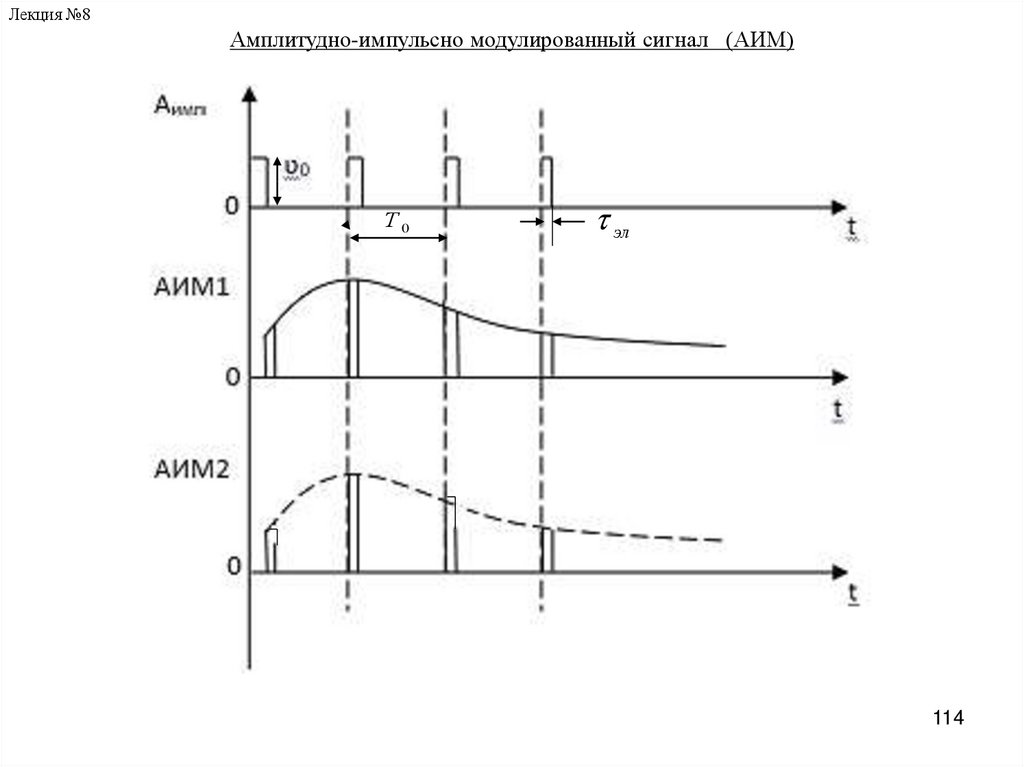


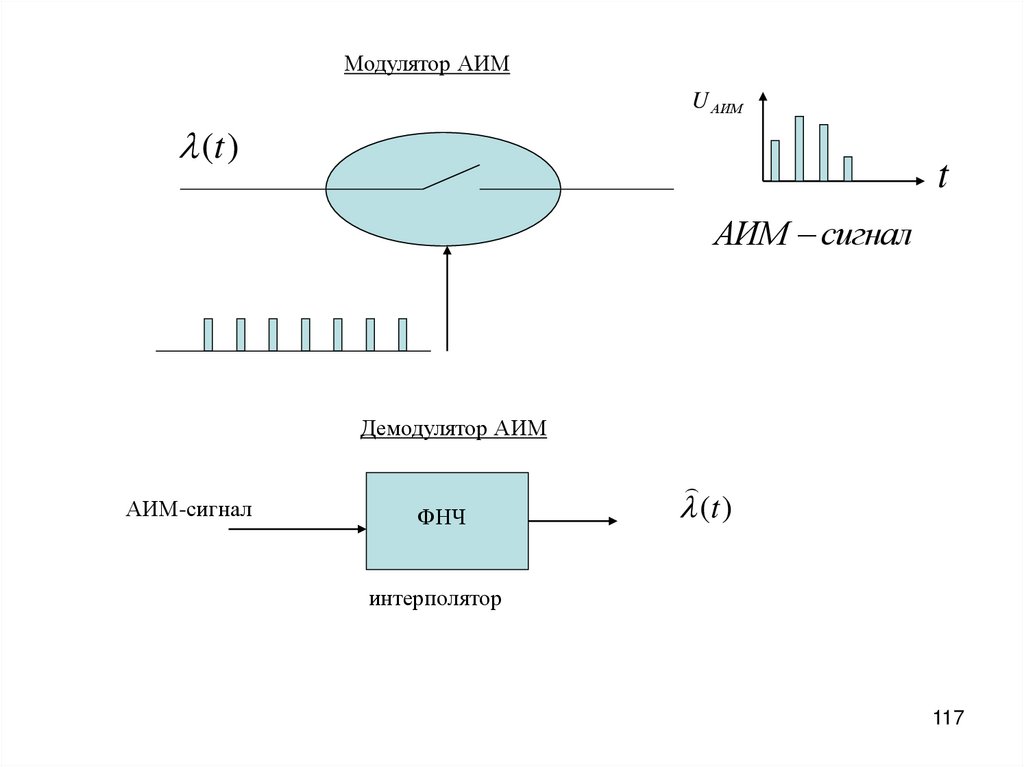


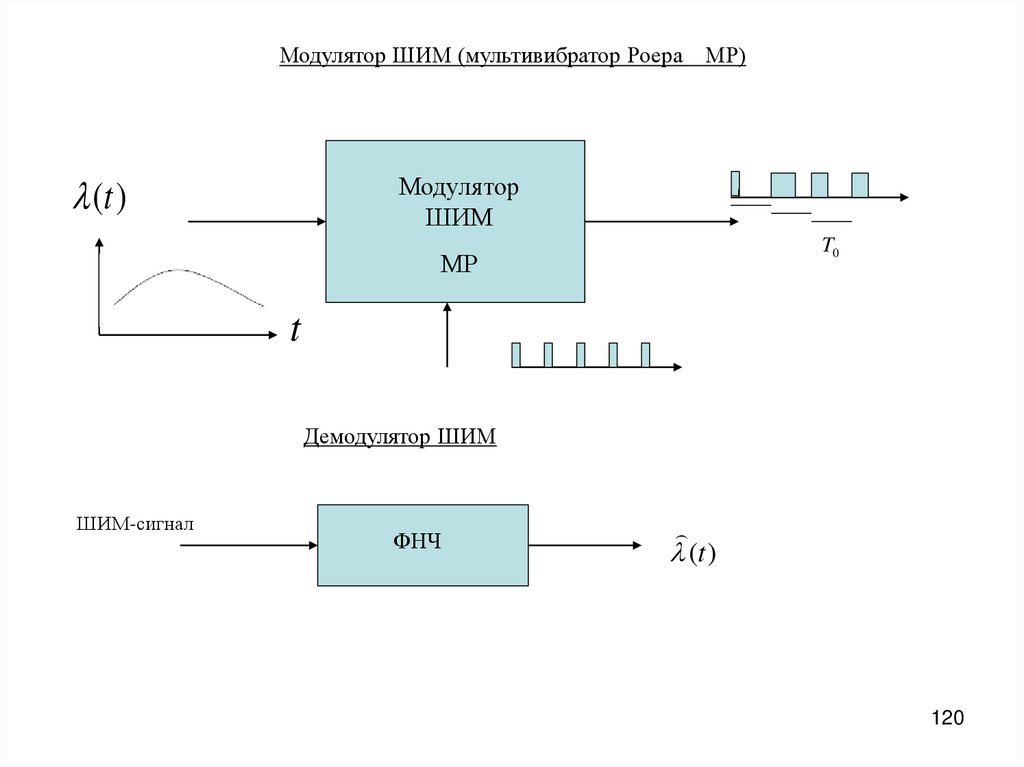

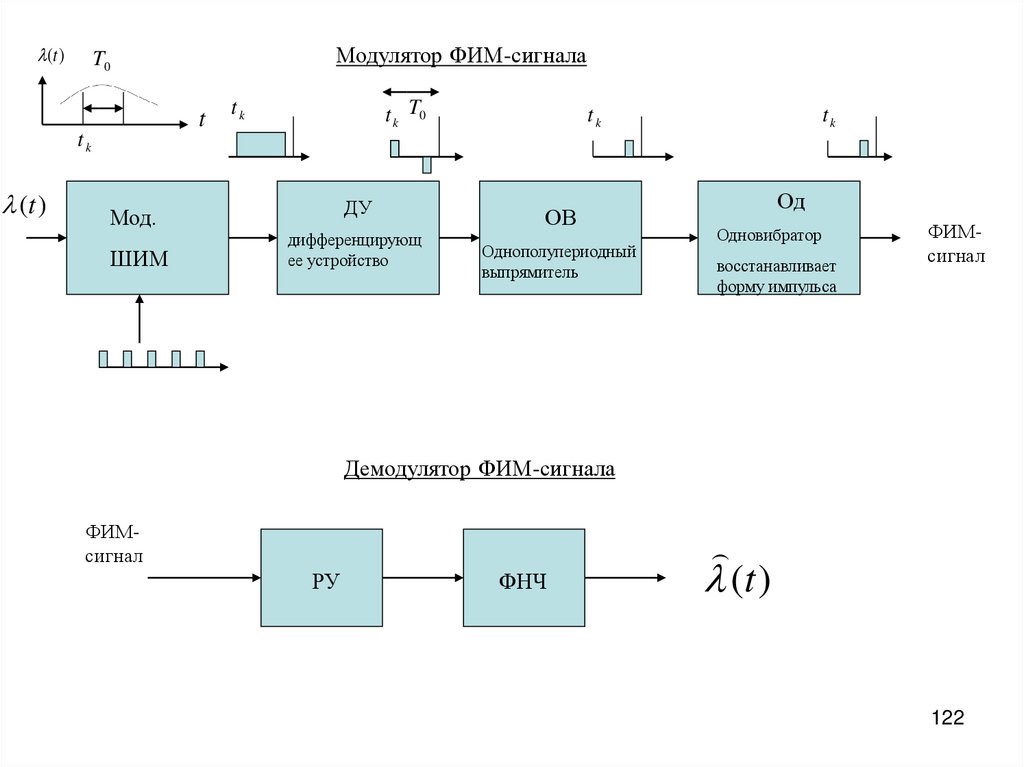



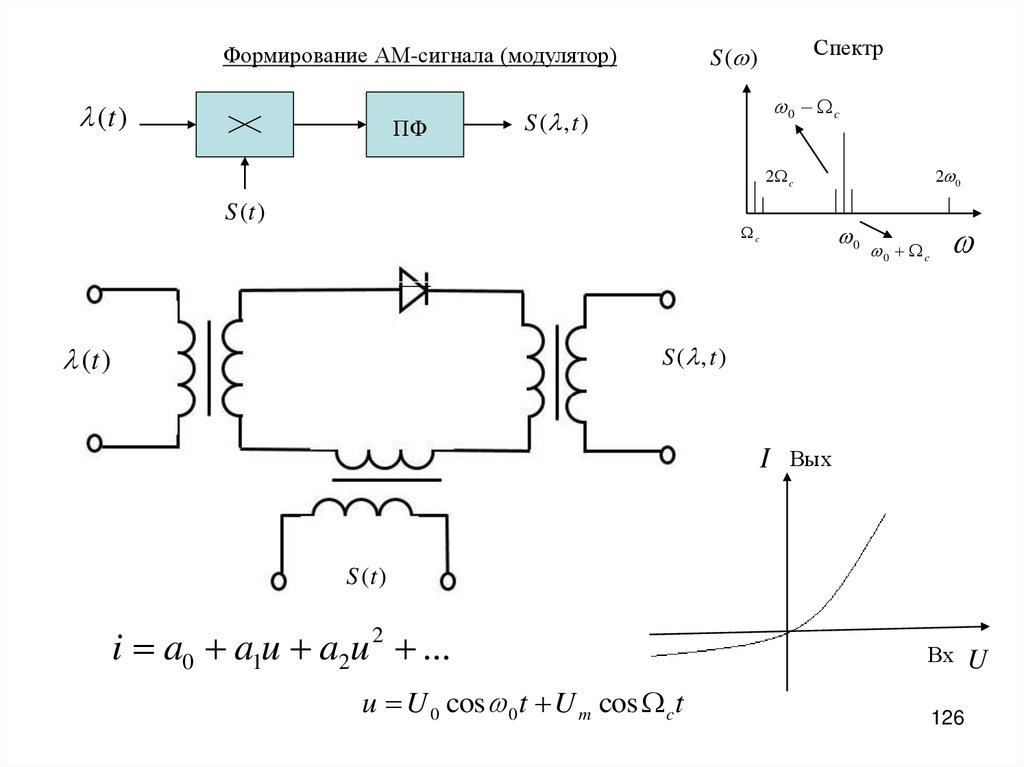
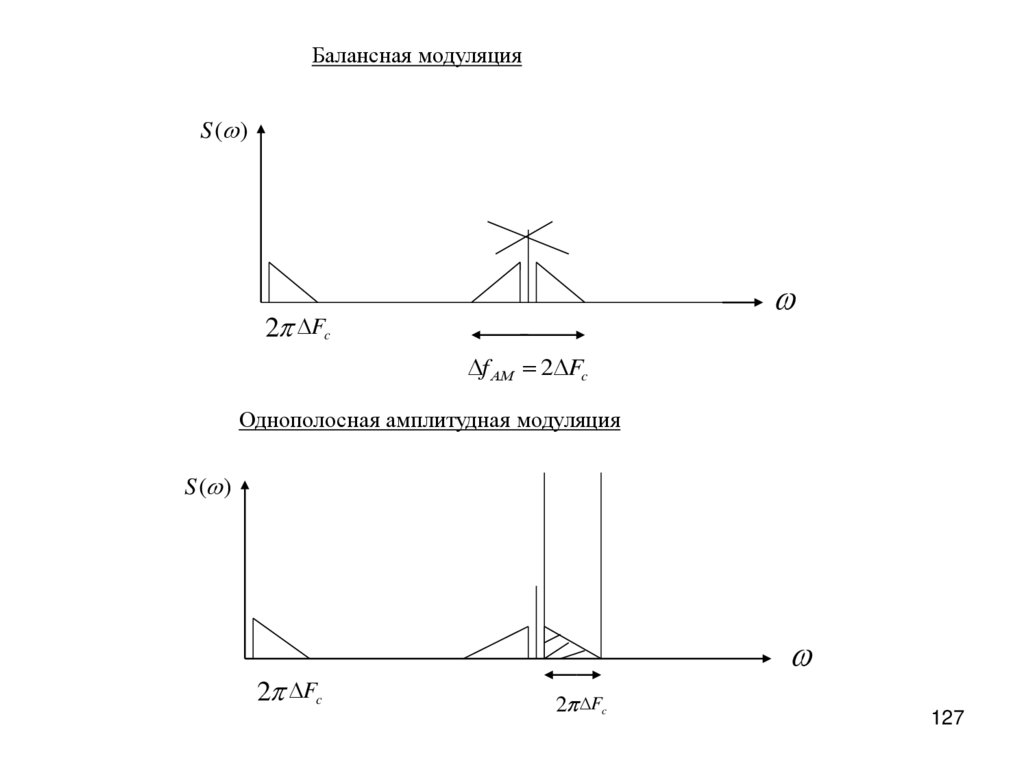
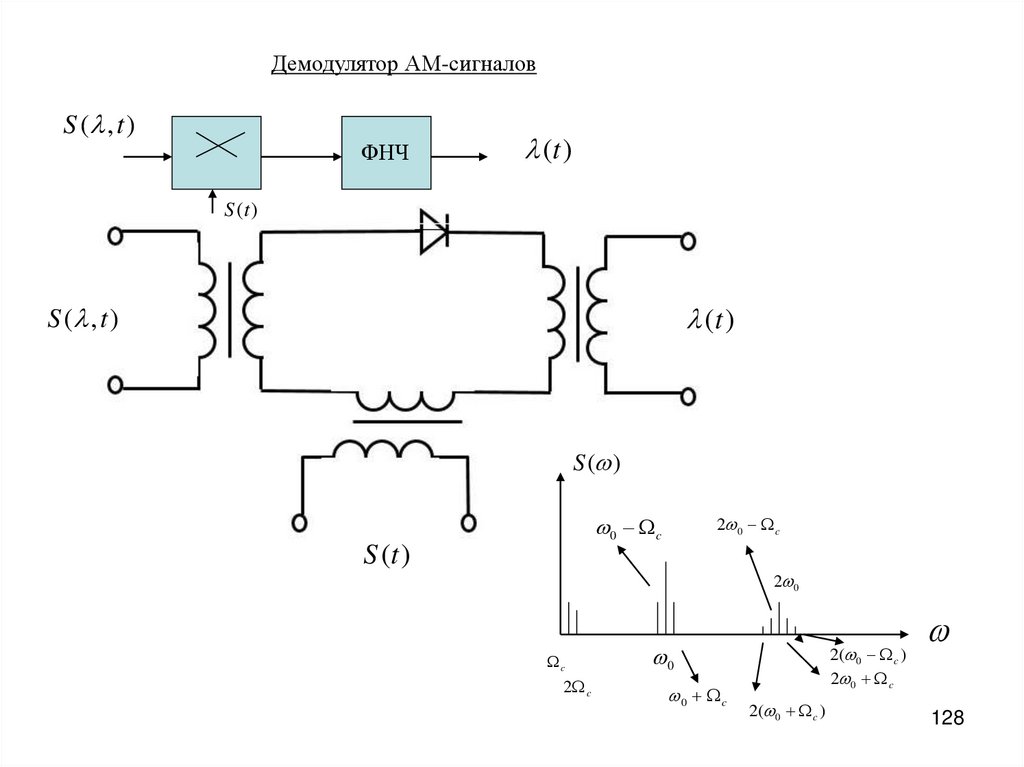

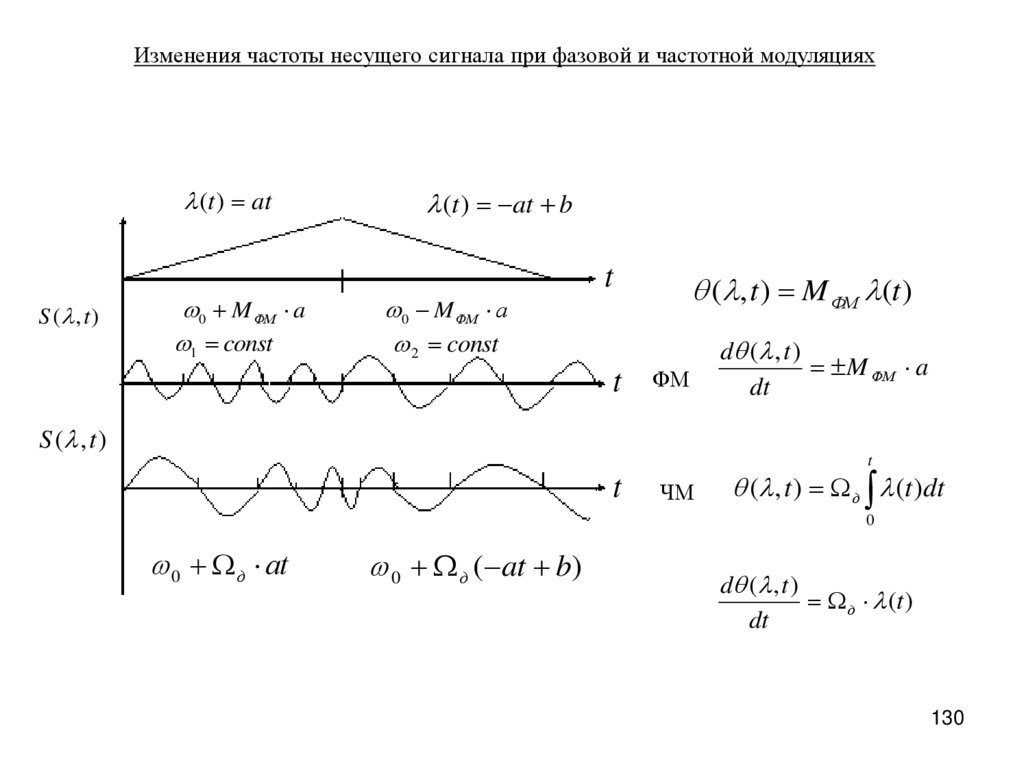
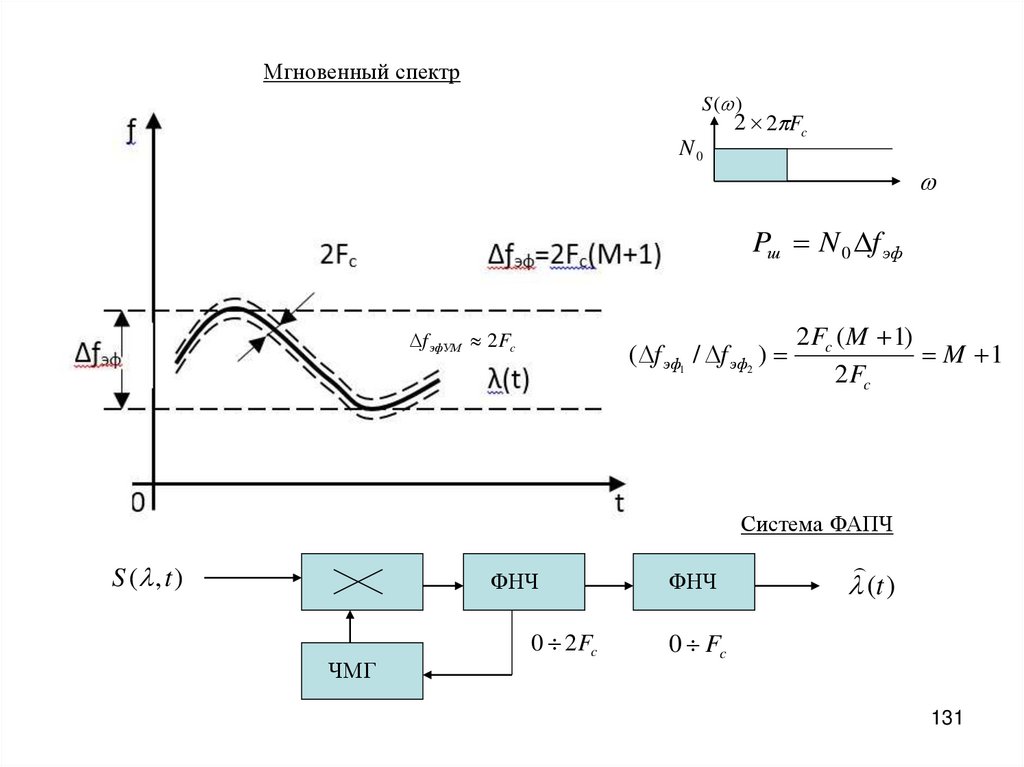




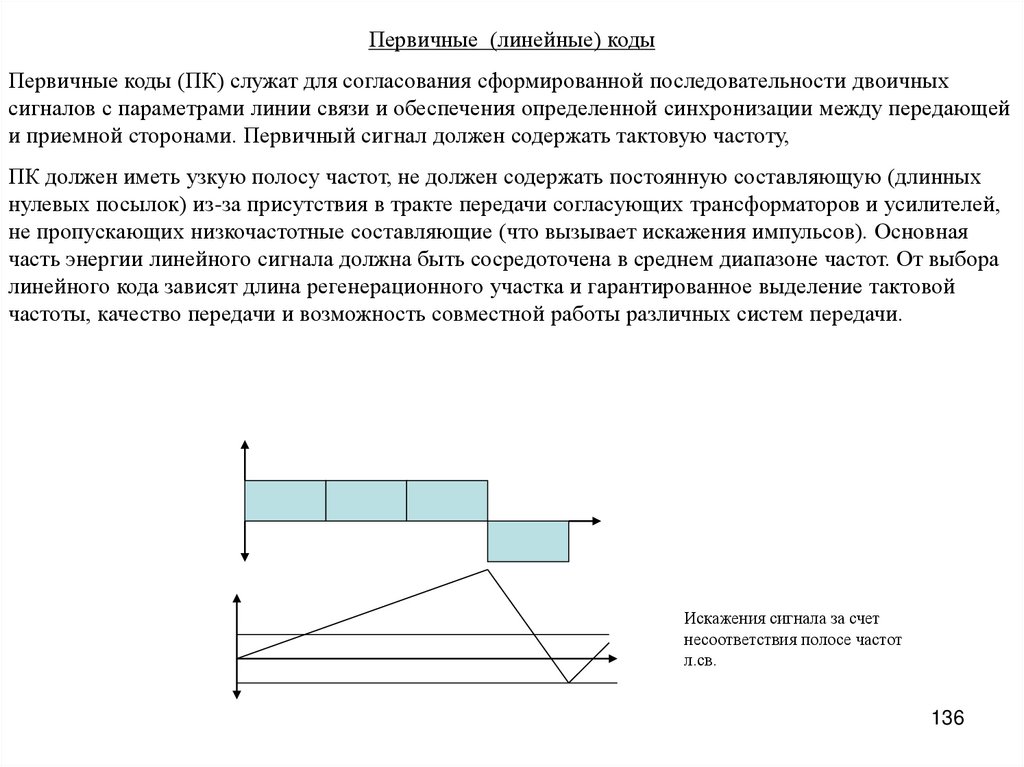
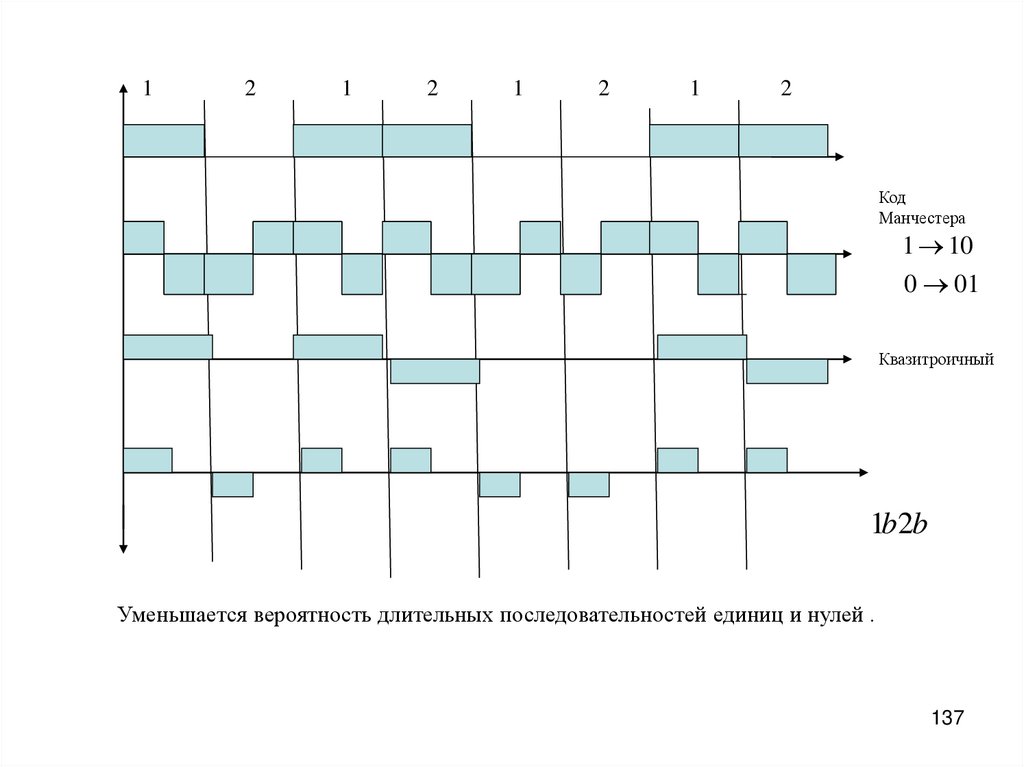





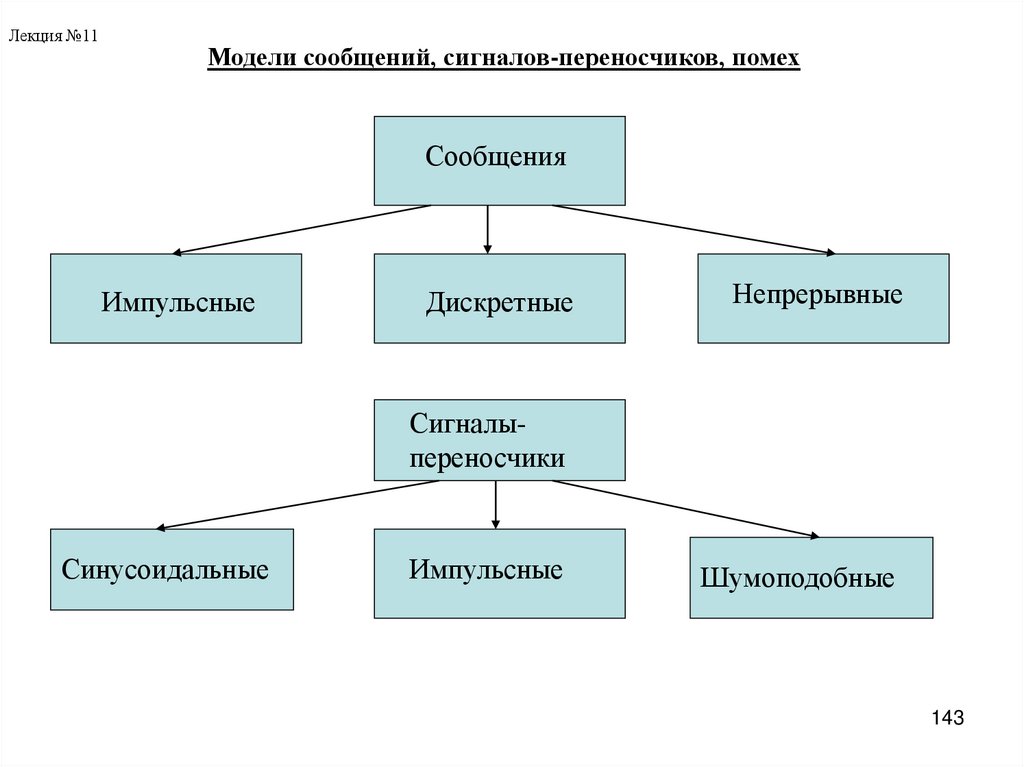
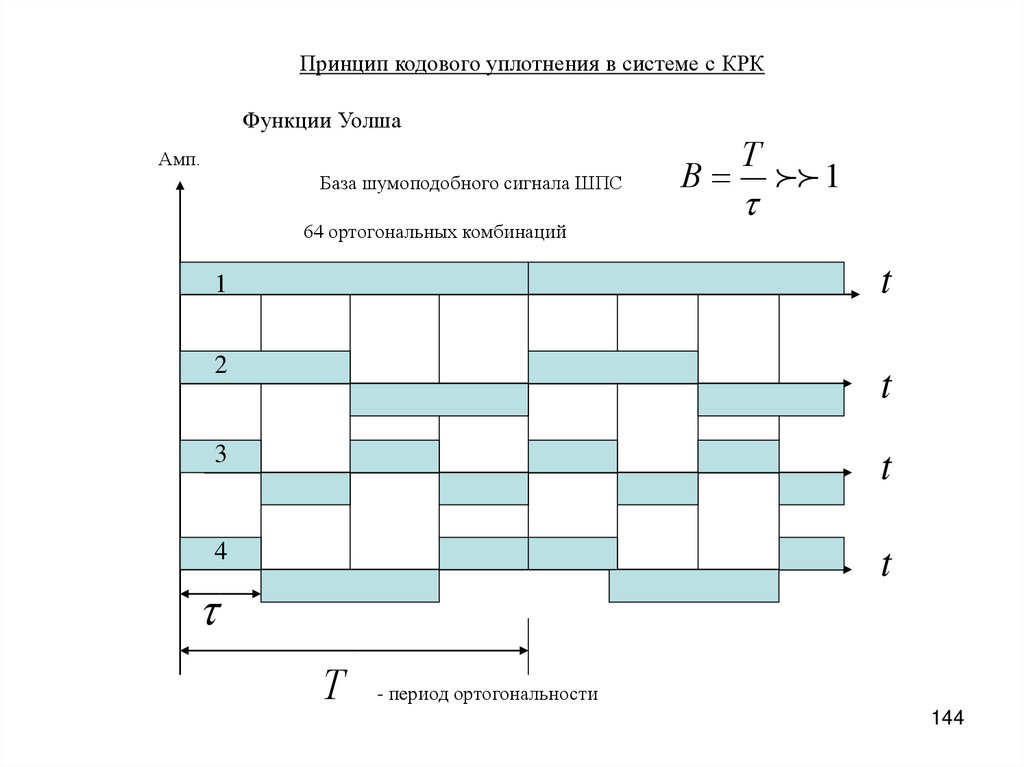

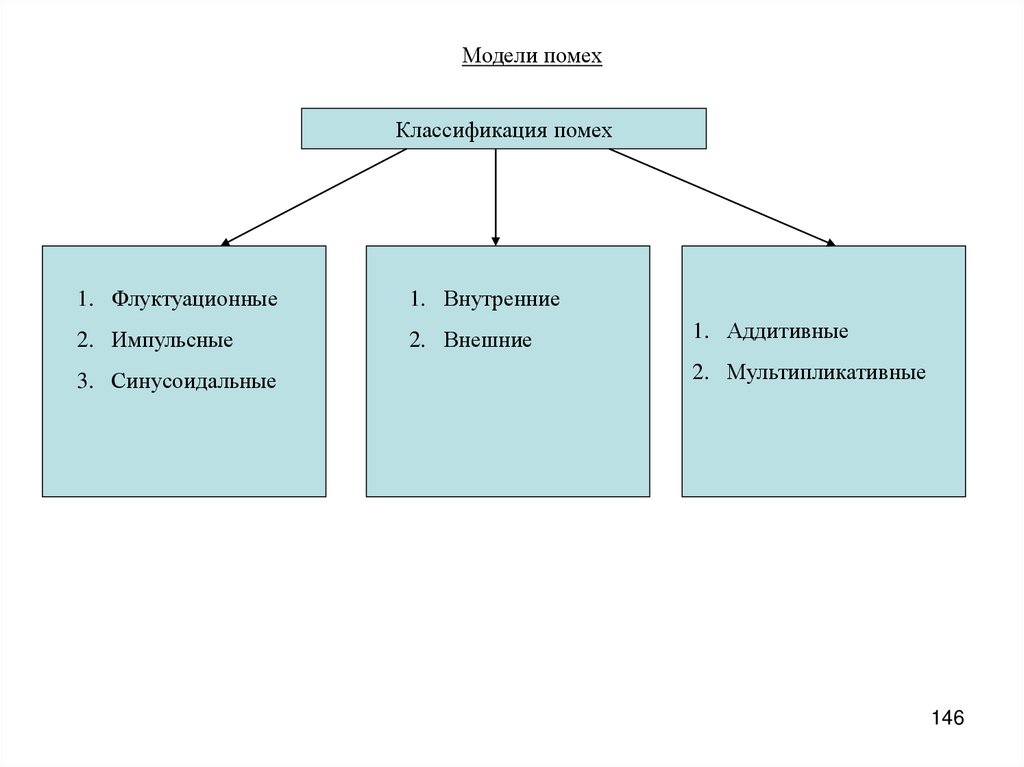
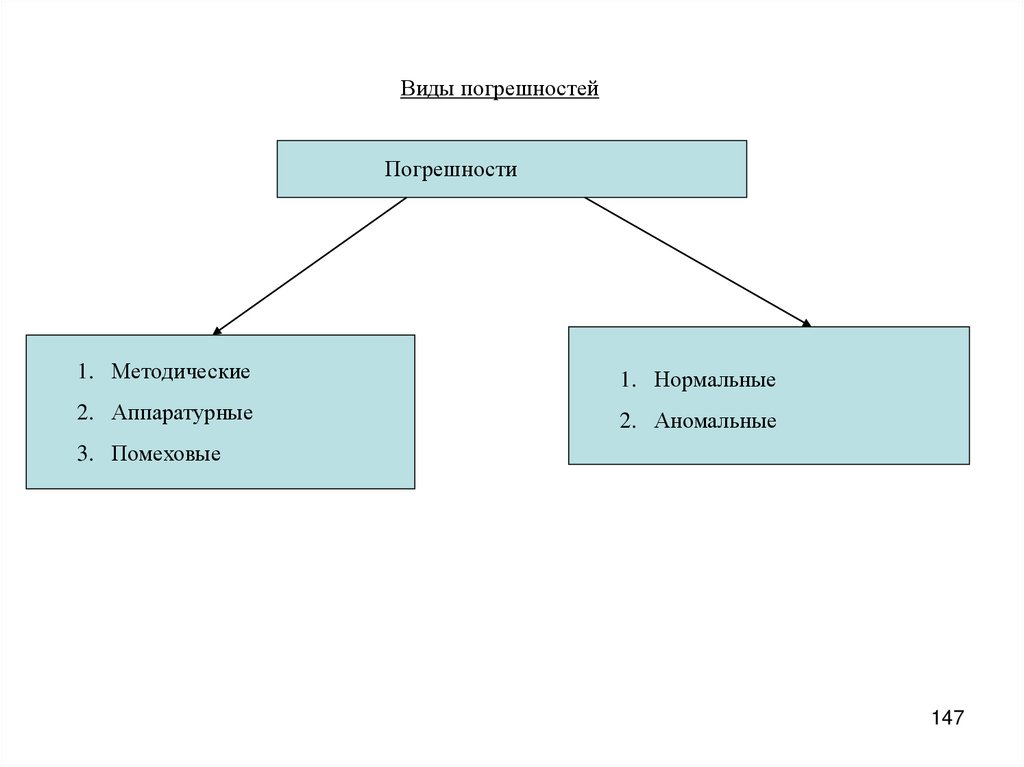
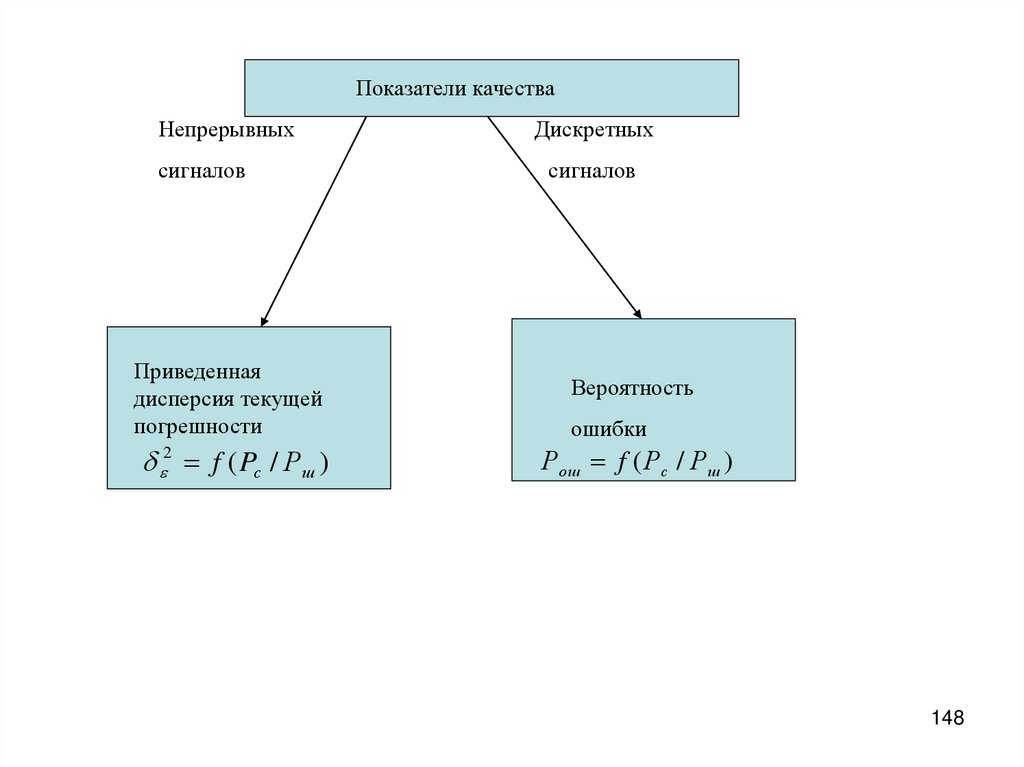




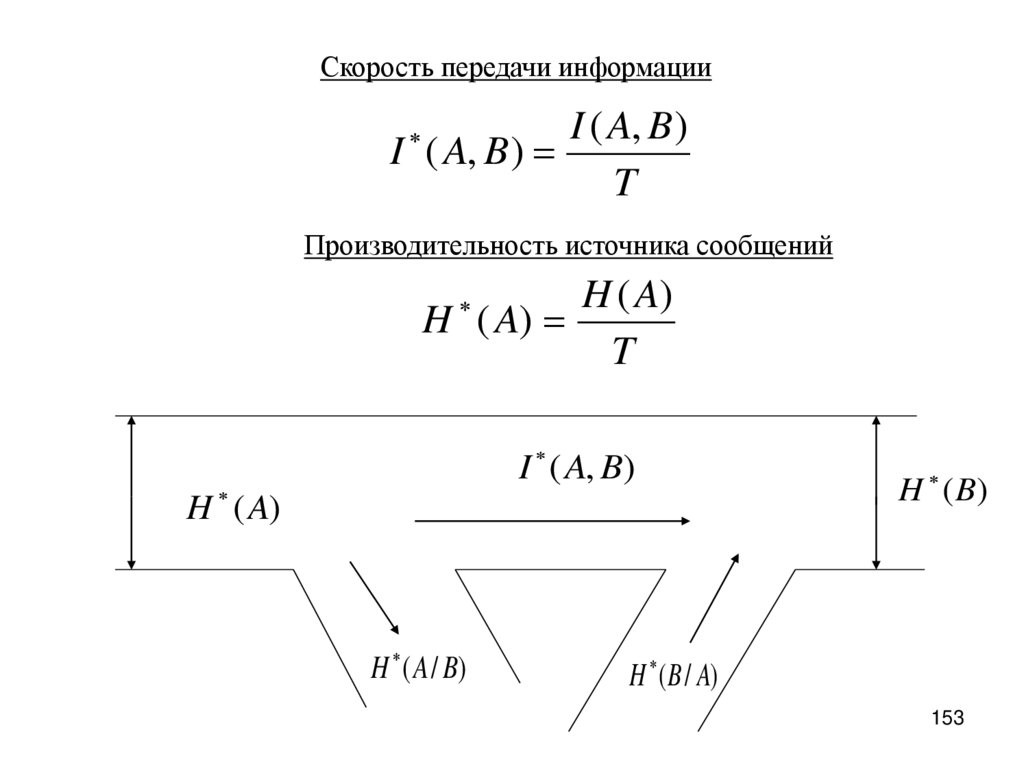
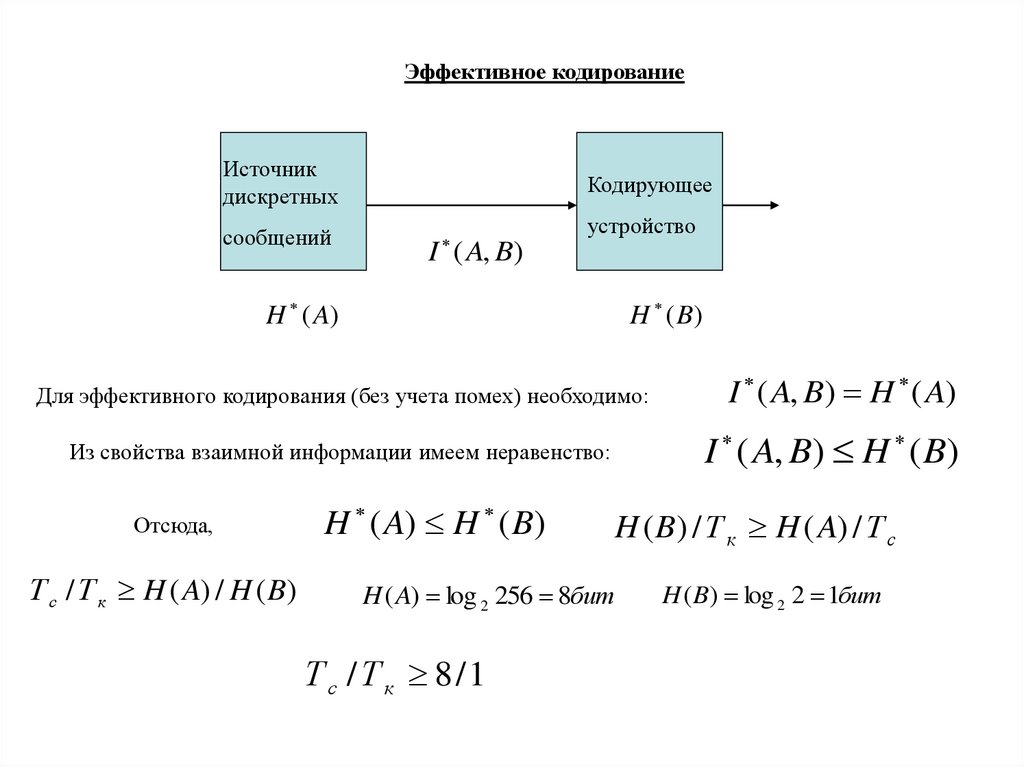
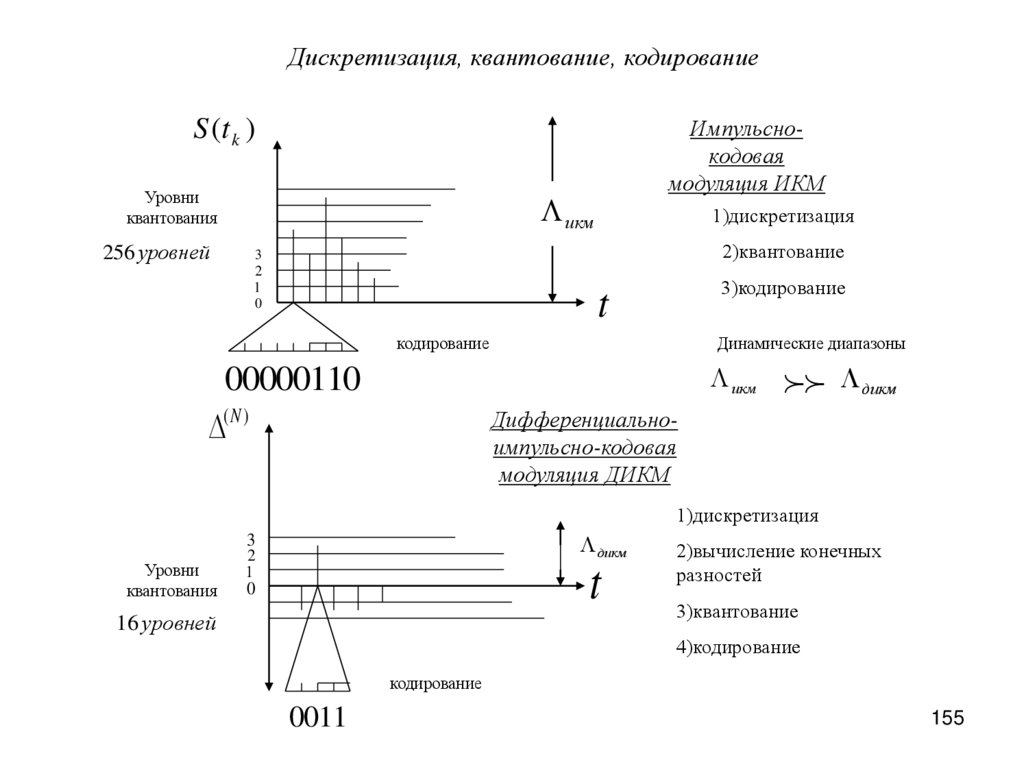




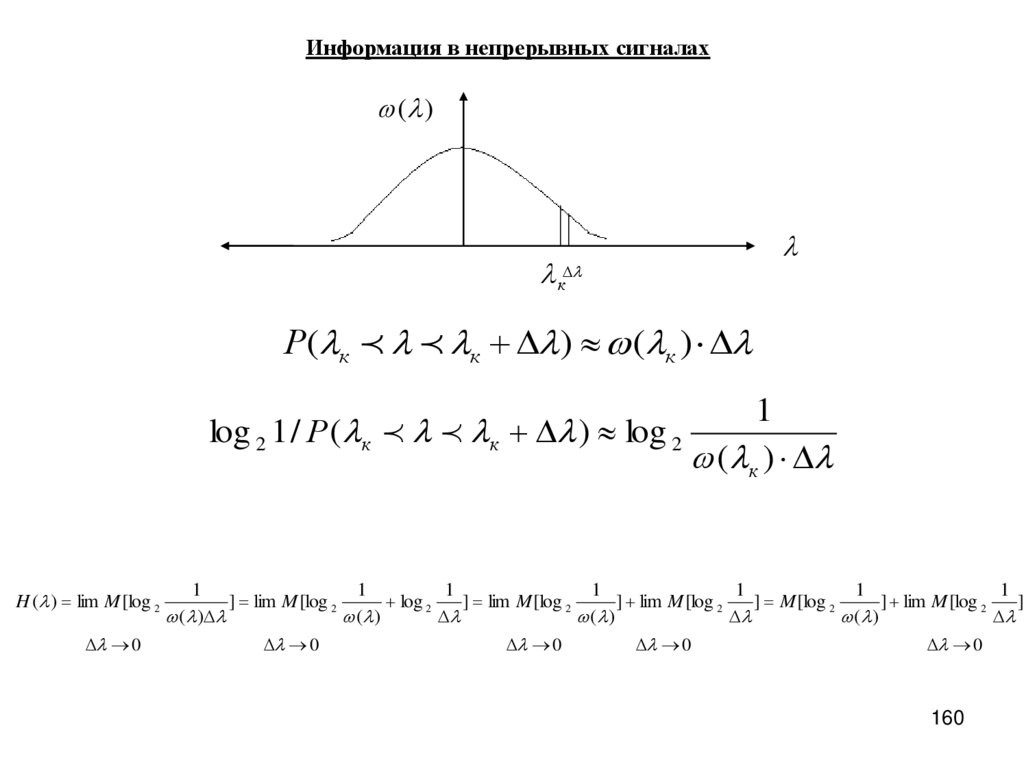



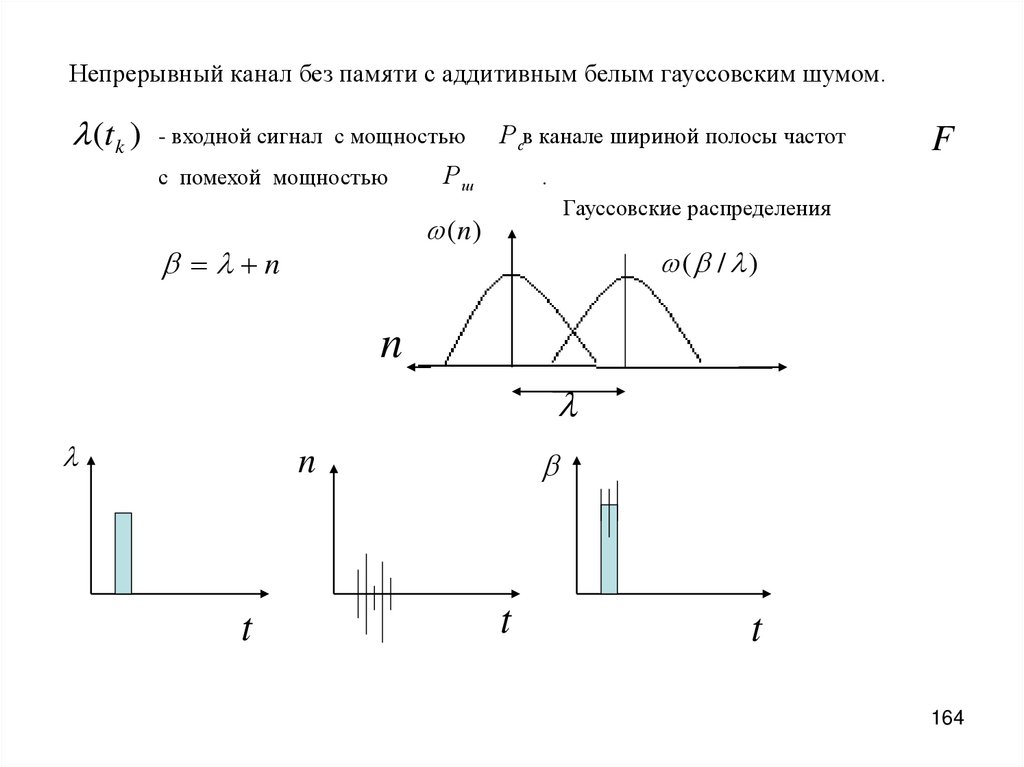

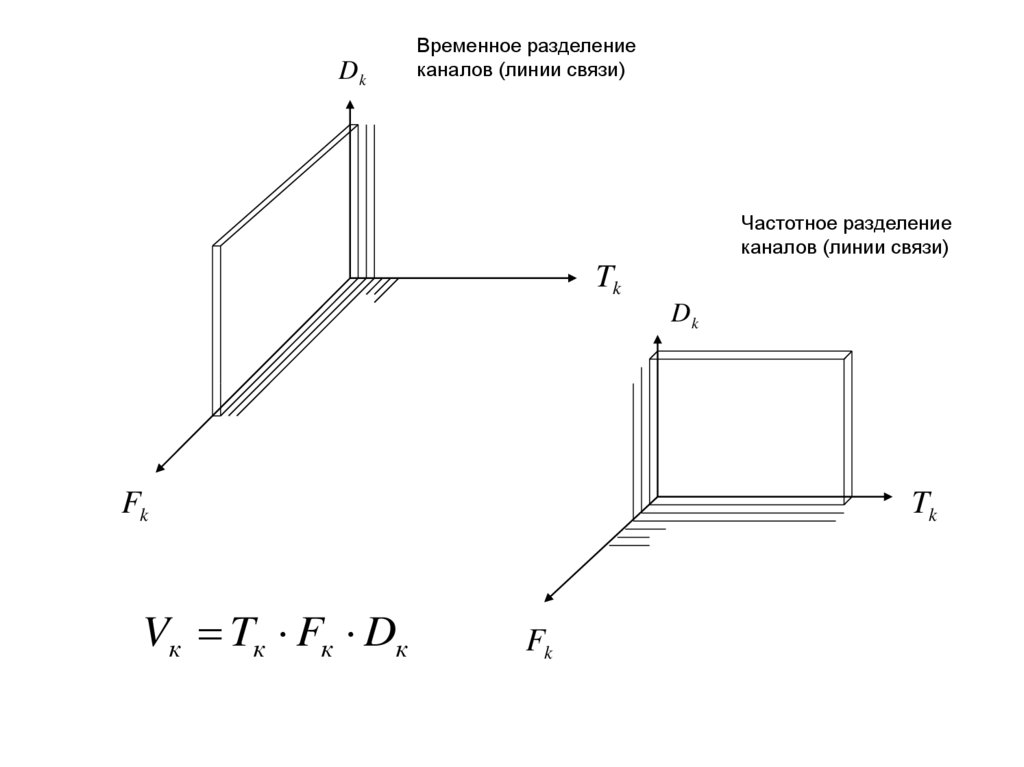



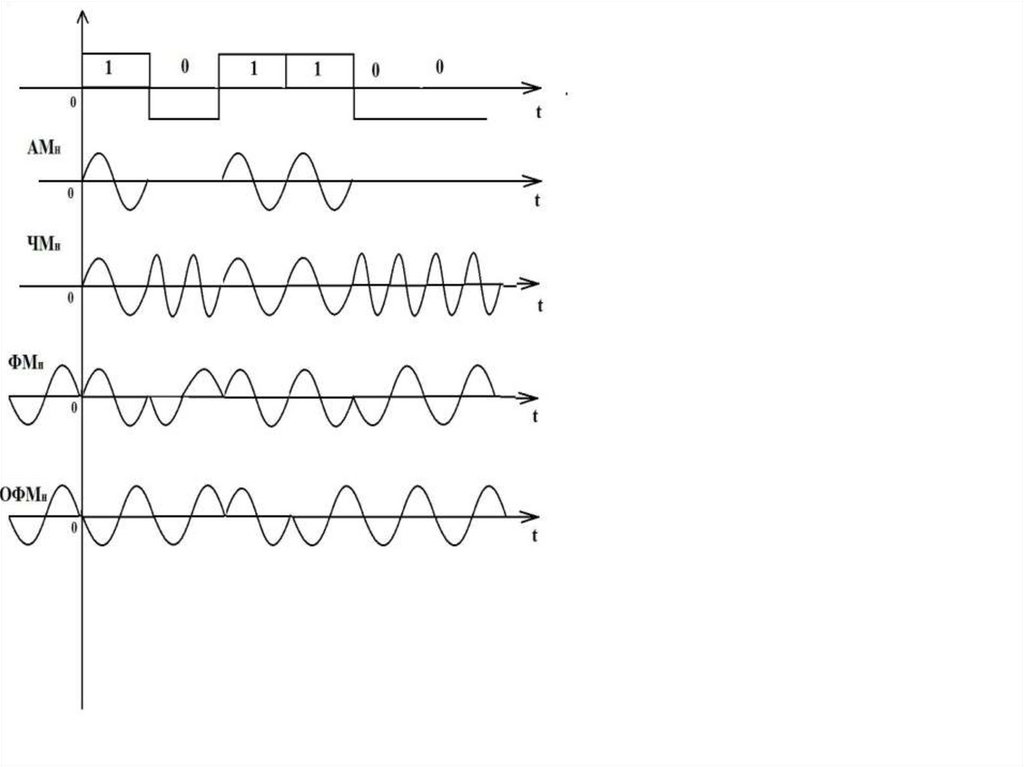

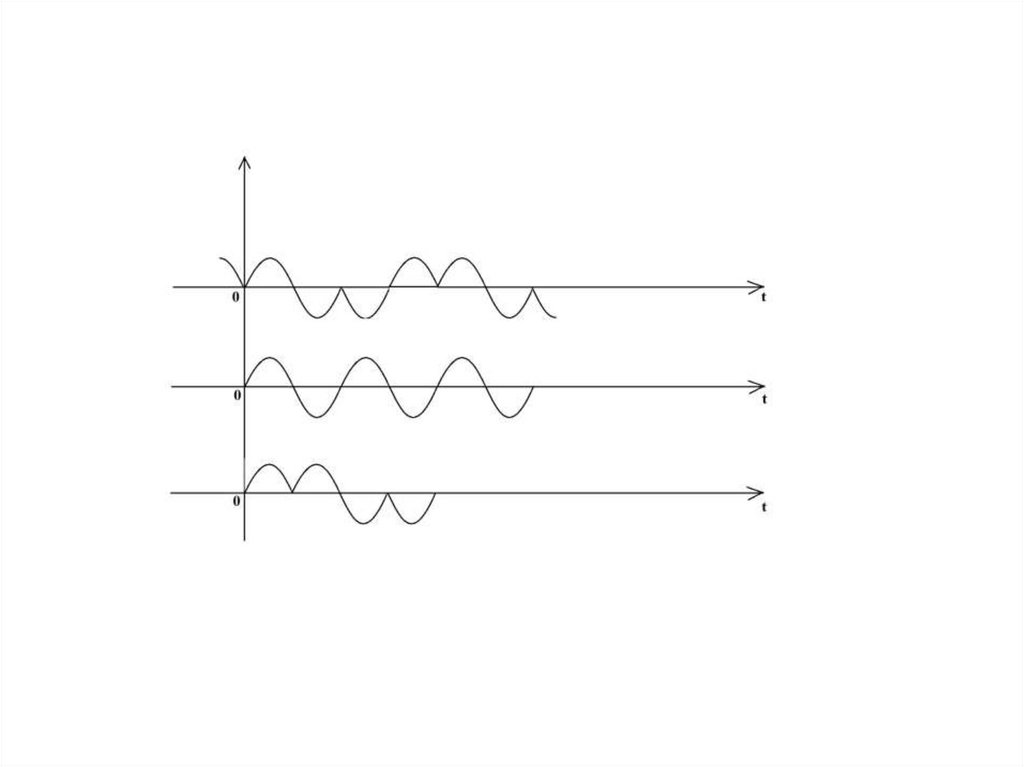
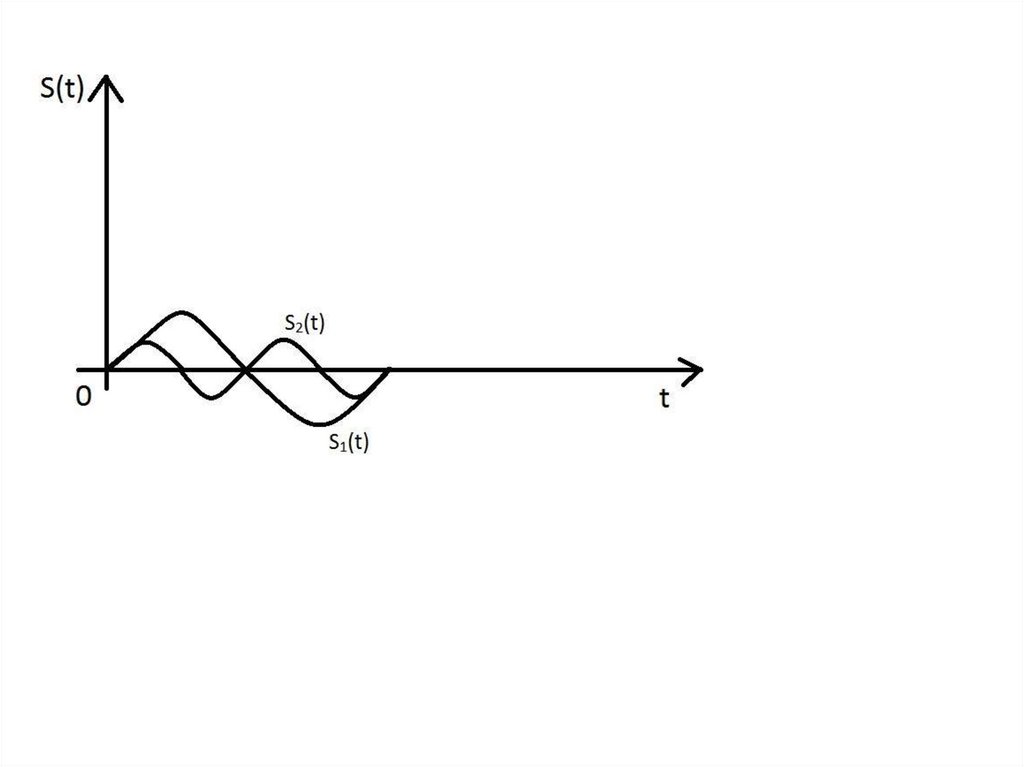
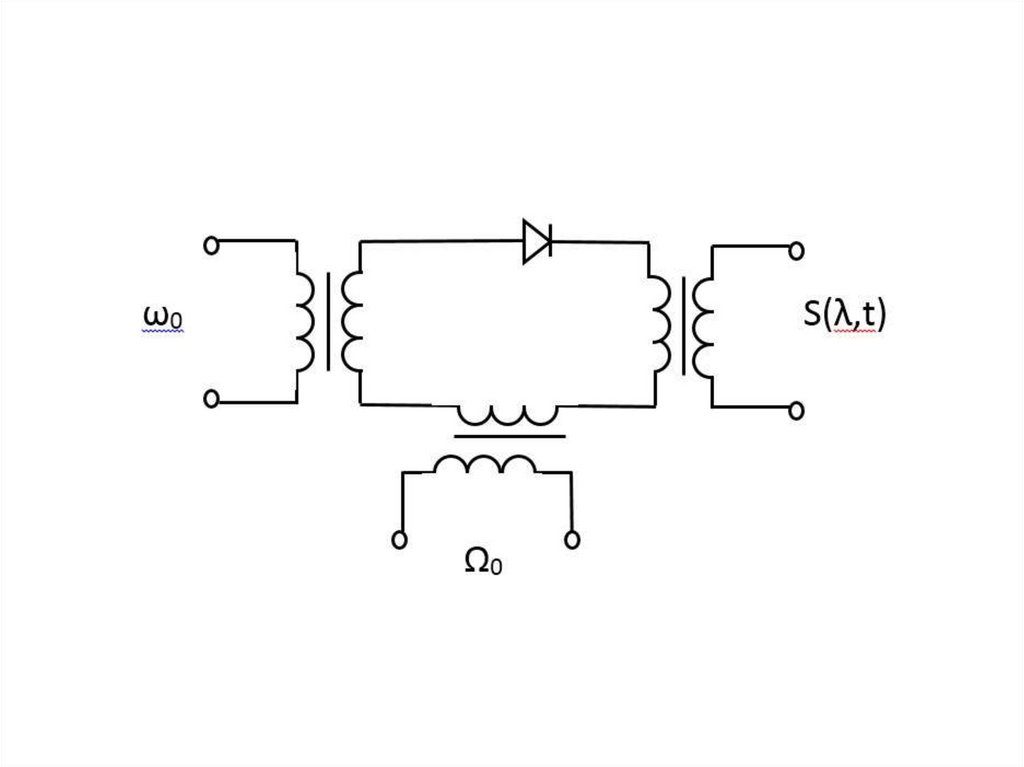
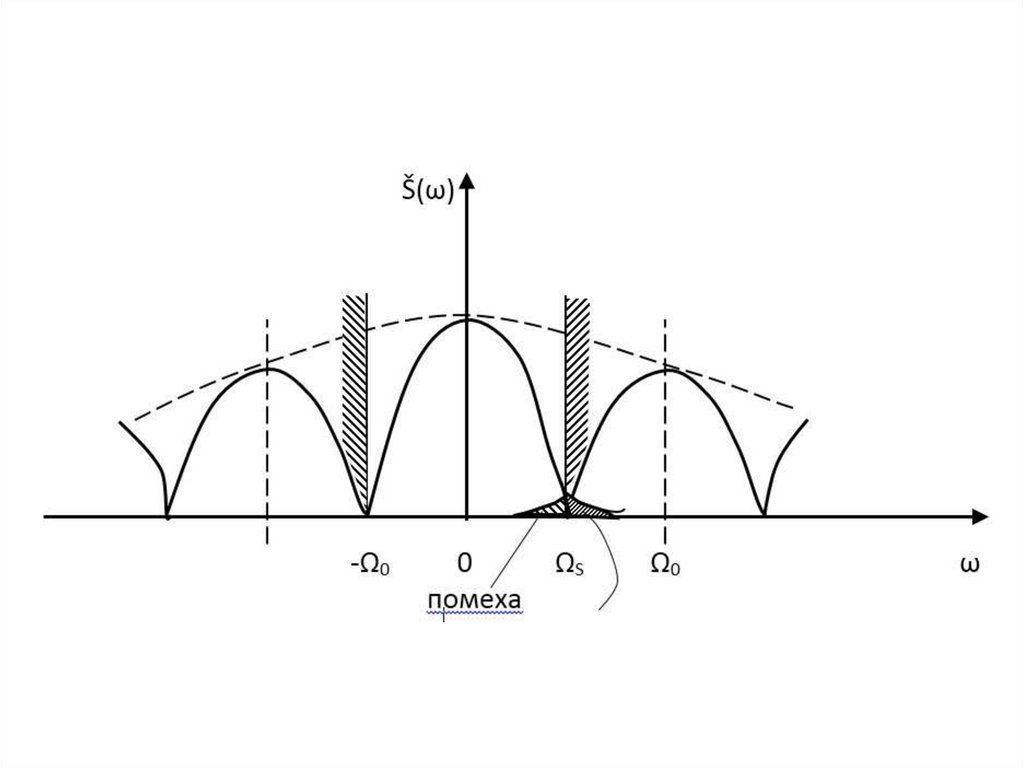



 electronics
electronics








