Similar presentations:
Кривые 2-го порядка. Аналитическая геометрия
1. Кривые 2-го порядка
Аналитическаягеометрия
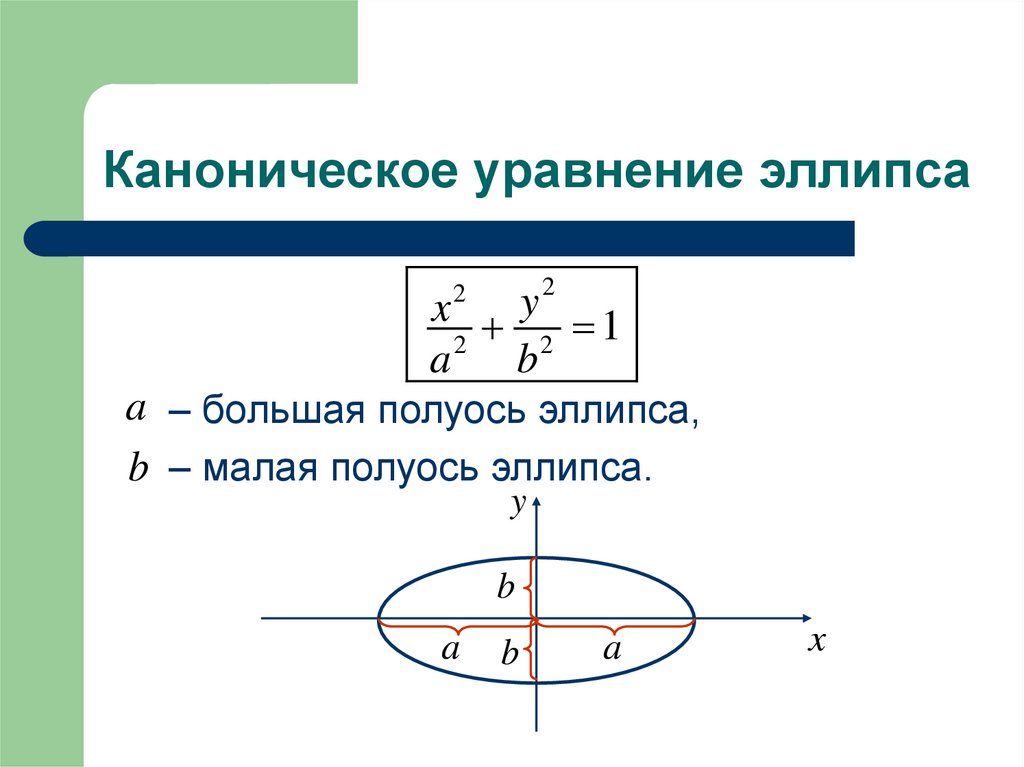
2. Каноническое уравнение эллипса
2y
x
1
2
2
a
b
2
a – большая полуось эллипса,
b – малая полуось эллипса.
y
b
a
b
a
x
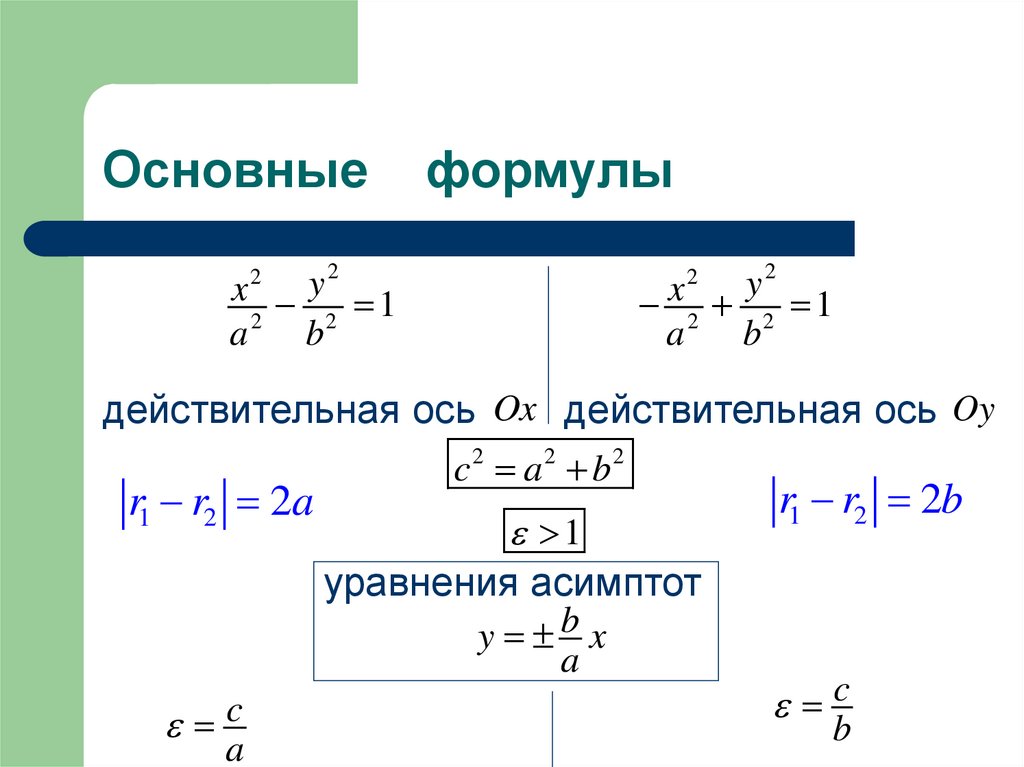
3. Основные формулы эллипса
2y
x
1
2
2
a
b
2
r1 r2 2a
a b
a c
c a
F1 c;0
F2 c;0
b2 a 2 c 2
c
a
b
c
r1 r2 2b
a b
F2 0;c
a
a
F1 0; c
c
b 2
a b2 c 2
c
b
4.
Нормальное уравнение эллипса с центромв точке xo , yo
x xo y yo 1
2
a2
2
b2
5. Каноническое уравнение гиперболы
2y
2
2
2
x
1,
b
c
a
a 2 b2
2
6. Основные формулы
2x2 y 1
a 2 b2
2
y2
x
2 2 1
a
b
действительная ось Ox действительная ось Oy
r1 r2 2a
c
a
c 2 a 2 b2
1
уравнения асимптот
y b x
a
r1 r2 2b
c
b
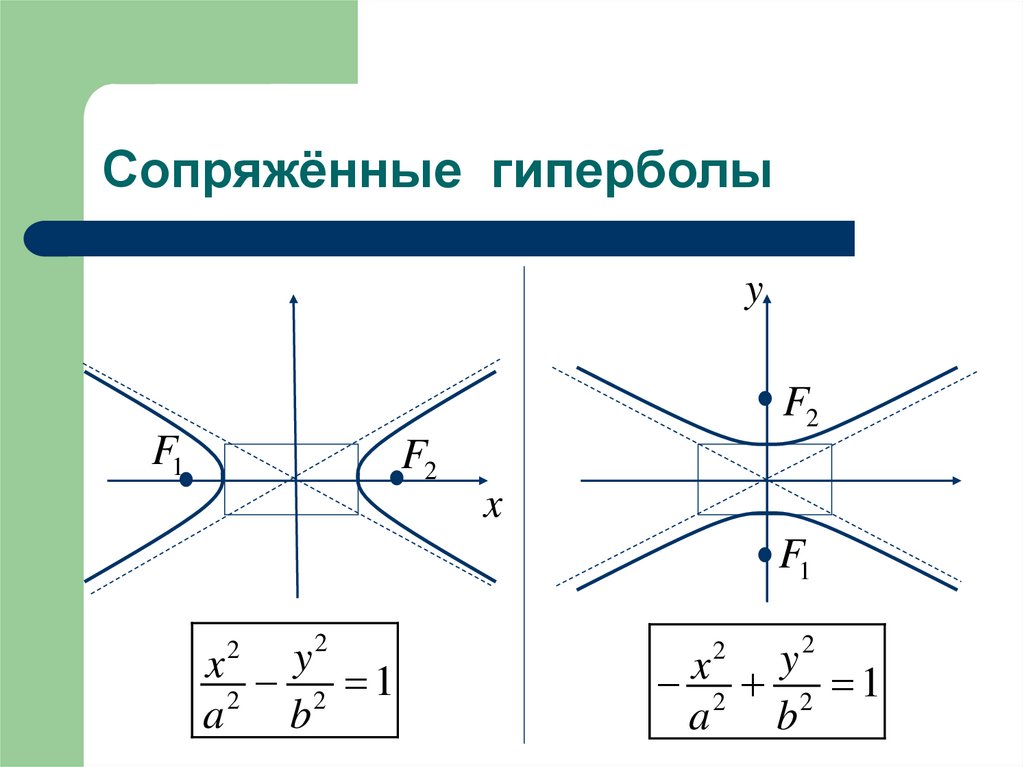
7. Сопряжённые гиперболы
yF2
F1
F2
x
F1
2
y
x
1
2
2
a
b
2
2
y
x2 2 1
a
b
2
8.
Нормальные уравнения гиперболы с центром вточке xo , yo
x xo
a
2
2
y yo 1
2
b
2
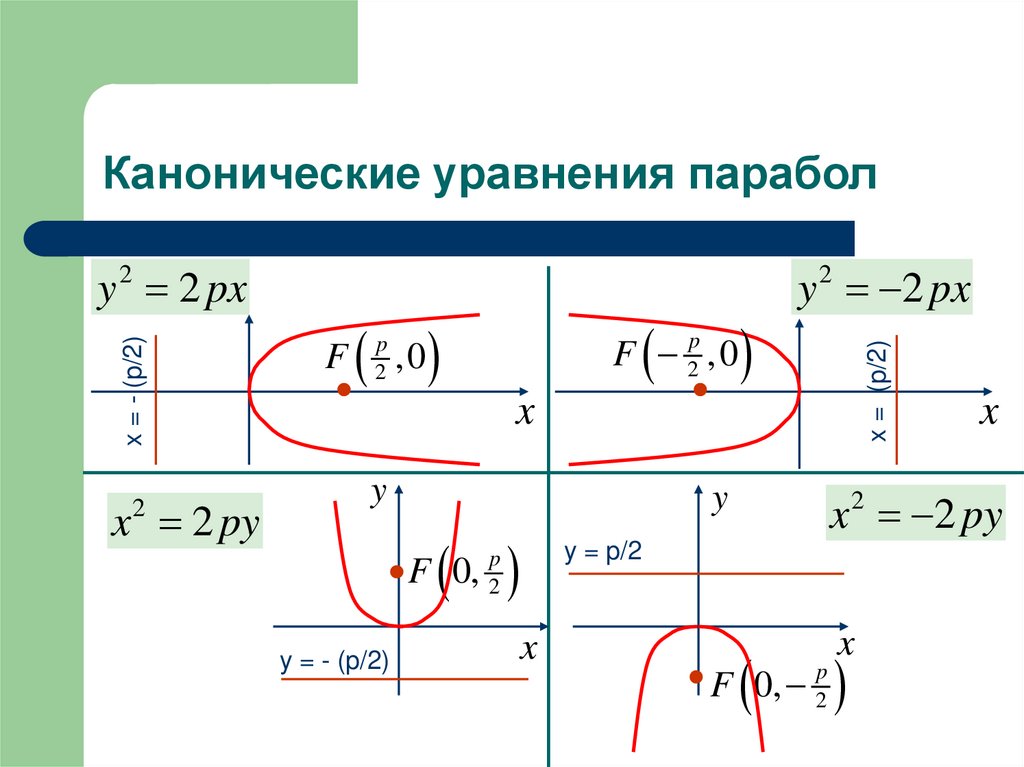
9. Канонические уравнения парабол
y 2 pxx 2 py
2
y 2 px
2
F
p
2
F 2p ,0
,0
x = (p/2)
x = - (p/2)
2
x
y
y
F 0,
y = - (p/2)
x 2 2 py
y = p/2
p
2
x
x
F 0, 2p
x
10. Нормальные уравнения парабол с вершиной в точке
xo , yoy yo 2 p x xo
2
x xo 2 p y yo
2







 mathematics
mathematics








