Скалярное произведение векторов. Геометрия. 7-9 класс

1.

2.

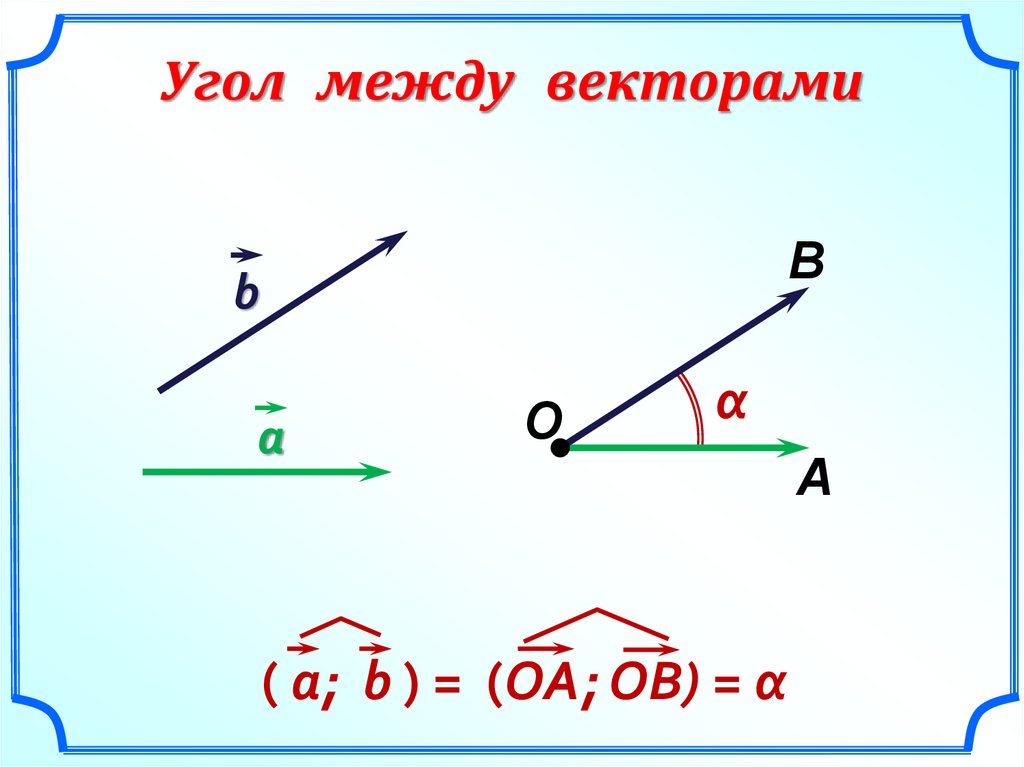
Угол между векторами
В
b
a
О
α
( a; b ) = (ОА; ОВ) = α
А

3.

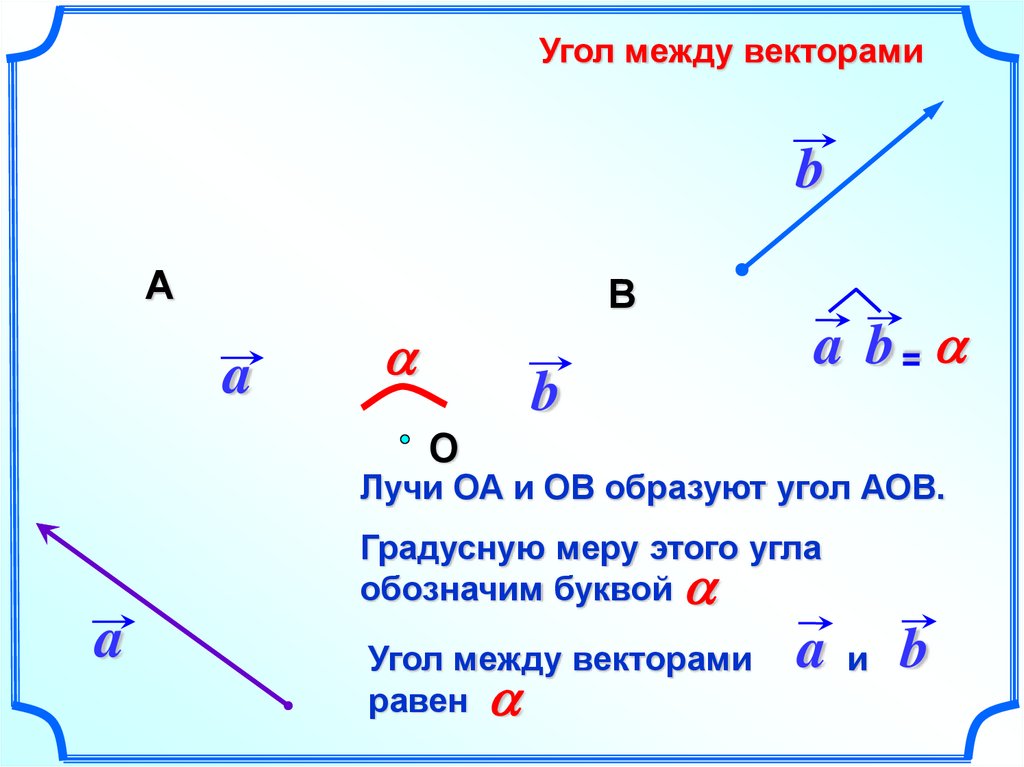
Угол между векторами
b
А
В
a
a
b
a b= a
О
Лучи ОА и ОВ образуют угол АОВ.
Градусную меру этого угла
обозначим буквой a
a
Угол между векторами
равен a
aи b

4.

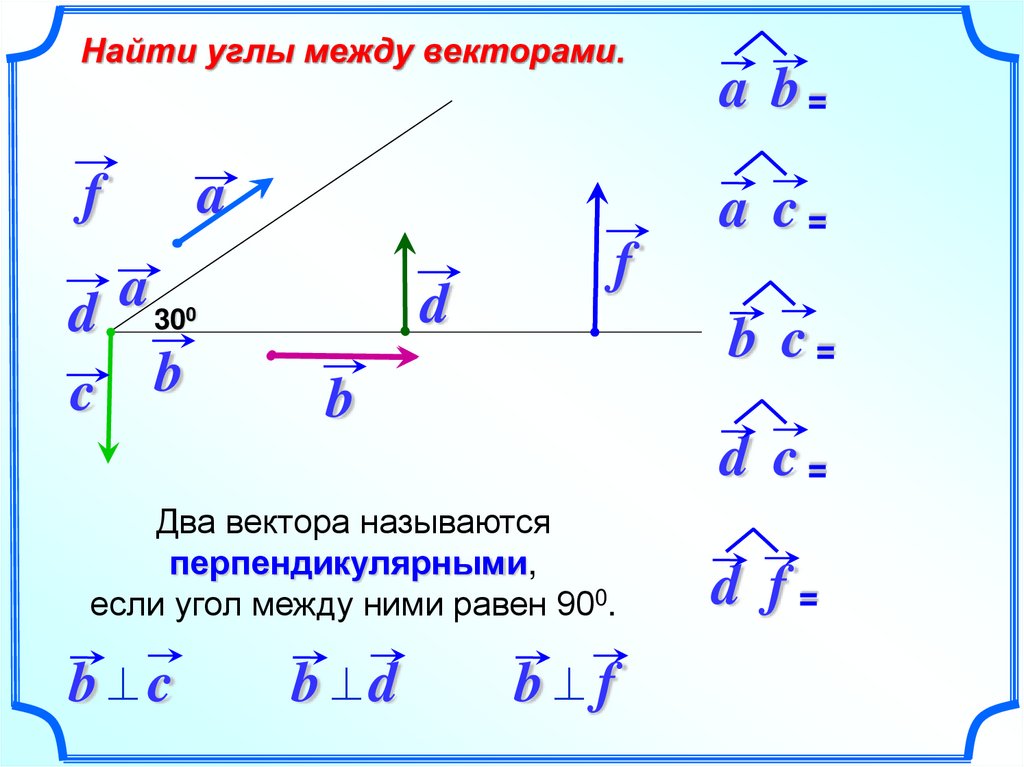
Найти углы между векторами.
f
a
a
d 30
c
b
a b=
a c=
d
0
f
b c=
b
d c=
Два вектора называются
перпендикулярными,
если угол между ними равен 900.
b^c
b ^d
b^f
d f=

5.

Определение скалярного
произведения
Скалярным произведением двух векторов называется
произведение их длин на косинус угла между ними.
a ∙ b = │a│∙│b│cos ( a; b )
Скалярное произведение ненулевых векторов равно
нулю тогда и только тогда, когда эти векторы
перпендикулярны.
a∙b=0 a^b

6.

a b = a b cos(a b )
Пример:
a 2,
b 3,
a угол между векторами а и b
a 135
0
a b 2 3 cos135 6 cos(180 45 )
0
2
6 cos 45 6
3 2
2
0

7.

Сумма векторов – вектор.
Разность векторов – вектор.
Произведение вектора на число – вектор.
Скалярное произведение векторов – число
(скаляр).
a b = a b cos(a b )
Скаляр – лат. scale – лестница, шкала.
Ввел в 1845г. У. Гамильтон, английский математик.

8.

Частный случай №1 0
0
a b = 90
b
a b = a b cos 900 = 0
a
a
b
Если векторы
и
перпендикулярны, то
скалярное произведение векторов равно нулю.
a b = 0 , то векторы a и b
Обратно: если
перпендикулярны.
Скалярное произведение ненулевых векторов равно
нулю тогда и только тогда, когда эти векторы
перпендикулярны.
a b =0
a ^b

9.

a b < 900
Частный случай №2
>0
a b = a b cos a > 0
b
a
Скалярное произведение ненулевых векторов
положительно тогда и только тогда , когда угол между
векторами острый.
a b > 0 a b < 900

10.

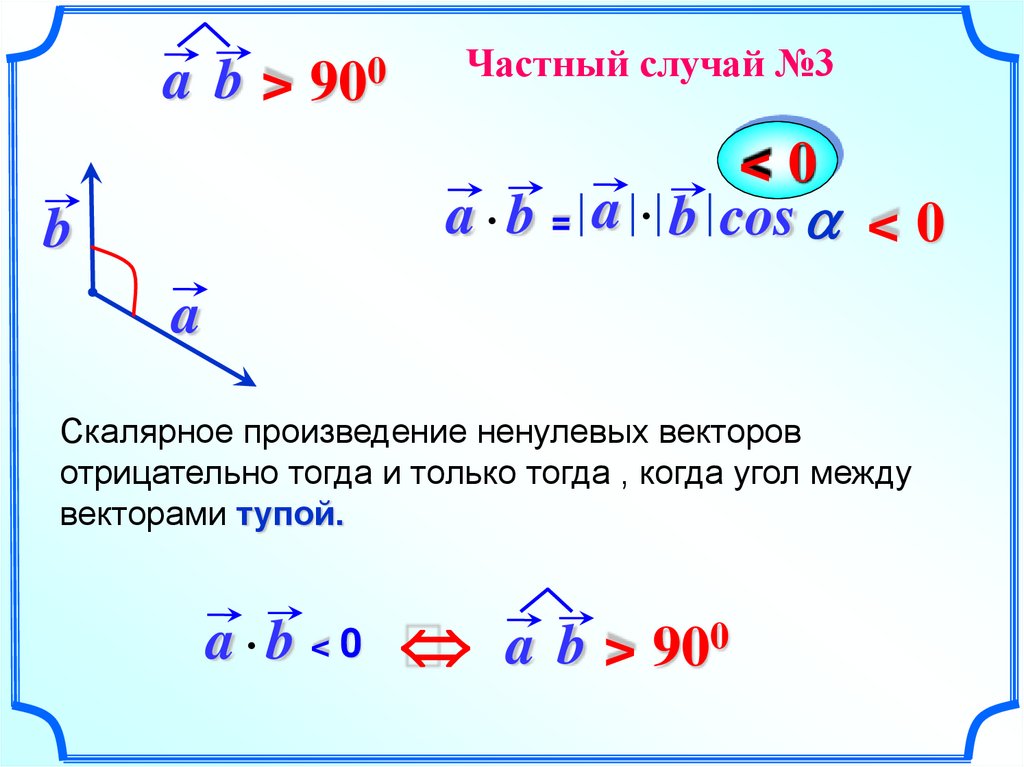
a b > 900
Частный случай №3
<0
a b = a b cos a < 0
b
a
Скалярное произведение ненулевых векторов
отрицательно тогда и только тогда , когда угол между
векторами тупой.
a b < 0 a b > 900

11.

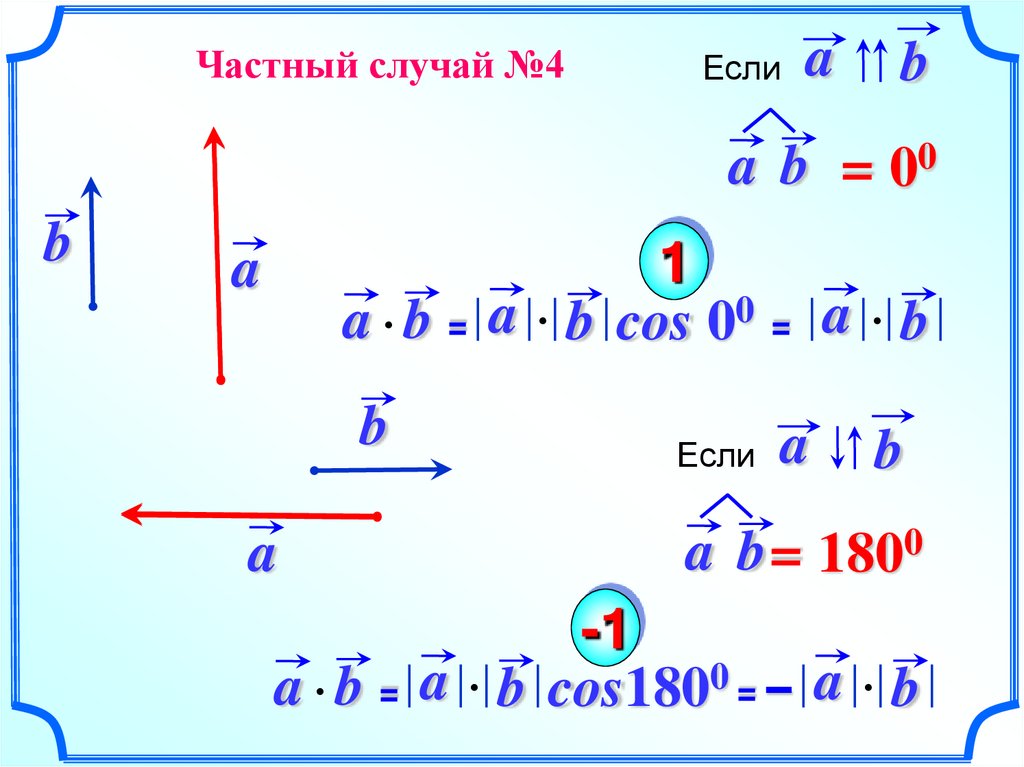
Частный случай №4
Если
a
b
a b = 00
b
1
a b = a b cos 00 = a b
a
b
a
Если
a
b
a b = 1800
-1
a b = a b cos1800 = – a b

12.

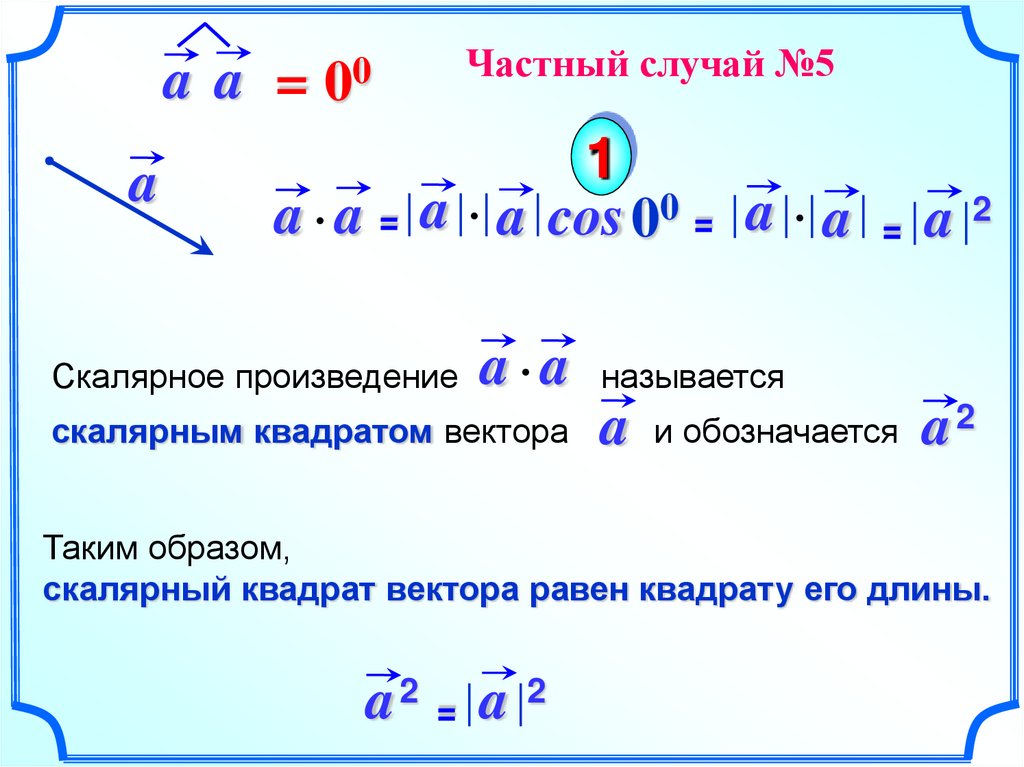
a a
a
= 00
Частный случай №5
1
a a = a a cos 00 = a a = a 2
a a называется
скалярным квадратом вектора a и обозначается a 2
Скалярное произведение
Таким образом,
скалярный квадрат вектора равен квадрату его длины.
a2 = a 2

13.

Скалярное произведение в
координатах
Теорема: скалярное произведение векторов
a{x1; y1} и b{x2; y2} выражается формулой
a ∙ b = x1x2 + y1 y2

14.

Скалярное произведение в
координатах
Следствие 1: косинус угла между ненулевыми
векторами a{x1; y1} и b{x2; y2} выражается формулой
cos α =
x1x2 + y1 y2
√x12 + y12 ∙ √x22 + y22
Следствие 2: ненулевые векторы a{x1; y1} и b{x2; y2}
перпендикулярны тогда и только тогда, когда
x1x2 + y1 y2 = 0

15.

Примечание:
В термине «скалярное произведение»
первое слово указывает на то, что
результат действия есть скаляр, т.е.
действительное число.
Второе слово подчеркивает, что для
этого действия имеют силу основные
свойства обычного умножения.

16.

Свойства скалярного
произведения
Для любых векторов
a, b и c и любого числа k
справедливы соотношения:
1о a2 ≥ 0, причем a2 > 0 при а ≠ 0.
2о a ∙ b = b ∙ a (переместительный закон).
3о ( a + b ) ∙ с = а ∙ с + b ∙ с (распределительный
закон).
4о ( k a ) ∙ b = k ( а ∙ b ) (сочетательный закон).

17.

Применение скалярного произведения в
физике
Работа А постоянной
силы F при перемещении
тела из точки М в точку
N, равна произведению
длин векторов силы и
перемещения на косинус
угла между ними.
Т.е. работа силы F
равна скалярному
произведению векторов
силы и перемещения
A F MN cos
A F MN

18.

Самое главное
• Скалярным произведением векторов называется
произведение их длин на косинус угла между ними
а b a b cos( а; b) cos (a; b)
a b
a b
• Скалярное произведение ненулевых векторов равно
нулю тогда и только тогда когда эти векторы
перпендикулярны
а b 0 a ^ b
• Скалярное произведение вектора самого на себя
называется скалярным квадратом вектора
а a a
2
• Скалярный квадрат вектора равен квадрату его длины.
2
a a
2

19.

Решение задач:
• № 1041
• №1044
• №1049