Физика. Лекция 2. Релятивизм. Волны. Акустика

1. Физика

Лекции студентам ФМиИТ
[email protected]
1

2. Лекция 2.

Релятивизм.
Волны. Акустика.
2

3. Принцип относительности Галилея

• Все механические явления протекают одинаково в
инерциальных системах отсчета
(выполняется при скоростях намного меньше скорости света в
вакууме)
Из принципа относительности Галилея вытекают как следствия :
• Инвариантность длины
• Инвариантность интервала времени
• Инвариантность ускорения
(Инвариантность означает независимость от перехода к другой
инерциальной системе отсчета)
• Закон сложения скоростей:
V V1 V2
Скорость тела (V) относительно неподвижной системы отчета
равна скорости тела (V1) в подвижной С.О. + скорость ( V2 )
подвижной С.О. относительно неподвижной С.О.
3

4.

4

5. Постоянство скорости света

5

6. Релятивистские преобразования координат (преобразования Лоренца)

• Чтобы объяснить экспериментальный факт
постоянства скорости света в различных
инерциальных системах отсчета, были
созданы преобразования Лоренца.
• Эти преобразования исходят из
однородности пространства и времени.
6

7. Следствия из преобразований Лоренца

• Относительность одновременности
События, происходящие одновременно в неподвижной с.о., в
подвижной с.о. могут происходить в разные моменты времени в
подвижной с.о.
• Сокращение длины
• Замедление времени
7

8. Сложение скоростей в релятивистской механике

Подвижная (штрихованная) система отсчета движется со
скоростью V вдоль оси х относительно неподвижной с.о.
8

9. Релятивистское уравнение движения

Аналог второго закона Ньютона
• р- релятивистский импульс,
• m - релятивистская масса
9

10.

10

11. Механическая волна

11

12.

Для продольных упругих
волн фазовая скорость
пропорциональна корню
квадратному из модуля
Юнга Е среды,
деленному на плотность
среды
Для поперечных упругих
волн фазовая скорость
пропорциональна корню
квадратному из модуля
сдвига G среды,
деленному на плотность
среды
12

13. Волновое уравнение

Волновое уравнение - это дифференциальное уравнение второго
порядка в частных производных, описывающее процесс
распространения возмущения в среде. Оно имеет вид:
2
s
1 2s
2 2
2
x
V t
Здесь S – смещение колеблющейся точки, V – скорость распространения
фронта волны (фазовая скорость ), x – координата, t - время
Уравнение плоской волны – частное решение волнового
уравнения:
S = A cos [w(t-x)/V)]
Длина волны l VT – расстояние между ближайшими точками
среды, колеблющимися в одинаковой фазе.
Поперечная волна
13

14. Эффект Допплера

Одним из примеров механических волн является звуковая волна.
Эффектом Допплера называют изменение частоты волн,
воспринимаемых наблюдателем, при движении источника волн
относительно наблюдателя.
V Vн
Обобщенная формула Допплера
n '''
n
V Vи
Верхние знаки «+» и «-» относятся к сближению источника и приемника,
нижние знаки – к удалению их друг от друга
Здесь V - скорость волны в среде, Vи - скорость источника относительно
среды, Vн - скорость наблюдателя (приемника) относительно среды, n частота при неподвижных относительно среды источнике и приемнике
волн
Эффект Допплера можно использовать для определения скорости
источника волн.
В медицине с помощью Э.Д. ультразвуковых волн определяют скорость
течения крови в кровеносных сосудах, скорости движения клапанов и
стенок сердца (допплеровская эхокардиография) и др.
В астрономии эффект Допплера позволяет измерять скорости звезд.
14

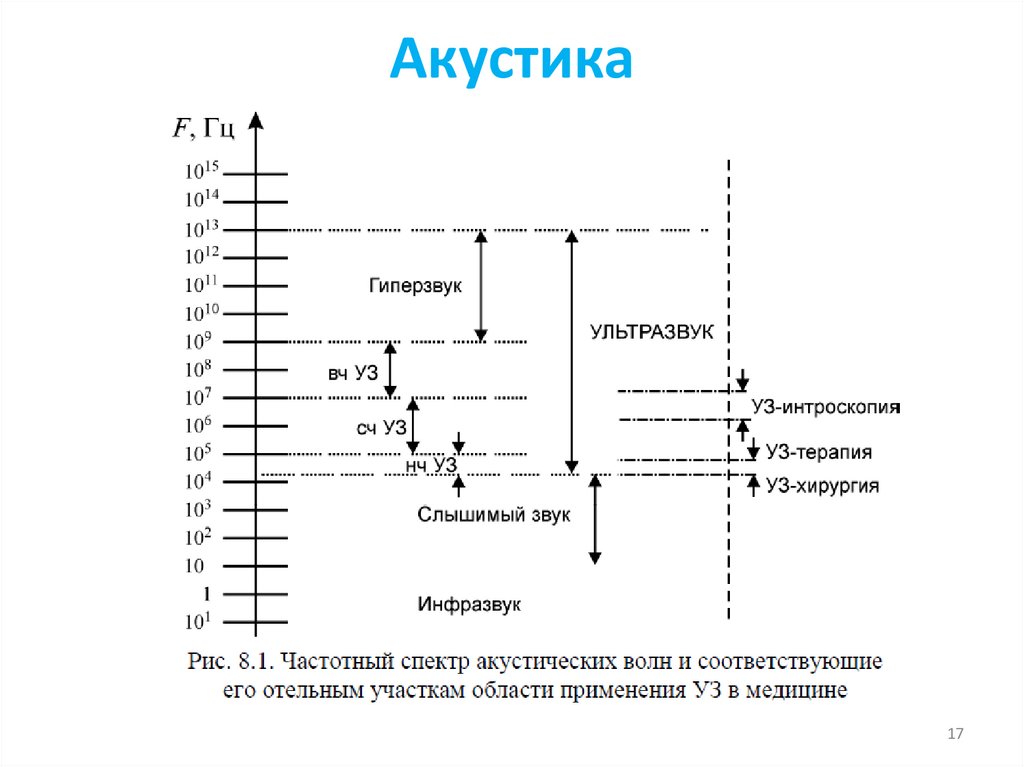
15. Акустика

15

16. Энергетические характеристики звука

16

17. Акустика

17

18.

18

19.

19

20.

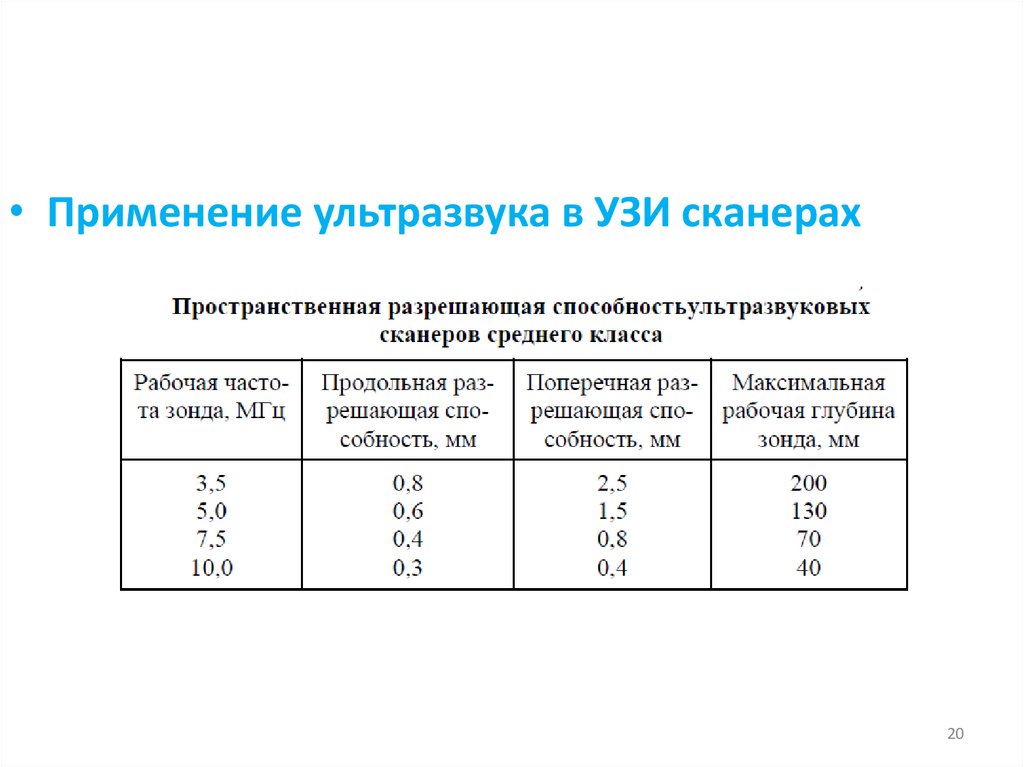
• Применение ультразвука в УЗИ сканерах
20

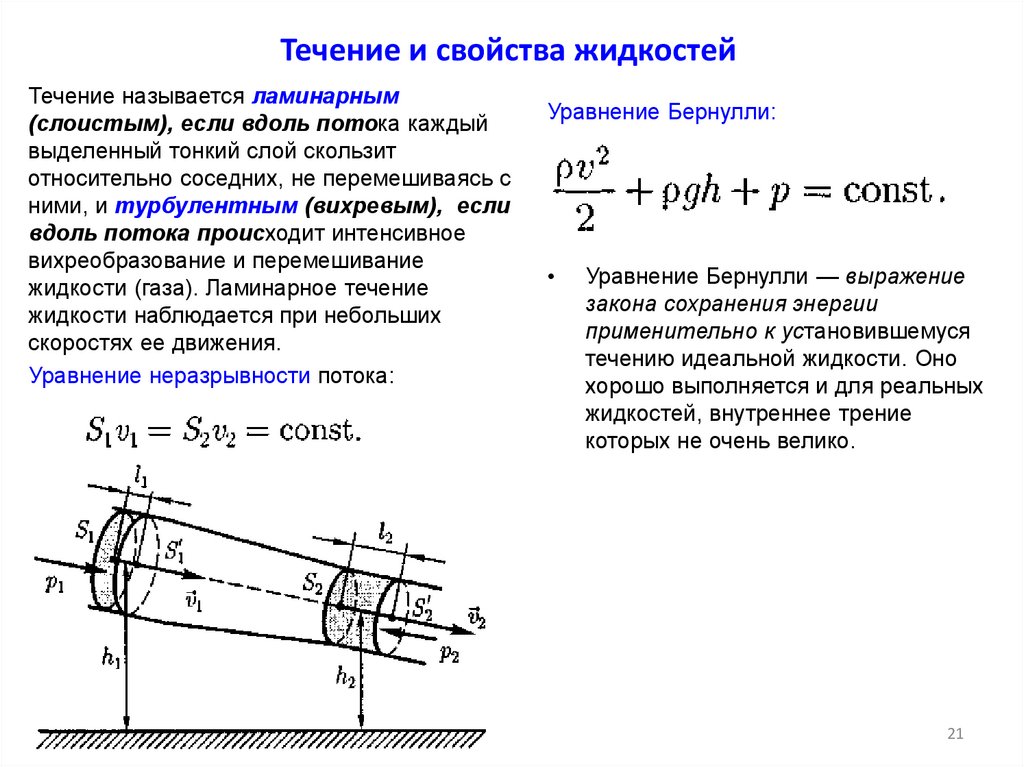
21. Течение и свойства жидкостей

Течение называется ламинарным
(слоистым), если вдоль потока каждый
выделенный тонкий слой скользит
относительно соседних, не перемешиваясь с
ними, и турбулентным (вихревым), если
вдоль потока происходит интенсивное
вихреобразование и перемешивание
жидкости (газа). Ламинарное течение
жидкости наблюдается при небольших
скоростях ее движения.
Уравнение неразрывности потока:
Уравнение Бернулли:
Уравнение Бернулли — выражение
закона сохранения энергии
применительно к установившемуся
течению идеальной жидкости. Оно
хорошо выполняется и для реальных
жидкостей, внутреннее трение
которых не очень велико.
21

22. Течение и свойства жидкостей

Вязкость жидкости. Уравнение Ньютона.
Ньютоновские и неньютоновские жидкости.
• При течении реальной жидкости отдельные
слои ее воздействуют друг на друга с силами,
касательными к слоям. Это явление
называют внутренним трением или вязкостью.
• (9.1) -Это уравнение Ньютона. Здесь η —
коэффициент пропорциональности,
называемый коэффициентом внутреннего
трения или динамической вязкостью (или
просто вязкостью). Вязкость зависит от
состояния и молекулярных свойств жидкости
(или газа). С повышением температуры
вязкость жидкостей уменьшается.
• Единицей вязкости является паскаль-секунда
(Па∙с). В СГС единица изм. 1 пуаз = 0,1 Па ∙с
• Для многих жидкостей вязкость не зависит от
градиента скорости dV/dx, такие жидкости
подчиняются уравнению Ньютона (9.1) и их
называют ньютоновскими. Жидкости, не
подчиняющиеся уравнению (9.1), относят к
неньютоновским.
• Кровь является неньютоновской жидкостью.
22

23. Течение вязкой жидкости по трубам. Формула Пуазейля

Пуазейль, изучая ламинарное течение
жидкости в круглой трубе, нашел закон
изменения скорости с расстоянием от оси
трубы
Это позволяет определить вязкость жидкости
из простых измерений
p 2 2
(R - r )
4 l
где R и l – радиус и длина трубы, V – объем
вытекающей из трубы жидкости за время t,
Δp - перепад давления на концах трубы.
R 4t p
8Vl
23