Особые точки ФКП. Нули функции комплексного переменного. Лекция 33. Часть 2

1.

ЛЕКЦИЯ 33
Часть 2. Особые точки ФКП
Нули функции комплексного переменного.
Необходимое и достаточное условие
существования нуля.
1

2.

Точка zₒподразумевается нулем функции f(z) , если
f(zₒ)=0.
Если окрестность точки , zₒ, │z-zₒ│<0, в которой
нет других нулей, кроме точки zₒ, то говорят, что
точка zₒ - изолированный ноль.
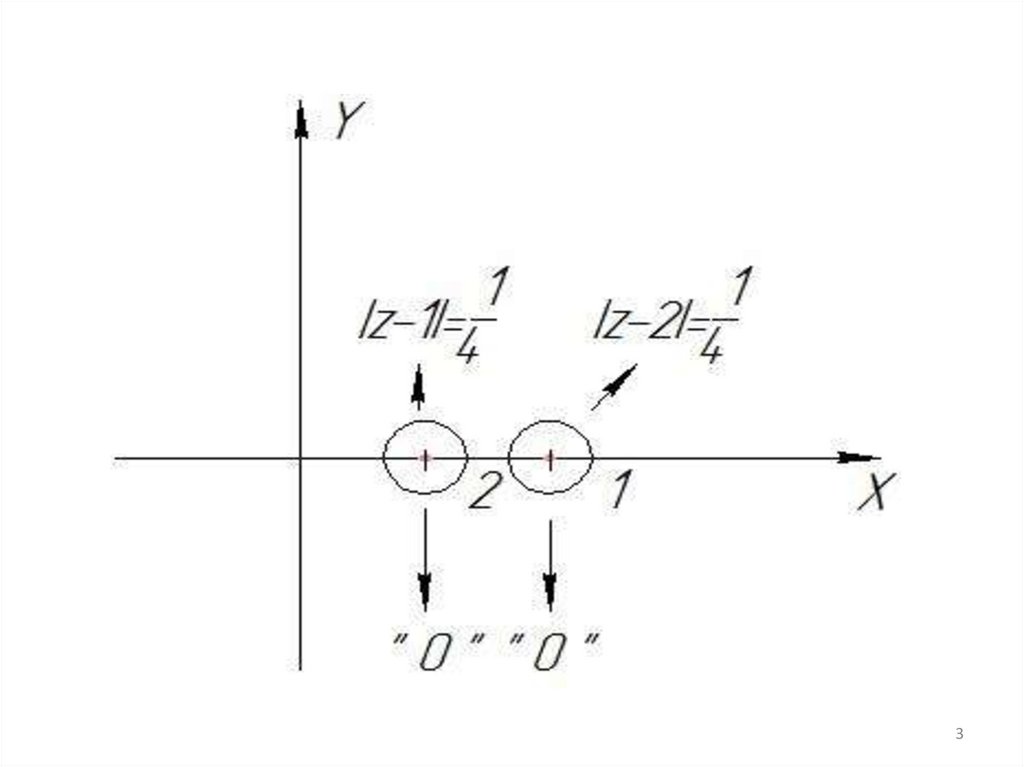
Пример: f(z)=(z-1)(z-2).
Построим около каждой точки окружности.
Внутри каждой области находится один . Когда
внутри области находится один ноль, то говорят
что точка, находящаяся внутри области –
изолированный ноль.
2

3.

3

4.

По определению точка zₒ называется "0" m-того
порядка функции , если f(zₒ)=0, f'(zₒ)=0, …, f⁽ᵐ⁾(zₒ)≠0.
Пример: f(z)=(z-1)² .
В точке zₒ=1 значение функции f(zₒ)=0.После
нахождения нуля функции необходимо определить
его порядок:
f' (z)=2(z-1)→ f'(zₒ)=0;
f''(z)=2 ≠0.
В данном случае "0" – второго порядка.
Пример 2: f(z)=z⁵⁰(eᶻ-1).
zₒ=0. Определить порядок нуля?
4

5.

Теорема (о порядке нуля, необходимое и
достаточное условие существования нуля
функции):
Для того, чтобы точка zₒ была нулем m-того порядка
аналитической функции f(z) необходимо и
достаточно, чтобы f(z) была представима в виде:
f ( z ) ( z z0 ) m ( z ) ,
где ( z ) - аналитическая функция в окрестности
точки zₒ;
( z ) 0.
Доказательство
5

6.

Функция f(z) представлена в виде:
f ( z ) ( z z0 ) m ( z ) .
Из аналитичности следует, что функция разлагается в
ряд Тейлора:
( z ) C0 C1( z z0 ) C2 ( z z0 ) 2 ... Cк ( z z0 ) к ...
После перемножения в выражении получим, что
функция представлена в виде:
f ( z ) C0 ( z z0 ) m C1( z z0 ) m 1 ... Cк ( z z0 ) m к ...
Коэффициент стоящий перед скобками
переобозначим , получим:
f ( z ) am ( z z 0 ) a m 1( z z 0 )
m
m 1
... am к ( z z0 )
m к
... 1
6

7.

Коэффициент ряда Тейлора
выражается по формуле:
(k )
f
( z0 )
ak
. 2
k!
Коэффициент ряда аₒ=0=f(z ₒ) и a₁=0= f'(zₒ) в силу
формулы (2).
a m 1 0
am 0
f ( m 1 ) ( z 0 )
( m 1 )!
f ( m ) ( z0 )
( m )!
. 3
.
Из соотношений (3) можно сделать вывод что точка
zₒ является нулем m-того порядка.
Необходимость
7

8.

Предположим , что точка zₒ – есть ноль m-того
порядка. По определению нуля : f(zₒ)=0, f'(zₒ)=0, …, f⁽ᵐ⁾
(zₒ)≠0.
Так как функция f(z) аналитическая в точке zₒ, то →
она расходится в ряд Тейлора:
k
f ( z ) ak ( z z 0 ) ,
k 0
где ak находится по формуле:
ak
f ( k ) ( z0 )
k!
.
Так как точка zₒ ноль m-того порядка то:
аₒ=0, а₁=0, …, am 1 0, am 0.
8

9.

С учетом этого разложение принимает вид:
m
m 1
f ( z ) a m ( z z 0 ) a m 1( z z 0 )
...
Ряд равномерно сходится в окрестность точки zₒ,
значит можно выносить функцию за знак ряда:
f ( z ) ( z z0 ) ( am am 1( z z0 ) am 2 ( z z0 ) ...
m
2
Сходится к ( z ) как степенной ряд.
Значит ( z ) в точке zₒ равно коэффициенту am 0.
Функция представима в виде:
f ( z ) ( z z0 ) m ( z ), где ( z0 ) 0.
Пример: f(z)=z⁵⁰(eᶻ-1).
zₒ=0
m=?
9

10.

Разложим функцию еᶻ в ряд Тейлора в окружности
2
3
k
z
z
z
нуля:
z
e
1 z
z2
2!
3!
z3
...
k 0 k!
2
;
zk
z
z
e 1 z
... z ( 1
...
...);
2!
3!
2! 3!
( k 1 )!
z
( z )
При z=0 значение функции ( z ) 0 1,
f ( z ) z 51 ( z ), (0) 1 0.
Изолированные особые точки:
Устранимые, полюсы и существенно особые точки
10

11.

Изолированные особые точки:
Устранимые, полюсы и существенно особые точки
Точка zₒ называется изолированной особой точкой
аналитической функции f(z), если такая
окрестность точки zₒ,0 z z0 что :
1. В этой окрестности нет особых точек функции f(z).
2. f(z) – аналитична в этой окрестности.
Определение: точка zₒ называется особой точкой
функции f(z), если в ней нарушается аналитичность
функции f(z).
Определение (изолированной особой точки):
zₒ особая точка функции f(z)называется изолированной

12.

особой, если такая окрестность точки zₒ,
0 z z0 такая что:
1. В окрестности нет других особых точек.
2. f(z) – аналитична в этой окрестности.
1
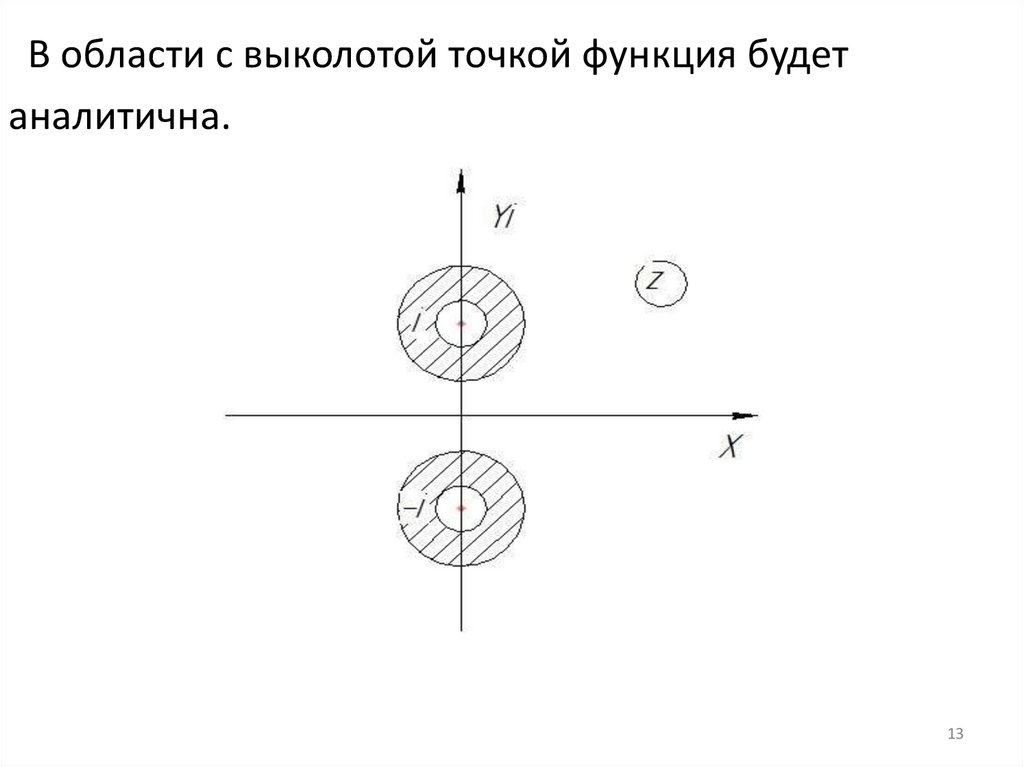
Пример: f ( z ) 2
имеет 2 особые точки:
z 1
zₒ=i, zₒ=-i.
В этих точках нарушается аналитичность функции.
В области с выколотой
точкой функция будет
аналитична
12

13.

В области с выколотой точкой функция будет
аналитична.
13

14.

В области с выколотой точкой функция будет
аналитична.
Изолированные точки классифицируются на:
1. Устранимые.
2. Полюсы.
3. Существенно особые.
Так как f(z) аналитична в окрестности особой точки
0 z z0 , значит она разлагается в ряд Лорана:
a k
k
f ( z ) ak ( z z 0 )
.
k
k 0
k 1 ( z z 0 )
правильная часть ряда
главная часть ряда
14

15.

По определению точка zₒ называется устранимой
особой точкой, если в разложении f(z) в ряд Лорана
присутствует только правильная
часть:
f ( z ) ak ( z z 0 ) k .
k 0
Так как ряд стоящий в правой части равномерно
сходится в точку zₒ, то:
k
lim
f
(
z
)
a
lim(
z
z
)
a0 0.
zk z0
0
z z
0
k 0
Этим свойством пользуются для определения
устранимых особых точек.
Пользуясь тем, что lim 0 и существует функция
в устранимой точке, можно доопределить:
15

16.

f(z)
f ( z ), z z0 ;
a0 , z z 0 .
е z 1
.
Пример: f ( z )
z
zₒ - аналитичность теряется.
Исследуем функцию на характер особой точки:
2
3
z
z
z
e 1 z
...;
2!
3!
e z 1
z
z
z
2
2!
z
z
3
3!
...
;
16

17.

Так как ряд равномерно
сходится,
то:
z
2
e
1
z
z z
1
... .
2! 3!
Перейдем к пределу в полученном выражении:
lim
z z0
e z 1
z
1.
Так как в разложении присутствует правильная часть
ряда Лорана, то точка zₒ- устранимая особая точка.
Полюсы
Изолированная особая точка zₒ называется полюсом
m-того порядка функции f(z), если в разложении
функции в ряд Лорана присутствует только m-членов
главной части, т. е. f(z) представима в виде:
17

18.

f ( z ) ak ( z z 0 )
k 0
k
a m
a 1
a 2
...
;
2
m
z z0 ( z z0 )
( z z0 )
lim f ( z ) ∞ .
Если m=1, то говорят, что такой полюс 1-го порядка
или простой полюс.
Пример: Исследовать характер особой точки
е z 1
функции f(z): f ( z ) 3 , z0 0.
f(z)
z
z
2
2!
z
z
3!
3
z
3
...
1
1 1 z
2
2! z 3!
4!
z
1
1 z 2
5!
...
главная часть правильная часть
Точка zₒ является полюсом 2-го порядка.
18