Similar presentations:
Применение теории планирования эксперимента при лабораторно-стендовых испытаниях и построении эмпирических моделей CУ
1.
ПРИМЕНЕНИЕ ТЕОРИИПЛАНИРОВАНИЯ ЭКСПЕРИМЕНТА
ПРИ ЛАБОРАТОРНО-СТЕНДОВЫХ ИСПЫТАНИЯХ
И ПОСТРОЕНИИИ ЭМПИРИЧЕСКИХ МОДЕЛЕЙ
СИСТЕМ УПРАВЛЕНИЯ И МЕХАТРОННЫХ СИСТЕМ И
МОДУЛЕЙ
2.
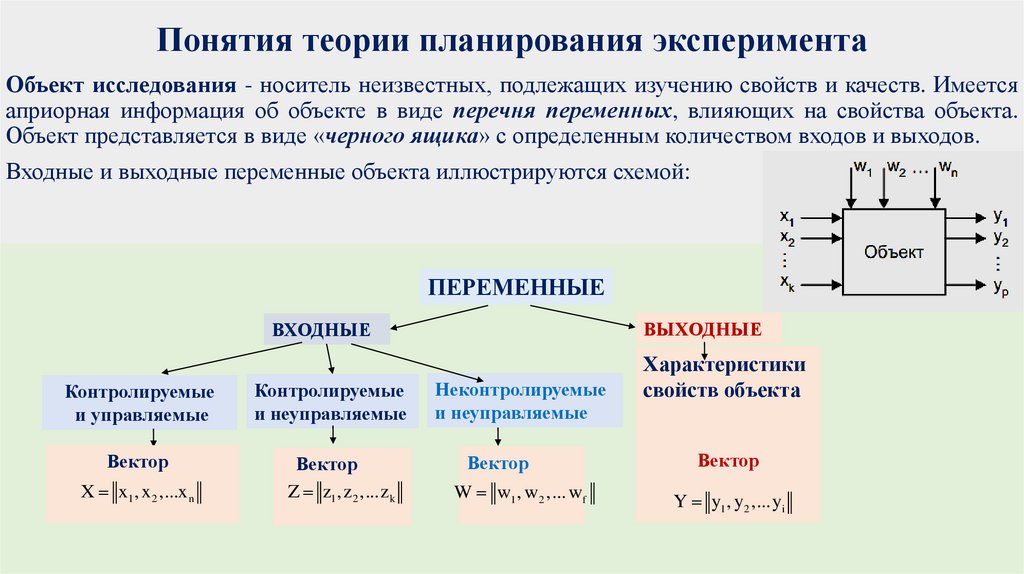
Понятия теории планирования экспериментаОбъект исследования - носитель неизвестных, подлежащих изучению свойств и качеств. Имеется
априорная информация об объекте в виде перечня переменных, влияющих на свойства объекта.
Объект представляется в виде «черного ящика» с определенным количеством входов и выходов.
Входные и выходные переменные объекта иллюстрируются схемой:
ПЕРЕМЕННЫЕ
ВЫХОДНЫЕ
ВХОДНЫЕ
Контролируемые
и управляемые
Контролируемые
и неуправляемые
Вектор
Вектор
Z z1 , z2 ,...zk
X x1 , x 2 ,...x n
Неконтролируемые
и неуправляемые
Вектор
W w1 , w2 ,... wf
Характеристики
свойств объекта
Вектор
Y y1 , y2 ,...yi
3.
Переменные X и Z называются факторами.Факторы могут меняться во времени как детерминированные (чаще всего факторы X) или
случайные (чаще всего факторы Z) переменные.
Пространство контролируемых переменных X образует факторное пространство.
Переменные неконтролируемые группы W – это мешающие переменные, под влиянием
которых показатели Y могут меняться систематически («дрейф объекта») или случайно (при
наличии случайной помехи, шумов).
Выходная переменная объекта, Y - зависимая переменная – называется отклик. Зависимость
отклика от рассматриваемых факторов - функция отклика. Геометрическое представление
функции отклика - поверхность отклика.
Объектами исследования при планировании эксперимента (ПЭ) могут быть: натурные
объекты; физические модели объектов; полные (нелинейные)
математические модели
объектов, полунатурные модели объектов.
Математическая модель (ММ) - это фраза на языке математики, отражающая свойства
объекта, его структуру и количественные связи. ММ, полученные с помощью ПЭ, - называются
экспериментальными.
Методы ПЭ предназначены для получения статистических ММ, вследствие чего сами эти
методы именуют статистическими методами.
4.
Планирование эксперимента - выбор плана эксперимента, удовлетворяющего заданнытребованиям. Планирование эксперимента - целенаправленное управление, которое реализуется
условиях неполного знания механизма изучаемого явления.
Эксперимент разделяют на пассивный и активный.
При пассивном эксперименте существуют только факторы группы Z, и экспериментато
находится в положении пассивного наблюдателя, фиксирующего изменения Z и отклика Y.
При активном эксперименте существуют лишь факторы группы X, и экспериментатор
соответствии с планом эксперимента может их целенаправленно изменять. Активный эксперимен
- основной предмет исследования теории планирования эксперимента.
Для активного эксперимента область действия - область возможных значений факторов X пр
экспериментировании. Область планирования - область значений факторов X, в которо
находятся точки, отвечающие условиям проведения опытов используемого плана эксперимента.
Точка плана - упорядоченная совокупность численных значений факторов, соответствующа
условиям проведения опыта; точка факторного пространства, в которой проводится эксперимен
Точке плана с номером g отвечает вектор:
.
Общая совокупность таких векторов образует план эксперимента, а совокупность различны
векторов - спектр плана
5.
Особенностью любой экспериментальной статистической ММ является то, что она неможет точно и полно описать поведение объекта в каждом конкретном опыте.
Статистическая модель описывает поведение объекта в среднем, характеризуя неслучайные
свойства объекта, которые в полной мере могут проявиться при многократном повторении
опытов в неизменных условиях. Из статистических ММ наибольший практический интерес
представляют регрессионные модели.
Регрессионная модель (модель регрессионного анализа) выражается соотношением:
Y = φ(x1 ,x 2 ,...x n ; z1 ,z 2 ,...z k ; c0 ,c1 ,c 2 ...cd )+e = φ(X, Z, C)+e
где С с0 , с1 , с 2 ,...сd - вектор параметров модели, причем вид функции φ полагают заданным,
а параметры модели неизвестны и подлежат определению из эксперимента.
На практике распространение получили регрессионные модели, которые линейны
относительно параметров. Линейные модели представляются в форме:
y 0f 0 (X, Z) 1f1 (X, Z) .. d f d (X, ,Z) e FT e
где FT f0 (X, Z),f1 (X, Z),..fd (X, Z) - вектор-строка базисных функций факторов X, Z, функций, не
зависящих от параметров модели; T 0 , 1 ,.. d - вектор параметров модели.
Линейные модели можно интерпретировать как разложение неизвестной функции отклика в
ряд по некоторой системе базисных функций (в тригонометрический ряд Фурье, в ряд по
различным системам ортогональных полиномов или функций, в ряд Тейлора и т.д.).
В последнем случае разложения функции отклика в ряд Тейлора имеют место
6.
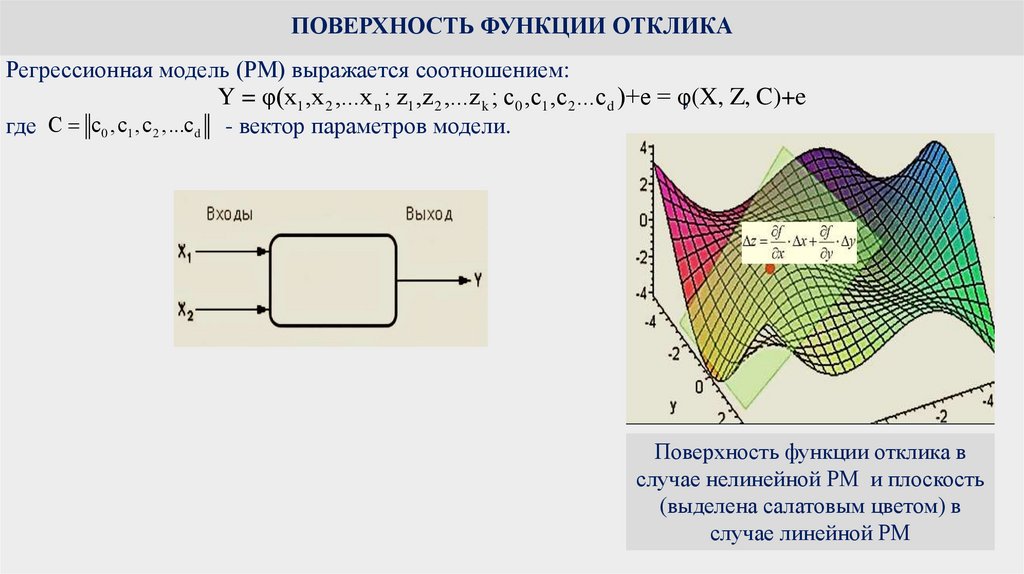
ПОВЕРХНОСТЬ ФУНКЦИИ ОТКЛИКАРегрессионная модель (РМ) выражается соотношением:
Y = φ(x1 ,x 2 ,...x n ; z1 ,z 2 ,...z k ; c0 ,c1 ,c 2 ...cd )+e = φ(X,
Z, C)+e
,
где С с0 , с1 , с 2 ,...сd - вектор параметров модели.
Поверхность функции отклика в
случае нелинейной РМ и плоскость
(выделена салатовым цветом) в
случае линейной РМ
7.
Уровнем фактора называют фиксированное значение фактора. Факторы могут различатьсяпо числу уровней, на которых возможна их фиксация в данной задаче. Понятие уровня
фактора часто используется при описании характерных точек из области действия
(планирования) фактора X j : минимальный X jmin и максимальный X jmax уровни, основной
уровень фактора X 0j , j = 1,2,..n.
Основной уровень фактора указывает такие условия эксперимента, которые представляют
наибольший интерес для исследователя в данный момент.
Обычно вектор X j0T X10 , X 02 ,..X 0n задает в факторном пространстве точку, являющуюся в какомто смысле центром области планирования, центром эксперимента. В ее окрестностях
располагаются все точки плана. Часто координаты X 0j выбираются с помощью соотношения:
X 0j
X jmin X jmax
2
;
X j
Интервал (шаг) варьирования фактора X j :
X jmax X jmin
2
,
так что X jmax X 0j X j , X jmin X 0j X j . Зная X 0j, X j , j = 1,2,..n, можно реализовать операцию
нормализации факторов (операцию перевода факторов в стандартизированный масштаб или к
безразмерной шкале). Операция нормализации сводится к изменению начала отсчета
x j x 0j
координатных осей и масштаба в соответствии с соотношением:
Xj
x j
Таким образом, для переменной x j в стандартизированном масштабе начало координат
совмещено с центром эксперимента, а в качестве единицы измерения используется шаг
варьирования фактора.
8.
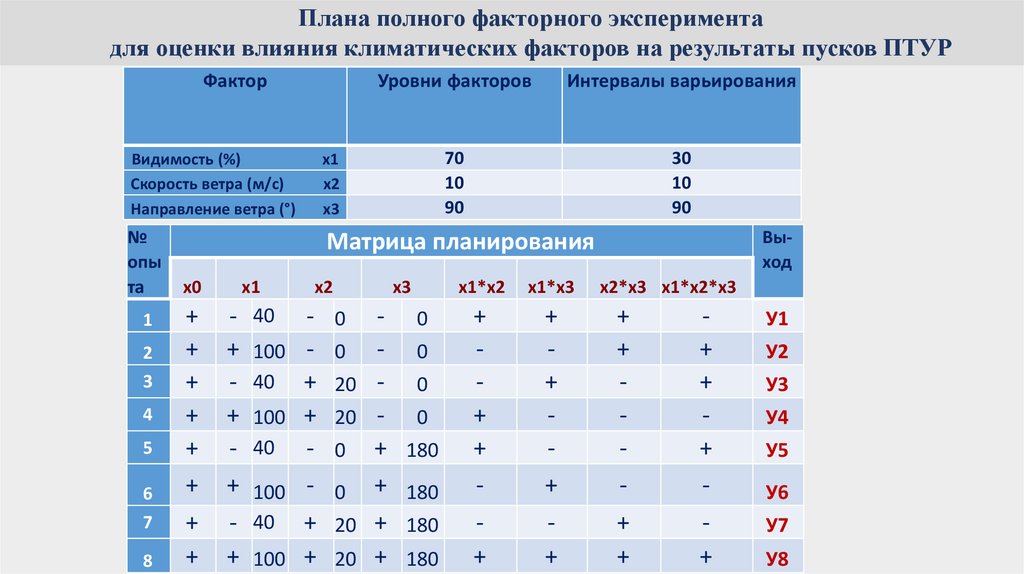
КОДИРОВАНИЕ ФАКТОРОВКодирование – это перевод натуральных значений уровней факторов в кодовые безразмерные
величины с целью построения стандартной матрицы эксперимента.





















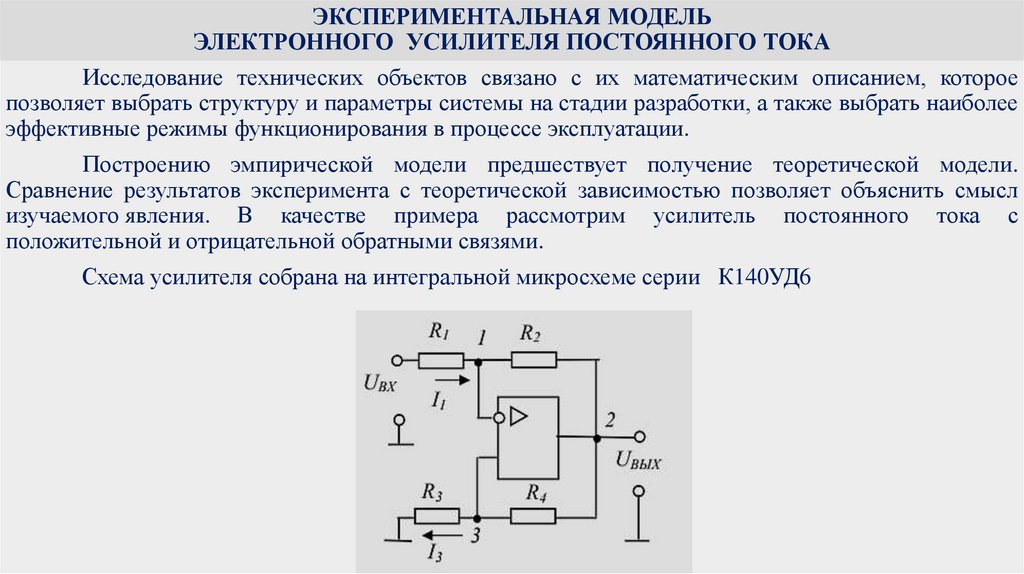








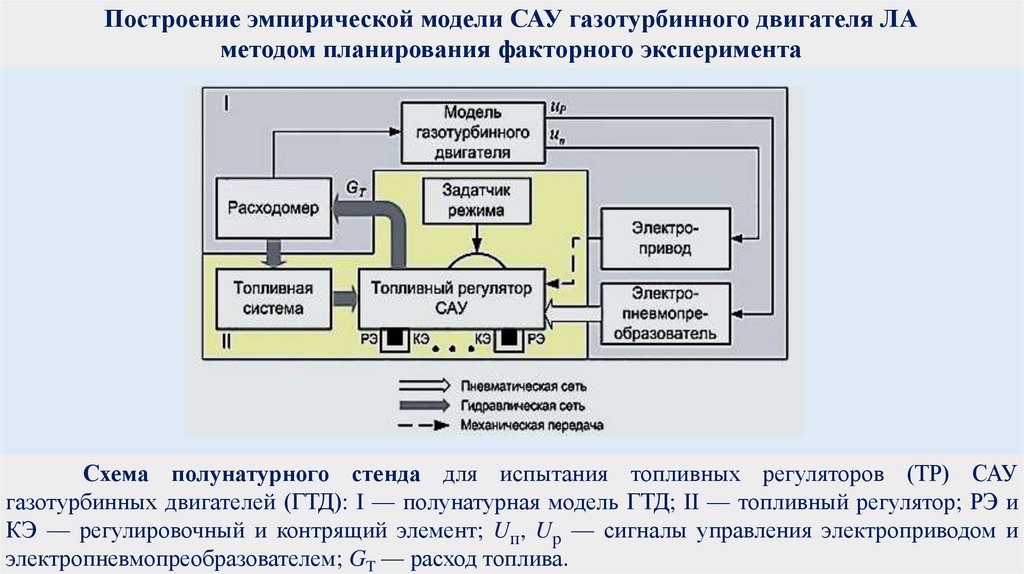


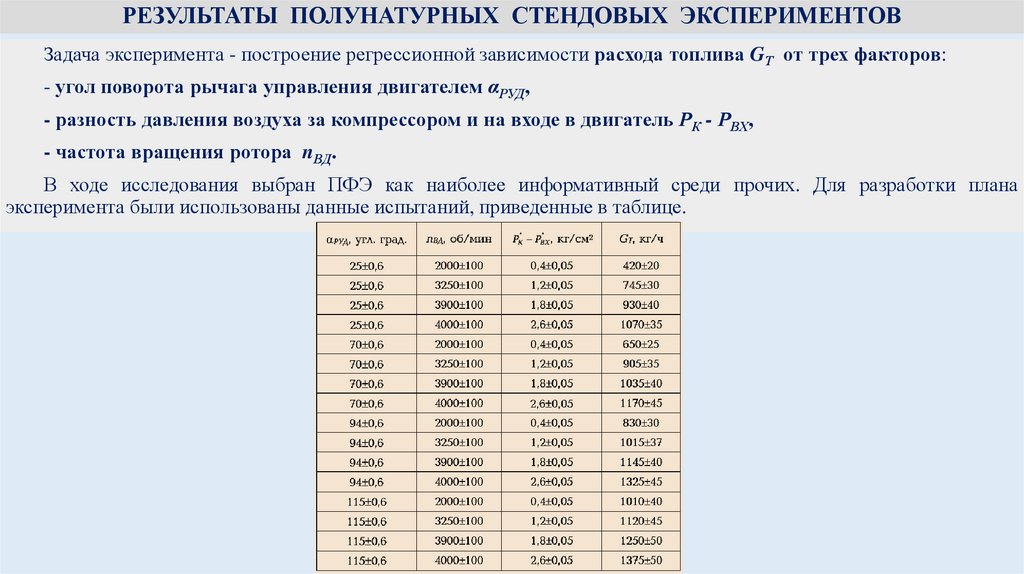





 physics
physics electronics
electronics








