Similar presentations:
Объект. Лекция № 3
1.
Лекция № 31
2.
y1x1
Объект
y
xr
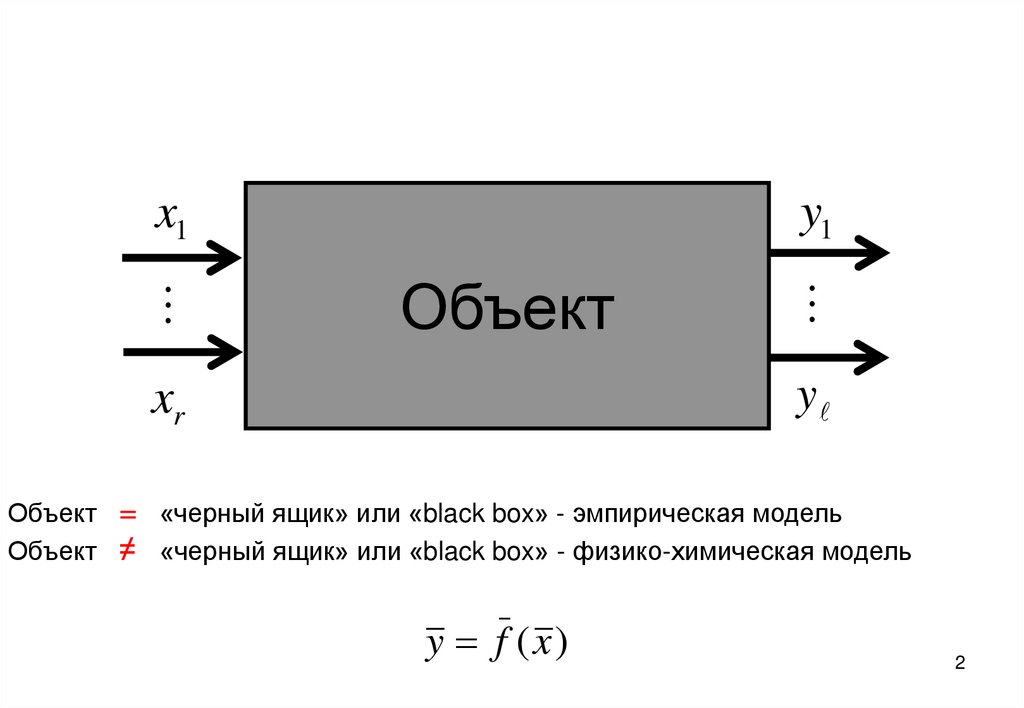
Объект = «черный ящик» или «black box» - эмпирическая модель
Объект ≠ «черный ящик» или «black box» - физико-химическая модель
y f (x )
2
3. I.Принципы построения теоретических физико-химических моделей
Последовательные этапы
Изучается теория процесса
Составляется система уравнения математического
описания (МО)
Выбирается алгоритм решения системы уравнений
МО, т.н. моделирующий алгоритм (МА)
МА реализуется на компьютере и получается
математическая модель (ММ)
Проверяется адекватность модели путем сравнения
расчетных результатов с экспериментальными
В случае отсутствия адекватности модели решается
задача идентификации,
3
4.
v1 C p10
T1
0
T2
v2 C p 2
T1
T2
FT KT
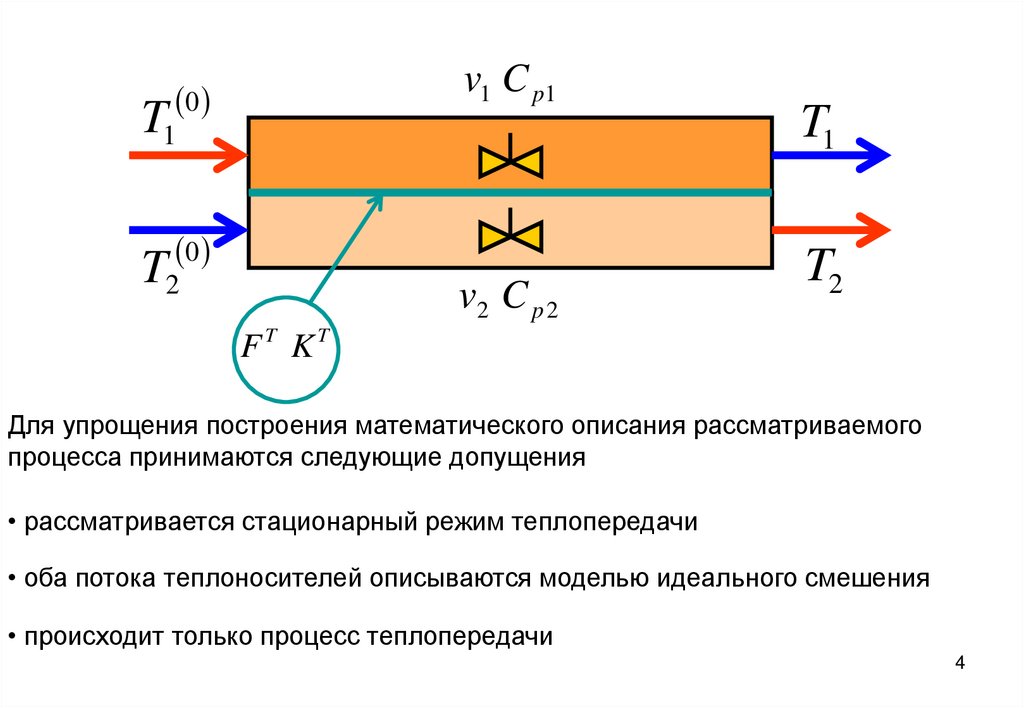
Для упрощения построения математического описания рассматриваемого
процесса принимаются следующие допущения
• рассматривается стационарный режим теплопередачи
• оба потока теплоносителей описываются моделью идеального смешения
• происходит только процесс теплопередачи
4
5.
( 0)1
( 0) ( 0)
p1 1
1. v C T
v1C p1T1 F q 0
T
T
1
2. q K T2 T1
T
1
( 0)
2
T
( 0) ( 0)
p2 2
3. v C T
v2C p 2T2 F q 0
T
T
2
4. q K T1 T2
T
2
T
q q q
T
T
1
T
2
5
6.
( 0)1
( 0) ( 0)
p1 1
v1C p1T1 F q 0
( 0)
2
( 0) ( 0)
p2 2
v2C p 2T2 F q 0
1. v C T
2. v C T
T
T
T
T
3. q K T2 T1
T
T
Принимается допущение о том, что константа теплопередачи через поверхность
теплообмена постоянна (KT = const)
Это означает, что теплоёмкости потоков постоянны и не зависят от температуры
В качестве определяемых переменных выбираем температуры потоков на
выходе из теплообменника Т1 и Т2 и локальную интенсивность теплопередачи
ΔqT
6
7.
Преобразуем систему путём подстановки в уравнения 1 и 2 выражения длялокальной интенсивности теплопередачи ΔqT:
1.
v C T
F K T F K T
T
1
T
T
p1 1
1
2
a12
a11
2.
T
T
T
1
a21
2
( 0) (0)
p1 1
b1
F K T v
C F K T
T
v C T
(0)
1
T
p2
2
v C T
a22
(0)
2
( 0) ( 0)
p2 2
b2
A x b;
a11 a12 T1 b1
a
21 a22 T2 b2
7
8.
137 Тема 02: Построение эмпирических статистических моделей ХТПМетодом обратной матрицы находим значения температур потоков на выходе из
теплообменника:
1
T1 a11 a12 b1
T a
2 21 a22 b2
Таким образом определяются температуры потоков Т1 и Т2 на выходе из
теплообменника.
8
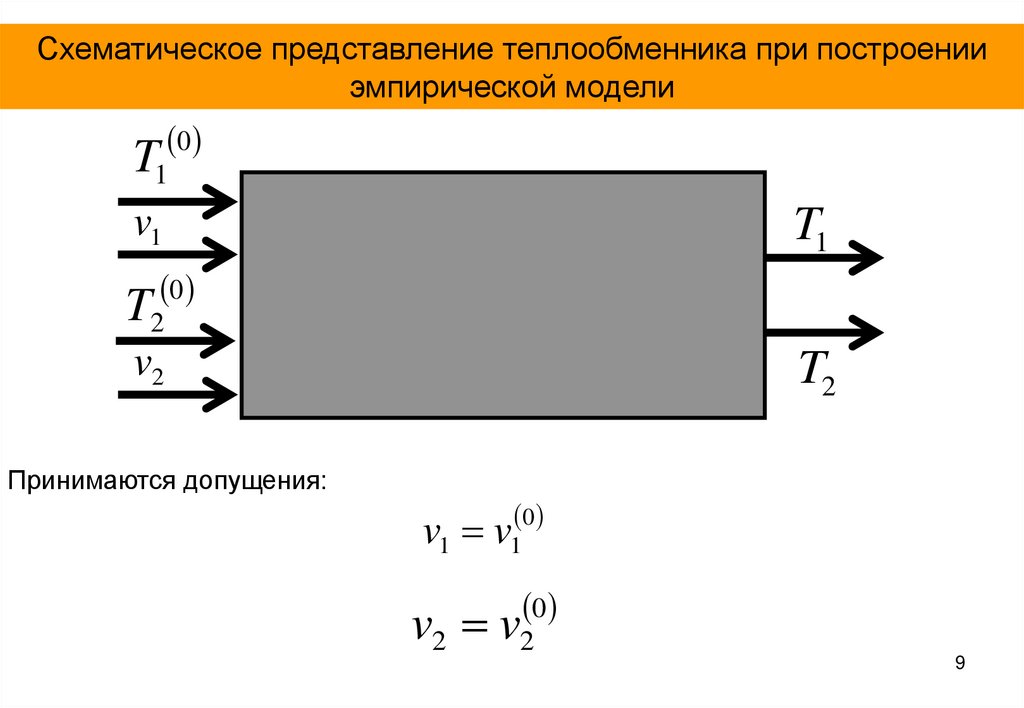
9.
Схематическое представление теплообменника при построенииэмпирической модели
0
T1
T1
v1
0
T2
v2
Принимаются допущения:
T2
0
v1 v1
0
v2 v2
9
10.
Основная задача при построении эмпирической моделитеплообменника
На основании обработки экспериментальных данных о функционировании
теплообменника получить две функциональные зависимости следующего вида:
0
0
0
0
T1 f1 (T1 , v1, T2 , v2 , a1 )
T2 f 2 (T1 , v1, T2 , v2 , a2 )
Где
a1, a2
- коэффициенты функциональных зависимостей
10
11.
Таблица результатов экспериментальныхисследований при построении эмпирической
модели теплообменника
11
12.
В общем случае:y f ( x, a )
y1 T1
y
y2 T2
где
0
x
1 T1
x
v
2
1
x
0
x3 T2
x4 v2
a - коэффициенты функциональных зависимостей:
y1 f1( x , a1 )
y2 f 2 ( x , a2 )
12
13. Пример решения задачи по теме «Моделирование простой гидравлической системы»
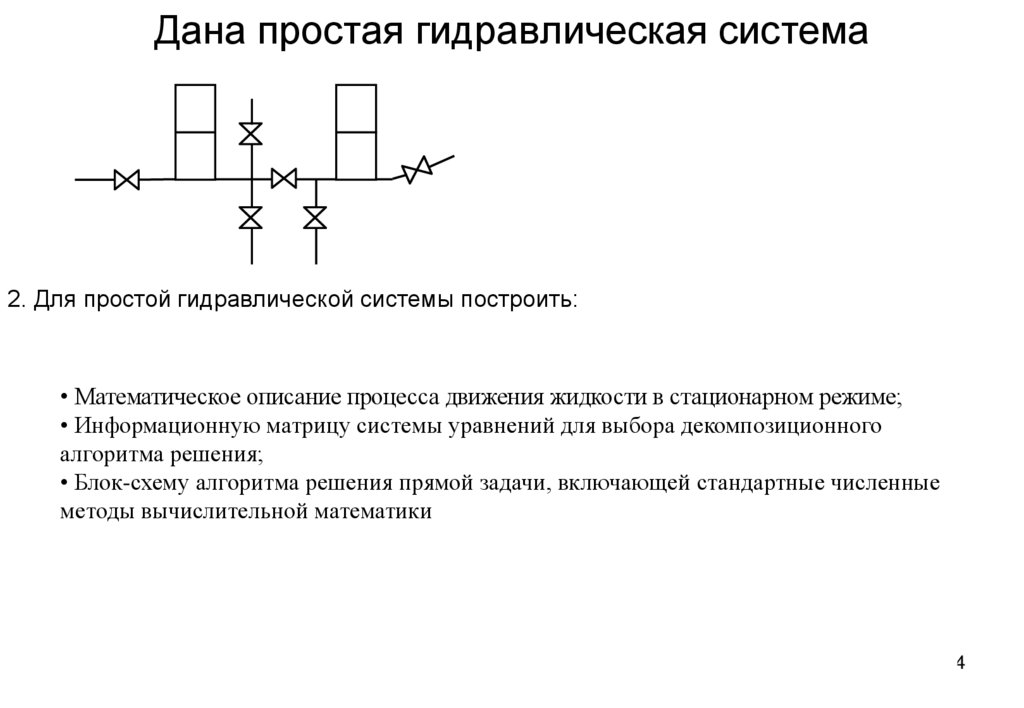
1314. Дана простая гидравлическая система
2. Для простой гидравлической системы построить:• Математическое описание процесса движения жидкости в стационарном режиме;
• Информационную матрицу системы уравнений для выбора декомпозиционного
алгоритма решения;
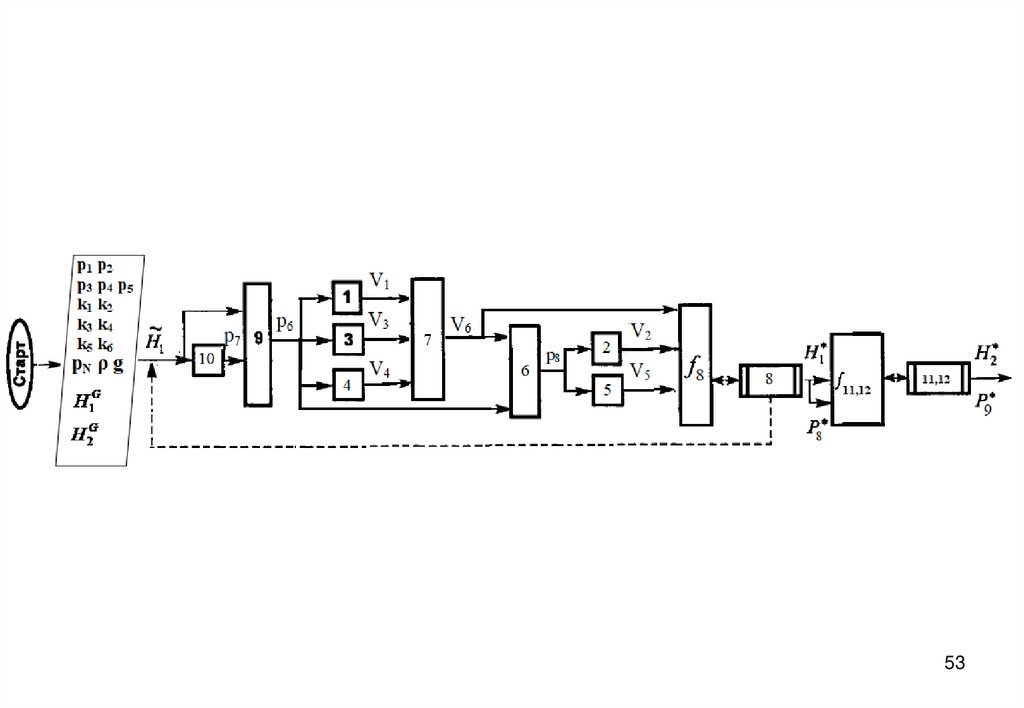
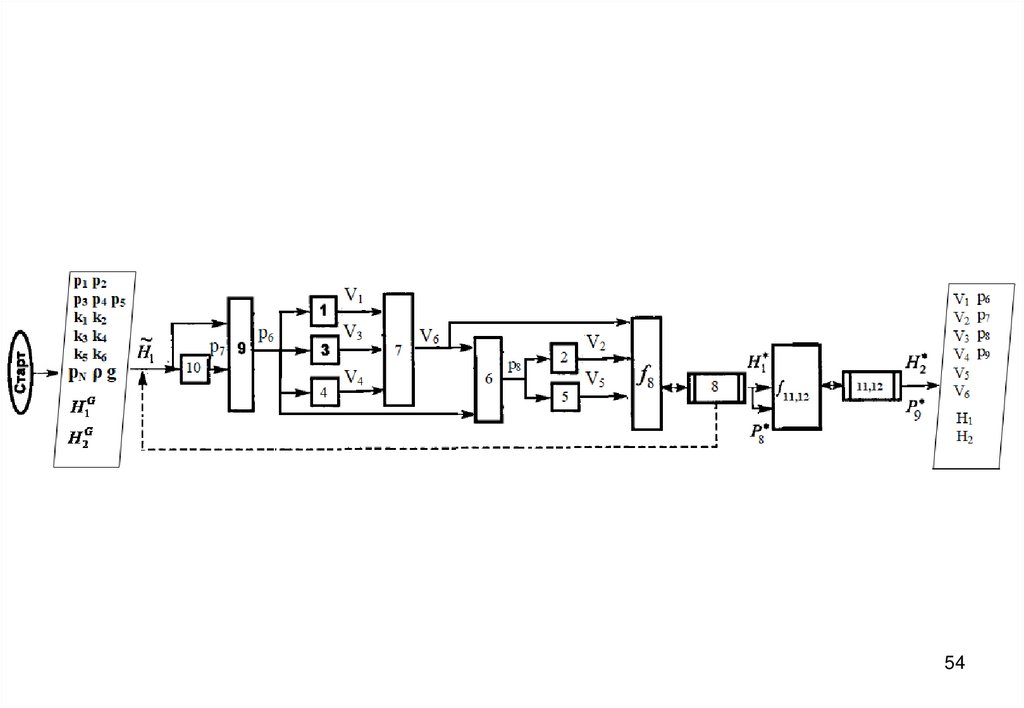
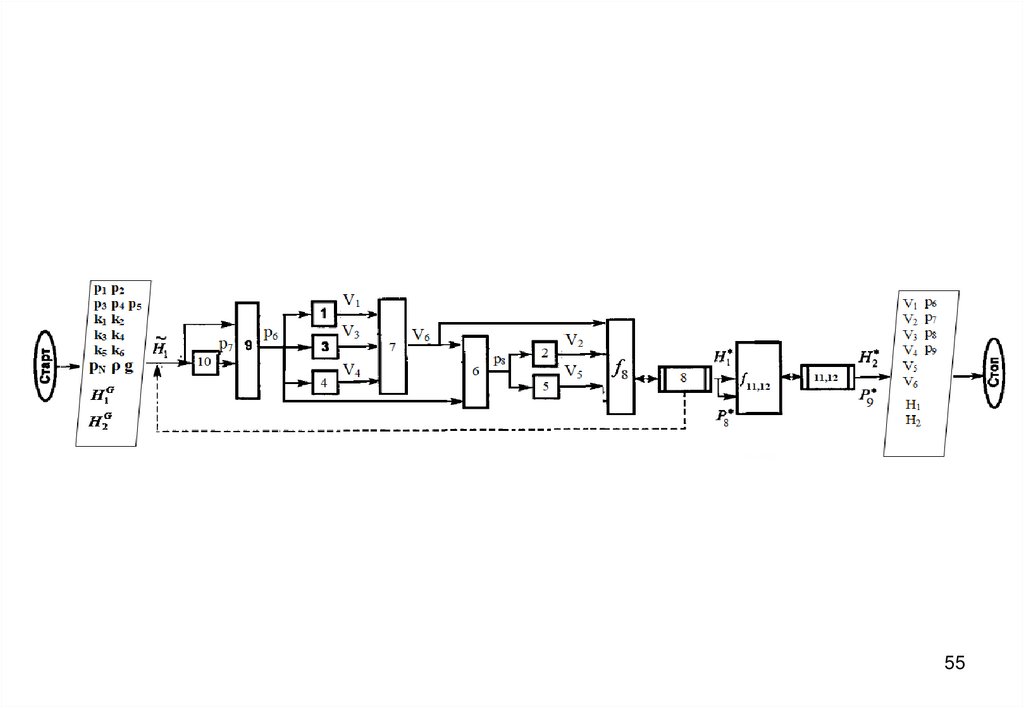
• Блок-схему алгоритма решения прямой задачи, включающей стандартные численные
методы вычислительной математики
14
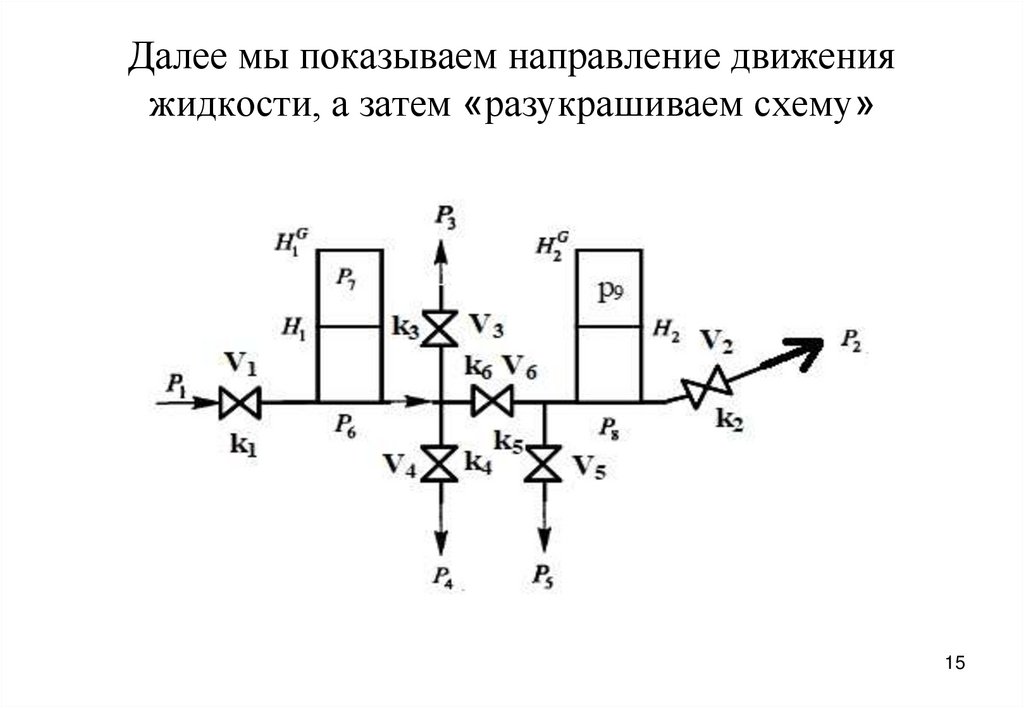
15. Далее мы показываем направление движения жидкости, а затем «разукрашиваем схему»
1516. Основные допущения при моделировании простой гидравлической системы:
Стационарный режим:Уравнения математического описания простой
гидравлической системы:
Уравнения для определения объёмного расхода
жидкости через вентили:
16
17.
1718.
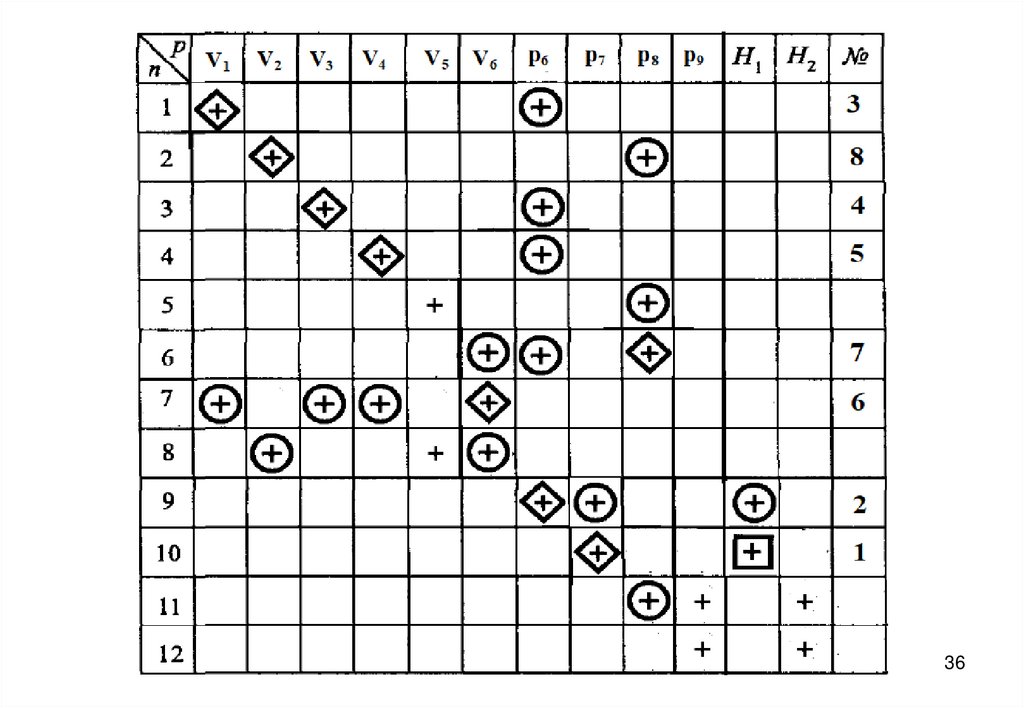
1. V1 k1 sgn( p1 p6 ) ( p1 p6 );18
19.
2. V2 k2 sgn( p8 p2 ) ( p8 p2 );19
20.
3. V3 k3 sgn( p6 p3 ) ( p6 p3 );20
21.
4. V4 k4 sgn( p6 p4 ) ( p6 p4 );21
22.
5. V5 k5 sgn( p8 p5 ) ( p8 p5 );22
23.
6. V6 k6 sgn( p6 p8 ) ( p6 p8 );23
24.
Балансовые уравненияКол-во балансовых ур.= кол-во емк.
7. V1 V3 V4 V6 ; или V1 V3 V4 V6 0
Приход
Расход
24
25.
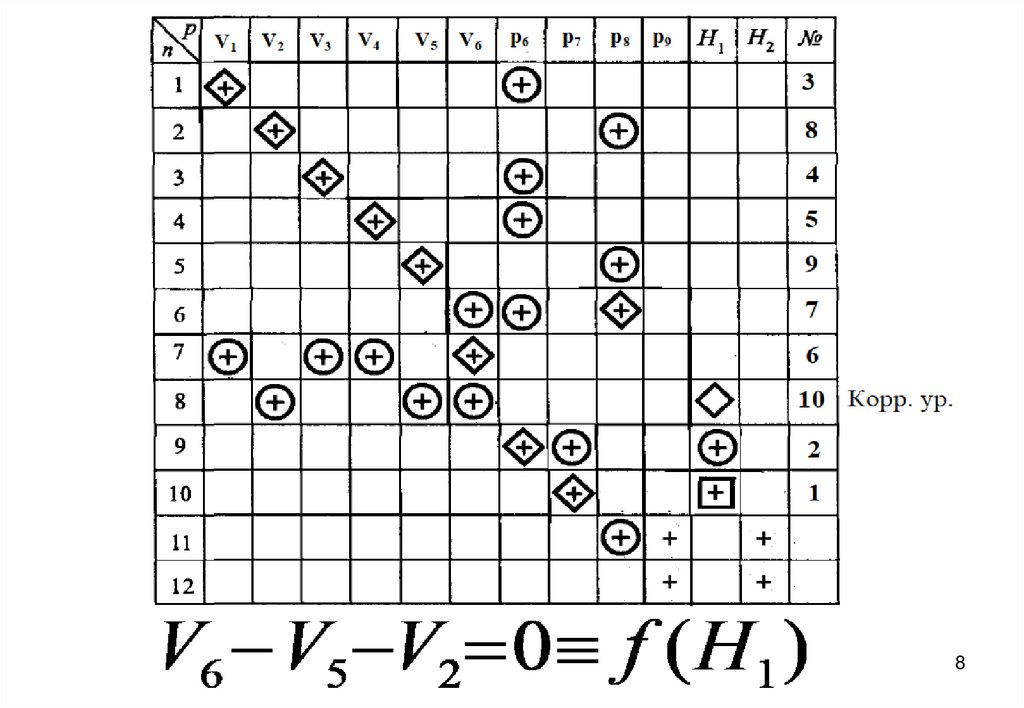
8. V6 V5 V2 ; или V6 V5 V2 0Приход
Расход
25
26.
9. p6 p7 gH1 ;G
1
H
10. p7 p N G
H1 H1
11. p8 p9 gH 2 ;
G
2
H
12. p9 p N G
H2 H2
26
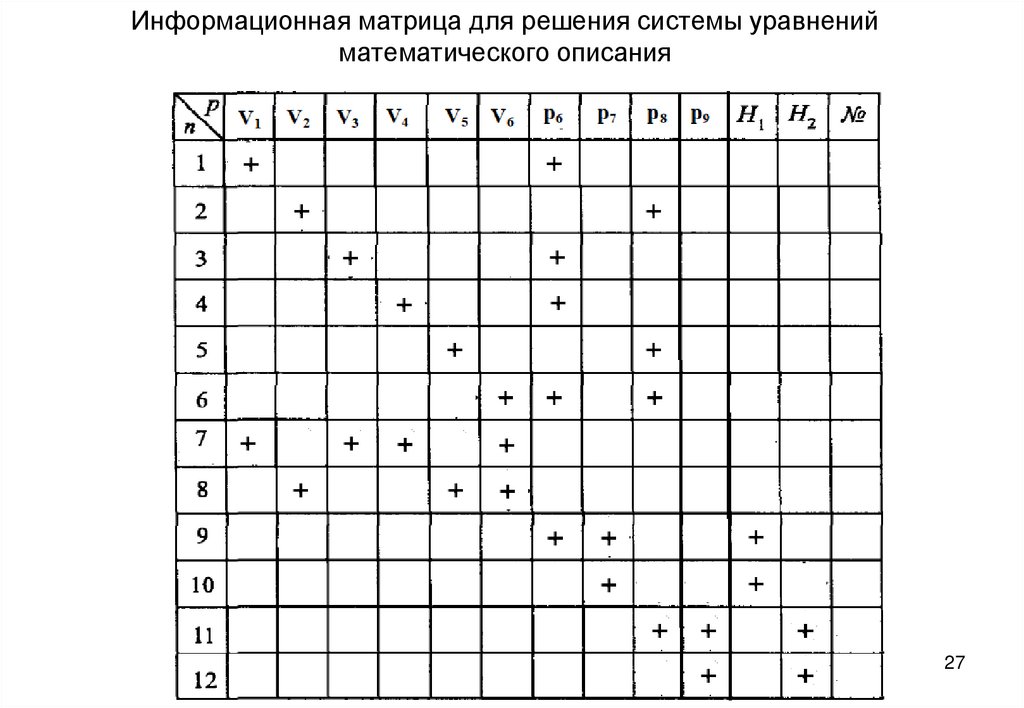
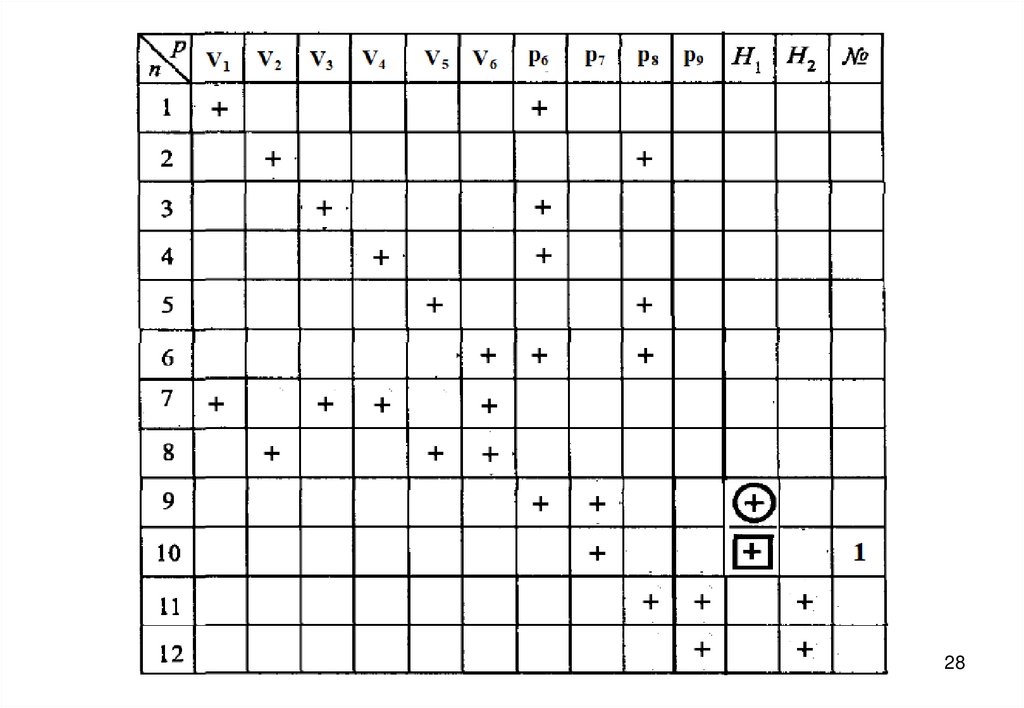
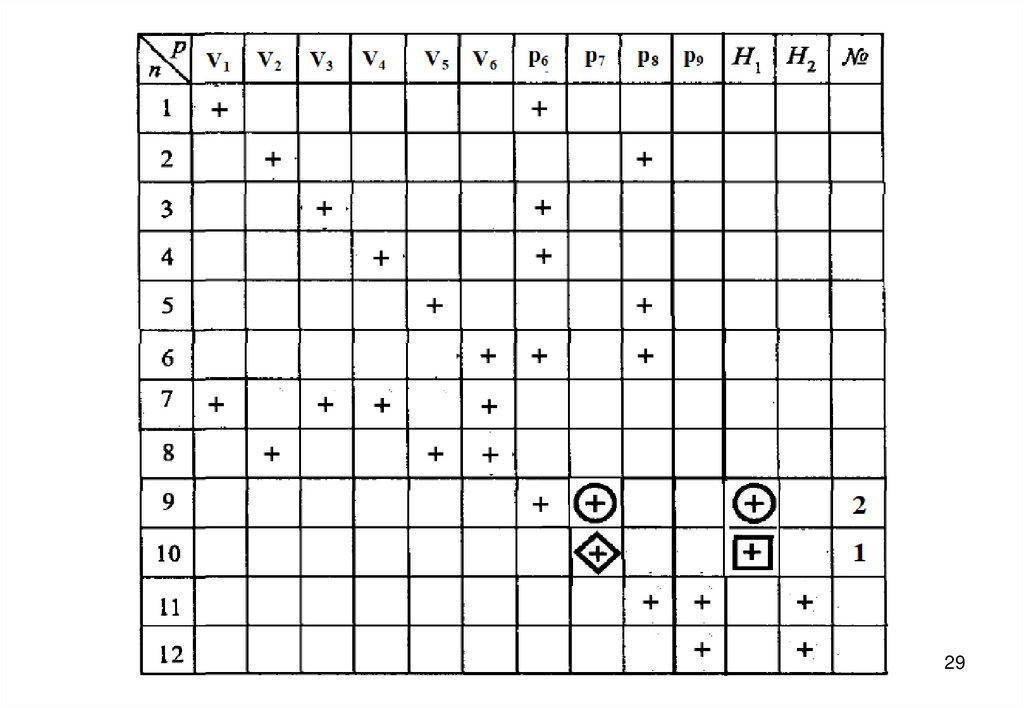
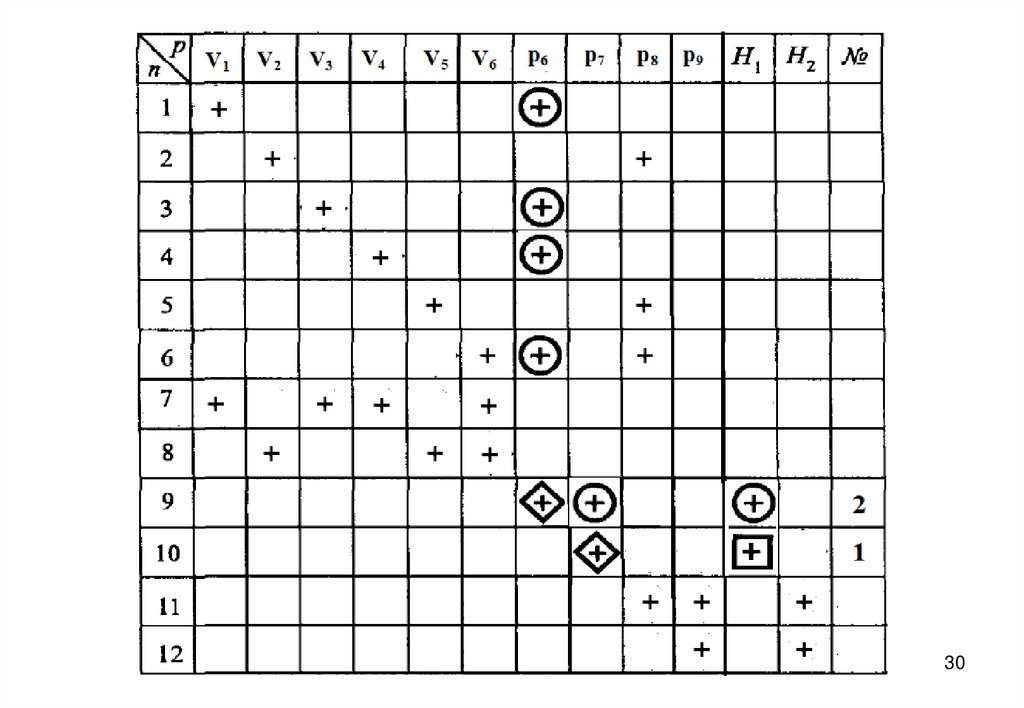
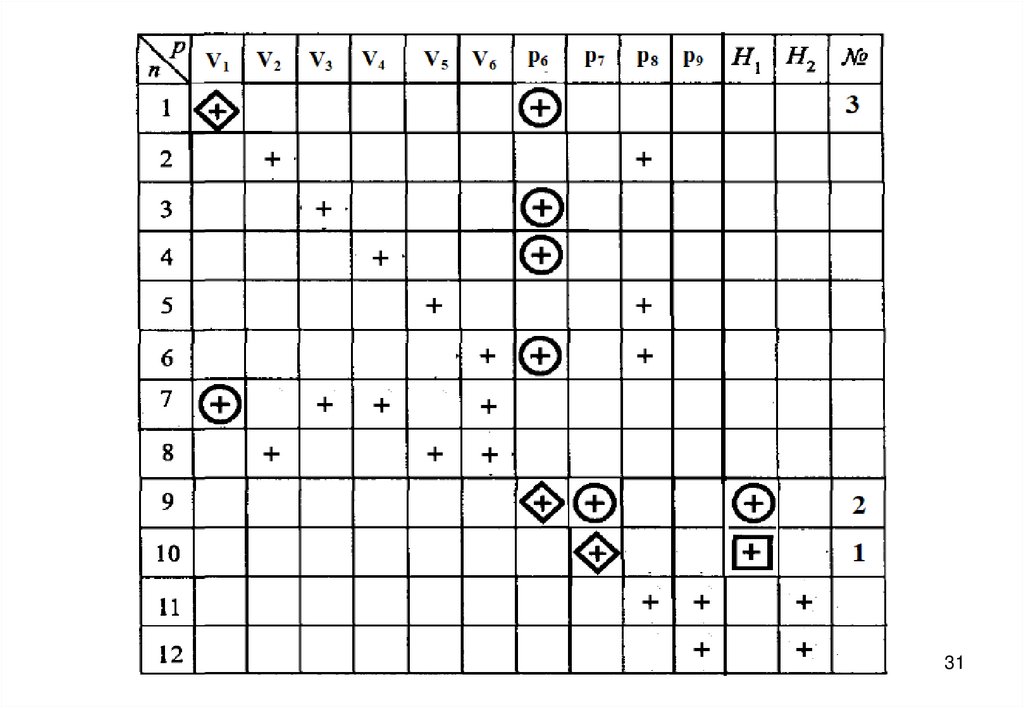
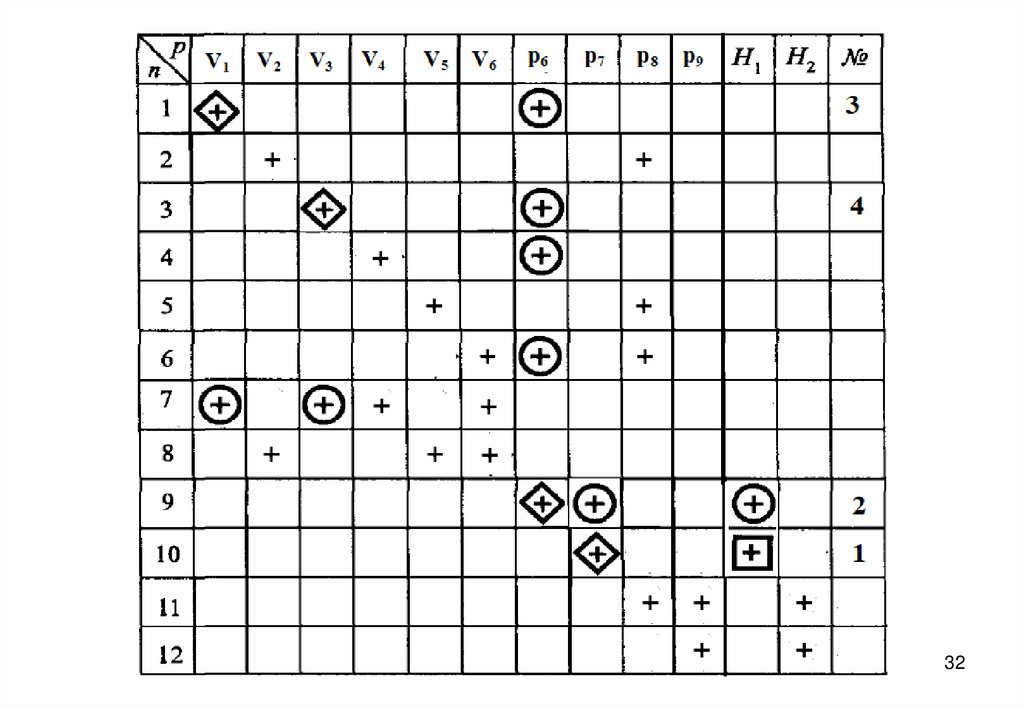
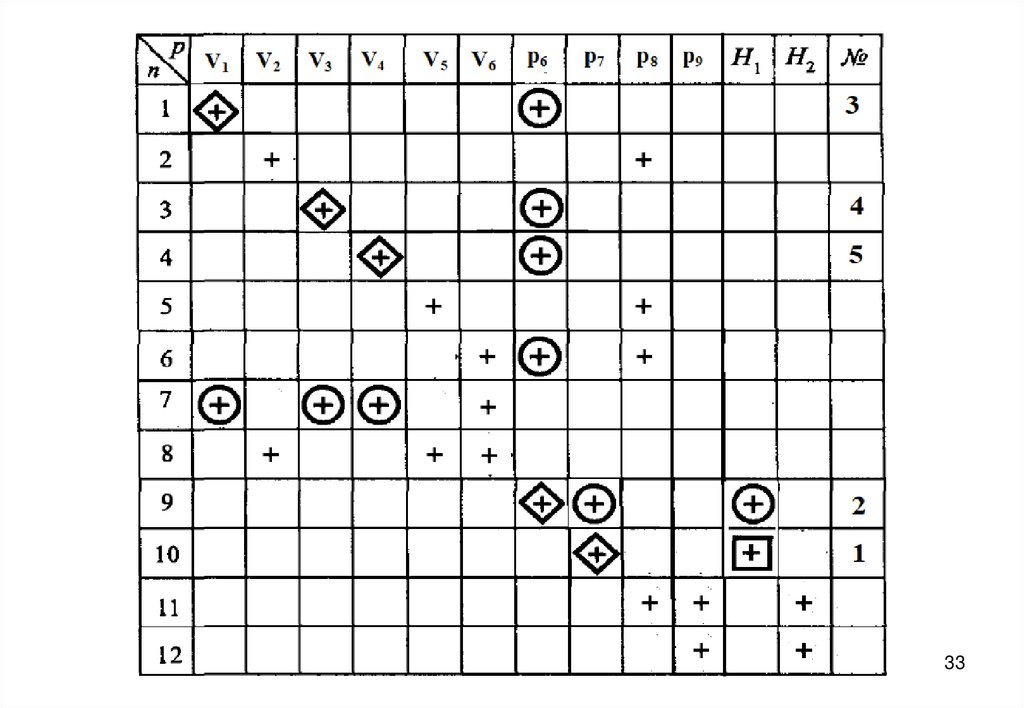
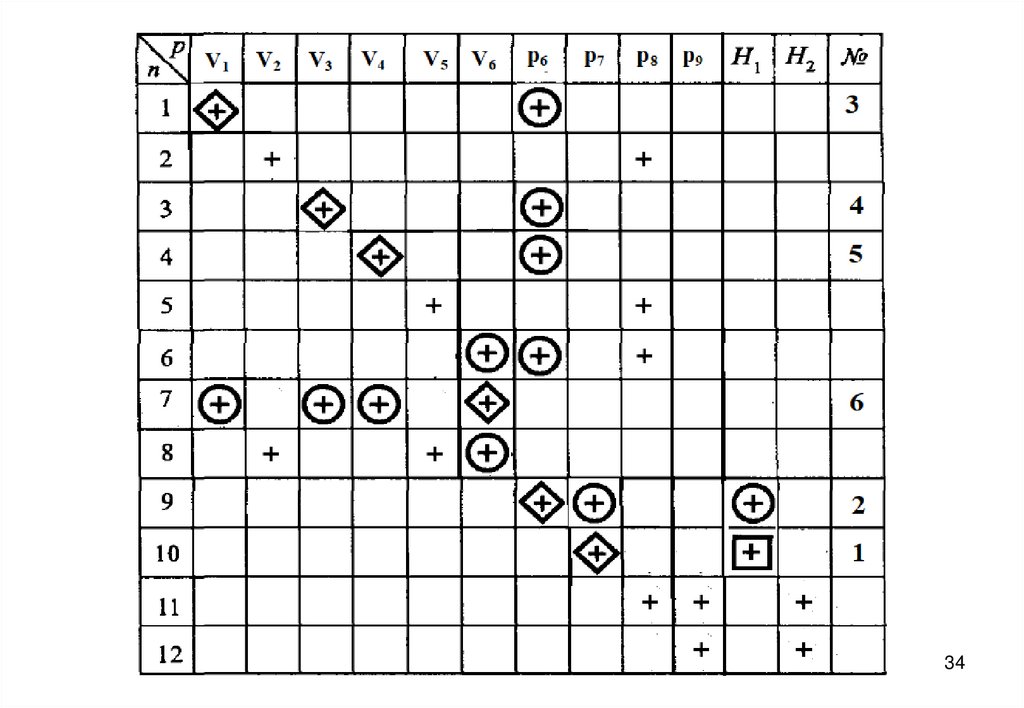
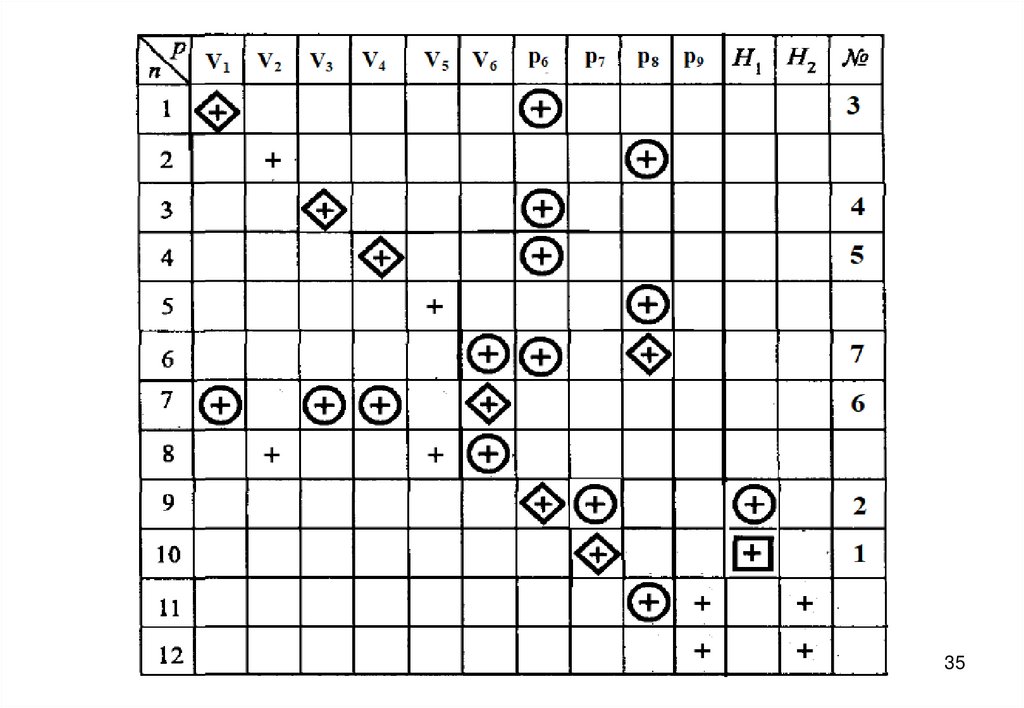
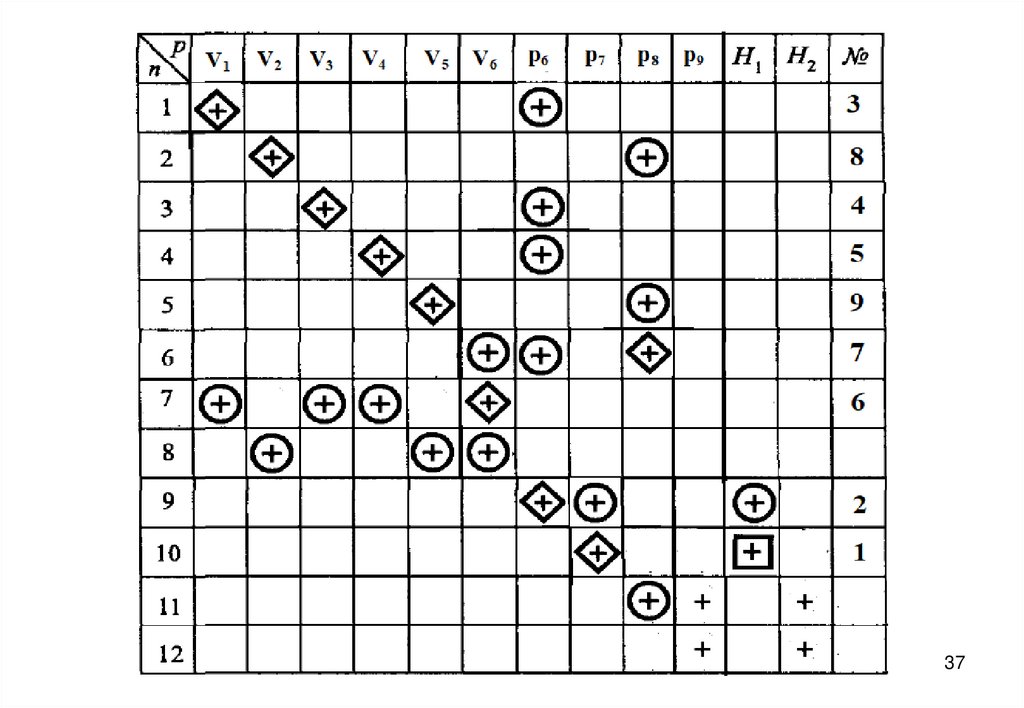
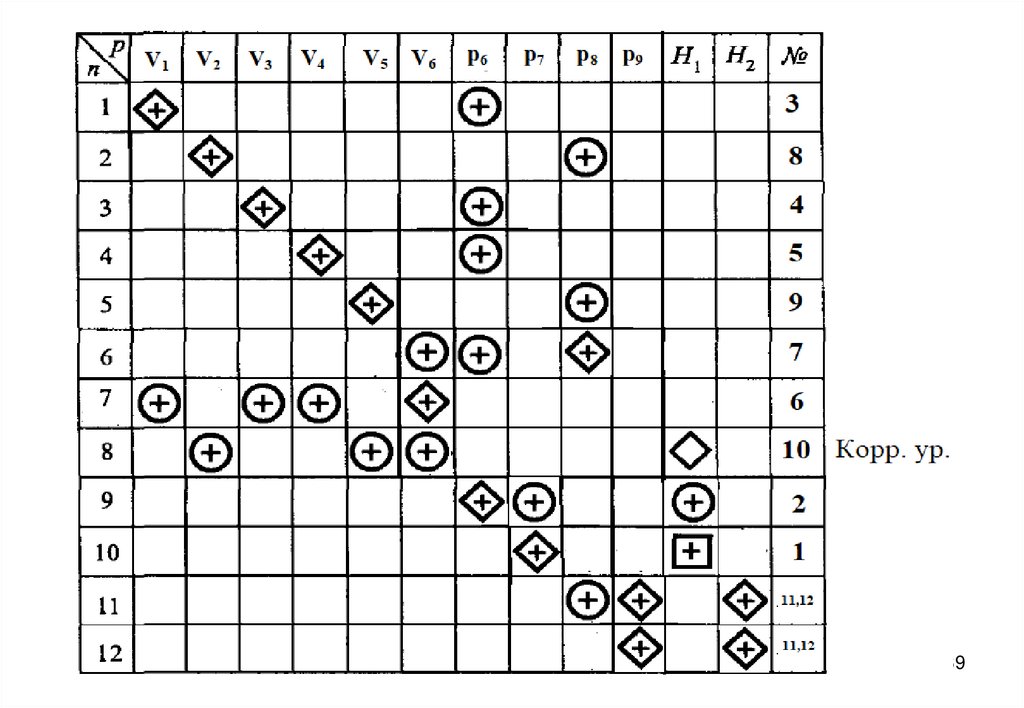
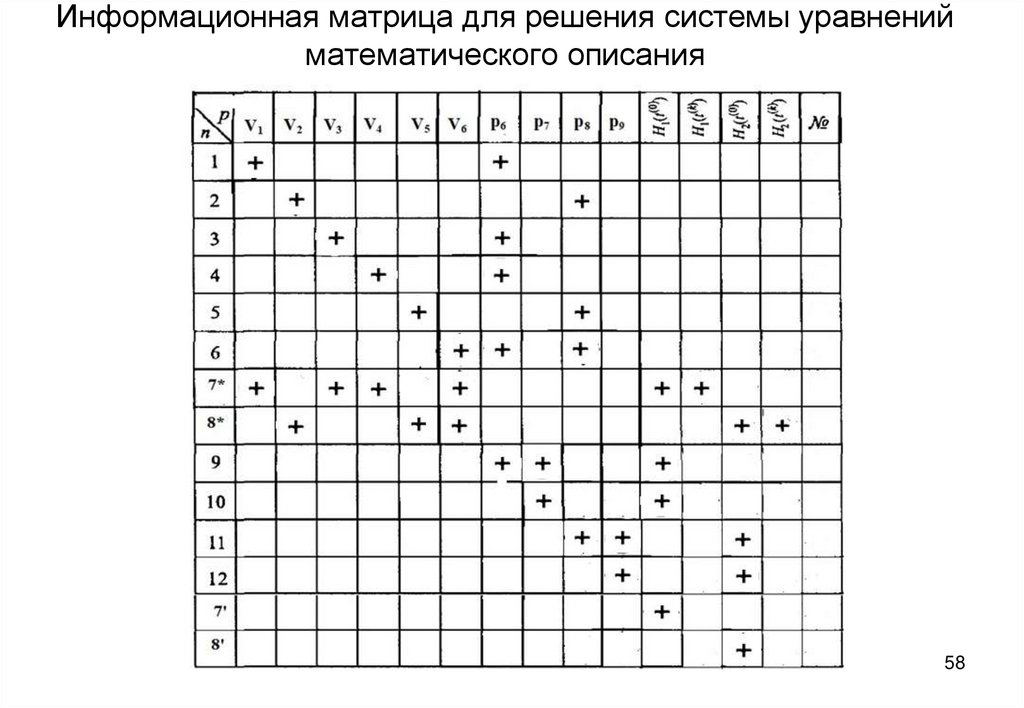
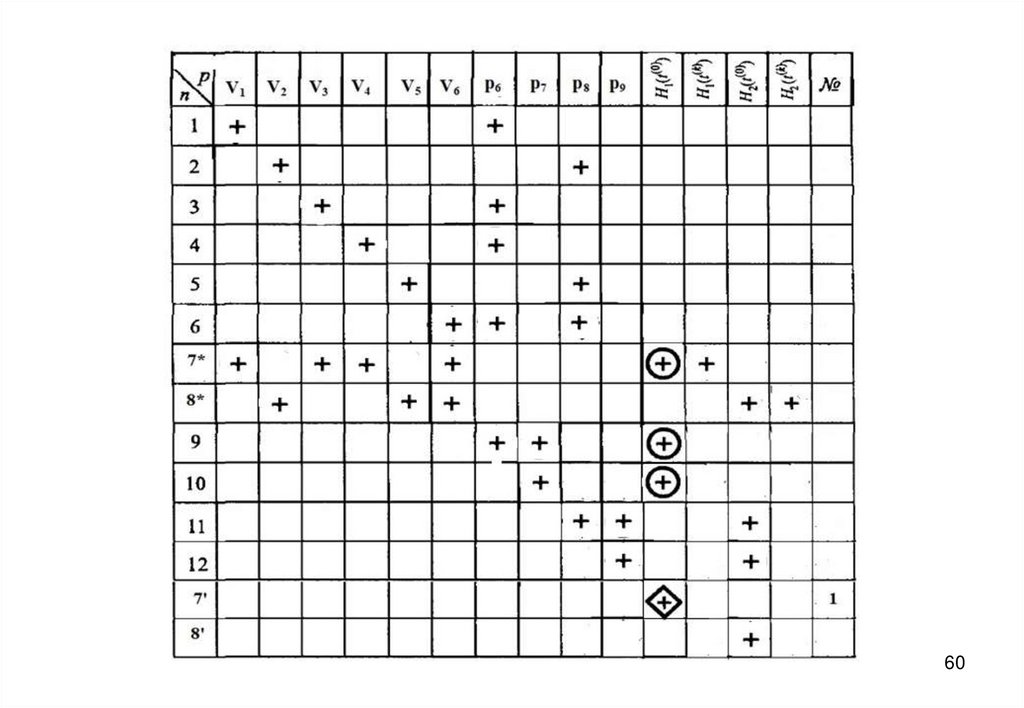
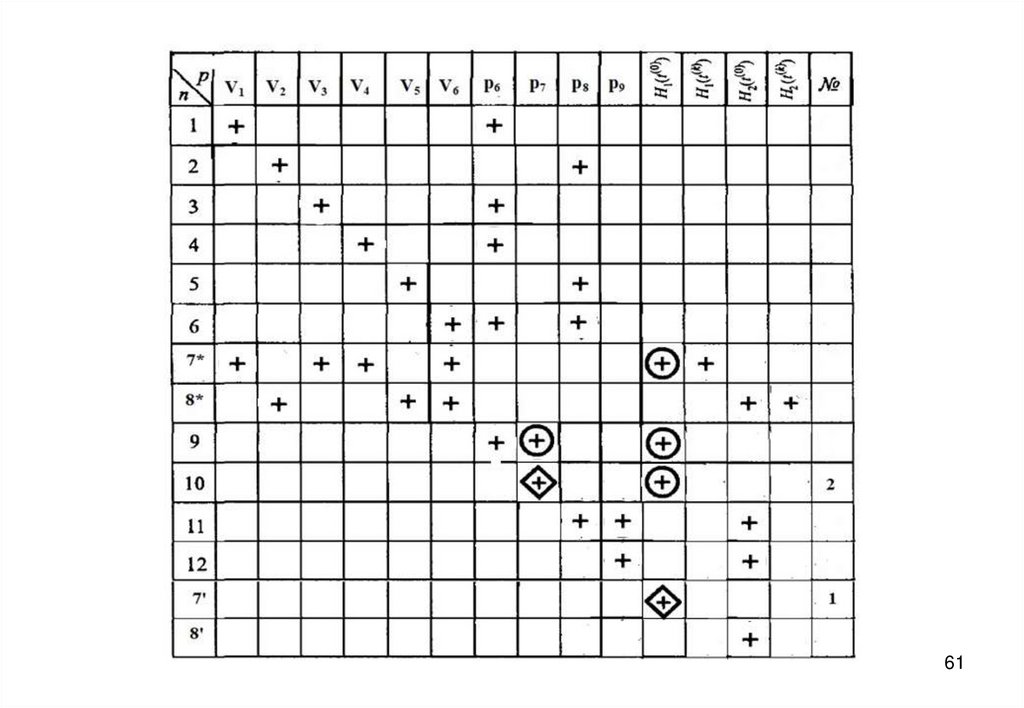
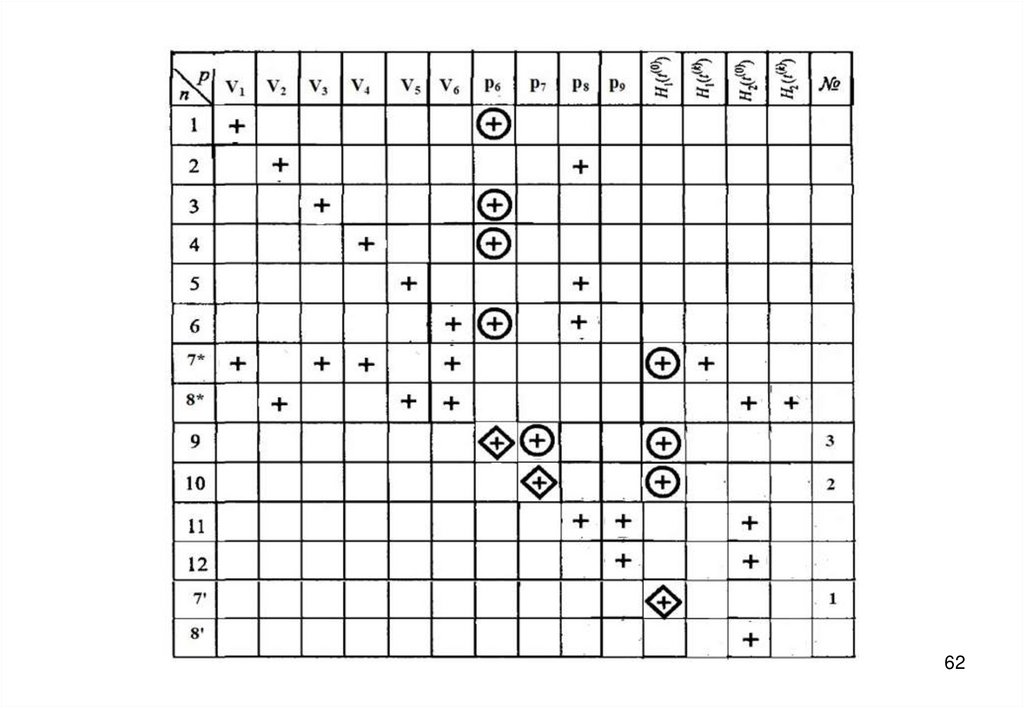
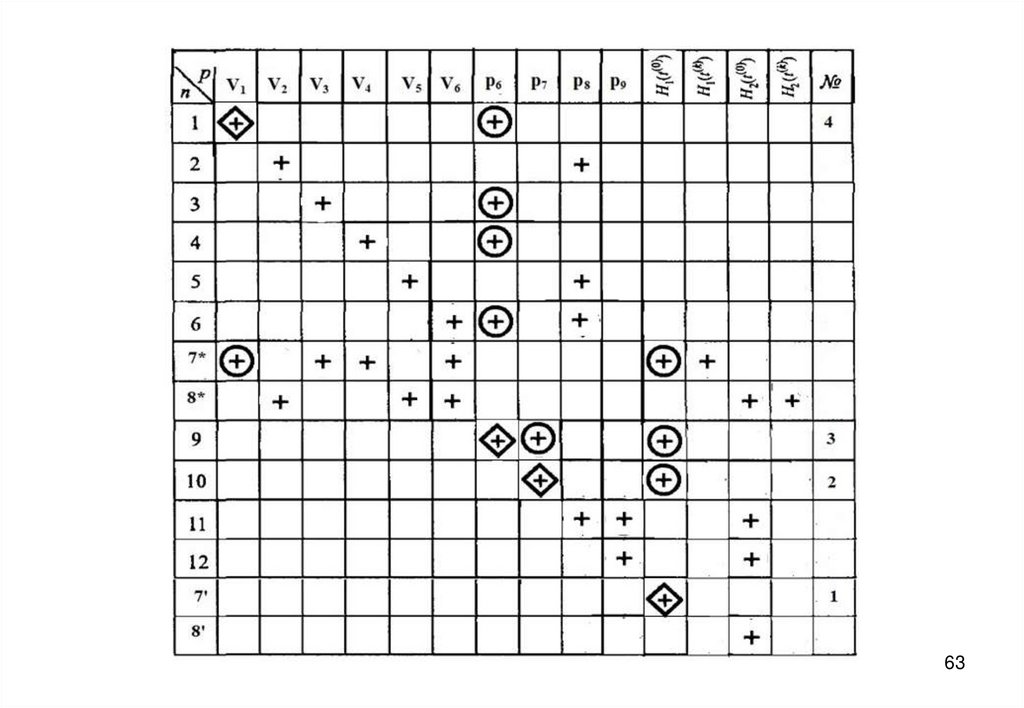
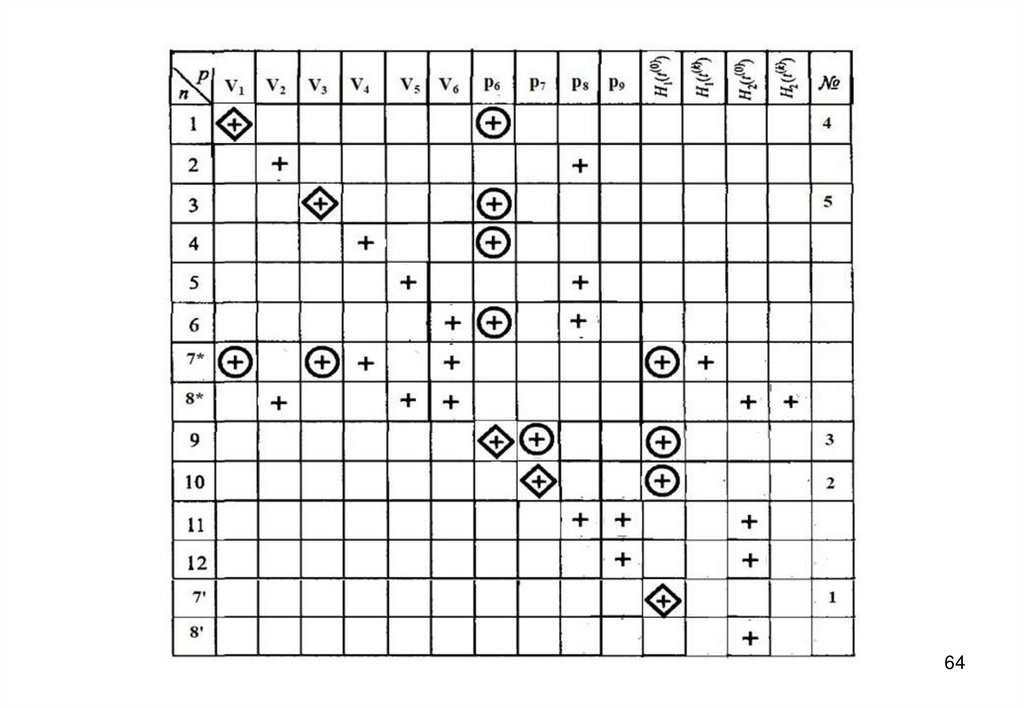
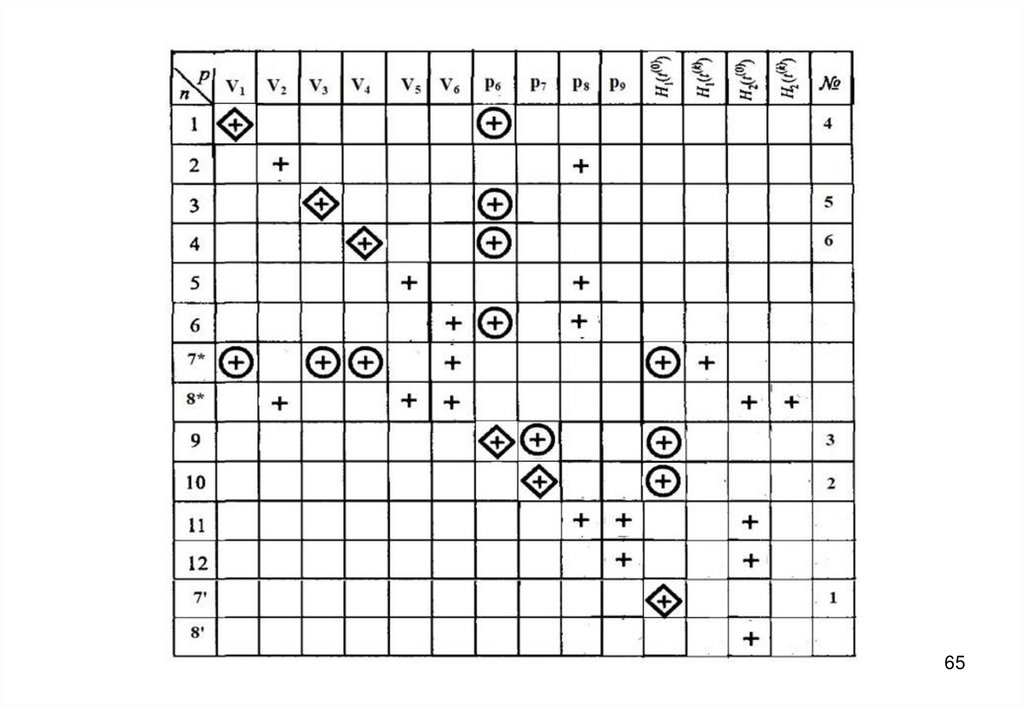
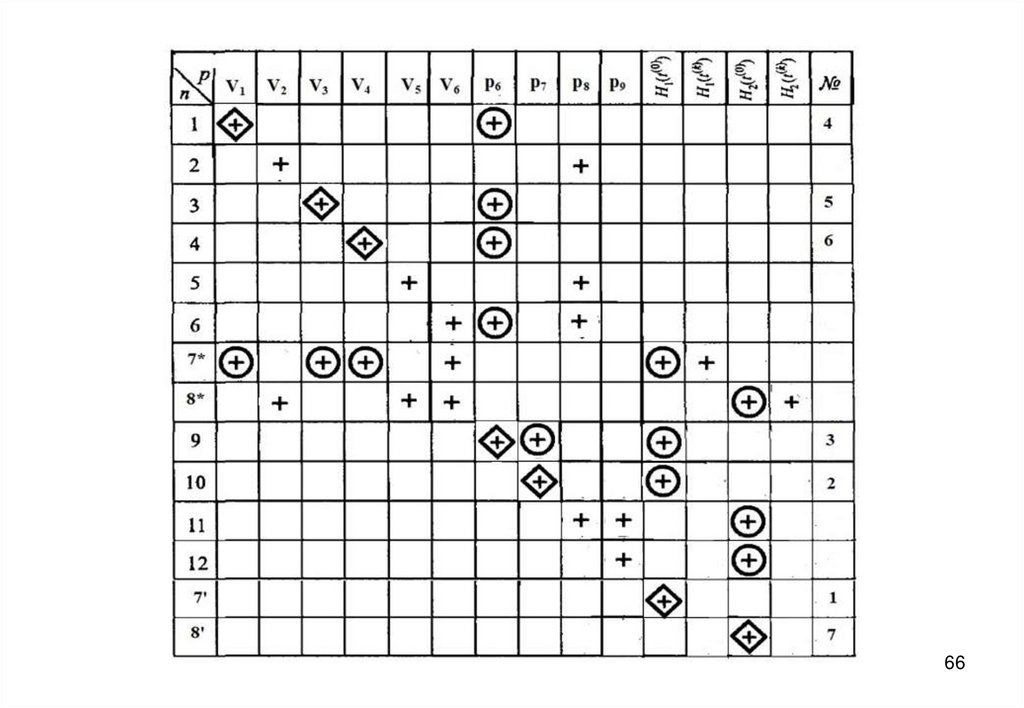
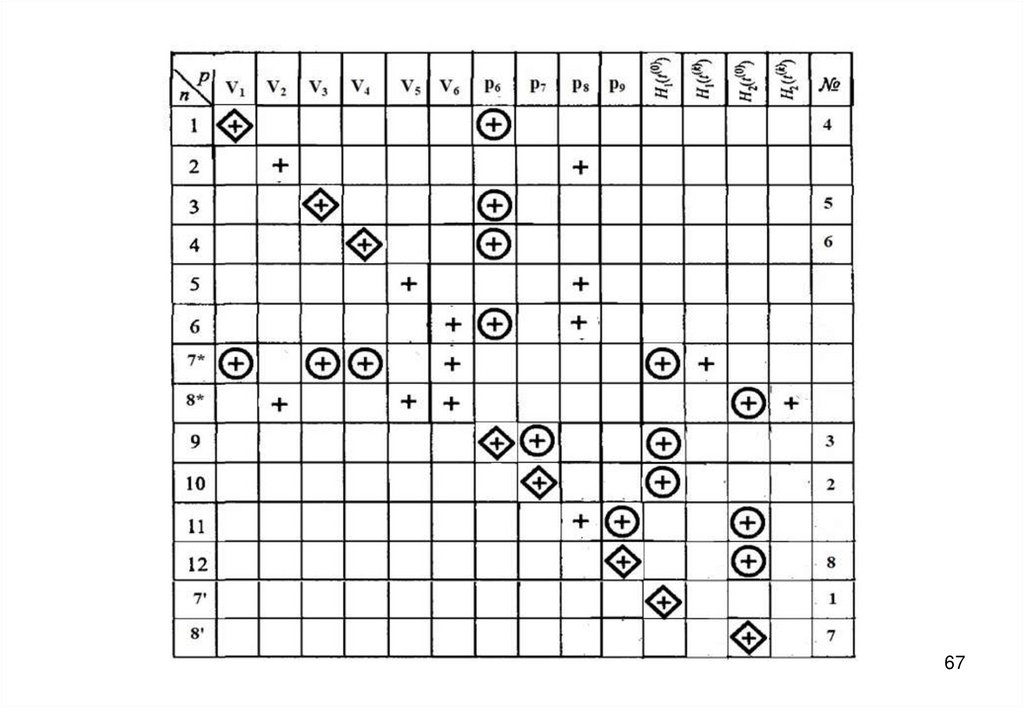
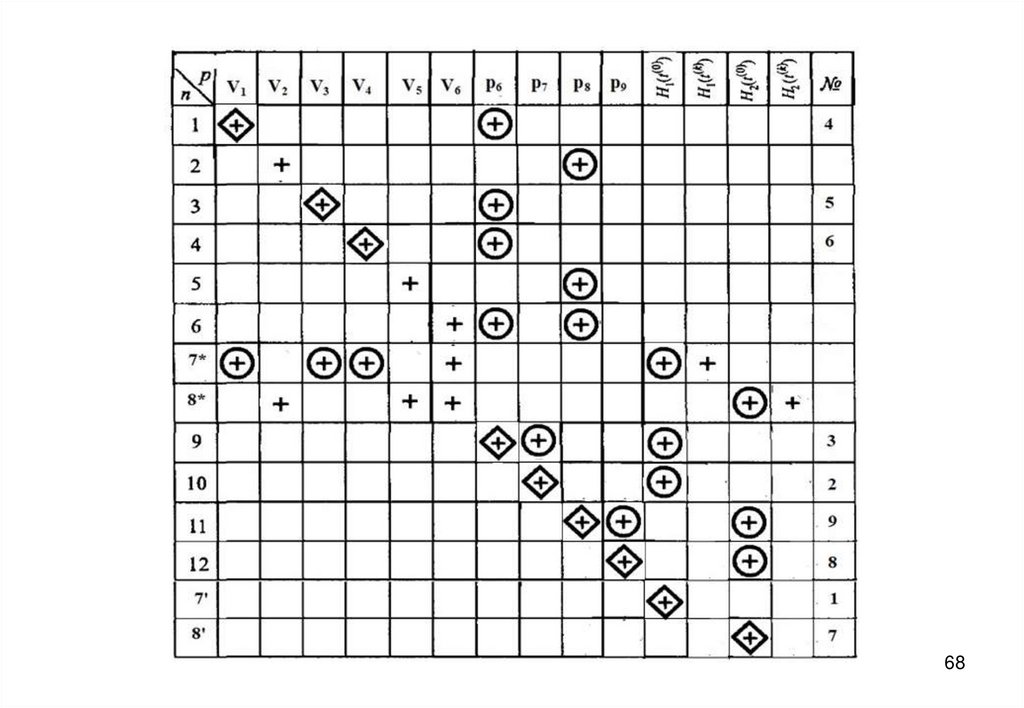
27. Информационная матрица для решения системы уравнений математического описания
2728.
2829.
2930.
3031.
3132.
3233.
3334.
3435.
3536.
3637.
3738.
3839.
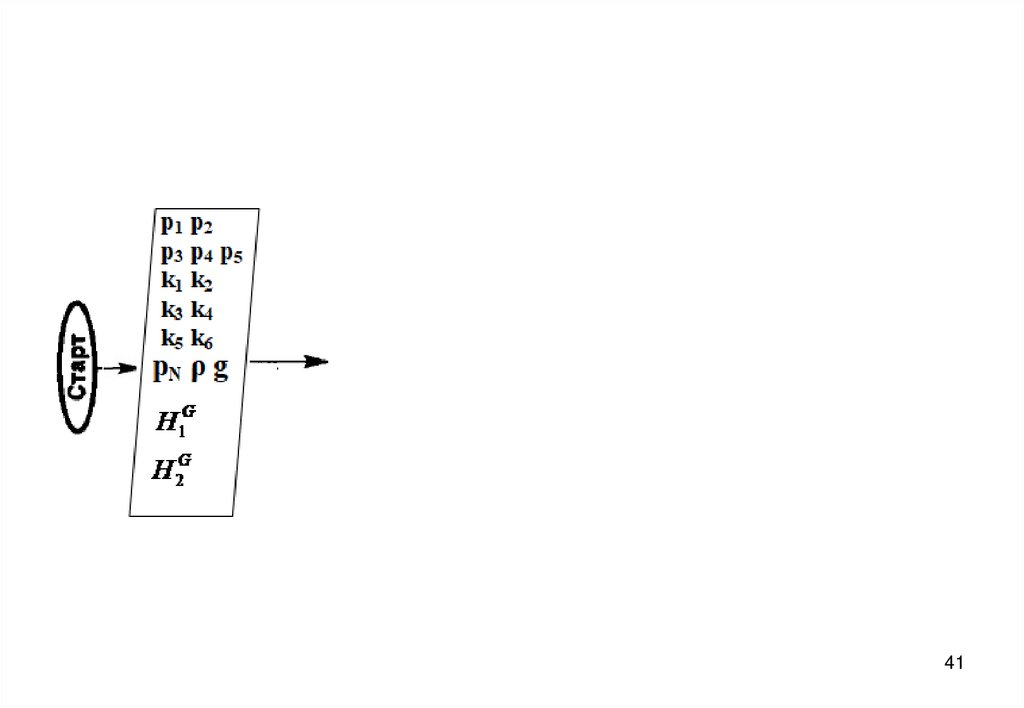
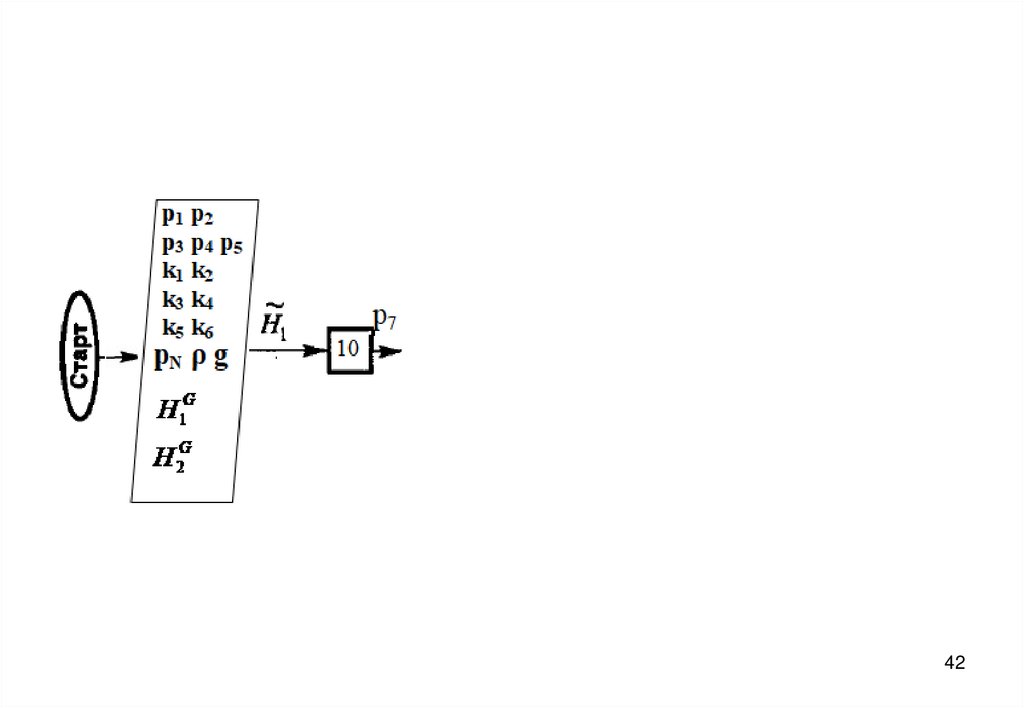
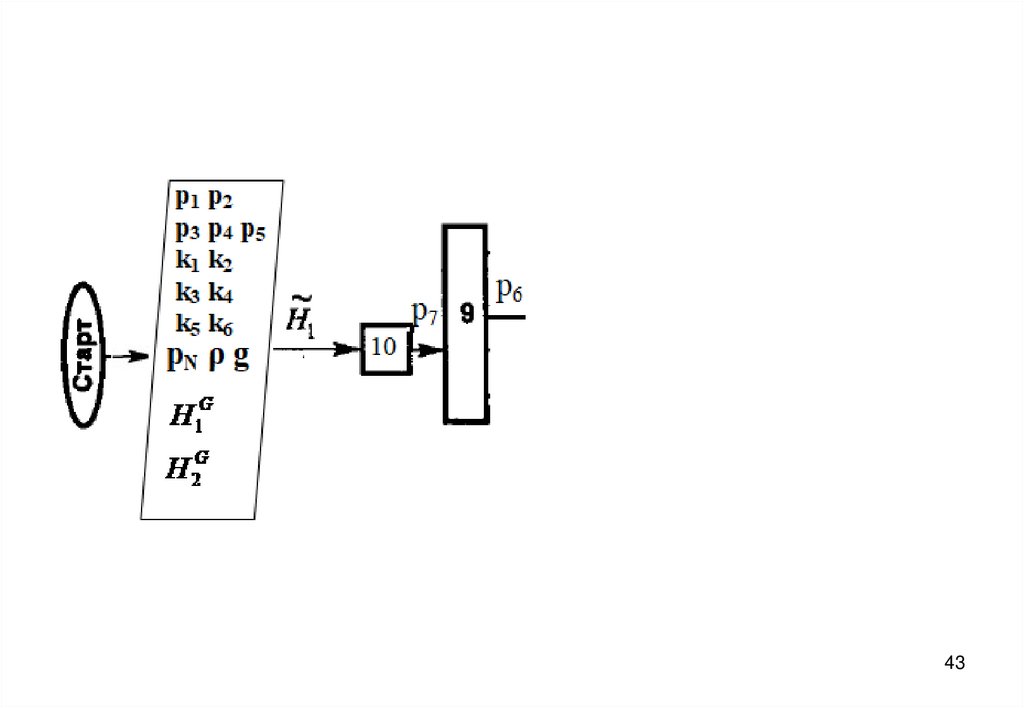
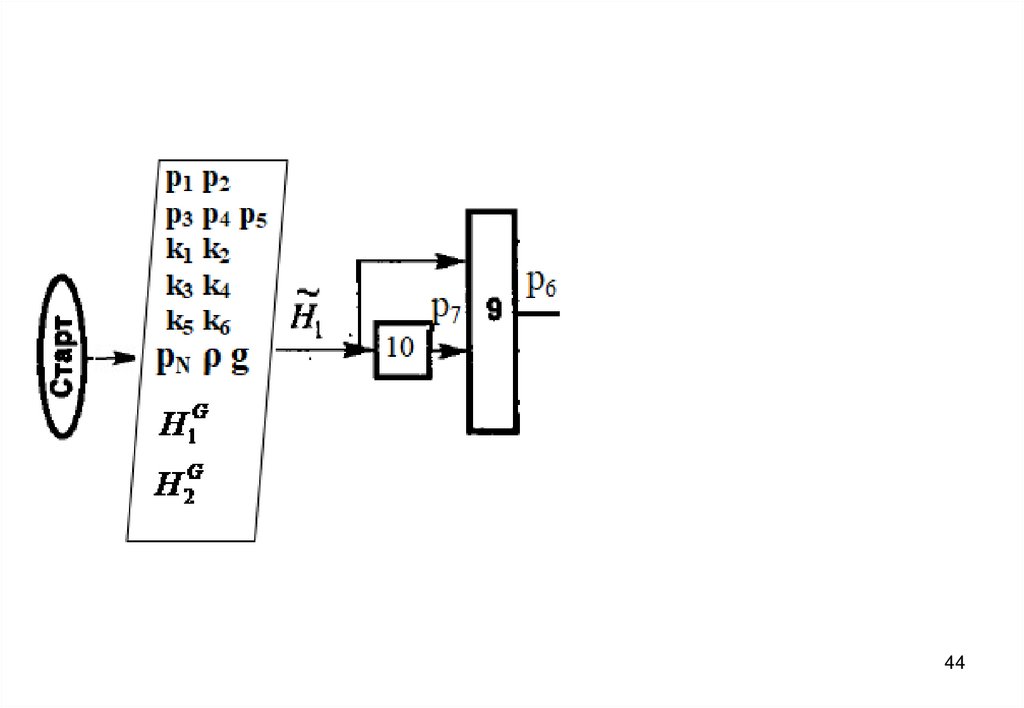
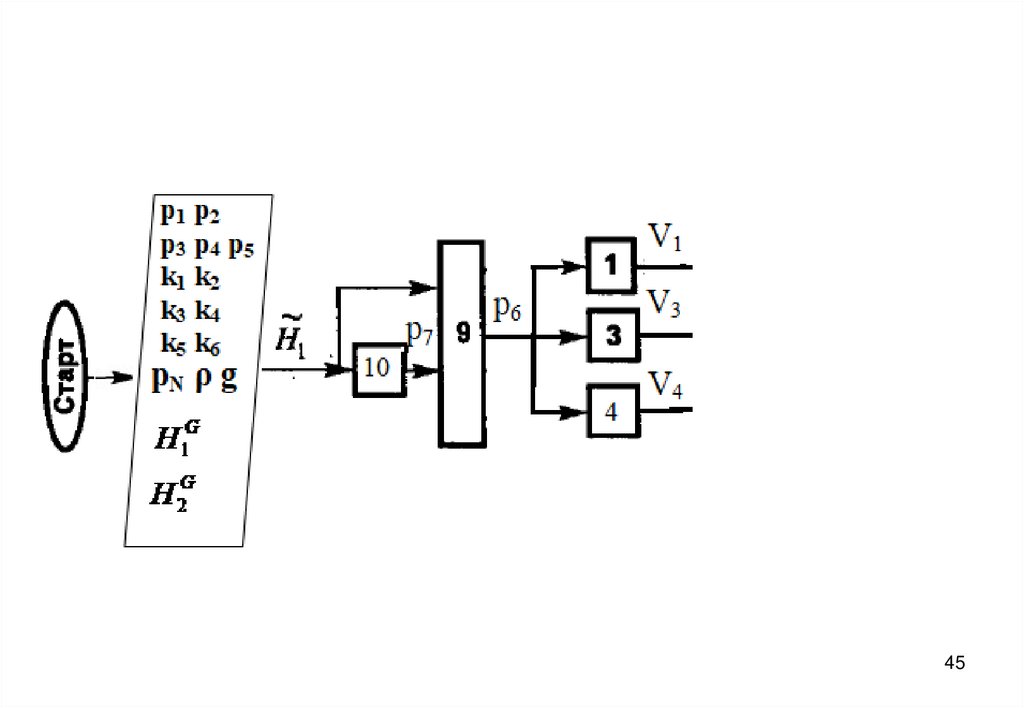
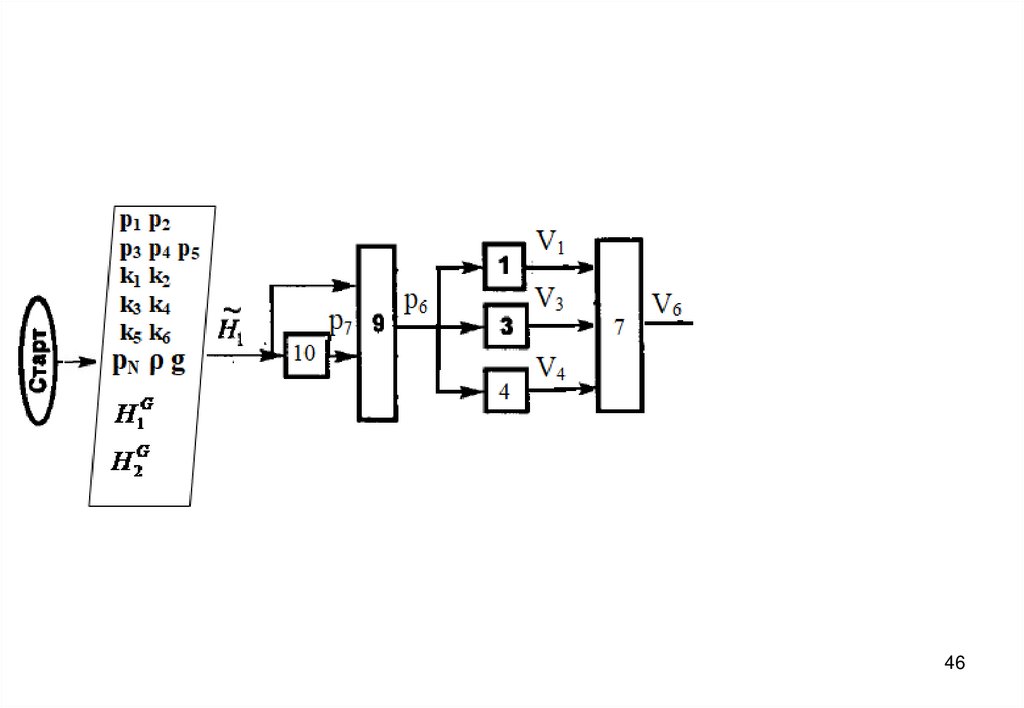
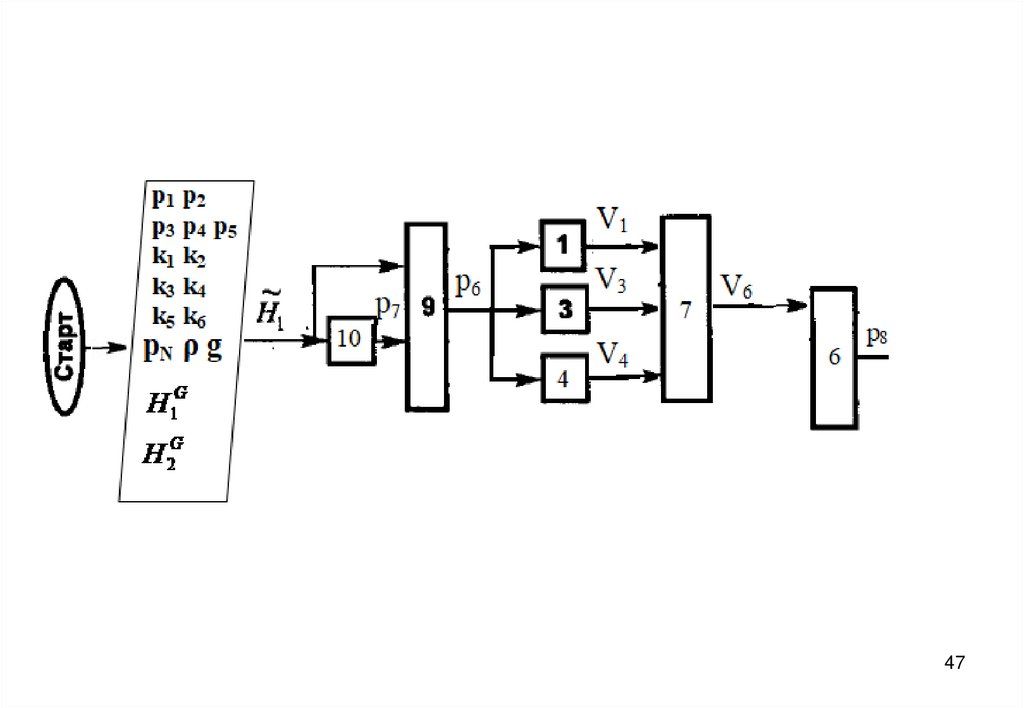
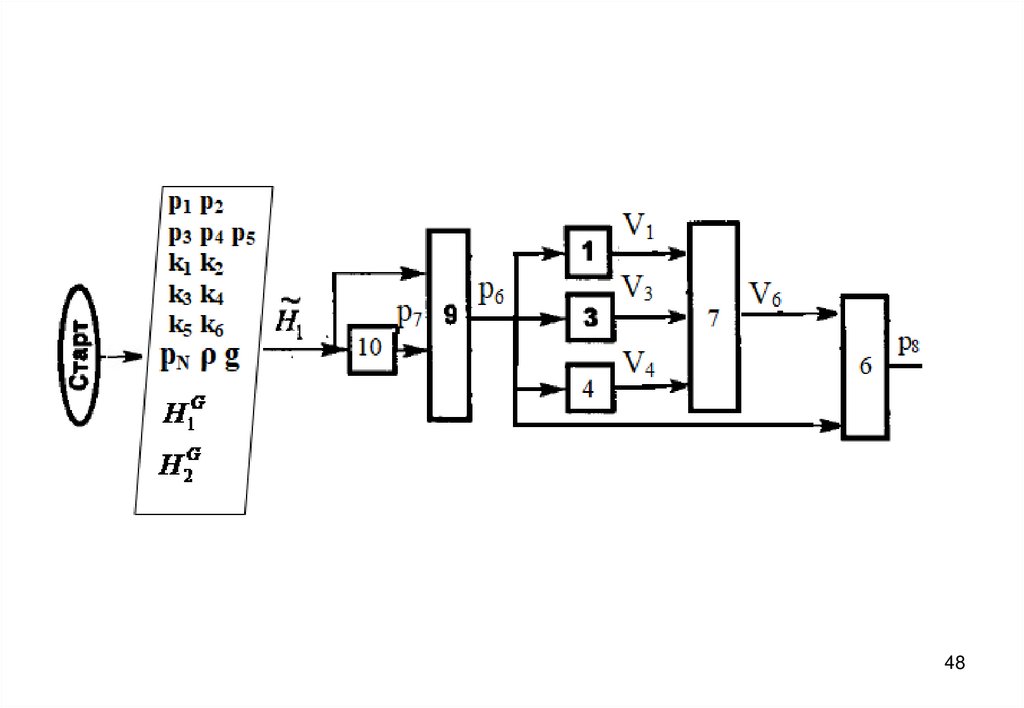
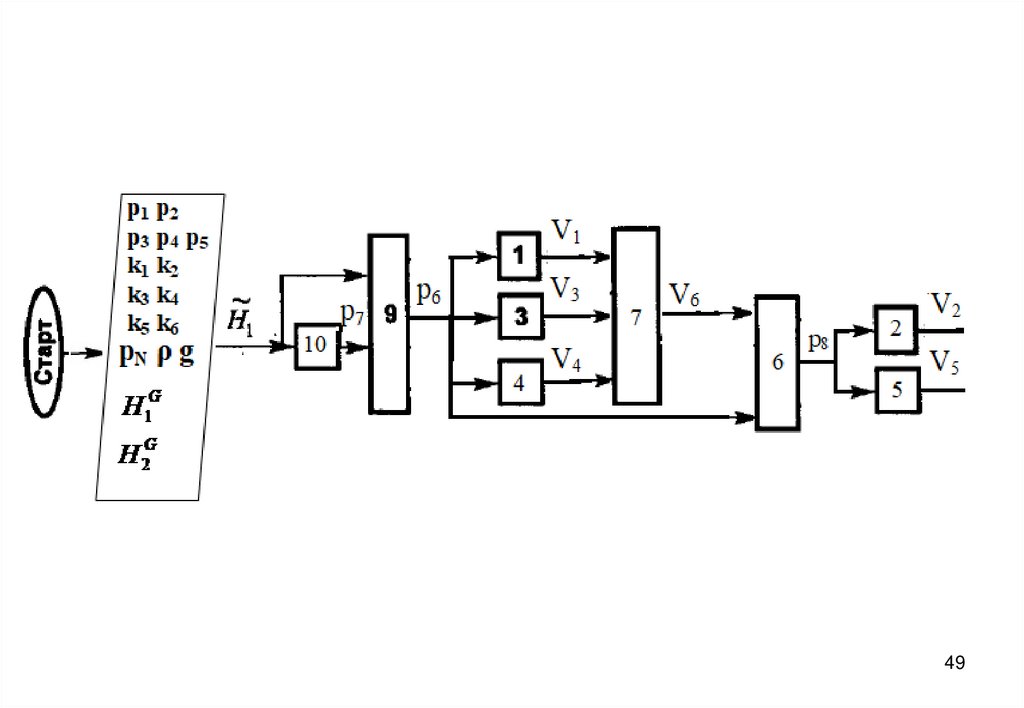
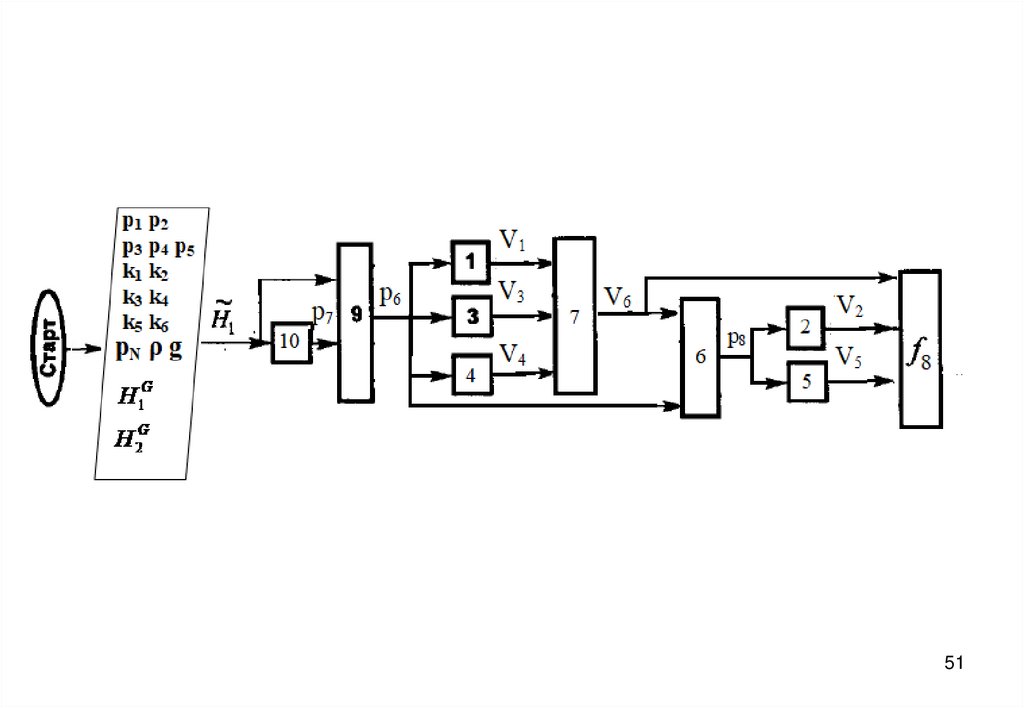
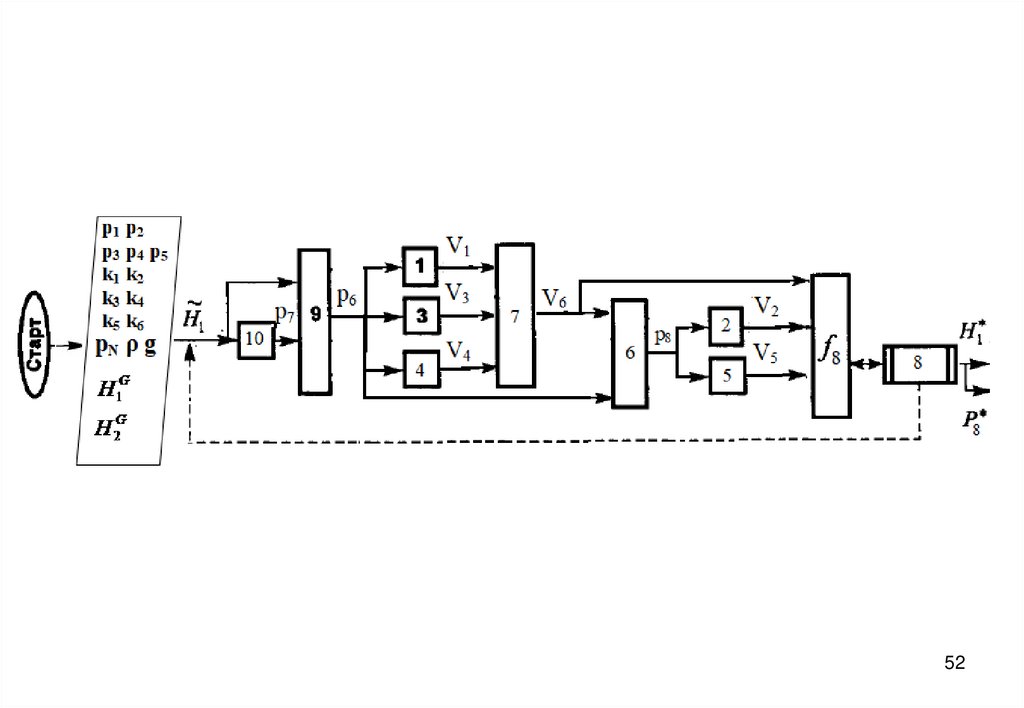
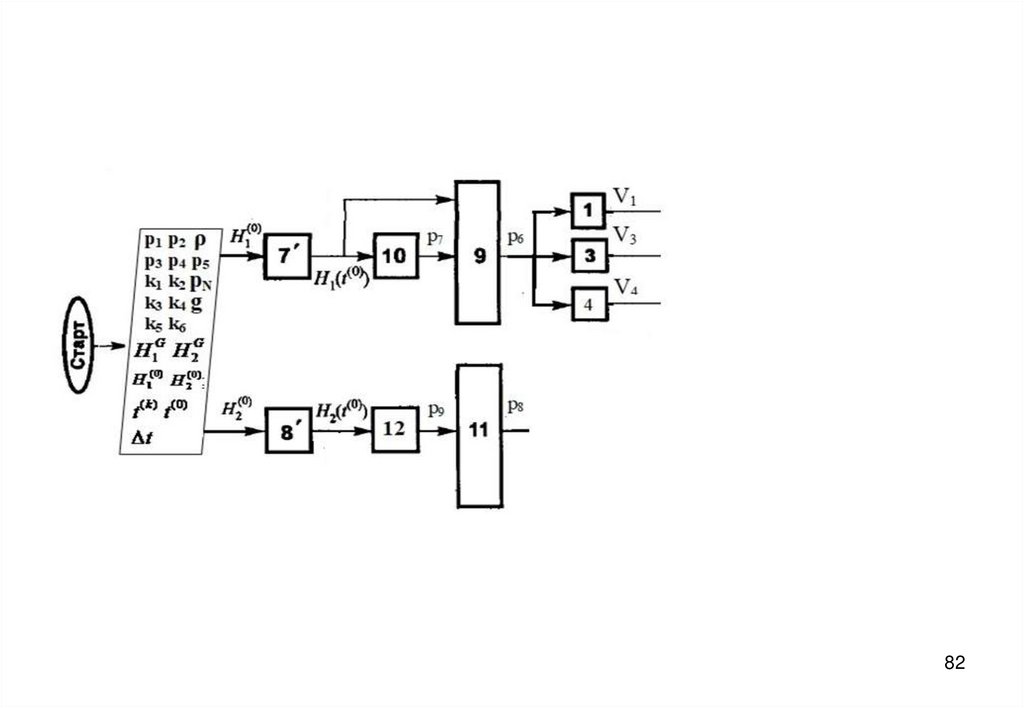
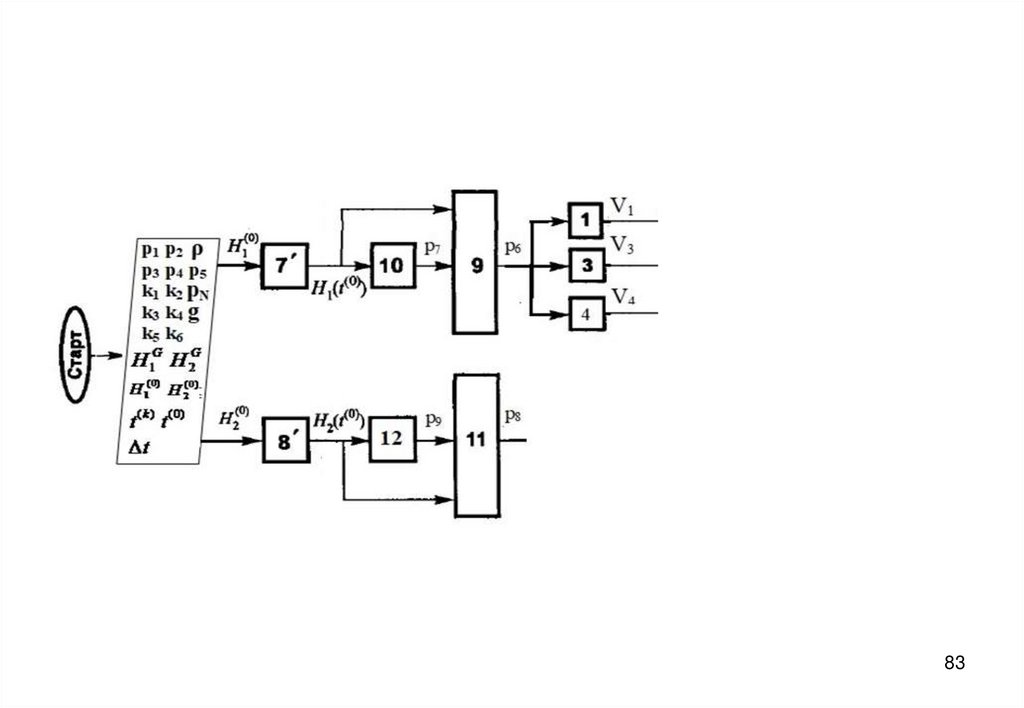
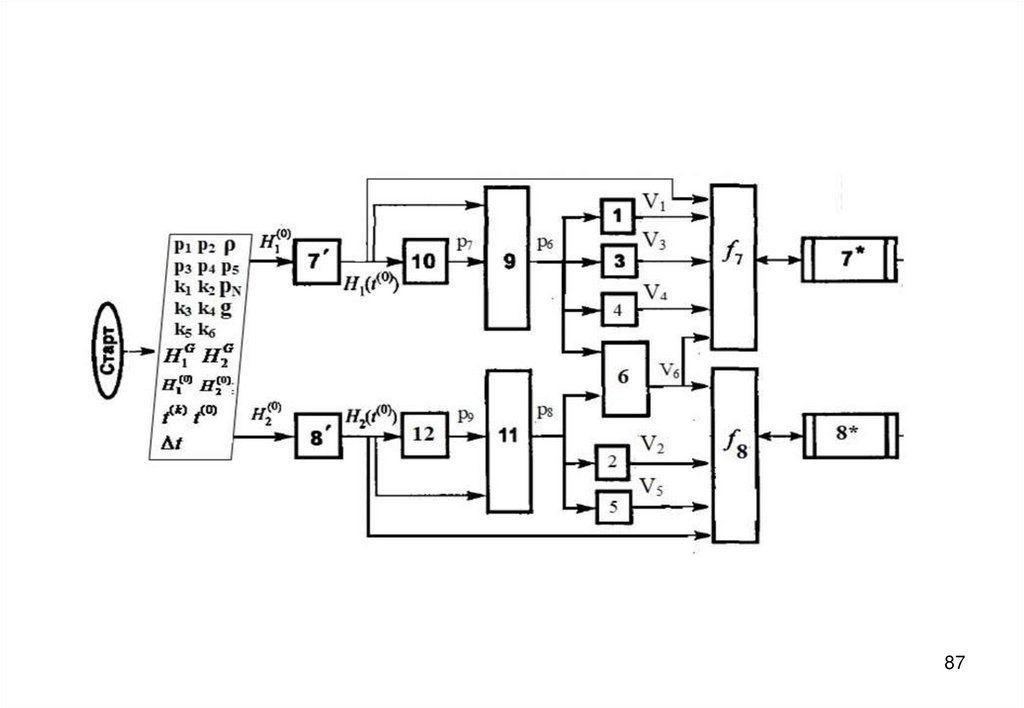
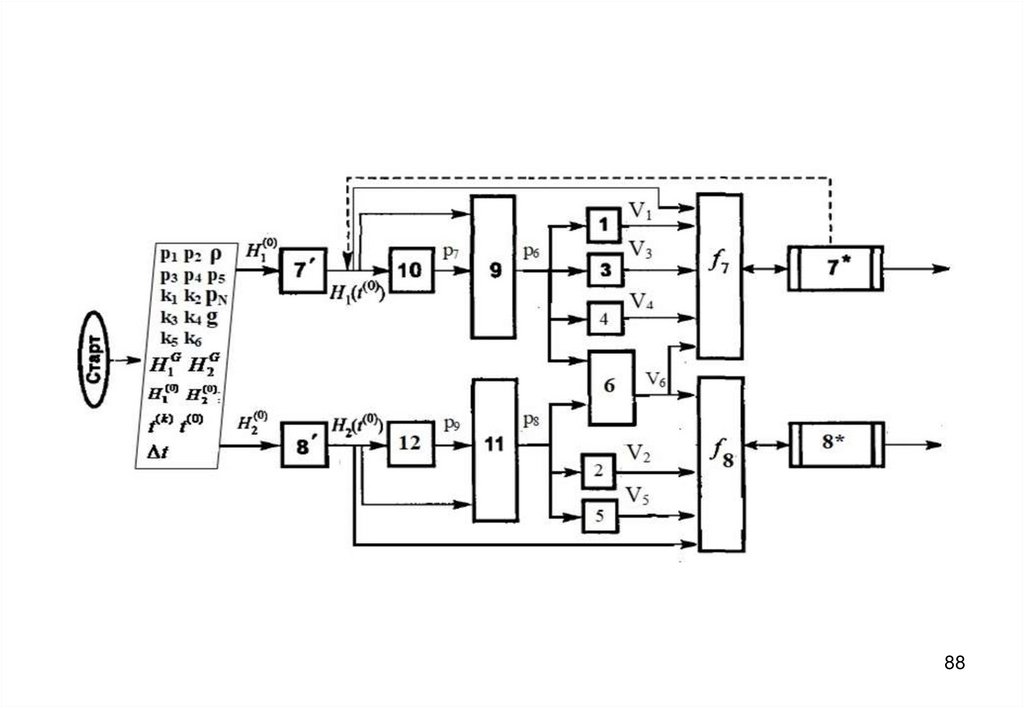
3940. Блок-схема алгоритма
4041.
4142.
4243.
4344.
4445.
4546.
4647.
4748.
4849.
4950.
5051.
5152.
5253.
5354.
5455.
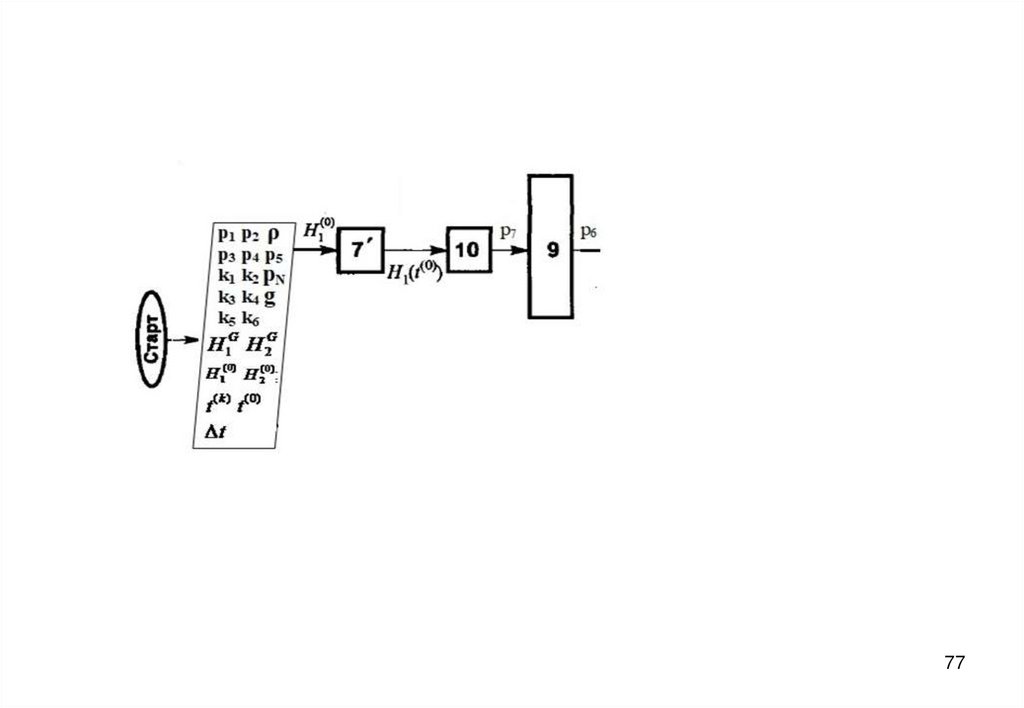
5556. Нестационарный (динамический) режим
dH11
7.
(V1 V3 V4 V6 ) f 7 ;
dt
S1
dH 2
1
8.
(V6 V5 V2 ) f 9 ;
dt
S2
7'.H1 (t
(0)
8'. H 2 (t
) H
(0)
(0)
1
) H
;
( 0)
2
;
56
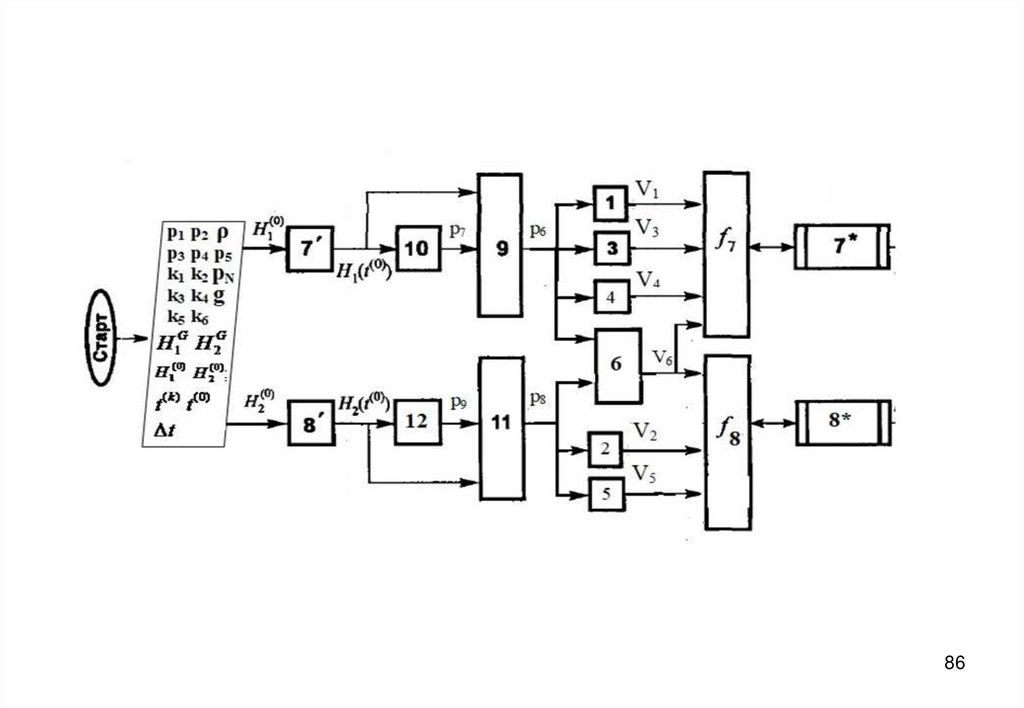
57. Дифференциальные уравнения записываются в конечно-разностной форме
H 1 (t ( k ) ) H 1 (t ( 0 ) ) 17 *.
(V1 V3 V4 V6 ) f 7 ;
t
S1
8* .
H 2 (t
7'.H 1 (t
(0)
8'. H 2 (t
(k )
) H 2 (t
t
) H
(0)
(0)
1
) H
(0)
)
1
(V6 V5 V2 ) f 9 ;
S2
;
(0)
2
;
57
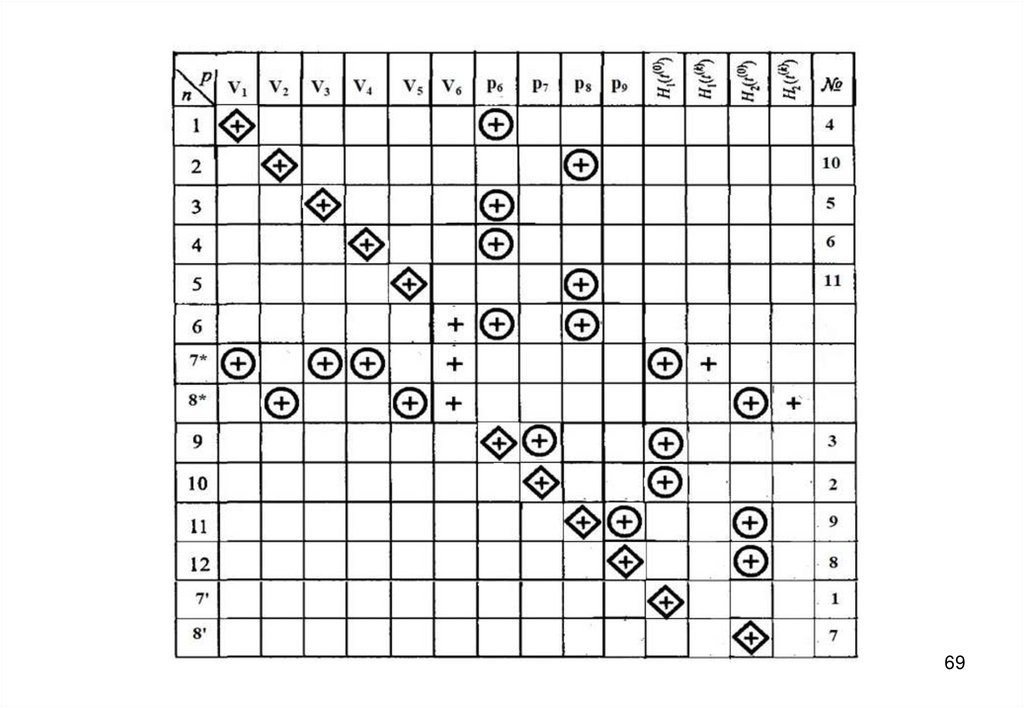
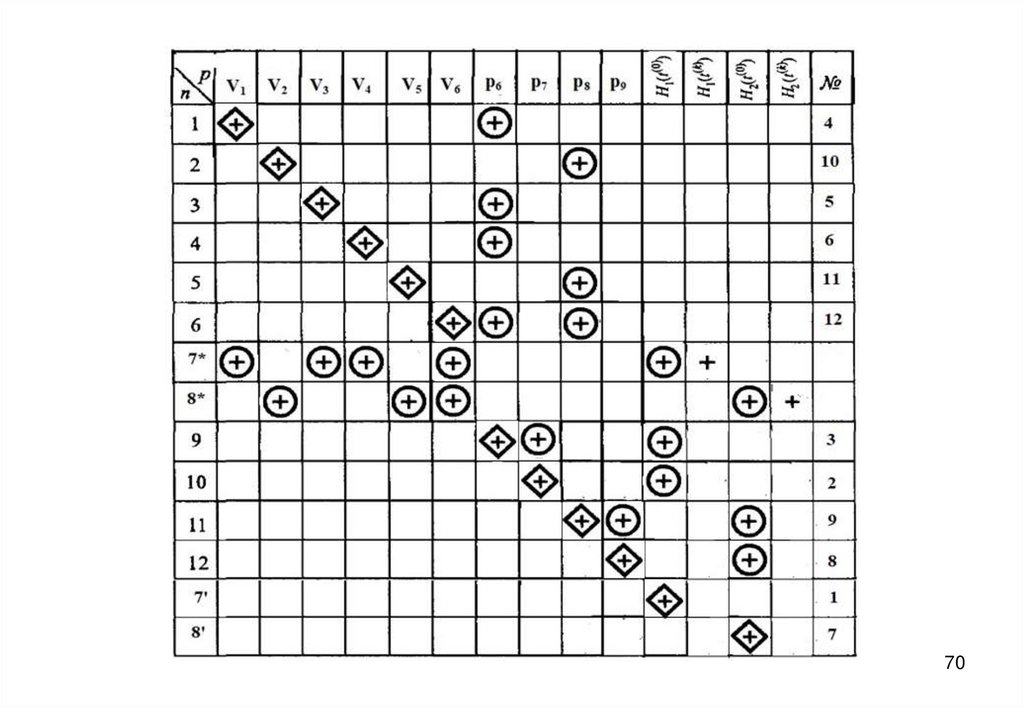
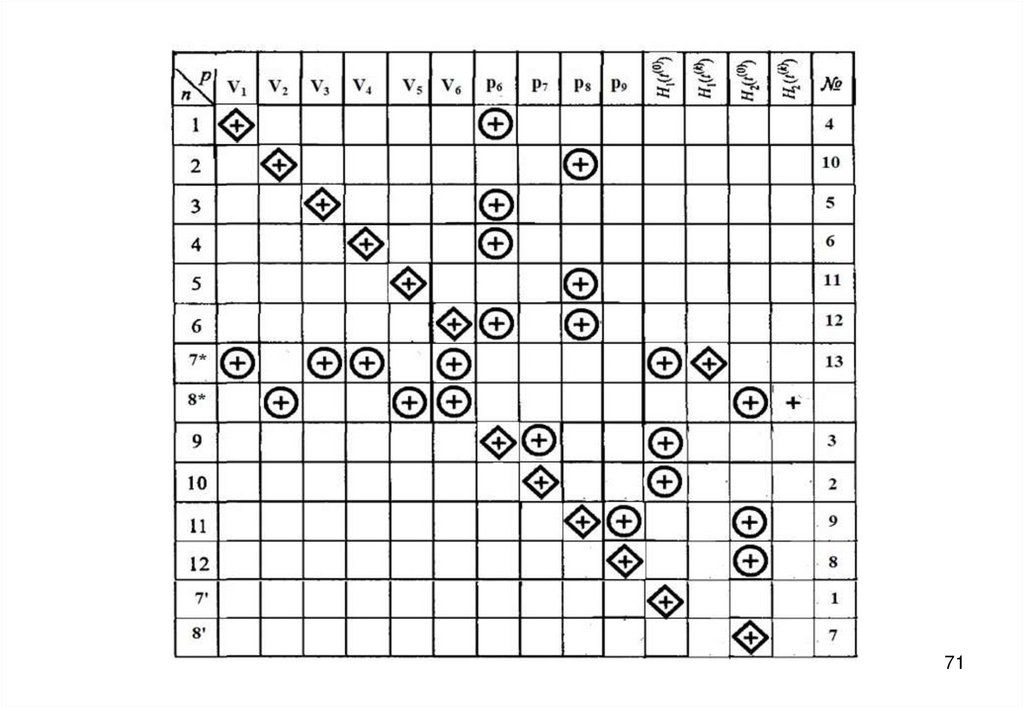
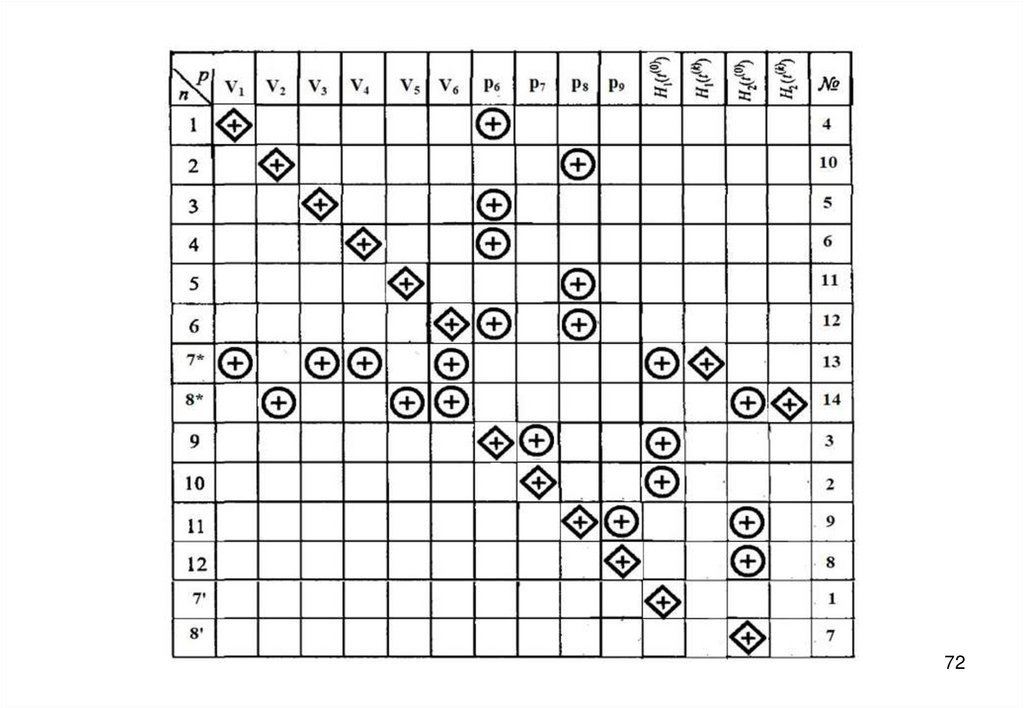
58. Информационная матрица для решения системы уравнений математического описания
5859.
5960.
6061.
6162.
6263.
6364.
6465.
6566.
6667.
6768.
6869.
6970.
7071.
7172.
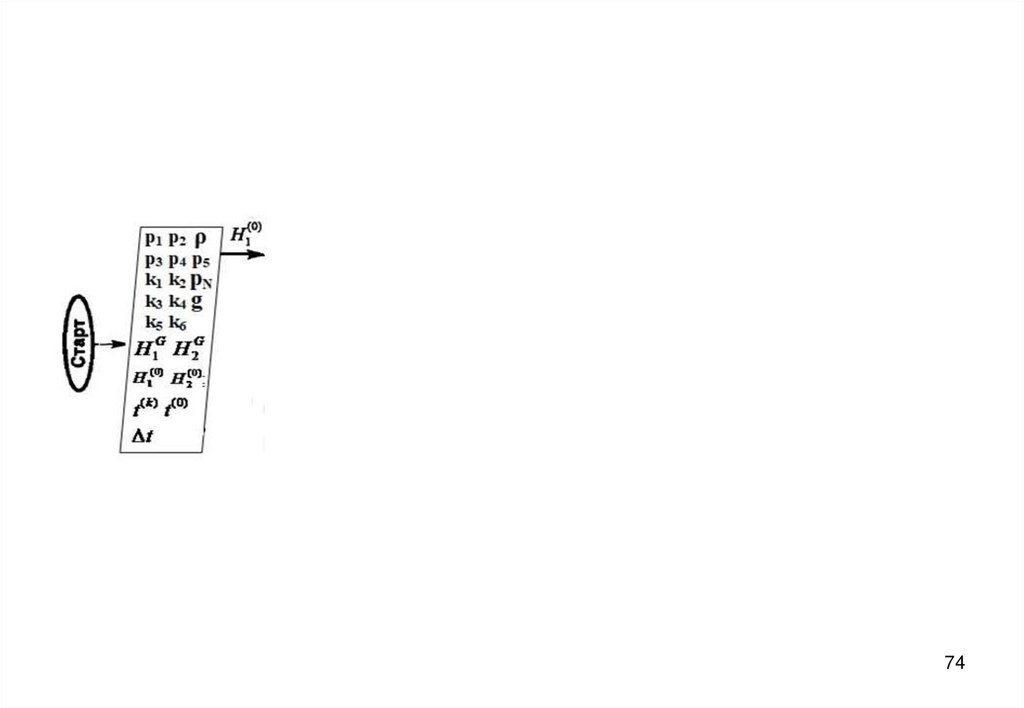
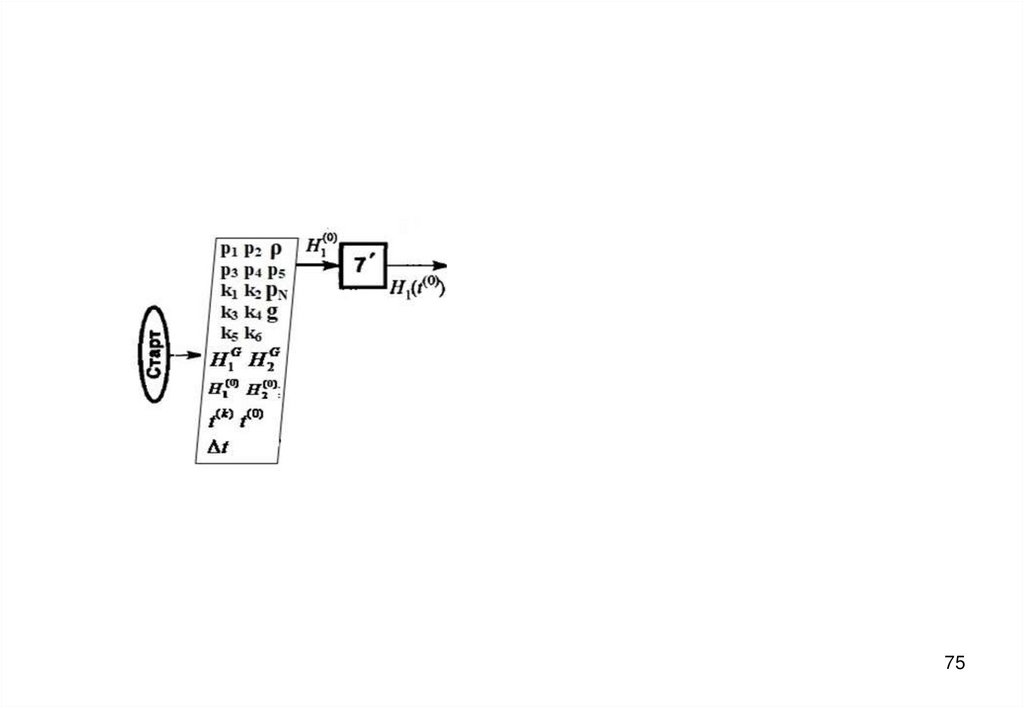
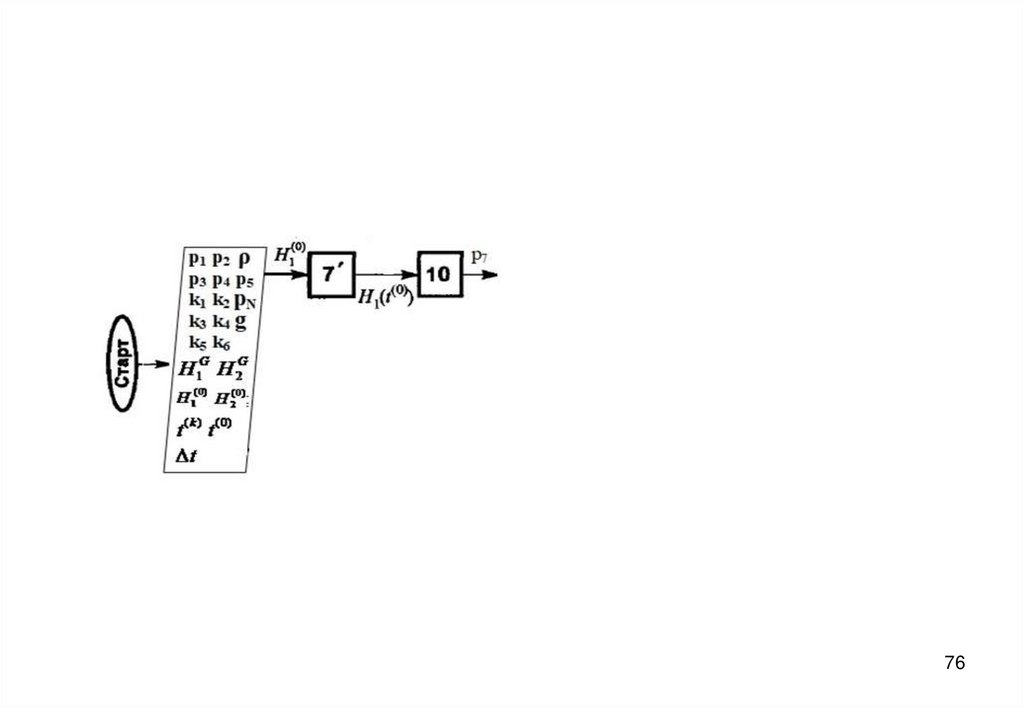
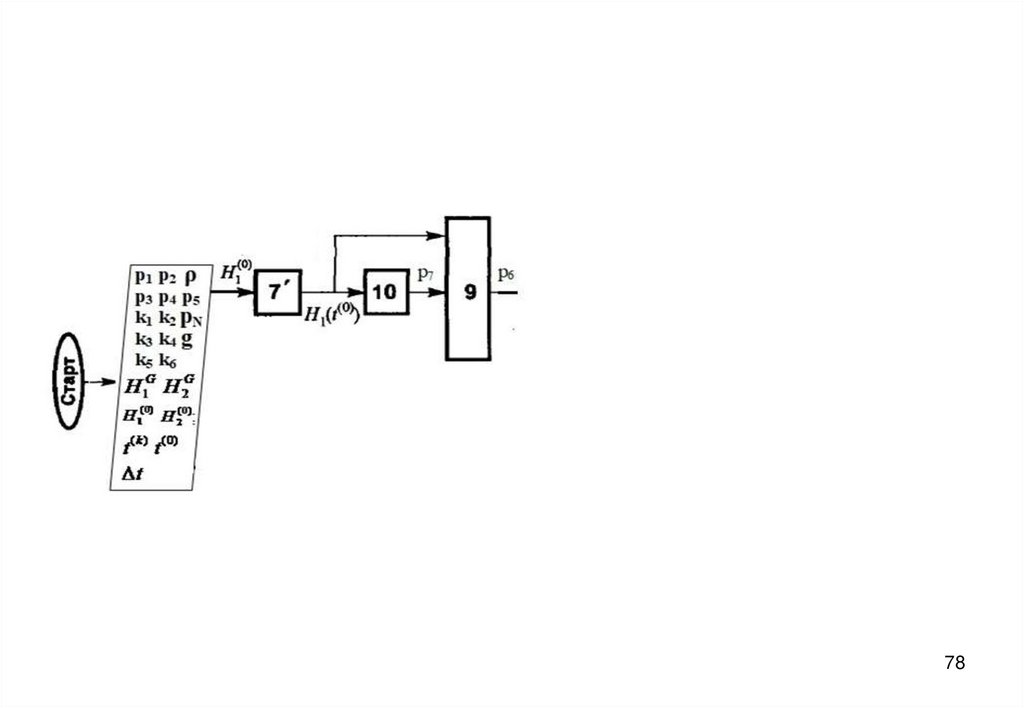
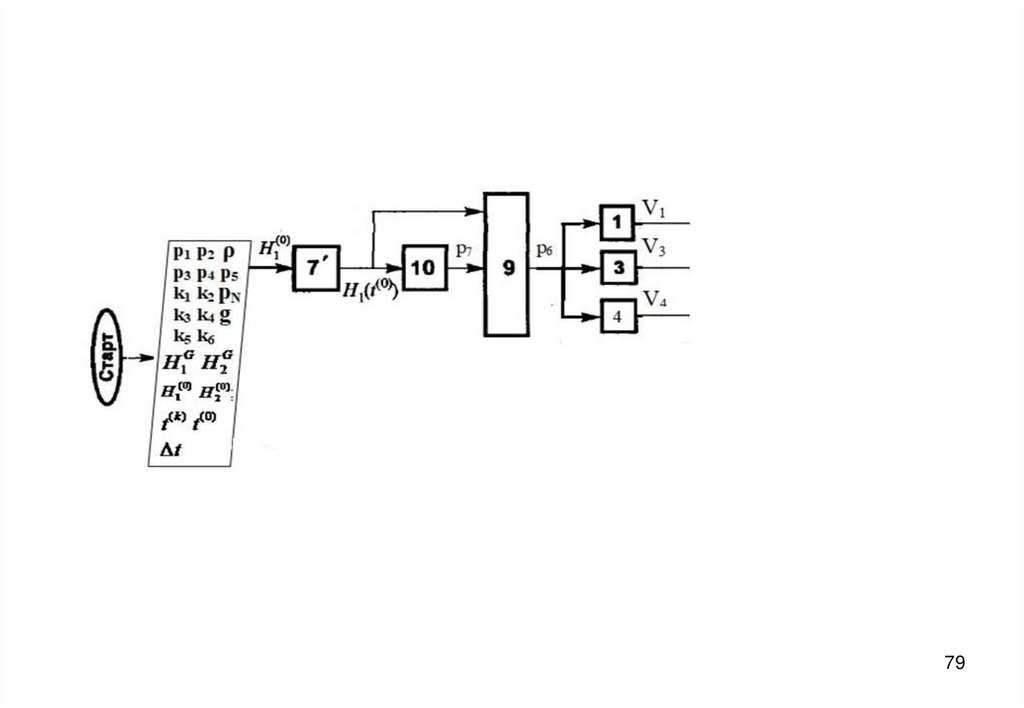
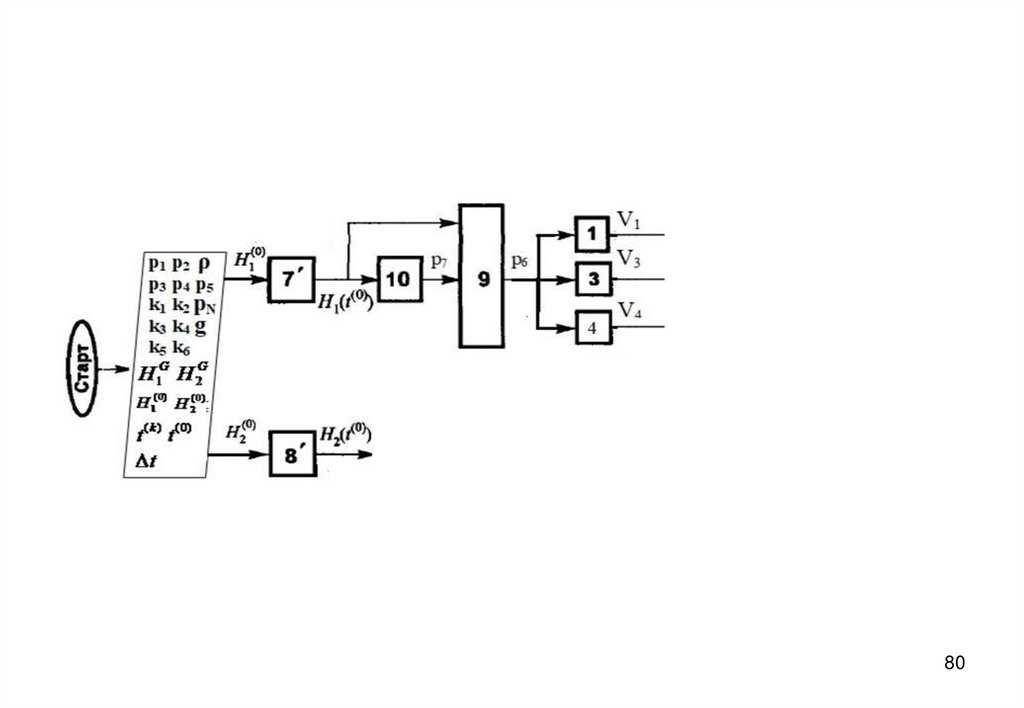
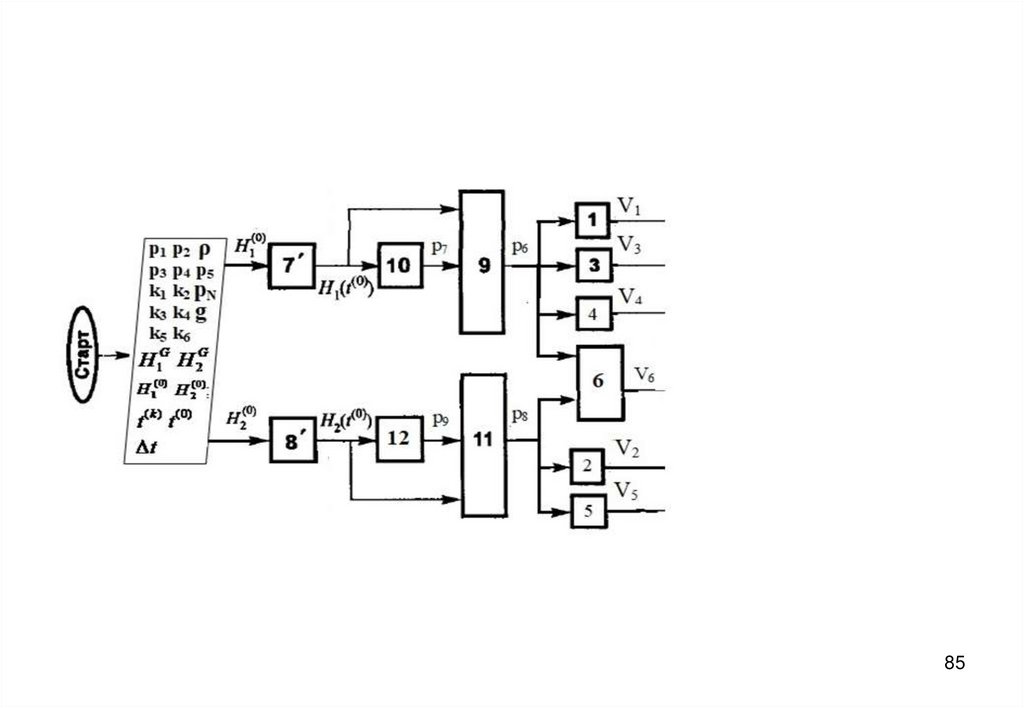
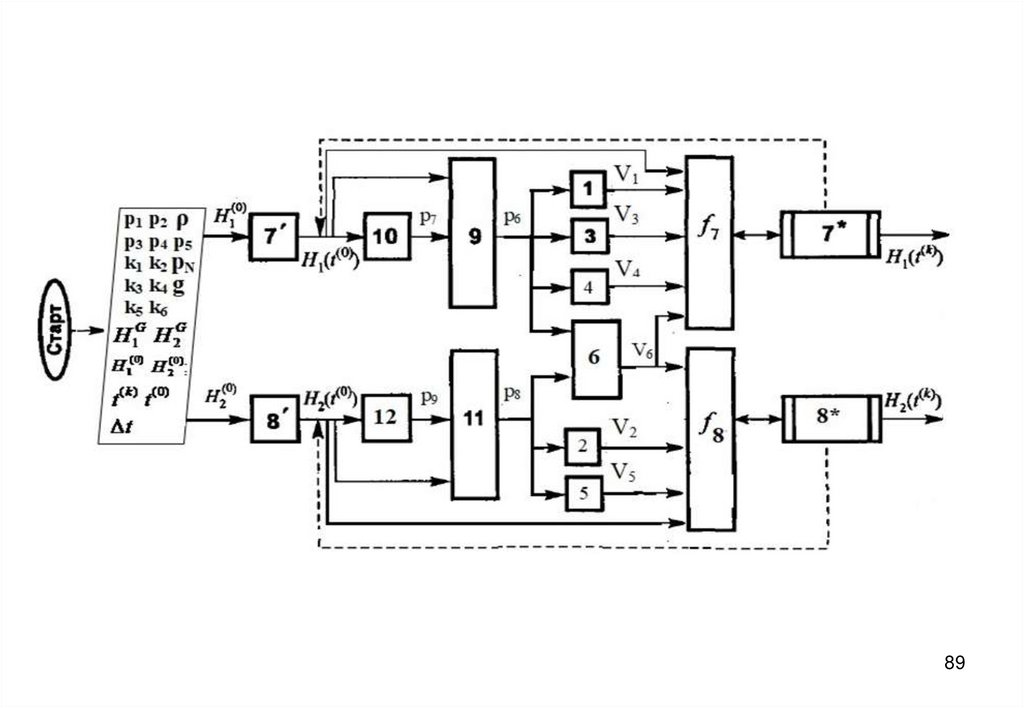
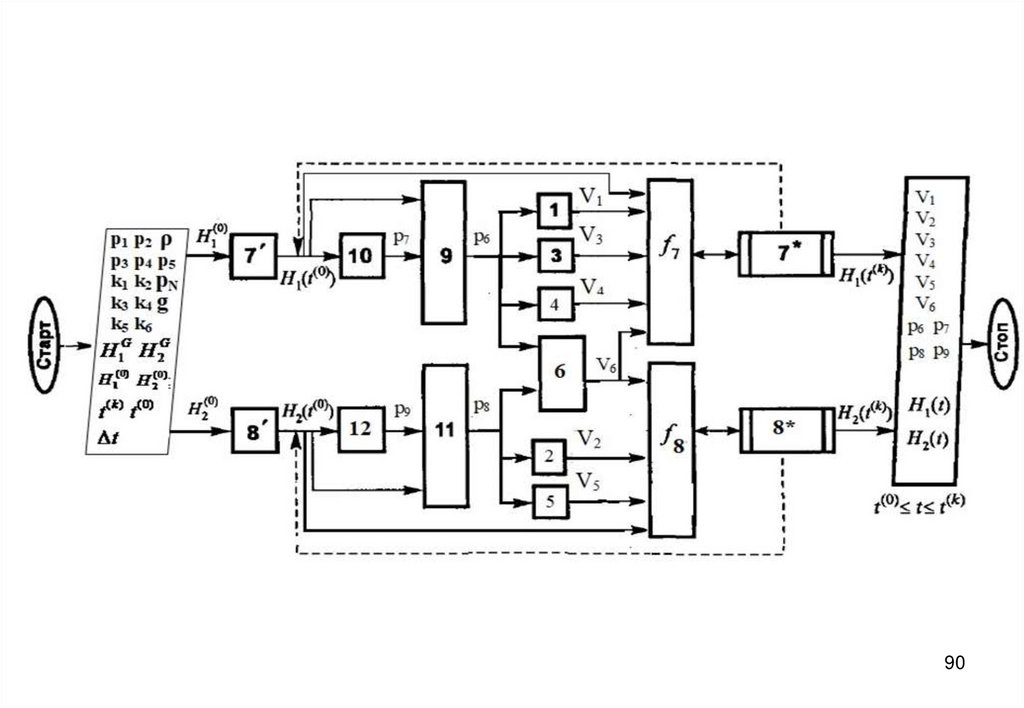
7273. Блок-схема алгоритма
7374.
7475.
7576.
7677.
7778.
7879.
7980.
8081.
8182.
8283.
8384.
8485.
8586.
8687.
8788.
8889.
8990.
9091.
Построение эмпирических моделейхимико-технологических процессов
91
92. Принципы построения эмпирических моделей по данным пассивных экспериментов
Последовательные этапы:92
93.
Проведение экспериментальных исследованийРазличают пассивный и активный эксперимент
Теория активного эксперимента позволяет оптимизировать
экспериментальные исследования и установить:
•количество экспериментальных измерений
•при каких значениях входных переменных надо проводить опыты
•реализовать эффективную методику обработки экспериментальных даных
•сократить число экспериментальных исследований
•обеспечивать достижение требуемых целей экспериментальных исследований
В пассивном эксперименте указанные параметры экспериментальных
исследований определяются опытом, эрудицией и интуицией исследователя.
При этом различают:
•лабораторный пассивный эксперимент – планируемый и целенаправленный
•промышленный пассивный эксперимент – наблюдаемый при протекании
технологических процессов
93
94.
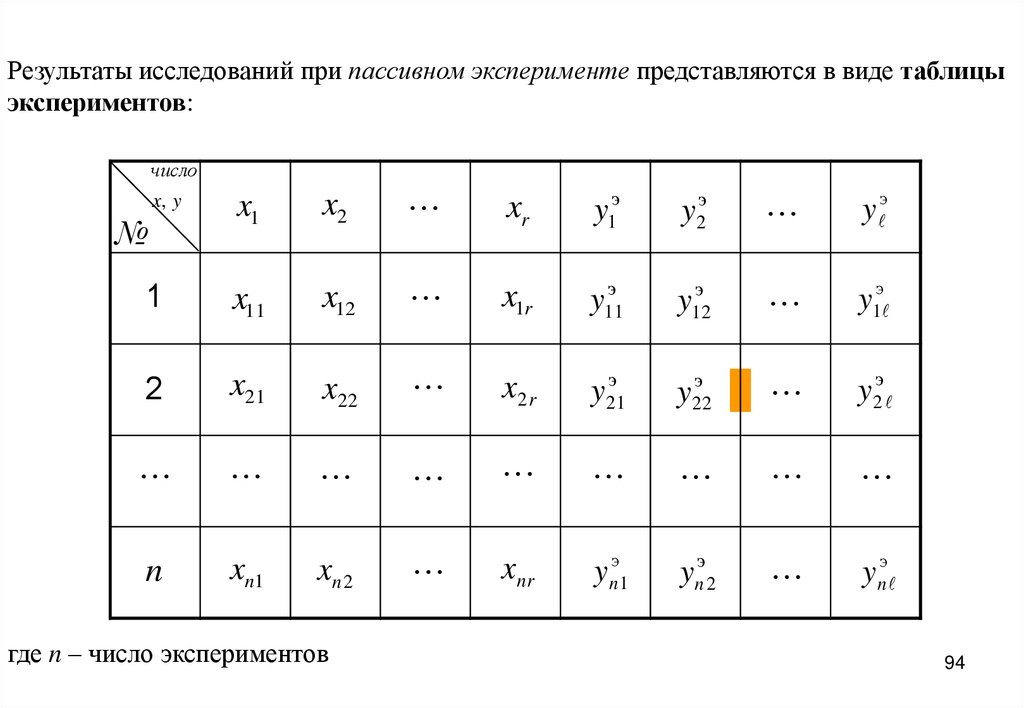
Результаты исследований при пассивном эксперименте представляются в виде таблицыэкспериментов:
число
x1
x2
xr
y1э
y2э
y э
1
x11
x12
x1r
y11э
y12э
y1 э
2
x21
x22
x2 r
э
y21
э
y22
э
y2
n
xn1
xn 2
xnr
y nэ1
ynэ 2
y nэ
x, y
№
где n – число экспериментов
94
95.
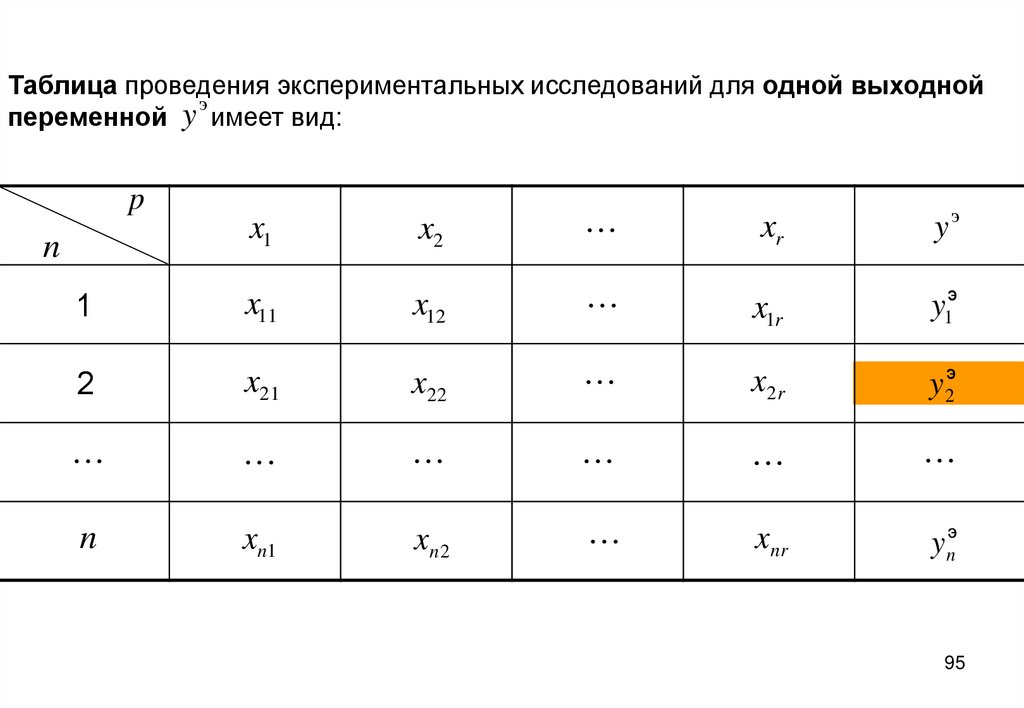
Таблица проведения экспериментальных исследований для одной выходнойэ
переменной y имеет вид:
p
x1
x2
xr
yэ
1
x11
x12
x1r
y1э
2
x21
x22
x2 r
y2э
n
xn1
xn 2
xnr
y nэ
n
95
96.
Выбор вида зависимости выходной переменной y от входнойпеременной x
Для этой цели анализируется следующая таблица экспериментов:
№
1
2
n
x
x1
x2
xn
э
y
э
y1
э
y2
э
yn
96
97.
137 Тема 02: Построение эмпирических статистических моделей ХТПII.2.1. Определение вида приближённого уравнения регрессии
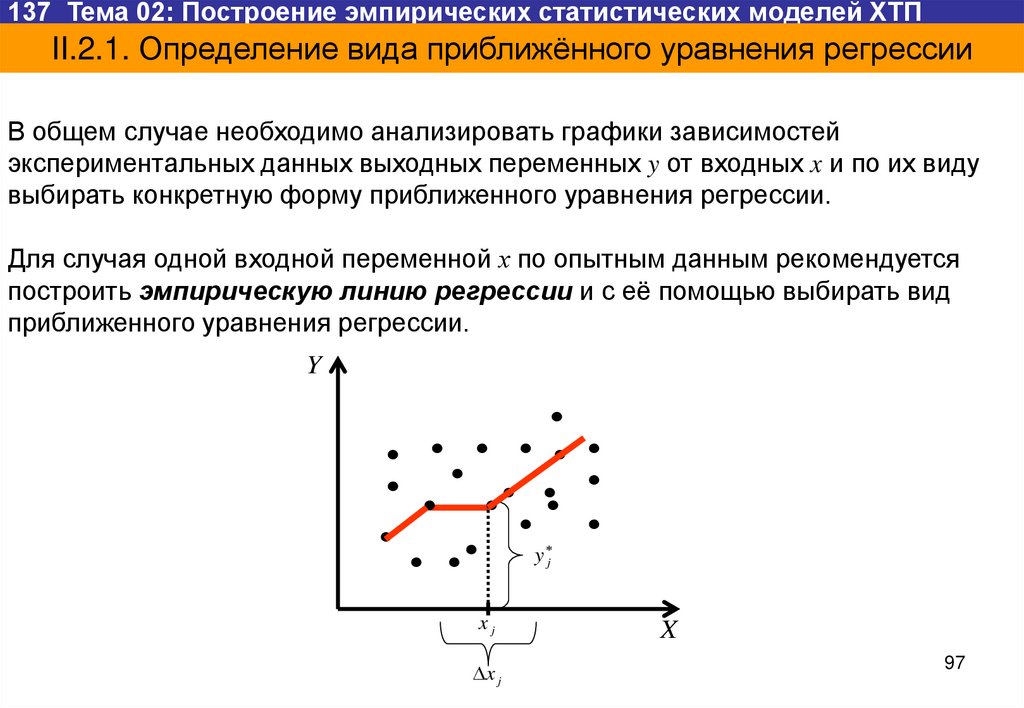
В общем случае необходимо анализировать графики зависимостей
экспериментальных данных выходных переменных y от входных x и по их виду
выбирать конкретную форму приближенного уравнения регрессии.
Для случая одной входной переменной х по опытным данным рекомендуется
построить эмпирическую линию регрессии и с её помощью выбирать вид
приближенного уравнения регрессии.
Y
y j
xj
x j
X
97
98.
При этом весь диапазон изменения x разбивается на s равных интервалов Δx.Все точки, попавшие в данный интервал x j , относят к его середине x j .
После этого подсчитывают частные средние y j для каждого интервала:
nj
j
y
y
i 1
nj
ji
, j 1,...s
n j число точек в интервале x j .
В результате объём выборки определяется по формуле:
s
n
j 1
j
n
99.
Эмпирическая линия регрессии y от x получается в виде ломанной линиипутём последовательного соединения отрезками прямой линии точек:
x , y ,
j
j
j 1,...s
При выборе вида приближенного уравнения регрессии для случая нескольких входных
переменных
x x1 ,...xm
T
может быть применён метод Брандона, который здесь не рассматривается.
99
100.
Определение коэффициентов уравнения регрессии – параметровэмпирических моделей методом наименьших квадратов
В соответствии с методологией регрессионного анализа в этом случае решается
задача аппроксимации экспериментальных данных методом наименьших
квадратов (МНК)
При этом предполагается, что вид уравнения регрессии или уравнение
эмпирической модели известно, т.е. решена задача структурной
идентификации модели.
Задача параметрической идентификации модели, т.е. определения
коэффициентов модели решается по МНК
Задачи структурной и параметрической идентификации моделей связаны
между собой и неудовлетворительное решение одной из них может приводить к
необходимости пересмотра результатов решения другой.
100
101.
В общем случае возможны два варианта:а) нелинейная относительно коэффициентов a модель – нелинейная регрессия
yˆ f ( x , a )
б) линейная относительно коэффициентов a модель – линейная регрессия
m
yˆ a j j x a0 0 x a1 1 x .... am m x
j 0
- линейные или нелинейные функции входных переменных
j x
a a0 , a1, ... am
- определяемые по МНК коэффициенты модели
yˆ a0 a1 x a2 x
2
2
0 x 1; 1 x x; 2 x x
101
102.
Преимущества линейных моделей1. Относительно несложная методика выбора вида модели
2. Простая процедура определения коэффициентов модели
3. Эффективная методика регрессионного и корреляционного анализа
Поэтому нелинейные модели, по возможности, стараются линеаризовать,
т.е. привести к линейному виду.
102
103.
Линеаризация уравнения Аррениусаk Ae
E RT
E 1
ln k ln A
R T
yˆ a0 0 ( x ) a1 1 ( x ), ãäå m 1
При этом:
yˆ ln k
a0 ln A
E
a1
R
0 ( x ) 1
1
1 ( x )
T
103
104.
Разновидности линейных уравнений регрессии•полиномиальное уравнение регрессия, когда
j x x
j
j 0,1,...m
и её разновидности:
линейное уравнение регрессии от одной переменной (m = 1):
yˆ a0 a1 x
параболическое уравнение регрессии (m = 2):
ˆy a0 a1 x a2 x 2
104
105.
•трансцендентные уравнения регрессии и их разновидности в видезависимостей:
yˆ a0 a1
показательного типа:
x
которая линеаризуется логарифмированием:
дробно-показательного типа:
yˆ a0 x
ln yˆ ln a0 x ln a1
a1
которая также линеаризуется логарифмированием:
ln yˆ ln a0 a1 ln x
•множественное уравнение регрессии, когда число входных переменных
больше 1:
yˆ a0 a1 x1 ... am xm
x0 1
105
106.
Для линейных и нелинейных моделей минимизируется критерийрассогласования расчетных и экспериментальных данных следующего вида:
n
Cr y y
где y
p
i и
p
i
i
2
i 1
y определяются при одном и том же значении элементов вектора
i
xi i 1,...n
n – общее число опытов (объём выборки).
При этом определяются оптимальные значения коэффициентов a , которые
обеспечивают наименьшее (в частном случае – минимальное) значение
106
критерия Cr
107.
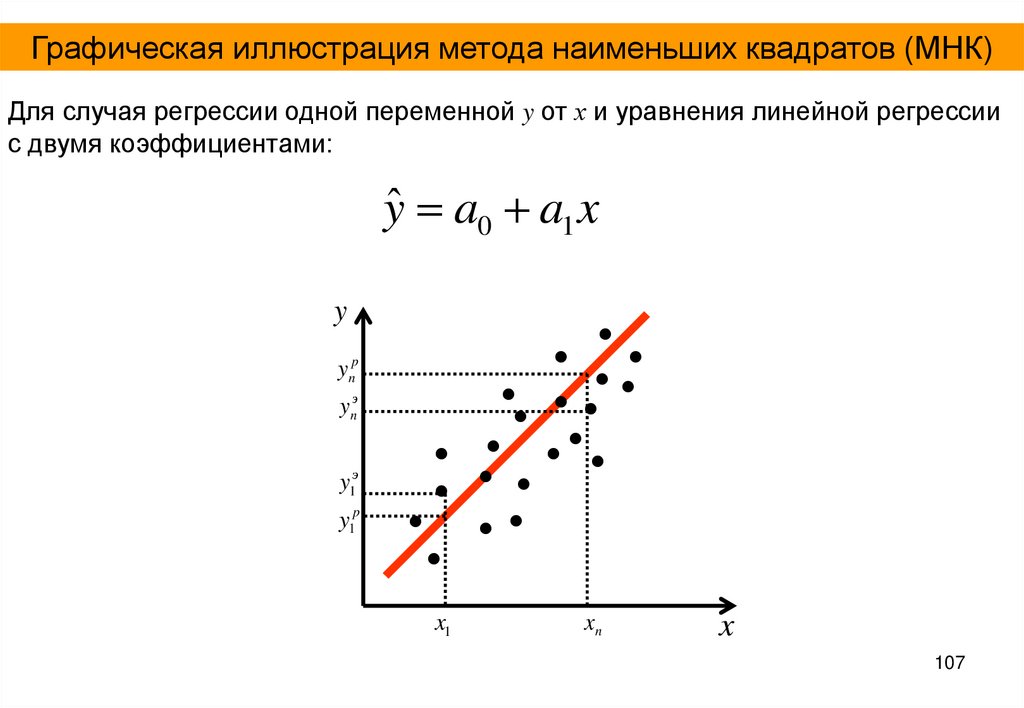
Графическая иллюстрация метода наименьших квадратов (МНК)Для случая регрессии одной переменной y от х и уравнения линейной регрессии
с двумя коэффициентами:
yˆ a0 a1 x
y
ynp
y nэ
y1э
y1p
x1
xn
x
107
108.
Для линейных и нелинейных уравнений регрессии с m + 1 коэффициентами:a a0 , a1 ,...am
T
критерий МНК также является функцией многих переменных от параметров a
Cr Cr a0 , a1 ,...am
108
109.
Для определения (подгонки) коэффициентов (параметров) модели необходимо,чтобы критерий МНК стал наименьшим.
Задача определения коэффициентов нелинейных моделей сводится к
реализации одного из алгоритмов оптимизации для определения минимума
критерия МНК:
2
n
p
i
i
доп
a a
i 1
min
y
y
a доп - допустимая область изменения параметров a - ограничения первого
рода.
В этом случае для определения коэффициентов необходимо реализовать
алгоритм оптимизации, позволяющий найти наименьшее значение критерия:
n
Cr a0 , a1 ,...am ( y y )
i 1
p
i
э 2
i
109
110.
Задача определения коэффициентов линейных моделей сводится к решениюсистемы линейных алгебраических уравнений (СЛАУ), исходя из необходимого
условия экстремума функции многих переменных
n
Cr a0 , a1 ,...am ( y y )
p
i
i 1
э 2
i
то есть СЛАУ, решаемая относительно коэффициентов:
a a0 , a1 ,...am
T
имеет вид:
Cr
0;
a0
Cr
Cr
0; ...
0
a1
am
110
111.
Вывод формулы для определения коэффициентов линейных илинеаризованных моделей
Матричная формула определения коэффициентов имеет вид:
1
ˆa y
T
T
111
112.
где матрицаФ
- это матрица вида
0 x1 1 x1
x x
1
2
0 2
n m 1
...
...
0 xn 1 xn
... m x1
... m x2
...
...
... m xn
элементы которой зависят от экспериментальных значений входных
переменных и вида функций x ;
э
вектор y - это вектор наблюдений экспериментальных значений выходной
переменной
э
В случае линеаризации моделей элементы матрицы Ф и вектора y
определяются из выражений, соответствующих выбору способа линеаризации.
112
113.
Для вывода этой формулы критерий МНК необходимо представить в виде:Cr a j j xi yi
i 1 j 0
n
m
2
и, воспользовавшись необходимым условием экстремума функции многих
переменных, решать полученную систему линейных алгебраических уравнений
(СЛАУ):
n
m
Cr
2 a j j xi yi 0 xi 0
a0
i 1 j 0
n m
Cr
2 a j j xi yi 1 xi 0
a1
i 1 j 0
..............................................................
n m
Cr
2 a j j xi yi m xi 0
am
i 1 j 0
113
114.
Перегруппировав члены в последней системе уравнений, можно записать СЛАУв виде:
m
n
n
a x x x y
j 0
j
i 1
j
i
u
i
i 1
u
i
i
( j, u 0,1,...m)
И, если ввести в рассмотрение информационную матрицу
uj
n
j 0,1,...m; u 0,1,...m :
uj u xi j xi
j 0,1,...m; u 0,1,...m
i 1
то она окажется квадратной, симметричной и значения её элементов зависят
только от входных переменных и конкретного вида функций j x
114
115.
В матричном виде информационную матрицу можно представить в видепроизведения транспонированной и исходной матрицы входных переменных :
T
Матрица, зависящая от входных переменных, имеет вид:
0 x1 1 x1
x x
0
2
1
2
n m 1
...
...
0 xn 1 xn
... m x1
... m x2
...
...
... m xn
Соответственно правую часть рассматриваемой СЛАУ можно записать:
115
116.
nbu u xi yi
(u 0,1,...m)
i 1
или в матричном виде:
T
b y
В результате СЛАУ, решаемая для определения коэффициентов эмпирической
модели, может быть представлена:
m
j 0
uj
a j bu
(u 0,1,...m)
или в матричном виде:
a b
116
117.
Если для определения коэффициентов использовать метод обратной матрицы,то получится:
1
1
a b
1
,
1
a b,
1
a b
117
118.
Матричная формула для определения коэффициентов линейной регрессии(параметров эмпирической модели):
1
ˆa y
T
T
Таким образом, для определения коэффициентов линейной или
линеаризованной регрессионной модели необходимо выполнить следующую
последовательность действий:
• сформировать вектор наблюдений
линеаризованных моделей);
y и вычислить его компоненты (только для
• сформировать и рассчитать компоненты матрицы, зависящей от входных переменных
;
118
119.
• транспонировать матрицуT
;
• перемножить транспонированную матрицу
T
на исходную матрицу
:
T
;
• выполнить обращение информационной матрицы -
T
;
• умножить полученную обратную матрицу на матрицу
• умножить полученный результат на вектор наблюдений
коэффициенты регрессии
â
;
1
T
и yполучить выборочные
119
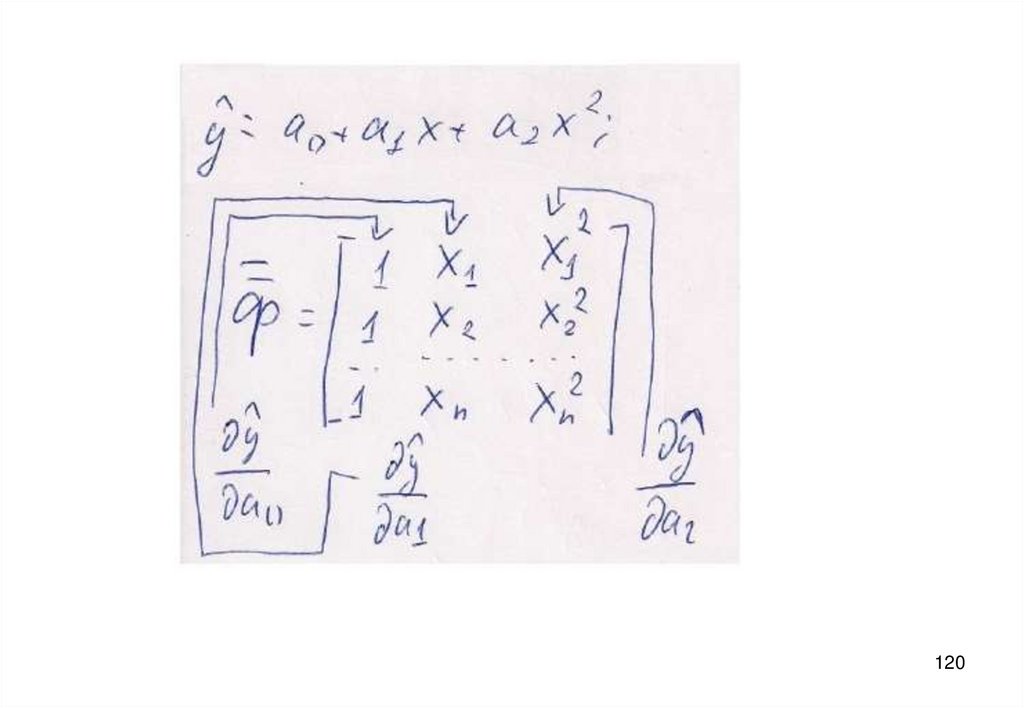
120.
120121.
121122.
Вывести матричную формулу для определения коэффициентов регрессии A, B, C иD в уравнении, связывающего давление насыщенного пара индивидуального
вещества (p) с температурой (Т) с помощью функции:
p exp( A BT CT DT )
2
3
Построить таблицу пассивного эксперимента. При обработке результатов
пассивного эксперимента линеаризовать регрессионную модель,
и
реализовать аналитический и алгоритмический подходы для получения
решения.
Таблица пассивного эксперимента:
№
эксперимента
Ti
piэ
1
Т1
p1э
2
Т2
p2э
….
….
n
Тn
….
p
э
n
122
123.
Линеаризация уравнения регрессии:ln p A BT CT DT
2
3
a0 A; a1 B; a2 C; a3 D;
Аналитический подход:
Критерий рассогласования расчётных и экспериментальных данных:
n
R ( yip yiэ ) 2 ;
i 1
yip a0 a1Ti a2Ti 2 a3Ti 3 ;
yiэ ln piэ ;
n
R (a0 a1Ti a2Ti 2 a3Ti 3 ln piэ ) 2 MIN
i 1
123
124.
Нахождение минимума критерия МНК по необходимому условию функции многихпеременных:
R
2
3
э
0; 2 ( a0 a1Ti a2Ti a3Ti ln pi ) 1 0;
a0
i 1
n
n
R
0; 2 ( a0 a1Ti a2Ti 2 a3Ti 3 ln piэ ) Ti 0;
a1
i 1
n
R
0; 2 ( a0 a1Ti a2Ti 2 a3Ti 3 ln piэ ) Ti 2 0;
a2
i 1
n
R
0; 2 ( a0 a1Ti a2Ti 2 a3Ti 3 ln piэ ) Ti 3 0;
a3
i 1
124
125.
Приведение СЛАУ к стандартному виду:n
n
n
n
n
i 1
i 1
i 1
i 1
i 1
a0 1 a1 Ti a2 Ti 2 a3 Ti 3 ln piэ ;
n
n
n
n
n
a0 Ti a1 Ti a2 Ti a3 Ti Ti ln piэ ;
2
i 1
3
i 1
n
4
i 1
n
i 1
n
i 1
n
n
a0 Ti a1 Ti a2 Ti a3 Ti Ti 2 ln piэ ;
2
i 1
3
i 1
n
4
i 1
n
5
i 1
n
i 1
n
n
a0 Ti a1 Ti a2 Ti a3 Ti Ti 3 ln piэ ;
3
i 1
4
i 1
5
i 1
6
i 1
i 1
125
126.
nTi
n
i 1
n
n
2
T
T
i
i
i 1 i 1
n 2 n 3
Ti Ti
i 1
i 1
n 3 n 4
Ti Ti
i 1
i 1
_
n
T
i 1
i
n
T
i 1
3
i
n
4
T
i
i 1
n
5
T
i
i 1
_
n
э
Ti
ln pi
i 1
i 1
n
a
n
4 0
э
T
T
ln
p
i
i
i
a
i 1
1 i 1
n
n
a2
5
2
э
T
T
ln
p
i
i
i
a
i 1
i
1
3
n
n
6
3
э
Ti
Ti ln pi
i 1
i 1
n
2
3
_
1 _
A a b a A b
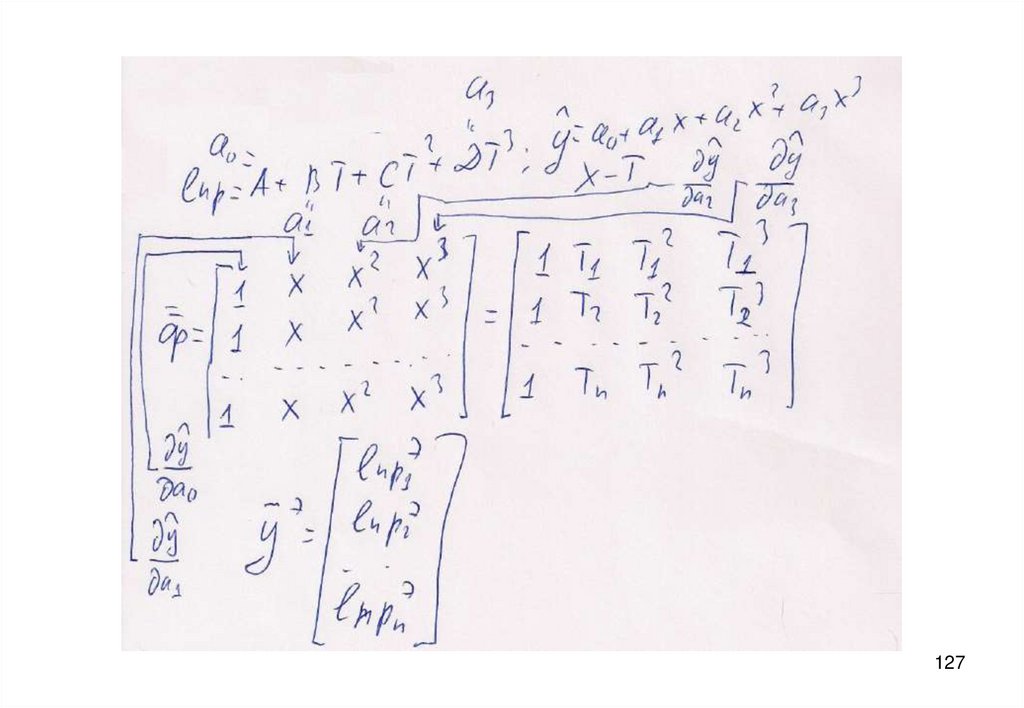
Алгоритмический подход:
Выбор стандартного типа уравнения регрессии:
Матрица, элементы которой зависят от вида уравнения регрессии и
_ э и вектор
значений входных переменных, при которых проведены опыты
y
126
127.
127128.
T_
T
_э
_
1 _
I 4 x 4 4 xn nx 4 ;
b 4 x 1 4 xn y ;
a 4 x1 I 4 x 4 b 4 x1 ;
a0
a
_
1
a
a2
a3
A a0 ; B a1 ; C a2 ; D a3 ;
128
129.
Вывести матричную формулу для определения коэффициентов регрессии A, B, C иD в уравнении, связывающего давление насыщенного пара индивидуального
вещества (p) с температурой (Т) с помощью функции:
B
p exp( A CT D ln T )
T При обработке результатов
Построить таблицу пассивного эксперимента.
пассивного эксперимента линеаризовать регрессионную модель,
и
реализовать аналитический и алгоритмический подходы для получения
решения.
Таблица пассивного эксперимента:
№
эксперимента
Ti
piэ
1
Т1
p1э
2
Т2
p2э
….
….
n
Тn
….
p
э
n
129
130.
Линеаризация уравнения регрессии:B
ln p A CT D ln T
T
a0 A; a1 B; a2 C ; a3 D;
Аналитический подход:
Критерий рассогласования расчётных и экспериментальных данных:
n
R ( yip yiэ ) 2 ;
i 1
1
y a0 a1 a2Ti a3 ln Ti ;
Ti
p
i
yiэ ln piэ ;
n
1
R (a0 a1 a2Ti a3 ln Ti ln piэ ) 2 MIN
Ti
i 1
130
131.
Нахождение минимума критерия МНК по необходимому условию функции многихпеременных:
1
R
э
0; 2 (a0 a1 a2Ti a3 ln Ti ln pi ) 1 0;
Ti
a0
i 1
n
1
1
R
э
0; 2 (a0 a1 a2Ti a3 ln Ti ln pi ) 0;
Ti
Ti
a1
i 1
n
n
R
1
0; 2 (a0 a1 a2Ti a3 ln Ti ln piэ ) Ti 0;
a2
Ti
i 1
n
R
1
0; 2 (a0 a1 a2Ti a3 ln Ti ln piэ ) ln Ti 0;
a3
Ti
i 1
131
132.
Приведение СЛАУ к стандартному виду:n
n
n
n
n
1
э
a0 1 a1 a2 Ti a3 ln Ti ln pi ;
i 1
i 1 Ti
i 1
i 1
i 1
n
n
n
n
n
1
1
1
1
a0 a1 2 a2 1 a3 ln Ti ln piэ ;
i 1 Ti
i 1 Ti
i 1
i 1 Ti
i 1 Ti
n
n
n
n
n
i 1
i 1
i 1
i 1
i 1
a0 Ti a1 1 a2 Ti 2 a3 Ti ln Ti Ti ln piэ ;
n
n
n
n
n
ln Ti
a0 ln Ti a1
a2 Ti ln Ti a3 ln 2 Ti ln Ti ln piэ
i 1
i 1 Ti
i 1
i 1
i 1
132
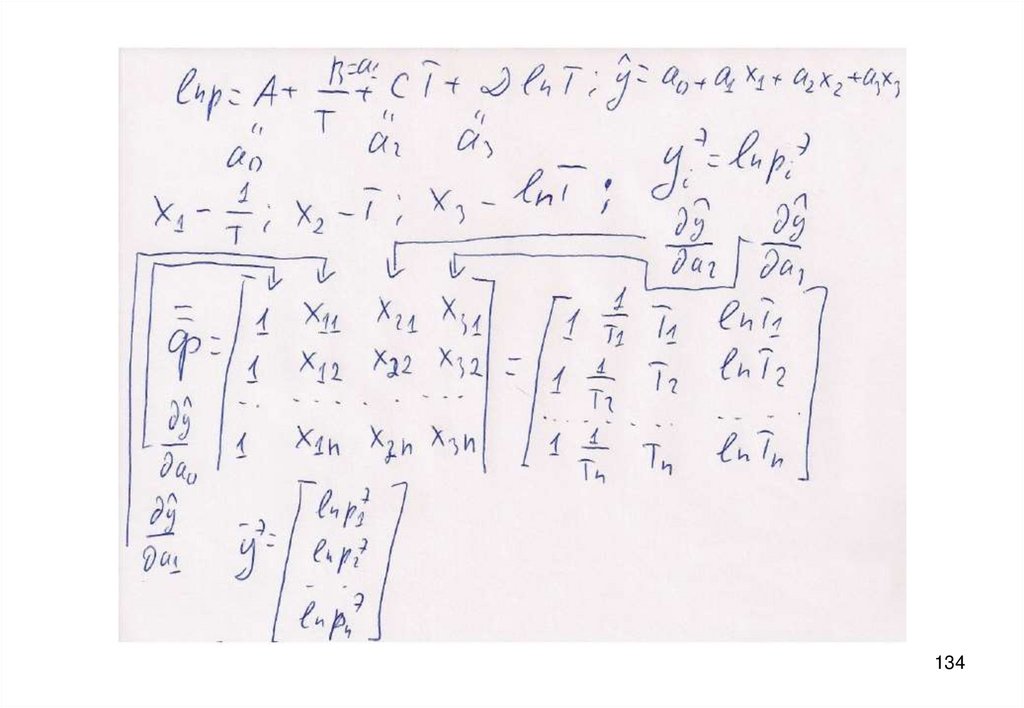
133.
nn
n
1
n
э
n
T
ln
T
i
i
ln pi
T
i 1 i
i 1
i 1
i 1
n
n
n 1
a0 n 1
1
1
э
n
ln T ln pi
2
i 1 Ti
i 1 Ti
i 1 Ti
a1 i 1 Ti
n
n
n
a2 n
2
э
Ti Ti ln Ti
Ti n
Ti ln pi
i 1
i 1
i 1
a3 i 1
n
n
n
n
n
ln Ti
2
э
Ti ln Ti ln Ti
ln Ti
ln Ti ln pi
i 1
i 1 Ti
i 1
i 1
i 1
_
_
_
1 _
A a b a A b
Алгоритмический подход:
Выбор стандартного типа уравнения регрессии:
Матрица, элементы которой зависят от вида уравнения регрессии и
_ э и вектор
значений входных переменных, при которых проведены опыты
y
133
134.
134135.
T_
T
_э
_
1 _
I 4 x 4 4 xn nx 4 ;
b 4 x 1 4 xn y ;
a 4 x1 I 4 x 4 b 4 x1 ;
a0
a
_
1
a
a2
a3
A a0 ; B a1 ; C a2 ; D a3 ;
135
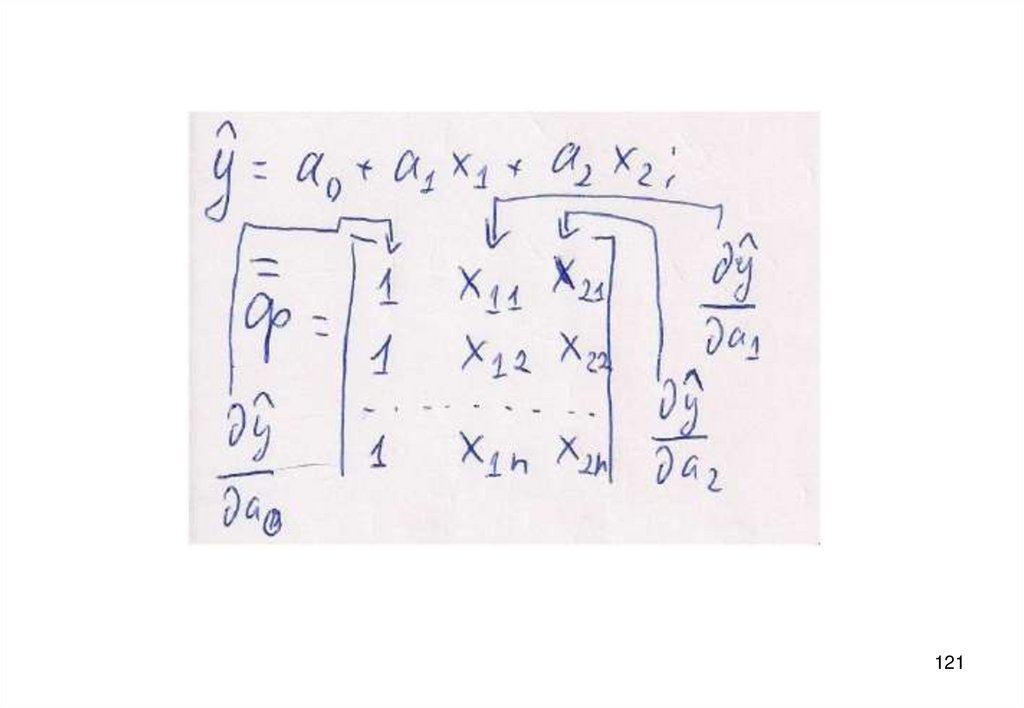
136.
Вывести матричную формулу для определения коэффициентов регрессии α, β1 и β2 вуравнении:
1
2
y x1 x2
Построить таблицу пассивного эксперимента. При обработке результатов
пассивного эксперимента линеаризовать регрессионную модель,
и
реализовать аналитический и алгоритмический подходы для получения
решения.
Таблица пассивного эксперимента:
№
эксперимента
x1i
x2i
yiэ
1
x11
X21
y1э
2
x12
X22
y2э
….
….
….
n
x1n
x2n
….
y nэ
136
137.
Линеаризация уравнения регрессии:ln y ln 1 ln x1 2 ln x2 ;
a0 ln ; a1 1 ; a2 2 ;
Аналитический подход:
Критерий рассогласования расчётных и экспериментальных данных:
n
R ( fi p fi э )2 ;
i 1
f i p a0 a1 ln x1i a2 ln x2i ;
f i э ln yiэ ;
n
R (a0 a1 ln x1i a2 ln x2i ln yiэ ) 2 MIN
i 1
137
138.
Нахождение минимума критерия МНК по необходимому условию функции многихпеременных:
R
0;
a0
R
0;
a1
R
0;
a2
n
2 (a0 a1 ln x1i a2 ln x2i ln yiэ ) 1 0;
i 1
n
2 (a0 a1 ln x1i a2 ln x2i ln y ) ln x1i 0;
i 1
э
i
n
2 (a0 a1 ln x1i a2 ln x2i ln yiэ ) ln x2i 0;
i 1
Приведение СЛАУ к стандартному виду:
138
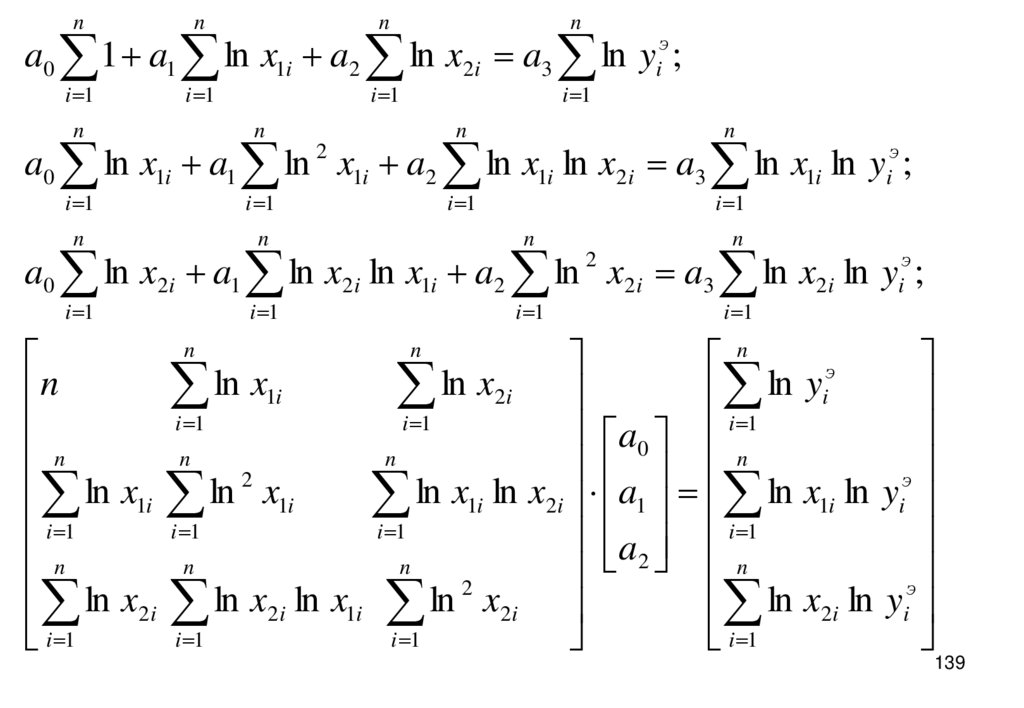
139.
nn
n
n
i 1
i 1
i 1
i 1
a0 1 a1 ln x1i a2 ln x2i a3 ln yiэ ;
n
n
n
n
i 1
i 1
i 1
i 1
n
n
a0 ln x1i a1 ln 2 x1i a2 ln x1i ln x2i a3 ln x1i ln yiэ ;
n
n
a0 ln x2i a1 ln x2i ln x1i a2 ln x2i a3 ln x2i ln y ;
2
i 1
i 1
i 1
i 1
э
i
n
n
n
э
ln x1i
ln x2i
n
ln yi
i 1
i 1
a0 i 1
n
n
n
n
2
э
ln x1i ln x2i a1 ln x1i ln yi
ln x1i ln x1i
i 1
i 1
i 1
a i 1
2 n
n
n
n
2
э
ln x2i ln x2i ln x1i ln x2i
ln x2i ln yi
i 1
i 1
i 1
i 1
139
140.
__
_
1 _
A a b a A b
Алгоритмический подход:
Выбор стандартного типа уравнения регрессии:
Матрица, элементы которой зависят от вида уравнения регрессии и _ э
значений входных переменных, при которых проведены опыты и вектор
f
f a0 a1 z1 a2 z 2 ; z1 ln x1 ; z 2 ln x2 ;
1 z11 z 21 1 ln x1 ln x21
1 z
1 ln x
z
ln
x
12
21
12
22
1 z1n z2 n 1 ln x1n ln x2 n
ln y1э
э
э
_
ln y2
f
ln ynэ
140
141.
TI 3 x 3 3 xn nx 3 ;
_
T
_
1 _
_
э
b 3 x 1 4 xn f nx 1 ;
a 3 x1 I 3 x 3 b 3 x 1 ;
a0
_
a a1
a2
exp( a0 ); 1 a1 ; 2 a2 ;
141
142.
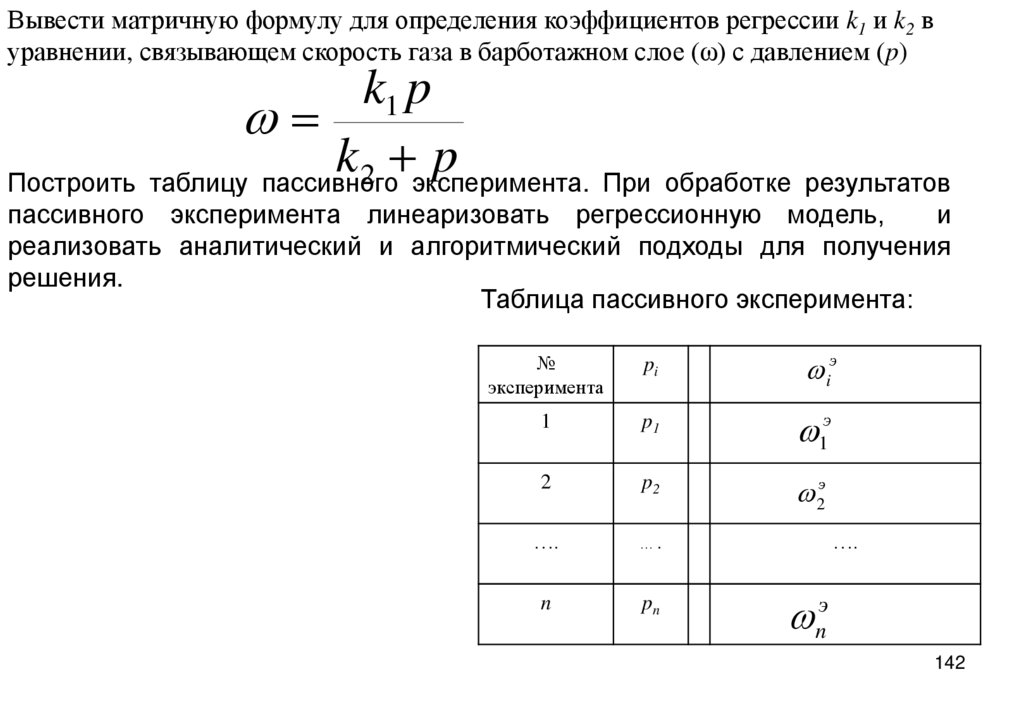
Вывести матричную формулу для определения коэффициентов регрессии k1 и k2 вуравнении, связывающем скорость газа в барботажном слое (ω) с давлением (p)
k1 p
k
p
2
Построить таблицу пассивного эксперимента. При обработке результатов
пассивного эксперимента линеаризовать регрессионную модель,
и
реализовать аналитический и алгоритмический подходы для получения
решения.
Таблица пассивного эксперимента:
№
эксперимента
pi
iэ
1
p1
1э
2
p2
2э
….
….
n
pn
….
nэ
142
143.
Линеаризация уравнениярегрессии:
k2 p 1 1 k2 1
;
;
k1 p k1 k1 p
1
1
k2
a0 ; a1 ;
k1
k1
Аналитический подход:
Критерий рассогласования расчётных и экспериментальных данных:
n
R ( yip yiэ ) 2 ;
i 1
1
y a0 a1 ;
pi
p
i
y
э
i
1
э
i
;
n
1
1 2
R (a0 a1 э ) MIN
pi i
i 1
143
144.
Нахождение минимума критерия МНК по необходимому условию функции многихпеременных:
1
1
R
0; 2 (a0 a1 p э ) 1 0;
i 1
i
i
a0
n
n
1
1
1
R
(a0 a1 э ) 0;
0; 2
pi i pi
i 1
a1
Приведение СЛАУ к стандартному виду:
n
n
i 1
i 1
a0 1 a1
n
a0
i 1
n
1
1
э
pi i 1 i
n
n
1
1
1 1
a1 2
э
pi
i 1 pi
i 1 pi i
144
145.
nn 1
i 1 pi
n 1
1
a
э
p
i 1
i
0
i 1 i
n
n
1 a1
1 1
2
э
p
p
i 1
i
i 1 i i
n
_
_
_
1 _
A a b a A b
Алгоритмический подход:
Выбор стандартного типа уравнения регрессии:
э
_
Матрица, элементы которой зависят от вида уравнения регрессии и
значений входных переменных, при которых проведены опыты и вектор
y
1
1
p
1
1 x1
1 x 1 1
1
2
y a0 a1 x; x ;
p2
p
1 xn
1
1
pn
1
э
1
1
_э
э
y 2
1
э
n
145
146.
TI 2 x 2 2 xn nx 2 ;
_
T
_
1 _
_
э
b 2 x1 2 xn ynx1 ;
a 2 x1 I 2 x 2 b 2 x1 ;
a0
a
a1
1
1
k1 ; k 2 a1 ;
a0
a0
_
146


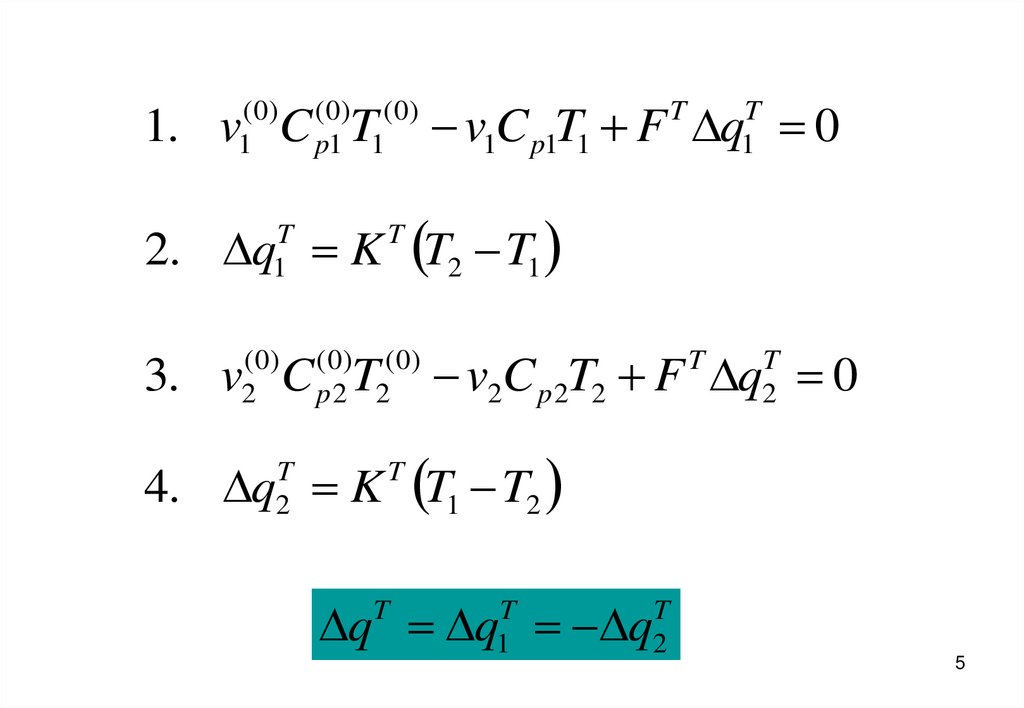








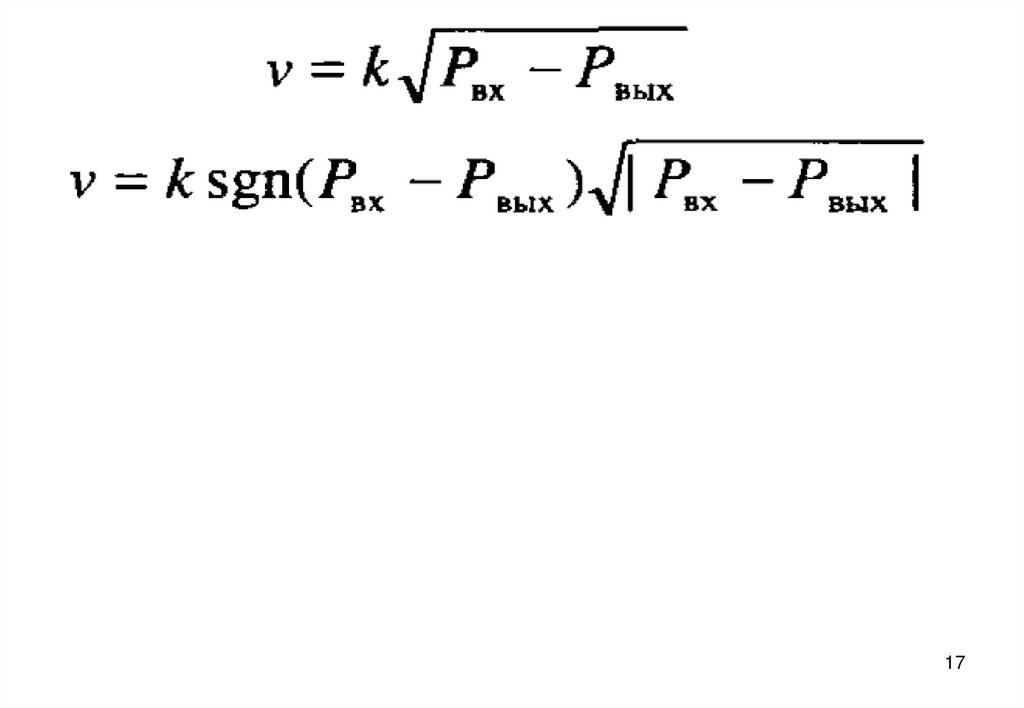
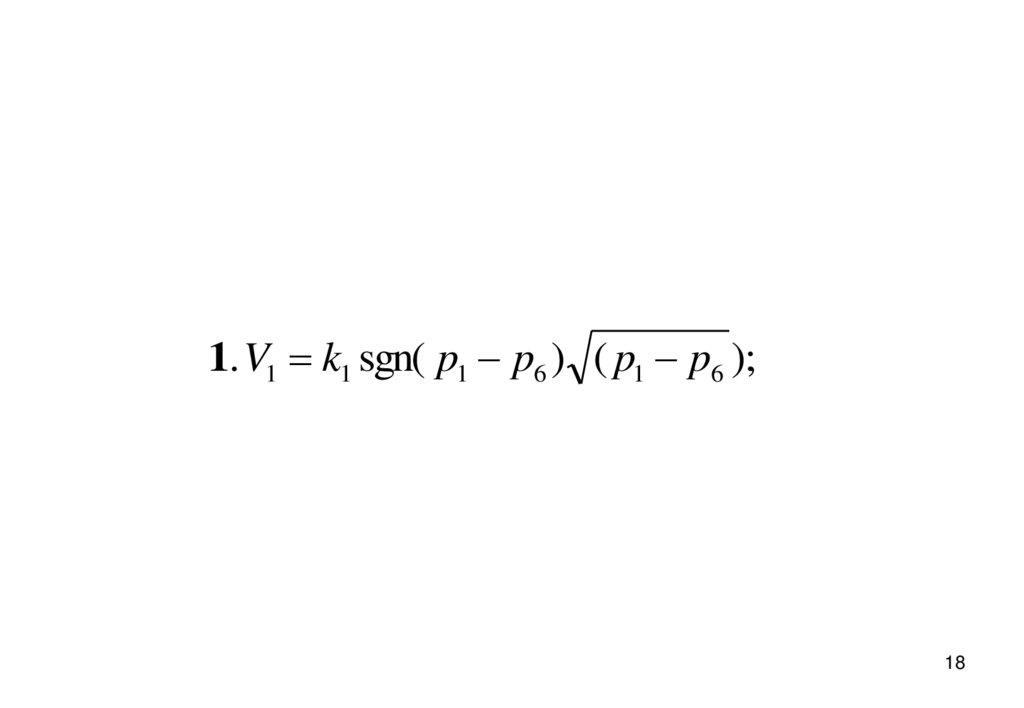
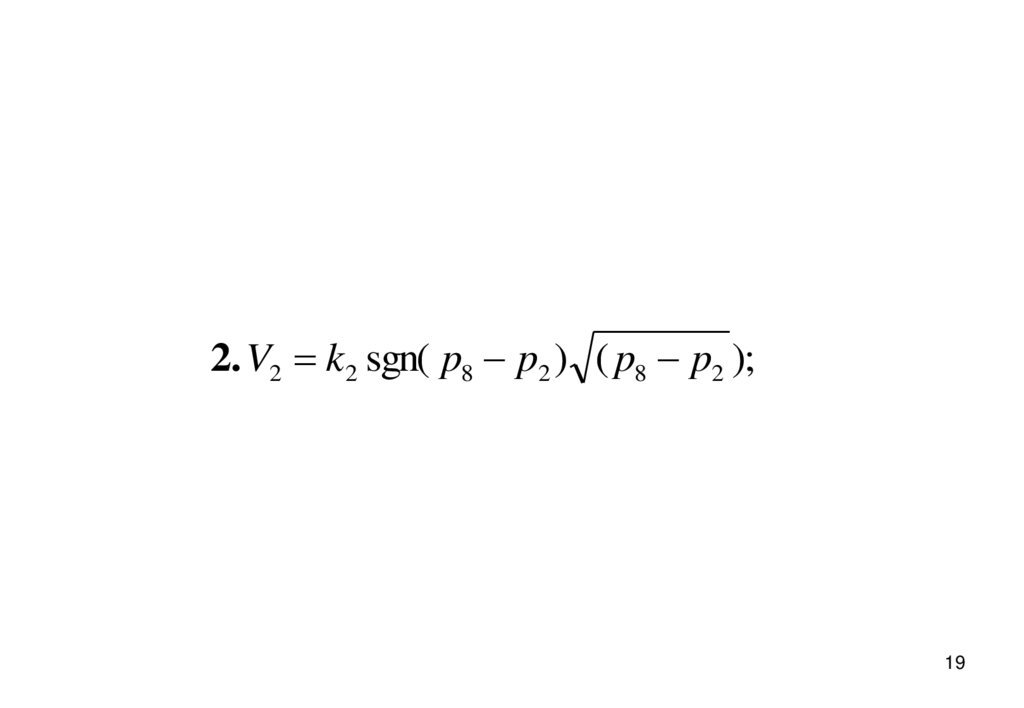
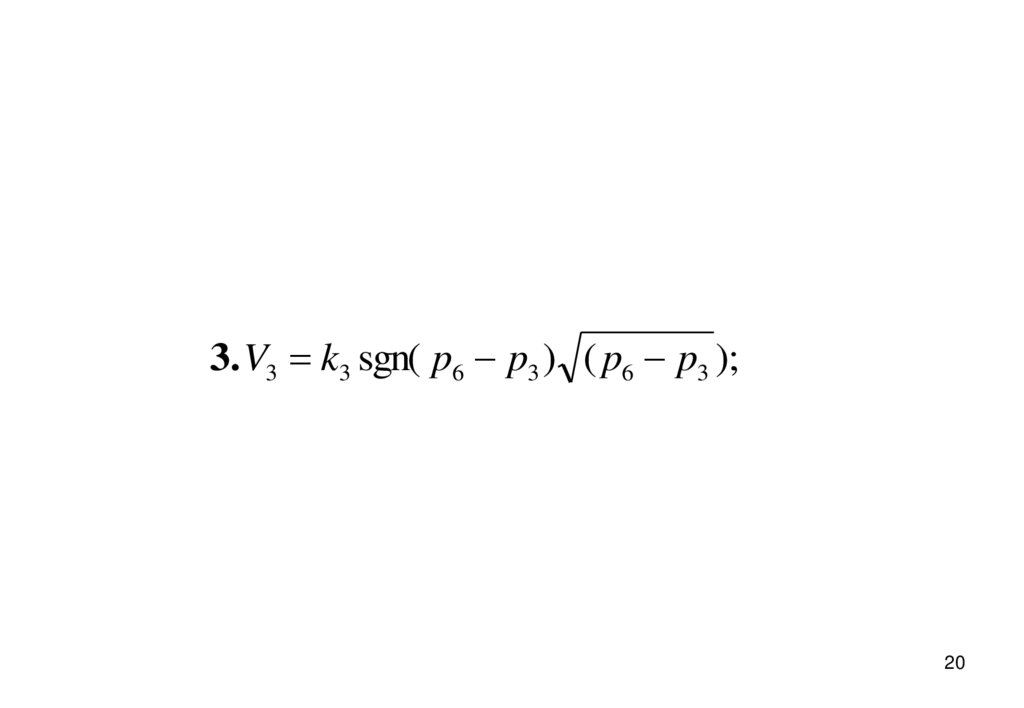
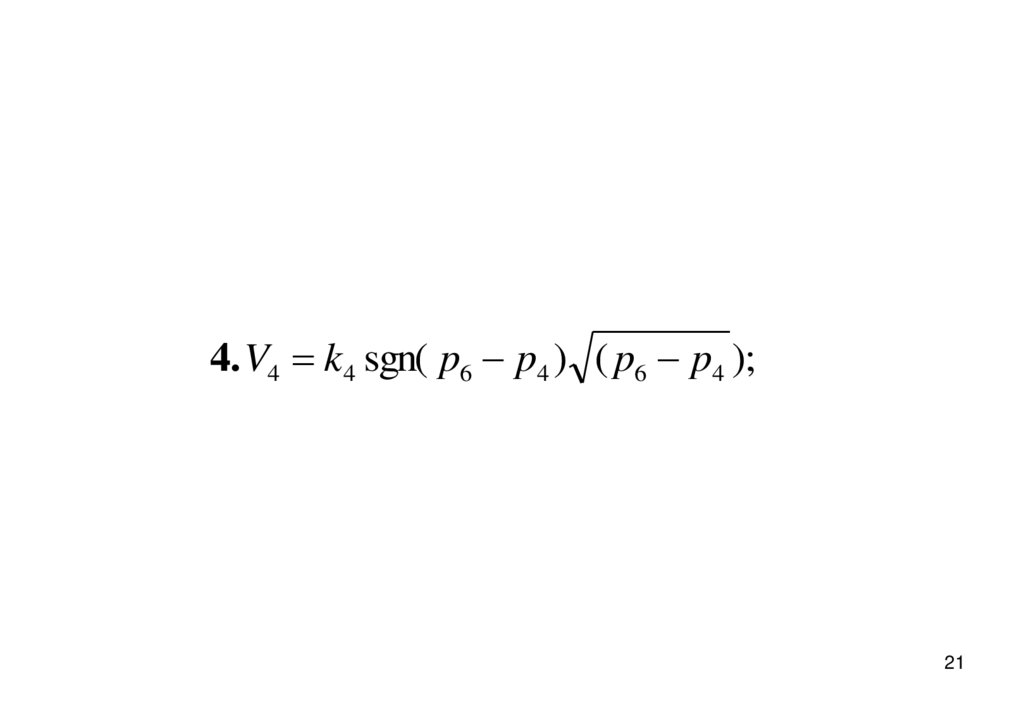
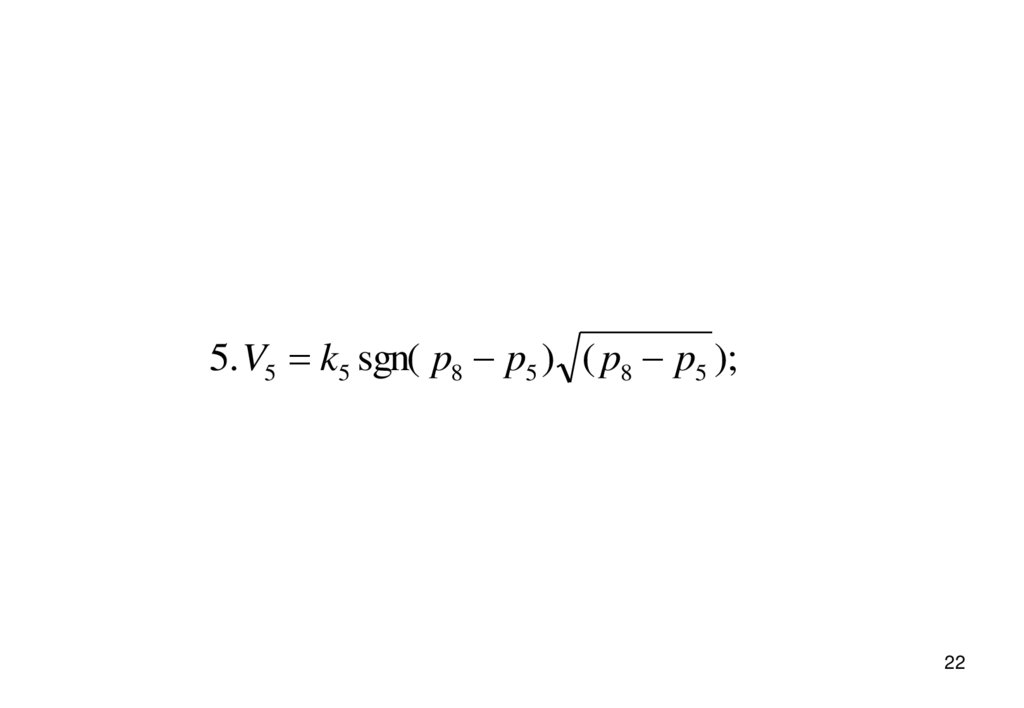
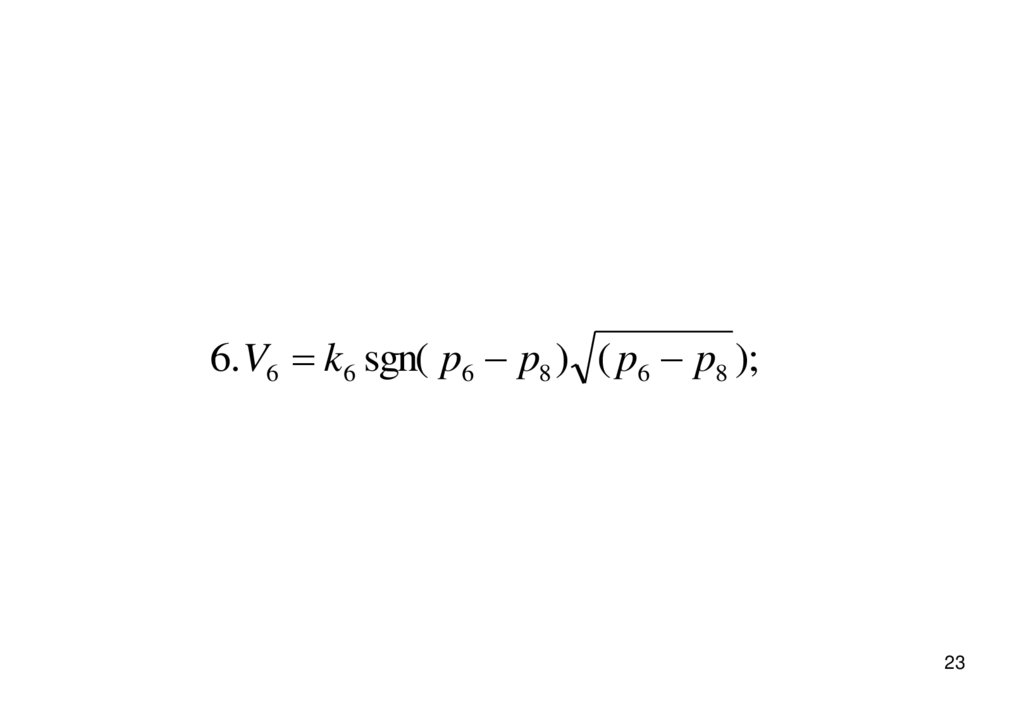

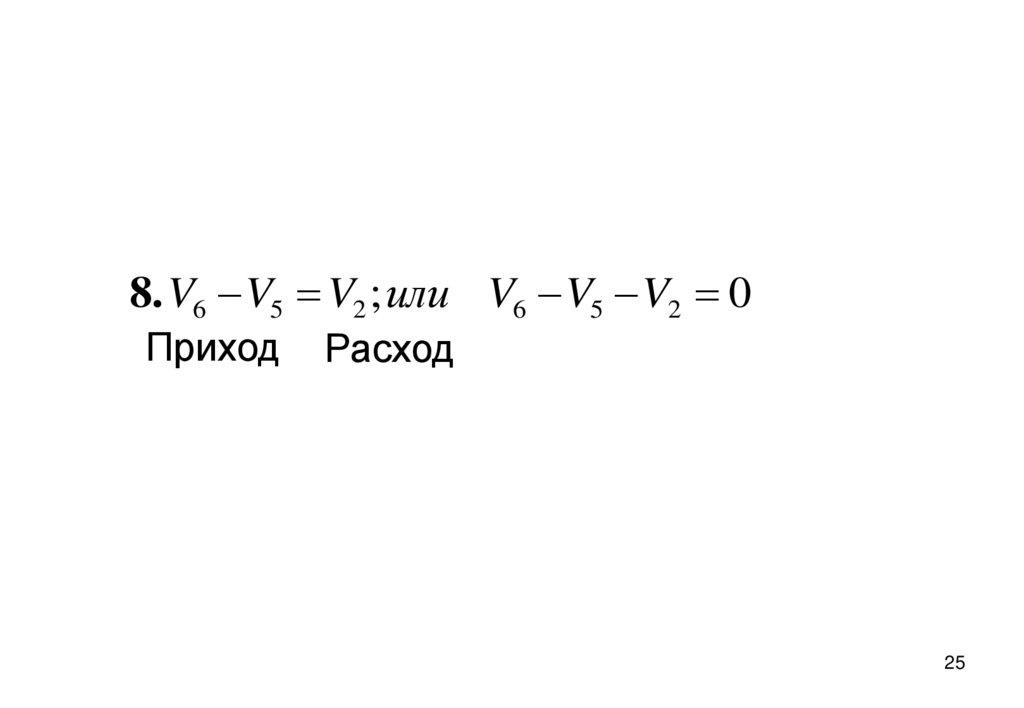
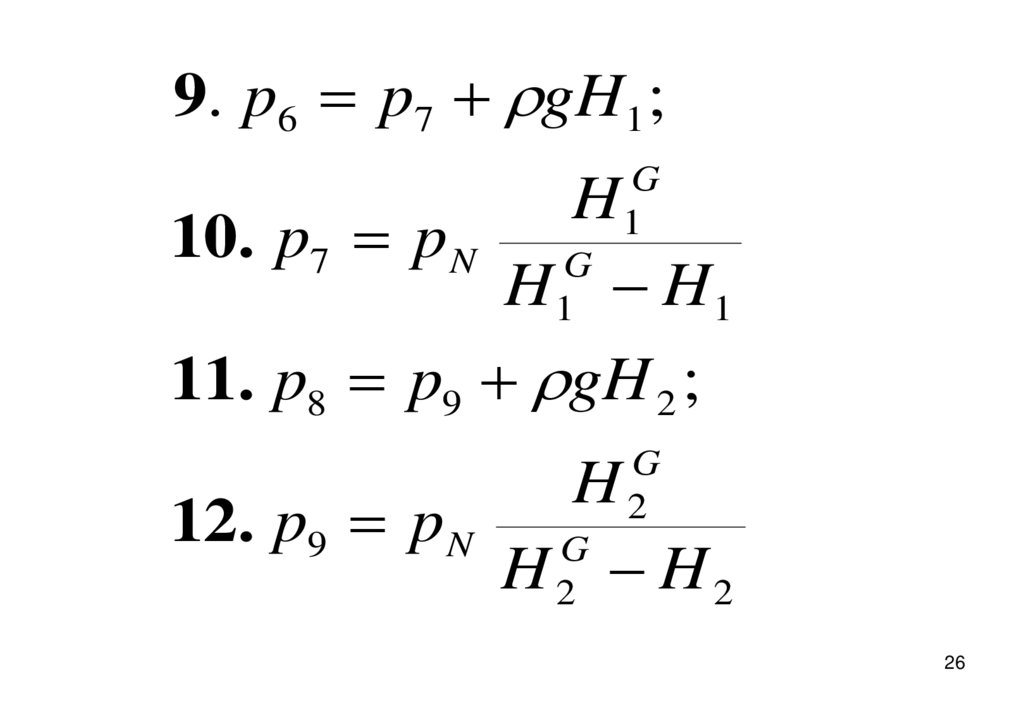





































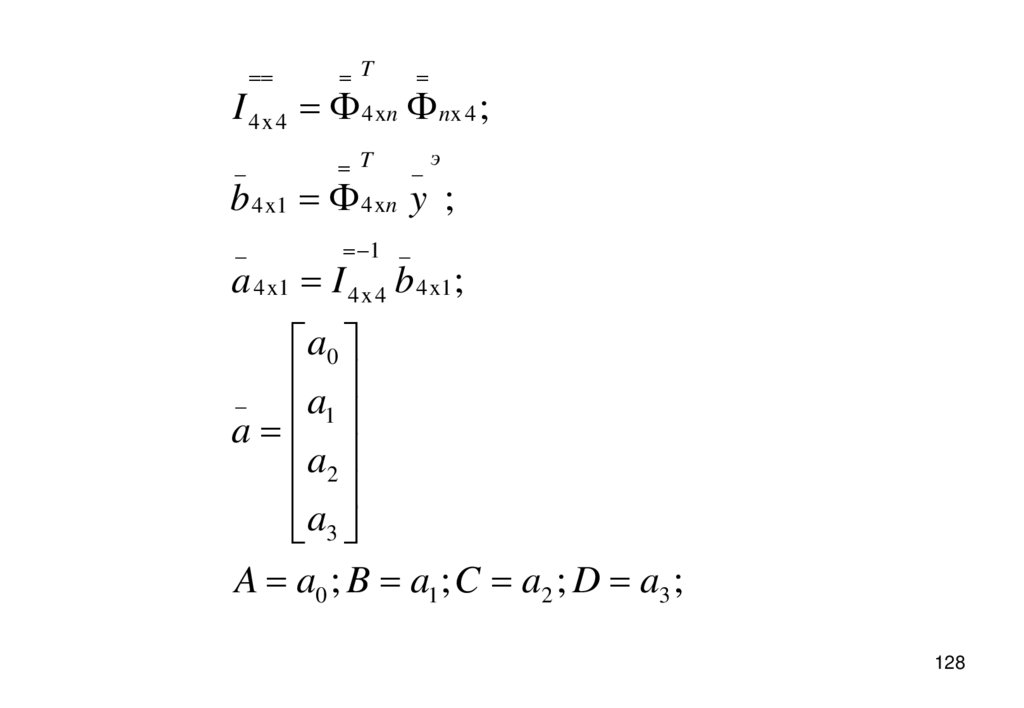





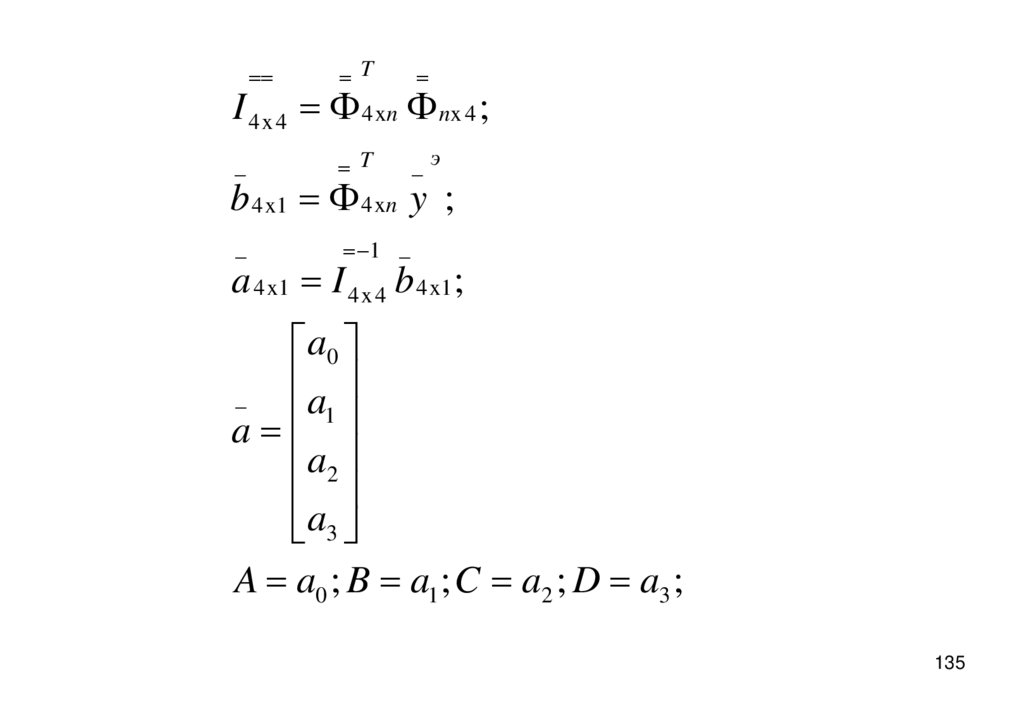




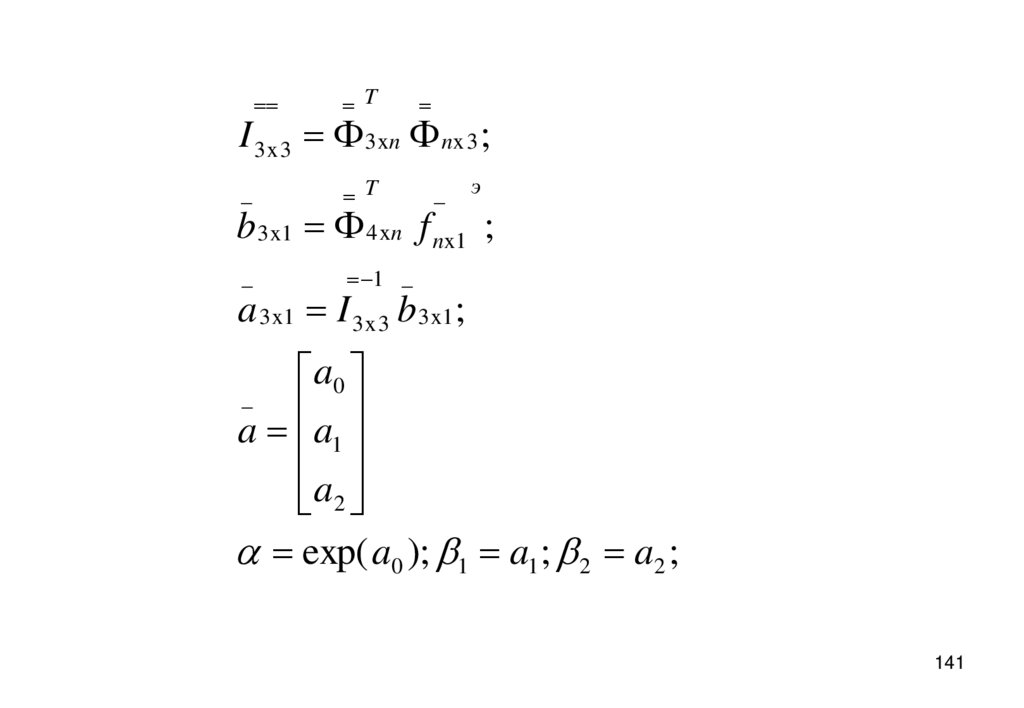



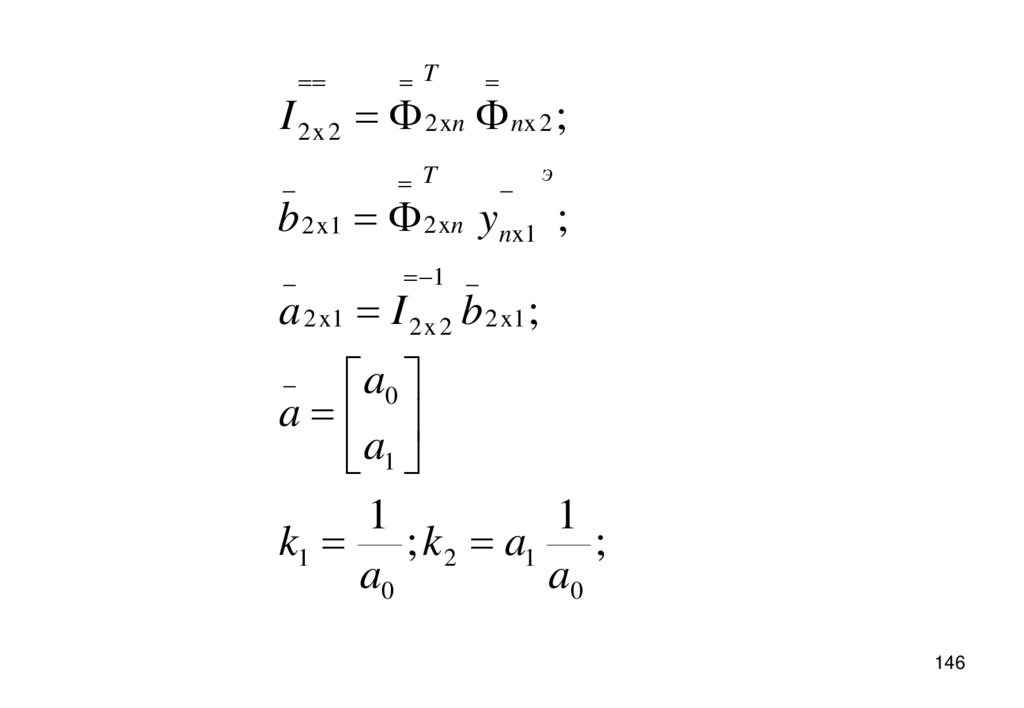
 physics
physics








