Similar presentations:
Метод паралельного проектування. Зображення просторових фігур фигур на площині
1.
• У стереометрії вивчаютьсяпросторові фігури, проте
на кресленні вони
зображуються у вигляді
плоских фігур. Яким же
чином слід зображувати
просторову фігуру на
площині? Зазвичай в
геометрії для цього
використовується
паралельне проектування
просторової фігури на
площину.
2.
Метод паралельногопроектування. Зображення
просторових фігур фигур на
площині
Воробьев Леонид Альбертович, г.Минск
3.
• Слово проекція виникло відлатинського projection кидання вперед, вдалину.
4.
Отже є геометрична фігура в просторі – точка А.А
5.
Оберемо в просторі довільну площину (її ми будемо називати площиноюпроекції)
і довільну пряму прямую a∦ (вона задає напрямок
паралельного проектування).
а
А
6.
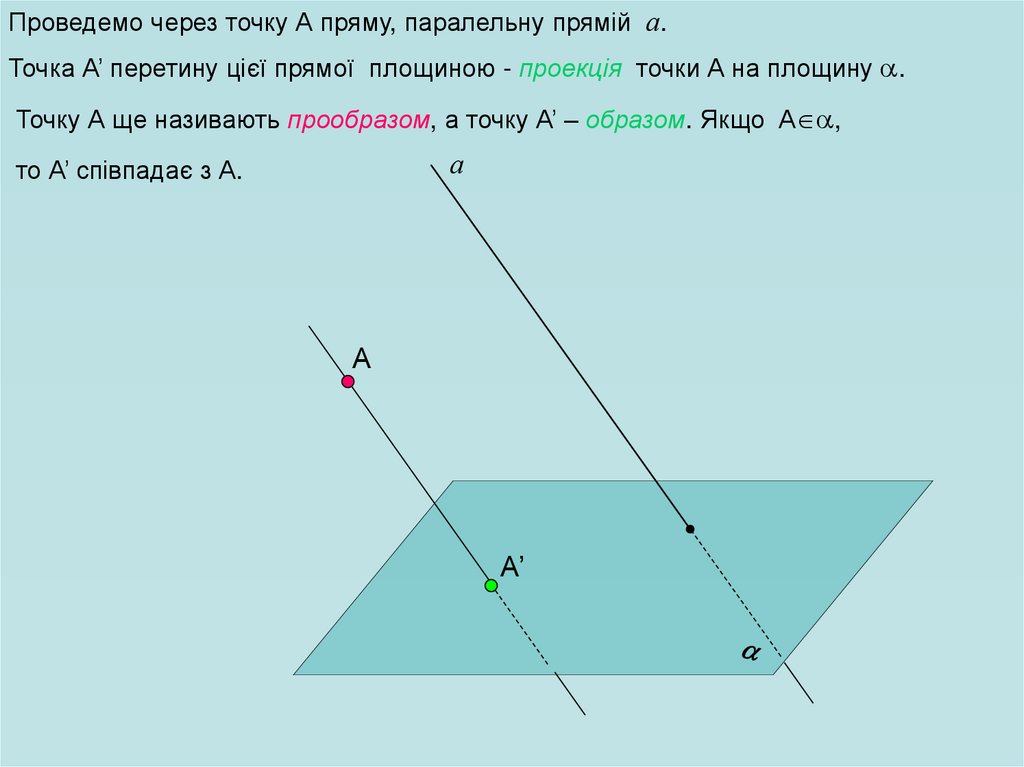
Проведемо через точку А пряму, паралельну прямій а.Точка А’ перетину цієї прямої площиною - проекція точки А на площину .
Точку А ще називають прообразом, а точку А’ – образом. Якщо А ,
а
то А’ співпадає з А.
А
А’
7.
Розглядаючи будь-яку геометричену фігуру як множину точок, можна побудувати взаданій площині проекцію даної фігури. Таким чином можна отримати зображення
(або «проекцію») будь-якої плоскої або просторової фігури на площині.
а
8.
Зауваження 1. При паралельному проектуванні непаралельного проектування паралельно площині проекції
а
А
обирають
напрямок
9.
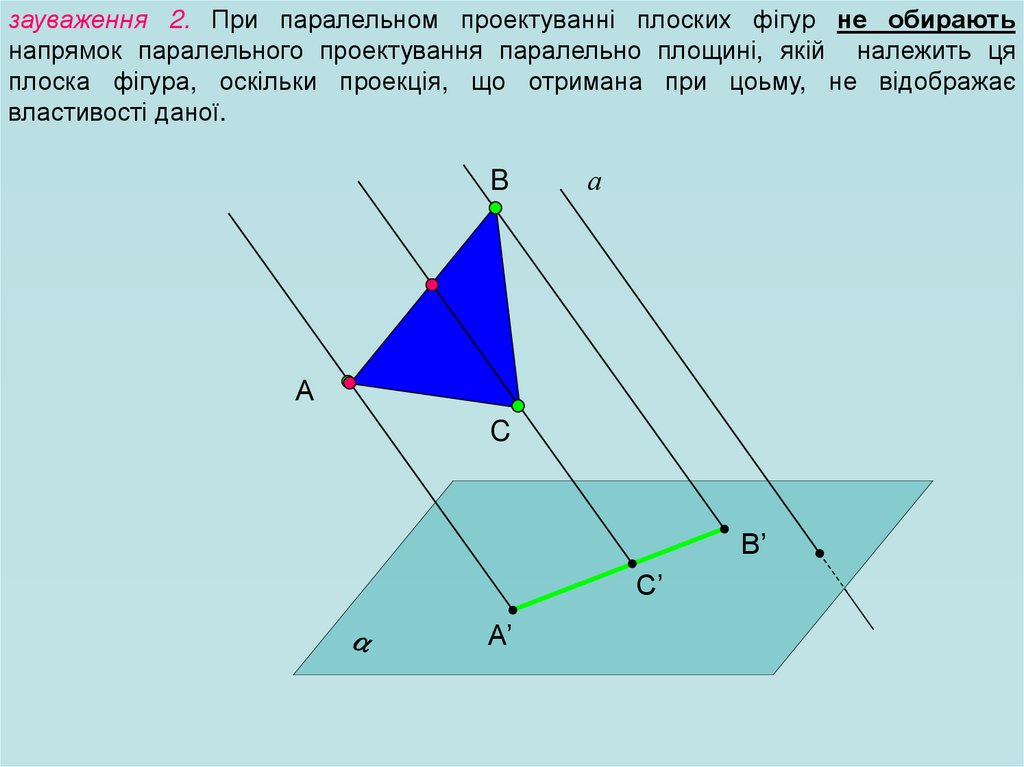
зауваження 2. При паралельном проектуванні плоских фігур не обираютьнапрямок паралельного проектування паралельно площині, якій належить ця
плоска фігура, оскільки проекція, що отримана при цоьму, не відображає
властивості даної.
B
а
А
C
B’
C’
А’
10.
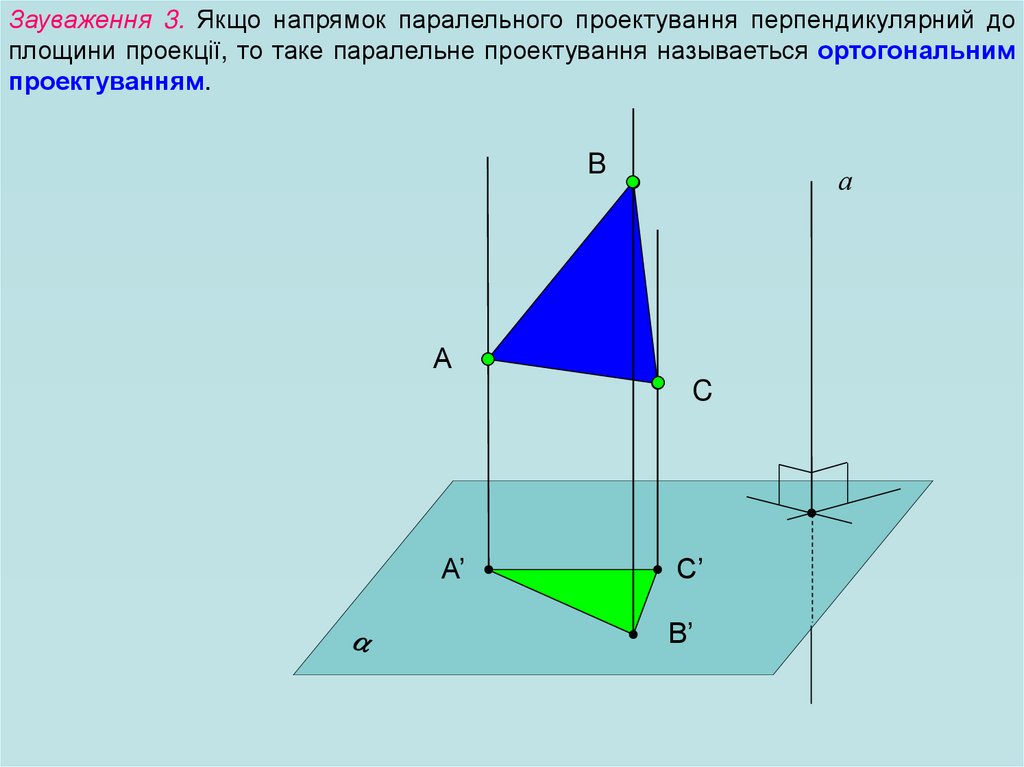
Зауваження 3. Якщо напрямок паралельного проектування перпендикулярний доплощини проекції, то таке паралельне проектування называеться ортогональним
проектуванням.
B
а
А
C
А’
C’
B’
11.
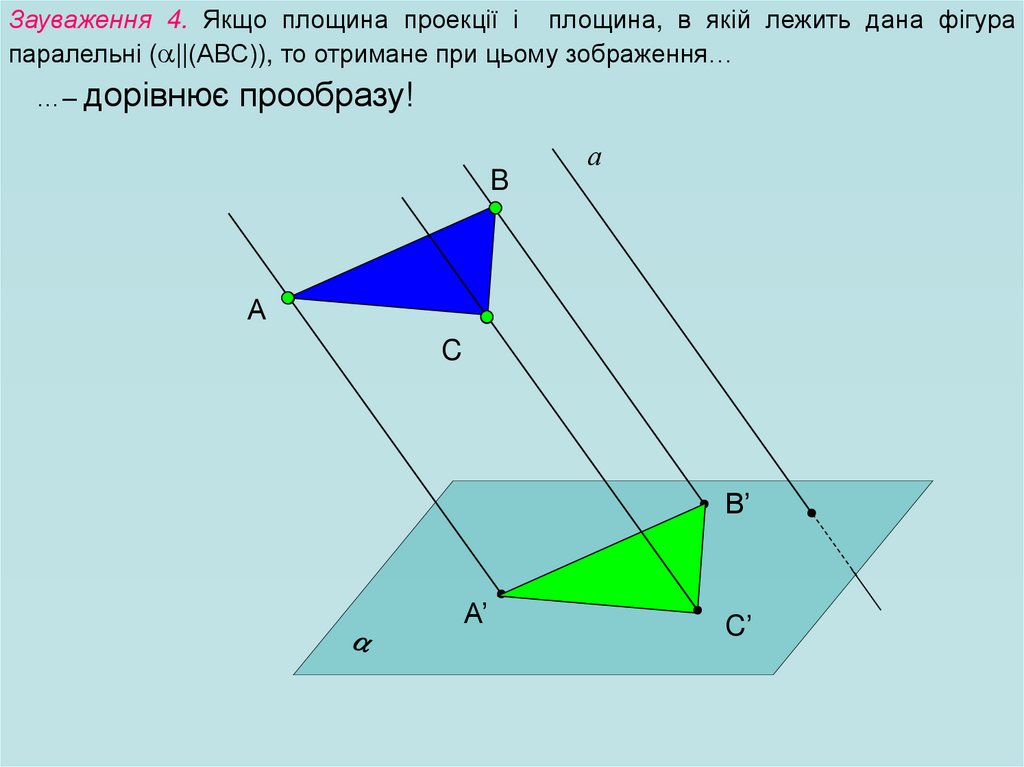
Зауваження 4. Якщо площина проекції і площина, в якій лежить дана фігурапаралельні ( ||(АВС)), то отримане при цьому зображення…
…– дорівнює прообразу!
B
а
А
C
B’
А’
C’
12.
Паралельне проектування володіє властивостями:1) паралельність прямих (відрізків, променів) зберігається;
B
а
D
A
C
B’
D’
A’
C’
AB CD A' B' C' D'
13.
Паралельне проектування володіє властивостями :1) паралельність прямих (відрізків, променів) зберігається;
2) відношення довжин відрізків, що лежать на паралельних або на одній прямій
зберігається;
B
а
М
D
A
C
М’
B’
D’
A’
C’
Якщо, наприклад, АВ=2CD, то А’В’=2C’D’ або
AM A' M '
MB M ' B'
14.
Паралельне проектування володіє властивостями :1) паралельність прямих (відрізків, променів) зберігається;;
2) ) відношення довжин відрізків, що лежать на паралельних або на одній прямій
зберігається;
3) Лінійні розміри плоских фігур (довжини відрізків, величини кутів) не
зберігаються (виключення – див. зауваження 4).
а
B
C
A
C’
A’
B’
15.
ЗБЕРІГАЮТЬСЯ1) Належність фігури до свого
класу фігур (точку зображають
точкою, відрізок – відрізком,
трикутник – трикутником
тощо;
2) Належність точок прямій;
3) Порядок розміщення точок
на прямій (внутрішню точку
відрізка зображають
внутрішньою точкою його
проекції);
4) Паралельність прямих;
5) Рівність (пропорційність)
відрізків, що лежать на
паралельних прямих або
на одній прямій.
НЕ ЗБЕРІГАЮТЬСЯ
1) Довжина відрізка;
2) Міра кута (зокрема прямий
кут зображають довільним
кутом);
3) Перпендикулярність прямих;
4) Рівність (пропорційність)
кутів;
5) Рівність (пропорційність)
відрізків, які лежать на
прямих, що перетинаються.
16.
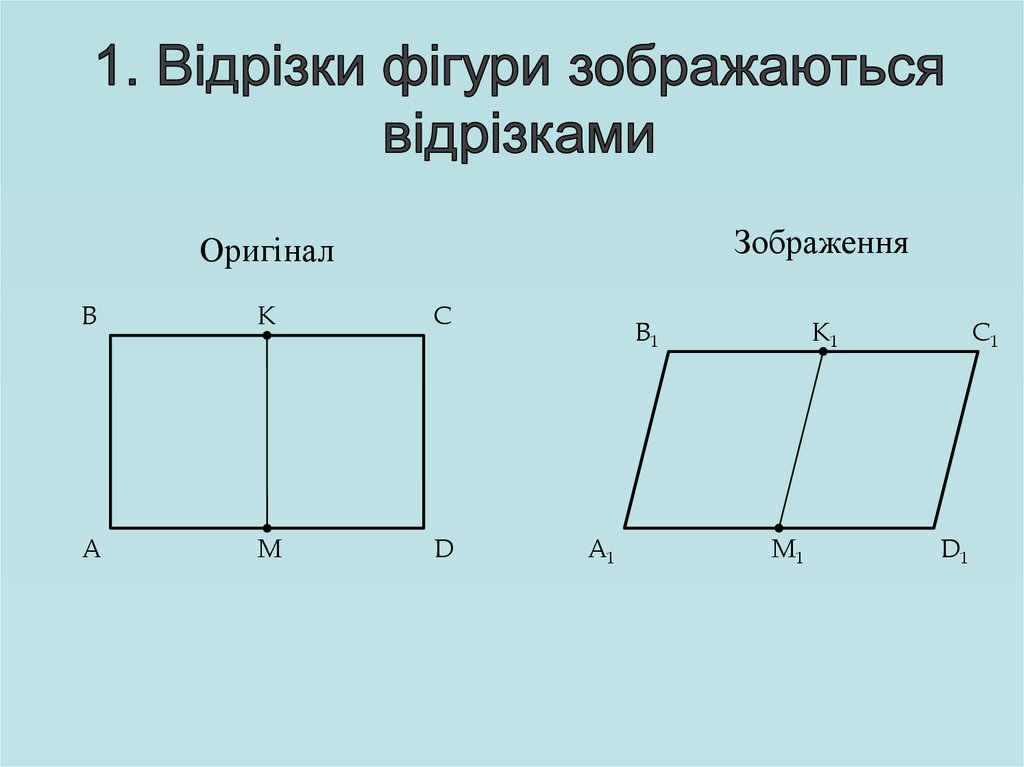
ЗображенняОригінал
B
K
C
A
M
D
B1
A1
K1
M1
C1
D1
17.
BC
D
А
Оригінал
B1
C1
D1
А1
Зображення
18.
ОригіналK
B
Зображення
C
B1
A
D
M
A1
K1
M1
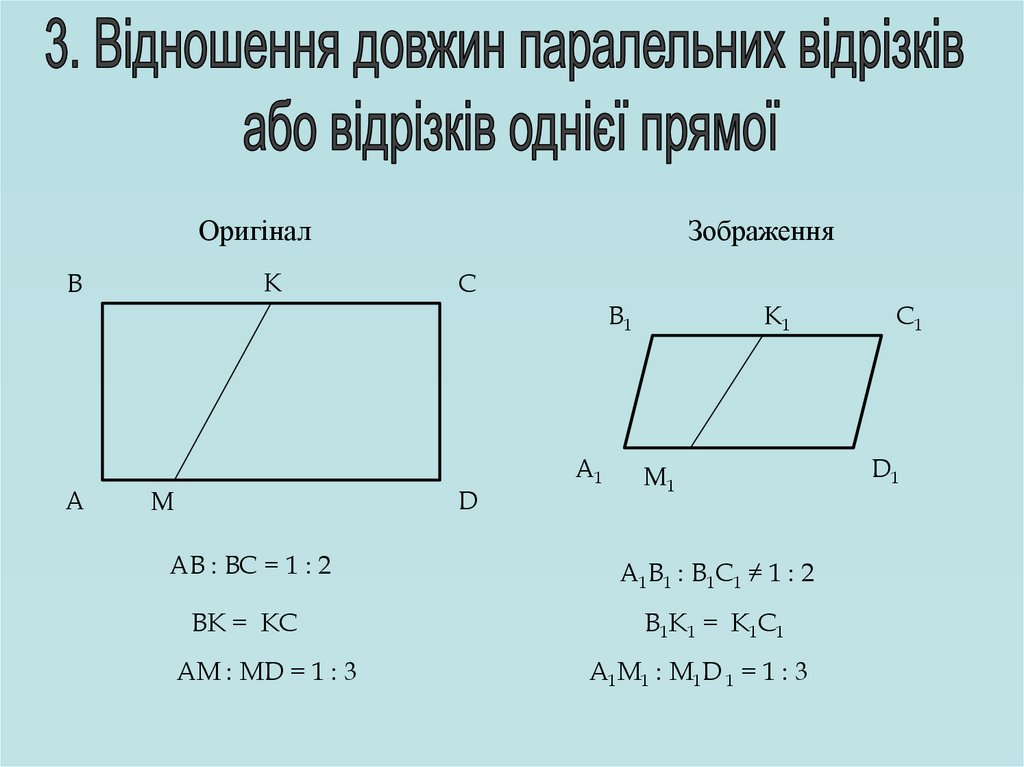
AB : BC = 1 : 2
A1B1 : B1C1 ≠ 1 : 2
BK = KC
B1K1 = K1C1
AM : MD = 1 : 3
A1M1 : M1D 1 = 1 : 3
C1
D1
19.
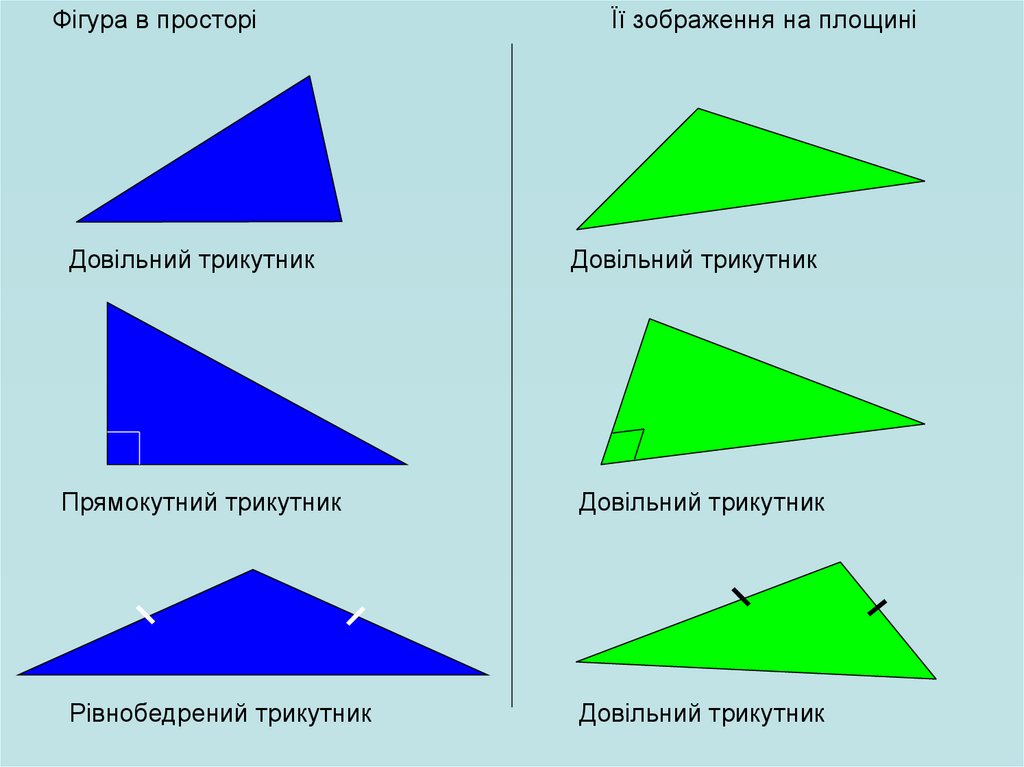
Фігура в просторіЇї зображення на площині
Довільний трикутник
Довільний трикутник
Прямокутний трикутник
Довільний трикутник
Рівнобедрений трикутник
Довільний трикутник
20.
Фігура в просторіРівносторонній трикутник
її зображення на площині
Довільний трикутник
Паралелограм
Довільний паралелограм
Прямокутник
Довільний паралелограм
21.
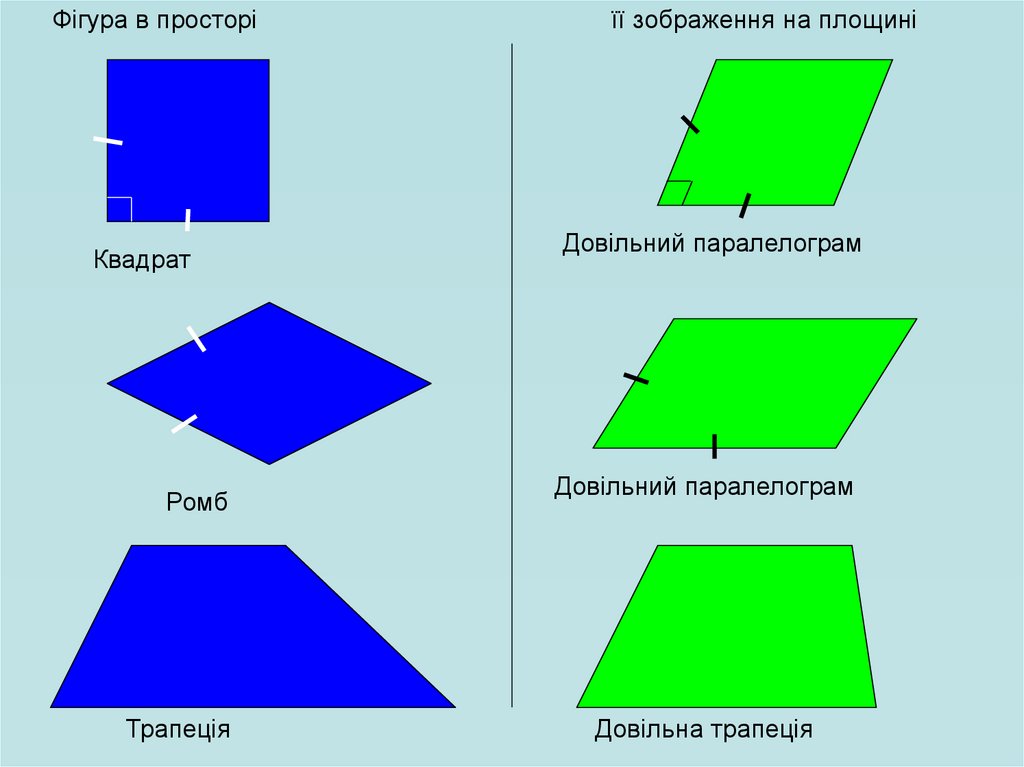
Фігура в просторіКвадрат
Ромб
Трапеція
її зображення на площині
Довільний паралелограм
Довільний паралелограм
Довільна трапеція
22.
Фігура в просторіїї зображення на площині
Рівнобічна трапеція
Довільна трапеція
Прямокутна трапеція
Довільна трапеція
Круг (коло)
Овал (еліпс)
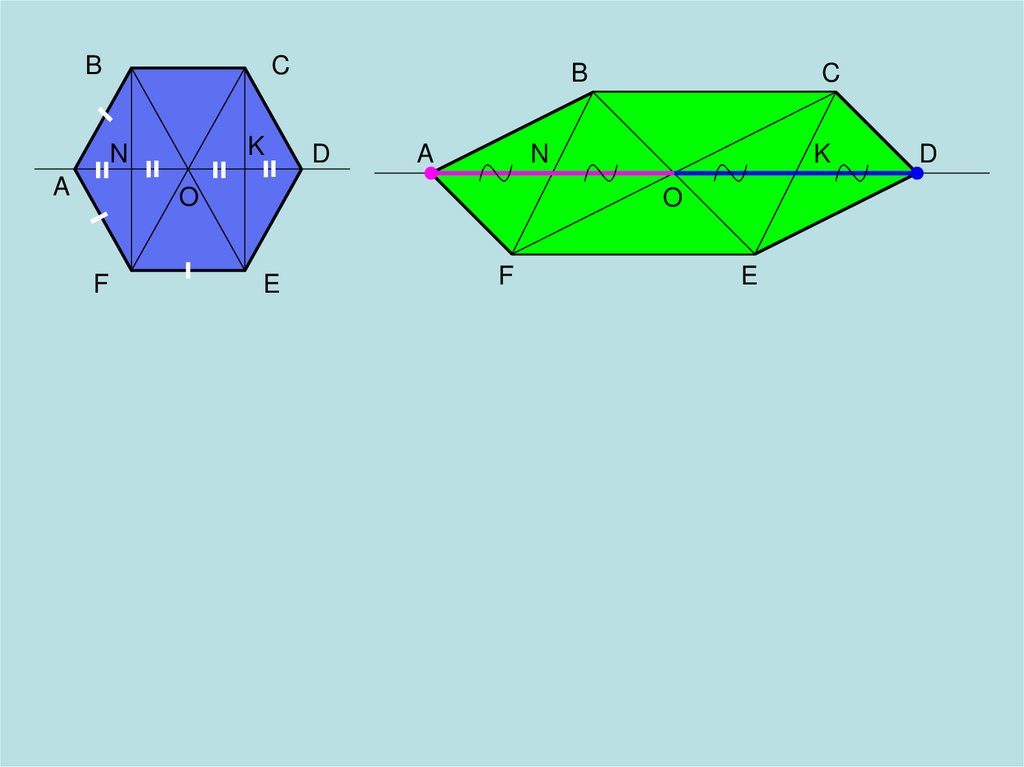
23.
BC
K
N
A
B
D
A
N
O
F
C
K
O
E
F
E
D
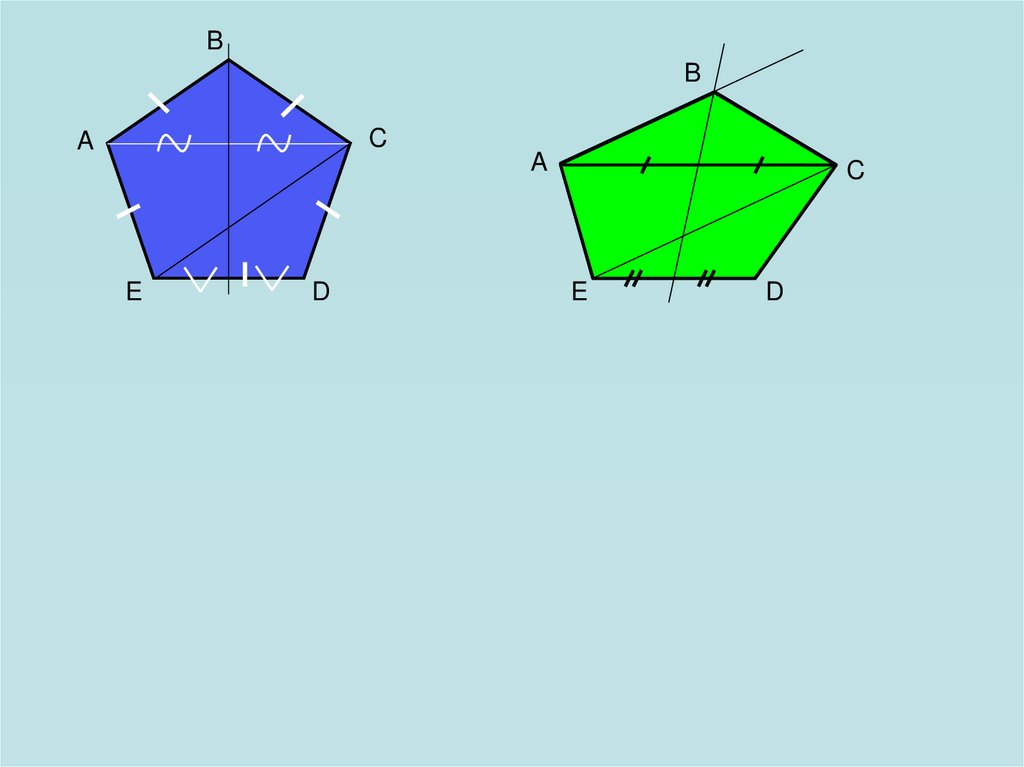
24.
BB
C
A
A
E
D
C
E
D
25.
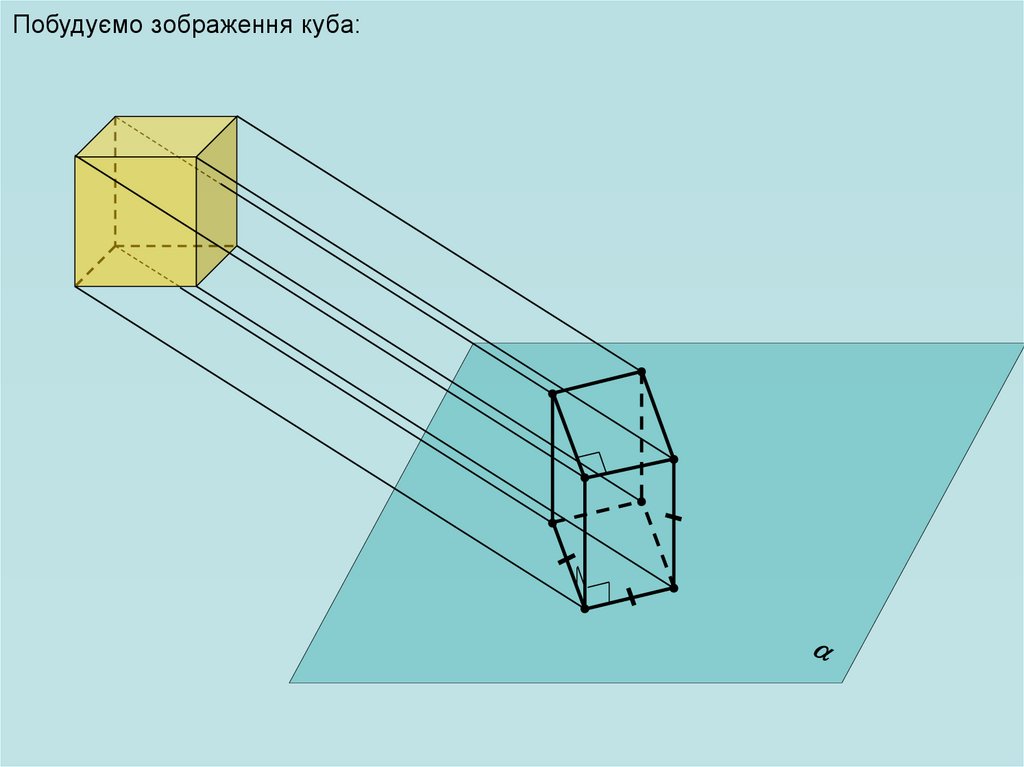
Побудуємо зображення куба:26.
Як побудувати паралельну проекціюплоскої фігури
Щоб побудувати паралельну проекцію
плоскої фігури, спочатку побудуйте її
оригінал. Потім, спираючись на оригінал,
виділіть властивості фігури:
• які збігаються під час паралельного
проектування (на них треба спиратися);
• які не збігаються під час паралельного
проектування (їх не
можна використовувати)
27.
1. У якому випадку паралельної проекцієювідрізка буде точка?
Відповідь: Якщо пряма паралельна напрямку
проектування.
2. У якому випадку паралельної проекцією двох
паралельних прямих є одна пряма?
Відповідь: Якщо площина, в якій лежать ці
прямі, паралельна напрямку проектування.
3. Які фігури можуть бути паралельними
проекціями двох мимобіжних прямих?
Відповідь: Дві прямі що перетинаються; дві
паралельні прямі; пряма і точка, що їй не
належить.
28.
4. Чи зберіжеться при паралельному проектуванні:а) довжина відрізка 30 см ; б) величина кута 900?
Відповідь: а), б) Ні.
5. Чи вірно, що якщо довжина відрізка дорівнює
довжині його паралельної проекції, то відрізок
паралельний площині проектування?
Відповідь: Ні.
• 6. Чи може паралельної проекцією прямокутного
трикутника бути: а) прямокутний трикутник; б)
рівнобедрений трикутник, в) різносторонній
трикутник?
• Відповідь: а), б), в) Так.
7. Чи може паралельною проекцією прямокутника
бути: а) квадрат; б) паралелограм, в) ромб; г)
трапеція?
• Відповідь: а), б), в) Так; г) ні.
29.
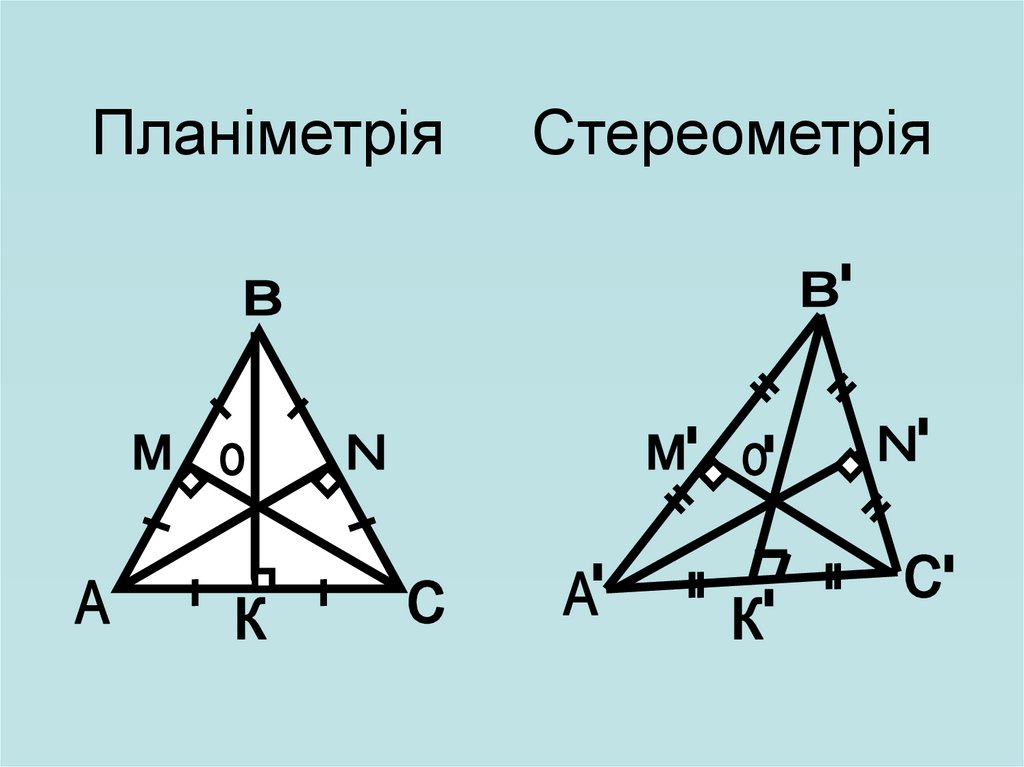
ПланіметріяСтереометрія
30.
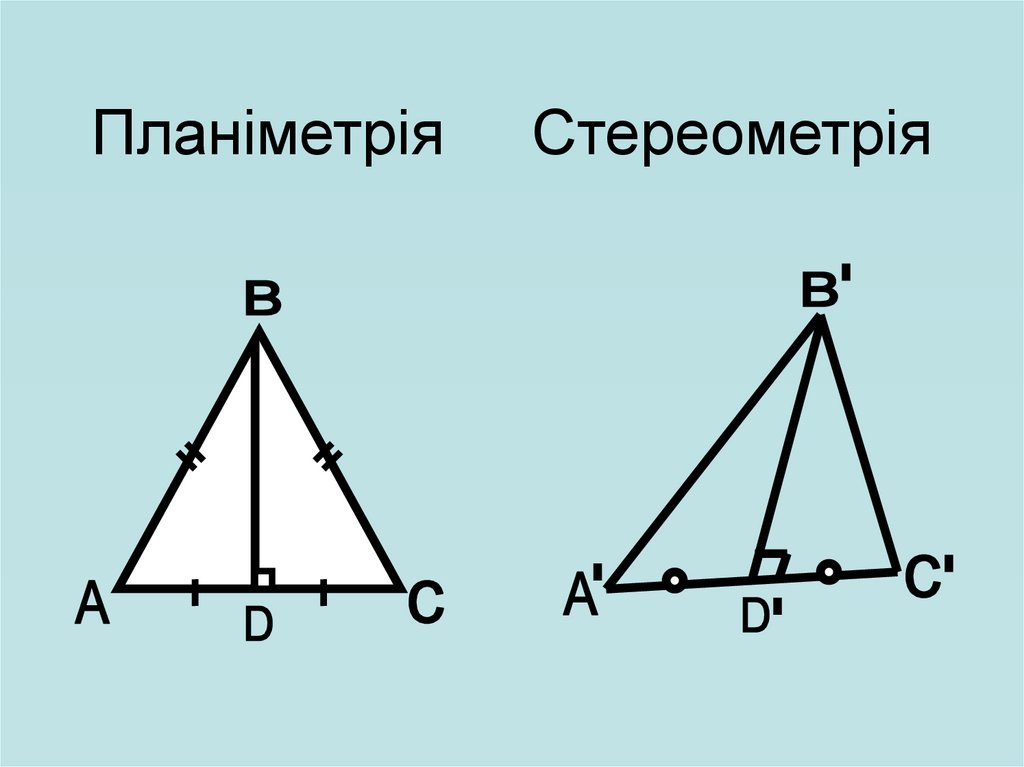
ПланіметріяСтереометрія
31.
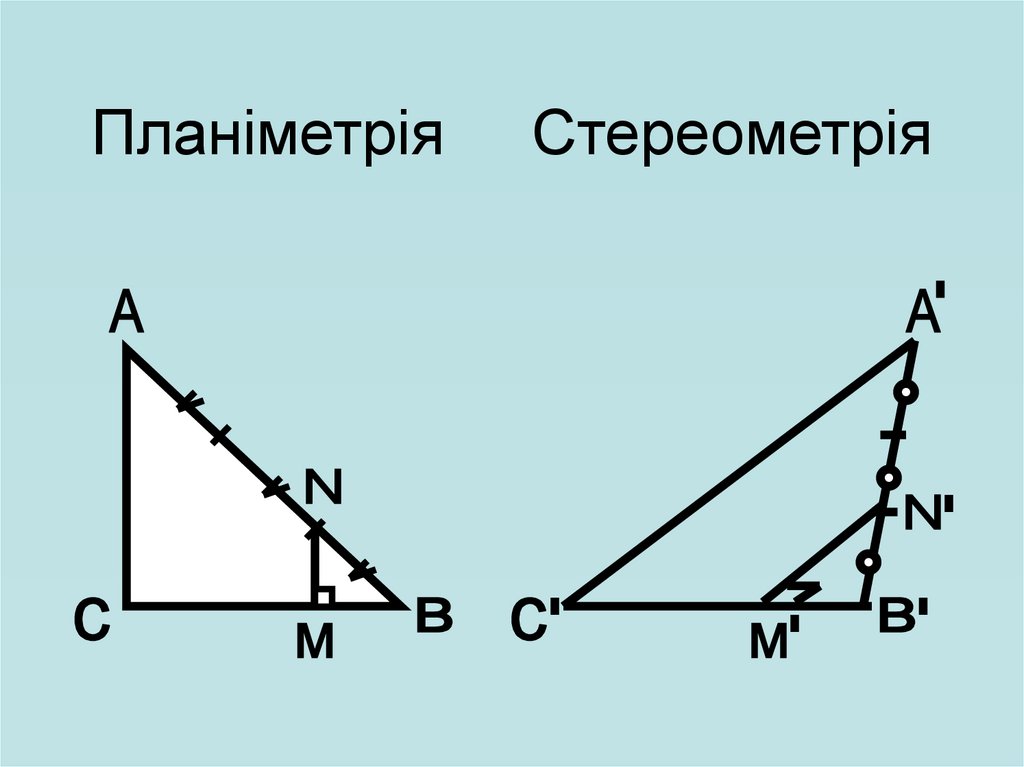
ПланіметріяСтереометрія
32.
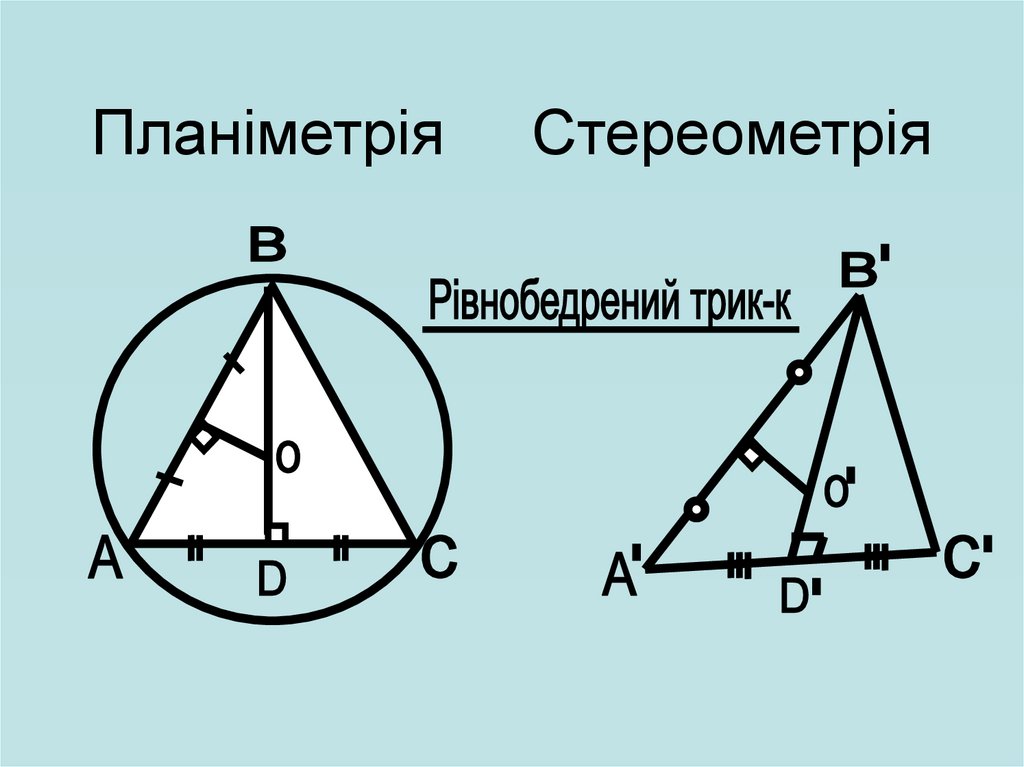
ПланіметріяСтереометрія
33.
ПланіметріяСтереометрія
34.
ПланіметріяСтереометрія
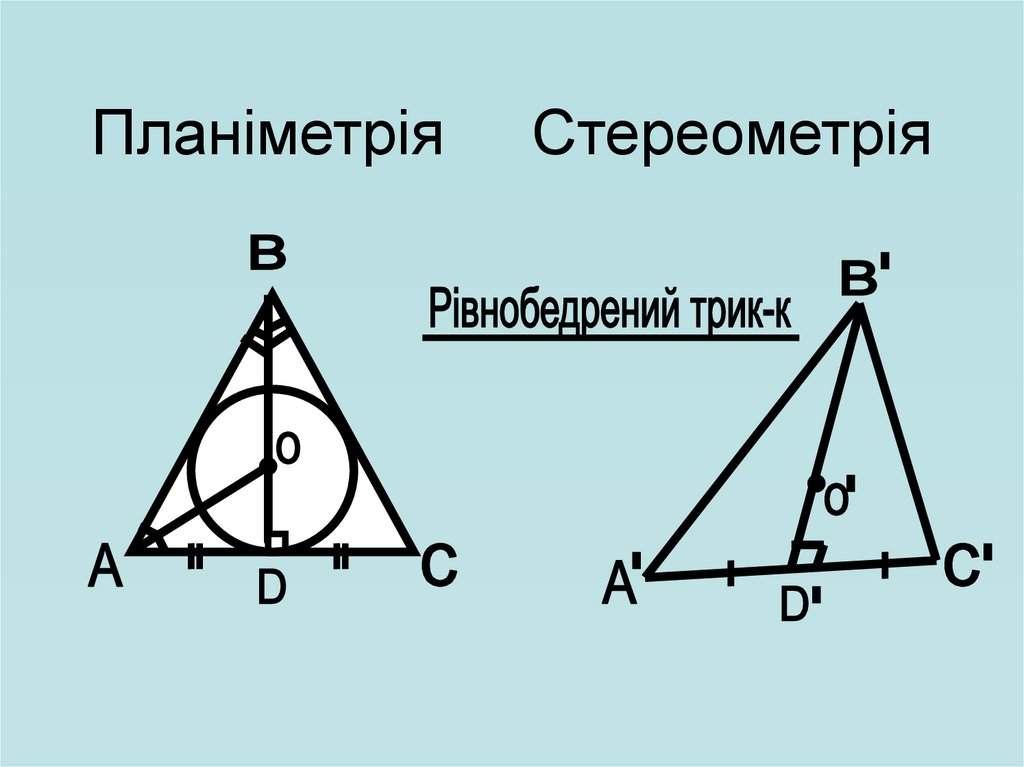
35.
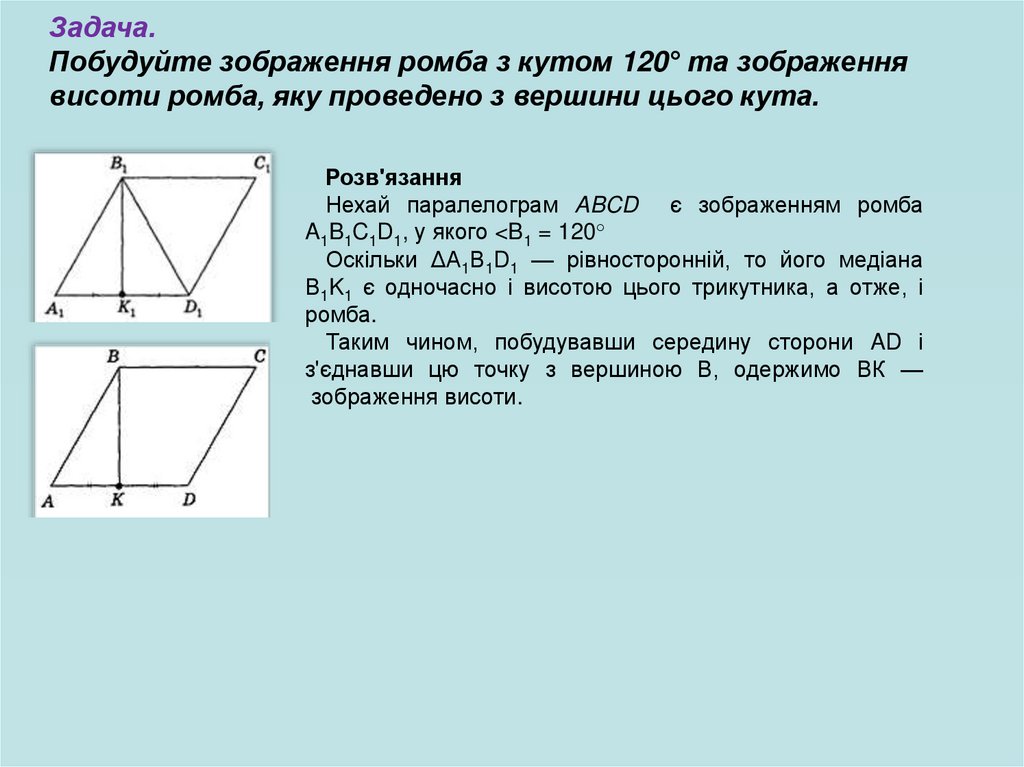
Задача. Побудувати зображенняправильного трикутника,
вписаного в коло.
Планіметрія
Стереометрі
я
36.
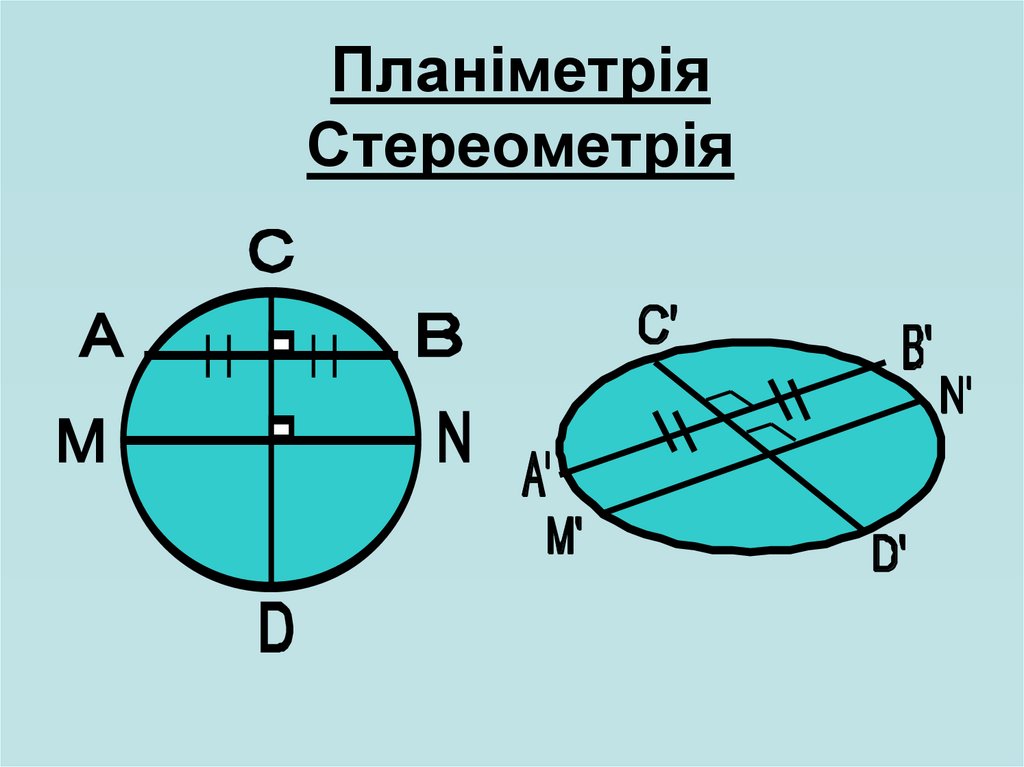
Задача.Планіметрія
Побудувати
зображення
квадрата,
вписаного
в
коло
.
Стереометрія
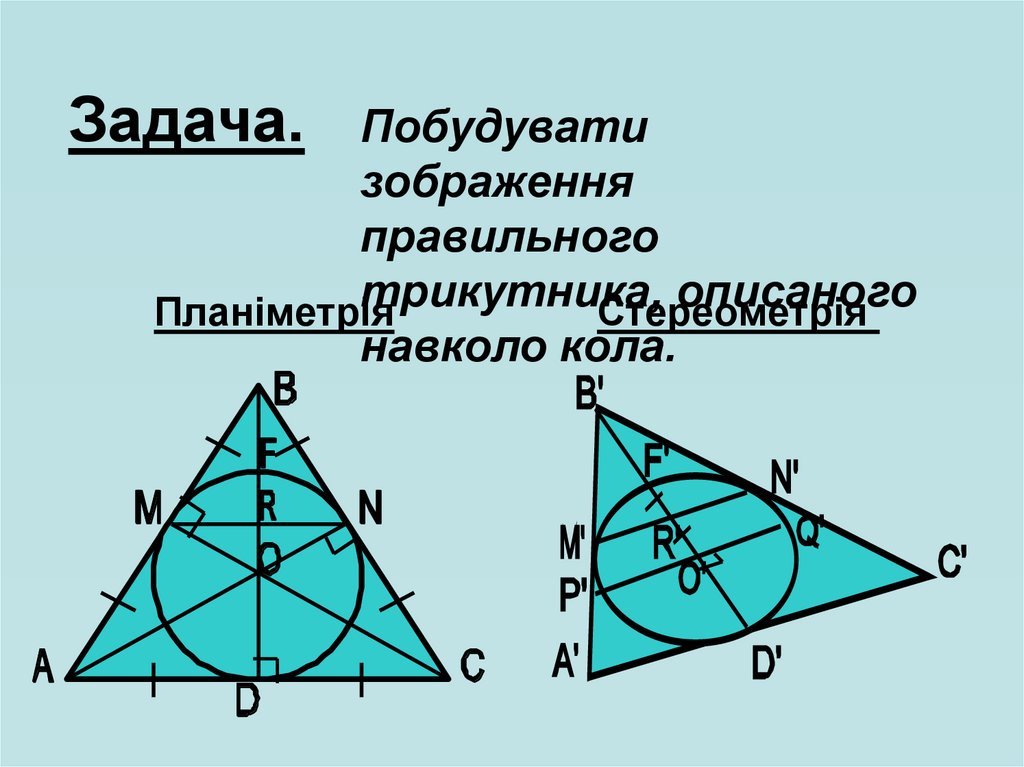
37.
Задача.Побудувати
зображення
правильного
трикутника,
описаного
Планіметрія
Стереометрія
навколо кола.
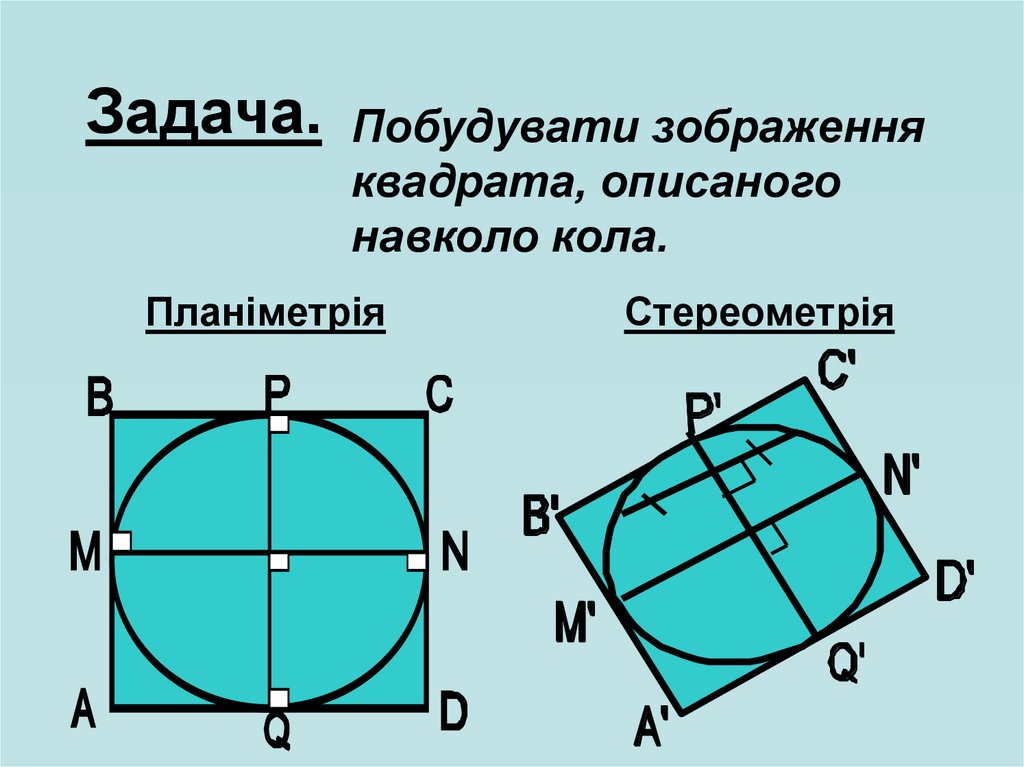
38.
Задача. Побудувати зображенняквадрата, описаного
навколо кола.
Планіметрія
Стереометрія
39.
Задача .ABCD - паралельна проекція рівнобічної трапеції A0B0С0D0, де
А
























 mathematics
mathematics








