Similar presentations:
Стереометрія. Основні поняття стереометрії. Аксіоми стереометрії та наслідки з них
1.
Стереометрія.Основні поняття стереометрії.
Аксіоми стереометрії та наслідки з них.
2.
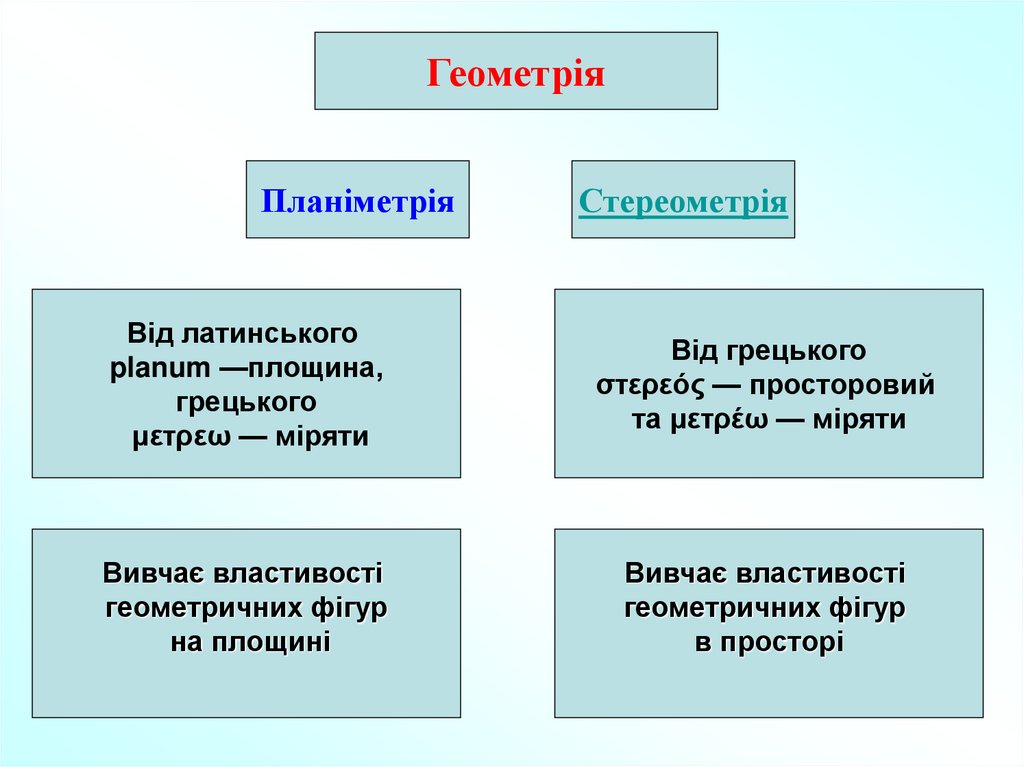
ГеометріяПланіметрія
Стереометрія
Від латинського
planum —площина,
грецького
μετρεω — міряти
Від грецького
στερεός — просторовий
та μετρέω — міряти
Вивчає властивості
геометричних фігур
на площині
Вивчає властивості
геометричних фігур
в просторі
3.
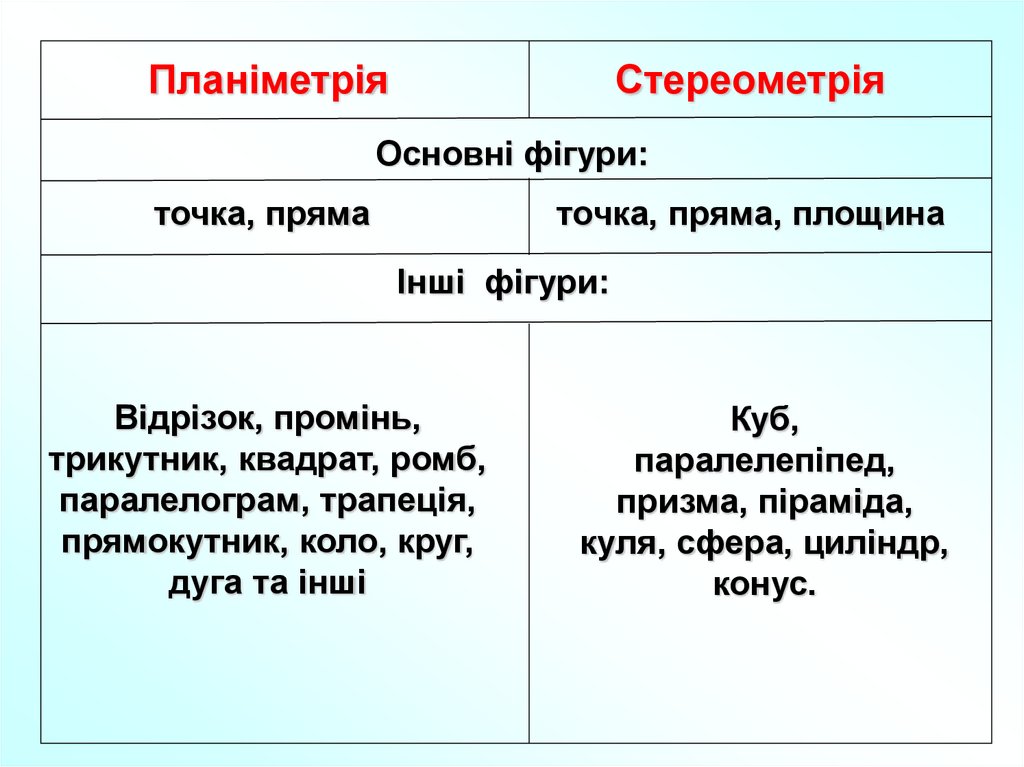
ПланіметріяСтереометрія
Основні фігури:
точка, пряма
точка, пряма, площина
Інші фігури:
Відрізок, промінь,
трикутник, квадрат, ромб,
паралелограм, трапеція,
прямокутник, коло, круг,
дуга та інші
Куб,
паралелепіпед,
призма, піраміда,
куля, сфера, циліндр,
конус.
4.
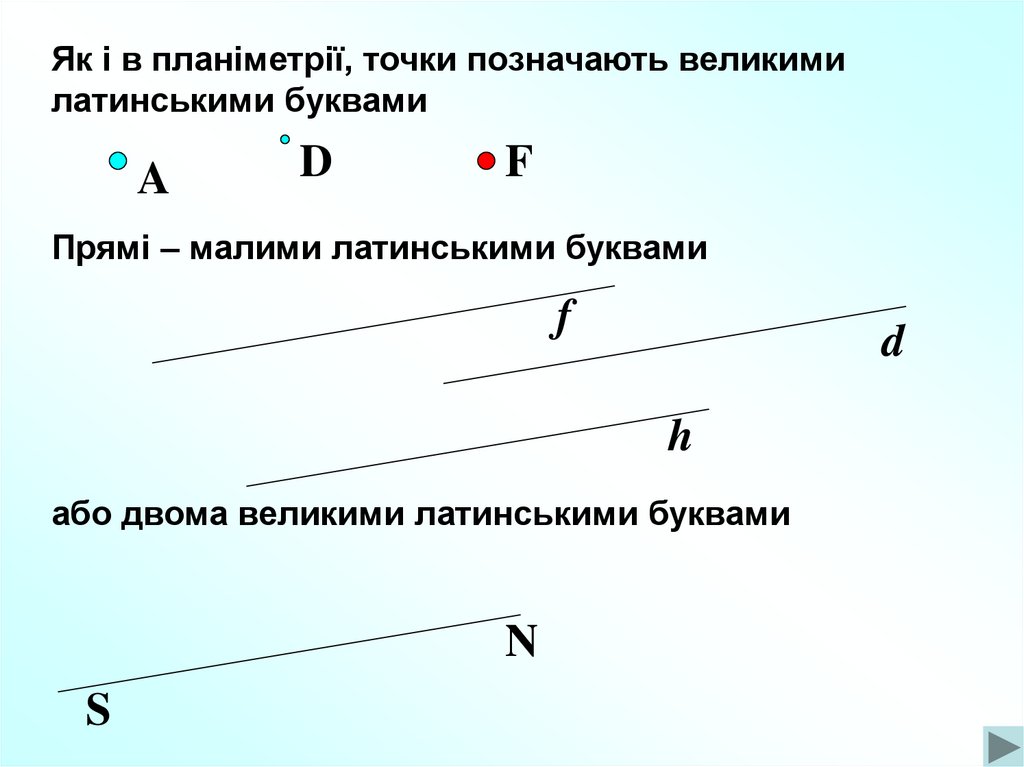
Як і в планіметрії, точки позначають великимилатинськими буквами
A
D
F
Прямі – малими латинськими буквами
f
d
h
або двома великими латинськими буквами
N
S
5.
Площини позначають малими грецькими буквамиНа малюнках площини зображають у вигляді
паралелелограмів. Площини є необмеженими,
ідеально рівними.
6. Математичні символи
• Точка А належитьплощині
• Точка А не
належить площині
• Пряма а лежить в
площині
• Пряма а не лежить
в площині
• Пряма а перетинає
площину в точці А
A
A
a
a
a A
7.
Аксіоми1. Яка б не була площина, існують точки,
що належать цій площині, і точки, які не
належать їй.
D
C
A
B
F
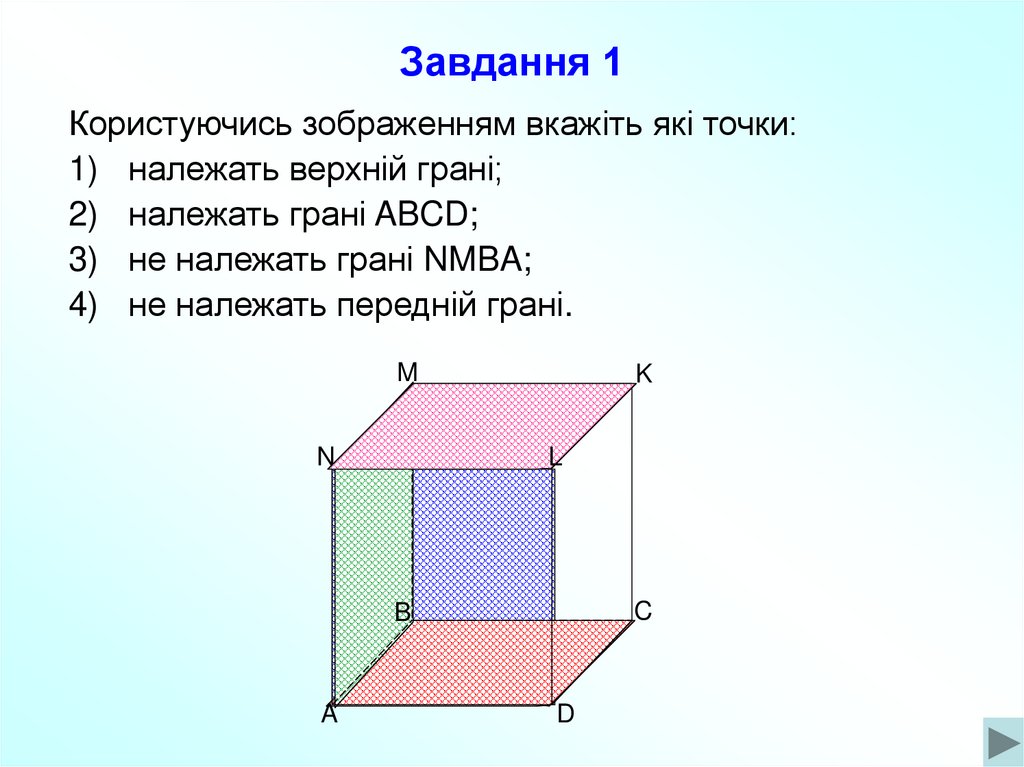
8. Завдання 1
Користуючись зображенням вкажіть які точки:1) належать верхній грані;
2) належать грані ABCD;
3) не належать грані NMBA;
4) не належать передній грані.
M
N
K
L
C
B
A
D
9.
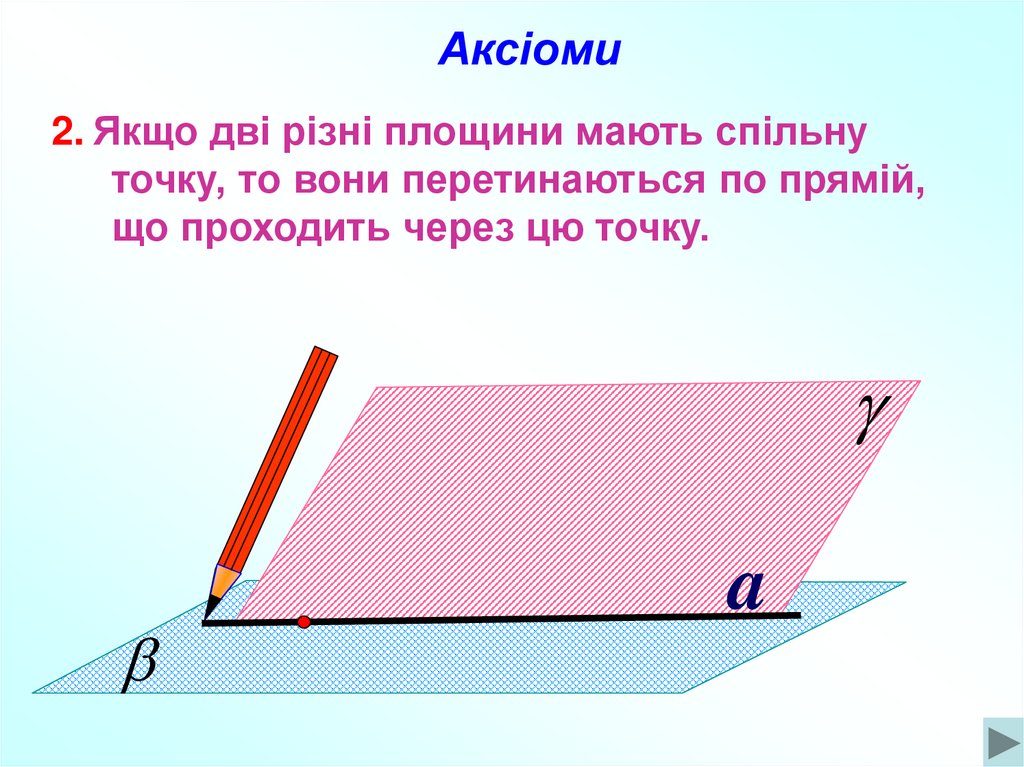
Аксіоми2. Якщо дві різні площини мають спільну
точку, то вони перетинаються по прямій,
що проходить через цю точку.
a
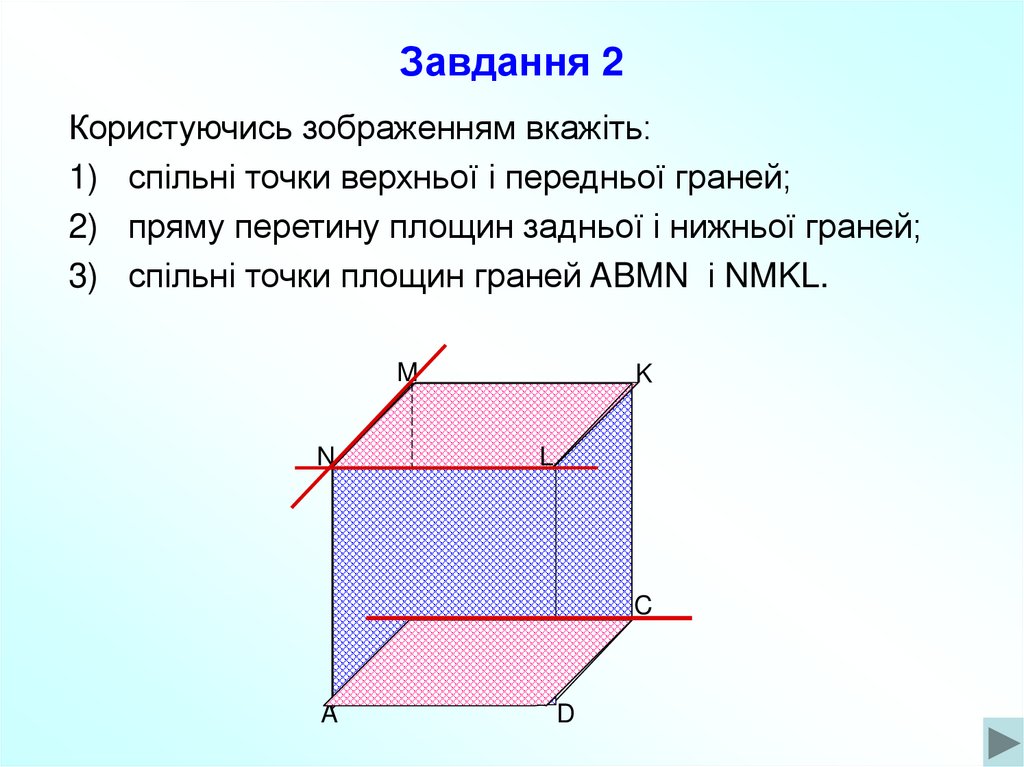
10. Завдання 2
Користуючись зображенням вкажіть:1) спільні точки верхньої і передньої граней;
2) пряму перетину площин задньої і нижньої граней;
3) спільні точки площин граней ABMN і NMKL.
M
N
K
L
C
B
A
D
11.
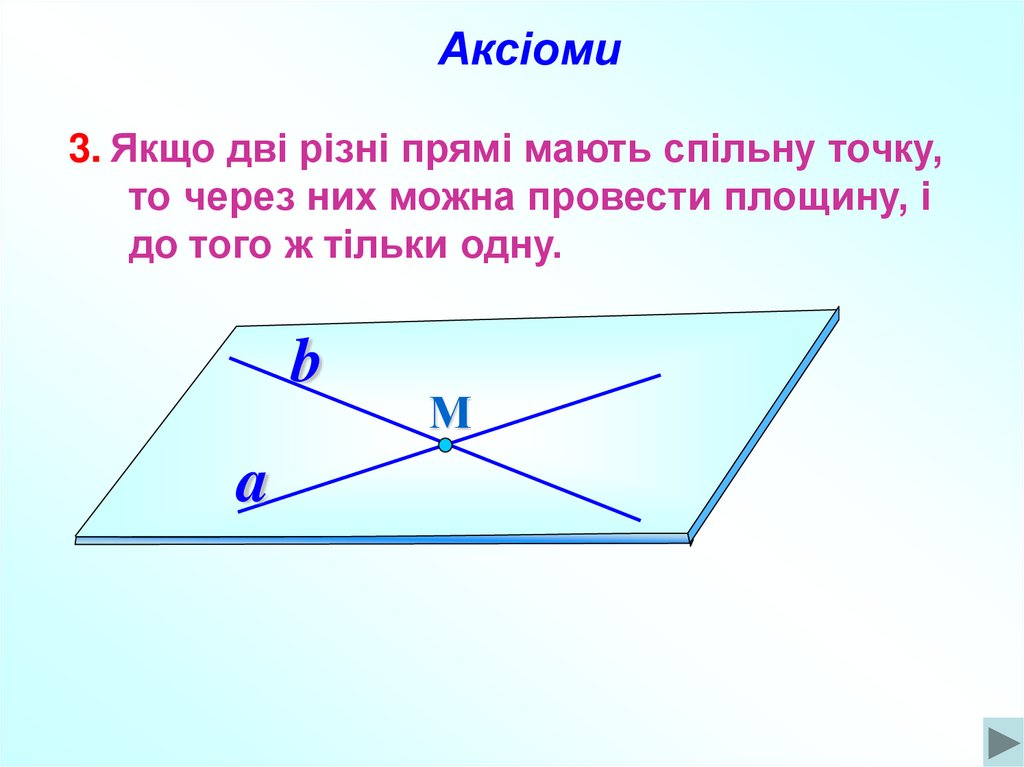
Аксіоми3. Якщо дві різні прямі мають спільну точку,
то через них можна провести площину, і
до того ж тільки одну.
b
a
М
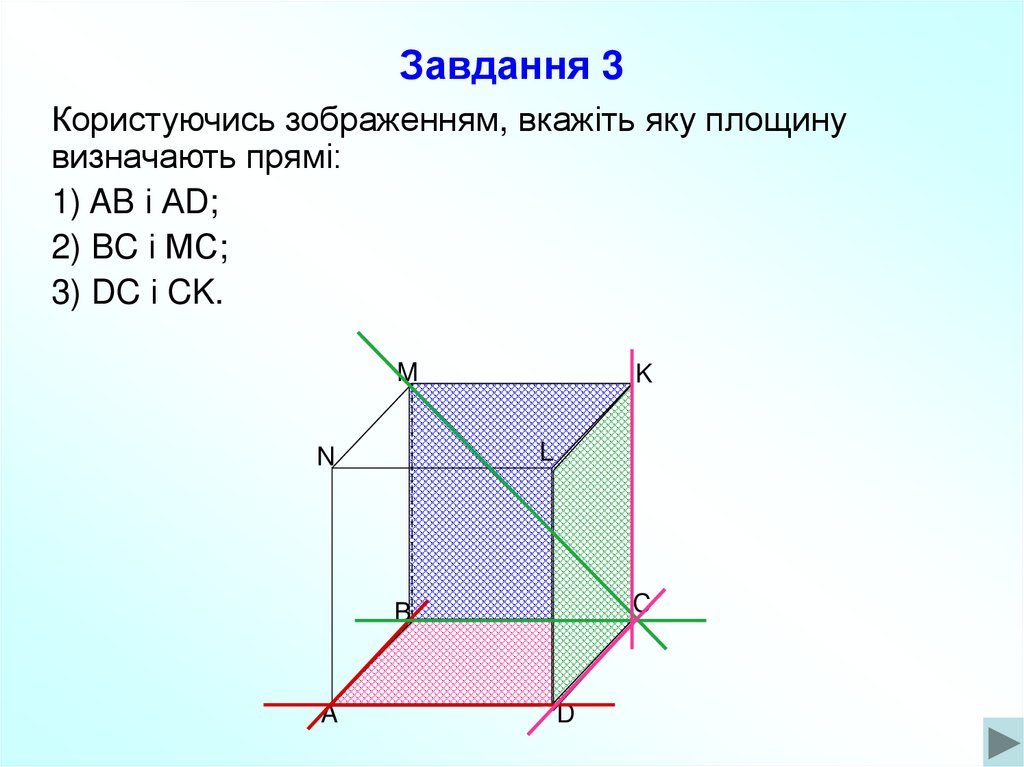
12. Завдання 3
Користуючись зображенням, вкажіть яку площинувизначають прямі:
1) AB і АD;
2) BC і МС;
3) DC і CK.
M
K
L
N
C
B
A
D




 mathematics
mathematics








