Similar presentations:
Гипотеза Максвелла. Ток смещения
1.
Гипотеза Максвелла. Токсмещения.
2.
Гипотеза Максвелла• Электрическое и магнитное
поля образуют единое
электромагнитное поле.
Переменное магнитное поле
порождает электрическое поле
Переменное электрическое
поле должно порождать
магнитное поле.
3.
Ток смещения4.
1. Математический способq
E
d
S
S
0
D
d
S
q
S
5.
Возьмем производную от зарядаdq d
DdS
dt dt S
dq
D
dS
dt S t
6.
I j dSS
D
j
d
S
d
S
S
S t
7.
• Плотность токасмещения в
данной точке
равна скорости
изменения вектора
электрического
смещения в этой
точке
D
jсм
t
8.
Ток смещенияD
I см jcм dS dS
t
S
S
9.
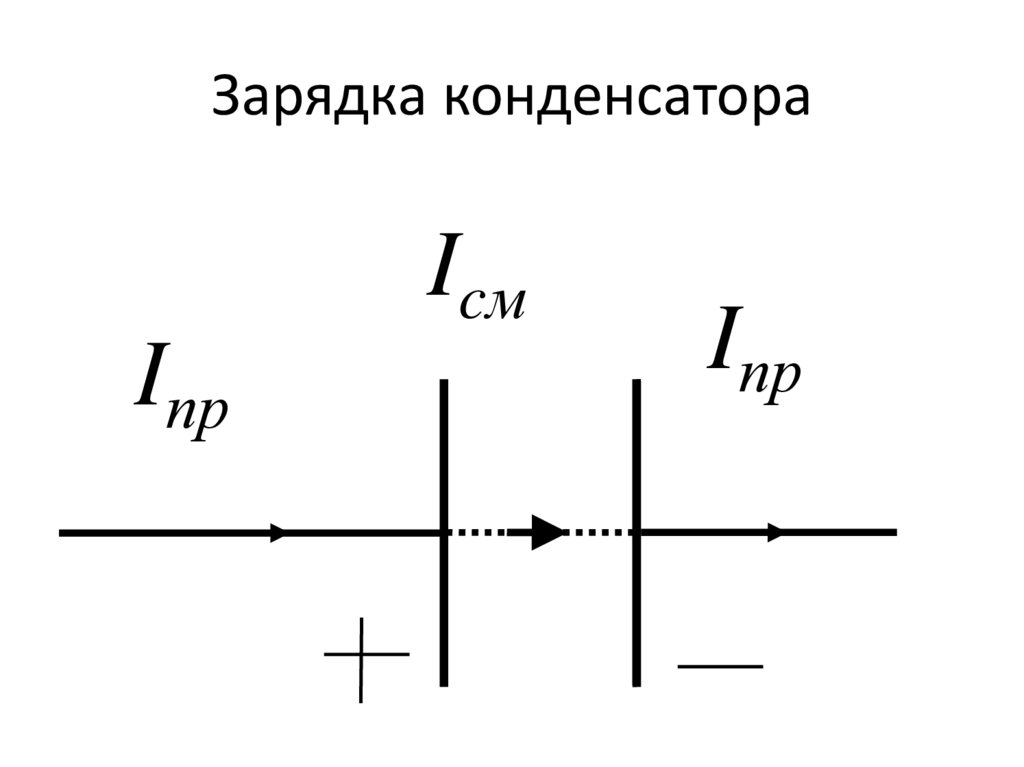
Зарядка конденсатораIcм
Iпр
Iпр
10.
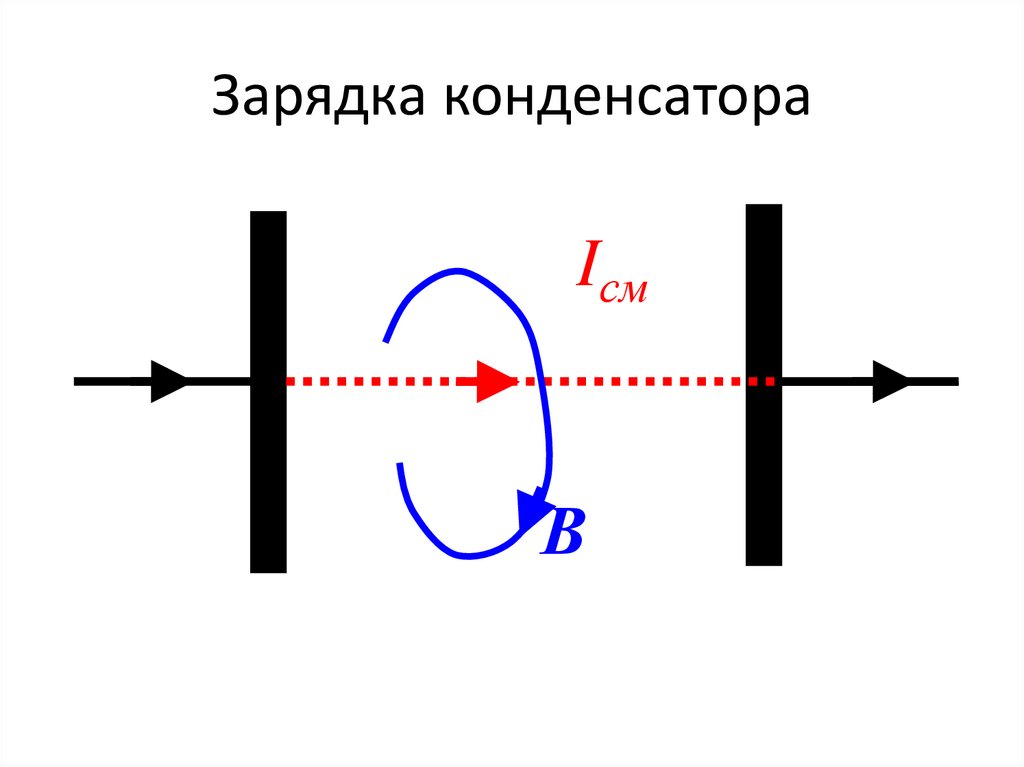
Зарядка конденсатораIсм
В
11.
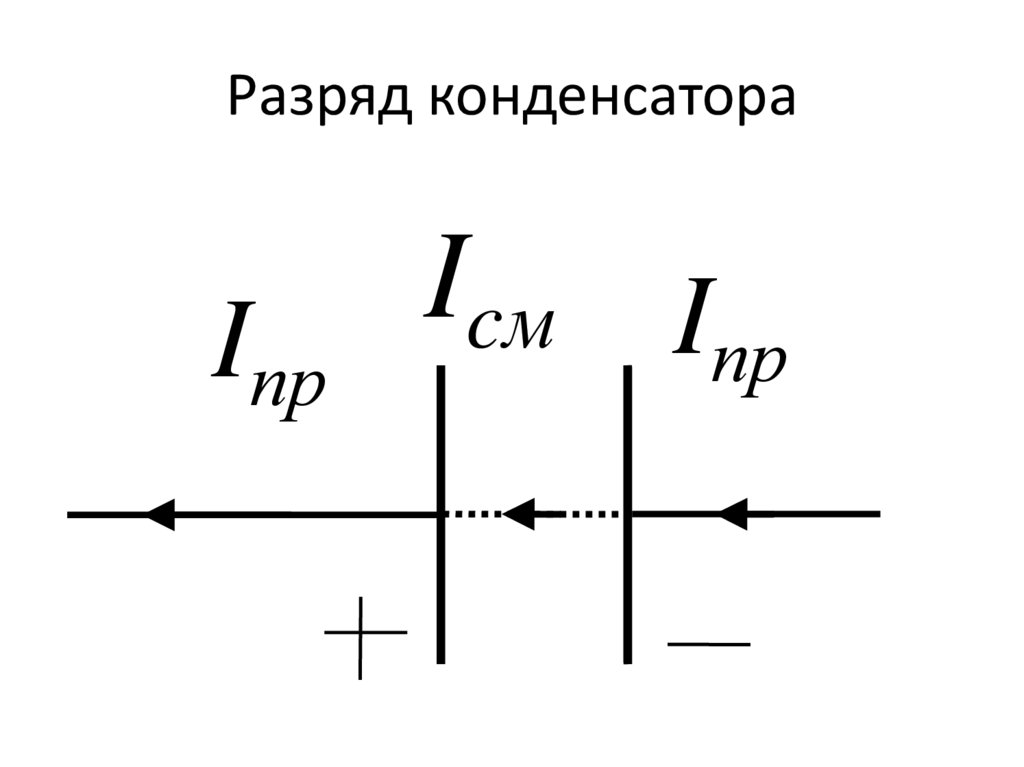
Разряд конденсатораIпр
Icм I
пр
12.
Разряд конденсатораIсм
В
13.
• По проводнику, соединяющемуобкладки, протекает ток
проводимости и этот ток не
проходит сквозь диэлектрик,
находящийся между
обкладками. Цепь замкнута
током смещения, протекающем
там, где нет проводника
14.
Гипотеза Максвелла• Ток смещения, так же, как и ток
проводимости является
источником вихревого
магнитного поля.
15.
Hd
l
(
I
I
)
CM
D
H
d
l
(
j
)
d
S
t
16.
Физический смысл• Источником магнитного поля
могут быть токи проводимости и
изменяющееся электрическое
поле.
17.
В диэлектрикеD 0E P
D
E P
jсм
0
t
t t
18.
• Протекание тока смещения несопровождается джоулевым
теплом
• Могут быть тепловые эффекты,
связанные с поляризацией.
19.
Опыт Эйхенвальда20.
Описание опыта1. Половинки диэлектрического
диска поляризованы в
противоположных направлениях
2. При вращении диска происходит
изменение поляризации
21.
3. При изменении направленияполяризации возникает ток
смещения
4. Магнитное поле этого тока
фиксируется магнитной
стрелкой.
22.
D 0E P23.
• Диск диэлектрический, токапроводимости в нем нет. При
вращении возникает магнитное
поле за счет изменения вектора
электрической индукции (за
счет изменения вектора
поляризации).
24.
Полная системауравнений
Максвелла в
интегральной форме
25.
1. Закон ФарадеяB
E
d
l
d
S
l
S t
26.
Математическая формулировка• Циркуляция вектора
напряженности электрического
поля по замкнутому контуру равна
скорости изменения магнитного
потока через поверхность,
натянутую на этот контур
27.
Физический смысл• Изменяющееся со временем
магнитное поле создает
электрическое поле вихревого
типа.
28.
2. Закон полного токаD
H
d
l
j
d
S
l
S np t
29.
Математическая формулировка• Циркуляция вектора магнитной
напряженности по замкнутому
контуру равна сумме тока
проводимости и скорости изменения
потока вектора электрического
смещения через поверхность,
натянутую на этот контур.
30.
Физический смысл• Магнитное поле создается
токами проводимости и
изменяющимся потоком
электрического смещения
31.
3. Теорема Гаусса для электрическогополя
D
d
S
dV
q
S
V
32.
Математическая формулировка• Поток вектора электрического
смещения через замкнутую
поверхность равен
электрическому заряду,
находящемуся внутри этой
поверхности.
33.
Физический смысл• Источником электрического
поля являются электрические
заряды.
34.
4. Теорема Гаусса для магнитного поляB
d
S
0
S
35.
Математическая формулировка• Поток вектора магнитной
индукции через замкнутую
поверхность равен нулю
36.
Физический смысл• Магнитных зарядов в природе
не существует
37.
5. Система материальных уравненийj E
D 0 E
B 0 H
38.
Основные понятиятеории поля
39.
1. Градиент скалярной функции• Вектор, показывающий
направление, в котором
функция возрастает быстрее
всего
40.
x, y, z скалярнаяфункция
;
;
координаты
x y z
градиента
41.
ij
k grad
x
y
z
42.
ПримерыE grad
F gradWпот
43.
Операторi j k
x
y
z
44.
Градиентgrad
Операторная форма записи
E
F Wnom
45.
gradi
j k
x
y
z
46.
2. Поток вектора• Скалярная величина,
пропорциональная числу линий
вектора, пересекающего данную
площадку
47.
An
dS
d A A dS
48.
Вектор площадкиdS dS n
n 1
49.
Поток вектораA A dS
S
50.
ПримерыM BdS
S
E EdS
S
51.
3. Дивергенция вектораz
A
S
x
y
52.
Сжимаем поверхность в точку(уменьшаем объем)
A
div
A
lim
V 0 V
53.
Дивергенция вектораd A
divA
dV
54.
Ax Ay Azdiv A
x y z
div A ( A)
55.
• Дивергенция – скалярнаявеличина. Может быть
положительной,
отрицательной и равной
нулю.
56.
• Если в данной точкеdivА>0, то в данной точке
имеется источник поля А
(линии выходят наружу)
57.
• Если в данной точкеdivA<0, то в данной точке
имеется сток поля А
(линии входят внутрь)
58.
• Если в данной точкеdivА=0, то в данной
точке источников и
стоков поля А нет.
59.
4. Циркуляция вектора60.
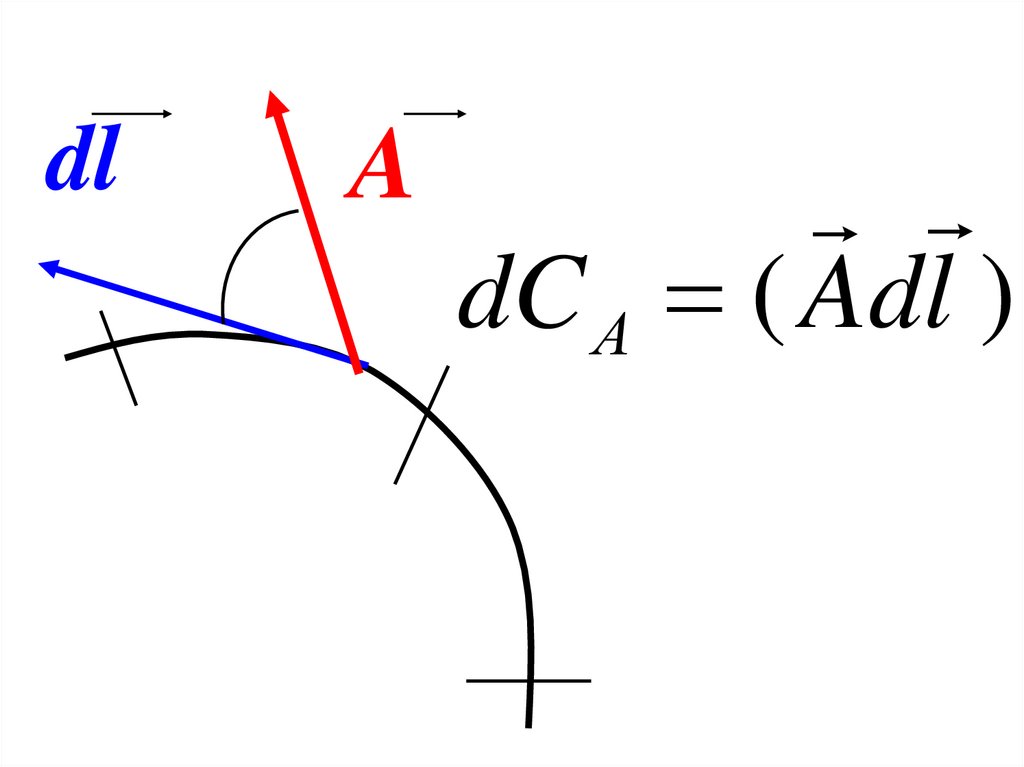
dlA
dC А ( Adl )
61.
Циркуляция вектора АC А A dl
l
62.
• Если циркуляция вектора равнанулю, то линии этого вектора не
замкнутые, имеют начало и
конец, либо уходят в
бесконечность
• Если циркуляция вектора не
равна нулю, то линии вектора
замкнутые
63.
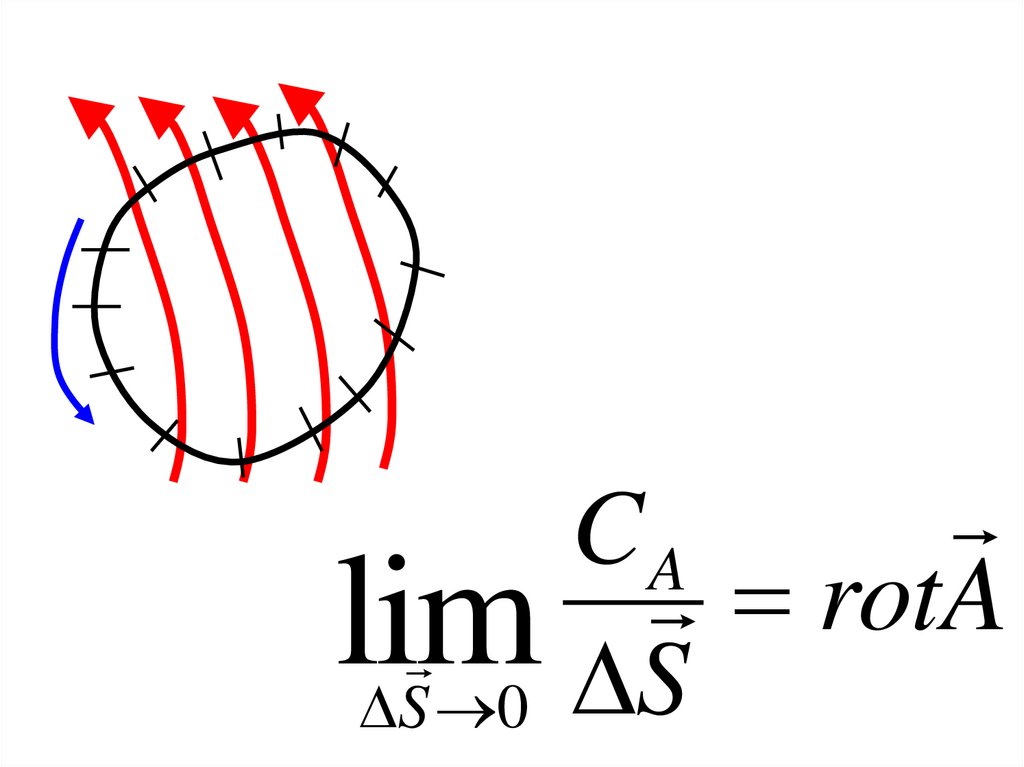
5. Ротор (вихрь) вектора• Контур интегрирования будем
стягивать в точку
64.
CArot
A
lim
S 0 S
65.
Ротор вектора АdC А
rotA A
dS
66.
iA
x
Ax
j
y
Ay
k
z
Az
67.
Ротор вектора А• Если ротор не равен нулю,
то в данной точке
существует поле вихревого
типа, линии которого
замкнуты.
68.
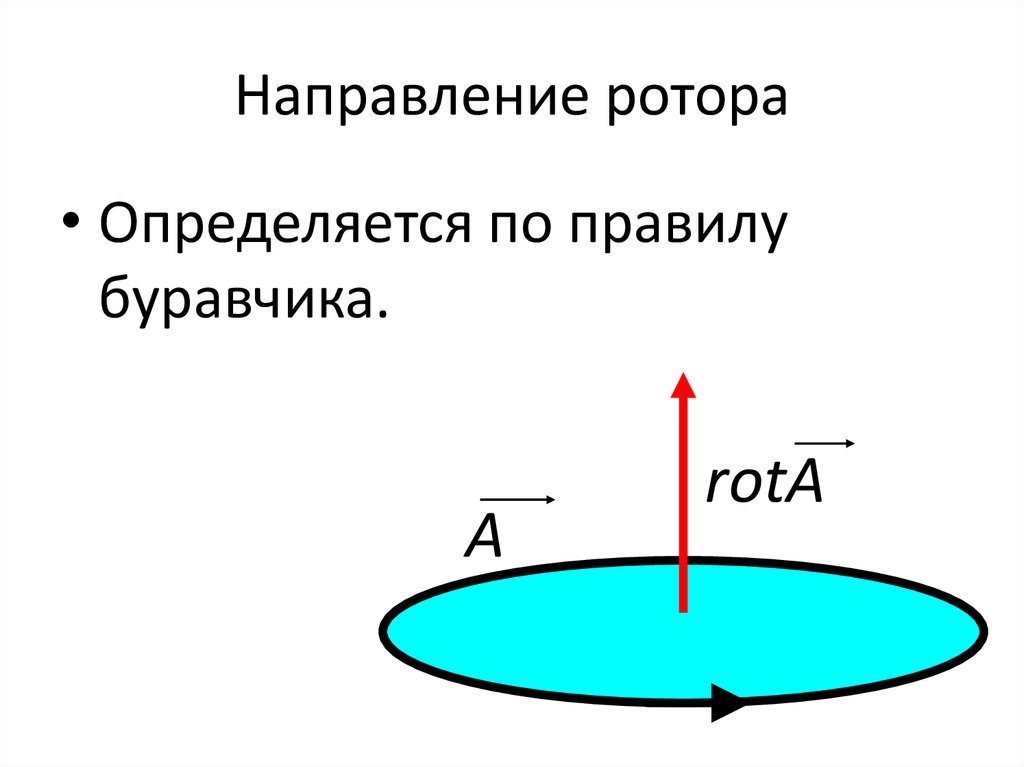
Направление ротора• Определяется по правилу
буравчика.
A
rotA
69.
Две теоремы70.
Теорема ГауссаA
d
S
div
A
dV
S
V
71.
• Поток вектора А череззамкнутую поверхность равен
дивергенции вектора А по
всему объему, ограниченному
этой поверхностью
72.
Теорема СтоксаA
d
l
(
rot
A
d
S
)
l
S
73.
• Циркуляция вектора А позамкнутому контуру равна
потоку ротора вектора А через
площадку, ограниченную этим
контуром
74.
Система уравненийМаксвелла в
дифференциальной и
операторной формах
75.
1. Закон Фарадея• Изменяющееся магнитное
поле создает электрическое
поле вихревого типа.
76.
BE
d
l
d
S
l
S t
77.
Применим теорему СтоксаЕ
d
l
(
rot
Е
d
S
)
l
S
78.
BrotE
t
B
E
t
79.
2. Закон полного тока• Источником магнитного поля
являются токи проводимости и
изменяющееся электрическое
поле
80.
DH
d
l
(
j
)
d
S
l
S t
81.
Нd
l
(
rot
Н
d
S
)
l
S
82.
DrotH j
t
D
H j
t
83.
3. Теорема Гаусса дляэлектрического поля
• Источником электрического
поля являются электрические
заряды
84.
Dd
S
dV
q
S
V
85.
Применим теорему ГауссаD
d
S
div
D
dV
S
V
86.
div D q( D ) q
87.
4. Теорема Гаусса для магнитного поля• Магнитных зарядов в природе
нет
88.
Bd
S
0
S
89.
Применим теорему ГауссаВ
d
S
div
В
dV
S
V
90.
div B 0( B ) 0
91.
Система материальных уравненийD 0 E
B 0 H
j E





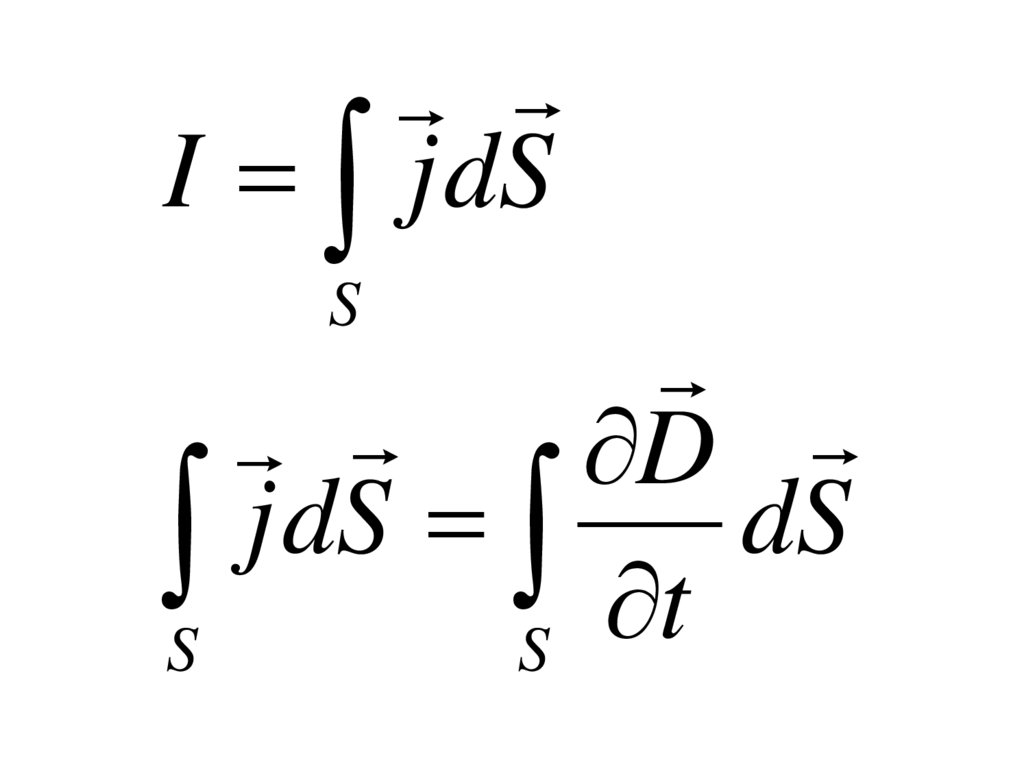































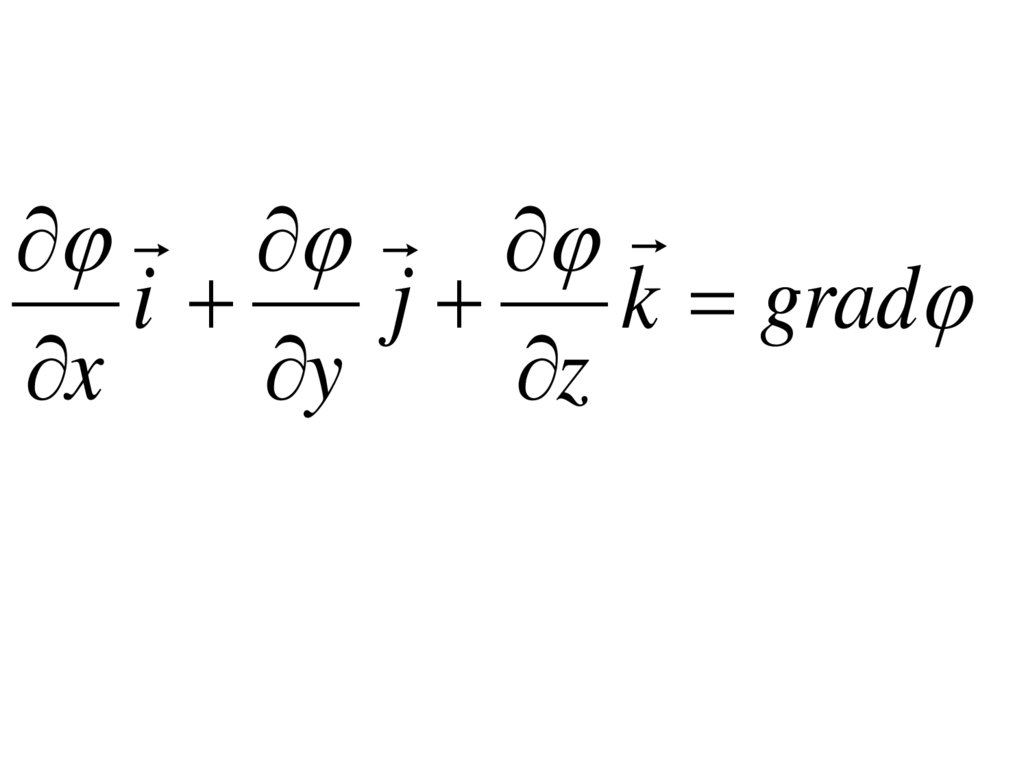
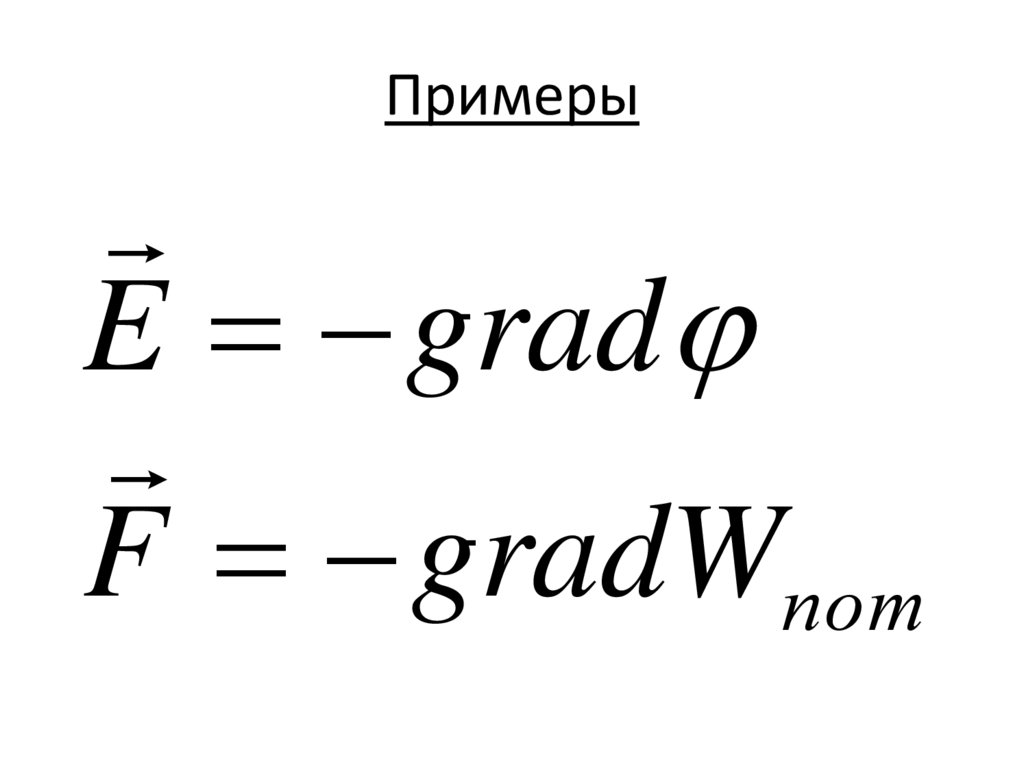





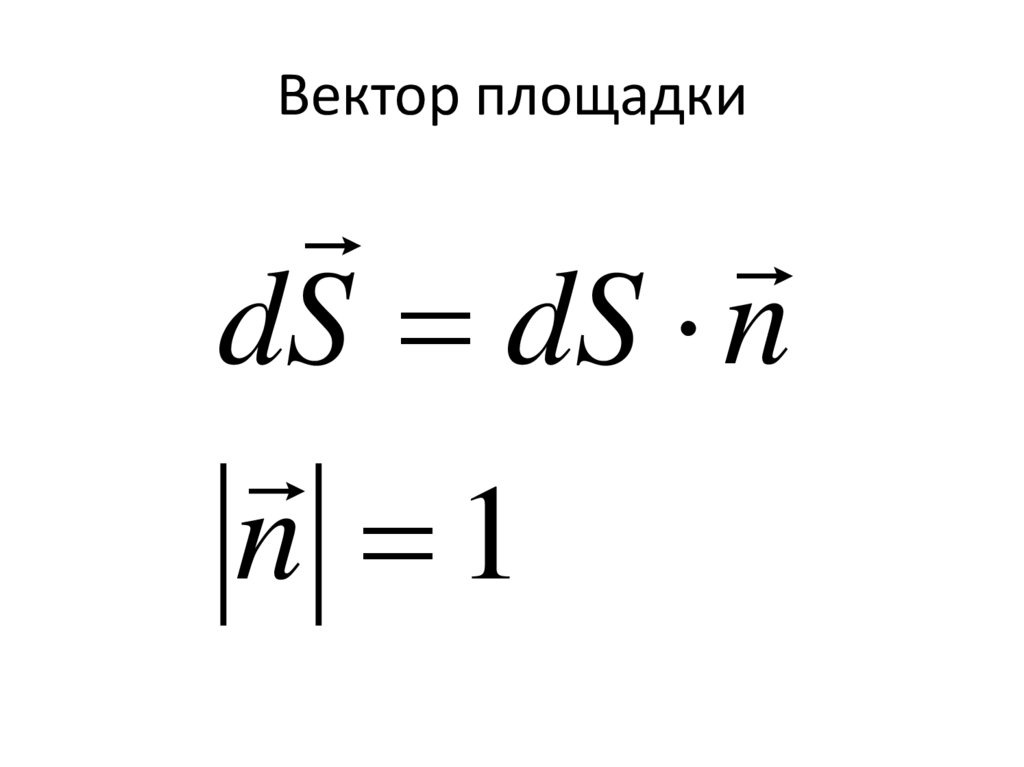

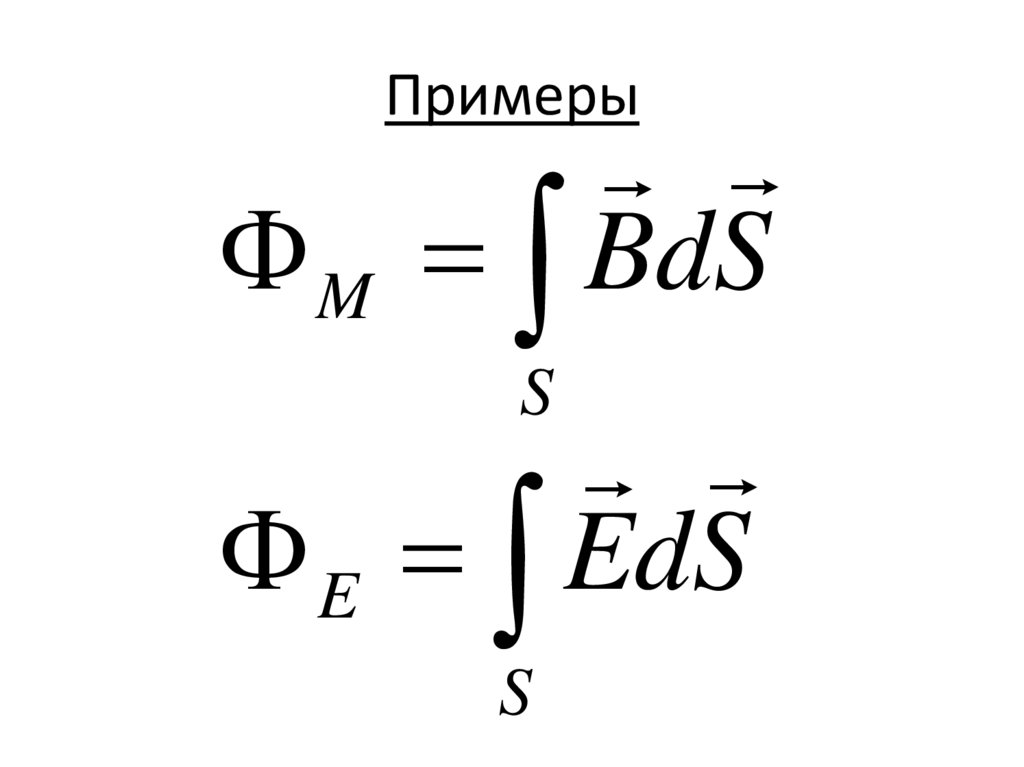



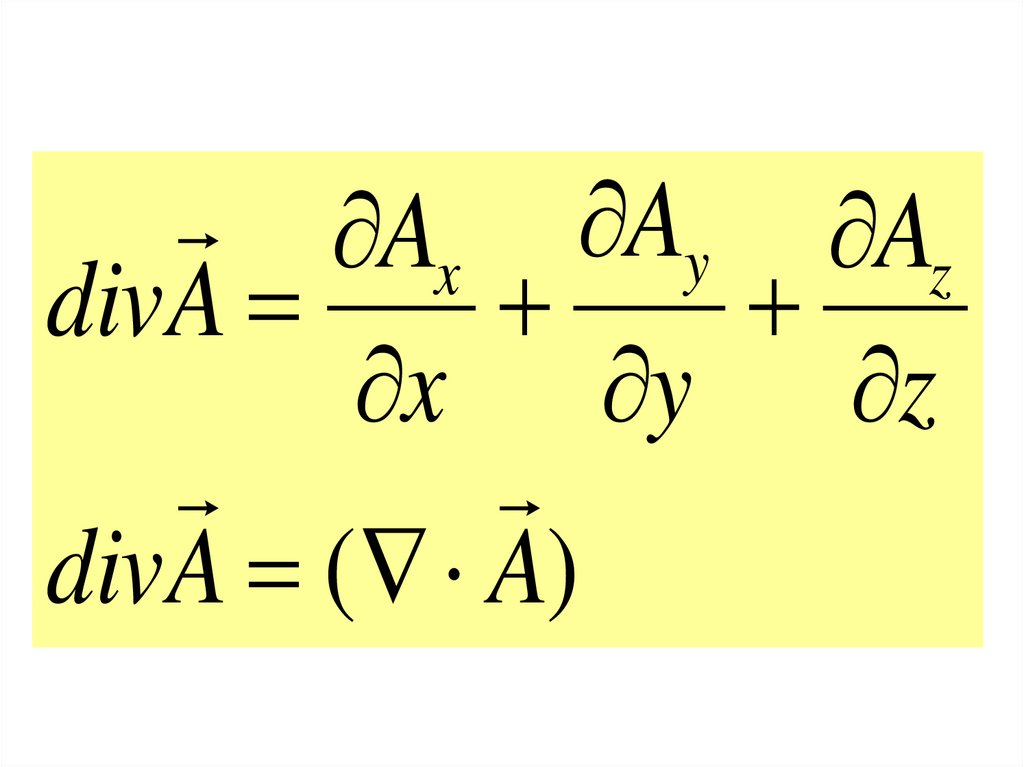




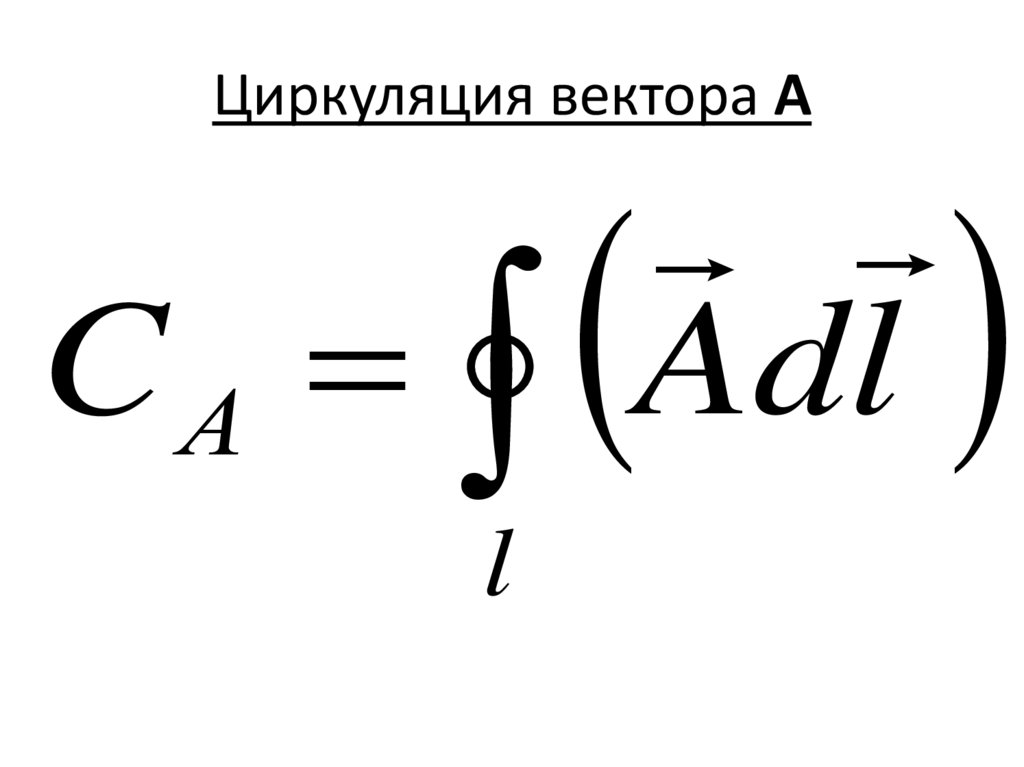



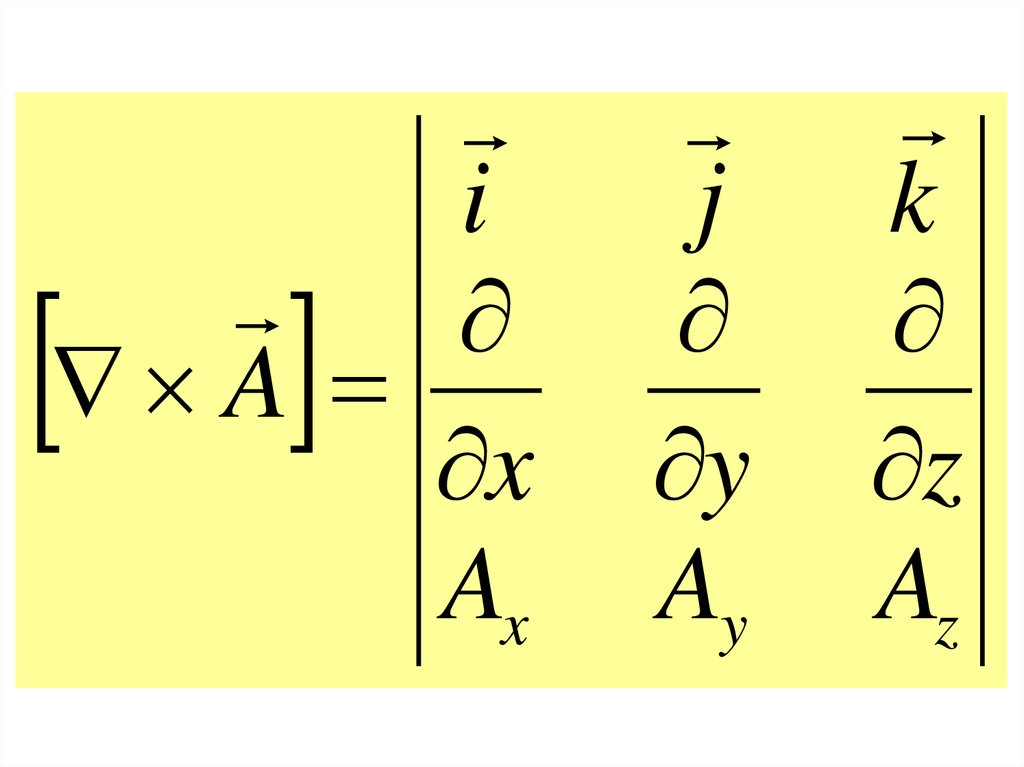








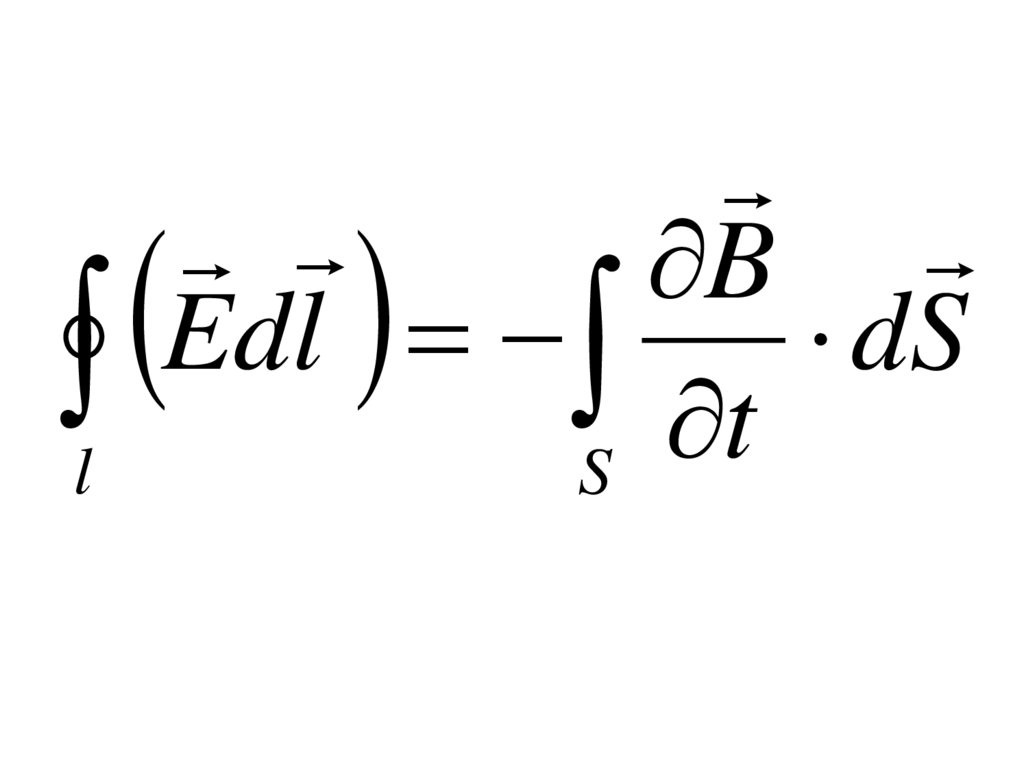
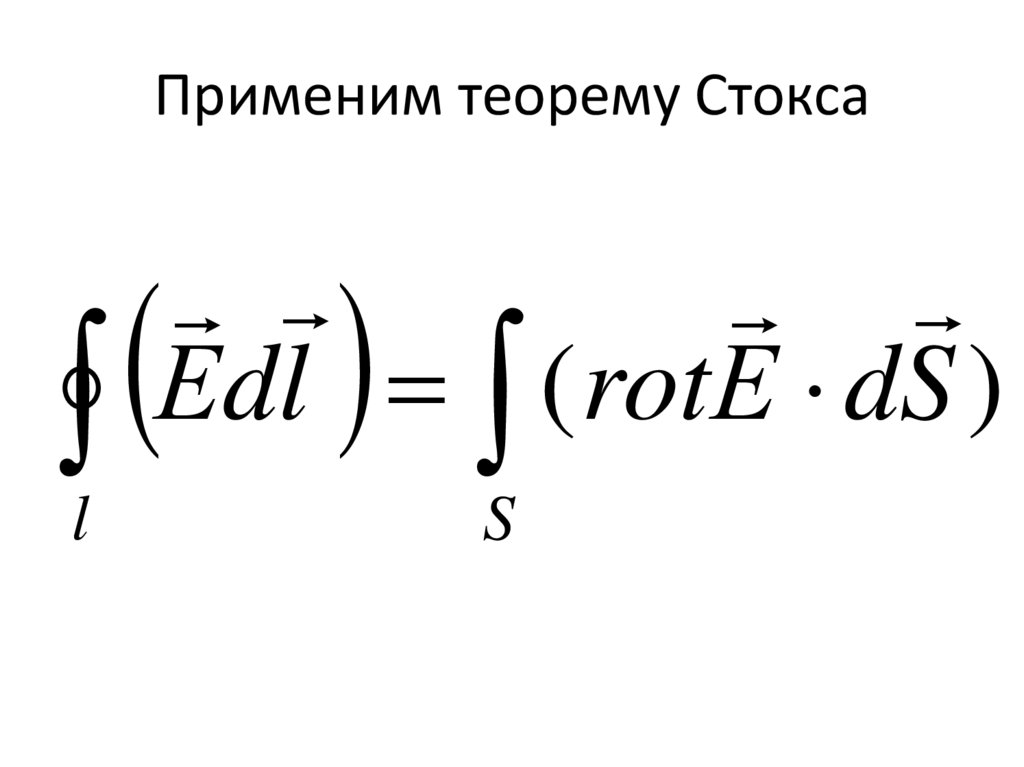




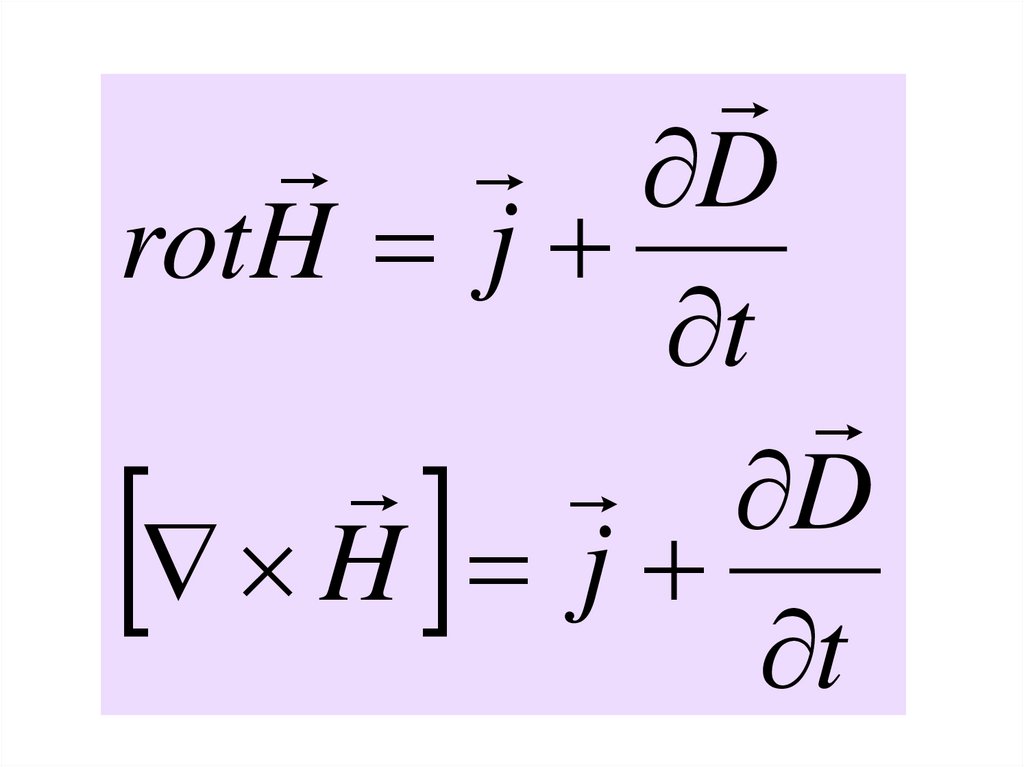



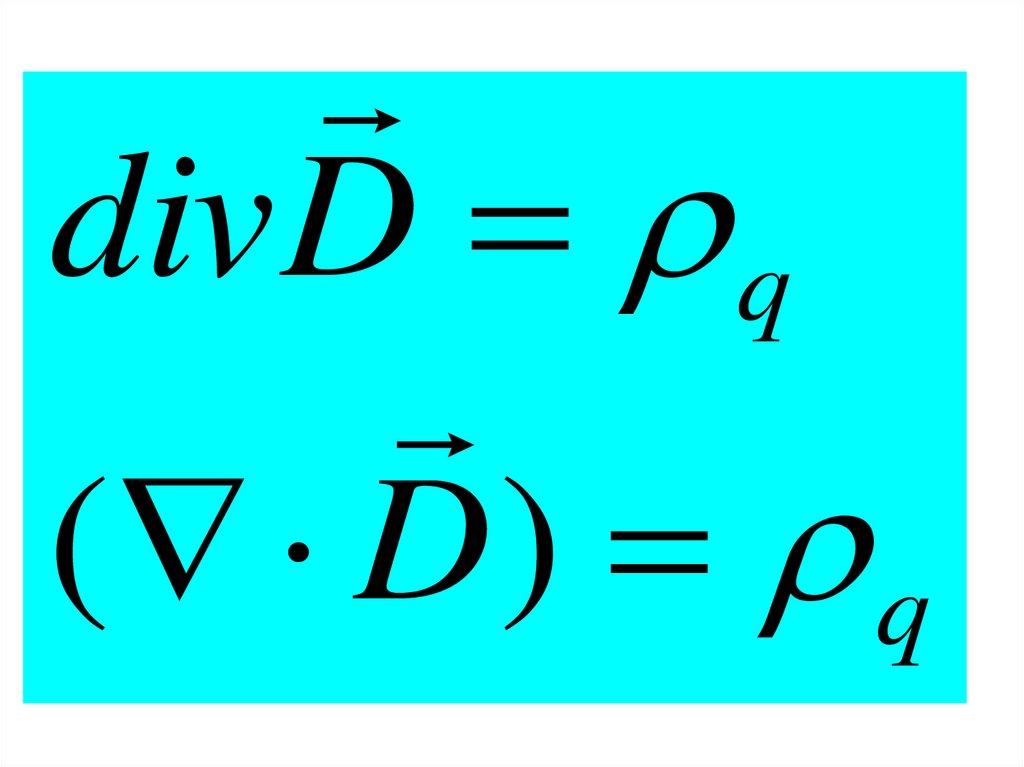

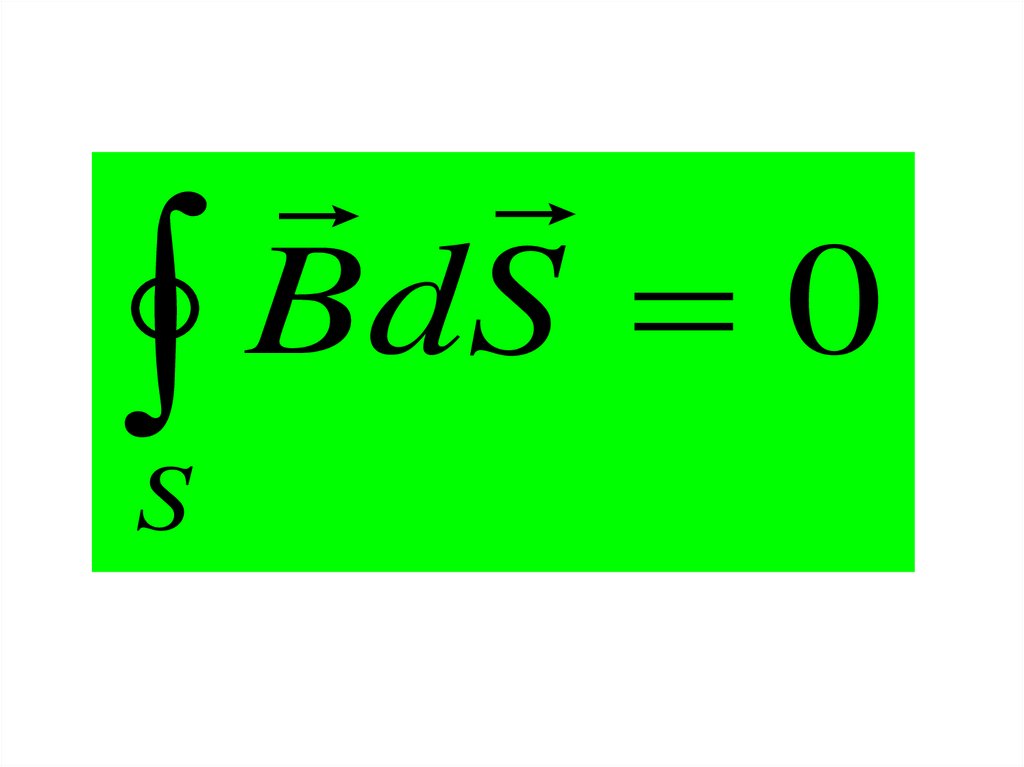

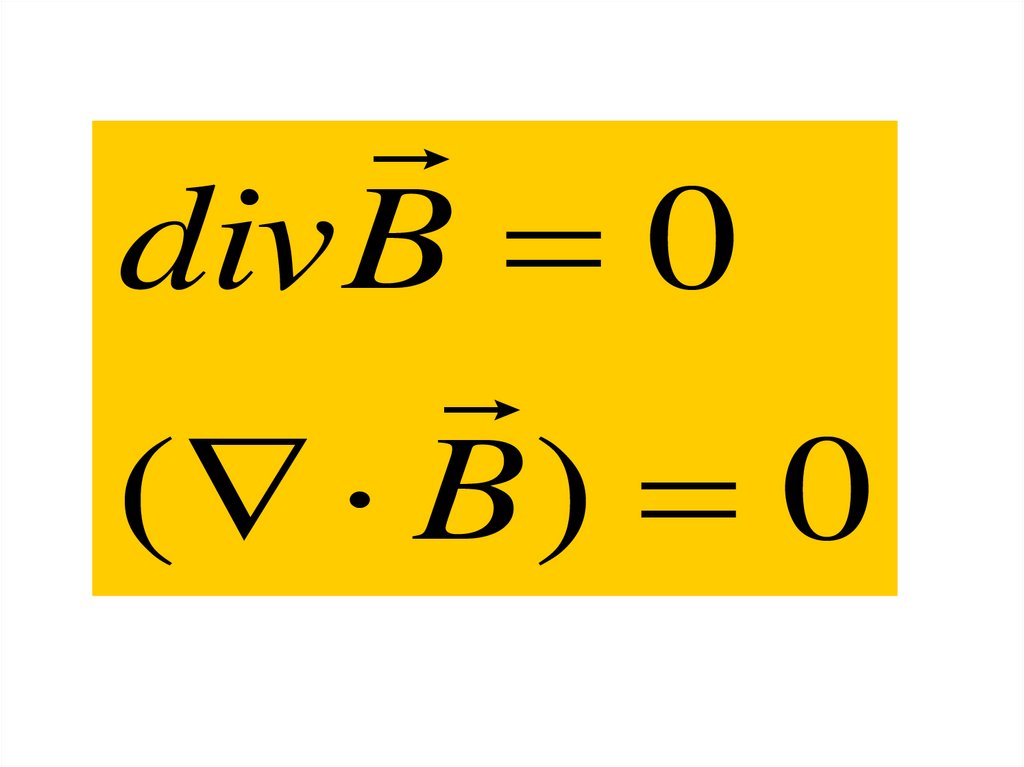

 physics
physics








