Алгоритмы и структуры данных

1. НИУ Высшая школа экономики Кафедра управления разработкой программного обеспечения

Алгоритмы и структуры
данных
2022-2023 учебный год
Нестеров Роман Александрович, PhD & Бессмертный Александр Игоревич
Департамент программной инженерии

2. Содержание курса

Do right things
Do things right

3. Алгоритмы и структуры данных

Основная литература
Хопкрофт Дж., Мотвани Р., Ульман Дж.
Введение в теорию автоматов, языков и
вычислений: Пер. с англ. - М.:
Издательский дом "Вильямс", 2008.
5

4. Do right things Do things right

Формальный язык
• Алфавит языка:
– Множество символов (букв)
• Язык – множество строк
• Строка (слово) :
– Последовательность символов
Примеры: “студент”, “123”, “house”, …
a , b , c , , z
6

5. Основная литература

Алфавит и строки
• Будем использовать алфавит из двух букв
a, b
• Строки (слова)
a
ab
abba
baba
u ab
v bbbaaa
w abba
aaabbbaabab
7

6. Формальный язык

Операции над строками
v b1b2 bm
w a1a2 an
v bbbaaa
w abba
• Конкатенация
wv a1a2 an b1b2 bm
wv abbabbbaaa
• Обращение
v
R
bm b2b1
v
R
aaabbb
8

7. Алфавит и строки

Итерация
w n ww
w
n
• Пример:
2
abba abbaabba
• Для любого слова w :
w
0
abba 0
9

8. Операции над строками

Операция *
• *- множество всех возможных слов в
алфавите
• Пример:
a , b
* , a , b , aa , ab , ba , bb , aaa , aab ,
*
a , b , aa , ab , ba , bb, aaa , aab ,
• Тогда язык в алфавите – любое
подмножество *
10

9. Итерация

Пример бесконечного языка
n n
L a b :n 0
ab
aabb
L
abb L
aaaaabbbbb
11

10. Операция *

Операции над языками
• Обычные теоретико-множественные операции:
a , ab, aaaa bb, ab {a , ab, bb, aaaa }
a , ab, aaaa bb, ab {ab }
a , ab, aaaa bb, ab a , aaaa
• Дополнение:
L * L
a , ba , b, aa , ab, bb, aaa ,
12

11. Пример бесконечного языка

Обращение, конкатенация
LR w R : w L
ab, aab, baba R ba , baa , abab
L1L2 xy : x L1 , y L2
a , ab, ba b, aa
ab , aaa , abb , abaa , bab , baaa
13

12. Операции над языками

Итерация
n
L LL
L
n
• Пример:
3
a , b a , b a , b a , b
aaa , aab , aba , abb, baa , bab, bba , bbb
• Специальный случай:
0
L
0
a , bba , aaa
14

13. Обращение, конкатенация

Еще пример
2
n n m m
L a b a b : n , m 0
L a n bn : n 0
2
aabbaaabbb L
15

14. Итерация

Замыкание * (звезда Клини)
0
1
2
L* L L L
• Пример:
,
a , bb ,
a , bb *
aa , abb , bba , bbbb,
aaa , aabb , abba , abbbb ,
16

15. Еще пример

Языки и автоматы

16. Замыкание * (звезда Клини)

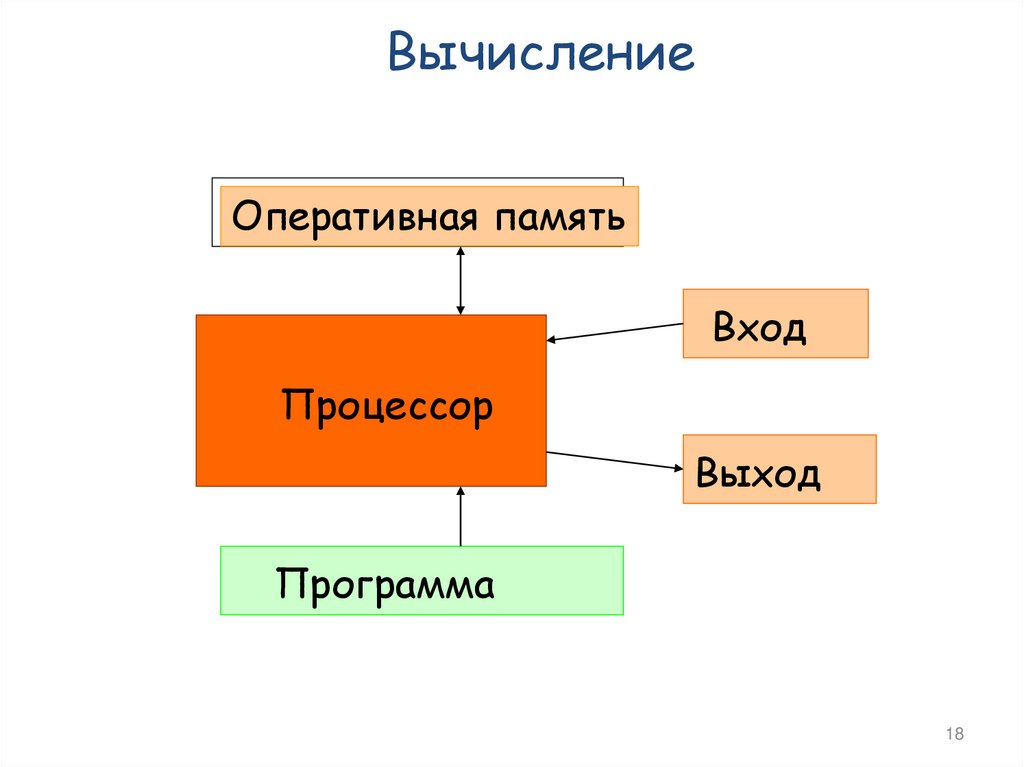
Вычисление
Оперативная память
Вход
Процессор
Выход
Программа
18

17. Языки и автоматы

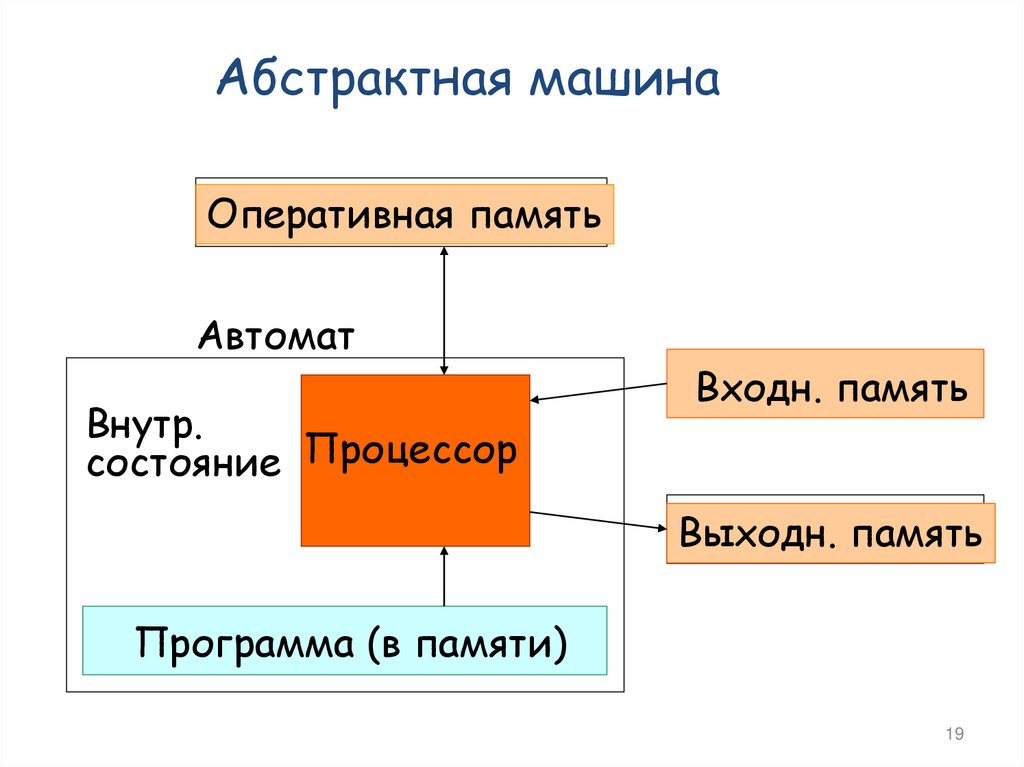
Абстрактная машина
Оперативная память
Автомат
Внутр.
состояние Процессор
Входн. память
Выходн. память
Программа (в памяти)
19

18.

Виды автоматов
В зависимости от оперативной памяти
• конечные автоматы
Нет оперативной памяти
• магазинные (стековые) автоматы
Стек
• машины Тьюринга
‘Неограниченная’ память
20

19.

Конечный автомат
Оперативная память
Конечный
автомат
Входн. память
Выходн. память
Слабые вычислительные возможности
21

20.

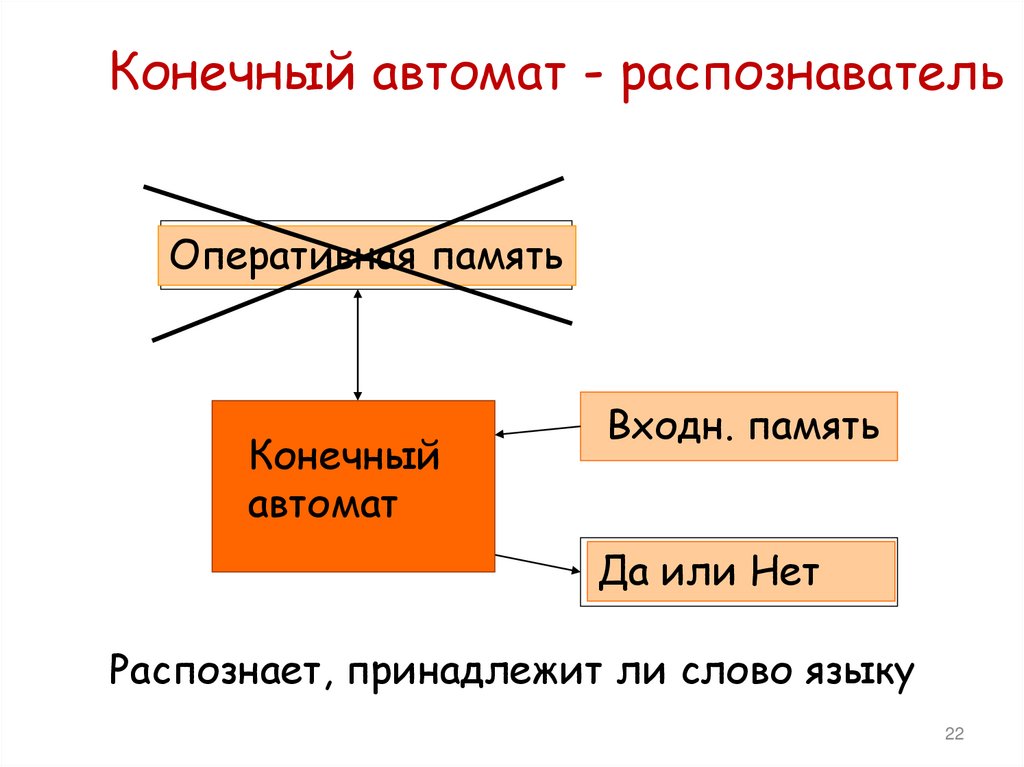
Конечный автомат - распознаватель
Оперативная память
Конечный
автомат
Входн. память
Да или Нет
Распознает, принадлежит ли слово языку
22

21.

Автомат-распознаватель
Вход
Строка
Конечный
автомат
Выход
“Да”
или
“Нет”
23

22.

Граф переходов автомата
аbba - распознаватель
a, b
q5
b
q0 a
a
a
b
q1 b q2 b q3 a
начальное
состояние
переход
состояние
a, b
q4
финальное
состояние
“Да”
24

23. Автомат-распознаватель

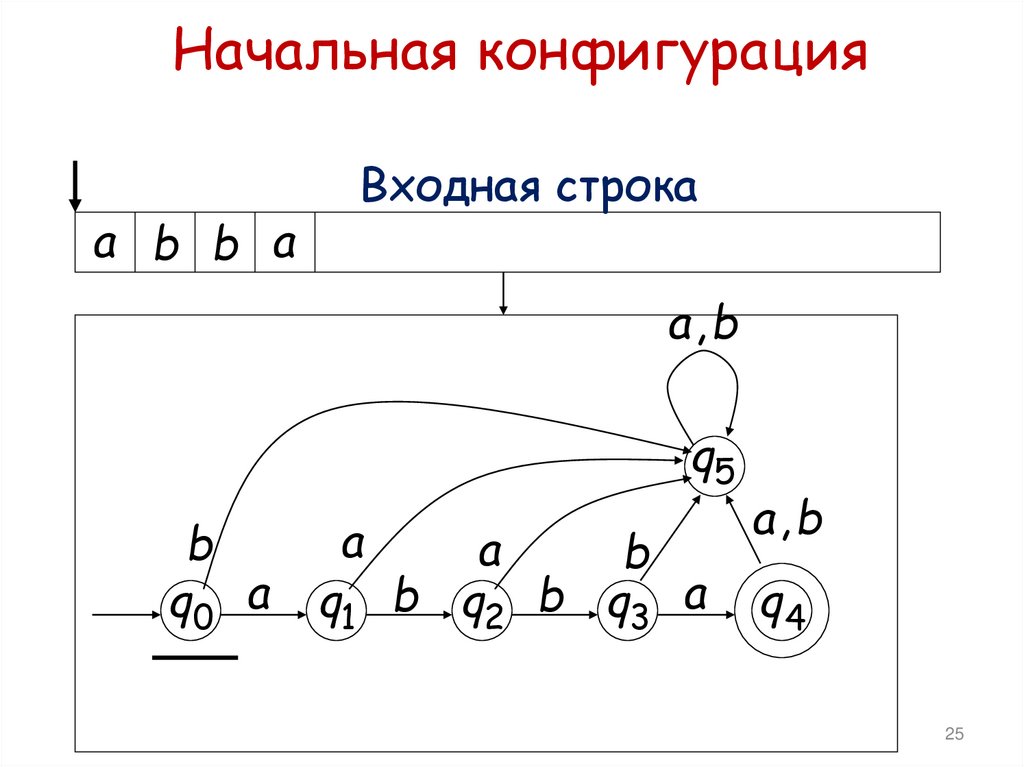
Начальная конфигурация
a b b a
Входная строка
a, b
q5
b
q0 a
a
a
b
q1 b q2 b q3 a
a, b
q4
25

24. Граф переходов автомата

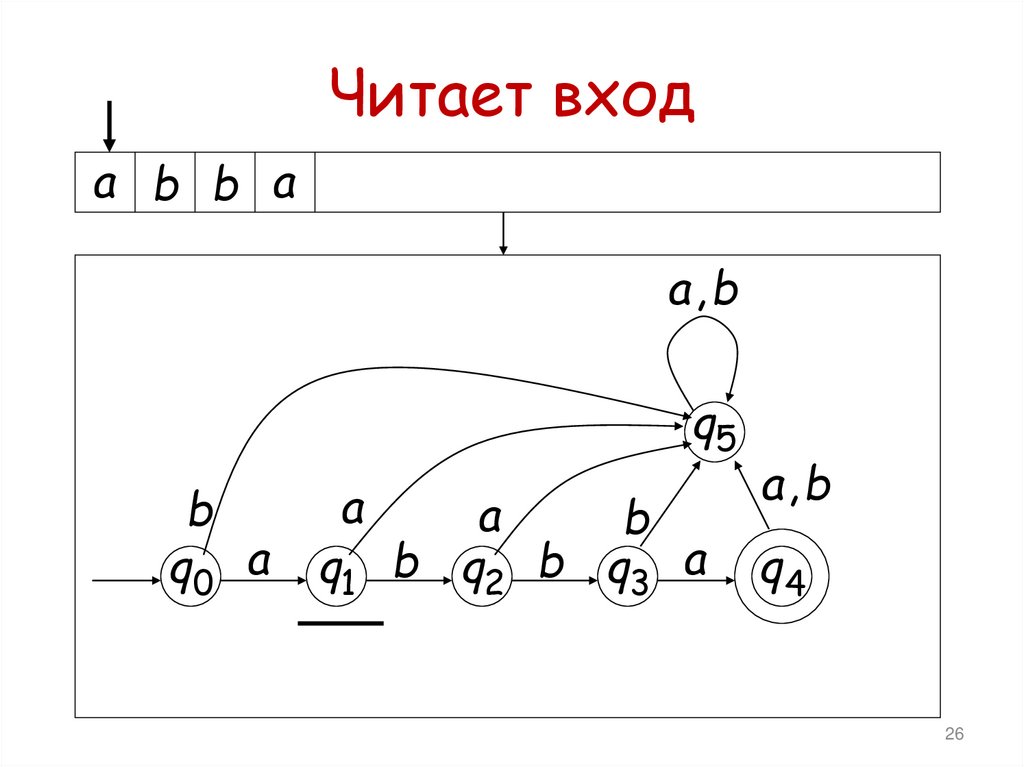
Читает вход
a b b a
a, b
q5
b
q0 a
a
a
b
q1 b q2 b q3 a
a, b
q4
26

25. Начальная конфигурация

a b b a
a, b
q5
b
q0 a
a
a
b
q1 b q2 b q3 a
a, b
q4
27

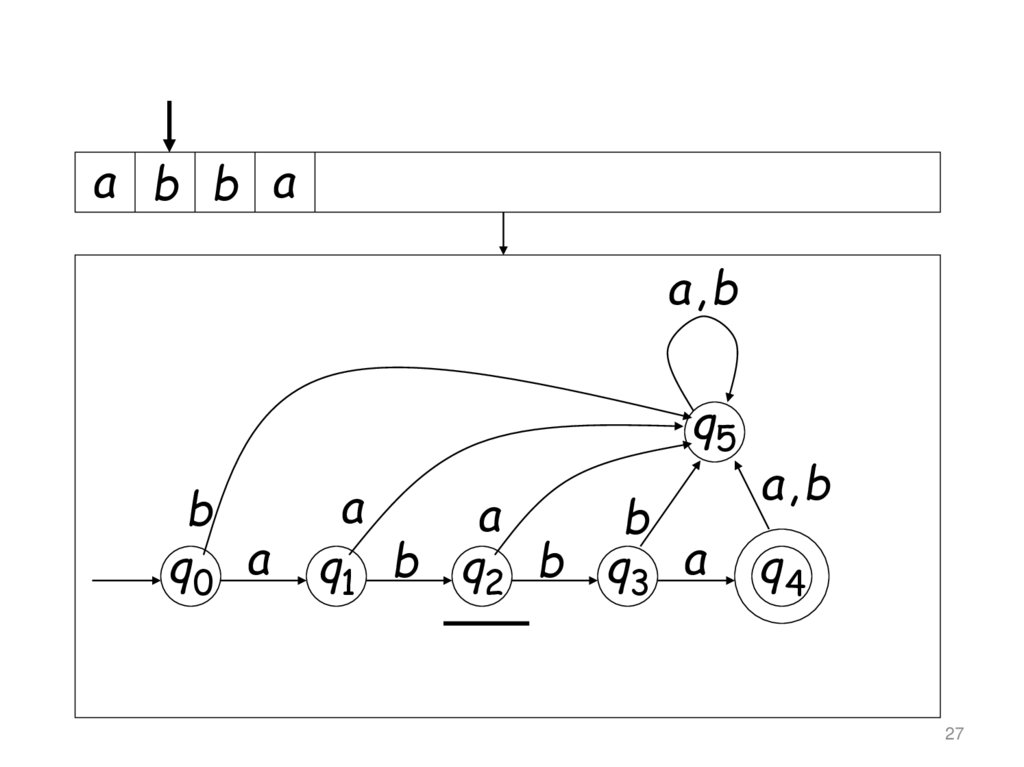
26. Читает вход

a b b a
a, b
q5
b
q0 a
a
a
b
q1 b q2 b q3 a
a, b
q4
28

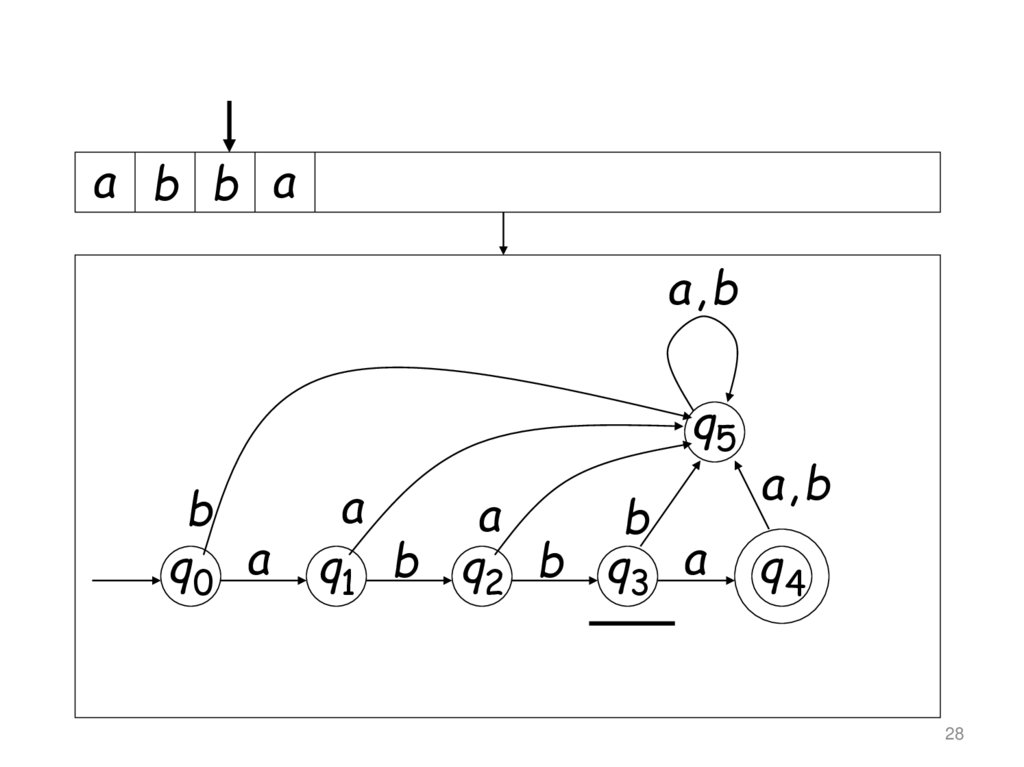
27.

a b b a
a, b
q5
b
q0 a
a
a
b
q1 b q2 b q3 a
a, b
q4
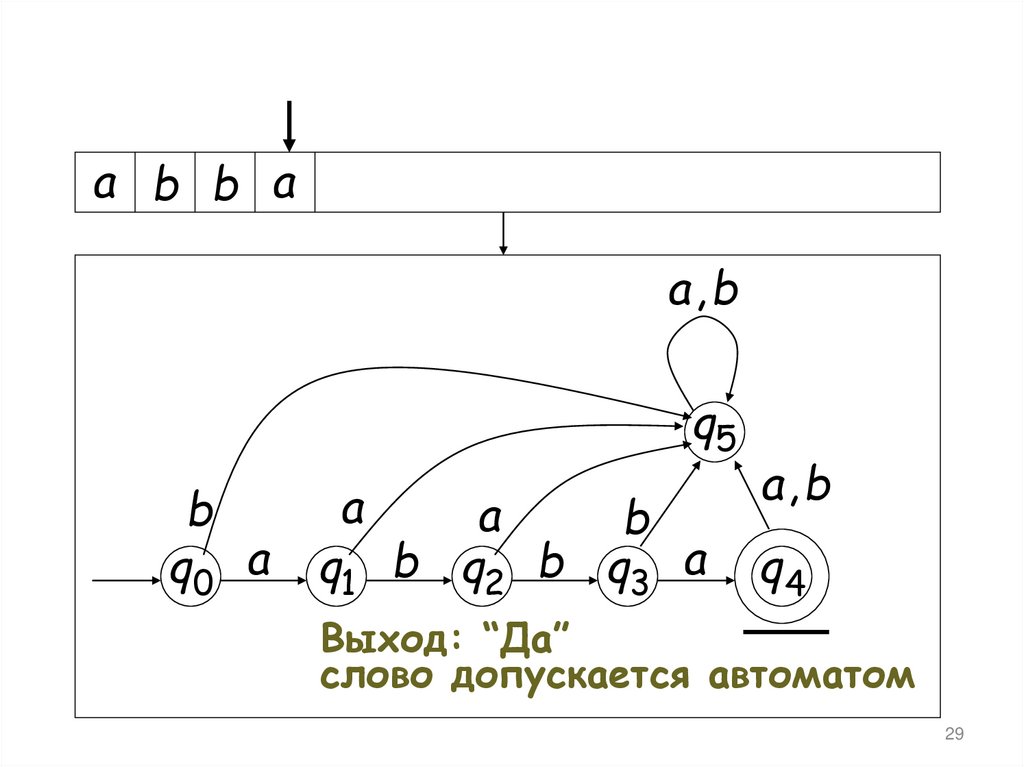
Выход: “Да”
слово допускается автоматом
29

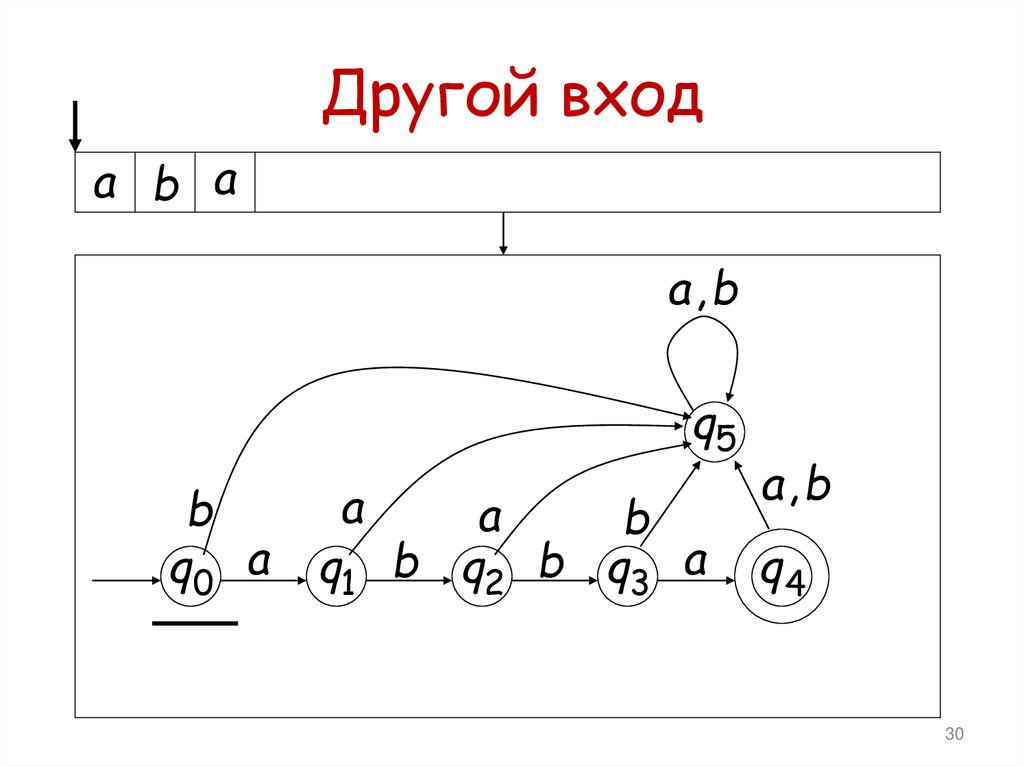
28.

Другой вход
a b a
a, b
q5
b
q0 a
a
a
b
q1 b q2 b q3 a
a, b
q4
30

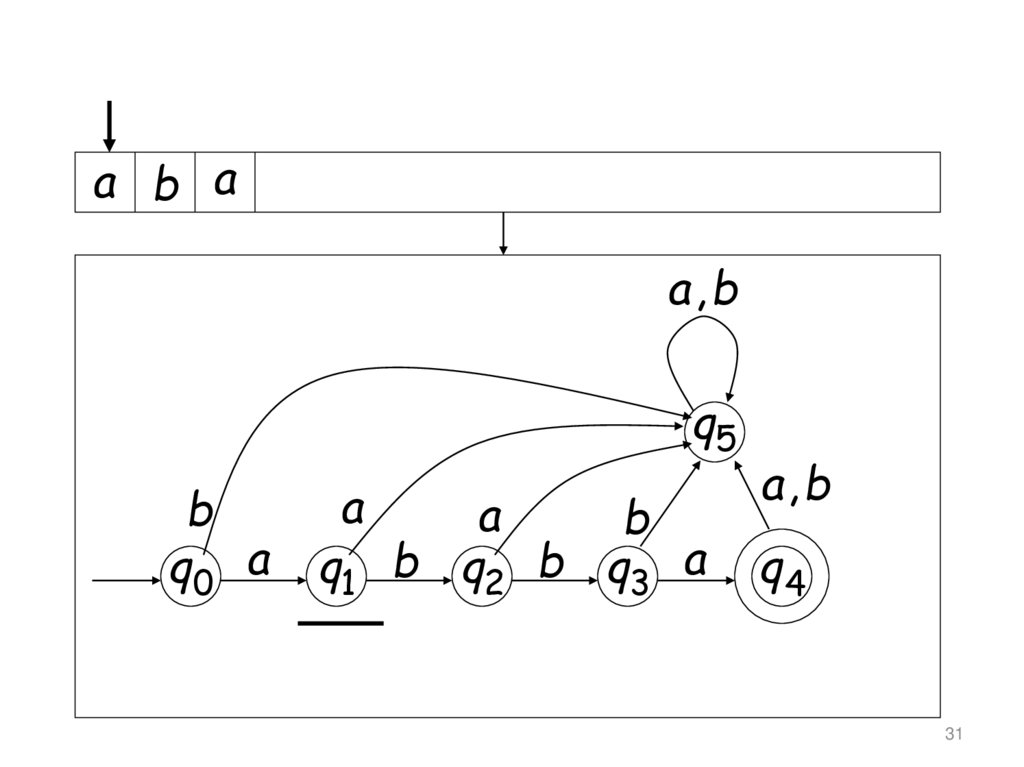
29.

a b a
a, b
q5
b
q0 a
a
a
b
q1 b q2 b q3 a
a, b
q4
31

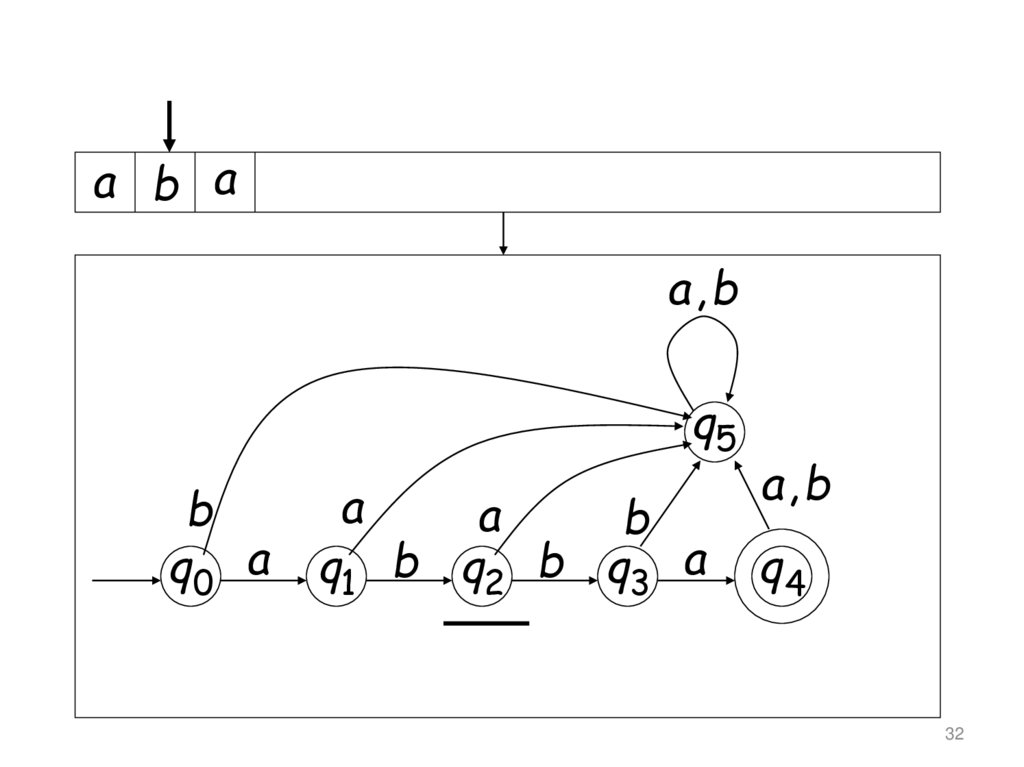
30. Другой вход

a b a
a, b
q5
b
q0 a
a
a
b
q1 b q2 b q3 a
a, b
q4
32

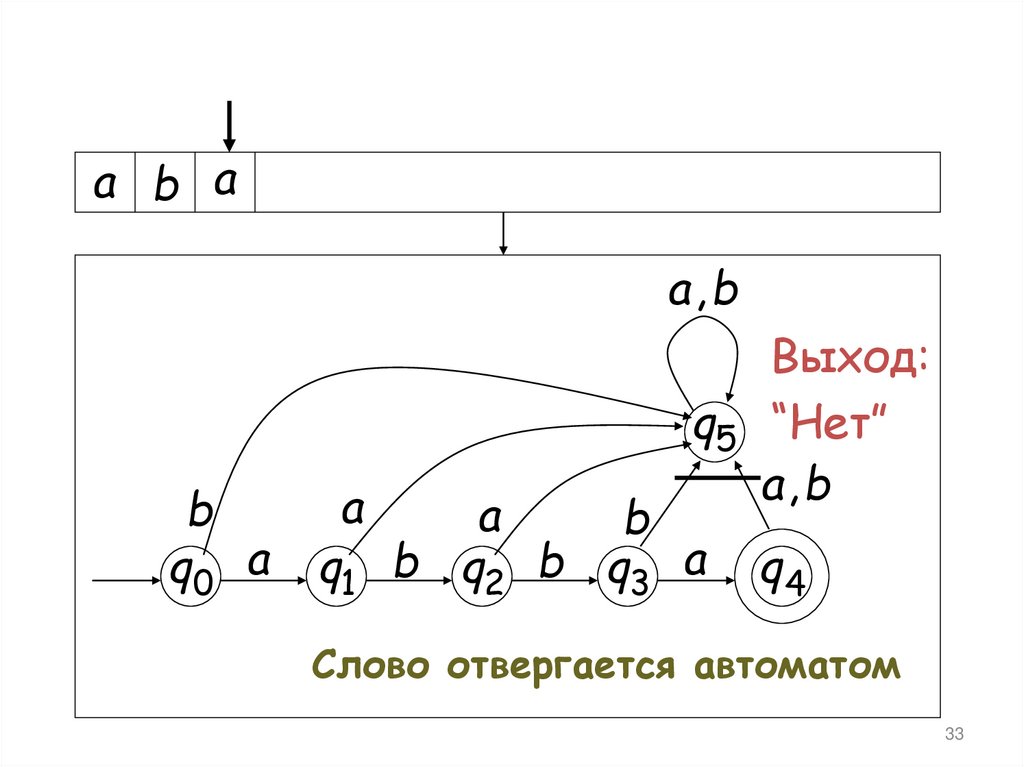
31.

a b a
a, b
b
q0 a
Выход:
q5 “Нет”
a, b
a
a
b
q1 b q2 b q3 a
q4
Слово отвергается автоматом
33

32.

Строгое определение ДКА
• Детерминированный конечный автомат (ДКА)
M Q , , , q0 , F
Q
: множество состояний
: входной алфавит
: функция переходов
q0 : начальное состояние
F
: множество заключительных состояний
34

33.

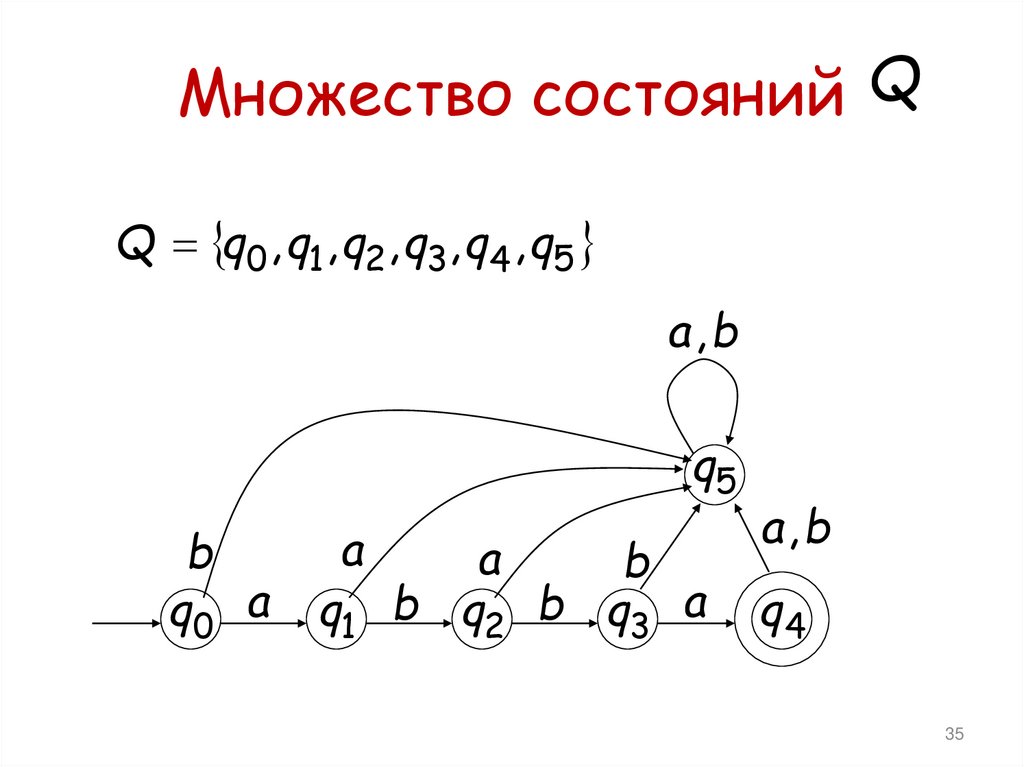
Множество состояний Q
Q q0 , q1 , q2 , q3, q4 , q5
a, b
q5
b
q0 a
a
a
b
q1 b q2 b q3 a
a, b
q4
35

34. Строгое определение ДКА

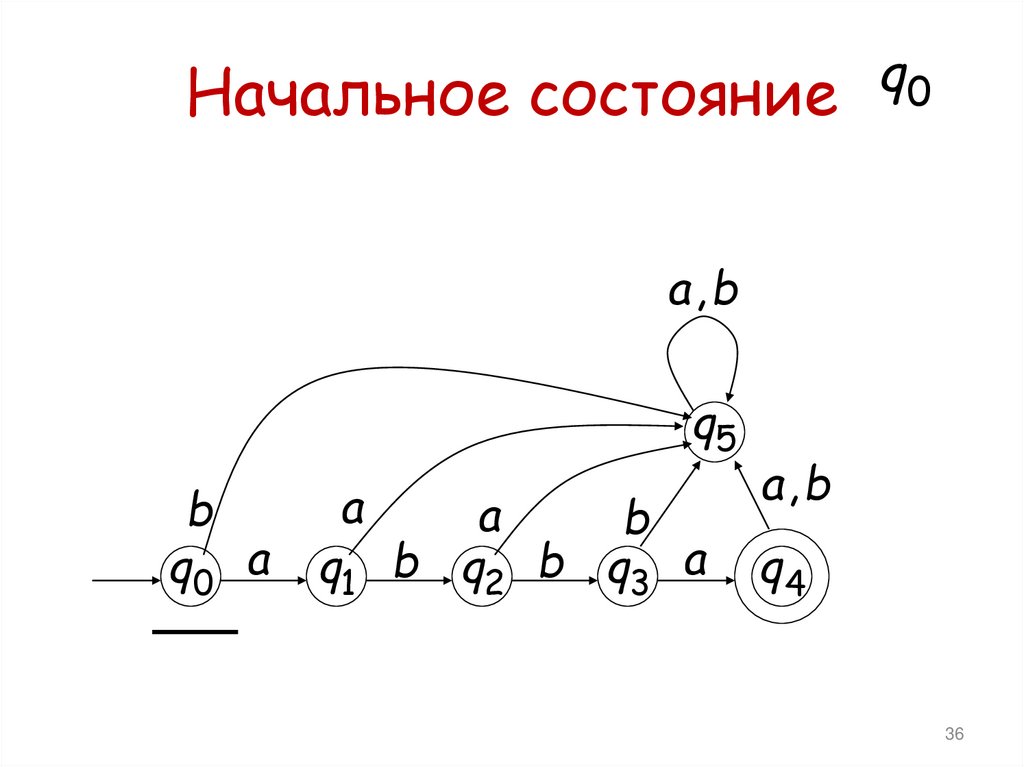
q
Начальное состояние 0
a, b
q5
b
q0 a
a
a
b
q1 b q2 b q3 a
a, b
q4
36

35. Множество состояний

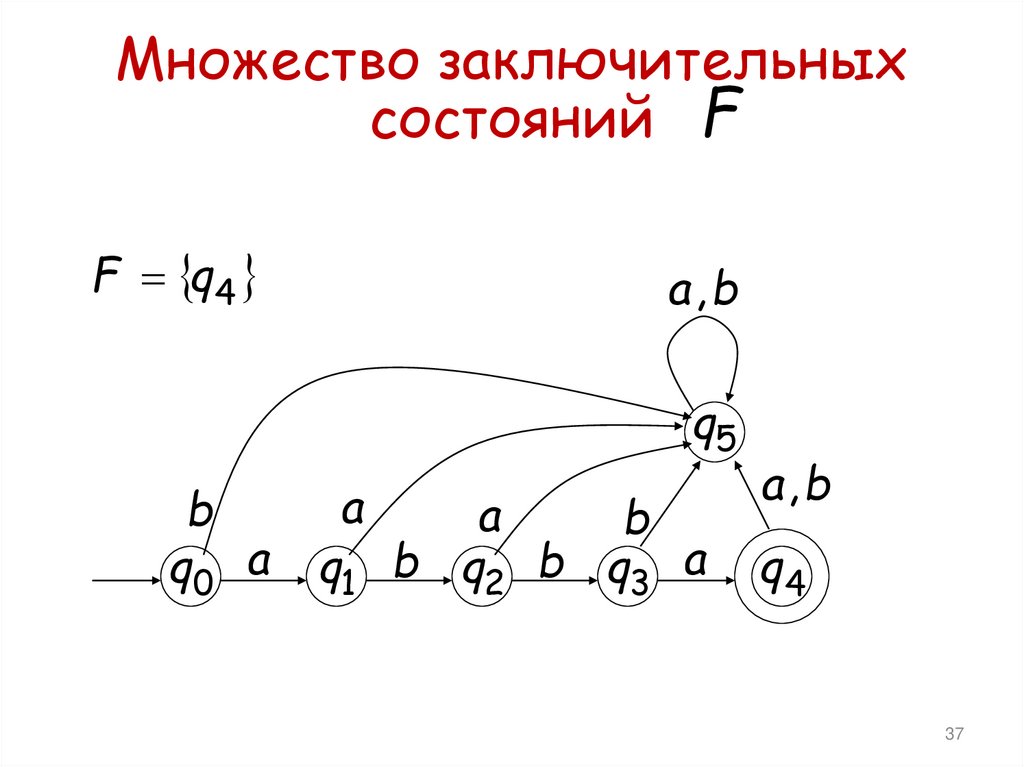
Множество заключительных
состояний F
F q4
a, b
q5
b
q0 a
a
a
b
q1 b q2 b q3 a
a, b
q4
37

36. Начальное состояние

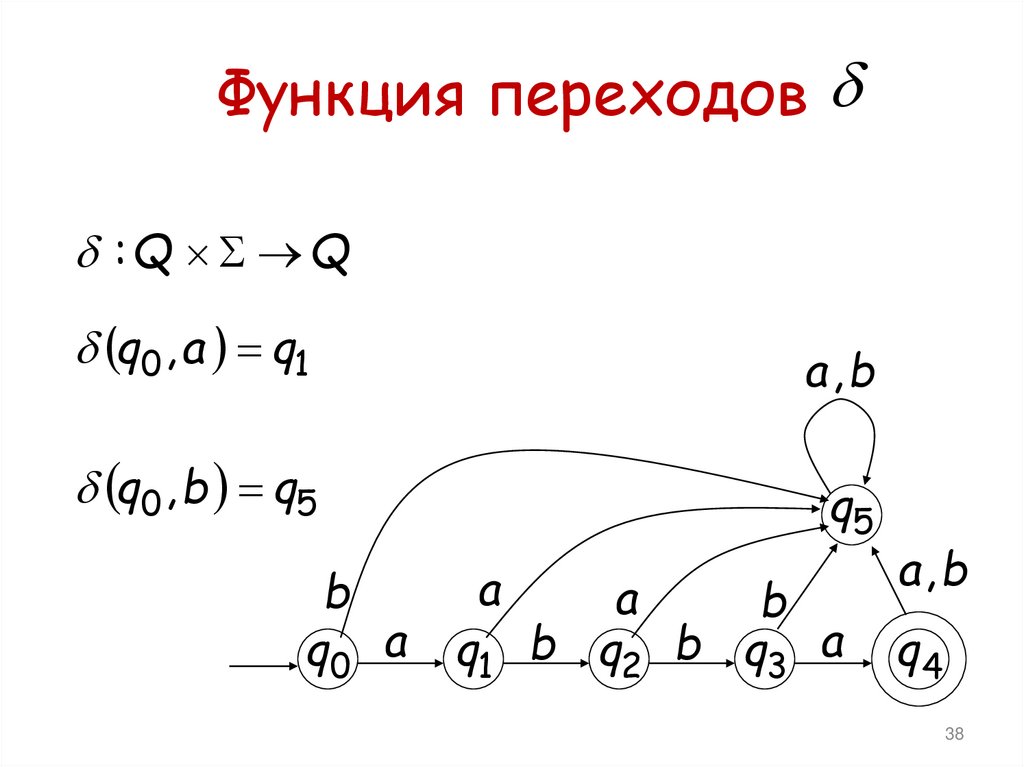
Функция переходов
:Q Q
q0 , a q1
a, b
q0 , b q5
q5
b
q0 a
a
a
b
q1 b q2 b q3 a
a, b
q4
38

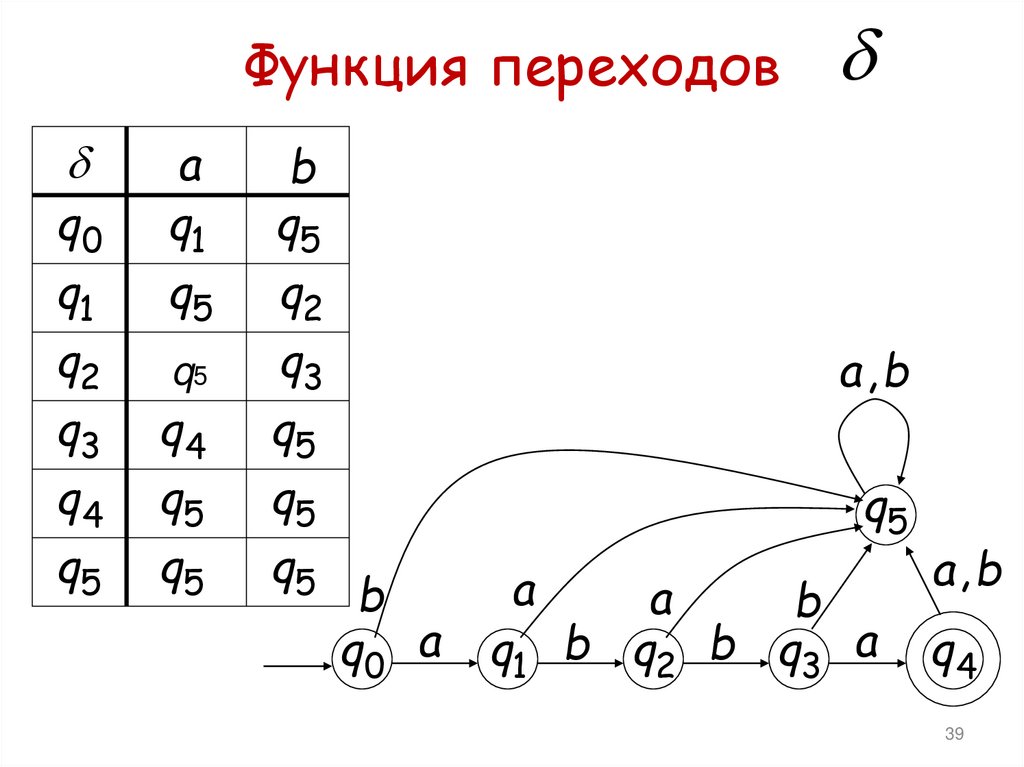
37. Множество заключительных состояний

q0
q1
q2
q3
q4
q5
a
q1
q5
qq25
q4
q5
q5
Функция переходов
b
q5
q2
q3
q5
q5
q5
a, b
q5
b
q0 a
a
a
b
q1 b q2 b q3 a
a, b
q4
39

38. Функция переходов

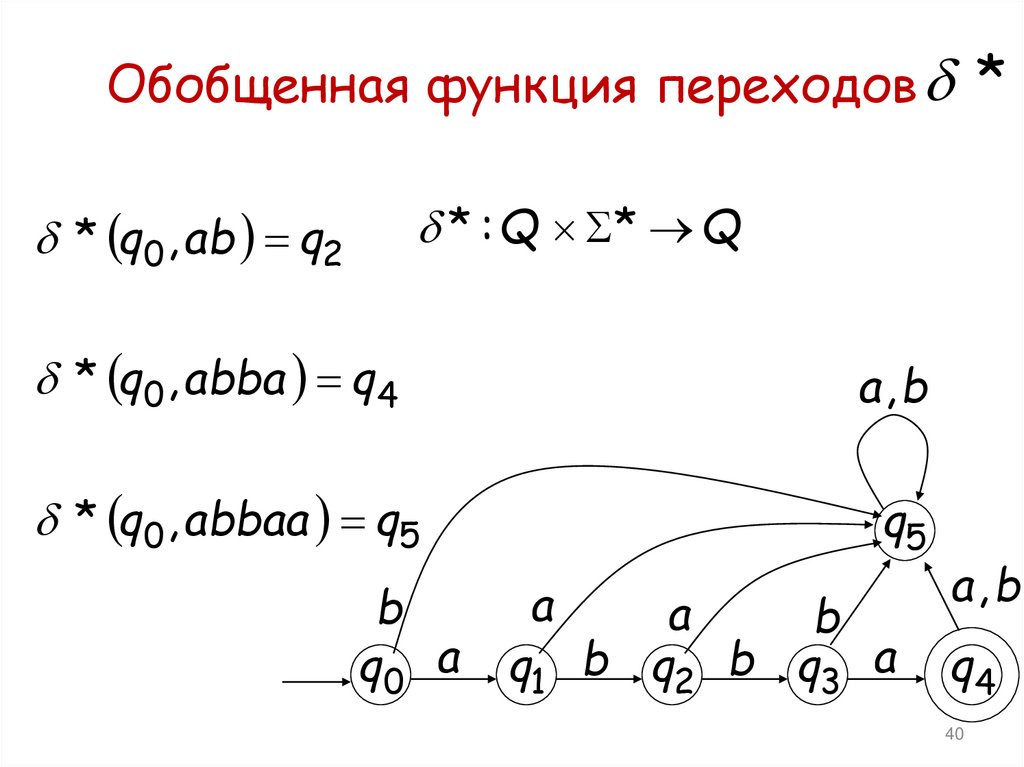
Обобщенная функция переходов *
* : Q * Q
* q0 , ab q2
* q0 , abba q4
a, b
* q0 , abbaa q5
q5
b
q0 a
a
a
b
q1 b q2 b q3 a
a, b
q4
40

39. Функция переходов

Язык, распознаваемый ДКА
Пусть M – ДКА
Определение:
Язык L M распознается автоматом M , если он
состоит из всех строк, допускаемых этим автоматом.
Другими словами:
L M = { строки, которые переводят M в
заключительное состояние}
41

40. Обобщенная функция переходов

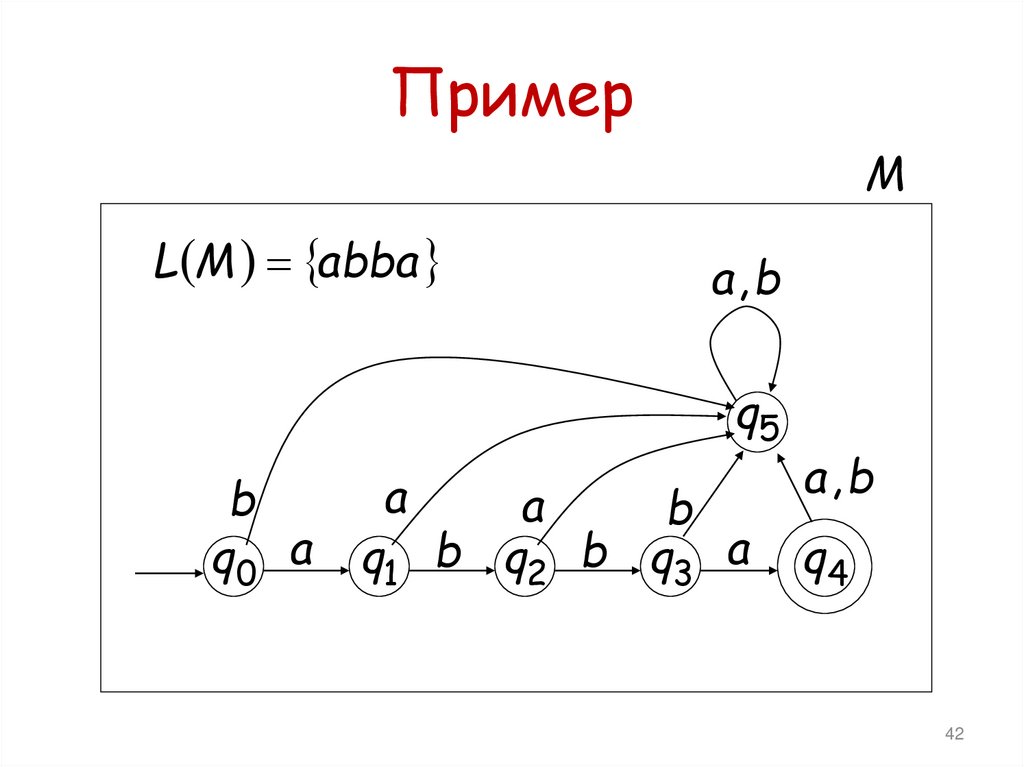
Пример
M
L M abba
a, b
q5
b
q0 a
a
a
b
q1 b q2 b q3 a
a, b
q4
42

41. Язык, распознаваемый ДКА

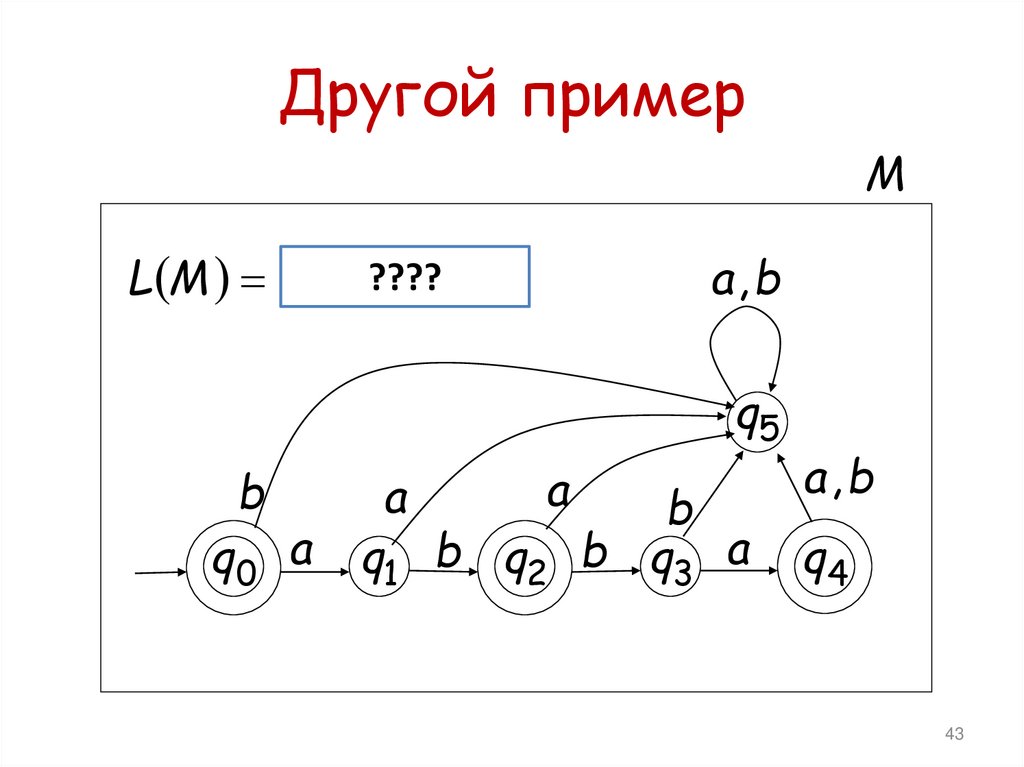
Другой пример
M
L M , ab????
, abba
a, b
q5
b
q0 a
a
a
b
q1 b q2 b q3 a
a, b
q4
43

42. Пример

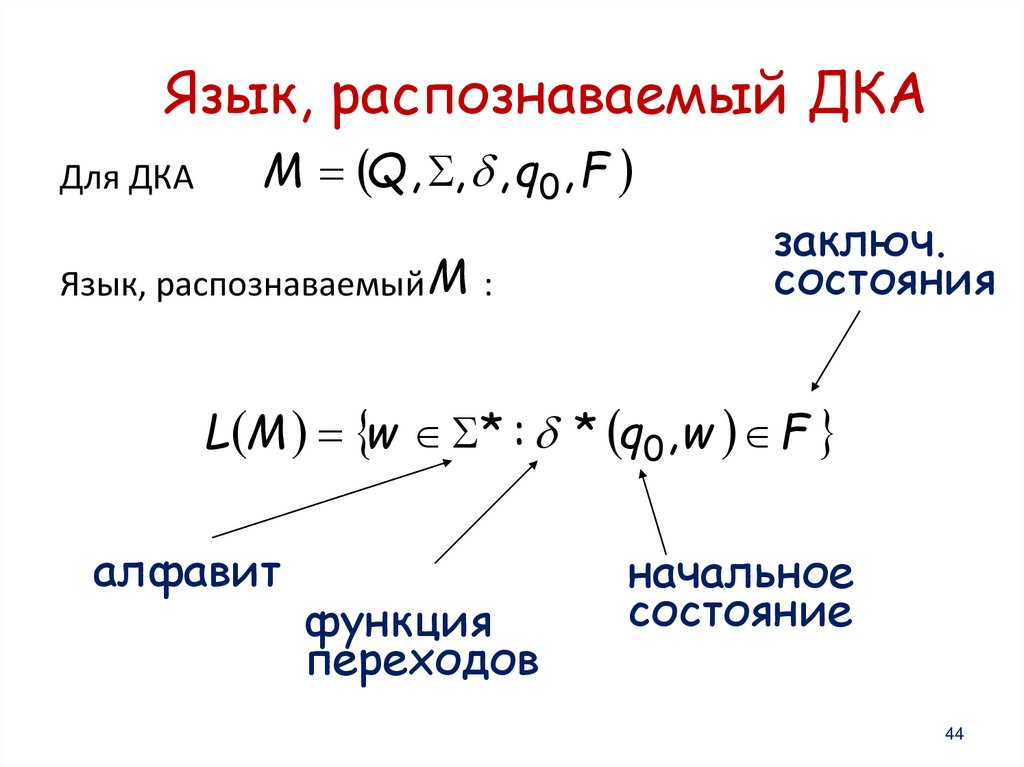
Язык, распознаваемый ДКА
M Q , , , q0 , F
Для ДКА
Язык, распознаваемый M :
заключ.
состояния
L M w * : * q0 , w F
алфавит
функция
переходов
начальное
состояние
44

43. Другой пример

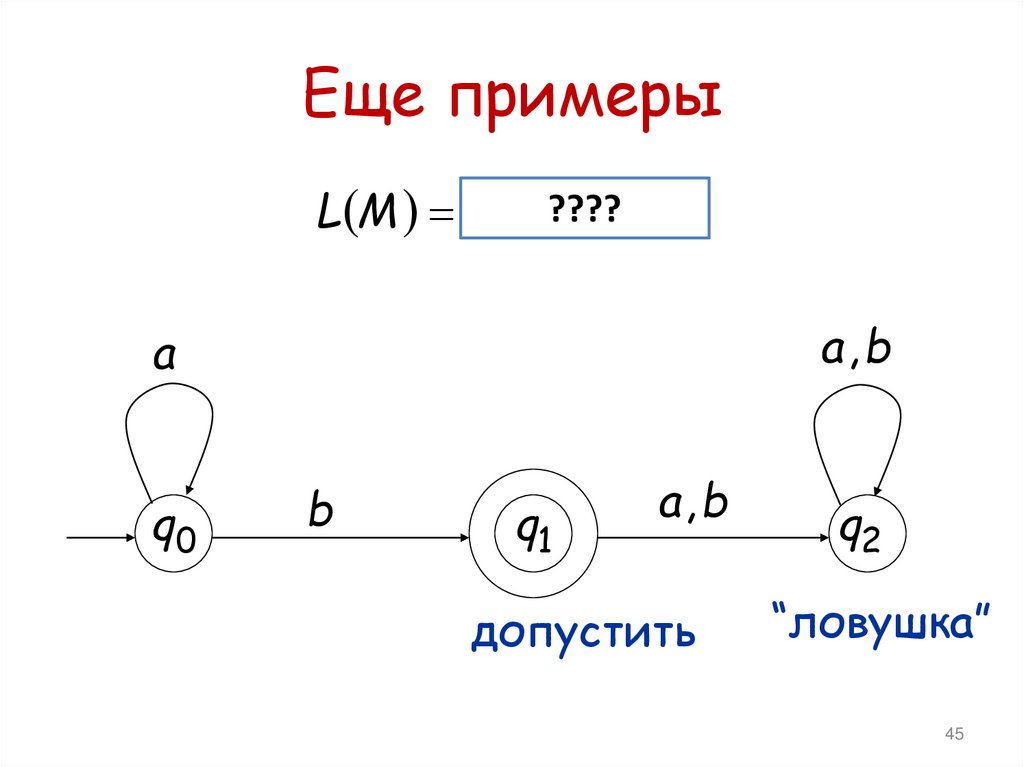
Еще примеры
L M a n b????
:n 0
a, b
a
q0
b
q1
a, b
допустить
q2
“ловушка”
45

44. Язык, распознаваемый ДКА

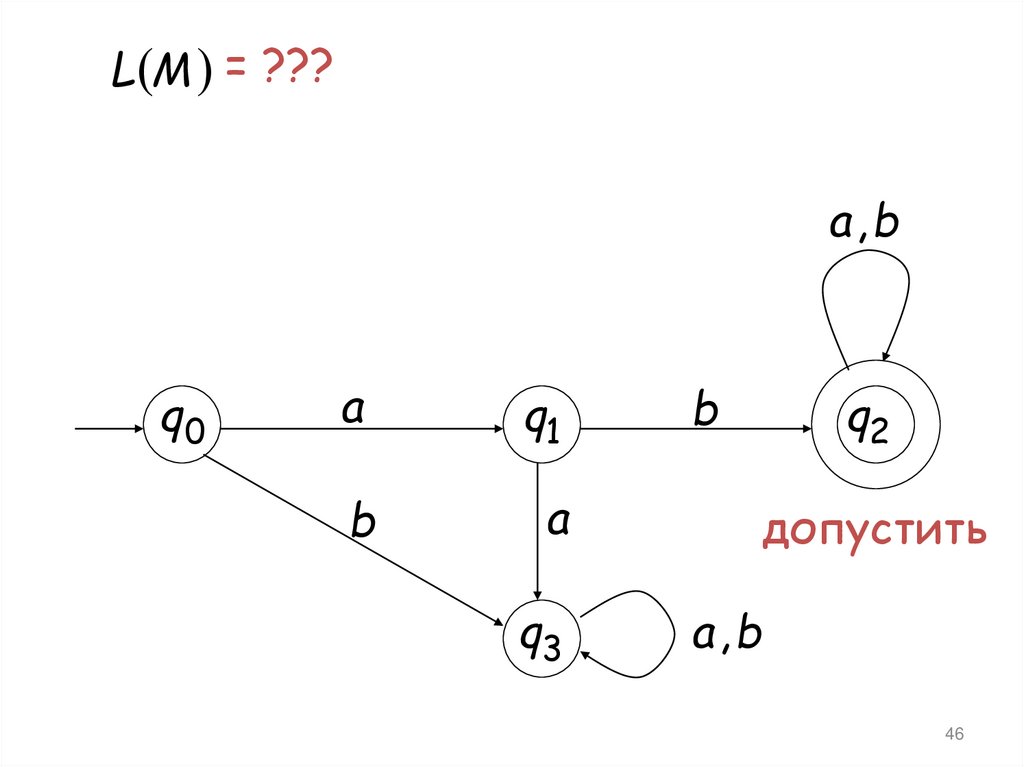
L M = ???
a, b
q0
a
q1
b
a
q3
b
q2
допустить
a, b
46

45. Еще примеры

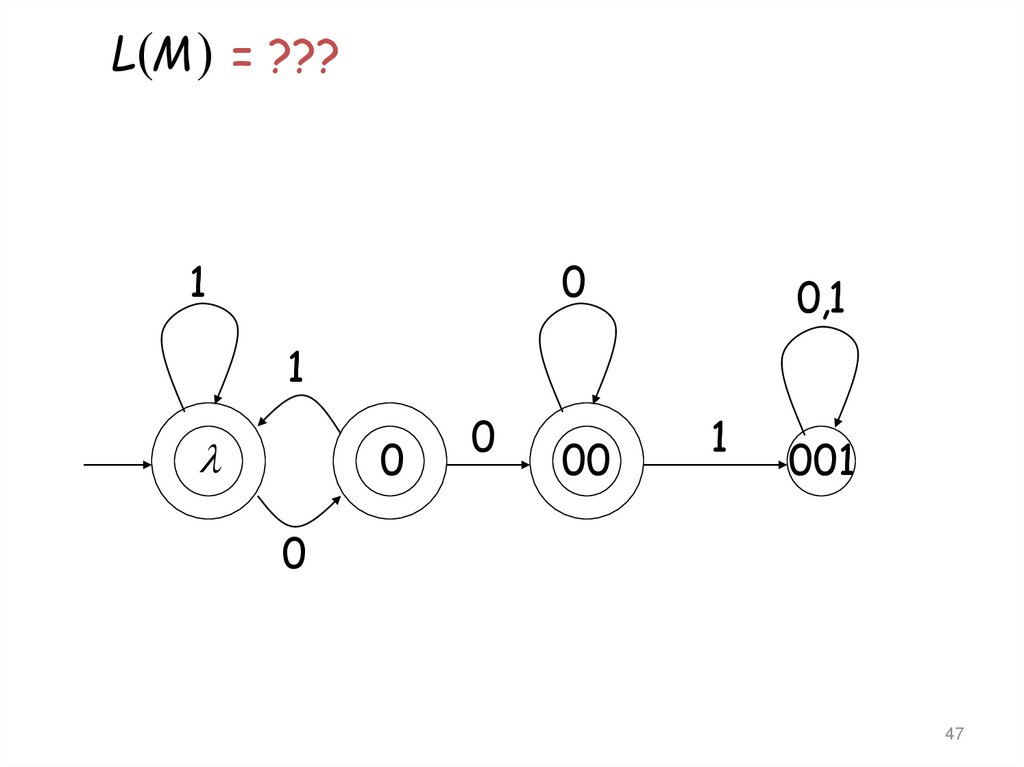
L M = ???
0
1
0,1
1
0
0
00
1
001
0
47

46.

Регулярные языки
Определение:
Язык L – регулярный, если существует ДКА M
такой, что L L M .
Все регулярные языки составляют класс регулярных
языков
48

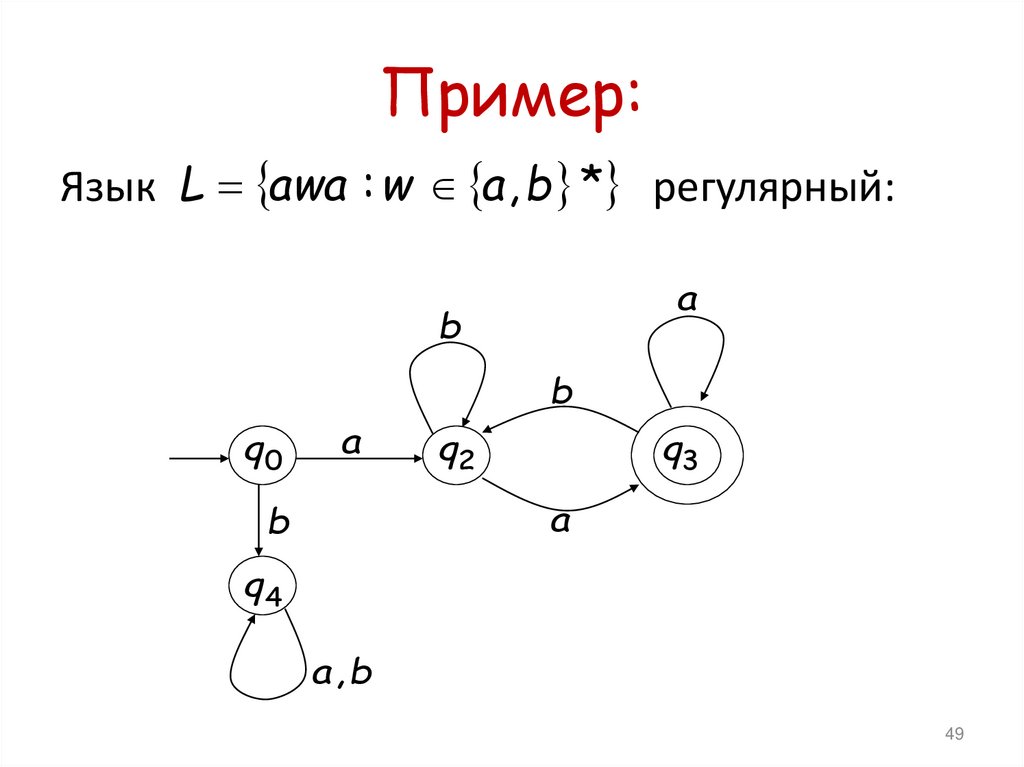
47.

Пример:
Язык L awa : w a , b * регулярный:
a
b
b
q0
a
q2
q3
a
b
q4
a, b
49

48. Регулярные языки

Недетерминированные
конечные автоматы (НКА)
Обобщение ДКА. Позволяет:
– выбирать следующее состояние из нескольких
возможных
• угадывание
– Помеченные пустым символом переходы.
• изменять состояние без чтения очередного
входного символа
Зачем? Большая гибкость.
– Проще строить, проще доказывать свойства.
50

49. Пример:

Как работает НКА ?
• Слово w допускается НКА, если существует
последовательность переходов (подсказок),
переводящая автомат в одно из заключительных
состояний (при этом слово полностью прочитано).
• Язык, распознаваемый НКА – множество всех
допускаемых слов.
51

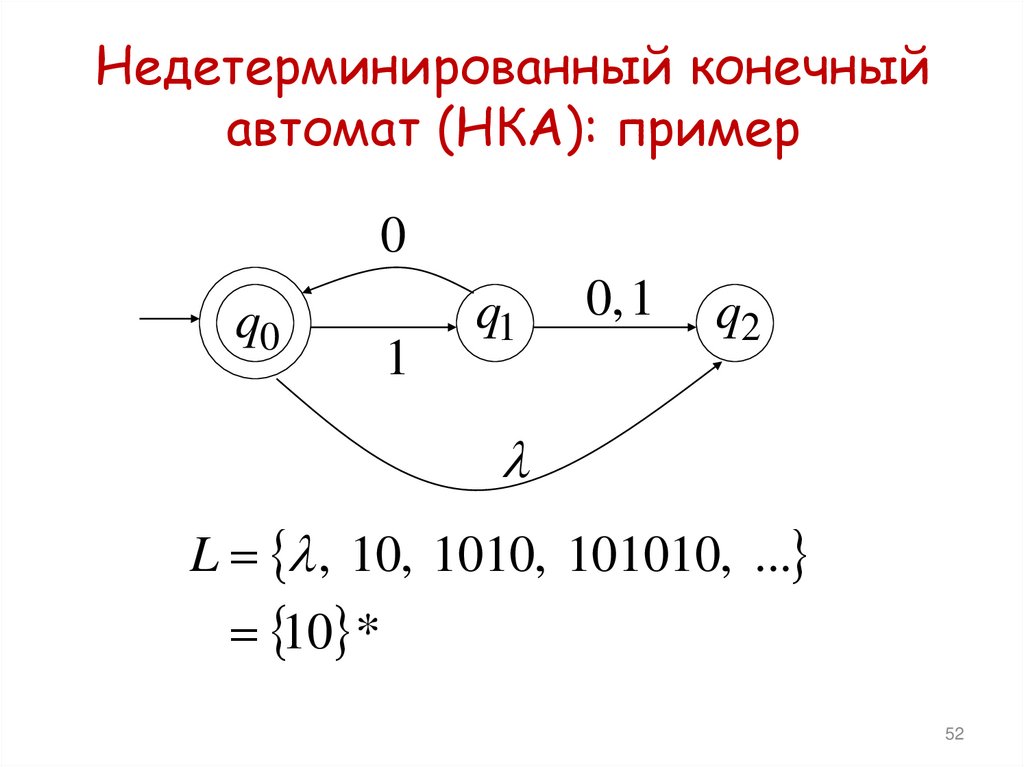
50. Недетерминированные конечные автоматы (НКА)

Недетерминированный конечный
автомат (НКА): пример
0
q0
1
q1
0, 1
q2
L , 10, 1010, 101010, ...
10 *
52

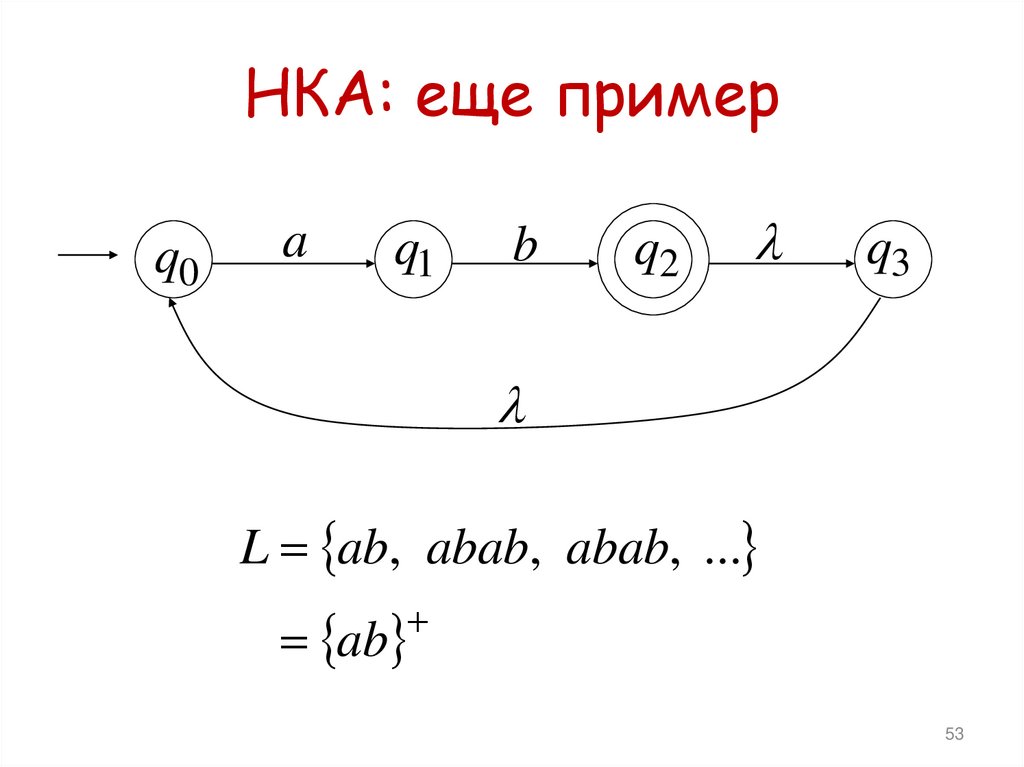
51. Как работает НКА ?

НКА: еще пример
q0
a
q1
b
q2
q3
L ab, abab, abab, ...
ab
53

52. Недетерминированный конечный автомат (НКА): пример

Определение НКА
M Q, , , q0 , F
Q : Мн-во состояний q0 , q1, q2
: Входной алфавит a, b
: Функция переходов
q0 : Начальное состояние
F : Заключительные состояния
54

53. НКА: еще пример

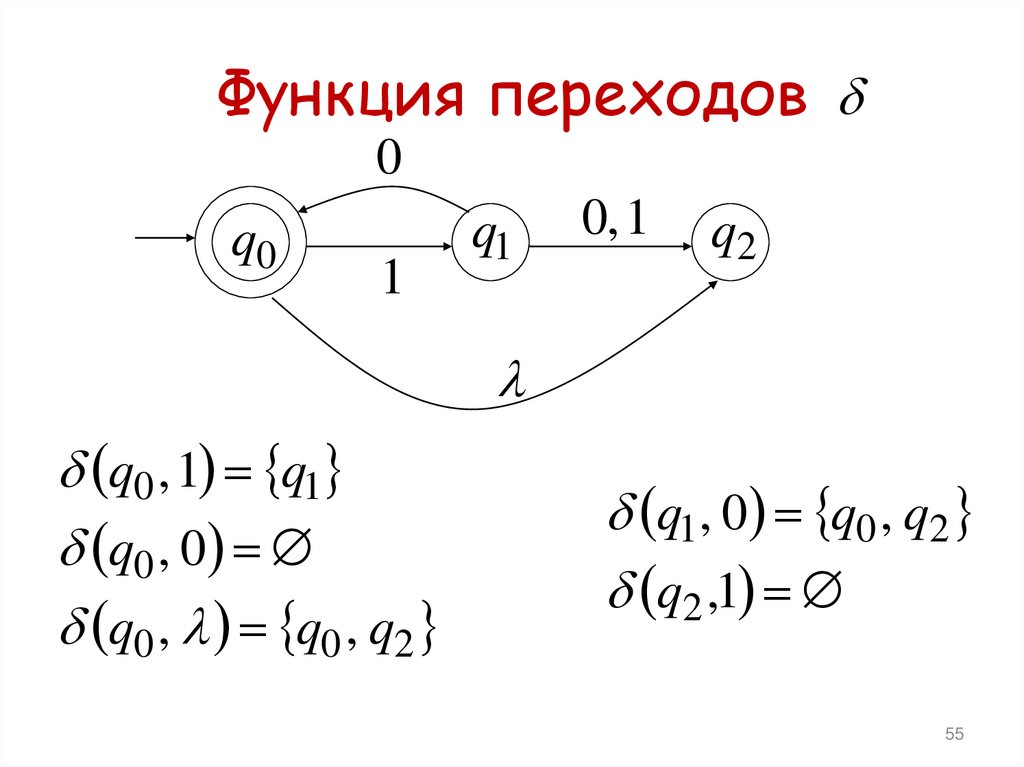
Функция переходов
0
q0
1
q1
0, 1
q2
q0 , 1 q1
q0 , 0
q0 , q0 , q2
q1, 0 q0 , q2
q2 ,1
55

54. Определение НКА

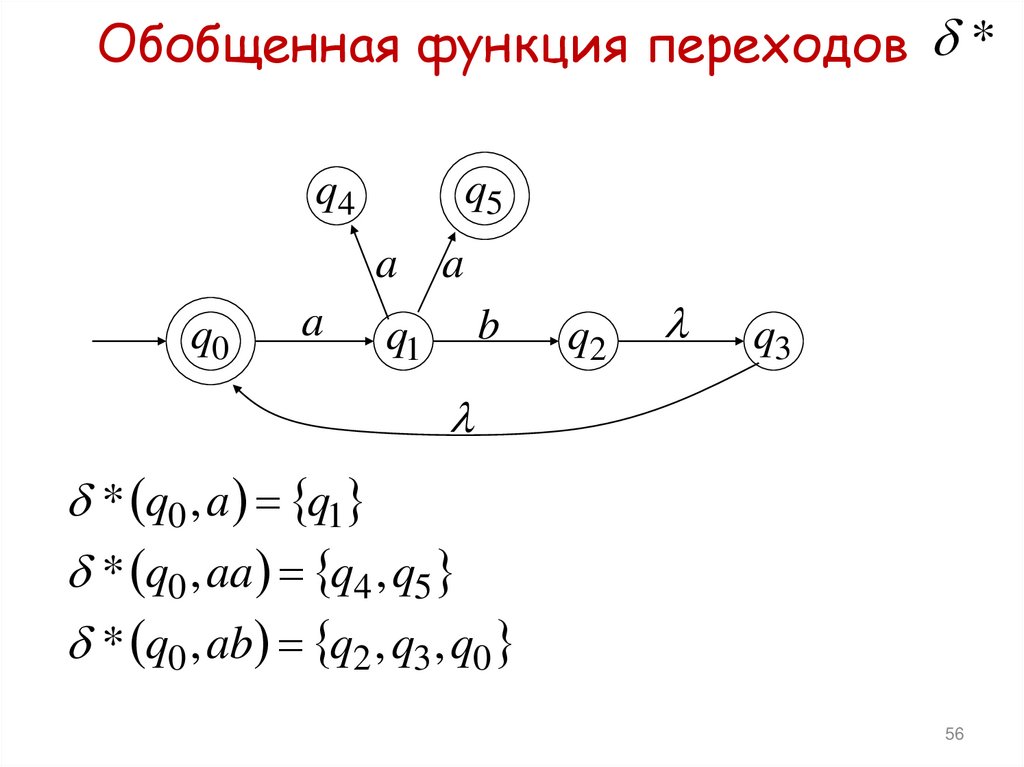
Обобщенная функция переходов *
q5
q4
a
q0
a
a
b
q1
q2
q3
* q0 , a q1
* q0 , aa q4 , q5
* q0 , ab q2 , q3 , q0
56

55. Функция переходов

Обобщенная функция переходов
q j * qi , w
в том и только том случае, когда
имеется путь от qi к q j
с пометкой w
57

56. Обобщенная функция переходов

Язык, допускаемый НКА M
F q0 , q5
q0
q5
q4
a
a
a
b
q1
q2
q3
* q0 , aa q4 , q5
* q0 , ab q2 , q3 , q0
aa L( M )
ab L M
58

57. Обобщенная функция переходов

Эквивалентность автоматов
Для ДКА и НКА :
Автоматы M1 и M 2 эквивалентны
если
L M1 L M 2
(т.е. их языки совпадают)
59

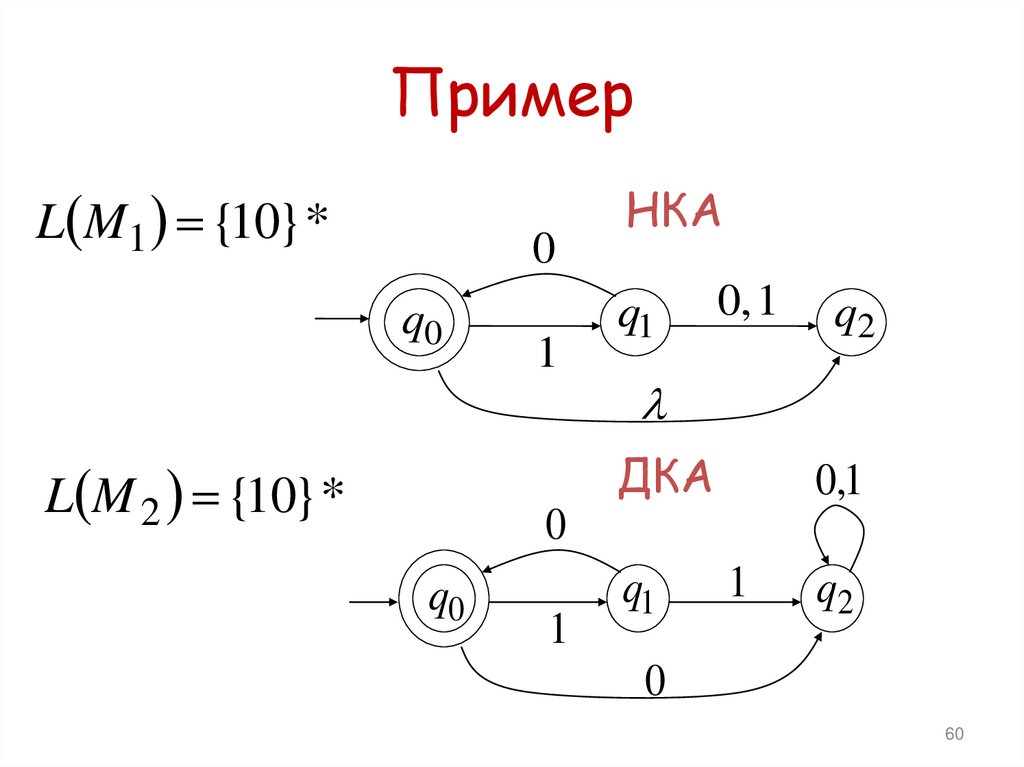
58. Язык, допускаемый НКА

Пример
L M1 {10} *
0
q0
1
НКА
q1
0, 1
ДКА
L M 2 {10} *
q2
0,1
0
q0
1
q1
1
q2
0
60

59. Эквивалентность автоматов

Эквивалентность НКА и ДКА
Любой ДКА является также НКА
Язык, распознаваемый ДКА будет
распознаваться также и НКА
Слабее ли ДКА, чем НКА?
Ответ: НЕТ!
Язык, распознаваемый НКА
распознается также и ДКА
Теорема. Для любого НКА можно
построить эквивалентный ему ДКА.
61

60. Пример

НКА и регулярные языки
Для любого НКА имеется
эквивалентный ДКА
Языки, распознаваемые ДКА –
регулярные
Класс языков, распознаваемых НКА,
совпадает с классом регулярных
языков.
62

61. Эквивалентность НКА и ДКА

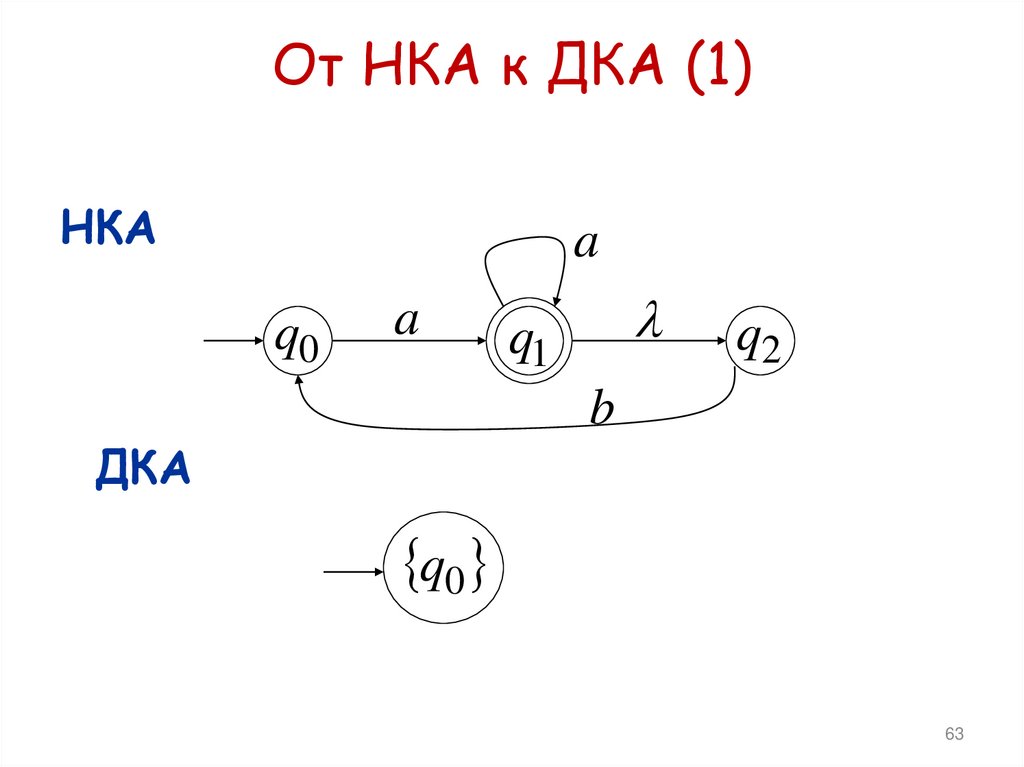
От НКА к ДКА (1)
НКА
a
q0
a
q1
q2
b
ДКА
q0
63

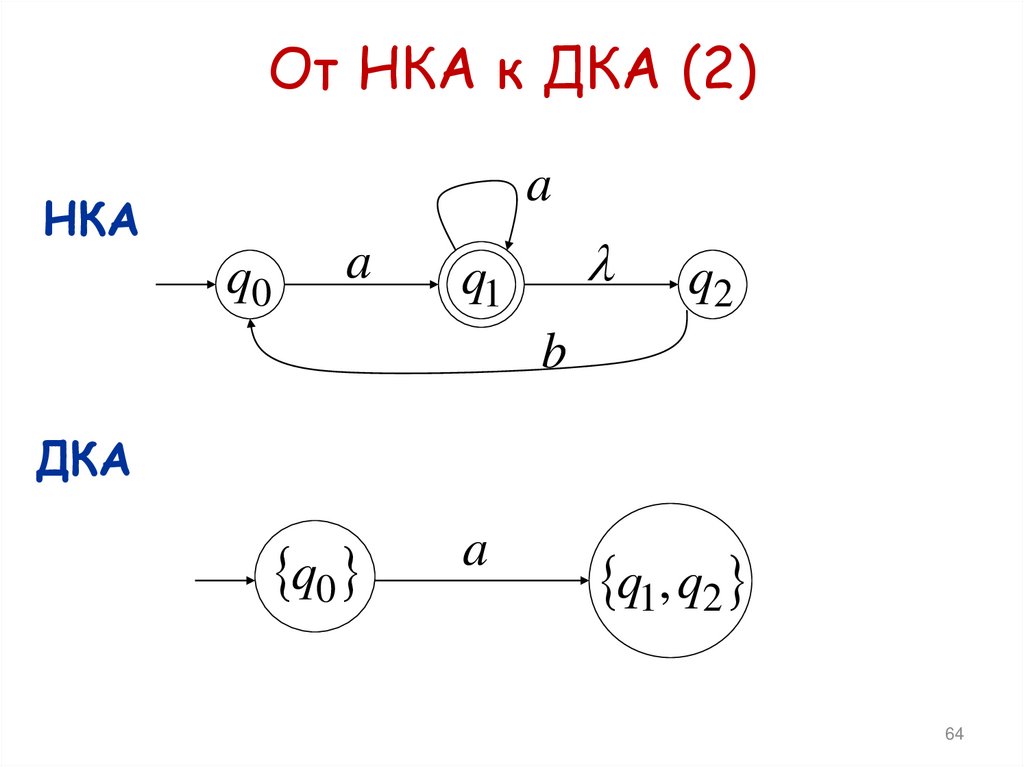
62. НКА и регулярные языки

От НКА к ДКА (2)
a
НКА
q0
a
q1
q2
b
ДКА
q0
a
q1, q2
64

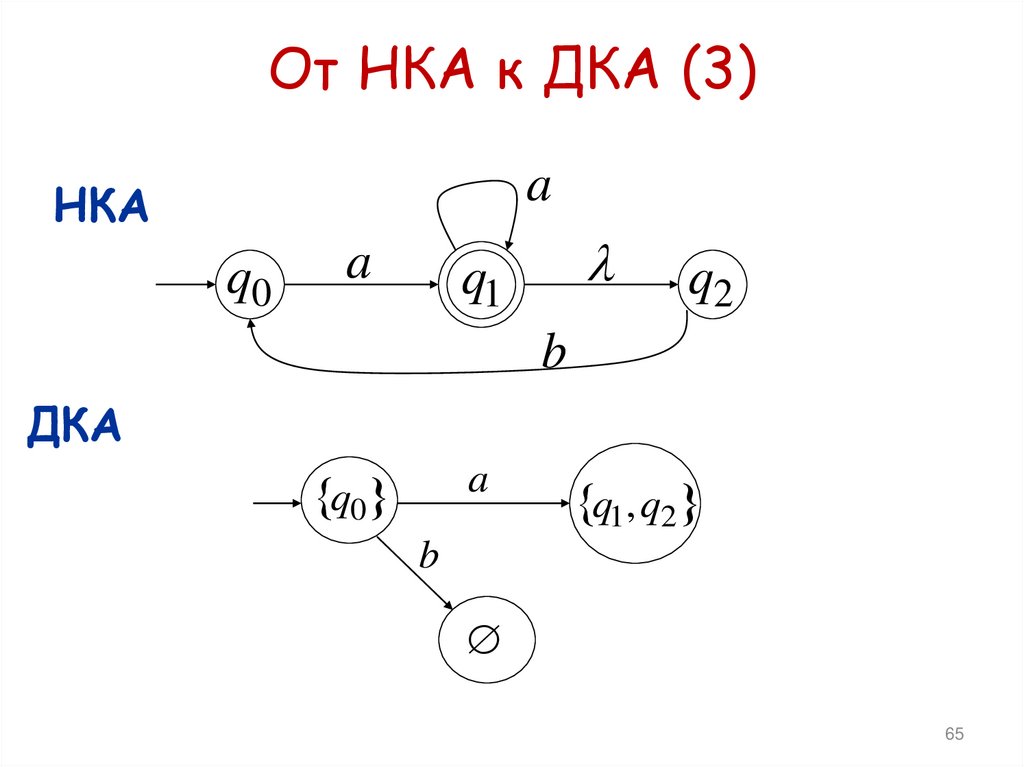
63. От НКА к ДКА (1)

От НКА к ДКА (3)
a
НКА
q0
a
q1
q2
b
ДКА
q0
a
q1, q2
b
65

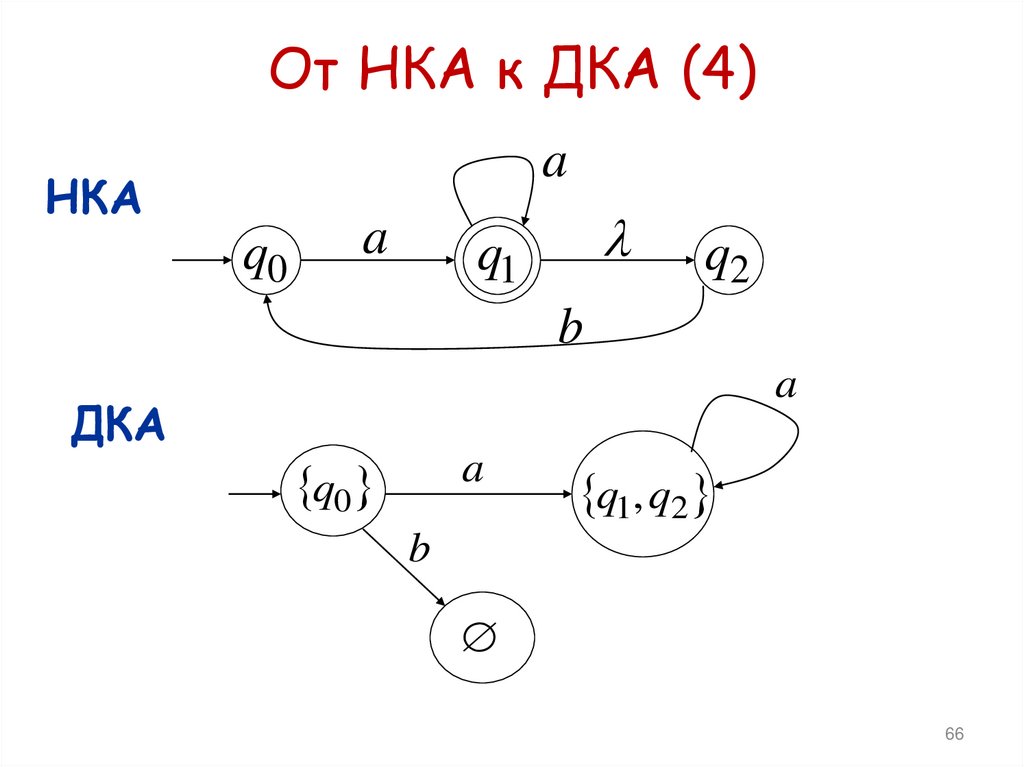
64. От НКА к ДКА (2)

От НКА к ДКА (4)
a
НКА
q0
a
q1
q2
b
ДКА
a
q0
a
q1, q2
b
66

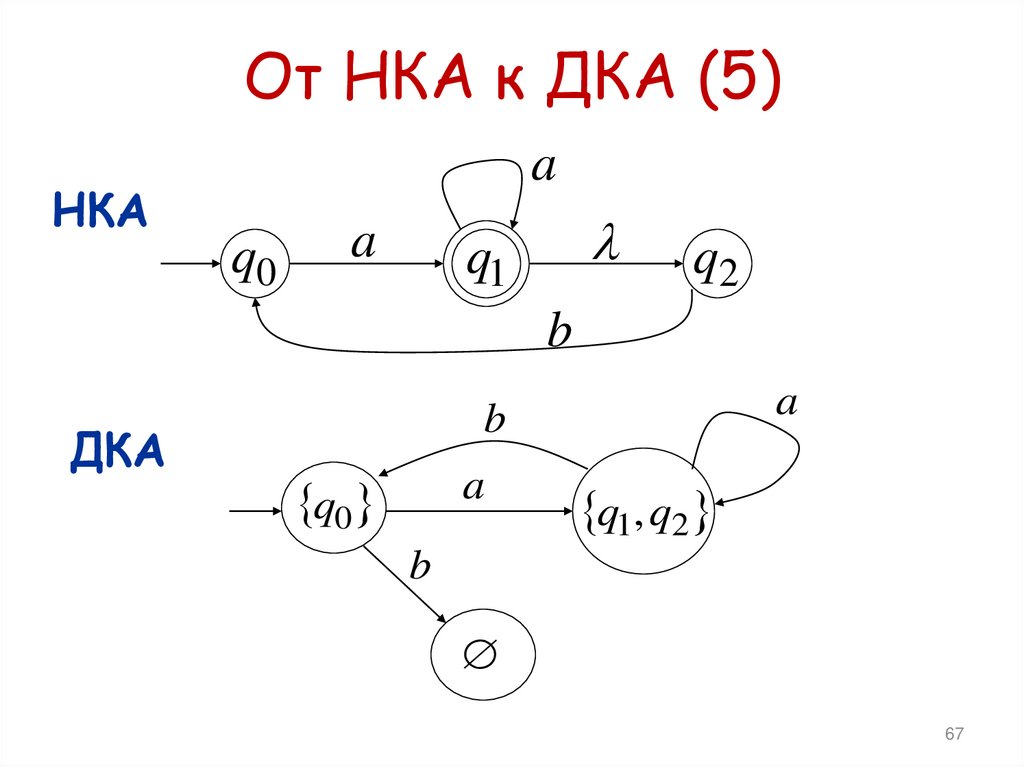
65. От НКА к ДКА (3)

От НКА к ДКА (5)
НКА
a
q0
a
q1
q2
b
ДКА
a
b
q0
a
q1, q2
b
67

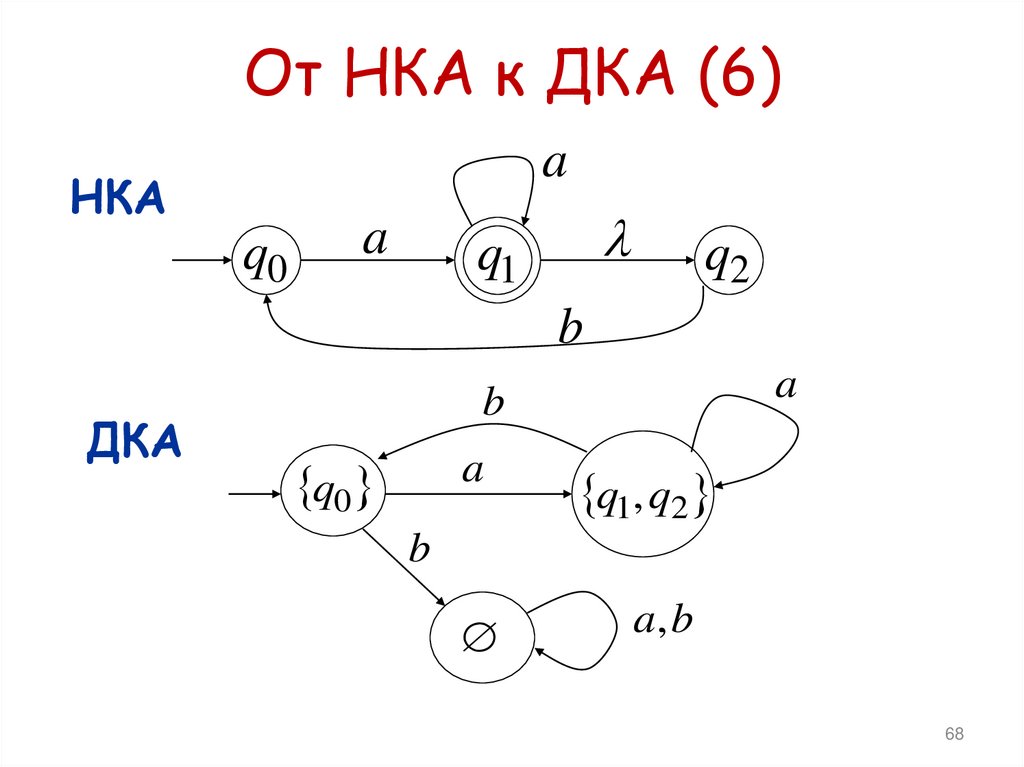
66. От НКА к ДКА (4)

От НКА к ДКА (6)
a
НКА
q0
a
q1
q2
b
ДКА
a
b
q0
a
q1, q2
a, b
b
68

67. От НКА к ДКА (5)

От НКА к ДКА (7)
НКА
a
q0
a
q1
q2
b
ДКА
a
b
q0
a
q1, q2
a, b
b
69

68. От НКА к ДКА (6)

От НКА к ДКА: суммируем
• Пусть дан НКА M
• Мы хотим построить эквивалентный ему ДКА M
такой, что L M L(M )
70

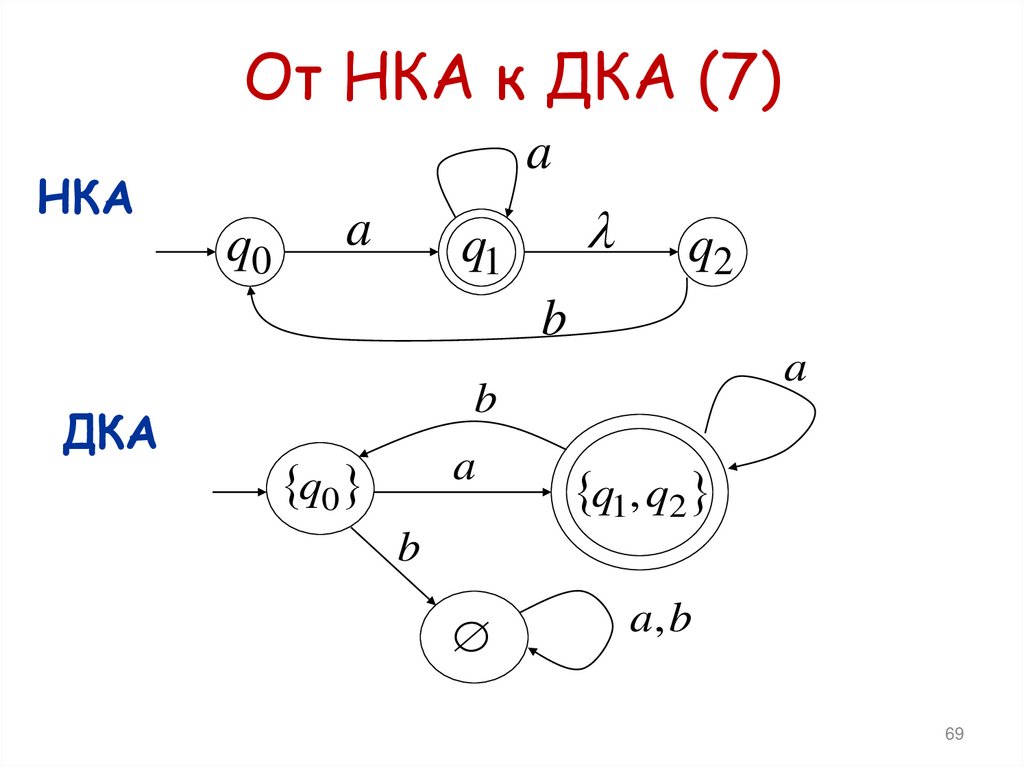
69. От НКА к ДКА (7)

• Пусть НКА имеет состояния
q0 , q1, q2 ,...
• Тогда состояния ДКА – множества состояний НКА
, q0 , q1 , q1, q2 , q3 , q4 , q7 ,....
71

70. От НКА к ДКА: суммируем

Алгоритм перевода НКА в ДКА
1. Начальное состояние НКА: q0
Начальное состояние ДКА: q0
72

71.

Пример
a
НКА
q0
a
q1
q2
b
ДКА
q0
73

72. Алгоритм перевода НКА в ДКА

2. Для каждого состояния ДКА qi , q j ,..., qm
вычислить в НКА
* qi , a ,
* q j , a , ...
- объединение
Пусть qi , q j ,..., qm
результатов этих вычислений.
Тогда добавляем переход
qi , q j ,..., qm , a qi , q j ,..., qm
74

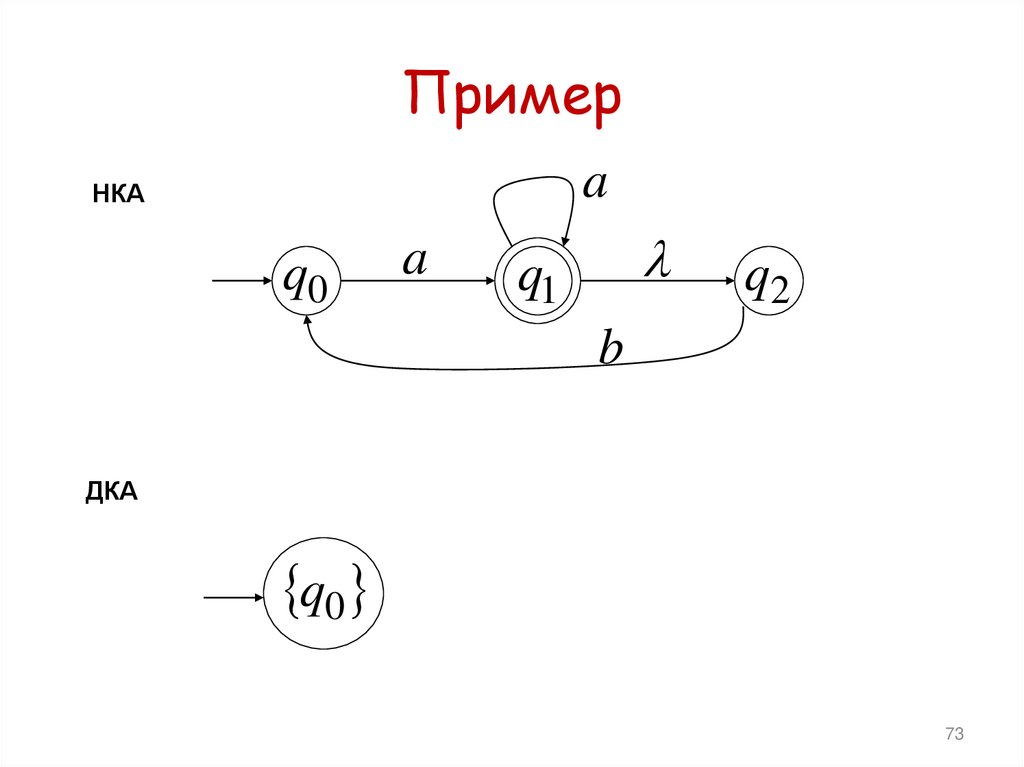
73. Пример

a
НКА
q0
a
q1
q2
b
* (q0 , a) {q1, q2}
ДКА
q0
a
q1, q2
q0 , a q1, q2
75

74. Алгоритм перевода НКА в ДКА

Повторять шаг 2 для всех входных символов, пока не
будут построены все возможные переходы.
76

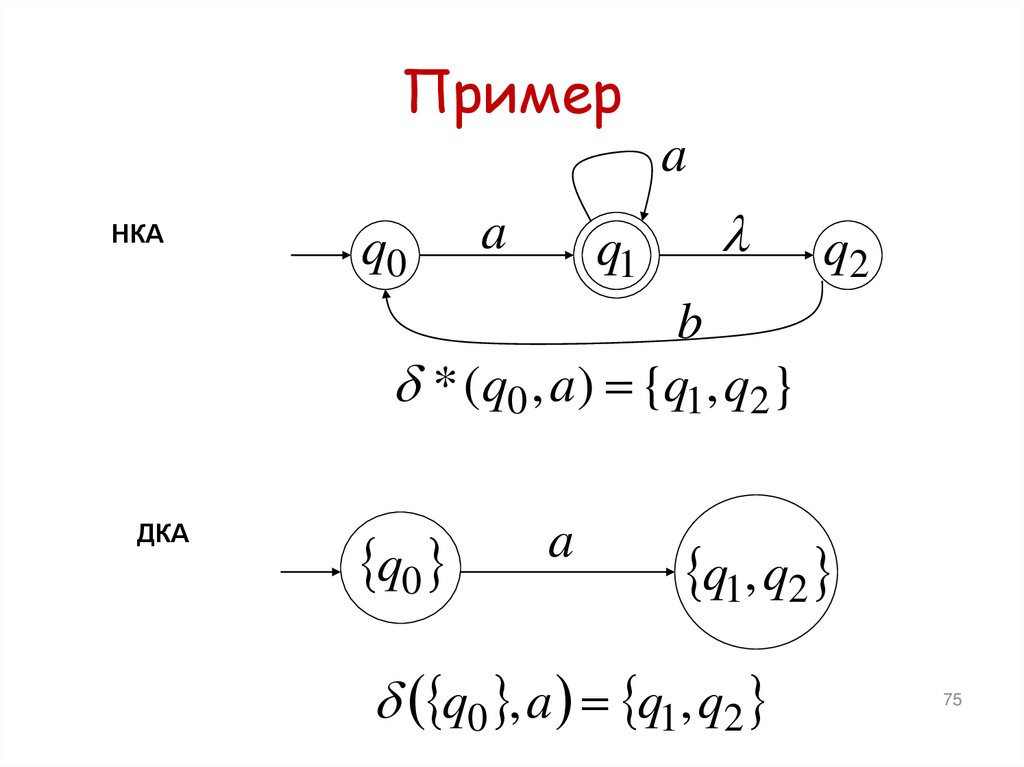
75. Пример

НКА
a
q0
a
q1
q2
b
ДКА
a
b
q0
a
q1, q2
a, b
b
77

76. Алгоритм перевода НКА в ДКА

3. Для каждого состояния ДКА
qi , q j ,..., qm
если состояние q j - заключительное в НКА
qi , q j ,..., qm
то
объявляется заключительным в ДКА
78

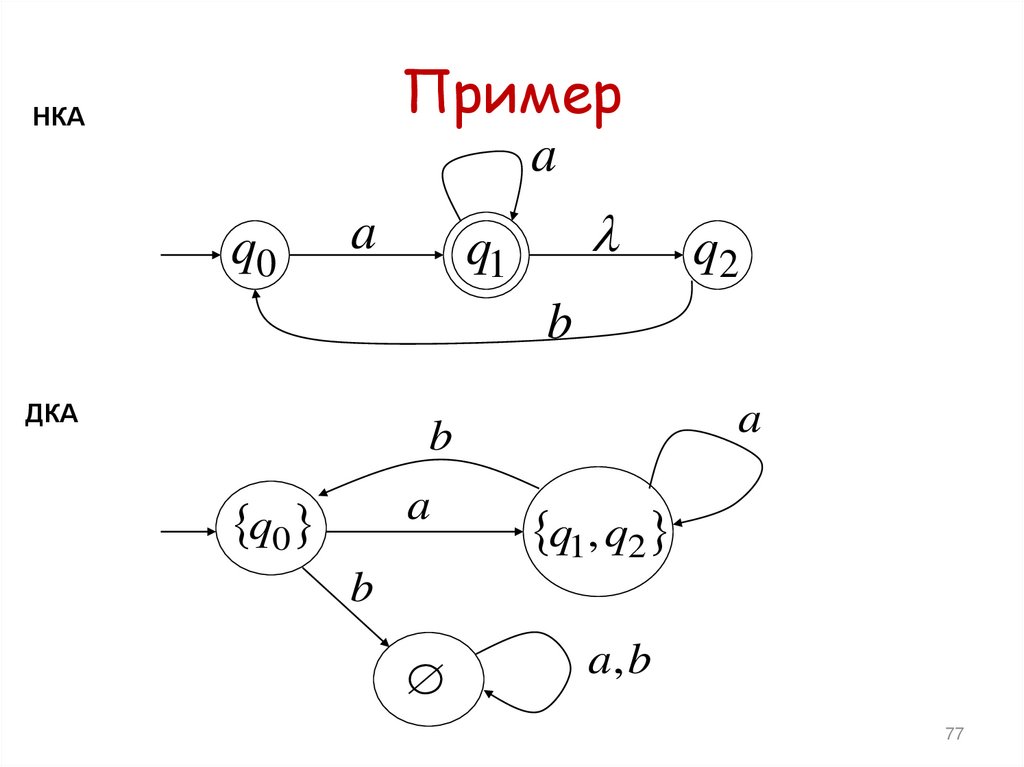
77. Пример

НКА
a
q0
a
q1
q2
b
a
b
ДКА
q0
a
q1 F
q1, q2
q1, q2 F
b
a, b
79

78. Алгоритм перевода НКА в ДКА

Теорема
Пусть M - произвольный НКА,
и пусть M - ДКА, получающийся из M
в результате описанной выше процедуры.
Тогда автоматы M и M эквивалентны, т.е.
L M L M
80

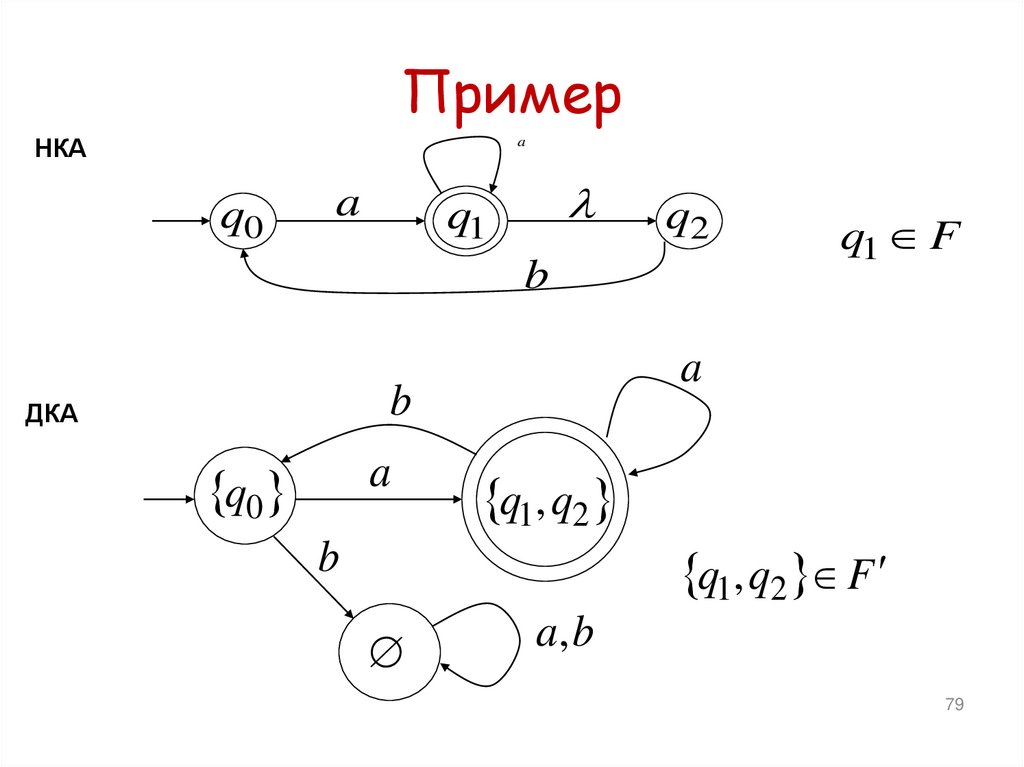
79. Пример

Заметим:
Для любого конечного автомата (ДКА и НКА) можно
построить эквивалентный НКА с одним
заключительным состоянием.
81

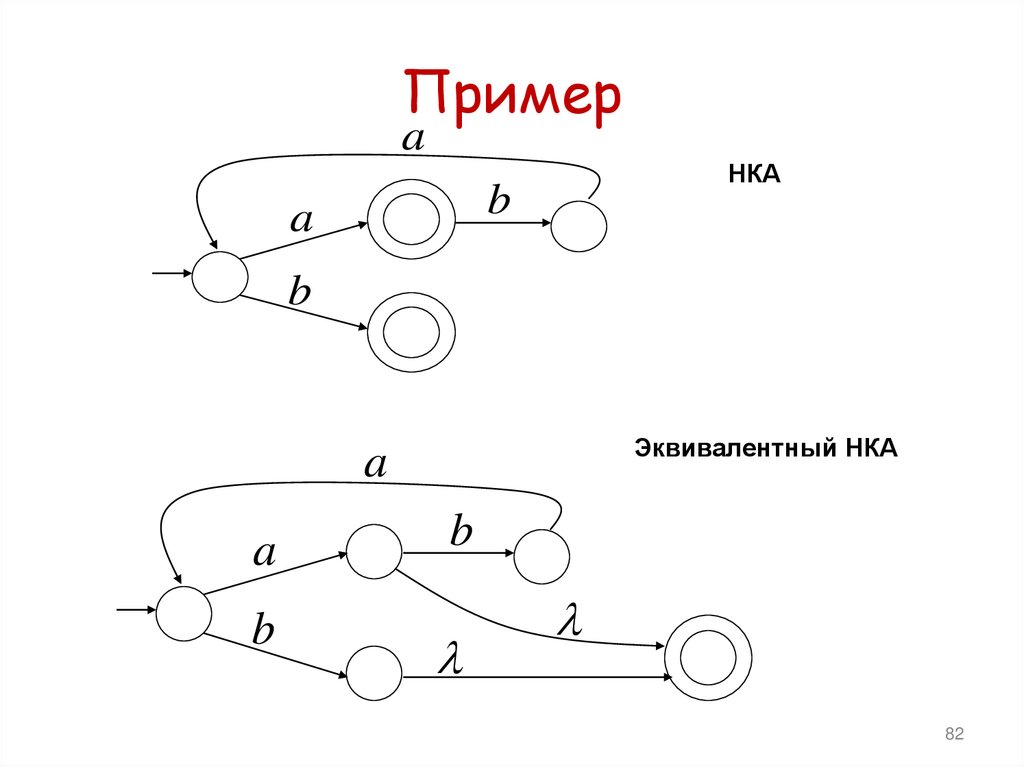
80. Теорема

Пример
a
НКА
b
a
b
Эквивалентный НКА
a
a
b
b
82

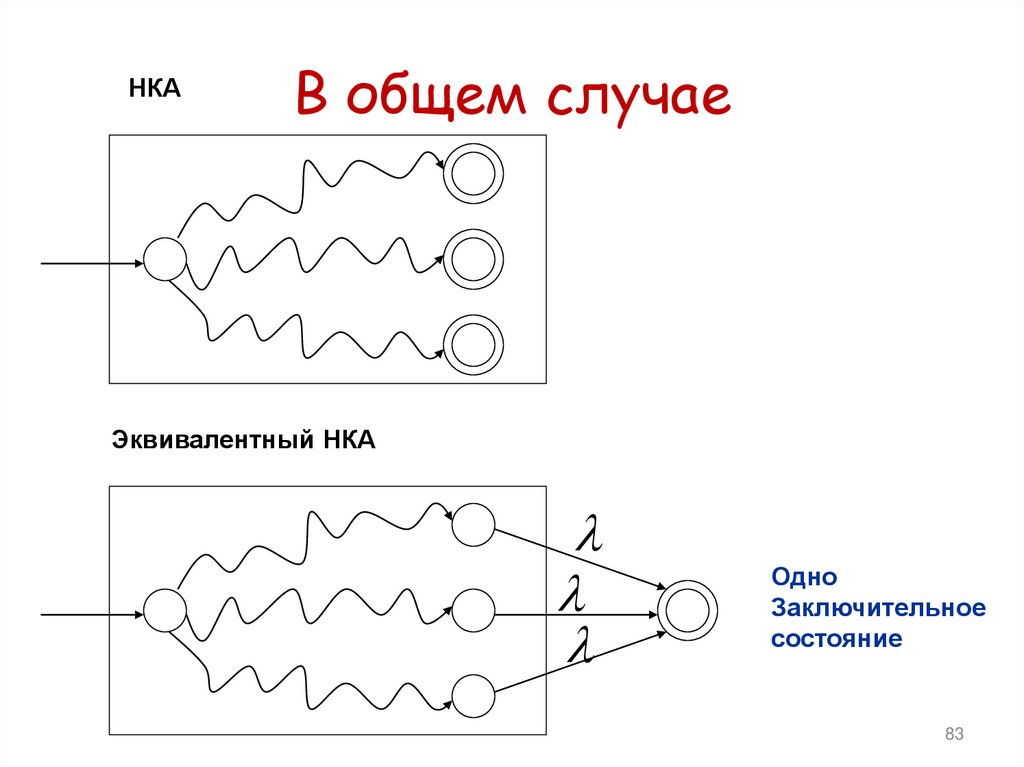
81. Заметим:

НКА
В общем случае
Эквивалентный НКА
Одно
Заключительное
состояние
83

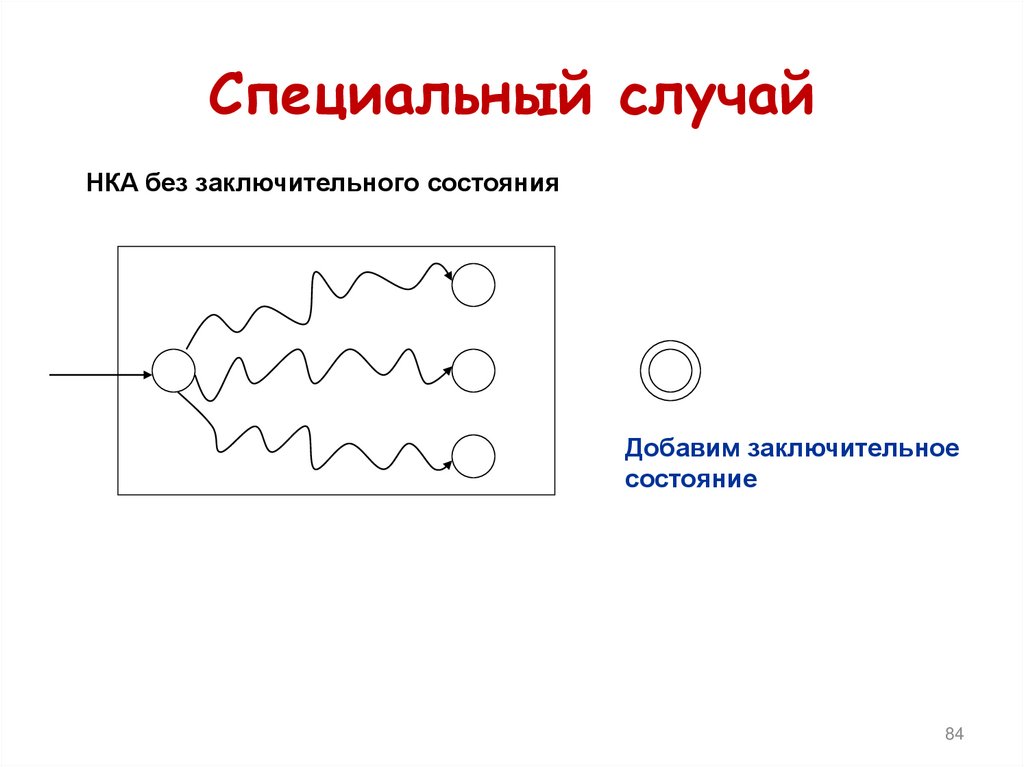
82. Пример

Специальный случай
НКА без заключительного состояния
Добавим заключительное
состояние
84

83. В общем случае

Свойства регулярных
языков

84. Специальный случай

Свойства
Пусть L1 и
Докажем:
L2 - регулярные языки
Объединение: L1 L2
Конкатенация: L1L2
Итерация: L1 *
Дополнение: L1
Регулярные
языки
Пересечение: L1 L2
86

85. Свойства регулярных языков

Говорят
Регулярные языки замкнуты относительно:
– объединения: L1 L2
– конкатенации: L1L2
– итерации: L1 *
L1
– дополнения:
– пересечения: L1 L2
87

86. Свойства

Доказательство
Пусть языки L1 и L2
допускаются НКА M1 и M 2 т.е.
L M1 L1
M1
L M 2 L2
M2
одно закл. состояние
88

87. Говорят

Пример
M1
L1 a b
n
a
b
M2
L2 ba
b
a
89

88. Доказательство

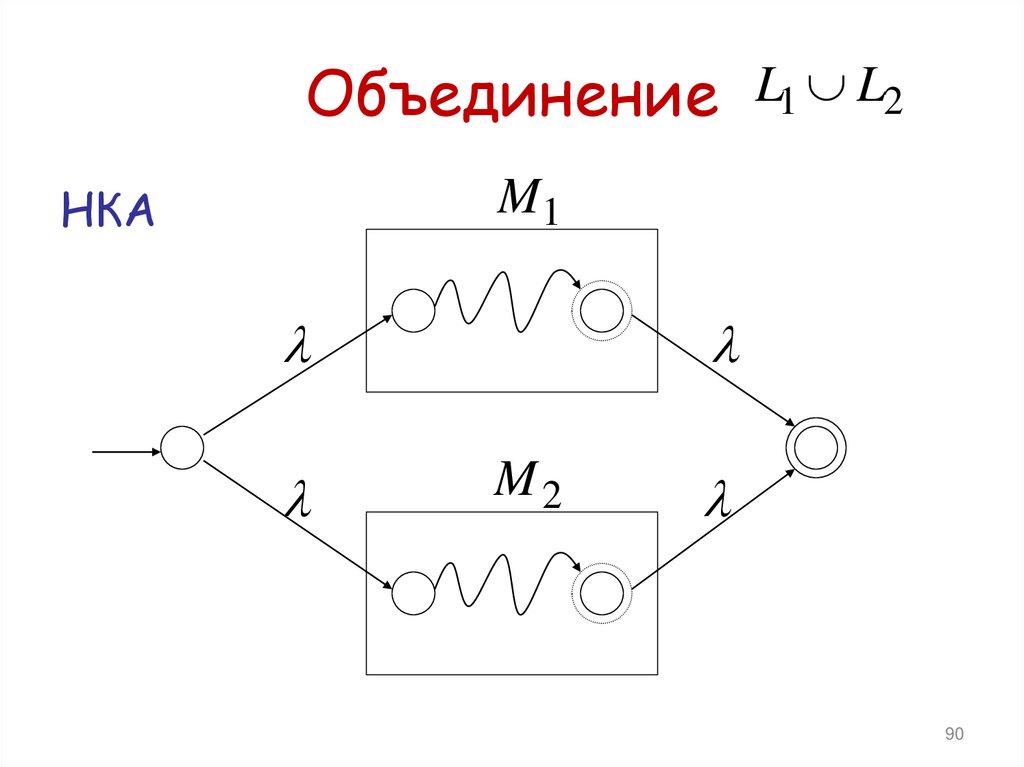
Объединение L1 L2
НКА
M1
M2
90

89. Пример

НКА для L1 L2 a nb b, a
L1 a nb
a
b
L2 ba
b
a
91

90. Объединение

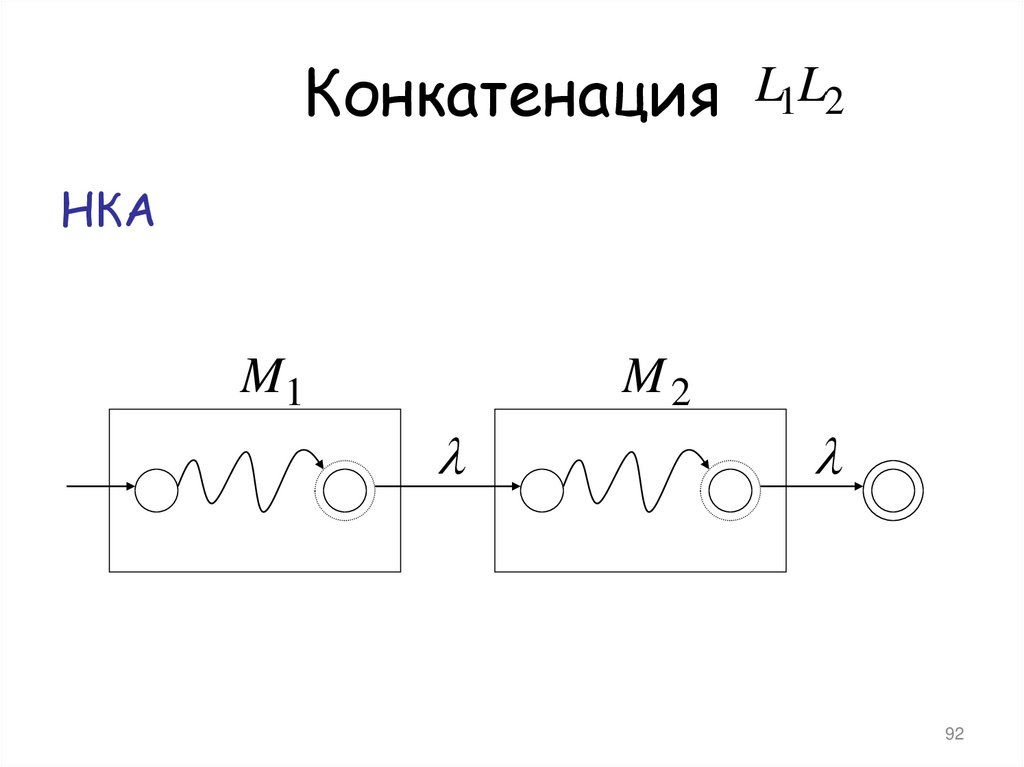
Конкатенация L1L2
НКА
M1
M2
92

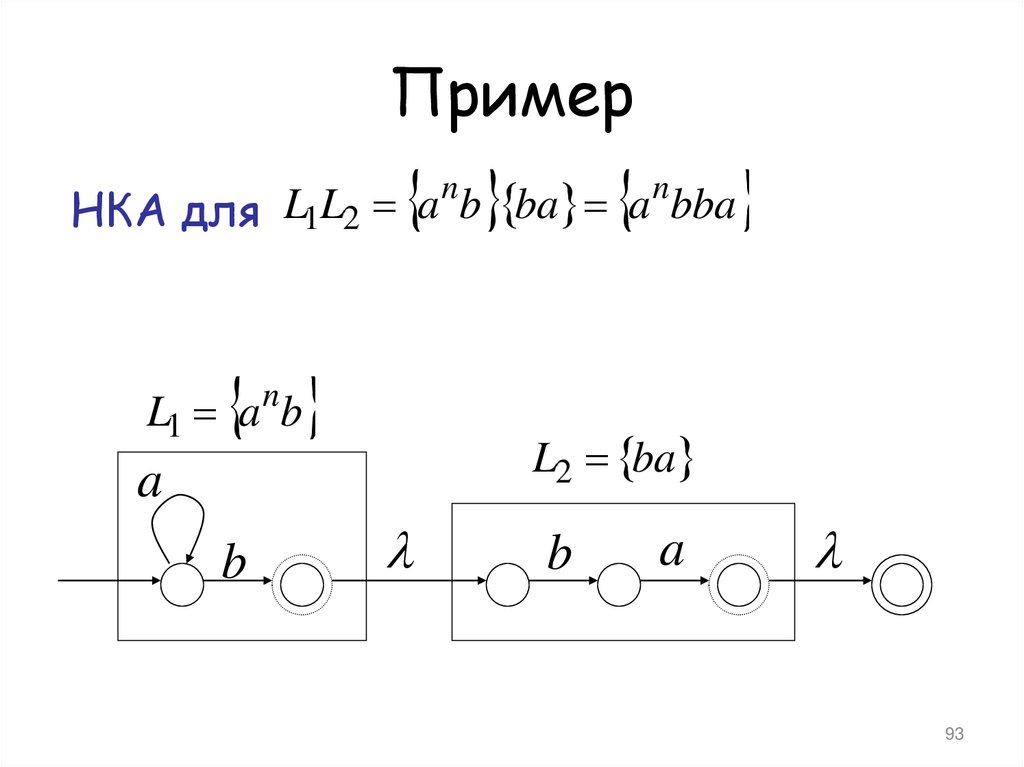
91. Пример

n
n
L
L
a
b
ba
a
bba
НКА для 1 2
L1 a nb
L2 ba
a
b
b
a
93

92. Конкатенация

Итерация L1 *
НКА
M1
94

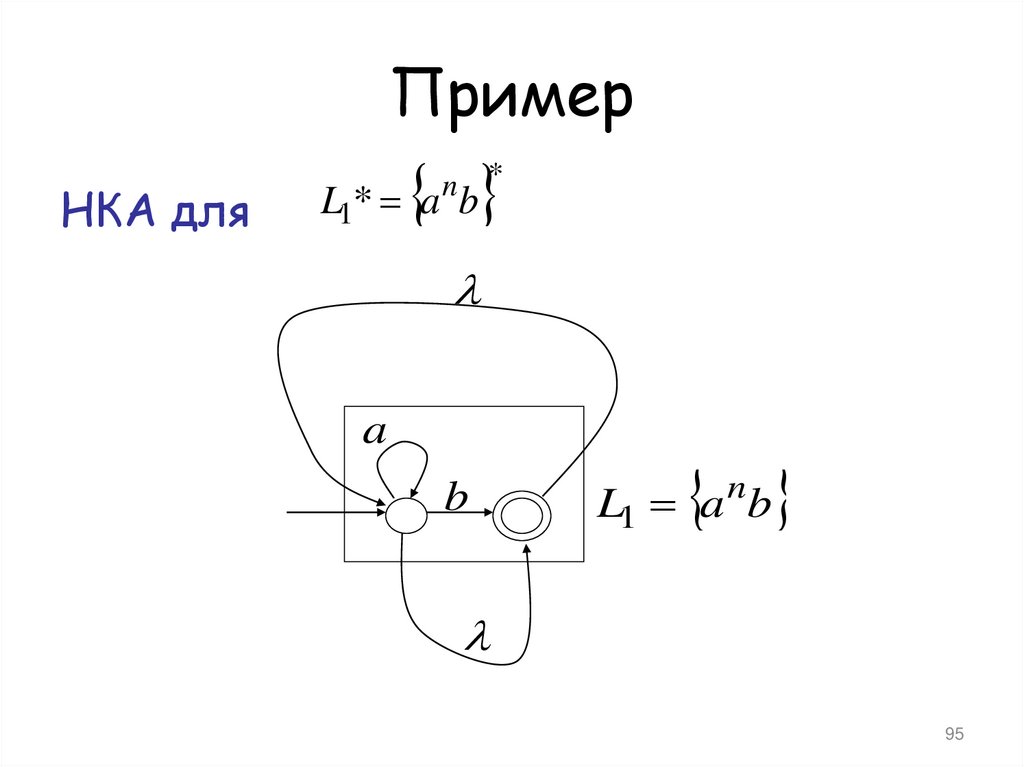
93. Пример

НКА для
n *
L1* a b
a
b
L1 a nb
95

94. Итерация

Дополнение
Для дополнения L языка L :
• Возьмем ДКА M который допускает L и построим M
такой что:
– Каждое финальное состояние M является
нефинальным для M
– И наоборот нефинальное – финальным
• Получаем:
L M L M L
96

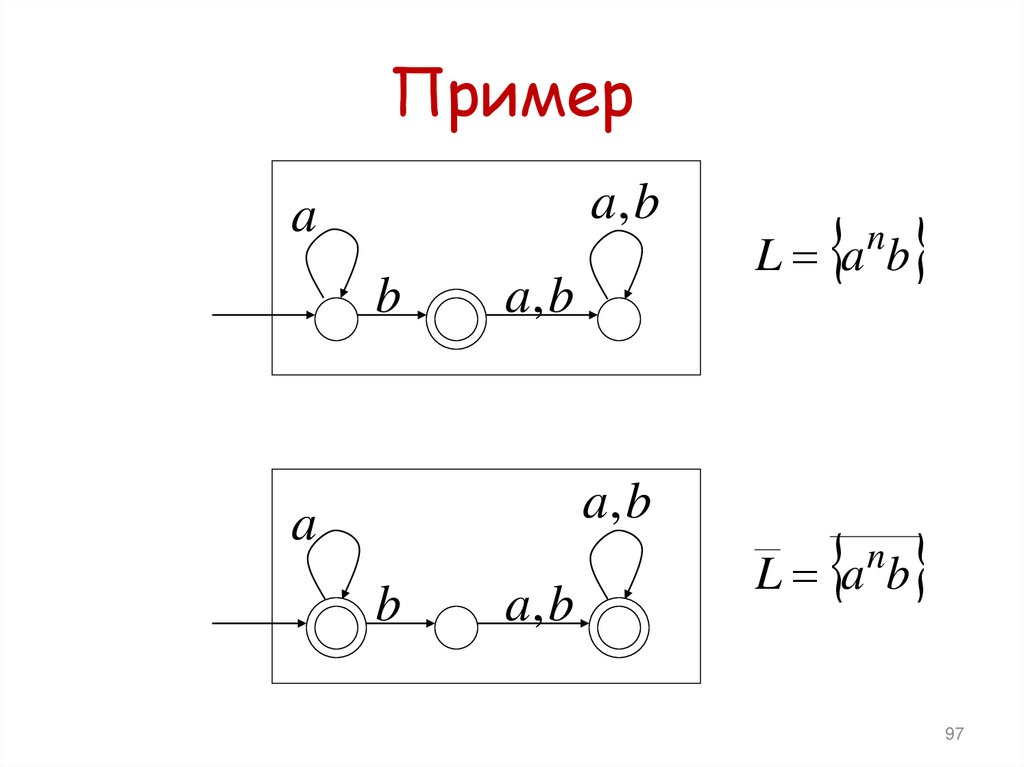
95. Пример

a, b
a
b
a, b
a, b
a
L a b
n
L a b
n
b
a, b
97

96. Дополнение

Пересечение
Для регулярных языков L1 и L2 :
L1 L2 L1 L2
L1 L2
регулярн
регулярн
L1
L1
L2
L2
регулярн
регулярн
L1 L2 L1 L2
L1 L2
регулярн
98

97. Пример

• Регулярные языки:
L2 bmba
L1 a k bl
k , l, m 0
Язык L1 L2 b b
m
регулярный
99